Konwersja AC CA

Definicje i model matematyczny próbkowania

Proces dyskretyzacji:

●

próbkowanie w czasie

●

kwantowanie wartości

●

kodowanie

Próbkowanie

Pobieranie z sygnału ciągłego próbek w określonych odstępach czasu

●

F

s

=

1

T

s

próbkowanie równomierne

●

próbkowanie nierównomierne

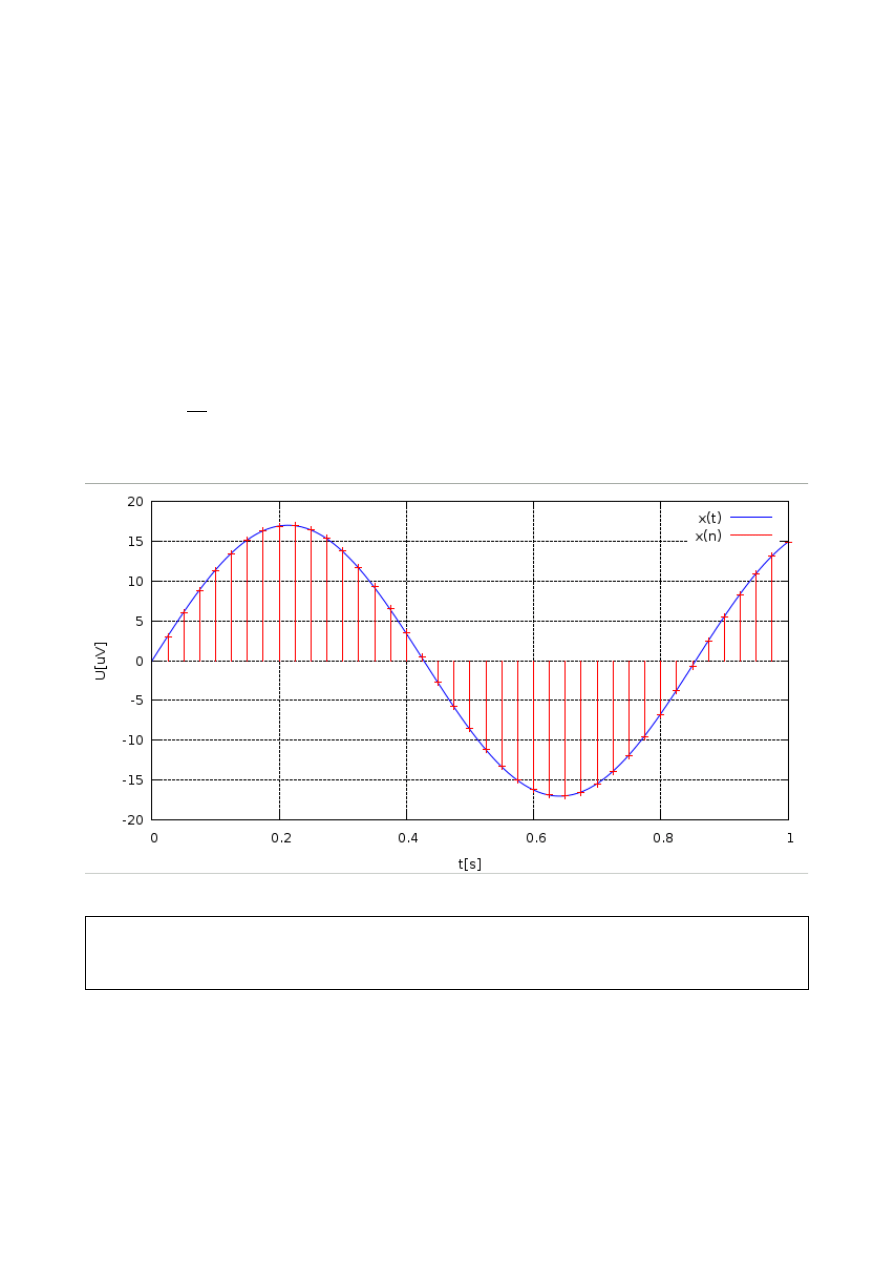
Fs=40;t=(0:0.001:1);n=(0:1/Fs:1);
xt=sin(2*pi*1*t); xn=sin(2*pi*1*n);

plot(t,xt,';x(t);',n,xn,'r.;x(n);');hold on;stem(n,xn,'r');hold off;

- 1 -

Ilustracja 1: Próbkowanie równomierne F

s

=

40[ Hz ]

Model matematyczny próbkowania

Próbkowanie to iloczyn funkcji grzebieniowej 

T

i sygnały ciągłego x

a



t

x  n=

T

x

a



t =x

a



nT  , n ∈ℤ

gdzie T =

1

F

s

Whittaker-Nyquist-Kotelnikov-Shannon – twierdzenie o próbkowaniu

F

s



2 f

g

Jeżeli nie spełnimy tego kryterium to wystąpi aliasing
Aliasing to przesunięcie i nałożenie się części widma sygnału
Przykład:

Fs=1000;N=1001;n=(0:N-1)/Fs;x=sin(2*pi*5*n);

m=(1:100:N);y=x(m);m=m/Fs; % dokładnie 10Hz
plot(n,x,'b;x(t);',m,y,'r;y(m);',m,y,'rx;;');

% inaczej zapisane
t=(0:0.001:1);xt=sin(2*pi*5*t);plot(t,xt);

Fs=10;n=(0:1/Fs:1);xn=sin(2*pi*5*n);
plot(t,xt,';x(t);',n,xn,'r*;x(n);',n,xn,'r');

Fs=1000;N=1001;n=(0:N-1)/Fs;x=sin(2*pi*7*n);
m=(1:125:N);y=x(m);m=m/Fs; % 8Hz

plot(n,x,'b;x(t);',m,y,'r;y(m);',m,y,'rx;;');
% inaczej zapisane

t=(0:0.001:1);xt=sin(2*pi*7*t);plot(t,xt);
Fs=8;n=(0:1/Fs:1);xn=sin(2*pi*7*n);plot(t,xt,n,xn,'r*');

plot(t,xt,';x(t);',n,xn,'r*;x(n);',n,xn,'r');

Odwracając tw. Shanona – nie jesteśmy w stanie odróżnić ciągłego sygnału o częstotliwości f

0

od innego o częstotliwości f

0



k∗F

s

, k ∈ℤ (pokazać na rysunku)

Żeby mieć gwarancję spełnienia warunku Nyquista stosuje się dolnoprzepustowe filtry
antyaliasingowe przed przetwornikiem AC. (pokazać rysunek z pasmami sygnału, pokazać co się
dzieje z szumem, że też się „zawija”)

Jeżeli chcemy dokonać decymacji

należy najpierw przefiltrować sygnał filtrem antyaliasingowym !!

- 2 -

Próbkowanie sygnału pasmowego

B= f

h

−

f

l

- pasmo

f

c

- częstotliwość środkowa

Aliasing pożyteczny – podpróbkowanie, próbkowanie z przesunięciem częstotliwości (pokazać
rysunek z pasmami, szumem i innymi pasmami)
Formuła wyboru częstotliwości próbkowania:

F

s



2B i

2 f

c

−

B

m



F

s



2 f

c



B

m1

, m∈ℕ (wyprowadzenie w Lyons)

np. dla sygnału FM f

l

=

87.5[MHz ] , f

h

=

108[MHz ]

stąd B=20 [MHz ] i f

c

=

97.75[ MHz]

!!! Uwaga problem !!! - Odwrócenie widmowe dla nieparzystych m

Kwantyzacja

Przetwornik AC ma skończoną liczbę bitów na reprezentację liczby- np. 8, 16, 24

x=b

B−1

2

B −1



b

B−2

2

B−2



b

2

2

2



b

1

2

1



b

0

=

∑

i=0

B−1

b

i

2

i

czyli w zapisie binarnym

x

bin

=

b

B−1

b

B−2



b

2

b

1

b

0

gdzie b

B−i

to wartości bitów 0 lub 1

Na B bitach można zapisać 2

B

różnych liczb.

Cały zakres pomiarów  x

min

, x

max

 podzielmy równomiernie na 2

B

przedziałów wtedy:



x

=



x

max

−

x

min



2

N

- 3 -

m

0

-

215,50

220

1

175,50

107,75

120

2

87,75

71,83

85

3

58,50

53,88

54

4

43,88

43,10

43,5

5

35,10

35,92

-

6

29,25

30,79

-

(2 f – B) / m

(2 f + B) / ( m +1 )

Fs

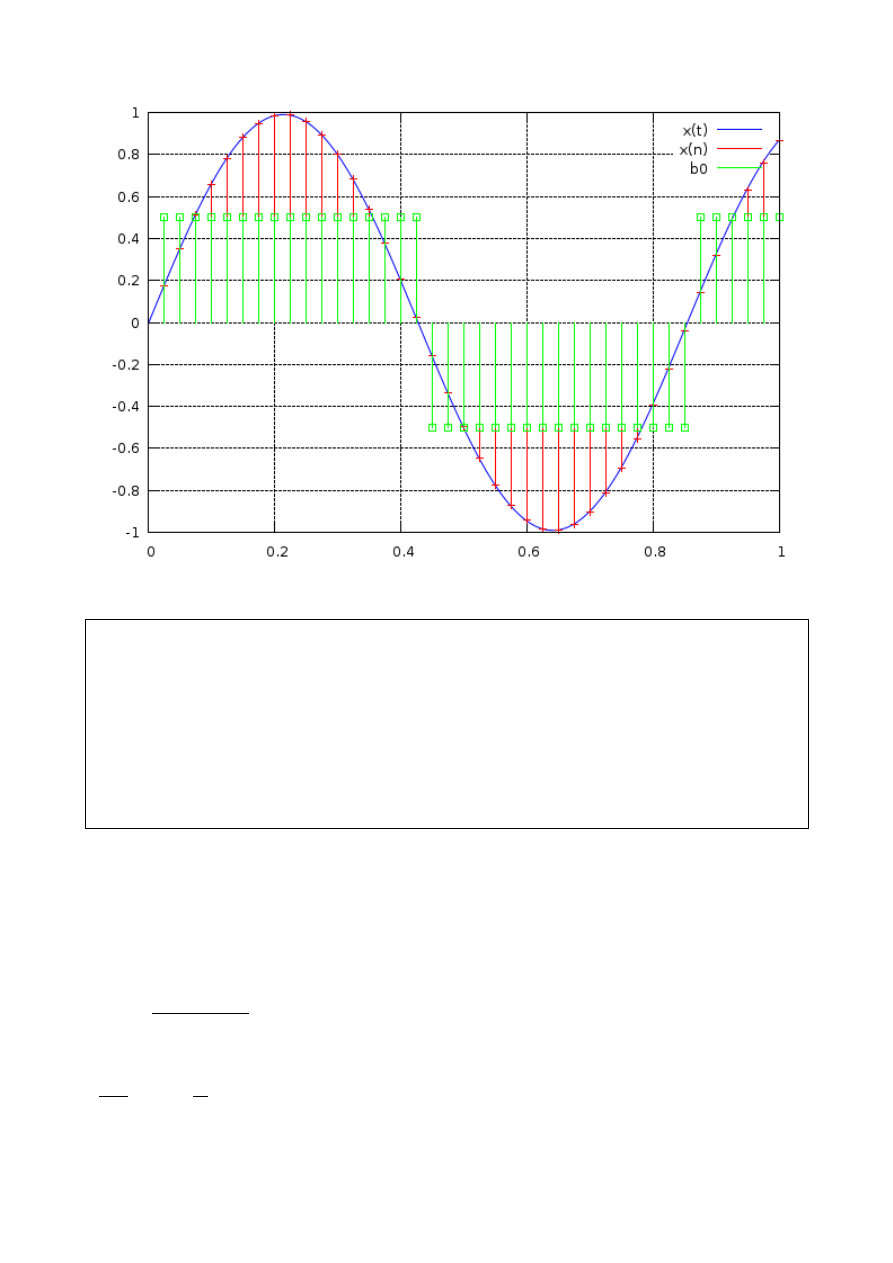
Przykład

N=1000;n=(0:N-1)./N;x=.99*sin(2*pi*1.17*n);
m=(25:25:N);y=x(m);m=m/N;

B=1; W=2^(B-1);z=(ceil(W*y)-0.5)/W;
plot(n,x,'b;x(t);',m,y,'ro;;',m,y,'r^;x(n);',m,z,'gx;;',m,z,'g^;b0;');

hold on;stem(m,y,'r');stem(m,z,'g');hold off;
%lub inaczej

t=(0:0.001:1);xt=0.99*sin(2*pi*1.17*t);
Fs=40;n=(0:1/Fs:1);xn=0.99*sin(2*pi*1.17*n);

B=2; W=2^(B-1);z=(ceil(W*xn)-0.5)/W;
plot(t,xt,'b;x(t);',n,xn,'ro;x(n);',n,z,'gx;z(n);');

hold on;stem(n,xn,'r');stem(n,z,'g');hold off;

Błąd kwantyzacji



x  n=Q[ x  n]=x  ne n

gdzie e n to błąd kwantyzacji
Dla sygnału −1≤x≤1, x ∈ℝ kwantyzator równomierny N-bitowy będzie
reprezentował/przypisywał następujące wartości

Q x=

⌊

2

N−1

x ⌋−0.5

2

N −1

Jeżeli jest zaokrąglenie do najbliższej wartości skwantowanej to

−

2



e n≤



2

- 4 -

Ilustracja 2: Kwantyzacja 1-bitowa

gdzie =2

−

B

Stosunek sygnał/szum SNR

SNR≈20 log

10



2

N

=

6.0206 N [dB ]

Przykład

B=2;N=1000;n=(1:N)./N;x=2*(n-.5);W=2^(B-1);z=(ceil(W*x)-0.5)/W;

plot(n,x,'b;x;',n,z,'r;z;',n,x-z,'g;e;');

Kodowanie

–

równomierne - w kodzie uzupełnienie do dwóch U2 (znaczenie bitów, przykład)

–

logarytmiczne – uLaw

–

zmiennoprzecinkowe - ??? dyskusyjne

Błędy próbkowania:

●

błąd kwantyzacji

●

szumy przetworników

●

jiter

●

nieliniowość

- 5 -