www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
(OKE Ł
ÓD ´
Z
)
POZIOM PODSTAWOWY
7
MARCA
2008
C
ZAS PRACY
: 120
MINUT
Z
ADANIE
1
(3
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c 2x
2
< −
260
+
53x. Podaj wszystkie liczby całkowite, które spełniaj ˛
a t˛e
nierówno´s´c.
R
OZWI ˛
AZANIE
Zapiszmy nierówno´s´c w postaci
2x
2
−
53x
+
260
<
0
i liczymy standardowo, z
∆-y.
∆
=
53
2
−
4
·
2
·
260
=
2809
−
2080
=
729
=
27
2
x
1
=
53
−
27
4
=
26
4
=
13
2
x
2
=
53
+
27
4
=
80
4
=
20.
Mo ˙zemy teraz naszkicowa´c wykres tej funkcji Wida´c teraz, ˙ze rozwi ˛
azaniem nierówno´sci
jest przedział
13
2
, 20
=
6
1
2
, 20
.
Je ˙zeli chodzi liczby całkowite w tym przedziale, to s ˛
a to wszystkie liczby całkowite z prze-
działu
h
7, 19
i
, czyli
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
Materiał pobrany z serwisu
1
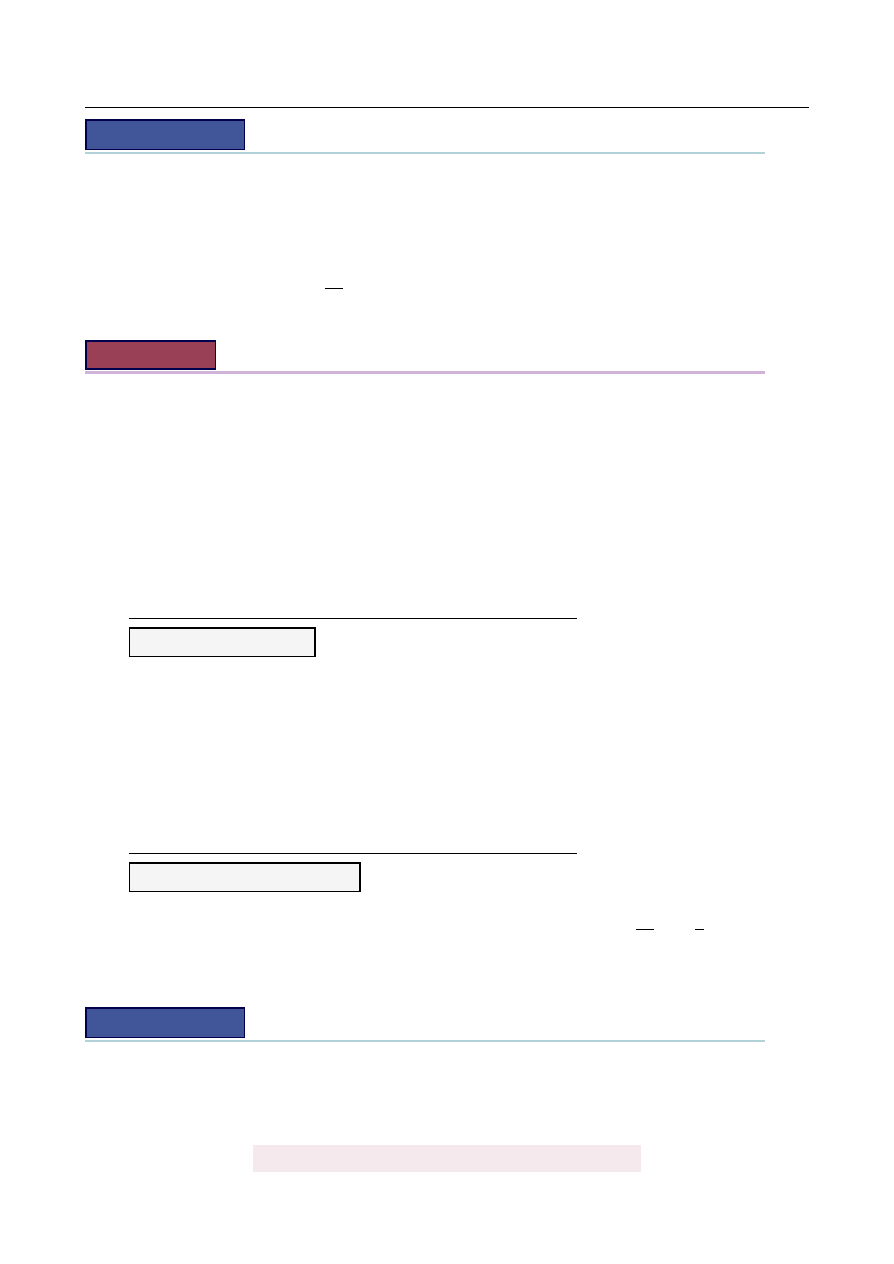
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
2
(6
PKT
.)
Dany jest wielomian W
(
x
) =
x
3
+
2x
2
−
9x
−
18.
a) Wyznacz pierwiastki tego wielomianu.
b) Sprawd´z, czy wielomiany W
(
x
)
i P
(
x
) = (
x
+
2
)(
x
2
−
2x
+
4
) + (
x
+
2
)(
2x
−
13
)
s ˛
a
równe.
c) Uzasadnij, ˙ze je´sli x
>
√
10 , to x
3
+
2x
2
−
9x
−
18
>
0.
R
OZWI ˛
AZANIE
a) ˙Zeby znale´z´c pierwiastki, wstawiamy do wielomianu dzielniki wyrazu wolnego, czyli
liczby
−
1, 1,
−
2, 2,
−
3, 3,
−
6, 6,
−
9, 9,
−
18, 18 tak długo a ˙z dla jakiej´s wyjdzie 0 – wy-
chodzi ju ˙z dla
−
2. Jak ju ˙z mamy pierwiastek, to dzielimy wielomian przez
(
x
+
2
)
.
Robimy to tak jak umiemy, schemat Hornera, dzielenie wielomianów lub grupowanie
odpowiednich czynników. My zrobimy to t ˛
a ostatni ˛
a metod ˛
a
x
3
+
2x
2
−
9x
−
18
=
x
2
(
x
+
2
) −
9
(
x
+
2
) =
= (
x
2
−
9
)(
x
+
2
) = (
x
−
3
)(
x
+
3
)(
x
+
2
)
.
Teraz widzimy, ˙ze pierwiastki to
−
2,
−
3, 3.
Odpowied´z:
−
2,
−
3, 3
b) Z poprzedniego podpunktu wiemy, ˙ze W
(
x
) = (
x
+
2
)(
x
2
−
9
)
. Zapiszemy teraz P
(
x
)
w postaci
(
x
+
2
)
cos i sprawdzimy czy cos
=
x
2
−
9.
P
(
x
) = (
x
+
2
)(
x
2
−
2x
+
4
) + (
x
+
2
)(
2x
−
13
) =
= (
x
+
2
)(
x
2
−
2x
+
4
+
2x
−
13
) = (
x
+
2
)(
x
2
−
9
)
i wyszło to samo, czyli s ˛
a równe. Oczywi´scie zamiast wył ˛
acza´c
(
x
+
2
)
przed nawias
mogli´smy wszystko powymna ˙za´c, ale rachunki byłyby znacznie gorsze.
Odpowied´z: Tak, s ˛
a równe.
c) Poniewa ˙z W
(
x
) = (
x
+
3
)(
x
+
2
)(
x
−
3
)
, to dla x
>
3 mamy W
(
x
) >
0 (bo ka ˙zdy z
czynników W
(
x
)
jest dodatni). Teraz wystarczy zauwa ˙zy´c, ˙ze
√
10
>
√
9
=
3.
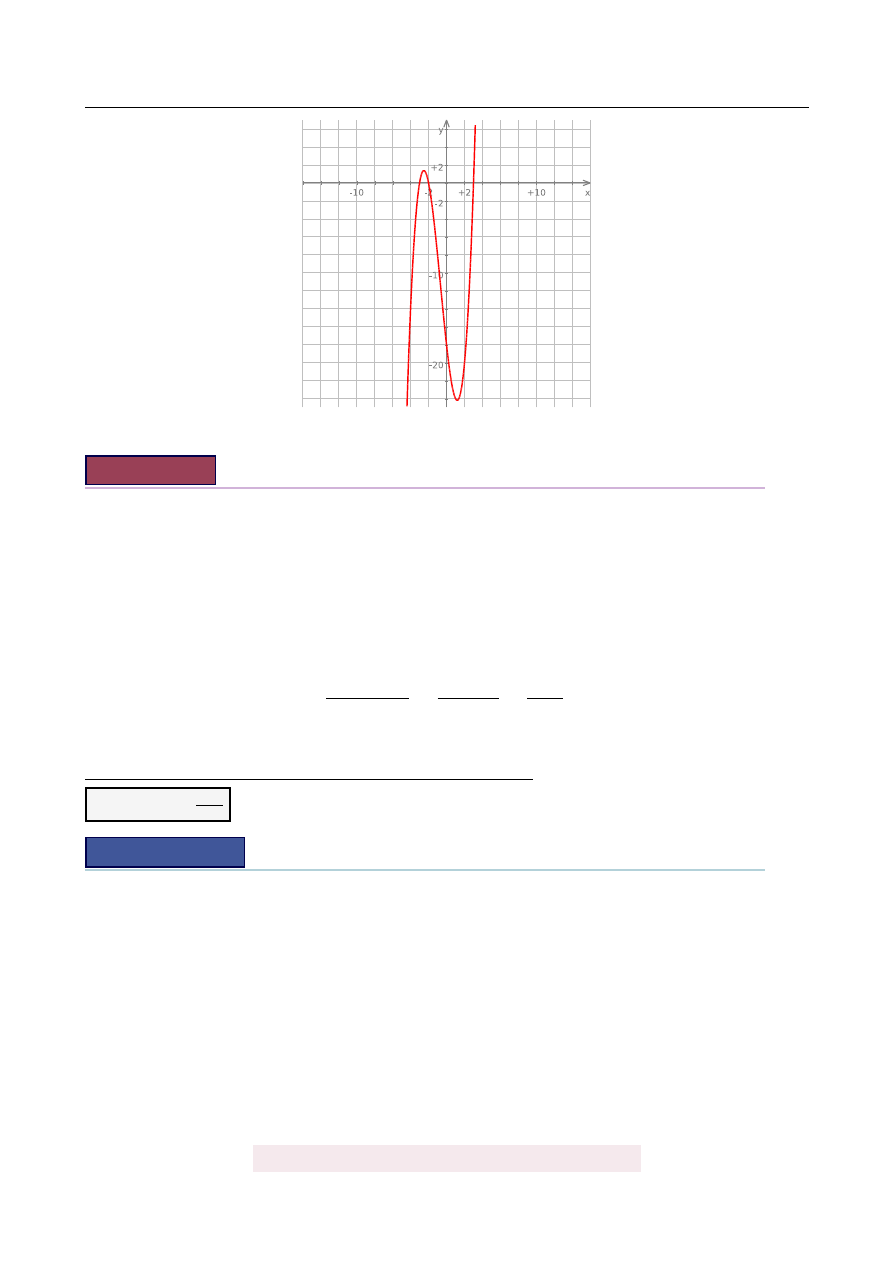
Na koniec, dla ciekawskich, wykres funkcji W
(
x
)
.
Z
ADANIE
3
(3
PKT
.)
Ka ˙zdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN.
Kod ten składa si˛e z czterech cyfr (cyfry mog ˛
a si˛e powtarza´c, ale kodem PIN nie mo ˙ze by´c
0000). Oblicz prawdopodobie ´nstwo, ˙ze w losowo utworzonym kodzie PIN ˙zadna cyfra si˛e
nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Najpierw policzmy ile jest wszystkich mo ˙zliwych numerów PIN. Ka ˙zd ˛
a z cyfr mo ˙zna wy-
bra´c na 10 sposobów, czyli wszystkich mo ˙zliwo´sci wyboru 4 cyfr jest jest 10
·
10
·
10
·
10
=
10
4
. Jeszcze trzeba odj ˛
a´c 1 PIN odpowiadaj ˛
acy 0000. W sumie mamy zatem 10
4
−
1
=
9999
mo ˙zliwych pinów.
A ile jest tych z ró ˙znymi cyframi? Pierwsz ˛
a cyfr˛e mo ˙zemy wybra´c dowolnie, czyli mamy
10 mo ˙zliwo´sci. Dla drugiej mamy ju ˙z tylko 9 mo ˙zliwo´sci (bo nie mo ˙zemy wzi ˛
a´c tej, któr ˛
a
wybrali´smy na pierwszym miejscu), dla trzeciej 8, a dla czwartej 7. Czyli razem jest 10
·
9
·
8
·
7 mo ˙zliwo´sci. Szukane prawdopodobie ´nstwo wynosi zatem
10
·
9
·
8
·
7
9999
=
10
·
8
·
7
1111
=
560
1111
.
Liczba 1111 oczywi´scie nie jest podzielna przez ani przez 2 ani przez 5. Mo ˙zna te ˙z spraw-
dzi´c, ˙ze nie dzieli si˛e przez 7. Oznacza to, ˙ze otrzymany ułamek jest nieskracalny.
Odpowied´z:
560
1111
Z
ADANIE
4
(3
PKT
.)
Dla dowolnych liczb rzeczywistych a i b okre´slamy liczby a
◦
b i a
∗
b w nast˛epuj ˛
acy sposób:
a
◦
b
=
liczba nie mniejsza spo´sród liczb a i b,
a
∗
b
=
liczba nie wi˛eksza spo´sród liczb a i b.
Na przykład: 7
◦
3
=
7, 15
◦
15
=
15, 7
∗
3
=
3,
(−
6
) ∗
4
= −
6,
(−
3
) ∗ (−
3
) = −
3.
Oblicz
a)
(−
5
) ◦
4
=
b)
(
2005
∗
2007
) ◦ (−
2006
) =
c)
(
5
◦
6
) ∗ (
2
◦
7
) =
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
a)
(−
5
) ◦
4
=
4.
Odpowied´z: 4
b)
(
2005
∗
2007
) ◦ (−
2006
) =
2005
◦ (−
2006
) =
2005.
Odpowied´z: 2005
c)
(
5
◦
6
) ∗ (
2
◦
7
) =
6
∗
7
=
6.
Odpowied´z: 6
Z
ADANIE
5
(3
PKT
.)
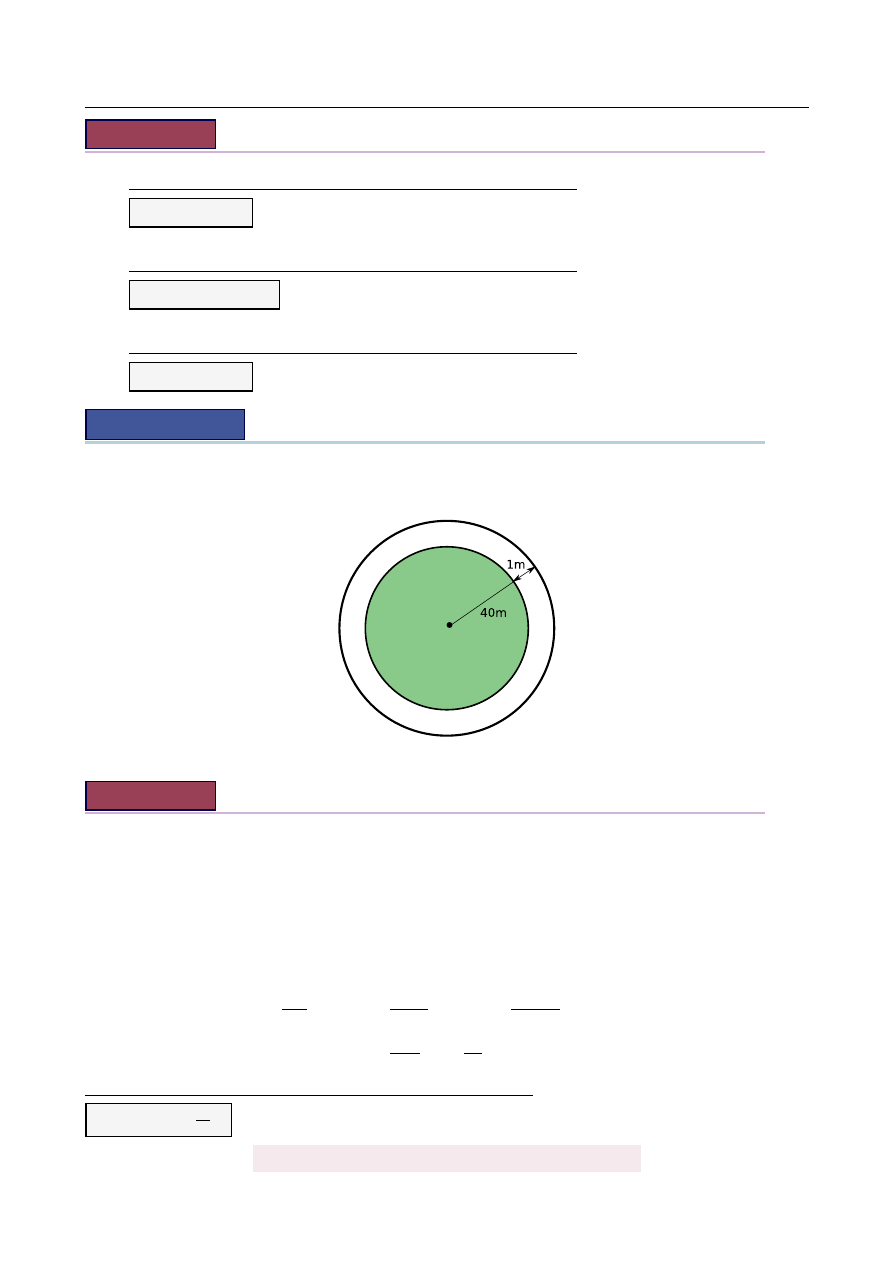
Ogrodnik opiekuj ˛
acy si˛e klombem w kształcie koła o promieniu 40 m chce go powi˛ekszy´c,
sadz ˛
ac wokół niego kwiatki na grz ˛
adce o szeroko´sci 1 m (patrz rysunek). Oblicz, o ile pro-
cent ogrodnik chce powi˛ekszy´c powierzchni˛e tego klombu.
R
OZWI ˛
AZANIE
˙Zeby obliczy´c o ile procent powi˛ekszy si˛e klomb, potrzebujemy zna´c aktualne pole klombu,
powiedzmy P i o ile si˛e powi˛ekszy – oznaczmy t˛e liczb˛e przez
∆P. Ze wzoru na pole koła
mamy
P
=
40
2
π
∆P
=
41
2
π
−
40
2
π
= (
41
2
−
40
2
)
π
=
= (
41
−
40
)(
41
+
40
)
π
=
81π.
Szukana zmiana procentowa pola to
∆P
P
·
100%
=
81π
40
2
π
·
100%
=
81
40
·
40
·
100%
=
81
4
·
4
%
=
81
16
%.
Odpowied´z:
81
16
%
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
6
(5
PKT
.)
Niesko ´nczony ci ˛
ag liczbowy
(
a
n
)
dla n
>
1 jest okre´slony wzorem
a
n
=
(
n
+
1
2
gdy n jest nieparzyste,
0
gdy n jest parzyste.
a) Uzupełnij tabelk˛e:
n
1
2
3
4
5
. . .
2005
2006
2007
2008
a
n
1
0
. . .
b) Oblicz
(
a
2005
)
a
2006
· (
a
2006
)
a
2007
· (
a
2007
)
a
2008
.
c) Oblicz sum˛e 2008 pocz ˛
atkowych wyrazów ci ˛
agu
(
a
n
)
.
R
OZWI ˛
AZANIE
a) Tabelk˛e uzupełniamy wprost z definicji ci ˛
agu
n
1
2
3
4
5
. . .
2005
2006
2007
2008
a
n
1
0
2
0
3
. . .
1003
0
1004
0
b) Korzystamy z wyliczonych wy ˙zej warto´sci
(
a
2005
)
a
2006
· (
a
2006
)
a
2007
· (
a
2007
)
a
2008
=
= (
1003
)
0
· (
0
)
1004
· (
1004
)
0
=
1
·
0
·
1
=
0.
Odpowied´z: 1
c) Jeszcze raz korzystaj ˛
ac z tabelki otrzymujemy, ˙ze szukana suma jest równa
S
=
1
+
2
+
3
+
. . .
+
1003
+
1004.
Jest to suma wyrazów ci ˛
agu arytmetycznego, wi˛ec
S
=
1
+
1004
2
·
1004
=
1005
·
502
=
504510.
Odpowied´z: 504510
Materiał pobrany z serwisu
5
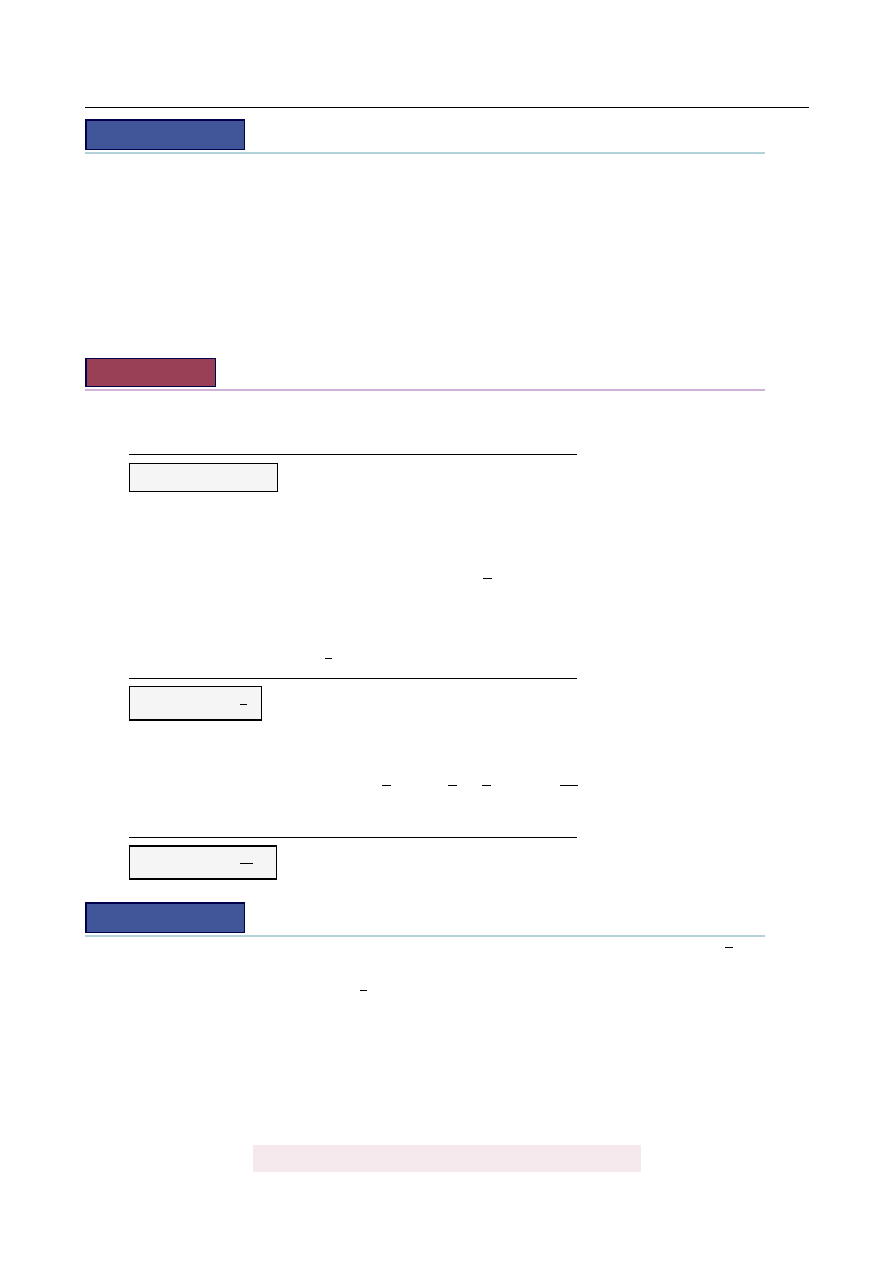
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
7
(3
PKT
.)
Z kraw˛edzi dachu podrzucono kamie ´n, który po 2 sekundach spadł na ziemi˛e. Wysoko´s´c
(wyra ˙zon ˛
a w metrach), na jakiej znajdował si˛e kamie ´n nad ziemi ˛
a po upływie t sekund od
chwili jego podrzucenia, opisuje funkcja h
(
t
) = −
5t
2
+
5t
+
10, gdzie t
∈ h
0, 2
i
.
a) Podaj, z jakiej wysoko´sci (od ziemi) kamie ´n został podrzucony.
b) Oblicz, po jakim czasie od momentu podrzucenia kamie ´n osi ˛
agn ˛
ał najwi˛eksz ˛
a wyso-
ko´s´c.
c) Oblicz najwi˛eksz ˛
a wysoko´s´c (od ziemi), na jak ˛
a wzniósł si˛e ten kamie ´n.
R
OZWI ˛
AZANIE
a) Wysoko´s´c z jakiej kamie ´n został podrzucony to dokładnie h
(
0
) =
10m (czyli wysoko´s´c
w chwili 0).
Odpowied´z: 10m
b) Poniewa ˙z funkcja wysoko´sci jest parabol ˛
a (o ramionach skierowanych w dół), oraz
współrz˛edna t wierzchołka jest równa
t
w
=
1
2
,
wi˛ec maksymalna wysoko´s´c odpowiada warto´sci w wierzchołku paraboli (tu jest wa ˙z-
ne, ˙ze wierzchołek jest w przedziale zmienno´sci t, czyli
h
0, 2
i
). Wierzchołek ten jest
osi ˛
agany po czasie t
w
=
1
2
.
Odpowied´z:
1
2
s
c) Na mocy poprzedniego podpunktu, wysoko´s´c maksymalna to
h
1
2
= −
5
4
+
5
2
+
10
=
45
4
.
Odpowied´z:
45
4
m
Z
ADANIE
8
(4
PKT
.)
Na rysunku przedstawiony jest wykres funkcji f okre´slonej wzorem f
(
x
) =
3
x
dla x
6=
0. Wykres ten przesuni˛eto o 2 jednostki w gór˛e wzdłu ˙z osi Oy. Otrzymano w ten sposób
wykres funkcji g o wzorze g
(
x
) =
3
x
+
2 dla x
6=
0.
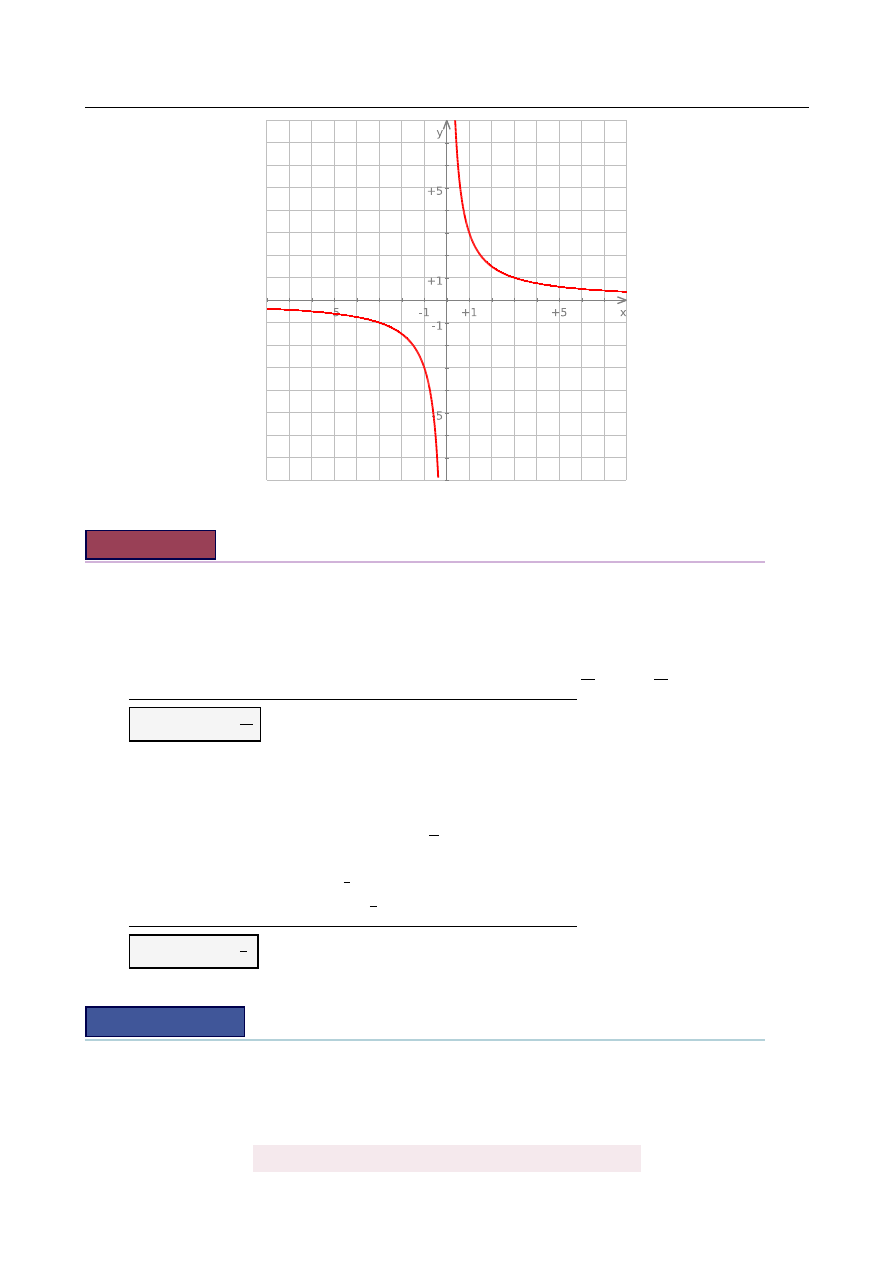
a) Narysuj wykres funkcji g.
b) Oblicz najwi˛eksz ˛
a warto´s´c funkcji g w przedziale
h
21, 31
i
.
c) Podaj, o ile jednostek wzdłu ˙z osi Ox nale ˙zy przesun ˛
a´c wykres funkcji g, aby otrzyma´c
wykres funkcji przechodz ˛
acy przez pocz ˛
atek układu współrz˛ednych.
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
a) Tak jak to jest opisane w tre´sci, trzeba wykres f przesun ˛
a´c o dwie jednostki w gór˛e -
rysunek.
b) Z narysowanego wykresu jest jasne, ˙ze na przedziale
h
21, 31
i
funkcja g jest malej ˛
aca.
Zatem najwi˛eksza warto´s´c na tym przedziale to g
(
21
) =
3
21
+
2
=
15
7
.
Odpowied´z:
15
7
c) Z rysunku wida´c, ˙ze kluczowe jest znalezienie punktu, w którym wykres przecina o´s
Ox. Musimy w tym celu rozwi ˛
aza´c równanie
3
x
+
2
=
0.
Łatwo wyliczy´c, ˙ze x
= −
3
2
. Zatem aby wykres g
(
x
)
miał miejsce zerowe w punkcie
(
0, 0
)
musimy go przesun ˛
a´c o
3
2
jednostki w prawo.
Odpowied´z:
3
2
Z
ADANIE
9
(4
PKT
.)
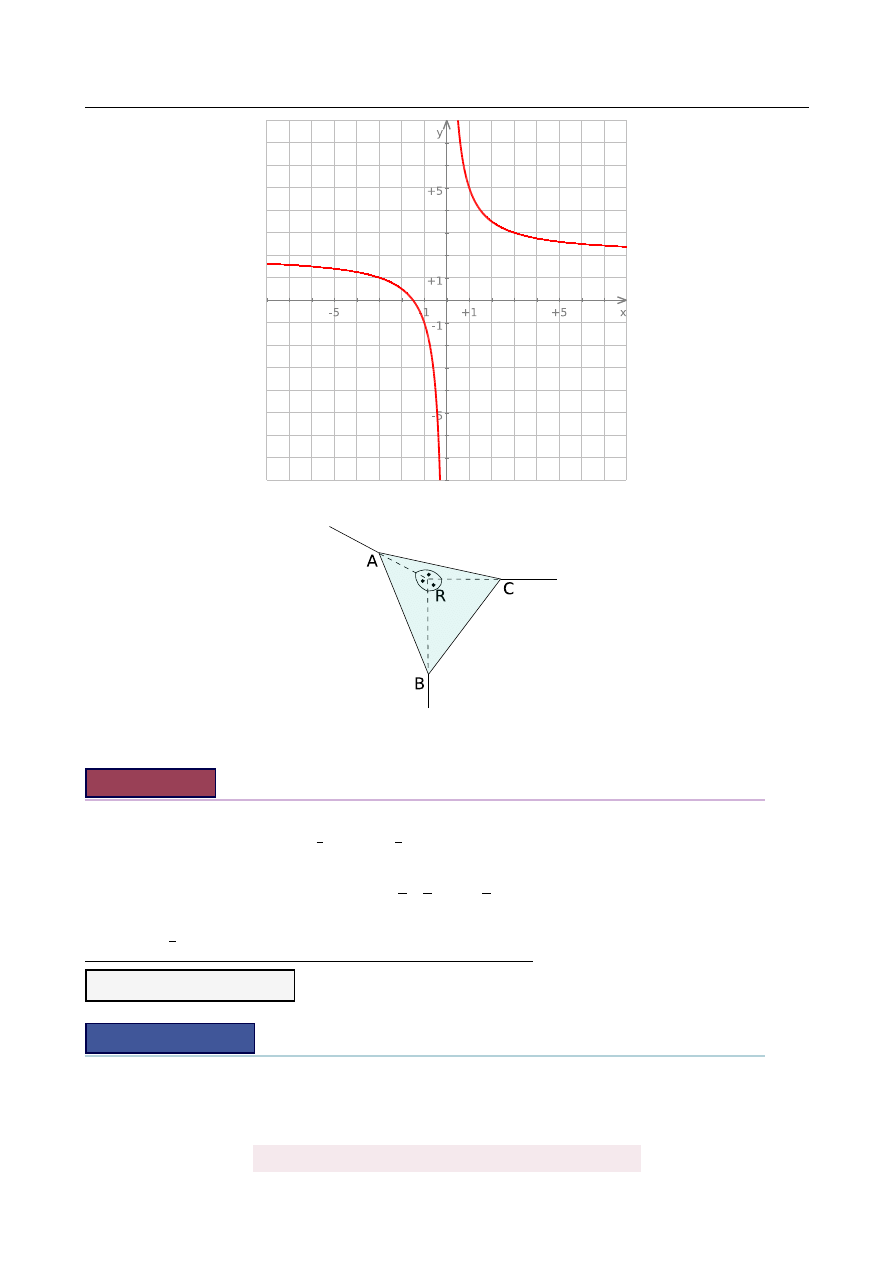
Naro ˙znik mi˛edzy dwiema ´scianami i sufitem prostopadło´sciennego pokoju nale ˙zy zama-
skowa´c trójk ˛
atnym fragmentem płyty gipsowo-kartonowej (patrz rysunek). Wiedz ˛
ac, ˙ze
RA
=
RB
=
RC
=
1m, oblicz obj˛eto´s´c naro ˙znika zamaskowanego t ˛
a płyt ˛
a. Wynik zaokr ˛
aglij
do 0,01 m
3
.
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Opisany naro ˙znik mo ˙zemy traktowa´c jak ostrosłup o podstawie ABR i wysoko´sci RC. Po-
niewa ˙z pole ABR jest równe
1
2
·
1
·
1
=
1
2
oraz RC
=
1, szukana obj˛eto´s´c wynosi
1
3
·
1
2
·
1
=
1
6
.
Poniewa ˙z
1
6
≈
0, 166, to po zaokr ˛
agleniu mamy V
=
0, 17m
3
.
Odpowied´z: V
=
0, 17m
3
Z
ADANIE
10
(4
PKT
.)
Na płaszczy´znie dane s ˛
a punkty A
= (
2, 3
)
i B
= (−
2, 1
)
(patrz rysunek). Zbadaj, czy
punkty K
= (
36, 21
)
i L
= (−
37,
−
15
)
le ˙z ˛
a po tej samej stronie prostej AB. Podaj odpowied´z
i jej uzasadnienie.
Materiał pobrany z serwisu
8

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zacznijmy od napisania równania prostej AB. Aby to zrobi´c, skorzystamy ze wzoru na pro-
st ˛
a przechodz ˛
ac ˛
a przez punkty A
= (
x
A
, y
A
)
i B
= (
x
B
, y
B
)
.
(
y
−
y
A
)(
x
B
−
x
A
) − (
y
B
−
y
A
)(
x
−
x
A
) =
0.
W naszej sytuacji mamy
(
y
−
3
)(−
2
−
2
) − (
1
−
3
)(
x
−
2
) =
0
−
4y
+
2x
+
8
=
0
y
=
1
2
x
+
2.
Ok, skoro mamy równanie prostej, to łatwo jest sprawdzi´c, czy punkt le ˙zy poni ˙zej, powy ˙zej
czy na tej prostej. Np. dla punktu K
= (
36, 21
)
, wstawiamy x
=
36 do równania prostej i
dostajemy y
=
20. To znaczy, ˙ze punkt na prostej o pierwszej współrz˛ednej 36 ma drug ˛
a
współrz˛edn ˛
a 20. Punkt K ma drug ˛
a współrz˛edn ˛
a 21, czyli jest powy ˙zej prostej. Podobnie
sprawdzamy, ˙ze punkt L te ˙z jest powy ˙zej prostej AB.
Odpowied´z: Punkty K i L le˙z ˛
a po tej samej stronie prostej AB.
Z
ADANIE
11
(4
PKT
.)
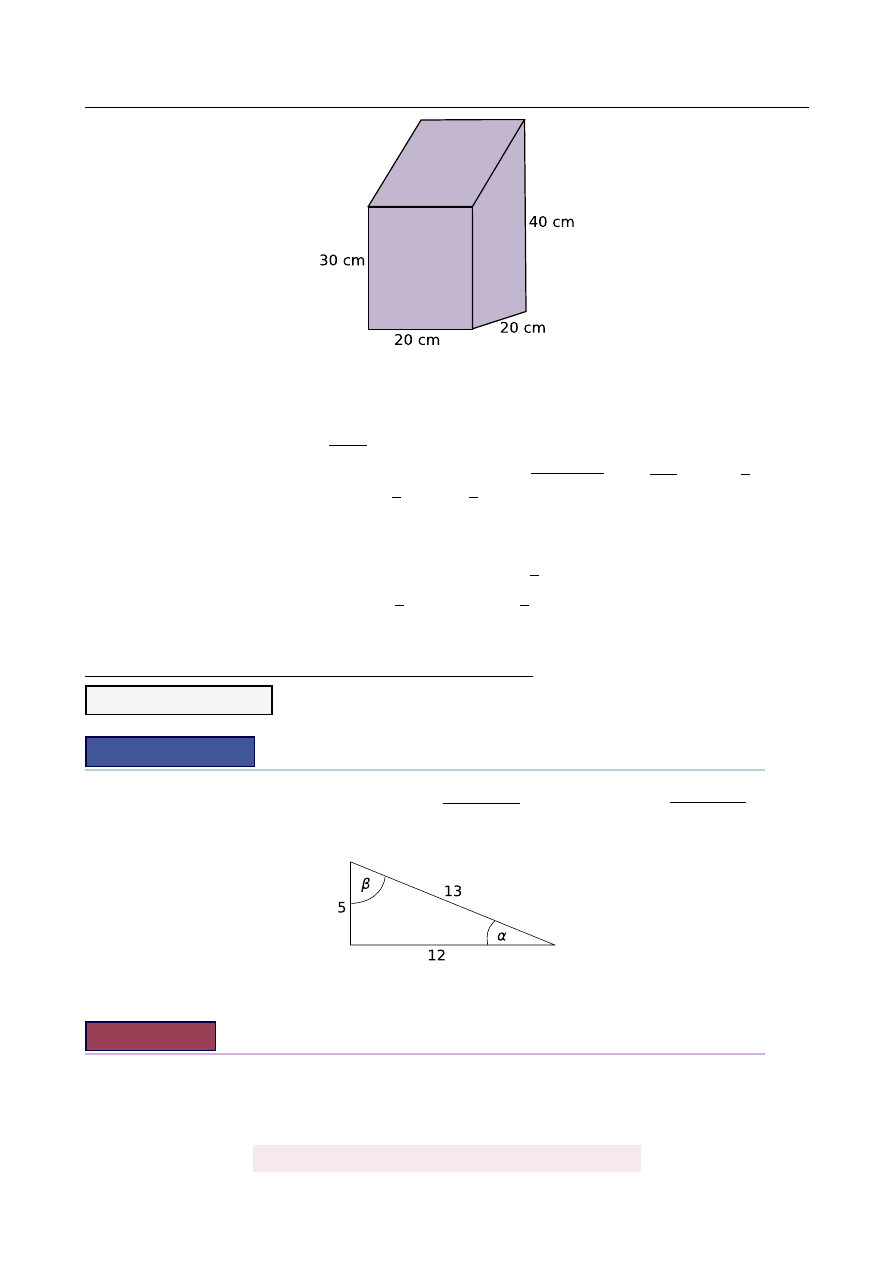
Spawacz ma wykona´c z blachy konstrukcj˛e, której podstaw ˛
a jest kwadrat a ´sciany boczne s ˛
a
prostopadłe do płaszczyzny podstawy. Wymiary elementów s ˛
a podane na rysunku. Oblicz
pole powierzchni tej konstrukcji (wszystkich sze´sciu ´scian). Wynik podaj z zaokr ˛
agleniem
do 1cm
2
.
R
OZWI ˛
AZANIE
Powierzchnia konstrukcji składa si˛e z:
• kwadratu w podstawie, pole: 20
2
=
400cm
2
,
• prostok ˛
ata z przodu, pole: 20
·
30
=
600cm
2
,
Materiał pobrany z serwisu
9
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
• prostok ˛
ata z tyłu, pole: 20
·
40
=
800cm
2
,
• dówch trapezów o polu:
30
+
40
2
·
20
=
700cm
2
,
• prostok ˛
ata u góry, jego sko´sny bok ma długo´s´c
√
20
2
+
10
2
=
√
500
=
10
√
5 (twier-
dzenie Pitagorasa), pole: 20
·
10
√
5
=
200
√
5cm
2
.
Zatem pole powierzchni całkowitej:
400
+
600
+
800
+
2
·
700
+
200
√
5
=
=
2400
+
200
√
5
=
200
(
16
+
√
5
) ≈
3647, 21.
Po zaokr ˛
agleniu P
=
3647.
Odpowied´z: P
=
3647
Z
ADANIE
12
(4
PKT
.)
Na rysunku oznaczono k ˛
aty oraz podano długo´sci boków trójk ˛
ata prostok ˛
atnego. Oblicz,
które z wyra ˙ze ´n ma wi˛eksz ˛
a warto´s´c: tg α
·
p1
−
cos
2
β
+
sin α czy tg β
·
√
1
−
cos
2
α
+
sin β.
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Spróbujmy przekształci´c podane wyra ˙zenie
tg α
·
q
1
−
cos
2
β
+
sin α
=
tg α
·
q
sin
2
β
+
sin α
=
tg α
·
sin β
+
sin α
=
tg α
·
sin
(
90
◦
−
α
) +
sin α
=
sin α
cos α
·
cos α
+
sin α
=
sin α
+
sin α
=
2 sin α
=
10
13
.
Przy tych przekształceniach korzystali´smy z nast˛epuj ˛
acych faktów:
• jedynka trygonometryczna,
• fakt, ˙ze sin β
>
0 (przy opuszczaniu pierwiastka),
• wzór redukcyjny sin
(
90
◦
−
α
) =
cos α.
Analogiczny rachunek pokazuje, ˙ze drugie z podanych wyra ˙ze ´n jest równe 2 sin β
=
24
13
–
trzeba we wszystkich powy ˙zszych przekształceniach pozamienia´c α i β miejscami. Wida´c
wi˛ec, ˙ze drugie wyra ˙zenie ma wi˛eksz ˛
a warto´s´c.
Odpowied´z: Drugie wyra˙zenie
Z
ADANIE
13
(4
PKT
.)
Wła´sciciel kiosku notował liczb˛e biletów komunikacji miejskiej sprzedanych w kolejnych
godzinach. Wyniki obserwacji zapisał w tabeli.
Czas obserwacji
Liczba biletów
5:00–6:00
2
6:00–7:00
3
7:00–8:00
9
8:00–9:00
8
9:00–10:00
6
10:00–11:00
4
11:00–12:00
3
12:00–13:00
3
13:00–14:00
3
14:00–15:00
5
15:00–16:00
8
16:00–17:00
6
a) Oblicz ´sredni ˛
a liczb˛e biletów sprzedawanych w ci ˛
agu 1 godziny.
b) Wynikiem „typowym” nazywamy wynik, który ró ˙zni si˛e od ´sredniej o mniej ni ˙z jed-
no odchylenie standardowe. Podaj wszystkie godziny, w których liczba sprzedanych
biletów nie była „typowa”.
Materiał pobrany z serwisu
11

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
a) Liczymy ´sredni ˛
a arytmetyczn ˛
a
x
=
2
+
4
·
3
+
4
+
5
+
2
·
6
+
2
·
8
+
9
12
=
60
12
=
5.
Odpowied´z: 5
b) Policzmy najpierw wariancj˛e
σ
2
=
=
(
5
−
2
)
2
+
4
(
5
−
3
)
2
+ (
5
−
4
)
2
+ (
5
−
5
)
2
+
2
(
5
−
6
)
2
+
2
(
5
−
8
)
2
+ (
5
−
9
)
2
12
=
=
9
+
16
+
1
+
0
+
2
+
18
+
16
12
=
62
12
=
31
6
.
Zatem odchylenie standardowe jest równe σ
=
q
31
6
≈
2, 27. To pozwala wyznaczy´c
godziny, które nie były „typowe”: 5:00-6:00, 7:00-9:00, 15:00-16:00.
Odpowied´z: 5:00-6:00, 7:00-9:00, 15:00-16:00
Materiał pobrany z serwisu
12
Wyszukiwarka
Podobne podstrony:
Zestaw 2 PP rozwiązania
Zestaw 1 PP rozwiązania
Zestaw 1 PP rozwiązania
zestaw 07 rozwiazania
Zestaw1 PR rozwiazania id 58873 Nieznany
2013 02 CEN PP rozwiązania
zestaw 05 rozwiazania
zestaw 06 rozwiazania
zestaw 10 rozwiązania
a6 jezyk polski pp rozwiazania Nieznany (2)
Zestaw 2 PR rozwiązania
2013 05 PP rozwiązania
MJA 1 PP rozwiazania id 303661 Nieznany
zestaw 08 rozwiazania
zestaw 04 rozwiazania
zestaw 03 rozwiazania
2013 05 ED PP rozwiązania
Chemia Ćwiczenia zestawy rozwiązane, Zestaw nr 7 rozwiazany, Zestaw 7
więcej podobnych podstron