
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
102
48
Całka oznaczona
Niech f:
R→R b dzie funkcj okre lon i ograniczon w przedziale [a, b].
Podzielmy przedział [a, b] na dowoln liczb odcinków (niekoniecznie równych), których długo ci s odpo-
wiednio równe
1
x
∆ ,
2
x
∆ ,...,
n
x
∆ . Oznaczmy ten podział przez Π. Zatem
}
...
:
]
,
[
{
1
2
1
0
1
b
x
x
x
x
x
a
x
x
n
n
i
i
=
<
<
<
<
<
=
=
Π
−
−
,
1
−
−
=
∆
i
i
i
x
x
x
.
Niech
ξ
1
,
ξ
2
,...,
ξ
n
oznaczaj punkty wybrane dowolnie, po jednym z ka dego odcinka:
}
,...,
2
,
1
,
:
{
)
(
1
n
i
x
x
i
i
i
i
=
≤
ξ
≤
ξ
=
Π
ω
−
Utwórzmy sum
(
)
n
n
x
f
x
f
x
f
S
∆
⋅
ξ
+
+
∆
⋅
ξ
+
∆
⋅
ξ
=
Π
ω
Π
)
(
...
)
(
)
(
)
(
,
2
2
1
1
.
Sum t nazywa si sum Riemanna funkcji f odpowiadaj c podziałowi
Π przedziału
]
,
[ b
a
i wyborowi
ω(Π)
punktów po rednich.
Znaczenie geometryczne sumy
(
)
)
(
,
Π
ω
Π
S
jest oczywiste, gdy funkcja f jest w przedziale [a, b] nieujemna.
Wówczas iloczyn
i
i
x
f
∆
⋅
ξ )
(
jest polem prostok ta o podstawie
i
x
∆ i wysoko ci
)
(
i
f
ξ . Suma
(
)
)
(
,
Π
ω
Π
S
jest sum
pól prostok tów o podstawach
1
x
∆ ,
2
x
∆ , ... ,
n
x
∆ i wysoko ciach
)
(
1
ξ
f
,
)
(
2
ξ
f
, ... ,
)
(
n
f
ξ .
Długo najwi kszego odcinka wchodz cego w skład podziału
Π oznaczamy δ(Π) i nazywamy
rednic podziału
Π
.
Zatem
}
...,
,
2
,
1
:
max{
)
(
n
i
x
i
=
∆
=
Π
δ
.
Definicja.
Je li istnieje liczba I taka, e ró nica
(
)
|
)
(
,
|
I
S
−
Π
ω
Π
jest dowolnie mała dla dostatecznie „drobnych” podziałów
Π i to niezale nie od wyboru ω(Π) punktów po rednich, to
liczb I nazywa si
całk oznaczon
funkcji f na przedziale [a, b] i oznacza symbolem
b
a
dx
x
f
)
(
.
Je li istnieje
b
a
dx
x
f
)
(
, to mówimy, e
funkcja
f
jest całkowalna w sensie Riemanna
w przedziale [a, b]. Liczb a na-
zywamy
granic doln
, liczb b
−
granic górn całki
. Ponadto przyjmujemy
0
)
(
=
a
a
dx
x
f
,
−
=
a
b
b
a
dx
x
f
dx
x
f
)
(
)
(
.
1
x
∆
2
x
∆
3
x
∆
4
x
∆
ξ
1
ξ
2
ξ
3
ξ
4
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
103
T
WIERDZENIE
(
o całkowalno ci funkcji ci głej
).
Je eli funkcja f jest ci gła w przedziale, to jest całkowalna w tym przedziale.
T
WIERDZENIE
(
o całkowalno ci funkcji monotonicznej
).
Je eli funkcja f jest monotoniczna w przedziale, to jest w nim całkowalna.
F
AKT
.
(Leibniz, Newton).
Je li F jest funkcj pierwotn funkcji f w przedziale [a, b], to
)
(
)
(
)
(
a
F
b
F
dx
x
f
b
a
−
=
.
1.
π
2
0
3
sin
dx
x
Korzystaj c ze wzoru
−
−
−
+
⋅
−
=
dx
x
n
n
x
x
n
dx
x
n
n
n
2
1
sin
1
cos
sin
1
sin
znajdujemy funkcj pierwotn F funkcji
x
x
f
3
sin
)
(
=
:
x
x
x
dx
x
x
x
x
F
cos
cos
sin
sin
cos
sin
)
(
3
2
2
3
1
3
2
2
3
1
−
⋅
−
=
+
⋅
−
=
.
Dlatego
π
2
0
3
sin
dx
x
[
]
=
−
⋅
−
=
π
2
0
3
2
2
3
1
cos
cos
sin
x
x
x
3
2
1
3
2
1
0
2
3
1
0
2
3
2
0
2
1
2
2
3
1
0
cos
0
cos
0
sin
cos
cos
sin
=
−
⋅
−
−
−
⋅
−
π
π
π
.
2.
=
+
2
1
)
1
(x
x
dx
1
1
1
)
1
(
1
+
−
=
+
x
x
x
x
wymiernej
funkcji
rozkad
y
Zastosujem
[
]
3
4
2
1
2
1
ln
)
2
ln
1
(ln
3
ln
2
ln
|
1
|
ln
|
|
ln
1
1
1
=
−
−
−
=
+
−
=
+
−
=
x
x
dx
x
x
3.
=
+
=
+
+
−
−
−
−
2
3
2
2
3
2
)
1
(
1
2
x
dx
x
x
dx
dt
dx
t
x
dx
dt
=
=
=
+
1
1
2
1
2
1
1
2
1
1
2
2
1
1
2
2
1
3
2
1
]
[
=
−
=
−
=
=
=
−
−
−
−
−
−
=
+
−
−
=
+
−
t
dt
t
t
dt
Uwaga!
W porównaniu ze stosowaniem podstawie w całce nieoznaczonej mamy zasadnicz zmian ;
musimy pami ta o zmia-
nie granic całkowania
.
4.
=
+
4
0
1
x
dx
tdt
dx
t
x
t
x
2
,
2
=
=
=
=
+
=
=
=
2
4
0
0
1
2
t
tdt
=
+
−
+
2
0
1
1
1
2
t
dt
t
=
+
−
2
0
1
1
1
2
dt
t
[
]
=
+
−
2
0
1
ln
2
t
t
[
] [
]
3
ln
2
4
0
1
ln
0
2
2
1
ln
2
2
−
=
+
−
−
+
−
5.
=
−
e
x
x
dx
1
2
)
(ln
1
dx
dt
x
t
x
=
=
1
ln
=
−
=
=
=
2
1
ln
0
1
ln
2
1
e
t
dt
[
]
6
0
2
1
0
0
6
2
1
π
=
−
=
π
arcsin
arcsin
arcsint
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
104
6.
3
1
ln dx
x
Znajdujemy funkcj pierwotn funkcji podcałkowej (stosuj c metod całkowania przez cz ci).
=
dx
x
ln
x
v
u
v
x
u
x
=
=
′
=
′
=
1
1
ln
C
x
x
dx
x
x
+
=
−
=
ln
ln
.
Dlatego (reguła Leibniza – Newtona)
3
1
ln dx
x
[
]
2
3
ln
3
)
1
1
ln
1
(
3
3
ln
3
ln
0
3
1
−
=
−
⋅
−
−
=
−
⋅
=
x
x
x
.
7.
π
0
2
cos x
x
Do wyznaczenia funkcji pierwotnej zastosujemy wzór na całkowanie przez cz ci:
=
dx
x
x cos
2
x
v
x
u
x
v
x
u
sin
2
cos
2
=
=
′
=
′
=
=
⋅
−
=
xdx
x
x
x
sin
2
sin
2
x
v
u
x
v
x
u
cos
1
sin
−
=
=
′
=
′
=
=
=
−
−
−
−
=
]
cos
cos
[
2
sin
2
dx
x
x
x
x
x
C
x
x
x
x
x
+
+
+
sin
cos
2
sin
2
Dlatego (reguła Leibniza – Newtona)
π
−
=
+
⋅
⋅
+
−
π
+
π
π
+
π
π
=
+
+
=
−
π
π
2
0
sin
0
cos
0
2
0
sin
0
sin
cos
2
sin
]
sin
cos
2
sin
[
cos
0
1
0
2
0
1
0
2
0
2
0
2
x
x
x
x
x
x
x
8.
dx
x
x arctg
⋅
1
0
Do wyznaczenia funkcji pierwotnej zastosujemy wzór na całkowanie przez cz ci
=
⋅
dx
x
x arctg
2
2
1
2
1
1
x
v
x
u
x
v
x
u
=
+
=
′
=
′
= arctg
=
+
−
=
dx
x
x
x
x
2
2
2
1
2
2
1
1
arctg
=
+
−
+
−
dx
x
x
x
x
2
2
2
1
2
2
1
1
1
1
arctg
+
−
−
=
dx
x
x
x
)
1
1
1
(
2
2
1
2
2
1
arctg
C
x
x
x
x
+
+
−
=
arctg
arctg
2
1
2
1
2
2
1
Dlatego (reguła Leibniza – Newtona)
=
⋅
dx
x
x arctg
1
0
[
]
=
+
−
1
0
2
1
2
1
2
2
1
x
x
x
x
arctg
arctg
2
1
4
1
0
2
1
0
2
1
2
1
2
1
2
1
0
0
1
1
4
4
−
π
=
+
−
+
−
π
π
arctg
arctg
arctg
arctg
9. Nie ka da funkcja okre lona i ograniczona na
]
,
[ b
a
jest całkowalna na
]
,
[ b
a
, np. funkcja
=
]
1
,
0
[
,
1
]
1
,
0
[
,
0
)
(
odcinka
a
niewymiern
liczba
gdy
odcinka
wymierna
liczba
gdy
x
x
x
f
nie jest całkowalna na [0, 1].
Gdyby my dla ka dego podziału
Π dokonali wyboru punktów po rednich zło onego jedynie z punktów wymiernych
odcinka [0, 1], to suma całkowa byłaby równa 0, a gdyby wybór punktów po rednich zło ony był jedynie z punktów
niewymiernych odcinka [0, 1], to suma całkowa byłaby równa 1.
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
105
49
Zastosowania całki oznaczonej
Pole trapezu krzywoliniowego
, ograniczonego wykresem ci głej funkcji y = f(x), f(x)
≥ 0 dla x∈[a, b], osi x i prostymi
x = a, x = b jest równe
=
b
a
dx
x
f )
(
|
D
|
Pole trapezu krzywoliniowego
, ograniczonego z góry wykresem funkcji y = g(x), z dołu wykresem y = f(x) (f(x)
≥0 dla
x
∈[a, b]) oraz z boków prostymi x = a, x = b jest równe
[
]
−
=
∈
≤
≤
≤
≤
=
b
a
b
a
dx
x
f
x
g
C
g
f
x
g
y
x
f
b
x
a
y
x
)
(
)
(
|
|
,
)
(
)
(
:
)
,
(
0
]
,
[
D
D
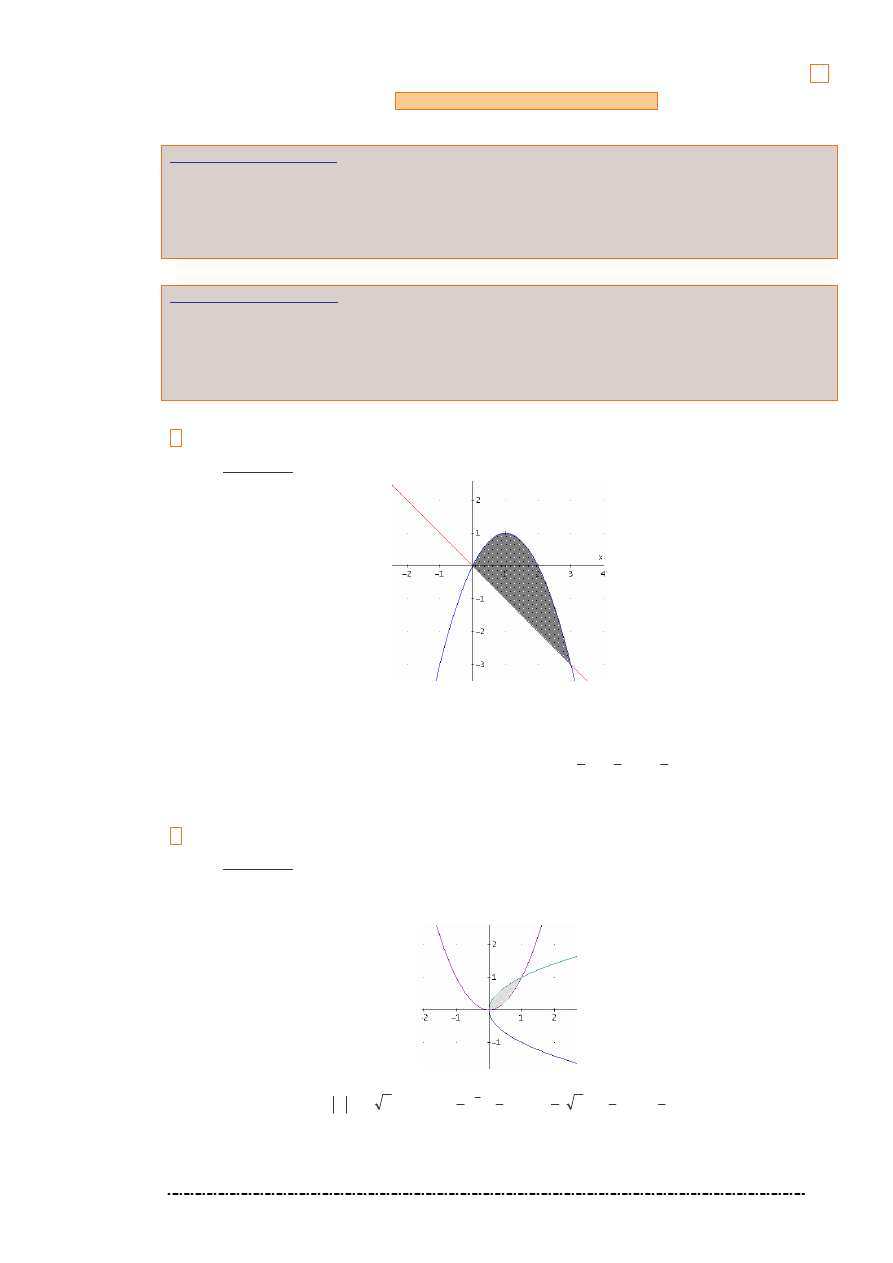
1. Oblicz pole obszaru ograniczonego wykresami funkcji
)
(
1
x
x
f
−
=
i
)
2
(
2
2
x
x
x
f
−
=
.
Rozwi zanie.
Punkty wspólne wykresów tych funkcji: (0,0), (3,
−3).
[
]
=
−
−
−
=
3
0
2
)
(
)
2
(
|
|
dx
x
x
x
D
[
]
2
9
3
0
3
3
1
2
2
3
3
0
2
)
3
(
=
−
=
−
x
x
dx
x
x
.
2. Oblicz pole obszaru zawartego mi dzy wykresami parabol
2
x
y
=
i
x
y
=
2
.
Rozwi zanie.
Punktami wspólnymi tych parabol s : (0, 0) i (1, 1). Dlatego
[
]
[
]
3
1
1
0
3
3
1
3
3
2
1
0
3
3
1
3
2
1
0
2
)
(
2
3
=
−
=
−
=
−
=
x
x
x
x
dx
x
x
D
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
106
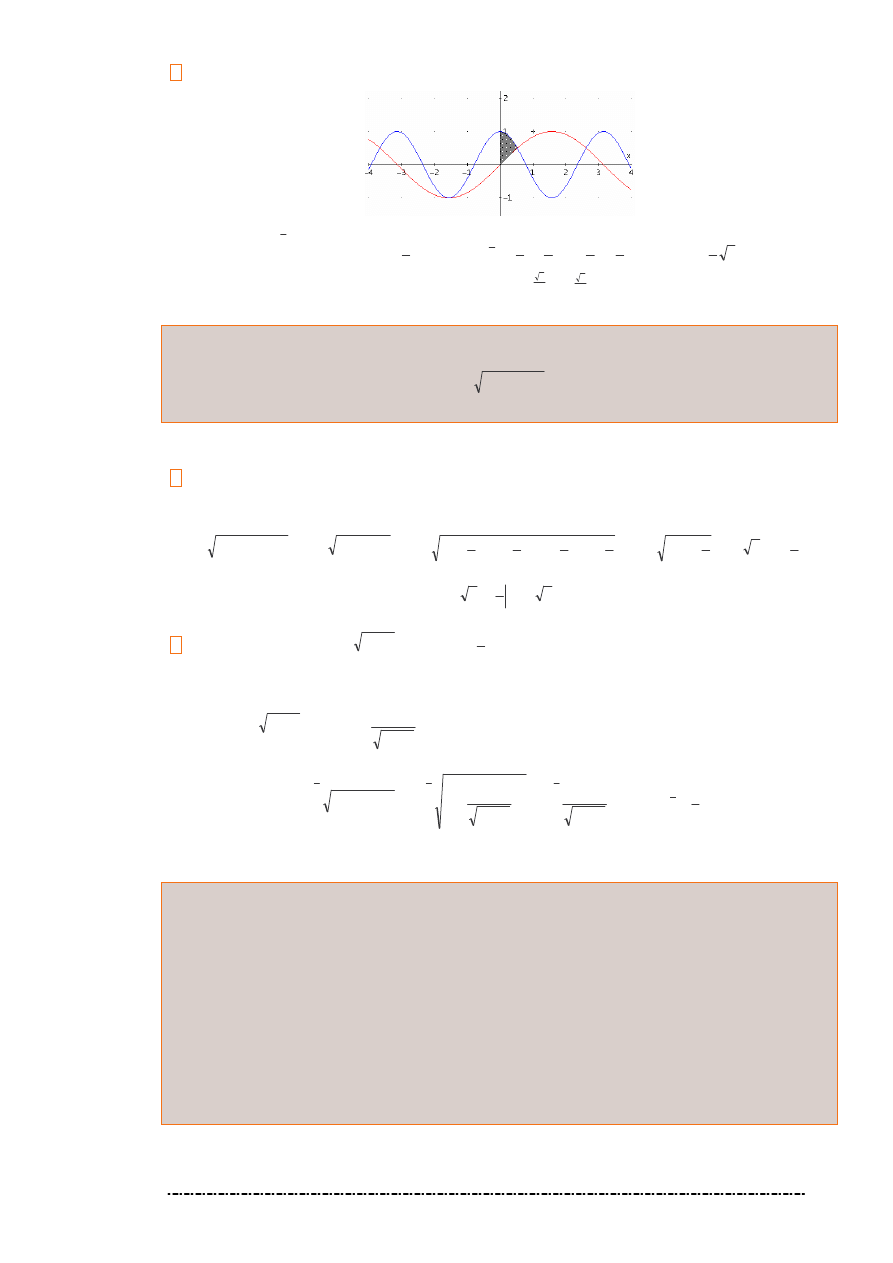
3. Obliczy pole obszaru ograniczonego wykresami funkcji
x
y sin
=
,
x
y
2
cos
=
,
0
≥
x
.
1
3
]
0
cos
0
sin
[
]
cos
sin
[
]
cos
2
sin
[
]
sin
2
[cos
|
|
4
3
1
0
2
1
6
3
2
1
0
2
1
0
2
3
2
3
6
6
−
=
+
−
+
=
+
=
−
=
π
π
π
π
x
x
dx
x
x
D
Krzywa
[ ]
R
∈
→
∋
)
(
,
:
)
(
x
f
x
b
a
L
, klasy
1
C , ma długo
(
)
′
+
=
b
a
dx
x
f
L
2
)
(
1
4. Oblicz długo łuku sinusoidy
x
y sin
=
,
]
,
0
[
π
∈
x
.
Rozwi zanie.
π
π
+
=
′
+
=
0
2
0
2
cos
1
]
)
[(sin
1
dx
x
dx
x
L
π
−
+
+
=
0
2
2
2
2
2
2
2
2
sin
cos
sin
cos
dx
x
x
x
x
=
=
π
0
2
2
cos
2
dx
x
=
π
0
2
cos
2
dx
x
π
=
0
2
sin
2
2
x
2
2
=
.
5. Obliczy długo krzywej
2
1 x
y
−
=
, gdzie
]
,
0
[
2
1
∈
x
.
Rozwi zanie.
Dla funkcji
2
1 x
y
−
=
mamy
2
1 x
x
y
−
−
=
′
. Zatem
[
]
=
+
=
2
1
0
2
)
(
'
1
dx
x
f
L
π
=
=
−
=
−
−
+
6
1
0
0
2
0
2
2
2
1
2
1
2
1
]
[arcsin
1
1
1
x
x
dx
dx
x
x
Niech
b
t
a
t
f
≤
≤
),
(
, b dzie pr dko ci (intensywno ci ) wpływu towarów w chwili t do magazynu. Wów-
czas
b
a
dt
t
f )
(
jest zapasem towarów w magazynie po upływie czasu od a do b.
Niech funkcja
)
(t
z
opisuje zysk, jaki przynosi urz dzenie U w chwili t, niech funkcja
)
(t
k
opisuje koszt eks-
ploatacji urz dzenia U w chwili t. Funkcja
)
(
)
(
)
(
t
k
t
z
t
f
−
=
opisuje rzeczywisty zysk osi gany z zainstalowania urz -
dzenia U w chwili t; niech a oznacza chwil uruchomienia urz dzenia U, b – maksymalny czas eksploatacji. Wówczas
b
a
dt
t
f )
(
jest równa zyskowi, jaki dało nam zainstalowanie urz dzenia U.
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
107
We my funkcj
[ ]
R
→
b
a
f
,
:
ci gł na przedziale
[ ]
b
a, . Obracaj c wykres funkcji f dookoła osi x, otrzymu-
jemy brył obrotow , której obj to liczymy ze wzoru
(
)
π
=
b
a
dx
x
f
2
)
(
Vol
za pole powierzchni -
(
)
dx
x
f
x
f
b
a
′
+
π
=
2
)
(
1
)
(
2
Pole
6. Obliczy obj to i pole powierzchni kuli o promieniu r.
Kula taka powstaje przez obrót krzywej
2
2
x
r
y
−
=
,
r
x
r
≤
≤
−
, wokół osi odci tych. Dlatego
(
)
π
=
b
a
dx
x
f
2
)
(
Vol
3
3
4
3
3
1
2
2
2
]
[
)
(
r
x
x
r
dx
x
r
r
x
r
x
r
r
π
=
−
π
=
−
π
=
=
−
=
−
;
(
)
dx
x
f
x
f
b
a
′
+
π
=
2
)
(
1
)
(
2
Pole
r
dx
r
dx
x
r
x
x
r
r
r
r
r
π
=
π
=
−
+
⋅
−
π
=
−
−
4
2
1
2
2
2
2
2
2
.
50
Całki niewła ciwe
1.
Je li funkcja
R
→
∞)
,
0
[
:
f
jest całkowalna w ka dym przedziale
[ ]
b
a
,
, gdzie
∞
<
< b
a
, to przyjmujemy
∞
→
∞
=
b
a
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
i przy warunku, e granica istnieje,
całk niewła ciw
nazywamy
zbie n
; w przeciwnym przypadku mówimy, e
całka
niewła ciwa
jest
rozbie na
.
2.
Je li funkcja
R
→
−∞ ]
,
(
:
b
f
jest całkowalna w ka dym przedziale
[ ]
b
a
,
, gdzie
b
a
<
<
−∞
, to przyjmujemy
−∞
→
∞
−
=
b
a
a
b
dx
x
f
dx
x
f
)
(
lim
)
(
i przy warunku, e granica istnieje,
całk niewła ciw
nazywamy
zbie n
; w przeciwnym przypadku mówimy, e
całka
niewła ciwa
jest
rozbie na
.
3.
Je li funkcja
R
R →
:
f
jest całkowalna w ka dym przedziale
[ ]
b
a
,
, to przyjmujemy
∞
∞
−
∞
∞
−
+
=
b
b
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
i przy warunku, e obie całki niewła ciwe po prawej stronie wzoru istniej ,
całk niewła ciw
nazywamy
zbie n
; w
przeciwnym przypadku mówimy, e
całka niewła ciwa
jest
rozbie na
.
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
108
4.
Zakładamy, e funkcja
R
→
)
,
[
:
b
a
f
jest całkowalna na ka dym przedziale
[
]
ε
−
b
a,
i nieograniczona na ka dym prze-
dziale
)
,
[
b
b
ε
−
. Przyjmujemy
ε
−
→
ε
+
=
b
a
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
0
i przy warunku, e granica istnieje,
całk niewła ciw
nazywamy
zbie n
; w przeciwnym przypadku mówimy, e
całka
niewła ciwa
jest
rozbie na
.
5.
Zakładamy, e funkcja
R
→
]
,
(
:
b
a
f
jest całkowalna na ka dym przedziale
[
]
b
a
,
ε
+
i nieograniczona na ka dym prze-
dziale
]
,
(
ε
+
a
a
. Przyjmujemy
ε
+
→
ε
+
=
b
a
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
0
i przy warunku, e granica istnieje,
całk niewła ciw
nazywamy
zbie n
; w przeciwnym przypadku mówimy, e
całka
niewła ciwa
jest
rozbie na
.
6.
Je eli funkcja f jest całkowalna na ka dym przedziale
[
]
α
−
c
a,
i
[
]
b
c
,
β
+
, nieograniczona na s siedztwie punktu c i
istniej całki niewła ciwe
b
c
c
a
dx
x
f
dx
x
f
)
(
,
)
(
to sum
+
b
c
c
a
dx
x
f
dx
x
f
)
(
)
(
nazywamy
całk niewła ciw funkcji nieograniczonej
f
na przedziale
[ ]
b
a, i piszemy
+
=
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
.
∞
1
2
x
dx
.
Funkcja
[
)
R
∈
→
∋
∞
2
1
,
1
:
x
x
f
jest ci gła na
[
)
∞
,
1
, a wi c całkowalna na ka dym przedziale
[ ]
b
,
1 . Dlatego
1
1
1
lim
1
lim
lim
1
1
2
1
2
=
+
−
=
−
=
=
∞
→
∞
→
∞
→
∞
b
x
x
dx
x
dx
b
b
b
b
b
∞
−
+
0
2
1 x
dx
Funkcja
(
]
R
∈
+
→
∋
∞
−
2
1
1
0
,
:
x
x
f
jest ci gła na
(
]
0
,
−∞ , a wi c całkowalna na ka dym przedziale
[ ]
0
,
a
. Dlatego
[
]
(
)
2
0
lim
lim
1
lim
1
0
0
2
0
2
π
=
−
=
=
+
=
+
−∞
→
−∞
→
−∞
→
∞
−
a
x
x
dx
x
dx
a
a
a
a
a
arctg
arctg

Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
109
−
3
0
2
)
1
(x
dx
.
Funkcja okre lona wzorem
2
)
1
(
1
)
(
−
=
x
x
f
nie jest ograniczona w s siedztwie punktu
1
=
c
. Dlatego badamy całk
=
−
1
0
2
)
1
(x
dx
ε
−
→
ε
−
+
1
0
2
0
)
1
(
lim
x
dx
=
−
−
=
ε
−
→
ε
+
1
0
0
1
1
lim
x
∞
=
−
ε
−
+
→
ε
)
1
1
(
lim
0
Poniewa jest ona rozbie na, wi c badana całka jest równie rozbie na.
Zadanie 1.
Oblicz
∞
⋅
2
ln x
x
dx
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na półprostej mamy
∞
=
=
⋅
=
⋅
∞
→
∞
→
∞
A
A
A
A
x
x
x
dx
x
x
dx
2
2
2
|]
ln
|
[ln
lim
ln
lim
ln
Dlatego wyj ciowa całka jest rozbie na (do wyznaczenia funkcji pierwotnej dla funkcji podcałkowej zastosowano pod-
stawienie
t
x
=
ln
).
Zadanie 2.
Oblicz
∞
+
1
2
1
dx
x
x
arctg
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na półprostej mamy:
=
+
dx
x
x
2
1
arctg
dt
dx
t
x
x
dx
dt
x
=
=
=
+
+
2
2
1
1
1
1
arctg
C
x
C
t
dt
t
+
=
+
=
=
2
2
1
2
2
1
)
(arctg
;
2
32
3
2
16
1
2
4
1
2
1
2
2
1
2
2
1
1
2
2
1
1
2
1
2
)
(
]
)
1
(
[
]
)
(
[
lim
]
)
(
[
lim
1
lim
1
π
=
π
−
π
=
=
−
=
=
+
=
+
∞
→
∞
→
∞
→
∞
arctg
arctg
arctg
arctg
arctg
A
x
dx
x
x
dx
x
x
A
A
A
A
A
Dlatego wyj ciowa całka jest zbie na (do wyznaczenia funkcji pierwotnej dla funkcji podcałkowej zastosowano podsta-
wienie
t
x
=
arctg
).

Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
110
Zadanie 3.
Oblicz
∞
−
⋅
2
2
1
x
dx
x
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na półprostej mamy
∞
=
−
=
−
⋅
=
−
⋅
=
−
⋅
∞
→
∞
→
∞
→
∞
A
A
A
A
A
A
x
x
dx
x
x
dx
x
x
dx
x
2
2
2
1
2
2
2
1
2
2
2
2
|]
1
|
ln
[
lim
1
2
lim
1
lim
1
Dlatego wyj ciowa całka jest rozbie na.
Zadanie 4.
Oblicz
∞
−
0
2
dx
xe
x
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na półprostej mamy
2
1
2
1
0
2
1
0
0
)
(
0
]
[
lim
lim
2
2
2
=
−
−
=
−
=
=
−
∞
→
−
∞
→
∞
−
A
x
A
A
x
A
x
e
dx
xe
dx
xe
Dlatego wyj ciowa całka jest zbie na (do wyznaczenia funkcji pierwotnej dla funkcji podcałkowej zastosowano podsta-
wienie
t
x
=
−
2
).
Zadanie 5.
Oblicz
∞
∞
−
+
⋅
1
2
2
x
dx
x
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na prostej mamy
∞
∞
−
∞
∞
−
+
⋅
+
+
⋅
=
+
⋅
0
2
0
2
2
1
2
1
2
1
2
x
dx
x
x
dx
x
x
dx
x
.
Poniewa
∞
=
+
=
+
⋅
=
+
⋅
∞
→
∞
→
∞
A
A
A
A
x
x
dx
x
x
dx
x
0
2
0
2
0
2
|]
1
|
[ln
lim
1
2
lim
1
2
,
co oznacza, e całka ta jest rozbie na, wi c wyj ciowa całka jest rozbie na (w takim przypadku nie musimy oblicza
drugiej całki).
Zadanie 6.
Oblicz
∞
∞
−
+
+
2
2
2
x
x
dx
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na prostej mamy
∞
−
−
∞
−
∞
∞
−
∞
∞
−
+
+
+
+
+
=
+
+
=
+
+
1
2
1
2
2
2
1
)
1
(
1
)
1
(
1
)
1
(
2
2
x
dx
x
dx
x
dx
x
x
dx
.
Poniewa
π
=
+
=
+
+
=
+
+
−
∞
→
−
∞
→
∞
−
2
1
1
1
2
1
2
)]
1
(
[
lim
1
)
1
(
lim
1
)
1
(
A
A
A
A
x
x
dx
x
dx
arctg
,
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
111
π
=
+
=
+
+
=
+
+
−
−∞
→
−
−∞
→
−
∞
−
2
1
1
1
2
1
2
)]
1
(
[
lim
1
)
1
(
lim
1
)
1
(
B
B
B
B
x
x
dx
x
dx
arctg
,
wi c
π
=
+
+
∞
∞
−
2
2
2
x
x
dx
.
Zadanie 7.
Oblicz
∞
∞
−
+
+
9
4
2
x
x
dx
.
Rozwi zanie.
Korzystaj c z definicji całki niewła ciwej na prostej mamy
∞
−
−
∞
−
∞
∞
−
∞
∞
−
+
+
+
+
+
=
+
+
=
+
+
2
2
2
2
2
2
5
)
2
(
5
)
2
(
5
)
2
(
9
4
x
dx
x
dx
x
dx
x
x
dx
.
Poniewa
π
=
=
+
+
=
+
+
−
+
∞
→
−
∞
→
∞
−
5
2
1
2
5
2
5
1
2
2
2
2
]
[
lim
5
)
2
(
lim
5
)
2
(
A
x
A
A
A
x
dx
x
dx
arctg
,
π
=
=
+
+
=
+
+
−
+
−∞
→
−
−∞
→
−
∞
−
5
2
1
2
2
5
1
2
2
2
2
]
[
lim
5
)
2
(
lim
5
)
2
(
B
x
B
B
B
x
dx
x
dx
5
arctg
,
zatem
π
=
+
+
∞
∞
−
5
1
2
9
4x
x
dx
.
Zadanie 8.
Oblicz
∞
∞
−
dx
x
f )
(
, je li
>
≤
≤
−
−
−
<
=
.
1
0
,
1
1
1
,
1
0
)
(
2
x
x
x
x
x
f
dla
dla
dla
Rozwi zanie.
π
=
−
=
⋅
+
−
+
⋅
=
−
∞
−
−
∞
−
∞
∞
−
2
1
1
1
2
1
1
1
2
1
1
0
1
0
)
(
dx
x
dx
dx
x
dx
dx
x
f
Do wyznaczenia funkcji pierwotnej dla funkcji podcałkowej zastosowano wzór
C
a
x
a
x
a
x
dx
x
a
+
+
−
=
−
arcsin
2
2
2
2
2
2
1
Zadanie 9.
Oblicz
∞
∞
−
dx
x
f )
(
, je li
π
>
π
≤
≤
<
=
.
0
,
0
cos
,
0
0
)
(
2
1
2
1
x
x
x
x
x
f
dla
dla
dla
Rozwi zanie.
1
]
[sin
cos
0
cos
0
)
(
2
1
2
1
2
1
2
1
0
0
0
0
=
=
=
⋅
+
+
⋅
=
π
π
∞
π
π
∞
−
∞
∞
−
x
dx
dx
dx
x
dx
dx
x
f

Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
112
Zadanie 10.
Oblicz
∞
∞
−
dx
x
f )
(
, je li
>
≤
≤
<
=
.
8
0
,
8
1
,
1
0
)
(
7
1
x
x
x
x
f
dla
dla
dla
Rozwi zanie.
1
0
0
)
(
8
1
7
1
8
8
1
7
1
1
=
=
⋅
+
+
⋅
=
∞
∞
−
∞
∞
−
dx
dx
dx
dx
dx
x
f
Zadanie 11.
Oblicz
1
0
x
dx
.
Rozwi zanie.
Funkcja podcałkowa nie jest ograniczona w prawostronnym s siedztwie dolnej granicy całkowania. W takim przypadku
– zgodnie z definicj – mamy
2
]
2
[
lim
lim
1
0
1
0
1
0
=
=
=
ε
→
ε
ε
→
ε
+
+
x
x
dx
x
dx
.
Zadanie 12.
Oblicz
−
1
0
2
1 x
dx
.
Rozwi zanie
Funkcja podcałkowa nie jest ograniczona w lewostronnym s siedztwie górnej granicy całkowania. W takim przypadku –
zgodnie z definicj – mamy
π
=
=
−
=
−
ε
−
→
ε
ε
−
→
ε
+
+
2
1
1
0
0
1
0
2
0
1
0
2
]
[arcsin
lim
1
lim
1
x
x
dx
x
dx
.
Zadanie 13.
Oblicz
π
4
1
0
dx
x
ctg
.
Rozwi zanie.
Funkcja podcałkowa nie jest ograniczona w prawostronnym s siedztwie dolnej granicy całkowania. W takim przypadku
– zgodnie z definicj – mamy
∞
=
=
=
π
ε
→
ε
π
ε
→
ε
π
+
+
4
1
4
1
4
1
|]
sin
|
[ln
lim
lim
0
0
0
x
dx
x
dx
x
ctg
ctg
.
Całka jest rozbie na.
Zadanie 14.
Oblicz
−
1
2
2
1
1 x
dx
x
.
Rozwi zanie
Funkcja podcałkowa nie jest ograniczona w lewostronnym s siedztwie górnej granicy całkowania. W takim przypadku –
zgodnie z definicj – mamy
1
]
1
[
lim
1
lim
1
1
0
2
0
1
2
0
1
2
2
1
2
1
=
−
−
=
−
=
−
ε
−
→
ε
ε
−
→
ε
+
+
x
x
dx
x
x
dx
x
.
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
113
Zadanie 15.
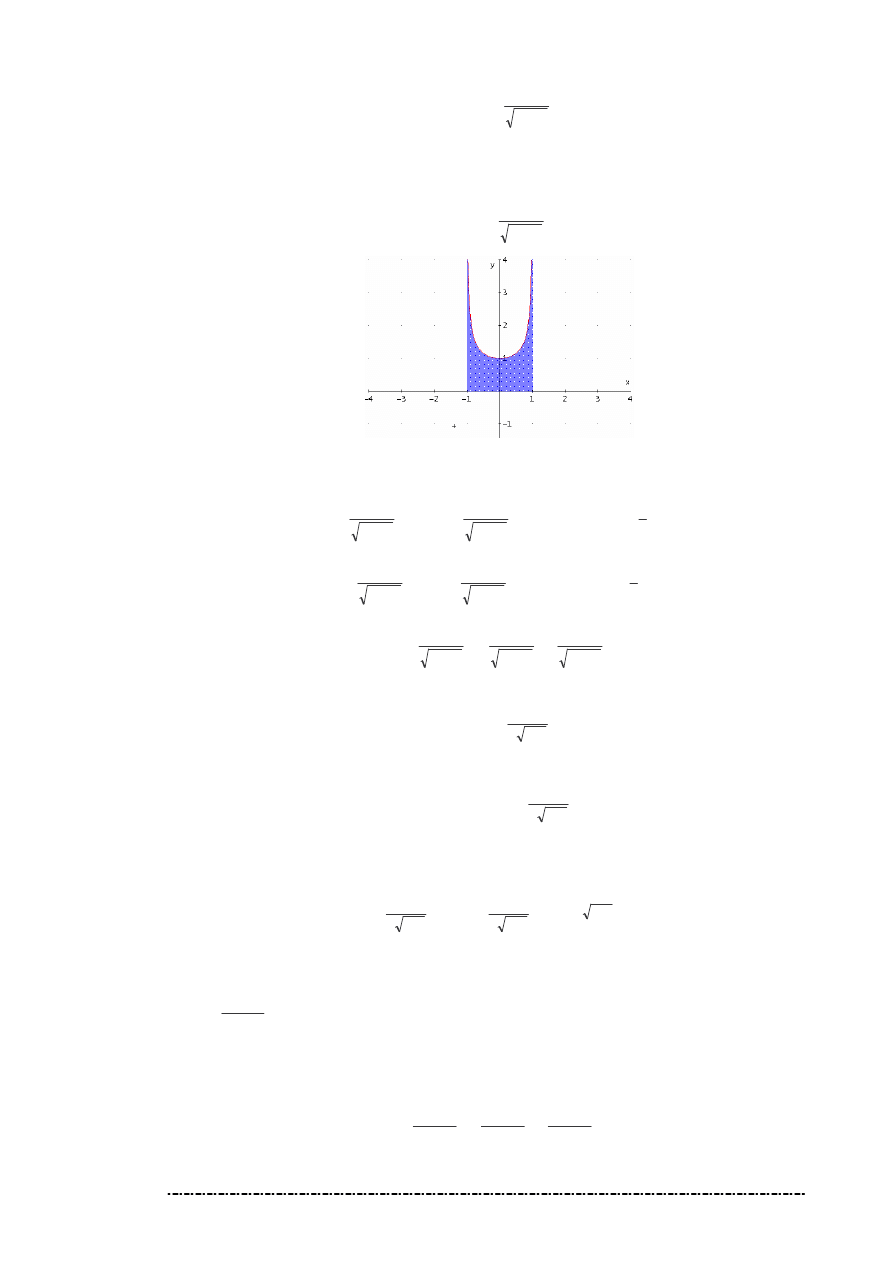
Oblicz pole obszaru ograniczonego wykresem funkcji
2
1
1
)
(
x
x
f
−
=
i osi odci tych.
Rozwi zanie.
Poniewa
)
1
,
1
(
−
=
f
D
, wi c
−
−
=
1
1
2
1
|
|
x
dx
D
.
Funkcja podcałkowa nie jest ograniczona w lewostronnym s siedztwie górnej granicy całkowania, ani w prawostronnym
s siedztwie dolnej granicy całkowania W takim przypadku – zgodnie z definicj – mamy
π
=
=
−
=
−
ε
+
−
→
ε
ε
+
−
→
ε
−
+
+
2
1
0
1
0
0
1
2
0
0
1
2
]
[arcsin
lim
1
lim
1
x
x
dx
x
dx
,
π
=
=
−
=
−
ε
−
→
ε
ε
−
→
ε
+
+
2
1
1
0
0
1
0
2
0
1
0
2
]
[arcsin
lim
1
lim
1
x
x
dx
x
dx
,
π
=
−
+
−
=
−
=
−
−
1
0
2
0
1
2
1
1
2
1
1
1
|
|
x
dx
x
dx
x
dx
D
.
Zadanie 16.
Oblicz pole obszaru ograniczonego wykresem funkcji
x
x
x
f
ln
1
)
(
=
, gdzie
e
x
≤
<
1
, i osi odci tych.
Rozwi zanie.
=
e
x
x
dx
D
1
ln
|
|
Funkcja podcałkowa nie jest ograniczona w prawostronnym s siedztwie dolnej granicy całkowania W takim przypadku –
zgodnie z definicj – mamy
2
]
ln
2
[
lim
ln
lim
ln
|
|
1
0
1
0
1
=
=
=
=
ε
+
→
ε
ε
+
→
ε
+
+
e
e
e
x
x
x
dx
x
x
dx
D
.
Zadanie 17.
Oblicz
−
3
0
2
)
1
(x
dx
Rozwi zanie.
Funkcja podcałkowa nie jest okre lona w punkcie
1
=
x
. W takim przypadku post pujemy nast puj co
−
+
−
=
−
3
1
2
1
0
2
3
0
2
)
1
(
)
1
(
)
1
(
x
dx
x
dx
x
dx
.
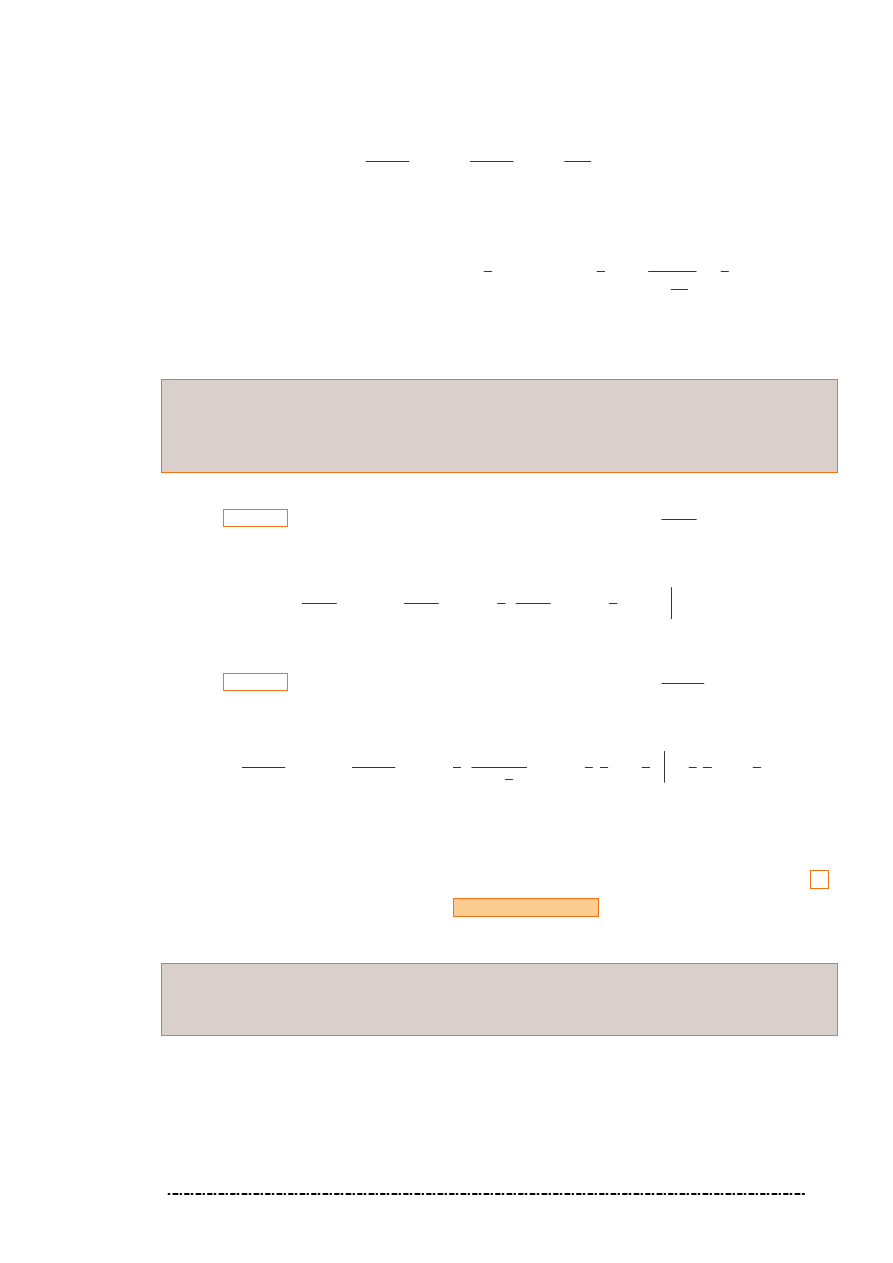
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
114
Teraz funkcja podcałkowa w pierwszej całce jest nieograniczona w lewostronnym s siedztwie górnej granicy całkowa-
nia, funkcja podcałkowa w drugiej całce jest nieograniczona w prawostronnym s siedztwie dolnej granicy całkowania.
Poniewa
∞
=
−
−
=
−
=
−
ε
−
→
ε
ε
−
→
ε
+
+
1
0
0
1
0
2
0
1
0
2
1
1
lim
)
1
(
lim
)
1
(
x
x
dx
x
dx
,
wi c wyj ciowa całka jest rozbie na (w takim przypadku nie musimy oblicza drugiej całki).
Zadanie 18.
[
]
4
1
2
0
4
1
1
2
4
1
0
1
0
1
0
1
4
1
ln
2
lim
)
1
ln
2
(
lim
ln
lim
ln
−
=
⋅
−
−
−
=
−
=
⋅
=
⋅
+
+
+
→
ε
ε
→
ε
ε
→
ε
x
x
x
x
dx
x
x
dx
x
x
Kryterium całkowe zbie no ci szeregu liczbowego.
Niech funkcja f b dzie dodatnia i malej ca w przedziale
)
,
1
[
∞ oraz niech
)
(n
f
a
n
=
,
1
≥
n
. Wówczas
Szereg
∞
=1
n
n
a
jest zbie ny
⇔ całka
∞
1
)
( dx
x
f
jest zbie na.
Przykład 1
°
Korzystaj c z kryterium całkowego zbadamy zbie no szeregu
∞
=
+
1
5
2
1
n
n
.
Poniewa całka
∞
=
+
=
+
=
+
=
+
∞
→
∞
→
∞
→
∞
A
A
A
A
A
A
x
dx
x
dx
x
dx
x
1
2
1
1
2
1
1
1
)
5
2
ln(
lim
5
2
2
lim
5
2
1
lim
5
2
1
nie jest zbie na, wi c szereg nie jest zbie ny.
Przykład 2
°
Korzystaj c z kryterium całkowego zbadamy zbie no szeregu
∞
=
+
1
2
4
9
1
n
n
.
Poniewa całka
)
(
)
(
lim
)
(
1
lim
4
9
1
lim
4
9
1
2
3
2
6
1
1
2
3
2
3
9
1
1
2
3
2
2
9
1
1
2
1
2
arctg
arctg
−
=
⋅
=
+
=
+
=
+
π
∞
→
∞
→
∞
→
∞
A
A
A
A
A
A
x
dx
x
dx
x
dx
x
jest zbie na, wi c szereg jest zbie ny.
51
Szeregi pot gowe
Definicja.
Szereg funkcyjny postaci
∞
=
−
0
0
)
(
k
k
k
x
x
a
, gdzie
k
a s stałymi, nazywamy
szeregiem pot gowym
o rodku w punkcie
R
x
∈
0
.
Mo na wykaza , e je li szereg pot gowy jest zbie ny w punkcie
0
≠
c
, to jest bezwzgl dnie zbie ny wewn trz prze-
działu
)|
|
|,
|
(
0
0
c
x
c
x
+
−
. Z powy szego wynika, e istnieje r takie, e w przedziale
)
,
(
0
0
r
x
r
x
+
−
szereg jest zbie ny,
a na zewn trz tego przedziału szereg jest rozbie ny. Liczb t nazywamy
promieniem zbie no ci
szeregu pot gowego.
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
115
Twierdzenie
o promieniu zbie no ci (Hadamard, d’Alembert, Cauchy):
Je li istnieje granica
λ
=
+
∞
→
n
n
n
a
a
1
lim
albo
λ
=
∞
→
n
n
n
a |
|
lim
to promie zbie no ci szeregu jest
=
λ
∞
∞
<
λ
<
λ
∞
=
λ
=
−
0
0
0
1
dla
dla
dla
r
Przykład 3
°
Okre l przedział zbie no ci szeregu
n
n
n
n
x
n
n
2
1
!
2
∞
=
.
Zastosujemy kryterium d’Alemberta.
e
x
n
n
x
n
n
x
x
n
n
x
n
n
w
w
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
2
2
2
2
)
1
(
2
1
1
1
2
1
lim
2
)
1
(
lim
2
!
2
)
1
(
)!
1
(
2
lim
|
|
|
|
lim
=
+
⋅
=
+
⋅
=
⋅
+
+
=
∞
→
∞
→
+
+
+
∞
→
+
∞
→
2
|
|
1
2
2
e
x
e
x
<
⇔
<
Szereg jest zbie ny w przedziale
)
,
(
2
2
e
e
−
.
Przykład 4
°
Okre l przedział zbie no ci szeregu
∞
=
+
+
+
1
)
2
)(
1
(
2
)
1
(
n
n
n
n
n
x
.
Zastosujemy kryterium d’Alemberta.
1
2
2
|
1
|
1
2
|
1
|
3
1
lim
2
|
1
|
|
|
|
|
lim
1
<
<
−
⇔
<
+
⇔
<
+
=
+
+
⋅
+
=
∞
→
+
∞
→
x
x
x
n
n
x
w
w
n
n
n
n
Ko ce przedziału zbie no ci:
∞
=
+
+
=
+
1
)
2
)(
1
(
1
2
1
n
n
n
x
jest szeregiem zbie nym.
∞
=
+
+
−
−
=
+
1
)
2
)(
1
(
)
1
(
2
1
n
n
n
n
x
jest szeregiem zbie nym bezwzgl dnie.
Szereg jest zbie ny w przedziale
]
1
,
3
[
−
.
Twierdzenie
(o rozwijaniu funkcji w szereg pot gowy).
Je li
1
° funkcja f ma w przedziale
)
,
(
0
0
δ
+
δ
− x
x
pochodne dowolnego rz du,
2
° dla ka dego
)
,
(
0
0
δ
+
δ
−
∈
x
x
x
spełniony jest warunek
0
)
(
!
)
(
lim
0
)
(
=
−
∞
→
n
n
n
x
x
n
c
f
,
to
∞
=
−
=
0
0
)
(
)
(
!
)
(
)
(
n
n
n
x
x
n
c
f
x
f
dla ka dego
)
,
(
0
0
δ
+
δ
−
∈
x
x
x
.
Szereg pot gowy wyst puj cy w tezie twierdzenia nazywa si
szeregiem Taylora
funkcji f w punkcie
0
x ; gdy
0
0
=
x
,
szereg ten nazywa si
szeregiem Maclaurina
.
Twierdzenie
(o ró niczkowaniu szeregu pot gowego):
Szereg pot gowy mo na ró niczkowa wyraz po wyrazie w przedziale
)
,
(
r
r
−
, gdzie r jest promieniem zbie no ci:
∞
=
−
−
∞
=
−
=
+
−
+
+
−
+
=
−
1
1
0
1
0
0
2
1
0
0
)
(
...
)
(
...
)
(
2
)
(
k
k
k
n
n
k
k
k
x
x
ka
x
x
na
x
x
a
a
x
x
a
dx
d
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
116
Po prawej stronie mamy tzw.
SZEREG POCHODNY
.
FAKT. Oba szeregi maj ten sam zbiór zbie no ci.
Twierdzenie
(o całkowaniu szeregu pot gowego):
Szereg pot gowy mo na całkowa wyraz po wyrazie w przedziale
)
,
(
r
r
−
, gdzie r jest promieniem zbie no ci:
∞
=
+
+
−
∞
=
=
+
+
+
+
+
=
0
1
1
1
1
1
3
2
3
1
2
1
2
1
0
0
0
...
...
k
k
k
k
n
n
n
x
k
k
k
x
a
x
a
x
a
x
a
x
a
dx
x
a
Przykład 5
°
...
1
1
1
3
2
+
+
+
+
=
−
x
x
x
x
Jest to szereg geometryczny zbie ny dla
1
|
|
<
x
.
Przykład 6
°
...
1
1
1
3
2
+
−
+
−
=
+
x
x
x
x
Jest to szereg geometryczny zbie ny dla
1
|
|
<
x
.
Przykład 7
°
x
x
dx
d
+
=
+
1
1
)]
1
[ln(
,
...
1
1
1
3
2
+
−
+
−
=
+
x
x
x
x
dla
1
|
|
<
x
.
∞
=
−
−
=
+
−
+
−
=
+
−
+
−
=
+
=
+
1
1
4
4
1
3
3
1
2
2
1
0
3
2
0
)
1
(
...
...)
1
(
1
1
)
1
ln(
k
k
k
x
x
x
k
x
x
x
x
dx
x
x
x
dx
x
x
jest szeregiem zbie nym dla
1
1
<
<
−
x
. Ponadto dla
1
=
x
jest zbie ny warunkowo. Kład c do tego wzoru warto
1
=
x
mamy
...
4
1
3
1
2
1
1
)
1
(
2
ln
1
1
+
−
+
−
=
−
=
∞
=
−
k
k
k
.
Przykład 8
°
...
1
1
1
6
4
2
2
+
−
+
−
=
+
x
x
x
x
Jest to szereg geometryczny (o ilorazie
2
x
−
) zbie ny dla
1
|
|
<
x
.
Jest zbie ny warunkowo (kryterium Leibniza) dla
1
=
x
. Zatem
...
1
1
1
)
(
6
4
2
2
+
−
+
−
=
+
=
x
x
x
x
x
dx
d
arctg
.
Dlatego
...
7
5
3
7
5
3
+
−
+
−
=
x
x
x
x
x
arctg
a nast pnie (dla
1
=
x
)
...
7
1
5
1
3
1
1
1
4
+
−
+
−
=
=
π
arctg
52
Szeregi trygonometryczne
Szereg postaci
∞
=
+
+
1
0
2
1
)
sin
cos
(
n
n
n
nx
b
nx
a
a
nazywa si szeregiem trygonometrycznym.
Je li f jest dowoln funkcj całkowaln w przedziale
]
,
[
π
π
−
, za współczynniki s obliczone na podstawie wzorów
π
π
−
π
=
dx
x
f
a
)
(
1
0
,
π
π
−
π
⋅
=
dx
nx
x
f
a
n
cos
)
(
1
,
π
π
−
π
⋅
=
dx
nx
x
f
b
n
sin
)
(
1
, to szereg
∞
=
+
+
1
0
2
1
)
sin
cos
(
~
)
(
n
n
n
nx
b
nx
a
a
x
f
Stanisław Kowalski: Wykłady z matematyki –
Całka oznaczona
– wykład 10 i 11
117
nazywa si szeregiem Fouriera
1
funkcji f.
Podamy jeden z warunków wystarczaj cych na to, aby szereg Fouriera funkcji f był zbie ny do f.
Je li funkcja
R
f
→
π
π
−
]
,
[
:
jest klasy
1
C na zbiorze
}
,
...,
,
,
,
{
\
]
,
[
2
1
π
π
−
π
π
−
n
x
x
x
,
}
...
2
1
π
<
<
<
<
<
π
−
n
x
x
x
, i ma
pochodn ograniczon , to w ka dym punkcie
}
,
...,
,
,
,
{
\
]
,
[
2
1
π
π
−
π
π
−
∈
n
x
x
x
x
szereg Fouriera funkcji f jest zbie ny do
)
(x
f
.
Przykład 1.
π
≤
<
<
<
π
−
−
=
.
0
1
,
0
)
(
2
1
x
x
x
f
dla
dla
Znajdujemy współczynniki szeregu Fouriera:
2
1
0
1
0
2
1
1
1
0
)
(
=
+
−
=
=
π
π
π
−
π
π
π
−
π
dx
dx
dx
x
f
a
;
0
cos
cos
cos
)
(
0
1
0
2
1
1
1
=
+
⋅
−
=
⋅
=
π
π
π
−
π
π
π
−
π
dx
nx
dx
nx
dx
nx
x
f
a
n
;
=
−
=
+
⋅
−
=
⋅
=
π
π
−
π
π
π
π
−
π
π
π
−
π
0
0
1
0
1
0
2
1
1
1
cos
2
cos
sin
sin
sin
)
(
n
nx
n
nx
dx
nx
dx
nx
dx
nx
x
f
b
n
−
=
−
π
=
=
−
−
π
=
π
−
=
+
π
−
π
−
=
π
π
1
2
)
1
2
(
3
2
0
]
)
1
(
1
[
2
3
2
cos
3
2
3
1
cos
2
cos
2
1
1
1
k
n
k
k
n
n
n
n
n
n
n
n
n
n
n
n
dla
dla
Dlatego
∞
=
+
π
π
+
+
=
+
+
+
+
0
1
2
1
3
4
1
5
1
3
1
3
4
1
)
1
2
sin(
...)
5
sin
3
sin
(sin
~
)
(
k
k
x
k
x
x
x
x
f
Przykład 2.
π
<
<
<
<
π
−
−
=
.
0
1
,
0
1
)
(
x
x
x
f
dla
dla
∞
=
+
π
π
+
=
+
+
+
0
1
2
1
4
5
1
3
1
4
)
1
2
sin(
...)
5
sin
3
sin
(sin
~
)
(
k
k
x
k
x
x
x
x
f
Przykład 3.
π
≤
≤
<
<
π
−
=
.
0
sin
,
0
0
)
(
x
x
x
x
f
dla
dla
∞
=
π
π
π
π
+
−
+
=
+
+
+
−
+
1
2
2
2
1
1
37
1
17
1
5
1
2
2
1
1
1
4
)
2
cos(
sin
...)
6
cos
4
cos
2
cos
(
sin
~
)
(
k
k
kx
x
x
x
x
x
x
f
Przykład 4.
|
|
)
(
x
x
f
=
∞
=
π
π
π
π
−
−
−
=
+
+
+
−
1
2
4
2
25
1
9
1
4
2
)
1
2
(
)
1
2
cos(
...)
5
cos
3
cos
(cos
~
)
(
k
k
x
k
x
x
x
x
f
1
J. Fourier – matematyk i fizyk francuski (1768 – 1830).
Wyszukiwarka
Podobne podstrony:
11 Wyklad OiSEid 12264 Nieznany (2)
c4 10 11 2011 id 97239 Nieznany
Algebra 10 10 11 Wyklad
zagadnienia, punkt 11, XI Całka oznaczona funkcji ograniczonej na [a,b]
PODSTAWY ZARZĄDZNIA 1,2,3,4,5,6,7,8,9,10,11 WYKŁADY
20 10 11 wykład 3
Instrukcja H, Poniedziałek - Materiały wiążące i betony, 06. (10.11.2011) Ćw H - Oznaczenie składu f
27 10 11 wykład 4
24 10 11 wykład 4
20 10 11 wykład 3
13 10 11 wyklad 2
27 10 11 wykład 4
Psychologia społeczna wykład$ 10 11
mat bud cwicz 10 11 id 282450 Nieznany
calka oznaczona Wronicz id 1079 Nieznany
więcej podobnych podstron