- 1 -
11. CHARAKTERYSTYKI CZASOWE UKŁADÓW SLS
11.1. WPROWADZENIE
A) SPLOT FUNKCJI
Niech dane będą dwie funkcje f
1
(t) i f
2
(t) całkowalne w każdym prze-
dziale (t
1
,t
2
), 0
≤t
1
≤t
2
<∞, wówczas splotem tych funkcji nazywać będziemy
funkcję q(t) określoną dla t
≥0 w sposób następujący
( )
( )
( ) (
)
τ
τ
τ
d
t
f
f
t
f
t
f
t
q
t
∫
−
=
=
0
2
1
2
1
*
)
(
(11.1)
Operację tworzenia splotu nazywamy splataniem funkcji f
1
(t) i f
2
(t) lub
ich mnożeniem splotowym.
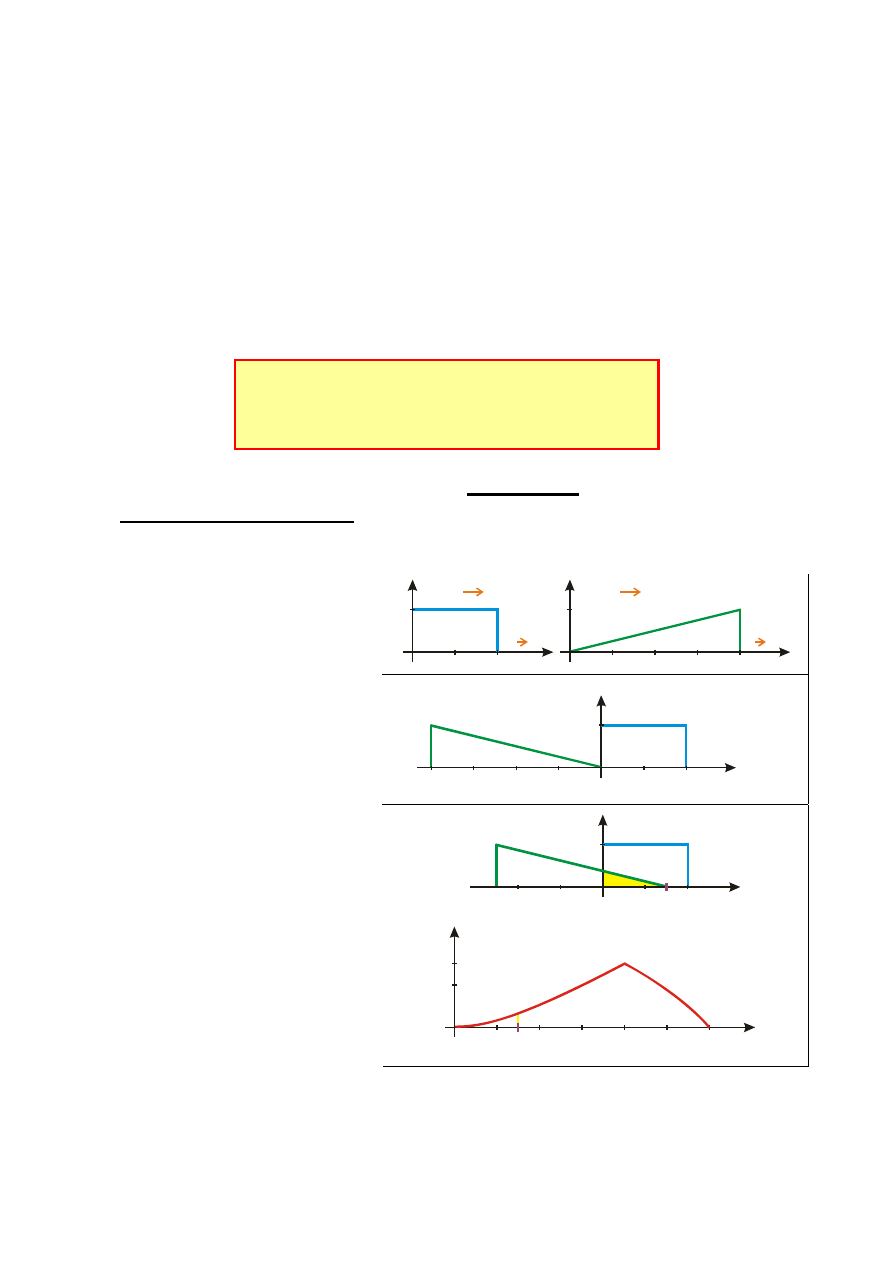
Interpretacja graficzna splotu
Rozpatrzmy funkcje f
1
(t) i f
2
(t)
- w pierwszym etapie wykreśla-
my funkcje f
1
(
τ) i f
2
(
τ) przyjmu-
jąc
τ za zmienną całkowania
1
2
1
f (t)
1
t
1
2
1
f (t)
2
3
4
f ( )
1
τ
f ( )
2
τ
τ
t
τ
W etapie drugim tworzymy
lustrzane odbicie f
2
(-
τ) funkcji
f
2
(
τ)
1
2
1
f ( )
1
τ
τ
f (- )
2
τ
-1
-2
-3
-4
1
2
1
f ( )
1
τ
τ
f (t - )
2 1
τ
-1
-2
t
1
Następnie przesuwamy funk-
cję f
2
(-
τ) wzdłuż osi τ o pewną
wartość, przyjmijmy t
1
– w efek-
cie uzyskujemy funkcję f
2
(t
1
-
τ).
Całkujemy iloczyn funkcji
f
1
(
τ)⋅f
2
(t
1
-
τ) ze względu na τ - jest
to pole pod krzywą wypadkową
funkcji f
1
(
τ) i f
2
(t
1
-
τ). Wartość
splotu f
1
(t)
∗f
2
(t) w chwili t=t
1
jest
równa temu polu powierzchni.
1
2
1
f (t)*f (t)
1
2
t
3
4
t
1
5
6
1,5
- 2 -
Własności splotu:
własność 1 - splatanie funkcji jest przemienne:
( )
( )
( )
( )
( ) (
)
(
) ( )
τ
τ
τ
τ
τ
τ
d
f
t
f
d
t
f
f
t
f
*
t
f
t
f
*
t
f
t
0
2
1
t
0
2
1
1
2
2
1
∫
∫
−
=
−
=
=
(11.2)
własność 2 - splatanie funkcji jest łączne:
( )
( )
( )
( )
( )
( )
[
]
( )
( )
[
]
( )
t
f
*
t
f
*
t
f
t
f
*
t
f
*
t
f
t
f
*
t
f
*
t
f
3
2
1
3
2
1
3
2
1
=
=
(11.3)
własność 3 - splatanie funkcji jest rozdzielne względem dodawania:
( )
( )
[
]
( )
( )
( )
( )
( )
t
f
*
t
f
t
f
*
t
f
t
f
*
t
f
t
f
3
2
3
1
3
2
1
+
=
+
(11.4)
splot funkcji f(t) z funkcją jednostkową 1(t)
( )
( )
τ
τ
d
f
1
*
t
f
t
0
∫
=
(11.5)
Zatem mnożenie splotowe funkcji f(t) przez funkcję jednostkową 1(t) jest równoznacz-
ne z całkowaniem funkcji f(t) w przedziale (0,t)
splot funkcji f(t) z funkcją impulsową Diraca
δ(t)
Na podstawie definicji
( ) ( ) ( ) ( )
( ) (
)
τ
τ
τ
δ
δ
δ
d
t
f
t
f
*
t
t
*
t
f
∫
∞
∞
−
−
=
=
Ponieważ
δ(t) istnieje tylko przy τ=0 - co oznacza, że należy brać pod uwagę wartość
funkcji f(t-
τ) tylko w punkcie τ=0, a więc f(t-τ) może być zastąpiona przez f(t). Za-
tem
( ) ( )
( ) ( )
( ) ( )
( )
1
t
f
d
t
f
d
t
f
t
*
t
f
⋅
=
=
=
∫
∫
∞
∞
−
∞
∞
−
τ
τ
δ
τ
τ
δ
δ
stąd
( ) ( )
( )
t
f
t
*
t
f
=
δ
(11.6a)
Ponadto
( ) (
)
(
)
0
0
t
t
f
t
t
*
t
f
−
=
−
δ
(11.6b)
- 3 -
B) TWIERDZENIE BORELA O SPLOCIE
Jedną z najważniejszych właściwości przekształcenia Laplace’a jest
twierdzenie o splocie tzw. twierdzenie Borela:
( )
( )
[
]
( ) ( )
s
F
s
F
t
f
t
f
2
1
2
1
*
⋅
=
L
(11.7a)
lub
( ) ( )
[
]
( )
( )
t
f
t
f
s
F
s
F
2
1
2
1
1
*
=
⋅
−
L
(11.7b)
gdzie:
( )
( )
[
]
( )
( )
[
]
t
f
s
F
,
t
f
s
F
2
2
1
1
L
L
=
=
C) TWIERDZENIE O TRANSFORMACIE POCHODNEJ SPLOTU
Transformata Laplace’a pochodnej splotu
( )
( )
[
]
( ) ( )
s
F
s
F
s
t
f
*
t
f
t
d
d
2
1
2
1
=
⎥
⎦
⎤
⎢
⎣
⎡
L
(11.8a)
czyli
( ) ( )
[
]
( )
( )
[
]
t
f
*
t
f
t
d
d
s
F
s
F
s
2
1
2
1
1
=
−
L
(11.8b)
- 4 -
D) CAŁKA DUHAMELA
( )
( )
[
]
( ) (
)
τ
τ
τ
d
t
f
f
t
d
d
t
f
t
f
t
d
d
t
∫
−
=
0
2
1
2
1
*
(11.9)
wyrażenie to nazywamy całką Duhamela (całką superpozycji)
Zgodnie z twierdzeniem o różniczkowaniu całki względem parametru
(jeśli obie funkcje f
1
(t) i f
2
(t) mają ciągłe pochodne dla t>0) napiszemy
( )
( )
[
]
=
t
f
t
f
t
d
d
2
1
*
( ) (
)
( )
( )
( ) (
)
τ
τ
τ
τ
τ
τ
d
t
f
f
f
t
f
d
t
f
f
t
d
d
t
t
∫
∫
−
+
=
−
=
+
0
'
2
1
2
1
0
2
1
0
(11.10a)
(
) ( )
( )
( )
(
) ( )
τ
τ
τ
τ
τ
τ
d
f
t
f
t
f
f
d
f
t
f
t
d
d
t
t
∫
∫
−
+
=
−
=
+
0
2
'
1
2
1
0
2
1
0
(11.10b)
a korzystając z przemienności splotu otrzymamy pozostałe postacie całki
Duhamela
( )
( )
[
]
( )
( )
(
) ( )
τ
τ
τ
d
f
t
f
0
f
t
f
t
f
*
t
f
t
d
d
t
0
'
2
1
2
1
2
1
∫
−
+
=
+
(11.10c)
( )
( )
[
]
( )
( )
( ) (
)
τ
τ
τ
d
t
f
f
t
f
0
f
t
f
*
t
f
t
d
d
t
0
2
'
1
2
1
2
1
∫
−
+
=
+
(11.10d)
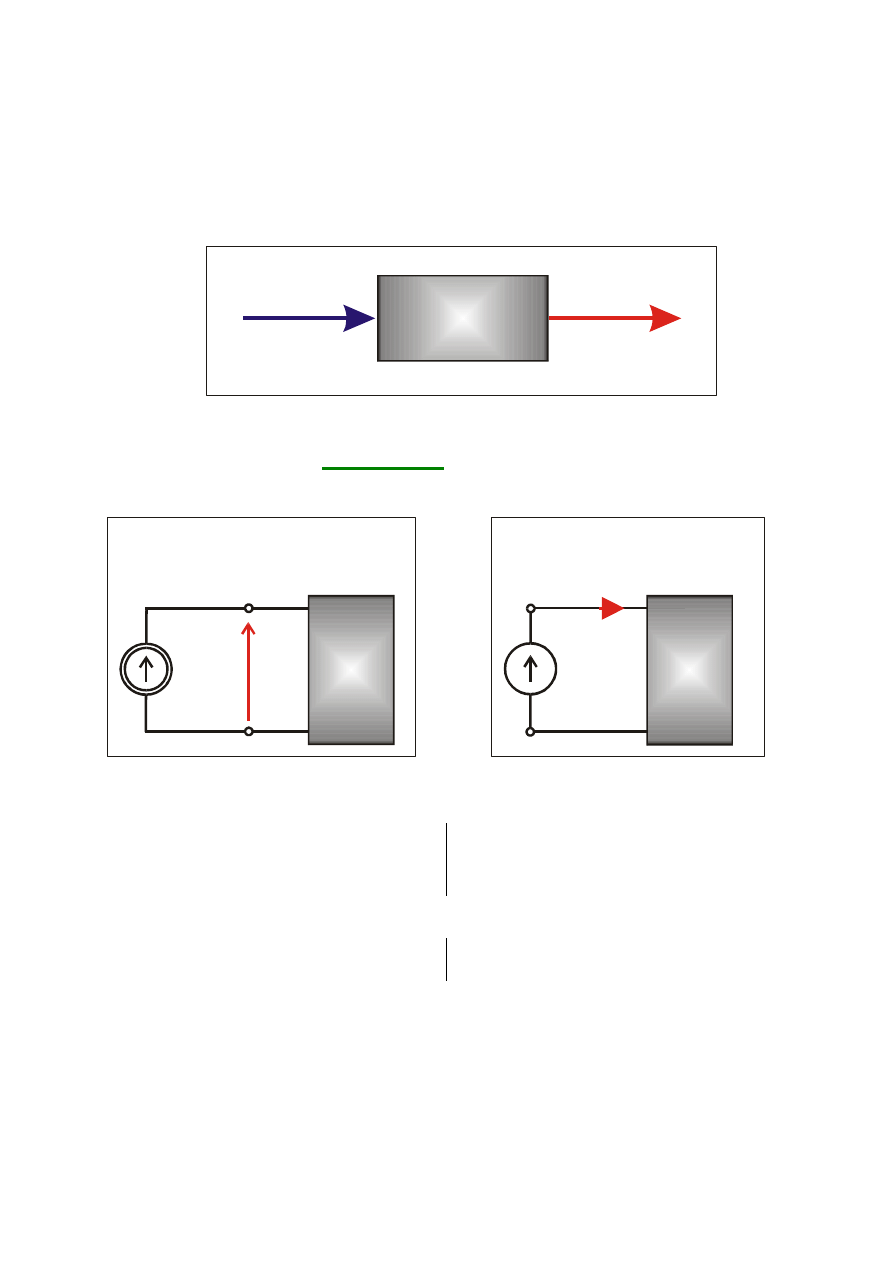
- 5 -
11.2. OPERATOROWE FUNKCJE UKŁADU
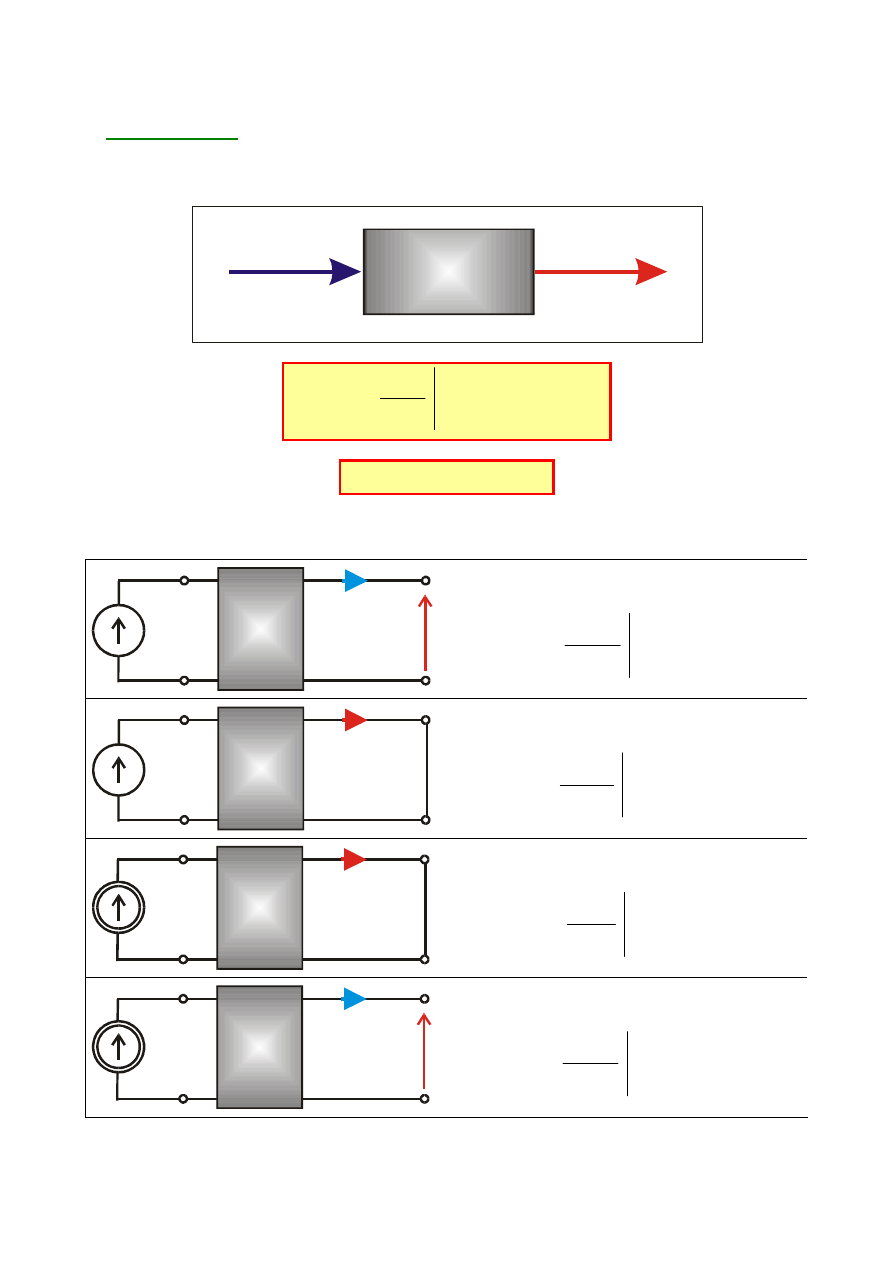
Rozpatrzmy układ elektryczny, na który działa wymuszenie przyczy-
nowe f(t) (napięciowe lub prądowe) i dla którego poszukiwaną funkcją jest
odpowiedź r(t) (prądowa lub napięciowa).
f t
( )
r t
( )
układ
SLS
Jeśli wielkości f(t) i r(t) występują na tych samych zaciskach to rozpa-
trywany układ staje się
dwójnikiem
. Jego stan opisany jest parą funkcji:
prądu wejściowego i napięcia
I (s)
Z
i (t)=f(t)
Z
U(s)
u(t)=r(t)
Z(s)
a)
b)
u (t)=f(t)
0
U (s)
0
I(s)
i(t)=r(t)
Y(s)
W zależności od wymuszenia odpowiedź wyznaczamy ze wzoru
( )
( ) ( )
s
I
s
Z
s
U
Z
=
(11.11a)
( ) ( ) ( )
s
U
s
Y
s
I
0
=
(11.11b)
gdzie:
Z(s) – operatorowa IMpedancja
Y(s) – operatorowa adMITANCJA
Dla obu tych funkcji układu spełniających związek
( ) ( )
1
s
Z
s
Y
=
(11.12)
stosujemy określenie :
operatorowa IMMITANCJA
- 6 -
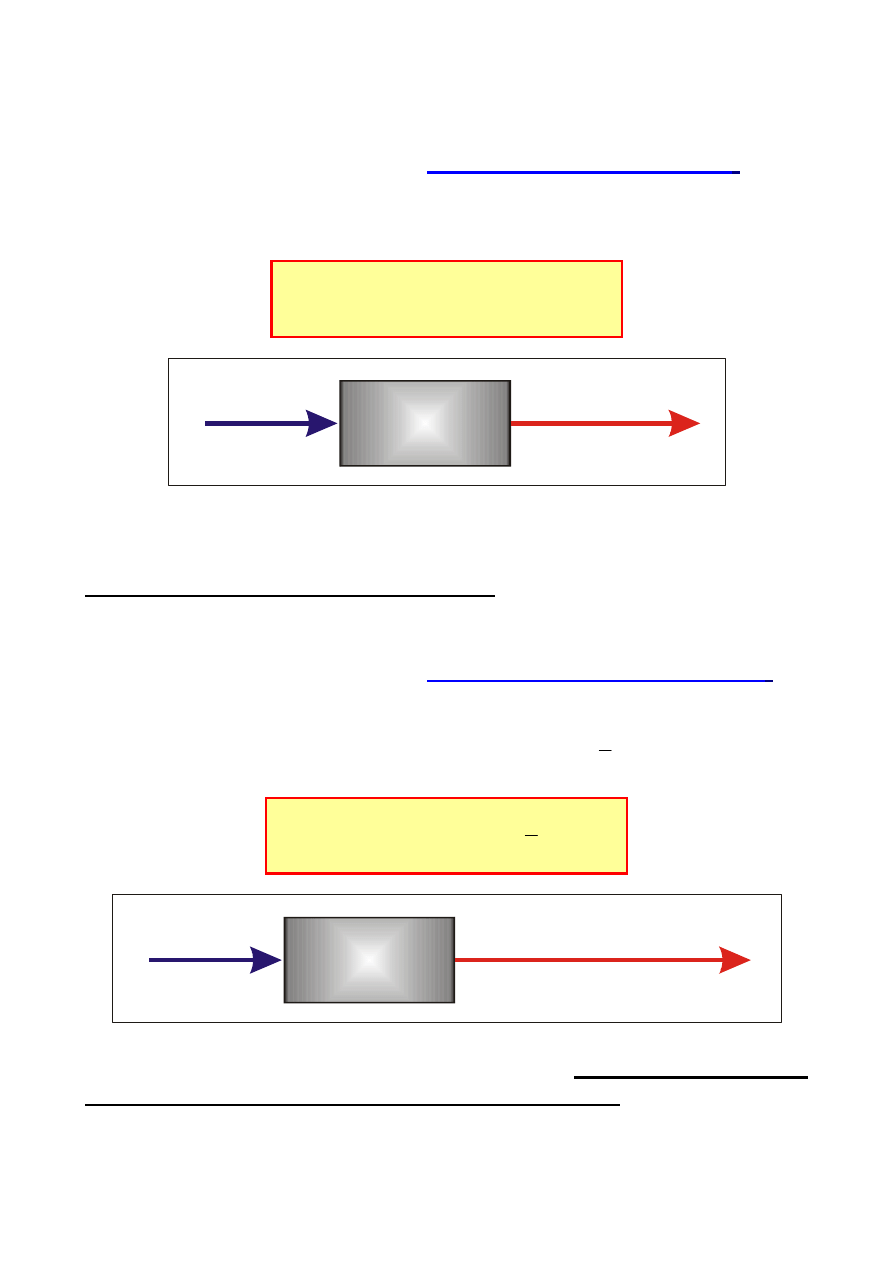
W przypadku wyodrębnienia dwóch par zacisków mamy do czynienia
z
czwórnikiem
. Jeśli wymuszenie jest związane z jedną bramą a odpo-
wiedź z drugą to relacje pomiędzy nimi - stosunek odpowiedzi do wymu-
szenia nazywamy
TRANSMITANCJĄ operatorową
.
F s
( )
R(s)
K(s)
( )
( )
( )
.
P
.
W
zerowych
przy
s
F
s
R
s
K
=
(11.13)
czyli
( )
( ) ( )
s
F
s
K
s
R
=
(11.14)
Wyróżniamy operatorową:
K (s)
u
I (s)=0
2
U (s)
2
U (s)
1
transmitancję napięciową
( )
( )
( )
( )
0
s
I
1
2
u
2
s
U
s
U
s
K
=
=
(11.15a)
K (s)
iu
I (s)=0
2
U (s)=0
2
U (s)
1
transmitancję prądowo-napięciową
( )
( )
( )
( )
0
s
U
1
2
u
i
2
s
U
s
I
s
K
=
=
(11.15b)
K (s)
i
I (s)
2
I (s)
1
U (s)=0
2
transmitancję prądową
( )
( )
( )
( )
0
s
U
1
2
i
2
s
I
s
I
s
K
=
=
(11.15c)
K (s)
ui
I (s)=0
2
U (s)
2
I (s)
1
transmitancję napięciowo-prądową
( )
( )
( )
( )
0
s
I
1
2
i
u
2
s
I
s
U
s
K
=
=
(11.15d)
- 7 -
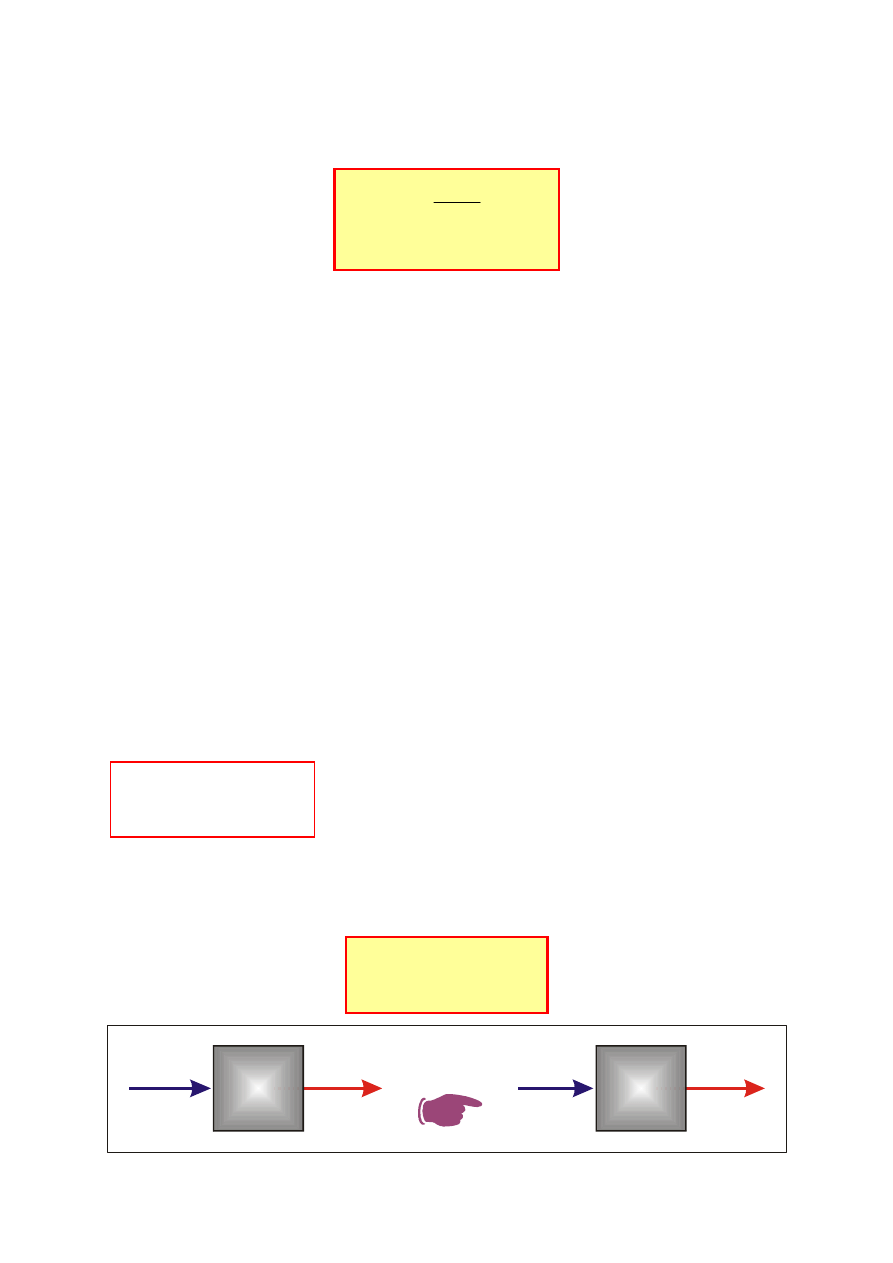
Rozpatrzmy dwa szczególne przypadki funkcji wymuszającej f(t)
①
Gdy funkcją wymuszającą jest
funkcja impulsowa Diraca
δ(t
)
Czyli
( ) ( )
( )
[ ]
( )
1
=
=
→
=
s
F
t
t
t
f
δ
δ
L
wówczas
( )
( ) ( )
( )
( )
s
K
s
K
s
F
s
K
s
R
=
=
=
1
(11.16)
F s
( )=1
R(s)=K(s)
K(s)
Oznacza to, że funkcja transmitancji K(s) jest tożsama z operatorową
odpowiedzią układu na wymuszenie impulsowe. Można zatem nazwać ją
operatorową funkcją impulsową układu.
②
Gdy funkcją wymuszającą jest
funkcja skoku jednostkowego 1(t
)
Czyli
( ) ( )
( )
[ ]
( )
s
s
F
t
t
t
f
1
1
1
=
=
→
=
L
wówczas
( )
( ) ( )
( )
( )
s
H
s
s
K
s
F
s
K
s
R
=
=
=
1
(11.17)
F s
( )=1/s
R(s)=K(s)/s=H(s)
K(s)
Tę szczególną odpowiedź H(s) nazywamy operatorową odpowie-
dzią układu na wymuszenie skokiem jednostkowym.
- 8 -
Zatem relacje pomiędzy operatorową funkcją impulsową układu K(s)
i operatorową odpowiedzią układu na wymuszenie skokiem jednostkowym
H(s) są następujące:
( )
( )
( )
( )
⎪⎭
⎪
⎬
⎫
=
=
s
H
s
s
K
s
s
K
s
H
(11.18)
Znajomość jednej z tych funkcji pozwala łatwo określić drugą.
11.3. CHARAKTERYSTYKI CZASOWE
Czasową charakterystykę układu o określonym wejściu i
wyjściu stanowi przebieg sygnału wyjściowego, gdy na wej-
ściu działa wymuszenie będące sygnałem wzorcowym.
Najczęściej używanymi sygnałami wzorcowymi w procesach bada-
nia układów są:
①
sygnał impulsowy
δ(t)
②
sygnał skoku jednostkowego 1(t)
______________________________
Rozpatrzmy ponownie zależność (11.14)
( )
( ) ( )
s
F
s
K
s
R
=
gdzie:
F(s) =
L
[
f(t)] – jest transformatą wymuszenia
K(s) =
L
[
k(t)] – jest transmitancją operatorową
Zatem zgodnie z twierdzeniem Borela (11.7b) oryginał odpowiedzi
r(t) określony jest funkcją splotu
( ) ( ) ( )
t
f
t
k
t
r
*
=
(11.19)
F s
( )
R(s)
K(s)
f(t)
r(t)
*k(t)
L
-1
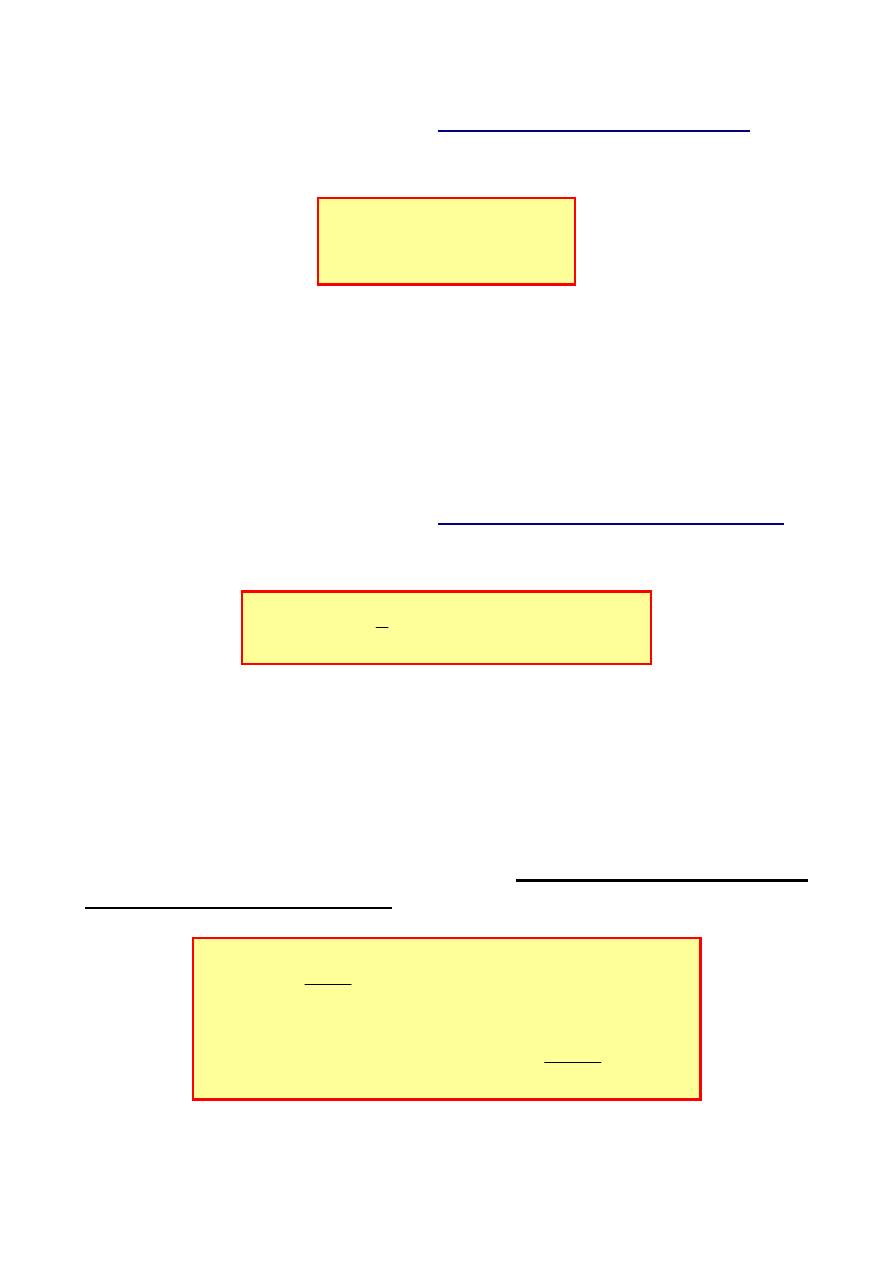
- 9 -
①
Jeśli
sygnałem wzorcowym
jest
funkcja impulsowa Diraca
δ(t)
to zgodnie z (11.19) i (11.16)
( ) ( ) ( ) ( )
( )
( )
[
]
( )
t
k
s
K
t
r
t
k
t
t
k
t
r
=
=
=
=
−1
*
L
δ
(11.20)
zatem
k(t)
– zwana
CHARAKTERYSTYKĄ IMPULSOWĄ UKŁADU
(
funkcją/charakterystyką impulsową)
jest tożsama z odpowiedzią układu na wymuszenie impulsem
Diraca.
②
Jeśli
sygnałem wzorcowym
jest
funkcja skoku jednostkowego 1(t)
to zgodnie z (11.17)
( )
( )
( )
[
]
( )
t
h
s
H
s
K
s
t
r
=
=
⎥⎦
⎤
⎢⎣
⎡
=
−
−
1
1
1
L
L
(11.21)
zatem
h(t)
– zwana
CHARAKTERYSTYKĄ SKOKOWĄ UKŁADU
(funkcją/charakterystyką przejściową)
jest tożsama z odpowiedzią układu na wymuszenie skokiem
jednostkowym.
Z relacji (11.18) wynikają następujące związki pomiędzy charakte-
rystykami czasowymi układu:
( )
( )
( )
( )
( )
( )
( )
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
⎯
⎯ →
⎯
=
=
⎯
⎯ →
⎯
=
−
−
∫
t
d
t
h
d
t
k
s
H
s
s
K
d
k
t
h
s
s
K
s
H
t
1
1
0
)
(
L
L
τ
τ
(11.22)
- 10 -
Znając charakterystykę czasową układu r
s
(t) jako odpowiedź na
sygnał wzorcowy f
s
(t), możemy wyznaczyć odpowiedź układu na do-
wolny sygnał przyczynowy, korzystając z zależności
( )
( )
( ) ( )
⎥
⎦
⎤
⎢
⎣
⎡
=
−
s
F
s
F
s
R
t
r
s
s
1
L
(11.23)
♦
Mając
charakterystykę impulsową k(t)
można wyznaczyć odpo-
wiedź układu na dowolny sygnał przyczynowy f(t), korzystając z twier-
dzenia Borela (
11.7
) oraz definicji splotu (
11.1
) i jego własności (
11.2
):
( ) (
)
τ
τ
τ
d
t
f
k
t
r
t
∫
−
=
0
)
(
(11.24a)
(
) ( )
τ
τ
τ
d
f
t
k
t
r
t
∫
−
=
0
)
(
(11.24b)
♦
Mając
charakterystykę skokową h(t)
można wyznaczyć odpowiedź
układu na dowolny sygnał przyczynowy f(t), korzystając z twierdzenia o
transformacie pochodnej splotu (
11.8
) oraz całki Duhamela (
10.10
):
( ) ( ) ( )
( ) (
)
τ
τ
τ
d
t
f
h
f
t
h
t
r
t
∫
−
+
=
0
'
0
(11.25a)
( ) ( ) ( )
(
) ( )
τ
τ
τ
d
f
t
h
t
f
h
t
r
t
∫
−
+
=
0
'
0
(11.25b)
( ) ( ) ( )
(
) ( )
τ
τ
τ
d
f
t
h
f
t
h
t
r
t
∫
−
+
=
0
'
0
(11.25c)
( ) ( ) ( )
( ) (
)
τ
τ
τ
d
t
f
h
t
f
h
t
r
t
∫
−
+
=
0
'
0
(10.25d)
- 11 -
11.4. ZWIĄZKI MIĘDZY CHARAKTERYSTYKAMI
CZASOWYMI I CZĘSTOTLIWOŚCIOWYMI
WPROWADZENIE
Znajomość transmitancji bądź immitancji operatorowej układu pozwa-
la wyznaczyć charakterystykę częstotliwościową stanu ustalonego dla
układu klasy SLS, stabilnego, prawie we wszystkich punktach
ω∈(0.∞),
przez proste podstawienie s=j
ω. Zatem
( )
( )
ω
ω
j
s
s
K
j
K
=
=
(11.26)
Wykorzystując jednostronne przekształcenie Laplace’a (10.13) mo-
żemy powyższe równanie przekształcić w zależność słuszną dla
ω∈(0.∞)
( )
( )
( )
∫
∫
∞
−
=
∞
−
=
=
0
0
t
d
e
t
k
t
d
e
t
k
j
K
t
j
j
s
t
s
ϖ
ω
ω
(11.27)
Otrzymujemy zatem
jednostronne przekształcenie Fouriera
, które istnieje
wtedy i tylko wtedy, gdy
( )
∞
<
∫
∞
dt
t
k
0
Jak wiemy K(j
ω), czyli charakterystyka amplitudowo-fazowa, jest
wielkością zespoloną, którą możemy przedstawić w postaci algebraicznej
lub wykładniczej:
( )
( )
( )
( )
( )
ω
ω
ω
ω
ω
j
K
j
j
K
j
e
K
e
j
K
j
K
arg
arg
=
=
- 12 -
ZWIAZKI GRANICZNE CHARAKTERYSTYK
Twierdzenie o wartości początkowej i końcowej funkcji f(t):
- jeśli
( )
( )
[ ]
t
f
s
F
L
=
oraz istnieje granica
( )
( )
+
→
=
+
0
lim
0
f
t
f
t
, to
( )
( )
+
∞
→
= 0
lim
f
s
sF
s
(11.28)
- jeśli
( )
( )
[ ]
t
f
s
F
L
=
oraz istnieje granica
( )
( )
∞
=
∞
→
f
t
f
t
lim
, to
( )
( )
∞
=
→
f
s
sF
s
0
lim
(11.29)
Zatem jeśli operatorową funkcją układu jest transmitancja K(s) a cha-
rakterystyka impulsowa posiada skończone granice zarówno dla t
→0
+
jak i
t
→∞, to słuszne są związki
( ) ( )
( )
( )
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
∞
=
+
∞
→
→
0
lim
lim
0
k
s
K
s
k
s
K
s
s
s
(11.30)
Jeśli weźmiemy pod uwagę charakterystykę skokową (przejściową)
układu, to możemy zapisać przy założeniu, że h(t) posiada granice zarów-
no dla t
→0
+
jak i t
→∞ oraz uwzględniając zależności (11.18)
( )
( ) ( )
( )
( )
( )
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
=
∞
=
=
+
∞
→
∞
→
→
→
0
lim
lim
lim
lim
0
0
h
s
K
s
H
s
h
s
K
s
H
s
s
s
s
s
(11.31)
następnie uwzględniając wzór (11.26) otrzymujemy:
- 13 -
( )
( ) ( )
( )
( )
( )
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
=
∞
=
=
+
∞
→
=
∞
→
→
=
→
0
lim
lim
lim
lim
0
0
h
K
s
K
h
K
s
K
j
s
s
j
s
s
ω
ω
ω
ω
ω
ω
(11.32)
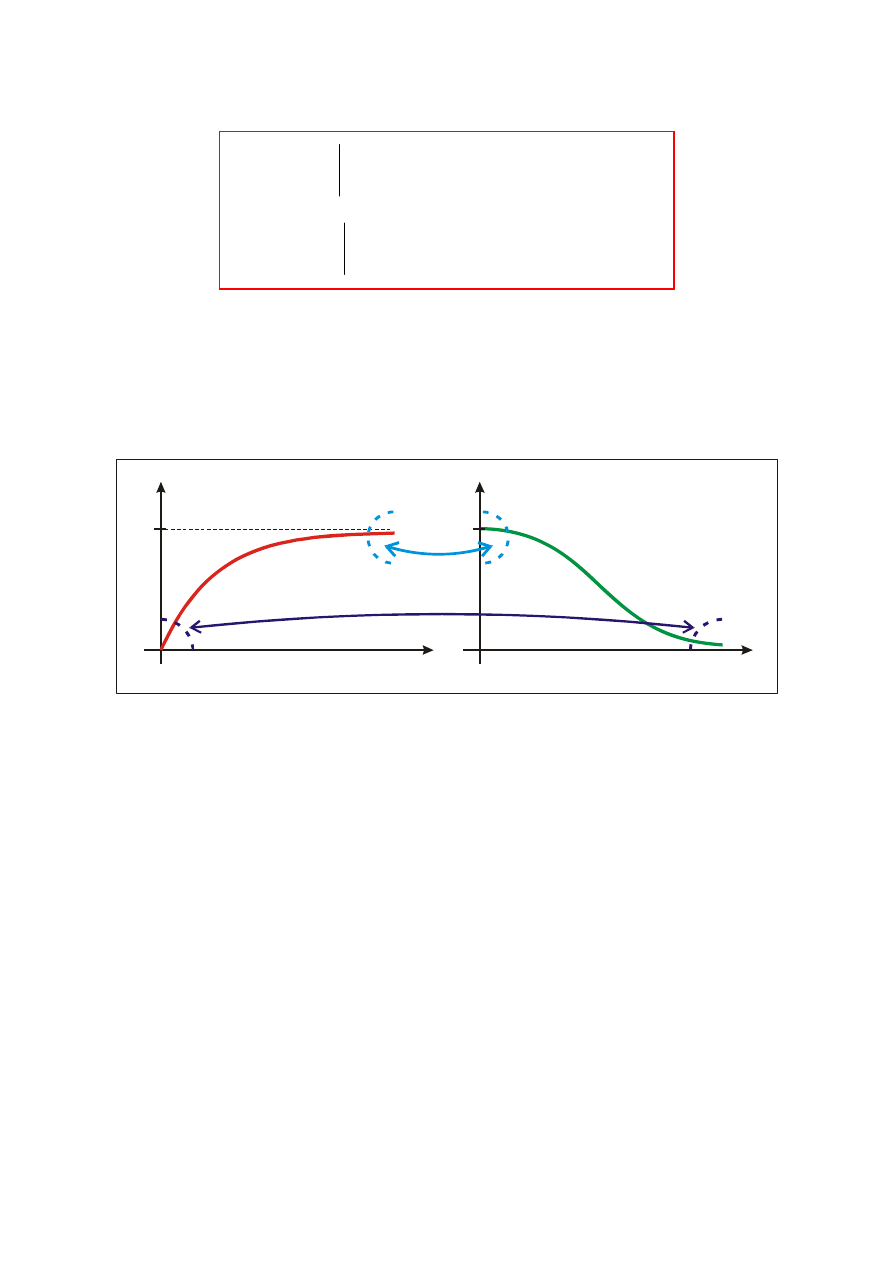
Są to związki o bardzo dużym znaczeniu praktycznym. Wynika z nich
jednoznacznie, że jeśli znamy np. charakterystykę amplitudową K(
ω), to
jej graniczne wartości określają jednoznacznie graniczne wartości funkcji
skokowej (przejściowej) h(t) i odwrotnie.
t
1
0
h(t)
ω
1
0
K( )
ω
ZWIĄZKI PARAMETRÓW CHARAKTERYSTYK
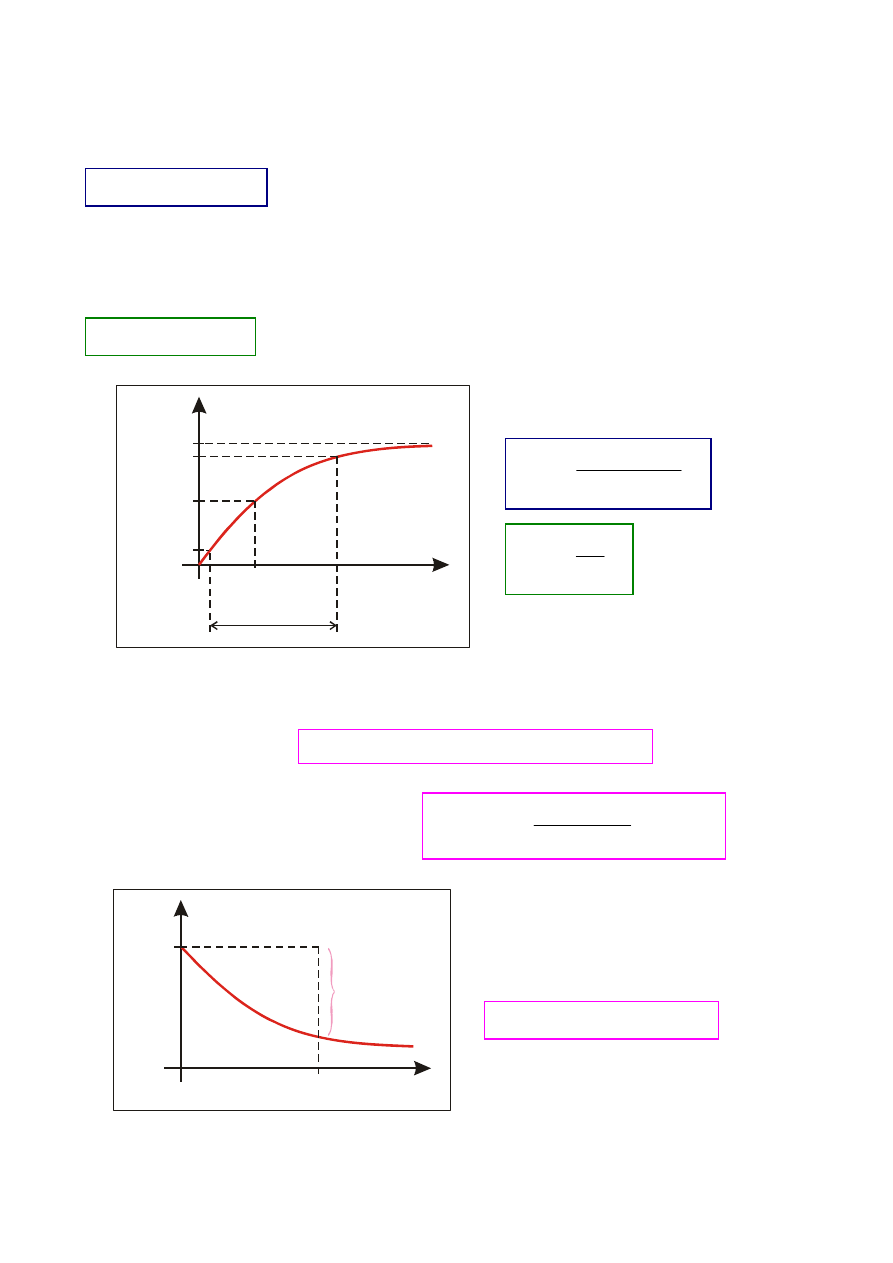
Jako podstawowe parametry charakterystyk czasowych przyjmuje się
między innymi:
t
n
– czas narastania,
t
o
– czas opóźnienia,
Z - zwis
- 14 -
Czas narastania t
n
- układu dolnoprzepustowego definiujemy jako czas
wzrostu charakterystyki skokowej (przejściowej)
układu od 0,1 do 0,9 wartości ustalonej
1
,
0
9
,
0
t
t
t
n
−
=
(11.33)
Czas opóźnienia t
o
- układu dolnoprzepustowego definiujemy jako czas
wzrostu charakterystyki skokowej (przejściowej)
układu od 0 do 0,5 wartości ustalonej
0
5
,
0
t
t
t
o
−
=
(11.34)
t
h =1
ust
0
h(t)
t
o
t
n
0,1
0,5
0,9
g
n
f
t
45
,
0
35
,
0
÷
=
(11.35)
g
o
f
t
1
,
0
=
(11.36)
Funkcję zwisu Z(t)
- układu górnoprzepustowego definiujemy:
( ) ( )
( ) ( ) ( )
t
h
h
t
h
t
h
t
Z
ust
−
=
−
=
0
(11.37)
lub funkcję zwisu w procentach
( ) ( ) ( )
( )
%
100
0
0
%
⋅
−
=
h
t
h
h
t
Z
(11.38)
t
h(0)
0
h(t)
t
i
Z(t
i
)
Dla małych wartości t
( )
t
f
t
Z
g
π
200
%
≈
(11.39)
- 15 -
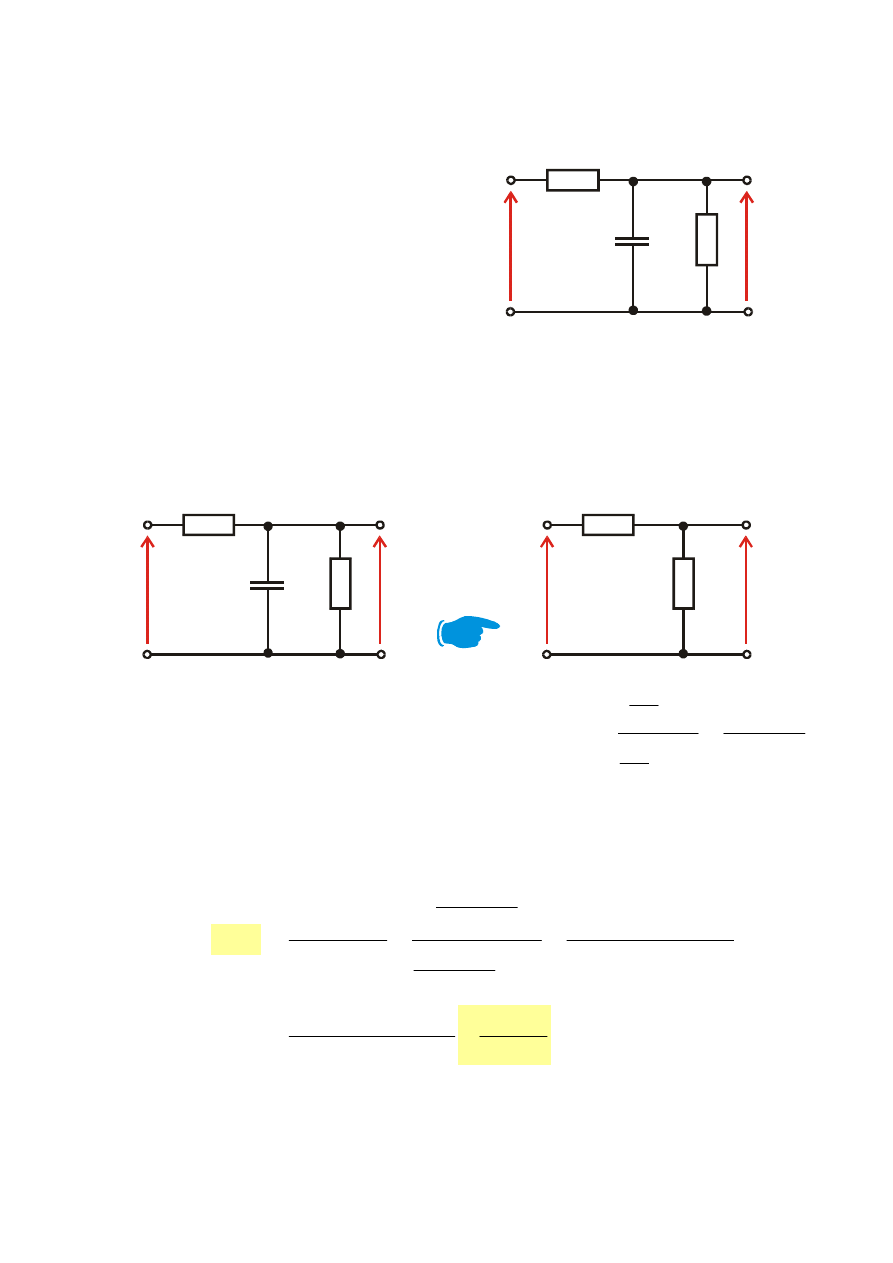
PRZYKŁAD
Dla układu przedstawionego na
rysunku, mając dane R
1
=9k
Ω,
R
2
=1k
Ω, C=1mF, wyznaczyć:
1. charakterystykę skokową,
2. czas narastania i opóźnienia,
3.
charakterystykę impulsową.
C
R
1
u
1
(t)
R
2
u
2
(t)
Ad.1.
• Podajemy skok jednostkowy na wejście układu i przedstawiamy
schemat operatorowy układu
1/sC
R
1
U
1
(s)
R
2
U
2
(s)
R
1
U
1
(s)
Z
2
(s)
U
2
(s)
gdzie:
( )
C
sR
R
R
sC
R
sC
s
Z
2
2
2
2
2
1
1
1
+
=
+
=
• Korzystając z dzielnika napięcia wyznaczamy operatorową funkcję
układu
( )
s
K
( )
( )
(
)
C
sR
R
R
R
R
C
sR
R
C
sR
R
R
s
Z
s
Z
2
1
2
2
1
2
2
2
2
1
2
2
1
1
1
+
+
=
+
+
+
=
+
=
C
R
sR
R
R
R
2
1
1
2
2
+
+
=
s
9
10
1
+
=
- 16 -
• Wyznaczamy operatorową odpowiedź układu na wymuszenie sko-
kiem jednostkowym (zależność 11.17)
( )
( )
(
)
s
s
s
s
s
s
K
s
H
9
10
1
9
10
1
+
=
+
=
=
UWAGA: znając H(s) możemy wyznaczyć (zal.11.31)
( )
( )
(
)
0
9
10
1
lim
9
10
1
lim
lim
0
=
+
=
+
=
=
∞
→
∞
→
∞
→
+
s
s
s
s
s
H
s
h
s
s
s
( )
( )
1
,
0
9
10
1
lim
lim
0
0
=
+
=
=
∞
→
→
s
s
H
s
h
s
s
• Wyznaczamy charakterystykę czasową skokową układu (zal.11.21)
( )
( )
[
]
(
)
⎥
⎦
⎤
⎢
⎣
⎡
+
=
=
−
−
s
s
s
H
t
h
9
10
1
1
1
L
L
(
)
a
s
s
1
+
1
−
L
→
(
)
t
a
e
1
a
1
−
−
Lp.9.
( )
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ +
=
⎥
⎦
⎤
⎢
⎣
⎡
+
=
−
−
−
9
10
1
9
1
9
10
9
1
10
9
1
1
1
1
s
s
s
s
s
s
t
h
L
L
L
( )
( )
1
1
1
9
10
1
9
1
9
10
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
− t
e
t
h
- 17 -
( )
( )
t
e
t
h
t
1
1
,
0
1
,
0
9
10
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
−
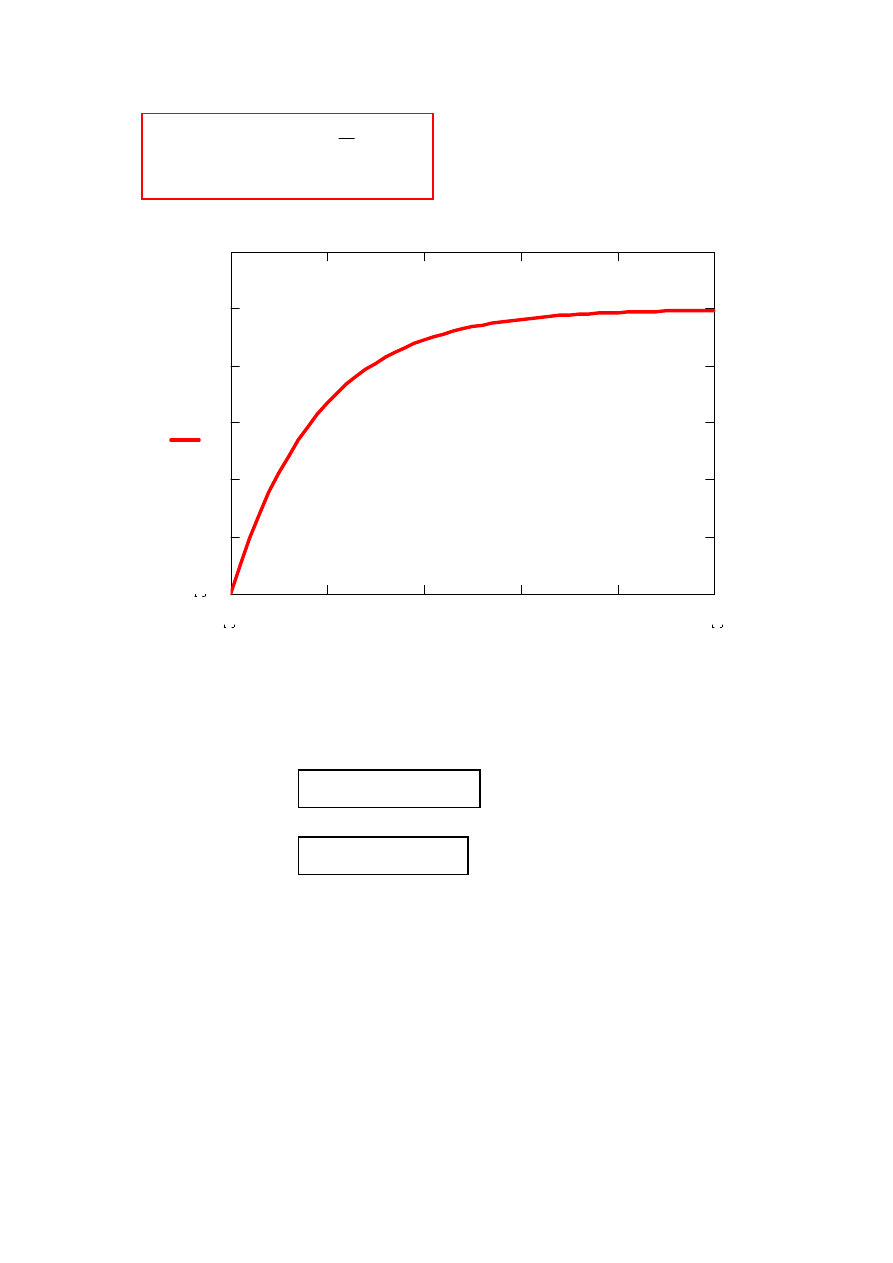
Ad.2.
Czas narastania t
n
-
1
,
0
9
,
0
t
t
t
n
−
=
Czas opóźnienia t
o
-
0
5
,
0
t
t
t
o
−
=
Wiemy już, że
( )
0
0
0
=
=
+
h
t
( )
1
,
0
=
∞
= h
t
ustal
0.12
0
h t
( )
5
0
t
0
1
2
3
4
5
0
0.02
0.04
0.06
0.08
0.1
- 18 -
( )
09
,
0
1
,
0
9
,
0
9
,
0
=
⋅
=
t
h
09
,
0
1
,
0
1
,
0
9
10
=
−
− t
e
1
,
0
09
,
0
1
,
0
9
10
−
=
−
− t
e
01
,
0
1
,
0
9
10
−
=
−
− t
e
1
,
0
9
10
=
− t
e
( )
1
,
0
ln
9
10 =
−
t
303
,
2
9
10
−
=
−
t
stąd:
073
,
2
9
,
0
=
t
( )
01
,
0
1
,
0
1
,
0
1
,
0
=
⋅
=
t
h
stąd:
095
,
0
1
,
0
=
t
czyli:
977
,
1
095
,
0
073
,
2
1
,
0
9
,
0
=
−
=
−
=
t
t
t
n
( )
05
,
0
1
,
0
5
,
0
5
,
0
=
⋅
=
t
h
stąd:
624
,
0
5
,
0
=
t
czyli:
624
,
0
0
624
,
0
0
5
,
0
=
−
=
−
=
t
t
t
o
- 19 -
Ad.3.
Sposób 1
Znając charakterystykę skokową, można wykorzystać zal. 11.22.
( )
( )
( )
( )
t
e
t
e
dt
d
t
d
t
h
d
t
k
t
t
1
9
10
1
,
0
1
1
,
0
1
,
0
9
10
9
10
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
=
−
−
( )
( )
t
e
t
k
t
1
9
1
9
10
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
Sposób 2
Znając operatorową funkcję układu
( )
s
s
K
9
10
1
+
=
wykorzystujemy zal.11.20:
( )
( )
[
]
( )
t
e
s
s
K
t
k
t
1
9
1
9
10
1
9
10
1
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎥⎦
⎤
⎢⎣
⎡
+
=
=
−
−
−
L
L
a
s
1
+
1
−
L
→
t
a
e
−
Lp.5.
0.12
0
k t
( )
5
0
t
0
1
2
3
4
5
0
0.02
0.04
0.06
0.08
0.1