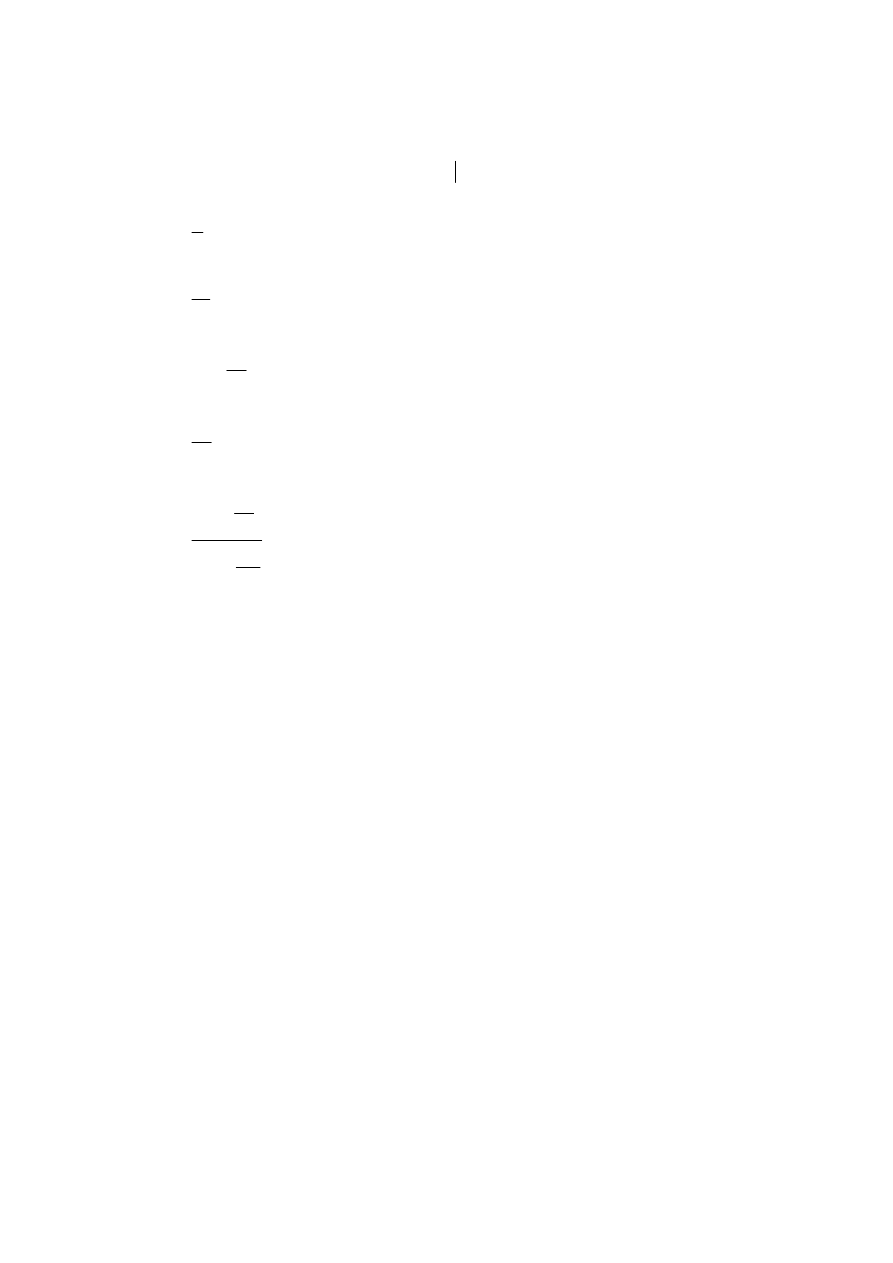
3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

1

Zadanie 1.

:\NRQXMHP\ NROHMQ\FK QLH]DOH*Q\FK U]XWyZ V\PHWU\F]Q PRQHW

Niech

n

S

R]QDF]D OLF]E RUáyZ RWU]\PDQ Z SRF]WNRZ\FK n rzutach.

3UDZGRSRGRELHVWZR ZDUXQNRZH

(

)

7

3

Pr

10

5

=

=

S

S

jest równe:

(A)

7

3

(B)

12

5

(C)

5

2

1

3

5

⋅









(D)

50

21

(E)

10

5

2

1

3

10

2

1

3

5

⋅









⋅









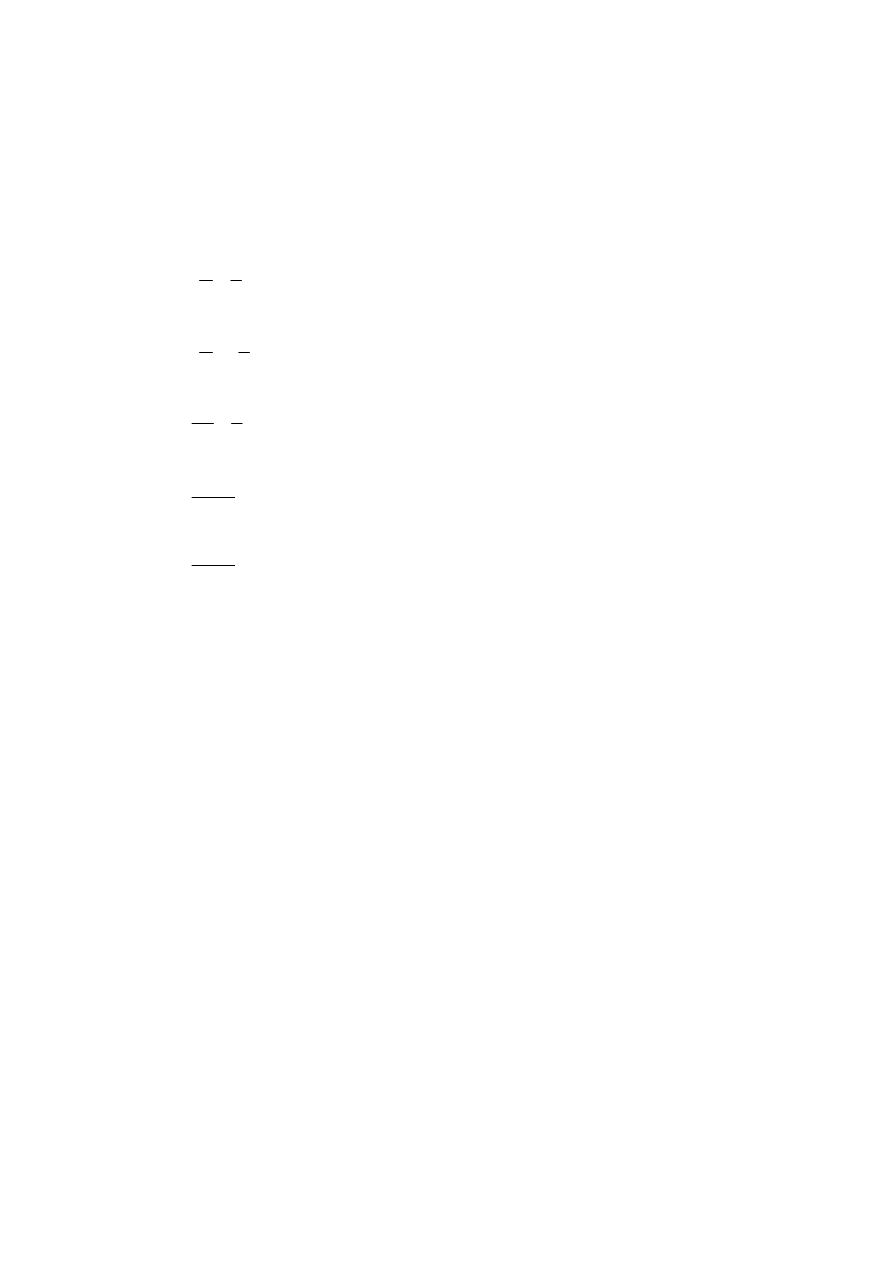
3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

2

Zadanie 2.

=Dáy*P\ *H ]PLHQQD ORVRZD X PD UR]NáDG Z\NáDGQLF]\ R JVWRFL







>

⋅

=

⋅

−

tym

poza

0

0

dla

)

(

x

e

x

f

x

X

λ

λ

Niech [x

@ R]QDF]D F]ü FDáNRZLW OLF]E\ x F]\OL QDMZLNV] OLF]E FDáNRZLW n WDN *H

x

n

≤

:DUWRü RF]HNLZDQD ]PLHQQHM ORVRZHM

[

]

5

.

0

+

=

X

N

Z\UD*D VL Z]RUHP

(C)







 +

2

1

1

λ

(D)

2

1

1

+









λ

(C)

[ ]

2

1

1

+

λ

(D)

1

5

.

0

−

⋅

λ

λ

e

e

(E)

1

1

−

λ

e

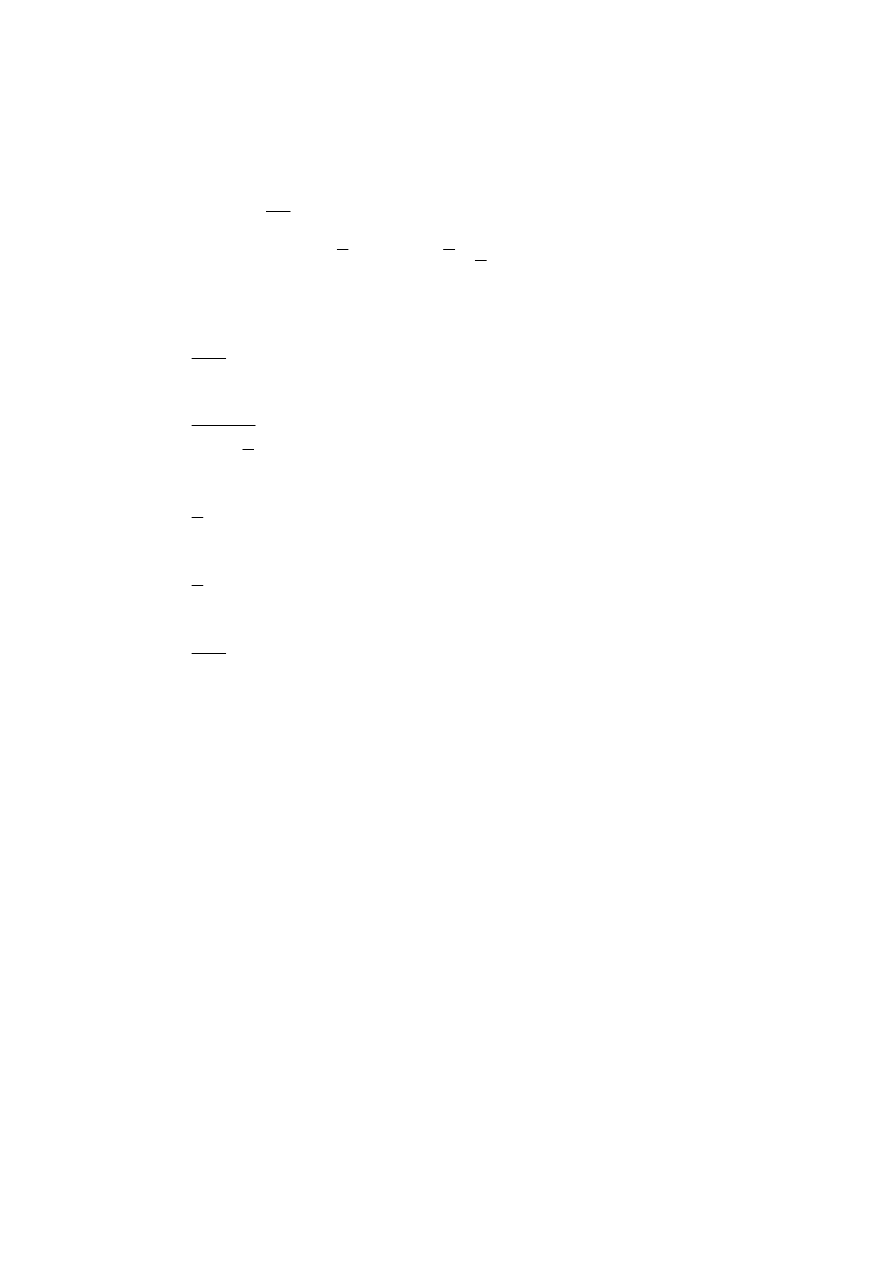
3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

3

Zadanie 3.

.D*GD ]H ]PLHQQ\FK ORVRZ\FK

n

X

X

X

,

,

,

2

1

PD WDN VDP ZDUWRü

RF]HNLZDQ

µ

:LDGRPR *H

(

)









≠

=

=

j

i

dla

j

i

dla

X

X

COV

j

i

2

,

2

2

σ

σ

Niech

( )

(

)

∑

=

−

⋅

=

n

i

i

X

X

c

c

S

1

2

2

, gdzie

∑

=

⋅

=

n

i

i

X

n

X

1

1

.

( )

c

S

2

MHVW QLHREFL*RQ\P HVW\PDWRUHP SDUDPHWUX

2

σ

MHOL c jest równe:

(A)

1

2

−

n

(B)

n

n

1

1

2

+

−

(C)

n

1

(D)

n

2

(E)

1

1

−

n

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

4

Zadanie 4. Zmienne losowe X i Y

V QLH]DOH*QH X PD UR]NáDG QRUPDOQ\ R ZDUWRFL

oczekiwanej 0 i wariancji 0.5. Y

PD UR]NáDG Z\NáDGQLF]\ R ZDUWRFL RF]HNLZDQHM

(

)

2

Pr

X

Y

>

wynosi:

(A)

2

1

(B)

π

2

1

(C)

π

e

(D)

e

1

(E)

2

2

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

5

Zadanie 5.

5R]ZD*P\ PRGHO UHJUHVML OLQLRZHM

i

i

i

x

a

Y

ε

+

⋅

=

,

,

4

,

3

,

2

,

1

=

i

gdzie

i

ε

V QLH]DOH*Q\PL ]PLHQQ\PL ORVRZ\PL R UR]NáDG]LH QRUPDOQ\P ] ZDUWRFL

RF]HNLZDQ L QLH]QDQ ZDULDQFM

2

σ

]D

4

3

2

1

,

,

,

x

x

x

x

V QLHORVRZ\PL SXQNWDPL ]

SU]HG]LDáX

[ ]

3

,

0

, natomiast a

MHVW QLH]QDQ\P ZVSyáF]\QQLNLHP :DULDQFMD HVW\PDWRUD

aˆ

RWU]\PDQHJR PHWRG QDMPQLHMV]\FK NZDGUDWyZ MHVW PLQLPDOQD MHOL

(

)

4

3

2

1

,

,

,

x

x

x

x

UyZQH V RGSRZLHGQLR

(A)

(

)

3

,

2

,

1

,

0

(B)

(

)

3

,

3

,

0

,

0

(C)

(

)

3

,

3

,

3

,

0

(D)

(

)

3

,

3

,

3

,

3

(E)













2

3

,

2

3

,

2

3

,

2

3

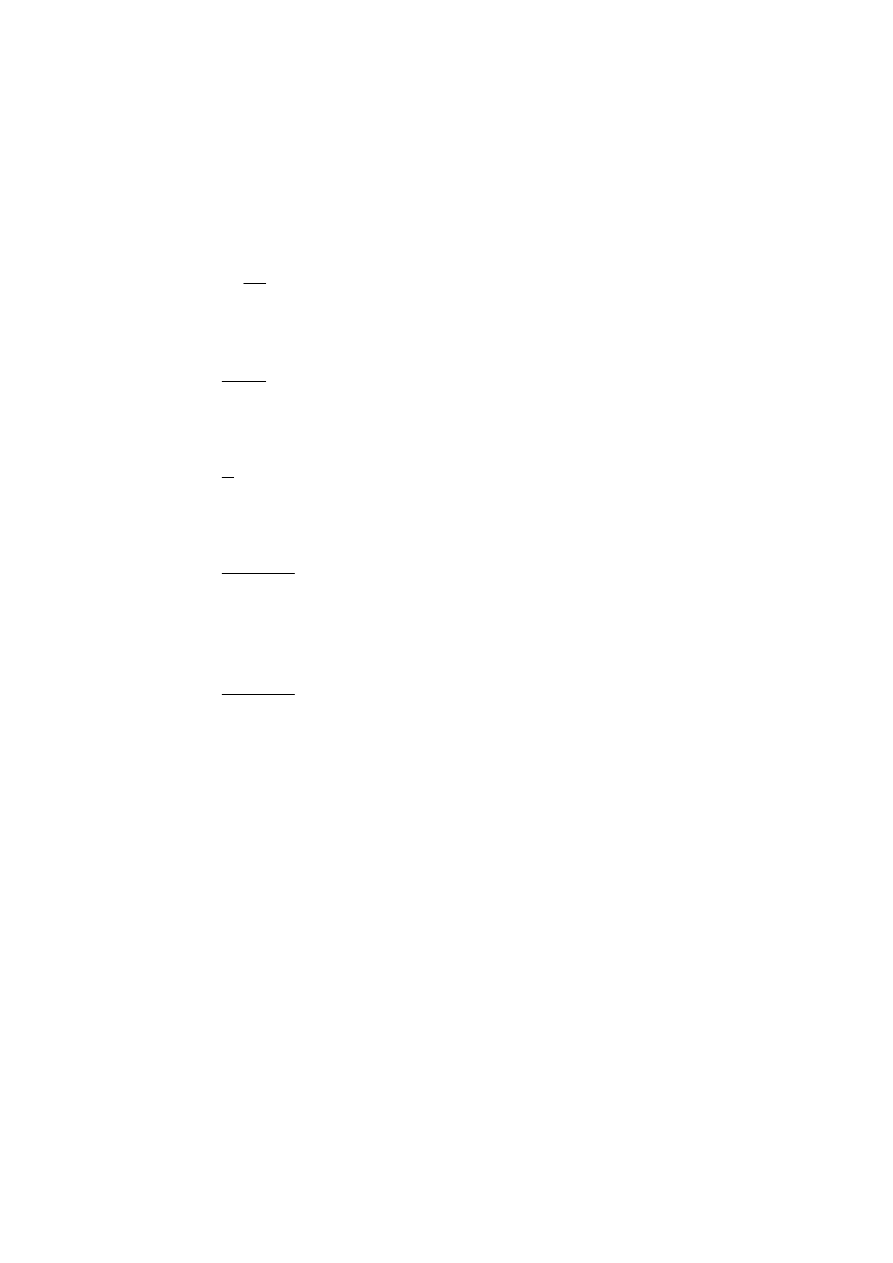
3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

6

Zadanie 6.

3U]\MPXMHP\ *H OLF]E\ Z\SDGNyZ

k

N

N

N

,

,

,

2

1

]JáRV]RQ\FK Z

kolejnych k

ODWDFK V QLH]DOH*Q\PL ]PLHQQ\PL ORVRZ\PL =DNáDGDP\ *H ]PLHQQD

i

N

PD UR]NáDG 3RLVVRQD ] ZDUWRFL RF]HNLZDQ UyZQ

i

m

⋅

λ

, gdzie

i

m

MHVW ]QDQ

OLF]E VDPRFKRGyZ XEH]SLHF]RQ\FK Z iW\P URNX ]D

λ

nieznanym parametrem.

(VW\PDWRU 1DMZLNV]HM :LDU\JRGQRFL

λ

ˆ parametru

λ

dany jest wzorem:

(A)

∑

=

=

k

i

i

i

m

N

1

ˆ

λ

(B)

∑

∑

=

=

=

k

i

i

k

i

i

m

N

1

1

ˆ

λ

(C)

∑

=

⋅

=

k

i

i

N

k

1

1

ˆ

λ

(D)

∑

∑

=

=

⋅

=

k

i

i

k

i

i

i

m

m

N

1

1

ˆ

λ

(E)

k

m

N

k

i

i

i

∑

=

⋅

=

1

ˆ

λ

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

7

Zadanie 7.

*VWRü ]PLHQQHM ORVRZHM X PD SRVWDü

R

x

e

x

f

x

∈

⋅

=

−

−

,

2

1

)

(

θ

θ

,

gdzie

θ

MHVW QLH]QDQ\P SDUDPHWUHP 5R]ZD*DP\ MHGQRVWDMQLH QDMPRFQLHMV]\ WHVW

hipotezy

0

:

0

=

θ

H

przeciw hipotezie alternatywnej:

0

:

1

>

θ

H

QD SR]LRPLH LVWRWQRFL

α

, gdzie

5

.

0

<

α

, oparty na pojedynczej obserwacji X.

Funkcja mocy tego testu

( )

θ

β

RVLJD ZDUWRü GOD

θ

równego:

(A)

α

ln

−

(B)

α

ln

4

3

ln

−

(C)











 ⋅

−

α

4

3

ln

(D)

4

ln

α

−

(E)

( )

α

⋅

−

2

ln

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

8

Zadanie 8. Niech

8

2

1

,

,

,

X

X

X

EG]LH SUyE ORVRZ ] UR]NáDGX QRUPDOQHJR ]

ZDUWRFL RF]HNLZDQ

θ

L ZDULDQFM 1LH]QDQ\ SDUDPHWU

θ

MHVW ] NROHL ]PLHQQ

ORVRZ R UR]NáDG]LH QRUPDOQ\P ] ZDUWRFL RF]HNLZDQ L ZDULDQFM 5R]ZD*DP\

%D\HV¶RZVNL SU]HG]LDá XIQRFL GOD SDUDPHWUX

θ

, to znaczy:

SU]HG]LDá

[ ]

b

a,

, gdzie

(

)

,

,

,

,

8

2

1

X

X

X

a

a

=

(

)

,

,

,

,

8

2

1

X

X

X

b

b

=

WDNL *H

(

)

(

)

8

2

1

8

2

1

,

,

,

Pr

05

.

0

,

,

,

Pr

X

X

X

b

X

X

X

a

>

=

=

<

θ

θ

.

-HOL SU]\MPLHP\ R]QDF]HQLH

∑

=

⋅

=

8

1

8

1

i

i

X

X

WR SU]HG]LDá

[ ]

b

a,

SU]\ELHUD SRVWDü

(A)

[

]

548

.

0

,

548

.

0

+

−

X

X

(B)

[

]

427

.

0

,

427

.

0

+

−

X

X

(C)









+

−

548

.

0

9

8

,

548

.

0

9

8

X

X

(D)









+

−

427

.

0

9

8

,

427

.

0

9

8

X

X

(E)

[

]

548

.

0

,

427

.

0

+

−

X

X

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

9

Zadanie 9.

àDFXFK 0DUNRZD PD SU]HVWU]H VWDQyZ

{

}

3

2

1

,

,

e

e

e

i macierz

SUDZGRSRGRELHVWZ SU]HMFLD





















2

1

3

1

6

1

0

1

0

3

1

3

1

3

1

.

=DNáDGDP\ *H Z FKZLOL áDFXFK ]QDMGXMH VL Z VWDQLH

1

e . Niech T

R]QDF]D FKZLO Z

NWyUHM áDFXFK SR UD] SLHUZV]\ ]QDMG]LH VL Z VWDQLH

2

e

:DUWRü RF]HNLZDQD ]PLHQQHM

losowej T wynosi:

(A)

1

(B)

2

(C)

3

(D)

∞

(E)

3

2

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

10

Zadanie 10.

( )

( )

( )

400

2

1

,

,

,

X

X

X

MHVW SUyE ORVRZ ] SHZQHJR UR]NáDGX FLJáHJR R

wariancji

2

σ

XVWDZLRQ Z SRU]GNX QLHPDOHMF\P W]Q WDN *H

( )

( )

( )

400

2

1

X

X

X

≤

≤

≤

. Niech m

EG]LH PHGLDQ UR]ZD*DQHJR UR]NáDGX 3U]\EOL*RQD

QD SRGVWDZLH &HQWUDOQHJR 7ZLHUG]HQLD *UDQLF]QHJR ZDUWRü

( )

(

)

m

X

≤

220

Pr

wynosi:

(A)

0.0149

(B)

0.0049

(C)

0.0532

(D)

0.0256

(E)













Φ

σ

20

, gdzie

Φ

MHVW G\VWU\EXDQW VWDQGDU\]RZDQHM ]PLHQQHM QRUPDOQHM

3UDZGRSRGRELHVWZR L VWDW\VW\ND

7.12.1996 r.

___________________________________________________________________________

11

Egzamin dla Aktuariuszy z 7 grudnia 1996 r.

3UDZGRSRGRELHVWZR L VWDW\VW\ND

Arkusz odpowiedzi

*

,PL L QD]ZLVNR ./8&= 2'32:,('=,

Pesel ...........................................

Zadanie nr

2GSRZLHG( Punktacja

♦

1

B

2

D

3

A

4

E

5

D

6

B

7

A

8

C

9

C

10

D

*

2FHQLDQH V Z\áF]QLH RGSRZLHG]L XPLHV]F]RQH Z Arkuszu odpowiedzi.

♦

:\SHáQLD .RPLVMD (J]DPLQDF\MQD