Metody probabilistyczne i statystyka
14 czerwca 2013
23:46
III+semestr Strona 1
Metody probabilistyczne i statystyka
14 czerwca 2013
23:46
III+semestr Strona 1
Definicja prawdopodobieństwa (aksjomatyczna).
1.
Definicja i własności dystrybuanty rozkładu prawdopodobieństwa.
2.
Sprawdzić, czy funkcja F(X)=1/Π(arctg(x)+1/2 Π) może być dystrybuantą rozkładu
prawdopodobieństwa.
3.
Definicja prawdopodobieństwa warunkowego.
4.
5.
6.
Udowodnić, że dla dowolnych dwóch zdarzeń P(A∪B)=P(A)+P(B) P(A∩B).
7.
Udowodnić, że: jeśli A⊂B, to P(A)≤P(B).
8.
Udowodnić, że dla każdego zdarzenia A prawdziwa jest nierówność P(A)≤1.
9.
Sformułować i udowodnić twierdzenie o prawdopodobieństwie zupełnym.
10.
Sformułować i udowodnić twierdzenie Bayesa.
11.
12.
Udowodnić, że P(a≤X<b)=P(X<b) P(X<a).
13.
14.
15.
16.
17.
Sformułować i udowodnić twierdzenie Poissona.
18.
19.
20.
21.
22.
23.
Zmienne losowe typu skokowego. Rozkład zmiennej losowej typu skokowego.
24.
Zmienne losowe typu ciągłego. Rozkład zmiennej losowej typu ciągłego.
25.
Twierdzenie Linderberga-Levy’ego
26.
27.
Definicja i własności estymatorów punktowych.
28.
Wyprowadzić wzór na estymator wartości oczekiwanej.
29.
Udowodnić, że średnia arytmetyczna jest nieobciążonym estymatorem wartości oczekiwanej.
30.
Udowodnić, że D^2 (x ̅ )=σ^2/n.
31.
32.
33.
Podać sposób konstrukcji prostej regresji.
34.
Z podziękowaniami dla Siergieja Łagierowa.
Opracowanie zagadnień na egzamin
23 stycznia 2014
15:28
III+semestr Strona 2
1.
2.
3.
Ciało zdarzeń
Prawdopodobieństwo
Niech oznacza przestrzeń zdarzeń elementarnych, a S ciało zdarzeń.
1.
2.
3.
Definicja prawdopodobieństwa (aksjomatyczna)
23 stycznia 2014
15:37
III+semestr Strona 3
Dystrybuanta w punkcie x to funkcja, która określa prawdopodobieństwo, że zmienna losowa
przyjmie wartość mniejszą niż x.
F jest niemalejąca (
)
1.
2.
F(x) jest lewostronnie ciągła (
3.
Zmienna losowa typu skokowego
Zmienna losowa typu ciągłego
1.
2.
przy założeniach dot. funkcji gęstości:
Dodatkowo, jeśli
Definicja i własności dystrybuanty rozkładu
prawdopodobieństwa.
23 stycznia 2014
15:37
III+semestr Strona 4
Funkcja musi być niemalejąca (dla takich
i
z jej dziedziny, że
,
a
także pierwsza pochodna musi być dodatnia)
1.
Granica w to 0
2.
Granica w to 1
3.
Jest lewostronnie ciągła
4.
Dla dowolnego
z dziedziny:
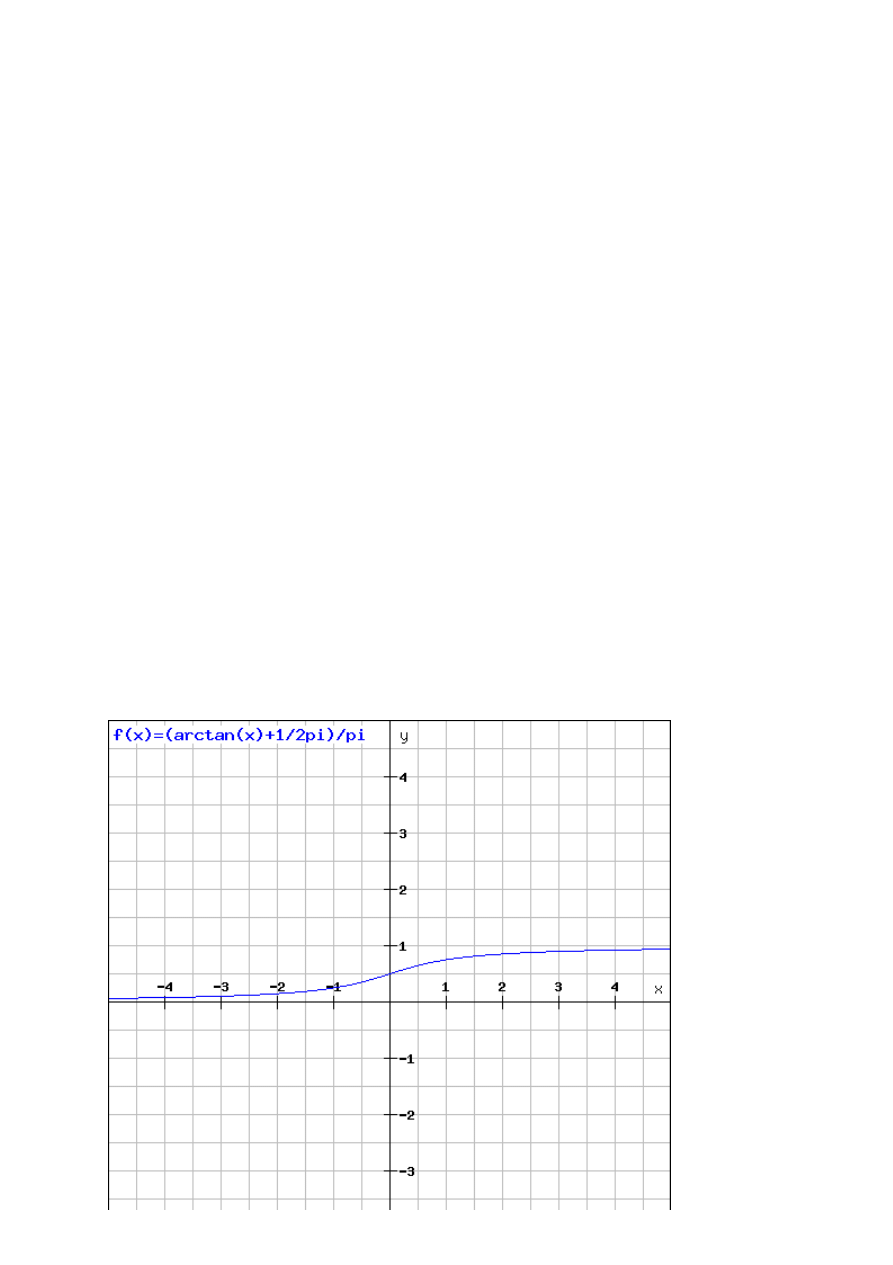
Zbiorem wartości badanej funkcji jest wycinek zbioru , a także spełnia ona wszystkie
własności dystrybuanty.
Pomocniczo, wykres:
Sprawdzić, czy funkcja
może
być dystrybuantą rozkładu prawdopodobieństwa.
23 stycznia 2014
15:37
III+semestr Strona 5
Prawdopodobieństwo warunkowe zdarzenia A pod warunkiem B, oznaczone symbolem to
prawdopodobieństwo zdarzenia A, obliczone przy założeniu, że zdarzenie B nastąpiło.
Jeżeli , to
Niezależność zdarzeń
nie zależy od , jeśli
.
Definicja prawdopodobieństwa warunkowego
23 stycznia 2014
15:37
III+semestr Strona 7
Z pierwszego i trzeciego aksjomatu prawdopodobieństwa oraz :
Udowodnić, że
23 stycznia 2014
15:37
III+semestr Strona 8
Udowodnić, że
23 stycznia 2014
15:37
III+semestr Strona 9
Wstępne spostrzeżenia:
Udowodnić, że dla dowolnych dwóch zdarzeń
23 stycznia 2014
15:37
III+semestr Strona 10
Udowodnić, że: jeśli , to
23 stycznia 2014
15:37
III+semestr Strona 11
Udowodnić, że dla każdego zdarzenia A prawdziwa jest
nierówność
23 stycznia 2014
15:37
III+semestr Strona 12
Układ zupełny
Twierdzenie
Jeżeli zdarzenie
( ) tworzą układ zupełny zdarzeń oraz
, to dla
dowolnego zdarzenia B zachodzi rowność
.
Dowód
Skoro zdarzenia
tworzą układ zupełny, to:
Zatem z trzeciego aksjomatu prawdopodobieństwa:
Z definicji prawdopodobieństwa warunkowego:
Stąd:
Sformułować i udowodnić twierdzenie o
prawdopodobieństwie zupełnym
23 stycznia 2014
15:37
III+semestr Strona 13
Twierdzenie
Jeżeli zdarzenia
( ) tworzą układ zupełny zdarzeń oraz B jest zdarzeniem takim, że
, to
, zachodzi wzór zwany wzorem Bayesa:
Dowód
Załóżmy, że
tworzą układ zupełny zdarzeń.
Z definicji prawdopodobieństwa warunkowego:
Z twierdzenia o prawdopodobieństwie całkowitym:
Sformułować i udowodnić twierdzenie Bayesa
23 stycznia 2014
15:37
III+semestr Strona 14
Funkcja określona w przestrzeni probabilistycznej , przekształcająca zbiór na zbiór .
Zmienna losowa to zbiór argumentów
, dla których spełniona jest zależność, że dla , wartości
zmiennej losowej są mniejsze od x. Zbiory te muszą być pozdbiorami ciała zdarzeń S.
Definicja zmiennej losowej
23 stycznia 2014
15:37
III+semestr Strona 15
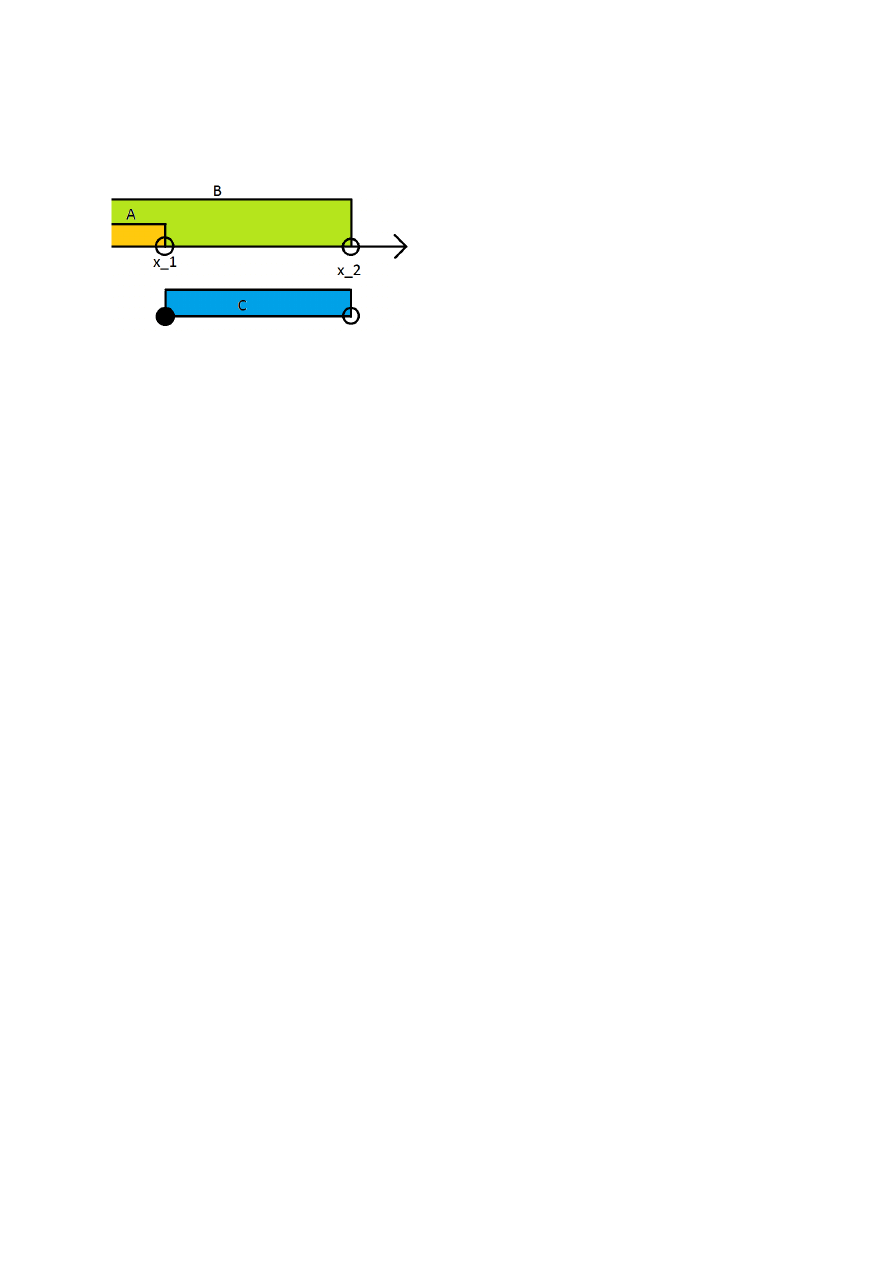
Udowodnić, że
23 stycznia 2014
15:37
III+semestr Strona 16
W schemacie Bernoulliego, n oznacza liczbę powtórzeń, p prawdopodobieństwo sukcesu (1-p zatem
prawdopodobieństwo porażki), a k liczbę sukcesów.
przyjmuje wartości
Wartość oczekiwana wynosi , a wariancja
.
Rozkład Bernoulliego
23 stycznia 2014
15:37
III+semestr Strona 17
przyjmuje wartości
Wartość oczekiwana i wariancja wynoszą
.
Rozkład Poissona
23 stycznia 2014
15:37
III+semestr Strona 18
Mówimy, ze zmienna losowa ma rozkład normalny o wartości oczekiwanej i wariancji
, co zapisujemy symbolicznie , jeżeli jej funkcja gęstości wyraża się wzorem:
Wykres funkcji gęstości w rozkładzie normalnym to tzw. krzywa dzwonowa (krzywa Gaussa)
W rozkładzie normalnym mediana, wartość oczekiwana i modalna są sobie równe.
Rozkład normalny
23 stycznia 2014
15:37
III+semestr Strona 19
Wartość oczekiwana zmiennej losowej typu skokowego wynosi
Po podstawieniu:
m
m
Podstawiamy
m
m
Z definicji dwumianu (symbolu) Newtona:
Wykazać, że wartość oczekiwana w rozkładzie
Bernoulliego wynosi np, gdzie n oznacza liczbę
doświadczeń, a p prawdopodobieństwo sukcesu w
pojedynczym doświadczeniu.
23 stycznia 2014
15:37
III+semestr Strona 20
Zmienna losowa
ma rozkład Bernoulliego określony wzorem
,
gdzie .
Jeśli maleje do 0 w ten sposób, że poczynając od pewnego
dla każdego
,
, gdzie , to
.
Dowód
Granica prawdopodobieństwa zmiennej losowej o rozkładzie Bernoulliego przy liczbie prób dążącej
do nieskończoności:
Skoro
, stosując podstawienie
i korzystając z faktu, że iloczyn
ma k czynników:
Sformułować i udowodnić twierdzenie Poissona
23 stycznia 2014
15:37
III+semestr Strona 21
Podstawiamy do wzoru
Napisać funkcję gęstości zmiennej losowej o rozkładzie
normalnym z wartością oczekiwaną 5 i odchyleniem
standardowym 7
23 stycznia 2014
15:37
III+semestr Strona 22
Podana funkcja gęstości jest f. g. w rozkładzie normalnym N(5,2) ( , ).
W r. n., wartość oczekiwana
.
Zatem wartość oczekiwana, modalna i mediana wynoszą 5, natomiast wariancja
4.
Podać wartość oczekiwaną, wariancję, wartość modalną i
medianę zmiennej losowej, której funkcja gęstości wyraża
się wzorem
23 stycznia 2014
15:37
III+semestr Strona 23
Parametr
Typ skokowy
Typ ciagły
Wartość oczekiwana
Wariancja
Odchylenie standardowe
Mediana
Modalna
x takie, że P(x) jest
największe
x takie, gdzie f(x) osiąga
maksimum
Parametry zmiennych losowych (średnia, wariancja,
odchylenie standardowe, mediana i wartość modalna)
23 stycznia 2014
15:37
III+semestr Strona 24
Udowodnić, że jeśli zmienna losowa X ma wartość
oczekiwaną m i odchylenie standardowe s, to zmienna
losowa
ma wartość oczekiwaną zero i
odchylenie standardowe 1
23 stycznia 2014
15:37
III+semestr Strona 25
Udowodnić, że jeśli zmienna losowa X ma wartość
oczekiwaną 7 i odchylenie standardowe 2, to zmienna
losowa
ma wartość oczekiwaną zero i
odchylenie standardowe 1.
23 stycznia 2014
15:37
III+semestr Strona 26
Zmienna losowa typu skokowego przyjmuje wartości ze zbioru zdarzeń elementarnych, który jest co
najwyżej przeliczalny (co najwyżej )
Rozkład zmiennej losowej typu skokowego
Znamy zdarzenia
oraz ich prawdopodobieństwa
.
Zmienne losowe typu skokowego. Rozkład zmiennej
losowej typu skokowego.
23 stycznia 2014
15:37
III+semestr Strona 27
Zmienna losowa typu ciągłego przyjmuje wartości ze zbioru nieprzeliczalnego.
Rozkład zmiennej losowej typu ciągłego
1.
2.
Funkcja gęstości f(x)
Zmienne losowe typu ciągłego. Rozkład zmiennej losowej
typu ciągłego
23 stycznia 2014
15:37
III+semestr Strona 28
Jeśli zbiór zmiennych losowych
o jednakowych rozkładach, mających wartość oczekiwaną m i
wariancję
, to ciąg
takich, że
jest zbieżny wg dystrybuant do zmiennej losowej , czyli dla każdego u zachodzi relacja
Twierdzenie Linderberga-Levy’ego
23 stycznia 2014
15:37
III+semestr Strona 29
Populacja - zbiór podlegający badaniu
Część populacji - próba (ciąg zmiennych losowych o rozkładzie populacji)
reprezentatywna
•
losowa
•
Cechy próby
Określenie populacji i próby
23 stycznia 2014
15:37
III+semestr Strona 30
Proces szacowania na podstawie obserwacji nazywamy estymacja a wyniki estymatorami.
Nieobciążoność
Estymator jest nieobciążony, jeśli wartość oczekiwana rozkładu estymatora jest równa wartości
szacowanego parametru:
Zgodność
Gdy liczebność próby rośnie, prawdopodobieństwo tego, że wartość estymatora różni się
dowolnie mało od parametru Q, zbliżą się do jedności.
Efektywność (możliwie najmniejsza wariancja)
Spośród zbioru wszystkich nieobciążonych estymatorów
, najefektywniejszym
nazywamy estymator o najmniejszej wariancji.
Definicja i własności estymatorów punktowych
23 stycznia 2014
15:37
III+semestr Strona 31
Metoda najmniejszych kwadratów
Wynik kolejnego pomiary
można przedstawić jako sumę pewnej mierzonej wartości x oraz błędu
pomiarowego , co zapisujemy
. Od wielkości
oczekujemy, aby suma jej kwadratów
była jak najmniejsza.
Wyprowadzenie wzoru na estymator wartości oczekiwanej
Dana jest obserwacja
. Wartość oczekiwana m to punkt, wokół którego najczęściej skupiają się
pomiary:
Niech dana będzie pewna funkcja Q(x), która dla danego parametru x zwróci sumę kwadratów błędu
pomiaru tej wielkości. Zbadajmy jej zachowanie dla wartości oczekiwanej m.
Ze względu na przyjętą metodę wyprowadzenia estymatora, otrzymana wartość m jest
przybliżeniem prawdziwej wartości m, dlatego oznacza się ją odpowiednim symbolem.
Wyprowadzić wzór na estymator wartości oczekiwanej
23 stycznia 2014
15:37
III+semestr Strona 32
Niech wartością oczekiwaną pomiaru
będzie m.
Zbadajmy, czy estymator jest nieobciążony:
Udowodnić, że średnia arytmetyczna jest nieobciążonym
estymatorem wartości oczekiwanej
23 stycznia 2014
15:37
III+semestr Strona 33
Niech odchylenie standardowe pomiaru
wyniesie .
Zbadajmy zachowanie
:
Udowodnić, że
.
23 stycznia 2014
15:37
III+semestr Strona 34
Współczynnikiem ufności nazwiemy oszacowanie pewnej zmiennej losowej za pomocą dwóch
innych zmiennych losowych
i
, ograniczających ją od góry i dołu.
gdzie .
Niech dane będą pomiary
o rozkładzie . Załóżmy, że jest znane. Ponadto,
, a także
. Z metody najmniejszych kwadratów:
Przeprowadźmy standaryzację do N(0,1):
Podsumowując:
Niech
Po przemnożeniu stronami przez
i dodaniu :
Zajmijmy się parametrem
. Niech oznacza dystrybuantę zmiennej losowej o rozkładzie
normalnym. Zauważmy, że . Sprawdźmy, jak zachowuje się dystrybuanta dla
przedziału
, gdy dane dla niego prawdopodobieństwo, tzw. współczynnik ufności wynosi
.
Wyprowadzić wzór na przedział ufności dla wartości
oczekiwanej na podstawie próby z populacji o rozkładzie
normalnym ze znanym odchyleniem standardowym
23 stycznia 2014
15:37
III+semestr Strona 35
Przedział ufności dla wartości oczekiwanej m przy znanym odchyleniu standardowym
III+semestr Strona 36
Hipoteza statystyczna to każde przypuszczenie dotyczące rozkładu prawdopodobieństwa badanej
cechy w populacji. Hipotezę statystyczną możemy zapisać w postaci:
gdzie F(x) oznacza dystrybuantę rozkładu populacji a pewien zbiór dystrybuant zwany zbiorem
hipotez dopuszczalnych, z których jedna jest przedmiotem badania.
Niech dany będzie poziom istotności , który określa prawdopodobieństwo, że przy poprawnej
hipotezie zerowej, wartości statystyki testowej znajdą się poza obszarem krytycznym:
Określa to ryzyko popełnienia tzw. błędu I rodzaju, czyli odrzucenia prawdziwej hipotezy.
Konstrukcja testu statystycznego odbywa się wg poniższego schematu.
Sformułowanie hipotezy zerowej i alternatywnej
Określenie statystyki testowej
Wyznaczenie obszaru krytycznego
Weryfikacja hipotezy
Jeżeli wartość statystyki testowej znajdzie się w obszarze krytycznym, należy ją odrzucić na rzecz
hipotezy alternatywnej. W przeciwnym przypadku, nie mamy podstaw do odrzucenia hipotezy
zerowej.
Podać przykład konstrukcji testu statystycznego dla
hipotezy
na podstawie próby
z populacji o rozkładzie normalnym ze
znanym odchyleniem standardowym
23 stycznia 2014
15:37
III+semestr Strona 37
Załóżmy, że dysponujemy n-elementową próbką:
Prostą , którą nazwiemy prostą regresji. Spróbujemy ją przybliżyć za pomocą kolejnych
danych z próbki.
Uogólniając:
, gdzie , a
oznacza błąd pomiarowy
Wykorzystajmy metodę najmniejszych kwadratów dla minimalizacji błędu
:
Niech dana będzie pewna funkcja będąca funkcją błędów pomiarowych (związana z metodą
najmniejszych kwadratów):
Zauważmy, że funkcja Q jest sumą stałych , stąd jej pochodne
oraz
. W związku z tym,
współczynniki prostej regresji a i b można obliczyć z zależności:
Konstrukcja prostej regresji
Niech dana będzie próbka
. Konstrukcja prostej regresji metoda
najmniejszych kwadratów polega na wyznaczeniu prostej zwanej prostą regresji, dla której suma
długości pionowych odcinków
łączących ja z punktami pomiaru będzie jak najmniejsza.
Podać sposób konstrukcji prostej regresji
23 stycznia 2014
15:37
III+semestr Strona 38
długości pionowych odcinków
łączących ja z punktami pomiaru będzie jak najmniejsza.
III+semestr Strona 39
