
Inżynieria Środowiska
2011/12
Materiały
do wykładu 11
15 12 2011
x
1
=
A
1
sin(ω t+ϕ
1
)
x
2
=
A
2
sin(ω t+ϕ
2
)
x = A
1
sin(ωt+ϕ
1
)+
A
2
sin(ωt+ϕ
2
) =
A sin(ω t+ϕ)
A =
√
A
1
2
+
A
2
2
+
2 A
1
A
2
cos(ϕ
1
−ϕ
2
)
składanie drgań równoległych
równe okresy
ϕ
1
=ϕ
2
A
1
=
A
2
⇒
A=2A
1
ϕ
1
−ϕ
2
=π
A
1
=
A
2
⇒
A=0
brak
wygaszenia
interferencja
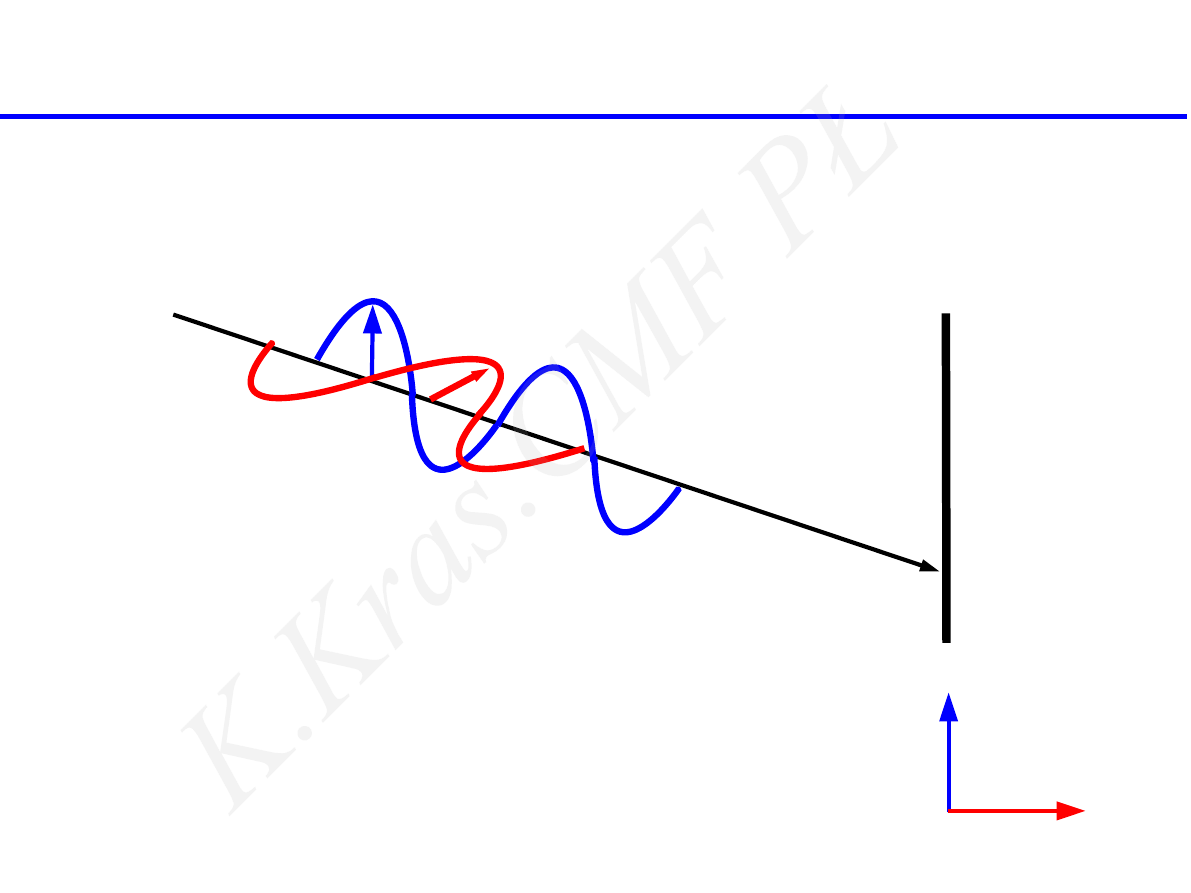
fale spolaryzowane liniowo
E
1
E
2
x
0
b
ϕ
0
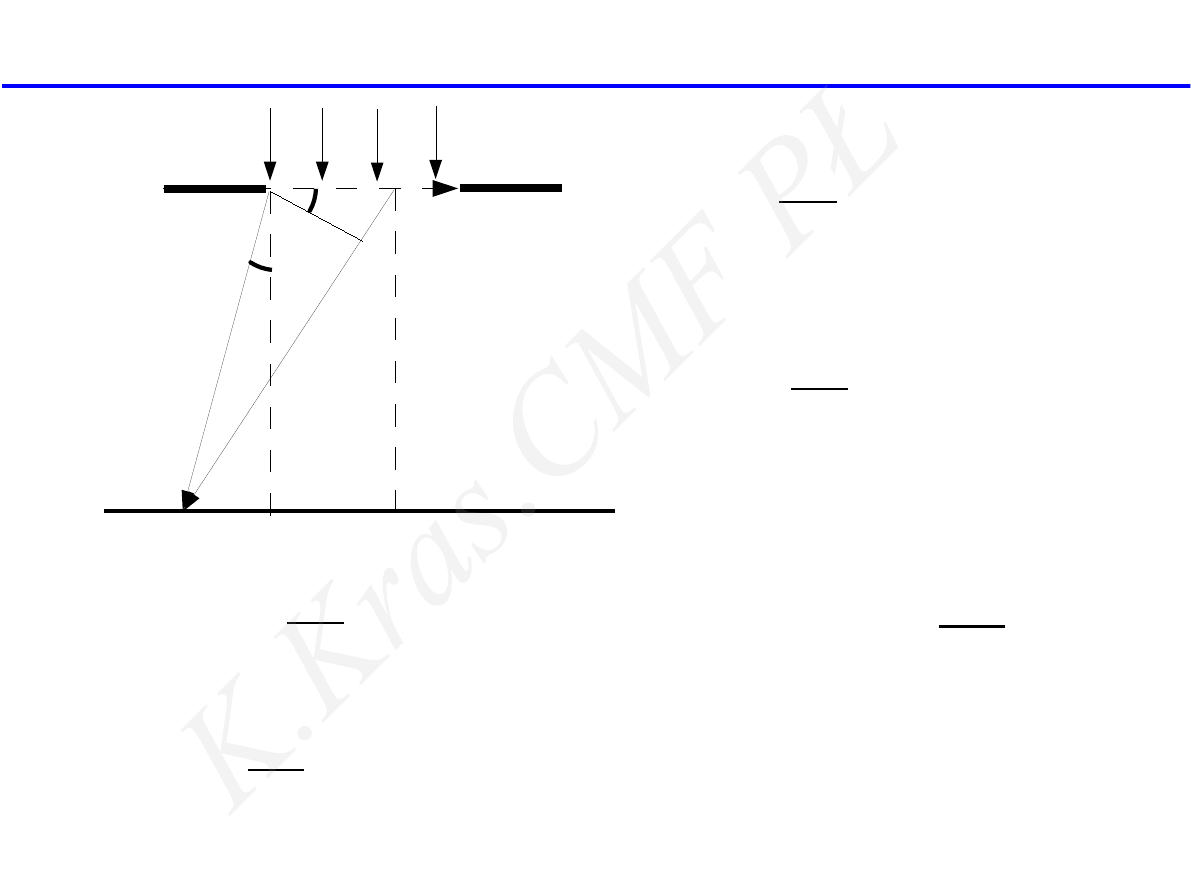
dyfrakcja na szczelinie ( fala płaska )
α
α
dE
P
(
x) =
E
0
b
dx sin(ω t−kx sin α)
E
P
=
∫
0
b
E
0
b
sin(ω t−kx sin α) dx
P
dE
P
(
0) =
E
0
b
sin(ω t)dx
dE
s
=
E
0
b
dx
k =
2π
λ
E
P
=
2 E
0
k b sin α
sin(
k b sin α
2
)
sin(
2ωt−k b sin α
2
)
amplituda fali wypadkowej w punkcie P
sin(
k b sin α
2
) =
0
b sin α = n λ
minima interferencyjne
k b sin α
2
≠
0
∧
n = 1,2,3... b≫λ
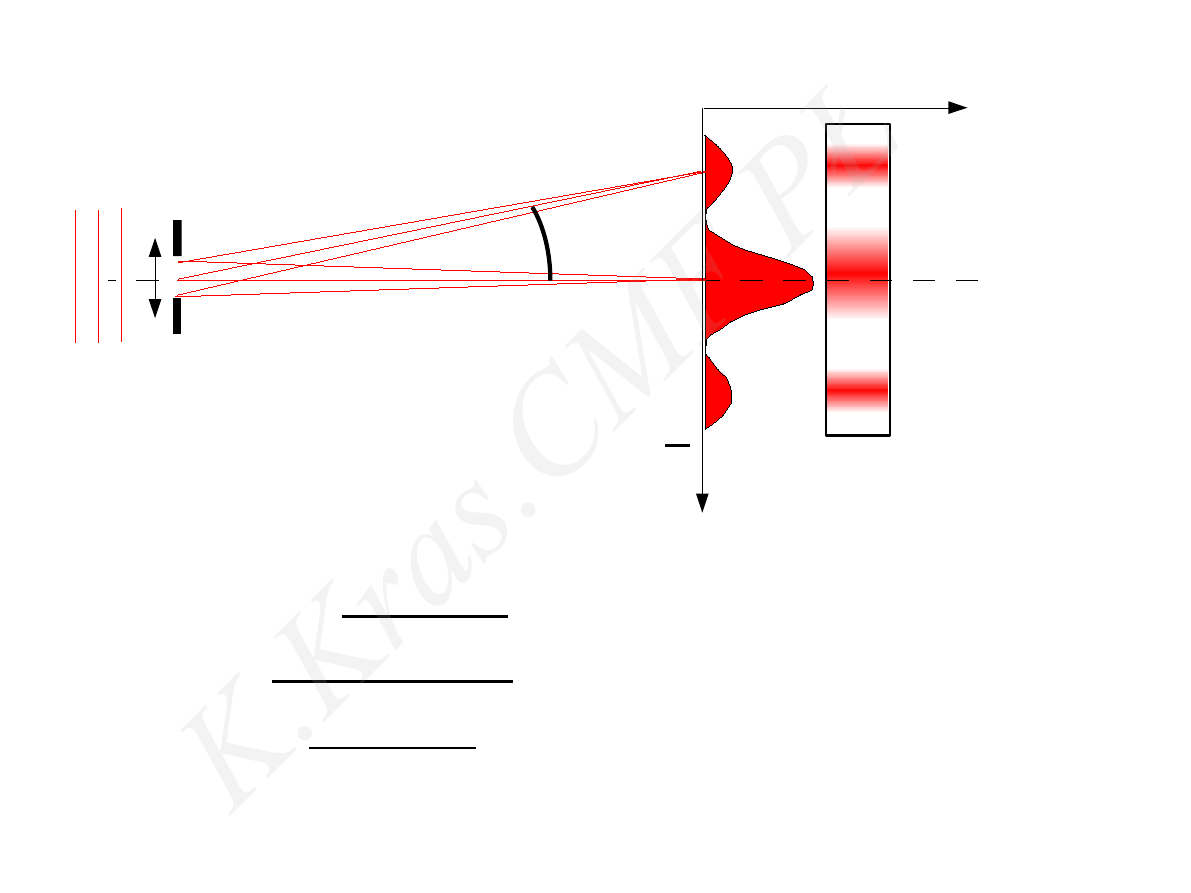
natężenie oświetlenia ekranu
n=1
n=−1
n=−2
n=2
α
sin α = n λ
b
b
I
α
=
I
0
(
sin
b k sin α
2
b k sin α
2
)
2
maksimum główne
α =
0
fala płaska
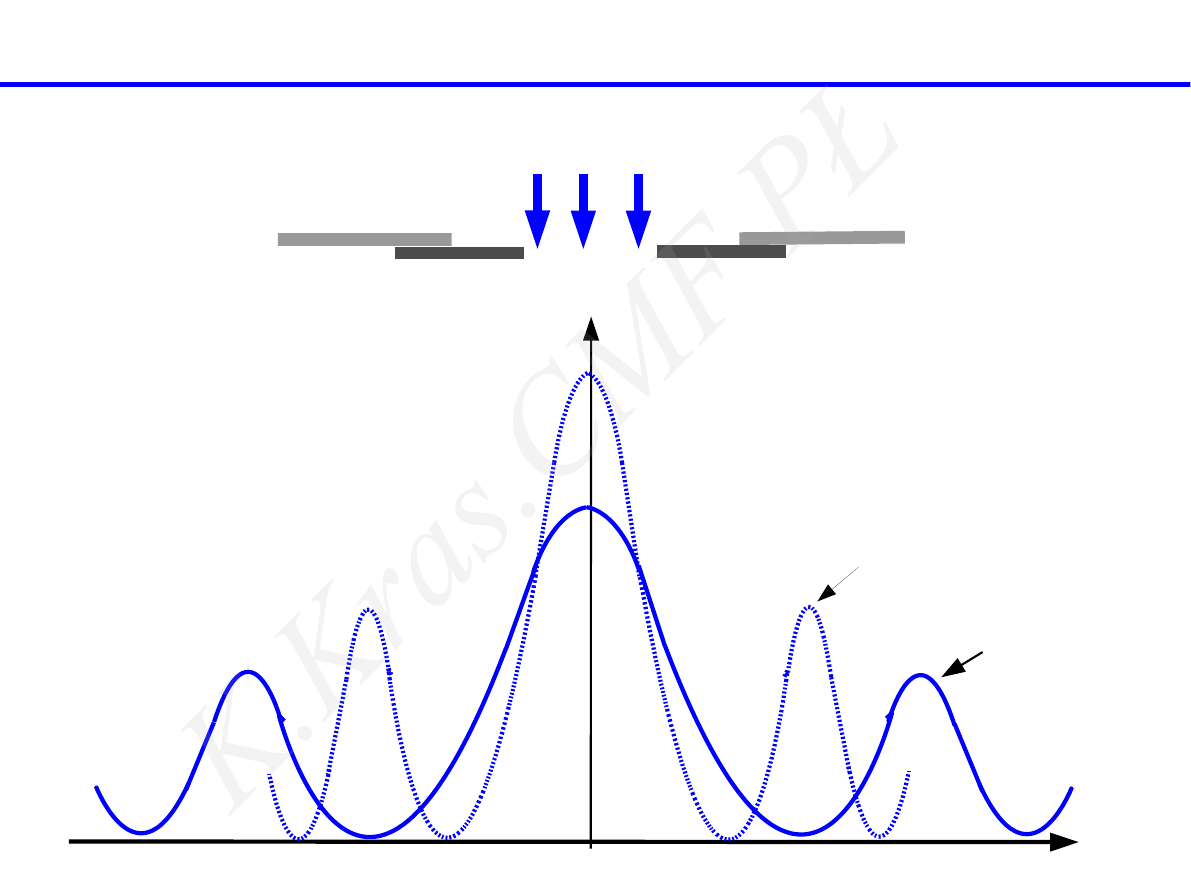
1
1
2
2
różne szerokości szczeliny
sin α
I
sinα
1
2
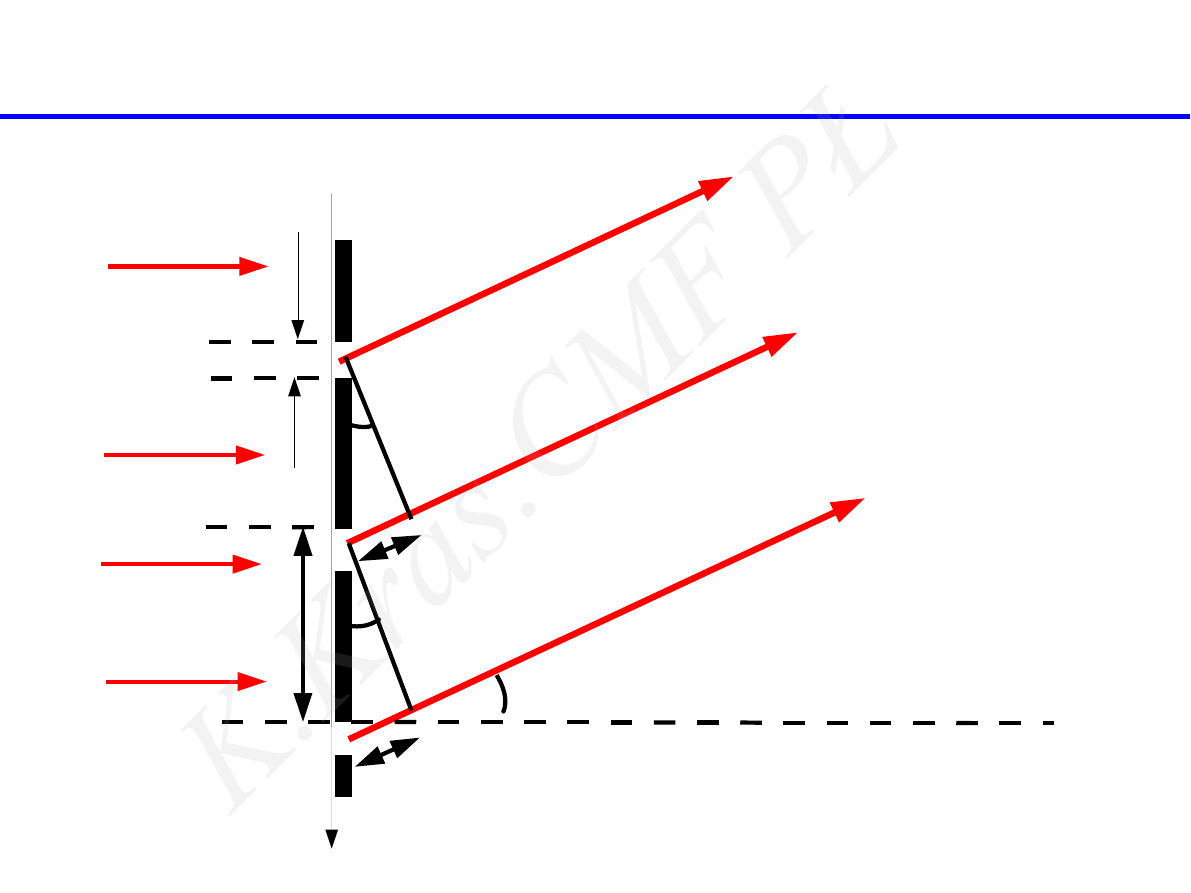
ϕ
ϕ
ϕ
Δ =
d sin ϕ
d
siatka dyfrakcyjna - N szczelin
fala płaska
b
x
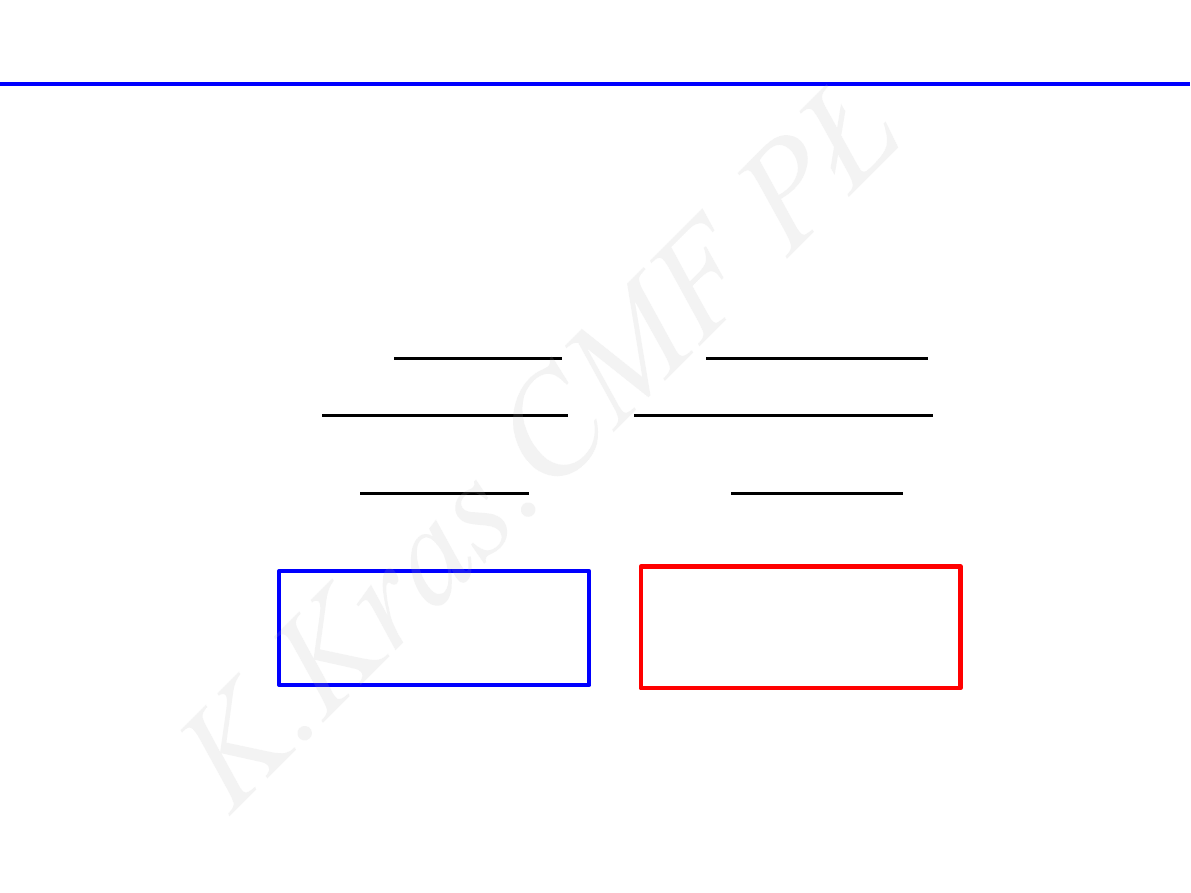
siatka dyfrakcyjna - natężenie wiązki
dyfrakcja
na szczelinie
interferencja
N szczelin
I
ϕ
=
I
0
(
sin
π
b sin ϕ
λ
π
b sin ϕ
λ
)
2
(
sin
N π d sin ϕ
λ
sin
π
d sin ϕ
λ
)
2
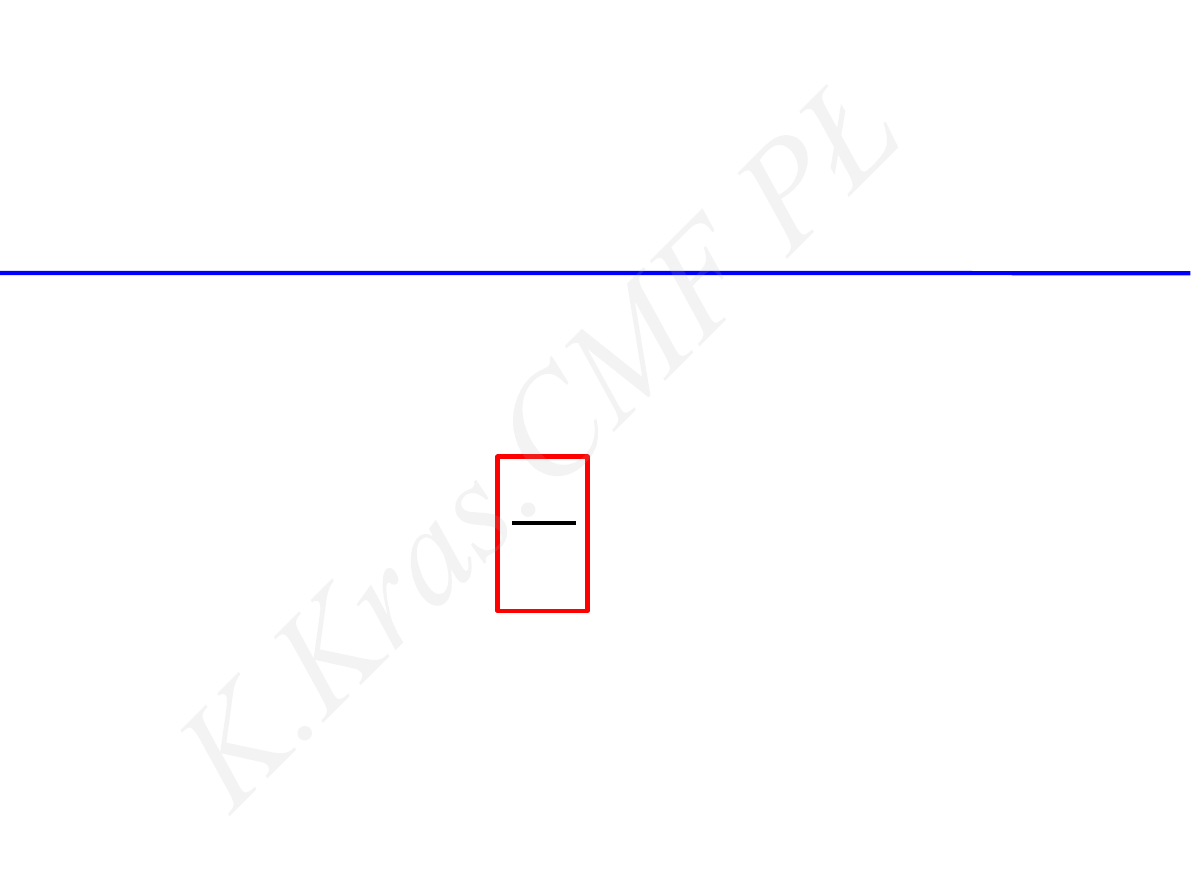
d sin ϕ = m λ
siatka dyfrakcyjna -maksima główne
s = 0,1,2 ,3...
d sin ϕ =
s
N
λ
tylko dla niecałkowitych wartości s/N
dla całkowitych s/N - maksima główne
siatka dyfrakcyjna -minima poboczne
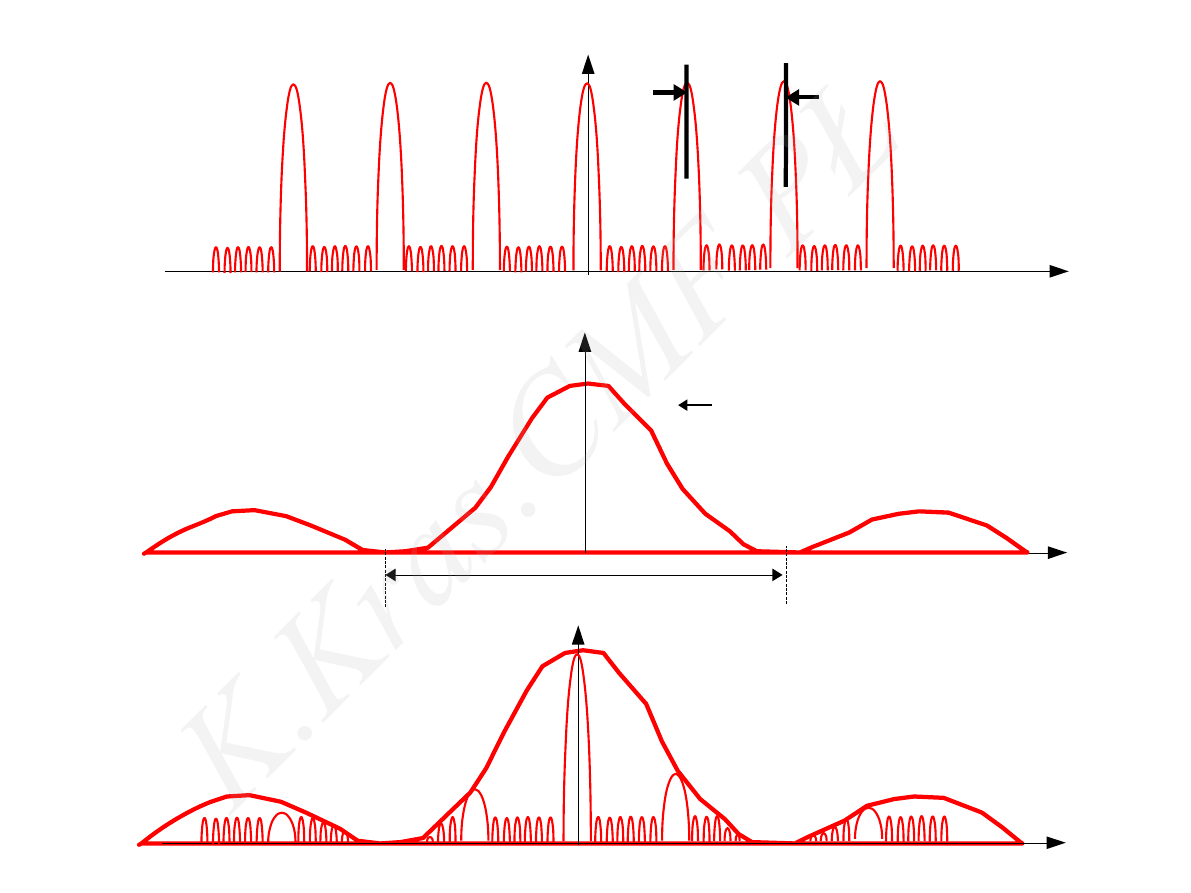
I
I
I
sin ϕ
sin ϕ
sin ϕ
N szczelin
1 szczelina
iloczyn
N-1
zależy od szerokości szczeliny b
zależy od odległości pomiędzy
szczelinami d
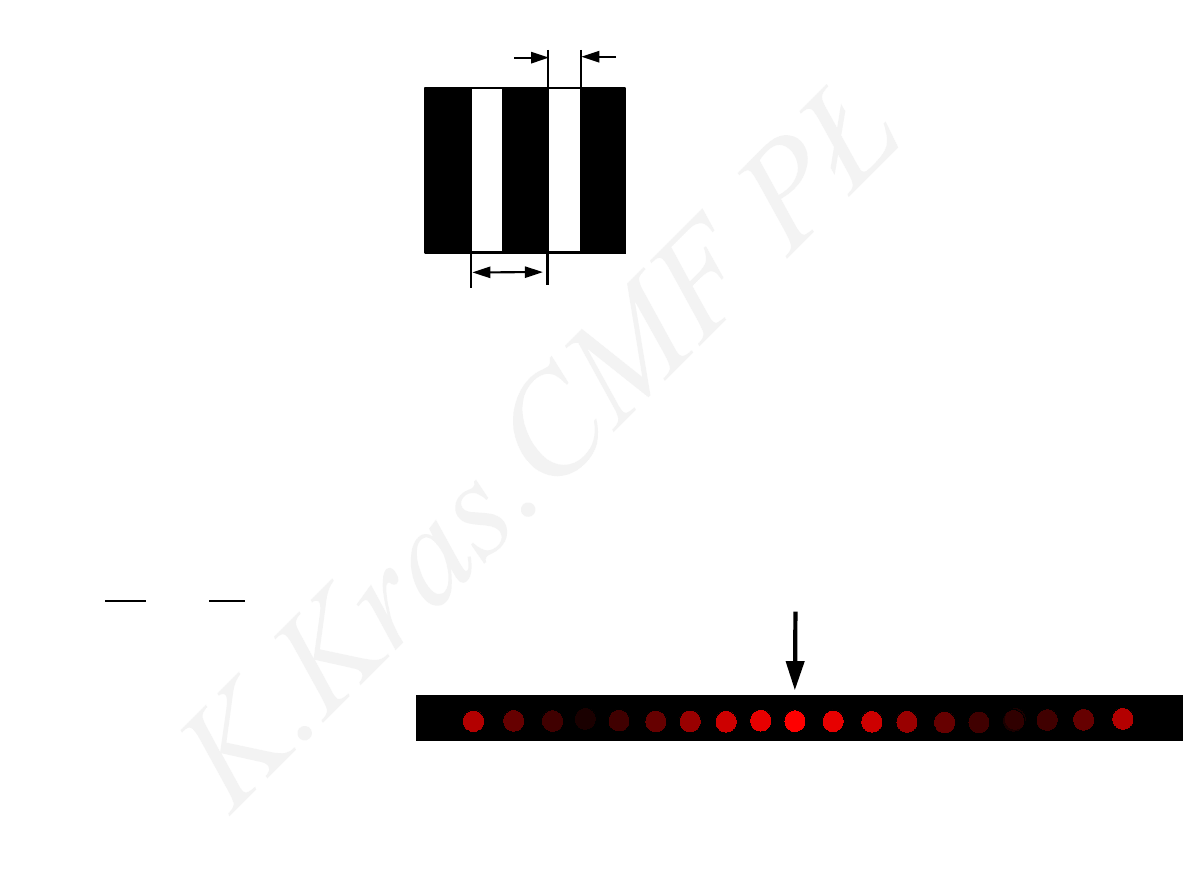
d
b
d =6b
d sin ϕ = m λ
b sin ϕ = n λ
m
n
=
d
b
=
6
m = 6, 12,18....
0
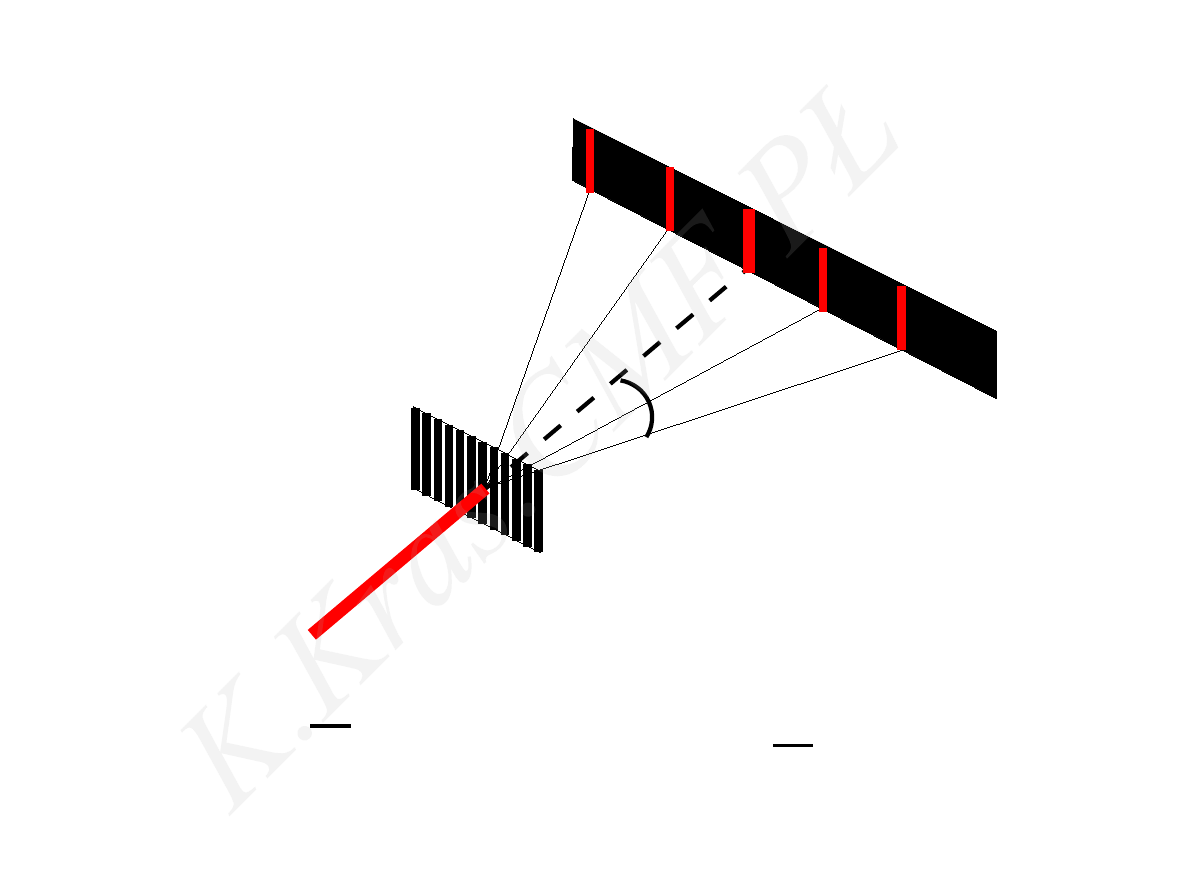
m=0
m=1
m=2
m=−1
m=−2
sin ϕ = m λ
d
≤
1
m≤
d
λ
ϕ
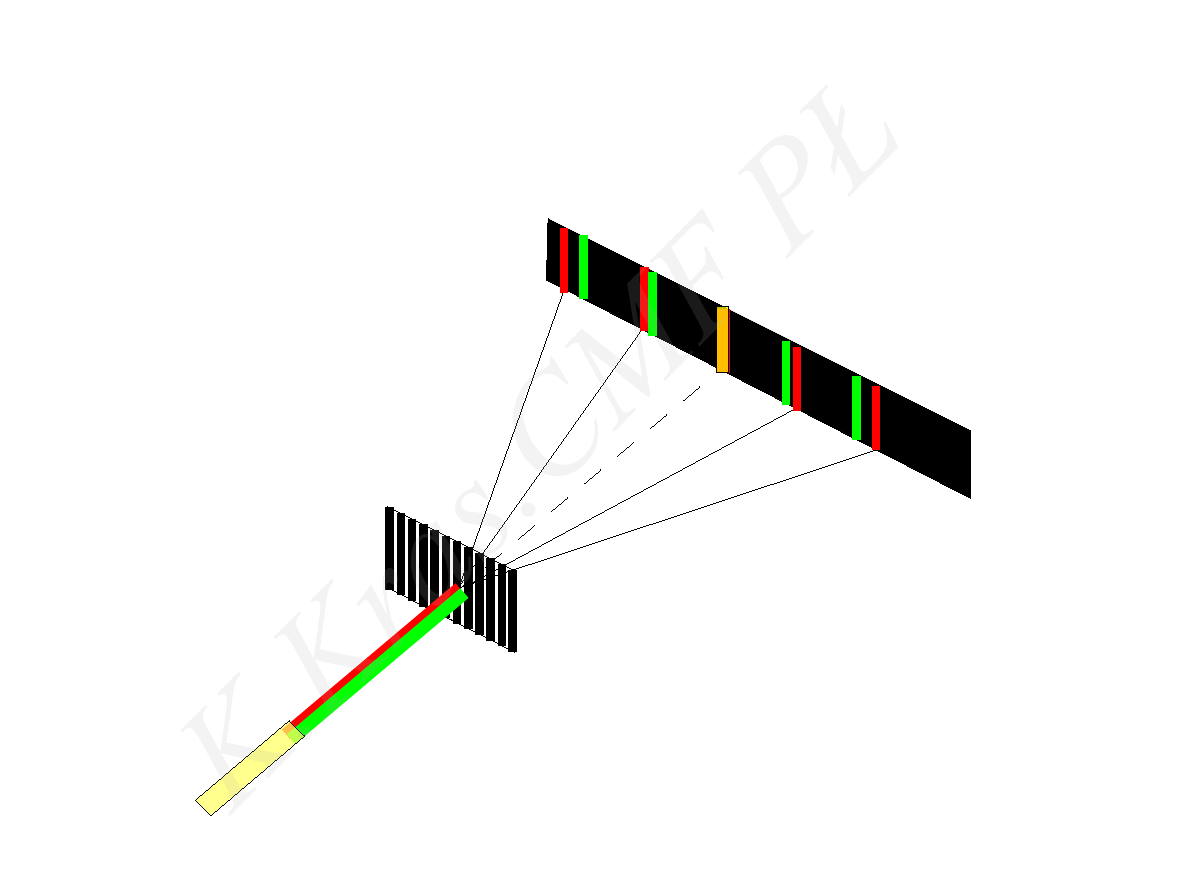
m=0
m=1
m=2
m=−1
m=−2
d
d sin ϕ = m λ
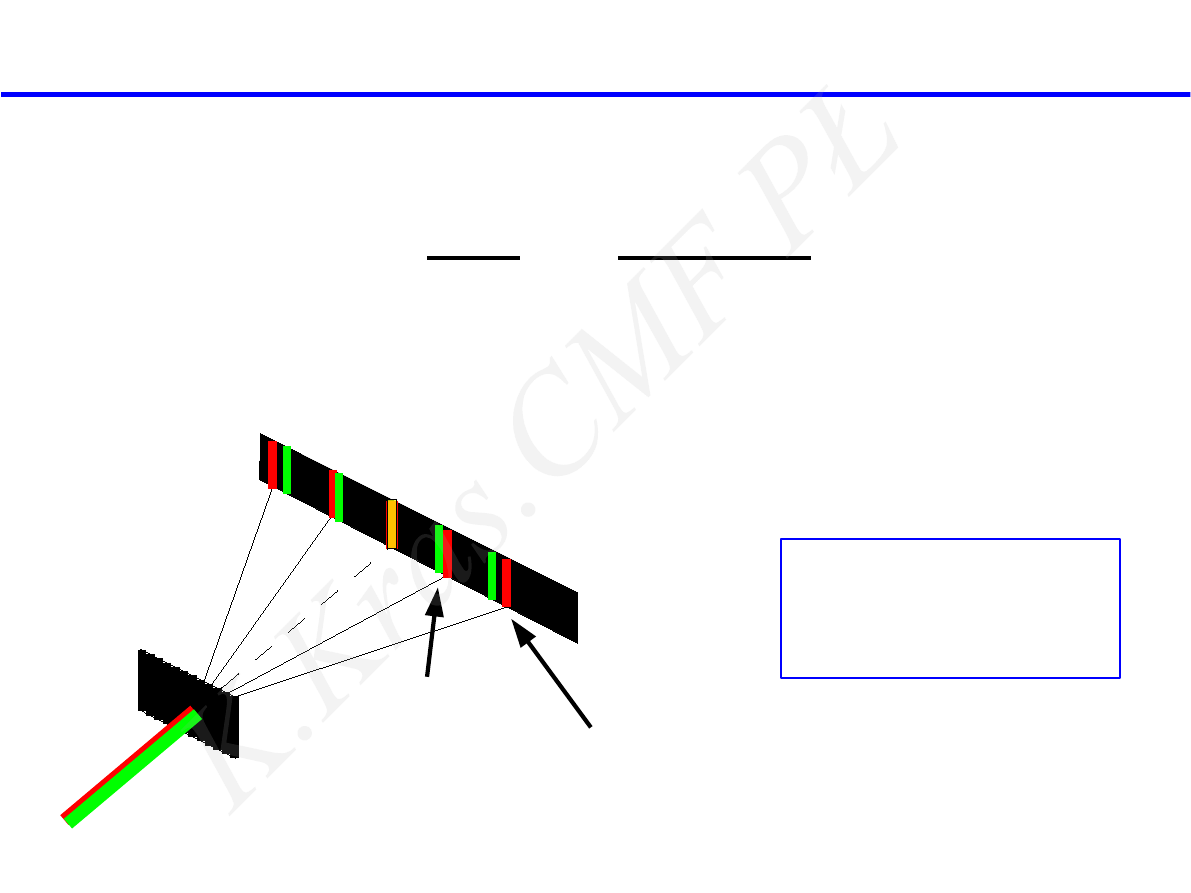
m=0
m=1
m=2
m=−1
m=−2
mniejsza
większa
dyspersja kątowa siatki dyfrakcyjnej
D =
∂ ϕ
∂ λ
=
m
d cos ϕ
D ∼ m
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
Wyszukiwarka
Podobne podstrony:
BOTANIKA - wyklad 11 - 15.12.2009, OGRODNICTWO UP LUBLIN, BOTANIKA, wykłady
LOGISTYKA W10, LOGISTYKA Wykład 11 15-12-2000
IS wyklad 14 15 01 09 MDW id 22 Nieznany
IS wyklad 14 15 01 09 MDW id 22 Nieznany
Wykład 11 15 16 Agnieszka Popławska Marketing
org miedz wyklad 11 15 05 07
15 12 2011 Wykład 11
AiR 11 12 wyklad 10 09 12 2011 MDW
FINANSE WYKLAD 5 (11 12 2011) id 171466
IS 2011 12 wyklad 13 12 01 2012 MDW
AiR 11 12 wyklad 08 25 11 2011 MDW
IS 2011 12 wyklad 10 08 12 2011 MDW
IS 2011 12 wyklad 12 05 01 2012 MDW
IS 2011 12 wyklad 09 01 12 2011 MDW
AiR 11 12 wyklad 11 16 12 2011 MDW
więcej podobnych podstron