
Fizyka: jak opracowywać pomiary
Sławomir Wolski
Katedra Fizyki Wydział Matematyki i Fizyki Stosowanej
Politechnika Rzeszowska
(Politechnika Rzeszowska)
1 / 16

Literatura
D. Holliday, R. Resnick, J. Walker, Podstawy Fizyki, Wydawnictwo
Naukowe PWN, Warszawa 2003
I.W. Sawieliew, Wykłady z fizyki, Wydawnictwo Naukowe PWN,
Warszawa, 2003
Fizyka I Pracownia, pod red. K. Kropa i K. Chłędowskiej, Oficyna
Wydawnicza Politechniki Rzeszowskiej, Rzeszów 2007
B.M. Jaworski, A.A Dietław, Fizyka. Poradnik encyklopedyczny,
Wydawnictwo Naukowe PWN, Warszawa
H.D. Young, R. A. Freedman, University Physics, Pearson New York,
2008
P. Hewit, Fizyka wokół nas, PWN, Warszawa 2005
I. N. Bronsztejn, K. A. Siemiendiajew, Matematyka. Poradnik
encyklopedyczny, Wydawnictwo Naukowe PWN, Warszawa 2000
(Politechnika Rzeszowska)
2 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
4
Przygotować tabelke pomiarową.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
4
Przygotować tabelke pomiarową.
5
Wykonać pomiary zgodnie z instrukcją (w skrypcie Fizyka I
Pracownia
) i zapisać wyniki. Zanotowac (jeśli trzeba) niepewności
pomiarów bezpośrednich.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
4
Przygotować tabelke pomiarową.
5
Wykonać pomiary zgodnie z instrukcją (w skrypcie Fizyka I
Pracownia
) i zapisać wyniki. Zanotowac (jeśli trzeba) niepewności
pomiarów bezpośrednich.
6
Zgodnie ze skryptem (Fizyka I Pracownia) dokonać obliczeń zadanych
wielkości.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
4
Przygotować tabelke pomiarową.
5
Wykonać pomiary zgodnie z instrukcją (w skrypcie Fizyka I
Pracownia
) i zapisać wyniki. Zanotowac (jeśli trzeba) niepewności
pomiarów bezpośrednich.
6
Zgodnie ze skryptem (Fizyka I Pracownia) dokonać obliczeń zadanych
wielkości.
7
Oszacowań niepewności pomiarowe.
(Politechnika Rzeszowska)
3 / 16

Jak wykonać sprawozdanie
1
Każdy zespół obowiązany jest do założenia teczki na sprawozdania.
Opis teczki powinien być zgodny z podanym wzorem.
2
Przygotować stronę tytułową zgodnie ze wzorem podanym na stronie:
http://www.prz.edu.pl/fizyka .
3
Opracować część teoretyczną: omówić fizyczne podstawy
doświadczenia. Podać najważniejsze wzory i prawa fizyczne.
4
Przygotować tabelke pomiarową.
5
Wykonać pomiary zgodnie z instrukcją (w skrypcie Fizyka I
Pracownia
) i zapisać wyniki. Zanotowac (jeśli trzeba) niepewności
pomiarów bezpośrednich.
6
Zgodnie ze skryptem (Fizyka I Pracownia) dokonać obliczeń zadanych
wielkości.
7
Oszacowań niepewności pomiarowe.
8
Podać wyniki końcowe razem z niepewnościami i zapisać wnioski.
(Politechnika Rzeszowska)
3 / 16

Zapisywanie wyników pomiarów
C
= (123.25 ± 0.35)µF
Wartość zmierzona
Niepewność pomiaru
C
= (1.2325 ± 0.0035) · 10
2
µF
(Politechnika Rzeszowska)
4 / 16

Zapisywanie wyników pomiarów
C
= (123.25 ± 0.35)µF
Wartość zmierzona
Niepewność pomiaru
C
= (1.2325 ± 0.0035) · 10
2
µF
Wyniki podajemy wraz z niepewnościami.
Liczba miejsc znaczących wyniku ma być taka sama jak niepewności
(niepewność determinuje dokładność podawanego wyniku).
Liczba miejsc znaczących
niepewności
nie powinna przekraczać
dwóch.
(Politechnika Rzeszowska)
4 / 16

Niepewności pomiarów
Niepewności typu A
Może ona być obliczona dla serii
pomiarów powtarzanych w jednakowych
warunkach.
Wynik pomiaru jest
średnią
arytmetyczną
¯
x
=
1
n
n
X
i
=1
x
i
.
Jako niepewność standardową u(¯
x
)
będziemy przyjmowali
odchylenie
standardowe
u
(¯
x
) =
s
P
n
i
=1
(x
i
− ¯x)
2
n
(n − 1)
.
(Politechnika Rzeszowska)
5 / 16

Niepewności pomiarów
Niepewności typu A
Może ona być obliczona dla serii
pomiarów powtarzanych w jednakowych
warunkach.
Wynik pomiaru jest
średnią
arytmetyczną
¯
x
=
1
n
n
X
i
=1
x
i
.
Jako niepewność standardową u(¯
x
)
będziemy przyjmowali
odchylenie
standardowe
u
(¯
x
) =
s
P
n
i
=1
(x
i
− ¯x)
2
n
(n − 1)
.
Niepewności typu B
Jest ona stosowana jeśli dostępny jest
tylko
jeden wynik pomiaru
, albo wyniki
są
powtarzalne
(miernik elektryczny,
suwmiarka itp.).
u
(x ) =
∆x
√
3
gdzie ∆x jest maksymalną niepewnością
pomiarową.
Zazwyczaj jako maksymalną
niepewnośc przyjmujemy działkę
elementarną przyrządu.
Często szacujemy maksymalną
niepewność uwzględniając inne
uwarunkowania pomiaru (np. refleks).
(Politechnika Rzeszowska)
5 / 16
Niepewności pomiarów
Niepewności typu AB
Jeśli oba typy niepewności (A i B) występują równocześnie obliczamy niepewność łączną
u
(x ) =
q
(u
A
(x ))
2
+ (u
B
(x ))
2
.
(Politechnika Rzeszowska)
6 / 16

Niepewności pomiarów
Niepewności typu AB
Jeśli oba typy niepewności (A i B) występują równocześnie obliczamy niepewność łączną
u
(x ) =
q
(u
A
(x ))
2
+ (u
B
(x ))
2
.
Niepewności wielkości złożonych
Jeśli wielkość obliczona jest funkcją kilku zmiennych (mierzonych wielkości), niepewność
wyznaczamy używająć metody
różniczki zupełnej
y
= f (x
1
, x
2
, · · · , x
n
), u(y ) =
v
u
u
u
t
N
X
j
=1
∂f
∂x
j
!
2
(u(x
j
))
2
gdzie ∂f /∂x
j
jest pochodną cząstkową.
(Politechnika Rzeszowska)
6 / 16

Podstawowe wzory dla pochodnych
Funkcja
Pochodna
stała C
0
x
α
αx
α−1
(Politechnika Rzeszowska)
7 / 16

Podstawowe wzory dla pochodnych
Funkcja
Pochodna
stała C
0
x
α
αx
α−1
sin x
cos x
cos x
− sin x
(Politechnika Rzeszowska)
7 / 16

Podstawowe wzory dla pochodnych
Funkcja
Pochodna
stała C
0
x
α
αx
α−1
sin x
cos x
cos x
− sin x
a
x
a
x
ln a
e
x
≡ exp(x) e
x
log
a
x
(log
a
e
)/x
ln x
1/x
(Politechnika Rzeszowska)
7 / 16

Podstawowe wzory dla pochodnych
Funkcja
Pochodna
stała C
0
x
α
αx
α−1
sin x
cos x
cos x
− sin x
a
x
a
x
ln a
e
x
≡ exp(x) e
x
log
a
x
(log
a
e
)/x
ln x
1/x
C f
(x )
C f
′
(x )
f
(x ) + g(x )
f
′
(x ) + g
′
(x )
(Politechnika Rzeszowska)
7 / 16

Podstawowe wzory dla pochodnych
Funkcja
Pochodna
stała C
0
x
α
αx
α−1
sin x
cos x
cos x
− sin x
a
x
a
x
ln a
e
x
≡ exp(x) e
x
log
a
x
(log
a
e
)/x
ln x
1/x
C f
(x )
C f
′
(x )
f
(x ) + g(x )
f
′
(x ) + g
′
(x )
f
(x )g(x )
f
′
(x )g(x ) + f (x )g
′
(x )
f
(x )/g(x )
[f
′
(x )g(x ) − f (x)g
′
(x )]/g
2
(x )
f
(g(x ))
f
′
(g(x ))g
′
(x )
(Politechnika Rzeszowska)
7 / 16

Przykład obliczania niepewności złożonych
Dla prawa elektrolizy Faradaya obliczyć niepewność pomiarową
równoważnika chemicznego k.
(Politechnika Rzeszowska)
8 / 16

Przykład obliczania niepewności złożonych
Dla prawa elektrolizy Faradaya obliczyć niepewność pomiarową
równoważnika chemicznego k.
Do obliczenia rónoważnika wykorzystujemy wzór k =
m
2
−m
1
I·t
.
(Politechnika Rzeszowska)
8 / 16

Przykład obliczania niepewności złożonych
Dla prawa elektrolizy Faradaya obliczyć niepewność pomiarową
równoważnika chemicznego k.
Do obliczenia rónoważnika wykorzystujemy wzór k =
m
2
−m
1
I·t
.
Niepewności u(m
1
), u(m
2
), u(t), u(I) szacujemy metodą B.
(Politechnika Rzeszowska)
8 / 16

Przykład obliczania niepewności złożonych
Dla prawa elektrolizy Faradaya obliczyć niepewność pomiarową
równoważnika chemicznego k.
Do obliczenia rónoważnika wykorzystujemy wzór k =
m
2
−m
1
I·t
.
Niepewności u(m
1
), u(m
2
), u(t), u(I) szacujemy metodą B.
Niepewność złożoną u(k) wyliczamy wg wzoru
u
(k) =
r
∂k
∂m
1
2
(u(m
1
))
2
+
∂k
∂m
2
2
(u(m
2
))
2
+
∂k
∂t
2
(u(t))
2
+
∂k
∂I
2
(u(I))
2
gdzie pochodne cząstkowe obliczamy w następujący sposób
∂k
∂m
1
=
−1
I · t
,
∂k
∂m
2
=
1
I · t
,
∂k
∂I
= −
m
2
− m
1
I
2
· t
,
∂k
∂t
= −
m
2
− m
1
I · t
2
.
(Politechnika Rzeszowska)
8 / 16
Niepewności rozszerzone i zapisywanie wyników
Niepewności rozszerzone
Wyniki pomiarów bedziemy podawać z niepewnością rozszerzoną U(x )
U
(x ) = k · u(x)
gdzie k jest współczynnikiem, który przyjmujemy z zakresu k = 2 ÷ 3.
(Politechnika Rzeszowska)
9 / 16

Niepewności rozszerzone i zapisywanie wyników
Niepewności rozszerzone
Wyniki pomiarów bedziemy podawać z niepewnością rozszerzoną U(x )
U
(x ) = k · u(x)
gdzie k jest współczynnikiem, który przyjmujemy z zakresu k = 2 ÷ 3.
Zapisywanie wyników
Dla niepewności standardowej:
m
= 1.02142(0.00035) kg lub m = 1.02142(35) kg.
Dla niepewności rozszerzonej
m
= (0.0214 ± 0.0038) kg lub m = (21.4 ± 3.8) · 10
−3
kg
.
(Politechnika Rzeszowska)
9 / 16

Porównywanie wyników doświadczeń
Pomiary prowadzone różnymi metodami
T
1
, U(T
1
) – pomiar pierwszą metodą.
T
2
, U(T
2
) – pomiar drugą metodą.
Wyniki są
zgodne
jeżeli spełniony jest warunek:
|T
1
− T
2
| < U(T
1
) + U(T
2
).
Porównywanie z wartością tablicową
Zakładamy, że dla wartości tablicowej T : U(T
1
) ≫ U(T ) ≈ 0
Jeśli spełniony jest warunek
|T
1
− T | < U(T
1
)
to wynik pomiaru zgadza się z wartością tablicową.
(Politechnika Rzeszowska)
10 / 16
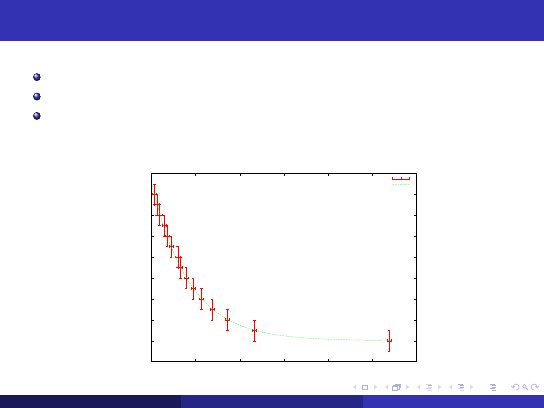
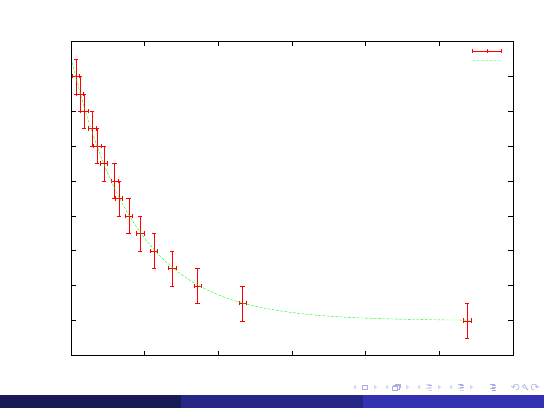
Wizualizacja danych doświadczalnych
Wykresy powinny zawierać
Dane doświadczalne wraz z słupkami (lub kwadratami) niepewności pomiarowych.
Opisane osie wraz z jednostkami.
Jeśli zachodzi potrzeba dopasowaną do punktów doświadczalnych krzywą
wg odpowiedniego modelu.
-20
0
20
40
60
80
100
120
140
160
0
20
40
60
80
100
120
I, [
µ
A]
t,[s]
dowiadczenie
dopasowanie
(Politechnika Rzeszowska)
11 / 16
Używanie programu GNUPLOT
Charakterystyka
http://gnuplot.info
Tworzenie wielu rodzajów wykresów.
Dopasowywanie danych.
Praca w konsoli.
Użycie wielu formatów przez definicje
terminali.
Łatwość tworzenia skryptów powłoki
i integracji z autorskimi programami.
Przygotowanie danych (plik
kondensator.txt
):
0.00
150
1.0
10
1.30
140
1.0
10
2.38
130
1.0
10
3.59
120
1.0
10
5.73
110
1.0
10
7.04
100
1.0
10
8.88
90
1.0
10
11.82
80
1.0
10
13.00
70
1.0
10
15.64
60
1.0
10
> set xlabel "t,[s]"
> set ylabel "I, [{/Symbol m} A]"
> plot ’kondensator.txt’ using 1:2:3:4 with xyerrorbars t "doświadczenie"
(Politechnika Rzeszowska)
12 / 16

Dopasowanie danych doświadczalnych
> y(x)= I0* exp(-x/tau)
> fit y(x) ’kondensator.txt’ using 1:2 via I0, tau
(Politechnika Rzeszowska)
13 / 16

Dopasowanie danych doświadczalnych
> y(x)= I0* exp(-x/tau)
> fit y(x) ’kondensator.txt’ using 1:2 via I0, tau
W wyniku otrzymamy parametry dopasowania i ich niepewności:
Final set of parameters
Asymptotic Standard Error
=======================
==========================
I0
= 150.449
+/- 1.088
(0.7232%)
tau
= 17.2512
+/- 0.2493
(1.445%)
correlation matrix of the fit parameters:
I0
tau
I0
1.000
tau
-0.742
1.000
(Politechnika Rzeszowska)
13 / 16

Dopasowanie danych doświadczalnych
> y(x)= I0* exp(-x/tau)
> fit y(x) ’kondensator.txt’ using 1:2 via I0, tau
W wyniku otrzymamy parametry dopasowania i ich niepewności:
Final set of parameters
Asymptotic Standard Error
=======================
==========================
I0
= 150.449
+/- 1.088
(0.7232%)
tau
= 17.2512
+/- 0.2493
(1.445%)
correlation matrix of the fit parameters:
I0
tau
I0
1.000
tau
-0.742
1.000
Możemy zdefiniować dopasowaną funkcję
>
y1(x)= 150.449* exp(-x/17.2512)
(Politechnika Rzeszowska)
13 / 16

Zapisanie wykresu do pliku
> y1(x)= 150.449* exp(-x/17.2512)
> set term post landscape
enhanced color
> set output "condensator.eps"
> set xlabel "t,[s]"
> set ylabel "I, [{/Symbol m} A]"
> plot ’kondensator.txt’ using 1:2:3:4 with xyerrorbars, y1(x) t "dopasowanie"
> set output
Uwaga: Wszystkie te komendy możemy zebrać w pliku kondensator.plt
i wywołać go w oknie konsoli.
(Politechnika Rzeszowska)
14 / 16
-20
0
20
40
60
80
100
120
140
160
0
20
40
60
80
100
120
I, [
µ
A]
t,[s]
dowiadczenie
dopasowanie
(Politechnika Rzeszowska)
15 / 16

Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
(Politechnika Rzeszowska)
16 / 16

Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
Znamy model teoretyczny zależności
y
= a · x + b.
(Politechnika Rzeszowska)
16 / 16

Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
Znamy model teoretyczny zależności
y
= a · x + b.
Zakładamy, że jedną wielkość (x )
znamy dokładnie, a druga (y ) jest
obarczona jednakową niepewnością.
(Politechnika Rzeszowska)
16 / 16

Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
Znamy model teoretyczny zależności
y
= a · x + b.
Zakładamy, że jedną wielkość (x )
znamy dokładnie, a druga (y ) jest
obarczona jednakową niepewnością.
Chcemy, aby bezwzględna suma
ochyłek od wartości średniej
¯
y
(x
i
) − y
i
= ¯
ax
i
+ ¯
b − y
i
była
minimalna.
(Politechnika Rzeszowska)
16 / 16
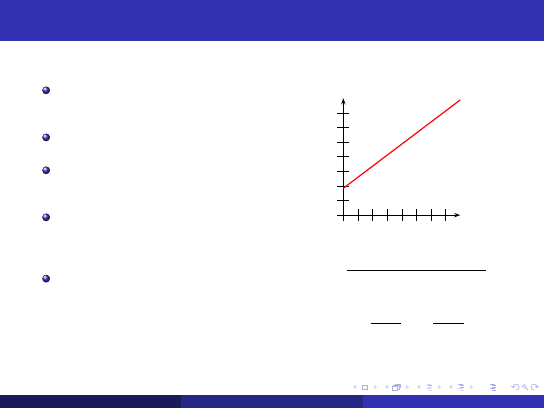
Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
Znamy model teoretyczny zależności
y
= a · x + b.
Zakładamy, że jedną wielkość (x )
znamy dokładnie, a druga (y ) jest
obarczona jednakową niepewnością.
Chcemy, aby bezwzględna suma
ochyłek od wartości średniej
¯
y
(x
i
) − y
i
= ¯
ax
i
+ ¯
b − y
i
była
minimalna.
Ogólnie dla wszystkich pomiarów
n
X
i
=1
¯
ax
i
+ ¯
b − y
i
2
= min
0
1
2
3
4
5
6
7
0 1 2 3 4 5 6 7
x
y
b
b
b
b
b
b
b
b
b
(Politechnika Rzeszowska)
16 / 16
Metoda najmniejszych kwadratów
Zakładamy że przedmiotem pomiaru
były dwie wielkości zależne x
i
, y
i
między sobą.
Znamy model teoretyczny zależności
y
= a · x + b.
Zakładamy, że jedną wielkość (x )
znamy dokładnie, a druga (y ) jest
obarczona jednakową niepewnością.
Chcemy, aby bezwzględna suma
ochyłek od wartości średniej
¯
y
(x
i
) − y
i
= ¯
ax
i
+ ¯
b − y
i
była
minimalna.
Ogólnie dla wszystkich pomiarów
n
X
i
=1
¯
ax
i
+ ¯
b − y
i
2
= min
0
1
2
3
4
5
6
7
0 1 2 3 4 5 6 7
x
y
b
b
b
b
b
b
b
b
b
¯
a
=
n
P
x
i
y
i
−
P
x
i
P
y
i
n
P
x
2
i
−
P
x
2
i
2
¯
b
=
P
y
i
n
− ¯a
P
x
i
n
(Politechnika Rzeszowska)
16 / 16

Metoda najmniejszych kwadratów w systemie GNUPLOT
Model dopasowania dla wahadła Oberbecka
t
2
= B + A · d
2
Procedura dopasowania
> obbk(x)=A*x+B
> fit obbk(x) ’oberbeck.txt’ using 1:2 via A, B
oberbeck.txt
dˆ2 tˆ2
0.21
52.02
0.19
43.69
0.17
41.42
0.16
37.55
0.14
34.97
0.12
31.51
0.11
29.27
Po wykonaniu procedury otrzymamy
Final set of parameters
Asymptotic Standard Error
=======================
==========================
A
= 181.434
+/- 11.06
(6.098%)
B
= 9.48893
+/- 1.67
(17.6%)
correlation matrix of the fit parameters:
A
B
A
1.000
B
-0.983
1.000
(Politechnika Rzeszowska)
17 / 16
Wyszukiwarka
Podobne podstrony:
PEM (12) Procedura obliczania niepewności pomiaru
przyklady obliczen niepewnosci 2012
Obliczam niepewność
Materały, przyklady obliczen niepewnosci 2012
Obliczanie niepewnosci dla cw 10, fiza
PEM (12) Procedura obliczania niepewności pomiaru
Obliczenia i niepewności doc
F2- Obliczenia i rachunek niepewności pomiarowej, Szkoła, Fizyka 02
Obliczenie wartości niepewności
Prezentacja JMichalska PSP w obliczu zagrozen cywilizacyjn 10 2007
3 ANALITYCZNE METODY OBLICZANIA PŁYWÓW
Obliczanie masy cząsteczkowej
Obliczanie powierzchni
2 Podstawy obliczania
NIEPEWNOŚĆ POMIARU
3 2 Ćwiczenie Obliczanie siatki kartograficznej Merkatora
więcej podobnych podstron