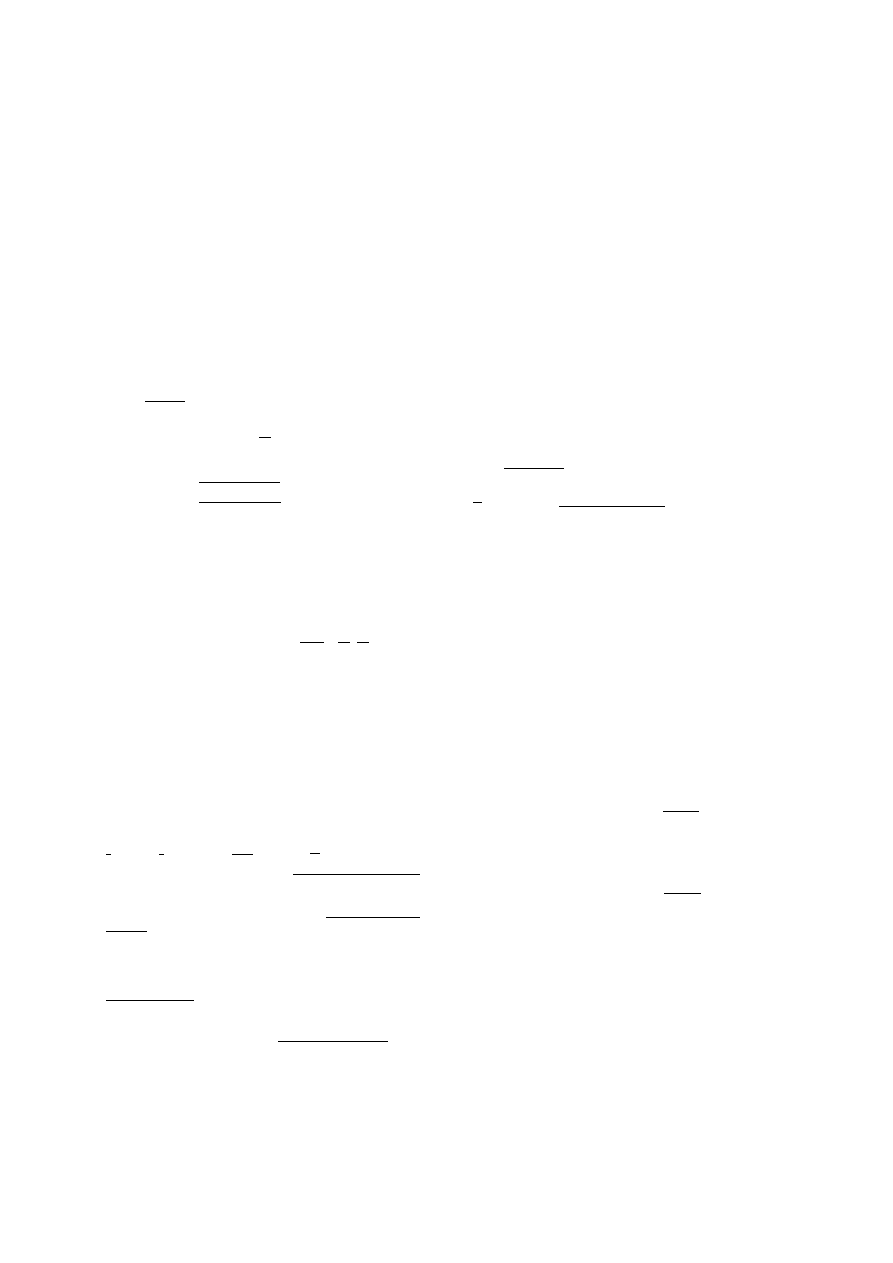
Otoczenie

punktu

o promieniu r jest zbiorem

wszystkich punktów P, których odległość od punktu

jest mniejsza

od r. Inaczej zbiór ten nazywamy kulą o środku w punkcie P0 i
promieniu r.
Sąsiedztwo

punktu

o promieniu r jest to zbiór

wszystkich punktów P, dla których

zatem

\{

}

Ciąg zbieżny: (def) ciąg punktów

przestrzeni

jest

zbieżny do punktu

wtedy i tylko wtedy, gdy

Twierdzenie:

Jeśli

to

Warstwicą funkcji

, odpowiadającą wartości c

nazywamy zbiór

TW.Weierstrassa Jeśli funkcja jest ciągła w <a,b> to jest w tym
przedziale ograniczona i istnieją punkty w których f przyjmuje
swoje kresy.
TW. Darboux Jeśli f jest ciągła w <a,b> oraz g jest
między f(a) i f(b) to istnieje co najmniej 1 pkt taki, że f(c) = g
(przyjmuje każdą wartość pośrednią między f(a) i f(b).
Pochodne CZ I RZ: Jeżeli istnieje skończona granica

to nazywamy ją pochodną cząstkową rzędu

pierwszego funkcji f względem zmiennej

w punkcie

i

oznaczamy symbolem

definicje dla:

Z podanej definicji wynika,

że obliczając

należy postępować tak jak przy obliczaniu

pochodnej kierunkowej funkcji zmiennej

traktując pozostałe

zmienne jak ustalone parametry.
Gradient funkcji w punkcie

nazywamy wektor pochodnych

cząstkowych

Pochodne CZ RZ II pochodne cząstkowe rzędu pierwszego
pochodnych cząstkowych

względem zmiennej

nazywamy pochodnymi cząstkowymi rzędu drugiego

i oznaczamy symbolem

DEF1. Funkcja f jest klasy

jeżeli ma na zbiorze X ciągłe

pochodne cząstkowe do rzędu n włącznie.
TW. Schwarza Jeżeli funkcja f ma w pewnym zbiorze otwartym
ciągłe pochodne cząstkowe mieszane rzędu drugiego

to w każdym punkcie tego zbioru są one równe.
Różniczka zupełna: wyrażenie

nazywamy różniczką zupełną funkcji f w

punkcie

i oznaczamy symbolem

DEF.2 Jeżeli funkcja f jest klasy

, to wyrażenie

nazywamy różniczką zupełną m funkcji f.

TW 1. (wzór Taylora) Jeżeli funkcja f jest klasy

w otoczeniu

punktu

, to da każdego punktu

istnieje takie punkt

że

Ekstrema: Funkcja f ma w punkcie

minimum lokalne właściwe

jeżeli istnieje takie sąsiedztwo punktu

że dla każdego punktu x

należącego do tego sąsiedztwa spełniona jest nierówność

Funkcja f ma w punkcie

maksimum lokalne

właściwe jeżeli istnieje takie sąsiedztwo punktu

że dla każdego

punktu x należącego do tego sąsiedztwa spełniona jest nierówność

. Jeżeli zamiast nierówności mocnej (>,<) zachodzi

nierówność słaba ( ), to mówimy, że funkcja f ma w

minimum (maksimum).
Minima i maksima (właściwe, niewłaściwe) nazywamy ekstremami.
Ekstremum jest lokalną własnością funkcji, charakteryzuje rozkład
wartości funkcji w dowolnie małym otoczeniu danego punktu. Nie
należy mylić ekstremów lokalnych z ekstremami globalnymi czyli z
wartości największą oraz wartością najmniejszą funkcji na zadanym
zbiorze.
TW2. Warunek konieczny istnienia ekstremum. Jeżeli funkcja f ma
w punkcie

ekstremum i ma w tym punkcie pochodne cząstkowe

rzędu pierwszego, to są one równe zero.

;

Punkty Stacjonarne: Punkty, w których spełniony jest
warunek

Macierz Hessego: macierz drugich pochodnych cząstkowych.
Jeżeli funkcja f jest klasy

w pewnym zbiorze, to macierz Hessego

dla punktów z tego zbioru jest macierzą symetryczną. Pochodne
mieszane są wówczas równe.
TW3. Warunek wystarczający istnienia ekstremum. Jeżeli funkcja f
jest klasy

w pewnym otoczeniu punktu

oraz

a

druga różniczka

jest określona dodatnio (macierz H(

)

jest dodatnio określona) to funkcja f ma w punkcie

Jeżeli funkcja f jest klasy

w pewnym

otoczeniu punktu

oraz

a druga różniczka

jest określona ujemnie (macierz H(

) jest ujemnie określona) to

funkcja f ma w punkcie

TW4 Warunek wykluczający ekstremum. Jeżeli funkcja f jest klasy

w pewnym otoczeniu punktu

oraz

i nie

spełniony jest żaden z warunków

lub

tzn.

istnieje

liczba

parzysta k taka, że

lub istnieją liczby nieparzyste k,l,

takie, że

to w punkcie

funkcja f nie ma

ekstremum.
DEF3 Mówimy, że funkcja f ma w punkcie

ekstremum

warunkowe związane warunkiem M, jeżeli funkcja f rozważana na
zbiorze

ma w punkcie

ekstremum lokalne.

Mnożniki Lagrange’a: Jeżeli f ma w

ekstremum lokalne

warunkowe to istnieją liczby

takie, że

POCHODNA kierunkowa: Jeżeli istnieje skończona granica

to nazywamy ją pochodną kierunkową funkcji f

w punkcie

w kierunku wektora v. Oznaczamy ją symbolem

Pochodna kierunkowa funkcji w punkcie

w

kierunku wektora

jest równa pochodnej cząstkowej funkcji f w

punkcie

względem i-tej zmiennej

.

TW5. Jeżeli funkcja f ma ciągłe pochodne cząstkowe pierwszego
rzędu w punkcie

jest dowolnym wektorem jednostkowym

to pochodna kierunkowa

jest iloczynem skalarnym wektora

gradientu i wektora v.

Płaszczyzna styczna: Jeżeli f jest klasy

w punkcie

to

równanie

jest

równaniem płaszczyzny stycznej do wykresu funkcji f w punkcie

.

Funkcja uwikłana: Jeżeli istnieje funkcja spełniająca w
każdym punkcie x z pewnego przedział I równość to
funkcję f nazywamy funkcją uwikłaną określoną równaniem
F(x,y)=0
TW6. O istnieniu i jednoznaczności funkcji uwikłanej. Jeżeli
funkcja F jest funkcją klasy

w pewnym otoczeniu punktu

oraz

to istnieje dokładnie jedna

funkcja uwikłana y=f(x) określona w pewnym przedziale

za pomocą równania spełnaijąca

warunek

. Funkcja ta ma w przedziale

ciągłą pochodną daną wzorem

Ekstremum funkcji uwikłanej: Jeżeli F jest klasy

w pewnym

otoczeniu punktu

oraz spełnione są warunki 1)

2)

3)

4)

to funkcja

uwikłana określona równaniem ma w punkcie

ekstremum właściwe gdy

a maksimum

właściwe gdy

DEF 4.Jeżeli dla każdego normalnego ciągu podziałów prostokąta
P ciąg sum całkowych

jest zbieżny do tej samej granicy

właściwej, niezależnej do wyboru punktów, to tę granicę nazywamy
całką podwójną funkcji f w prostokącie P i oznaczamy symbolem

TW7. Warunek wystarczający istnienia całki podwójnej w
prostokącie. Jeżeli funkcja f jest ciągła w prostokącie P, to jest w
nim całkowalna.
DEF5. Obszarem normalnym względem osi Ox nazywamy obszar

gdzie g,h są funkcjami

ciągłymi w przedziale <a,b>
Obszarem normalnym względem osi Oy nazywamy obszar

gdzie p,q są funkcjami

ciągłymi w przedziale <c,d>

DEF6. Obszar regularny. Obszarem regularnym na płaszczyźnie
nazywamy sumę skończonej liczby obszarów normalnych
(względem osi Ox i Oy) o parami rozłącznych wnętrzach.
TW8. O zamianie zmiennych w całce podwójnej. Jeżeli:
odwzorowanie przekształca wzajemnie
jednoznacznie wnętrze obszaru regularnego wnętrze obszaru
regularnego D. Funkcje x=x(u,v), y=y(u,v) są klasy

na pewnym

zbiorze otwartym zawierającym zbiór . Jakobian J J(u,v)

jest różny od zera wewnątrz obszaru . Funckcja

podcałkowa

f

jest

ciągła

na

D,

to:

DEF7. Jeżeli dla każdego normalnego ciąg podziałów
prostopadłościanu P ciąg sum całkowych

jest zbieżny do tej samej

granicy właściwej, niezależnej od wyboru punktów, to tę granicę
nazywamy całką potrójną funkcji f w prostopadłościanie P i
oznaczamy symbolem:

TW9. warunek wystarczający istnienia całki potrójnej w Prost.
Jeżeli funkcja f jest ciągła w prostopadłościanie P, to jest w nim
całkowalna.