POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ MECHANICZNY
KATEDRA MECHANIKI I INFORMATYKI STOSOWANEJ
LABORATORIUM MECHANIKI TECHNICZNEJ
Kod:
Instrukcja do ćwiczenia
DOŚWIADCZALNE WYZNACZANIE SIŁY KRYTYCZNEJ
PRZY WYBOCZENIU SPRĘŻYSTYM PRĘTA PROSTEGO
Autor: ADAM TOMCZYK
BIAŁYSTOK
2011
2
Cel ćwiczenia
Celem ćwiczenia jest doświadczalne wyznaczenie wartości siły krytycznej podczas
ś
ciskania pręta smukłego i porównanie tej siły z wartościami teoretycznymi. Badania należy
przeprowadzić dla prętów wykonanych z co najmniej dwóch rożnych materiałów o znacznie
różniących się właściwościach wytrzymałościowych.
Podstawy teoretyczne
Zagadnienie wyboczenia pręta prostego jest przedstawicielem szerszej grupy
zagadnień związanych z tzw. statecznością ustrojów. Zasadniczym problemem w tego typu
zagadnieniach jest znalezienie wartości pewnej siły nazywanej siłą krytyczną, przekroczenie
której powoduje utratę stateczności. Aby fizycznie przybliżyć czytelnikowi ten problem
rozważmy pręt pryzmatyczny o przekroju prostokątnym obciążony pewną osiową siłą P (zob.
np.
Niezgodziński T. i Niezgodziński M., 2004
). Rozpatrzmy sytuację, w której wartość siły
P jest na tyle mała, że po przyłożeniu pewnej siły poprzecznej Q (patrz rys. 1) pręt ulegnie
wyboczeniu jednak po usunięciu tej siły powraca do swego pierwotnego prostoliniowego
kształtu. W takiej sytuacji ustrój nazywamy statecznym. Jeżeli jednak siłę P będziemy
zwiększać to dojdziemy do sytuacji, w której po przyłożeniu poprzecznej siły Q pręt ulegnie
wyboczeniu jednak po jej zdjęciu już nie powróci do pierwotnej prostoliniowej postaci
pozostając w stanie równowagi krzywoliniowej. Oczywistym jest, że taki stan jest daleko
bardziej niebezpieczny, gdyż jak łatwo zauważyć oprócz zagadnienia prostego ściskania pręta
mamy tez do czynienia ze zginaniem. Omówiona powyżej sytuacja utraty stateczności
dotyczy tzw. prętów smukłych kiedy siła ściskająca działa w osi pręta. W praktyce wykonanie
pręta idealnie prostoliniowego jest w zasadzie niemożliwe. W takich przypadkach imperfekcji
kształtu należy więc mówić o mimośrodowym ściskaniu prętów smukłych. Tego typu
zagadnienia również zastały już dawno rozwiązane zaś czytelnik znajdzie informacje na ten
temat w odnośnej literaturze przedmiotu (np.
Niezgodziński T. i Niezgodziński M., 2004
).
Należy także przypomnieć, że zjawisko wyboczenia jest groźne jedynie dla tzw. prętów
smukłych. W przypadku tzw. prętów krępych nie jest ono brane pod uwagę. Oczywiście
granica pomiędzy prętem krępym i smukłym jest umowna.
Rys. 1. Schematyczne przedstawienie warunku
równowagi
prostoliniowej
oraz
utraty
stateczności przy ściskaniu pręta smukłego
(np.
Niezgodziński T. i Niezgodziński M.,
2004
)
Rys. 2. Schemat rozpatrywanego zagadnienia
3
Wartość wspomnianej wcześniej siły krytycznej można określić teoretycznie
wykorzystując równanie różniczkowe linii ugięcia pręta wyprowadzone przez Eulera.
Rozpatrzmy zatem pręt pryzmatyczny o długości l podparty przegubowo na końcach.
Załóżmy, że mamy do czynienia z sytuacją, w której siła osiowa P osiąga wartość krytyczną
P
kr
powodującą wyboczenie. Uwzględniając wprowadzony na rysunku 2 układ
współrzędnych (x,y) równanie różniczkowe linii ugięcia przyjmuje postać:
2
kr
2
d
d
y
EJ
P y
x
= −
.
(1)
Dzieląc obie strony powyższego równania przez sztywność EJ i przekształcając otrzymamy:
2
kr
2
d
0
d
P
y
y
EJ
x
+
=
.
(2)
Wprowadźmy oznaczenie:
2
kr
P
EJ
α
=
,
(3)
wówczas równanie (2) przyjmie postać:
2
2
2
d
0
d
y
y
x
α
+
=
.
(4)
Tego typu równania rozwiązujemy poszukując całki szczególnej mając do dyspozycji całkę
ogólną w postaci:
cos
sin
0
y
C
x
D
x
α
α
=
+
=
.
(5)
Stałe C i D znajdziemy formułując warunki brzegowe dla rozpatrywanego zagadnienia
(patrz rys. 2). Ponieważ pręt podparty jest na obu końcach tj. dla x = 0 i x = l poziome
przemieszczenie w tych punktach musi być równe zeru, zatem warunki brzegowe są
następujące:
(
)
(
)
1)
0
0,
2)
0.
y x
y x
l
=
=
= =
(6)
Korzystając z warunku 1) tj. podstawiając x = 0 otrzymamy C = 0. Z drugiego warunku
(pamiętając, że C = 0) dostaniemy:
sin
0
D
l
α
=
.
(7)
Równanie (7) jest spełnione w dwóch przypadkach. Po pierwsze kiedy D = 0 i wówczas
mamy do czynienia z trywialnym zagadnieniem kiedy brak jest wyboczenia, czyli postać
równowagi pręta jest prostoliniowa. Drugi przypadek dotyczy sytuacji gdy:
sin
0
l
α
=
.
(8)
Powyższe równanie jest spełnione dla
α
l =
π
n, gdzie n = 1, 2, 3 … . Pamiętając, że
α
2
= P
kr
/EJ mamy:
2
2
kr
2
P
n
EJ
l
α
2
π
=
=
.
(9)
4
Zatem wartość siły krytycznej przy której może nastąpić utrata stateczności określamy z
zależności:
2
2
kr
2
n
EJ
P
l
π
=
.
(10)
Należy się jeszcze zastanowić, który z dwóch głównych momentów bezwładności J należy
uwzględnić w obliczeniach – J
min
czy J
max
? Jeżeli np. rozpatrzymy pręt o przekroju
prostokątnym i wymiarach b
×
h, przy czym h > b, to w której z dwóch głównych centralnych
płaszczyzn bezwładności pręta nastąpi wyboczenie? Oczywiste jest, że pręt wyboczy się w
płaszczyźnie prostopadłej do dłuższego z boków. Zatem we wzorze (10) należy uwzględnić
minimalny moment bezwładności:
2
2
min
kr
2
n
EJ
P
l
π
=
.
(11)
Zwróćmy teraz uwagę że dla różnych wartości n mamy różne wartości siły krytycznej tj.:
dla n = 1:
min
kr
2
EJ
P
l
2
π
=
(12)
dla n = 2:
min
kr
2
EJ
P
l
2
4π
=
(13)
dla n = 3:
min
kr
2
EJ
P
l
2
9π
=
(14)
. . . itd.
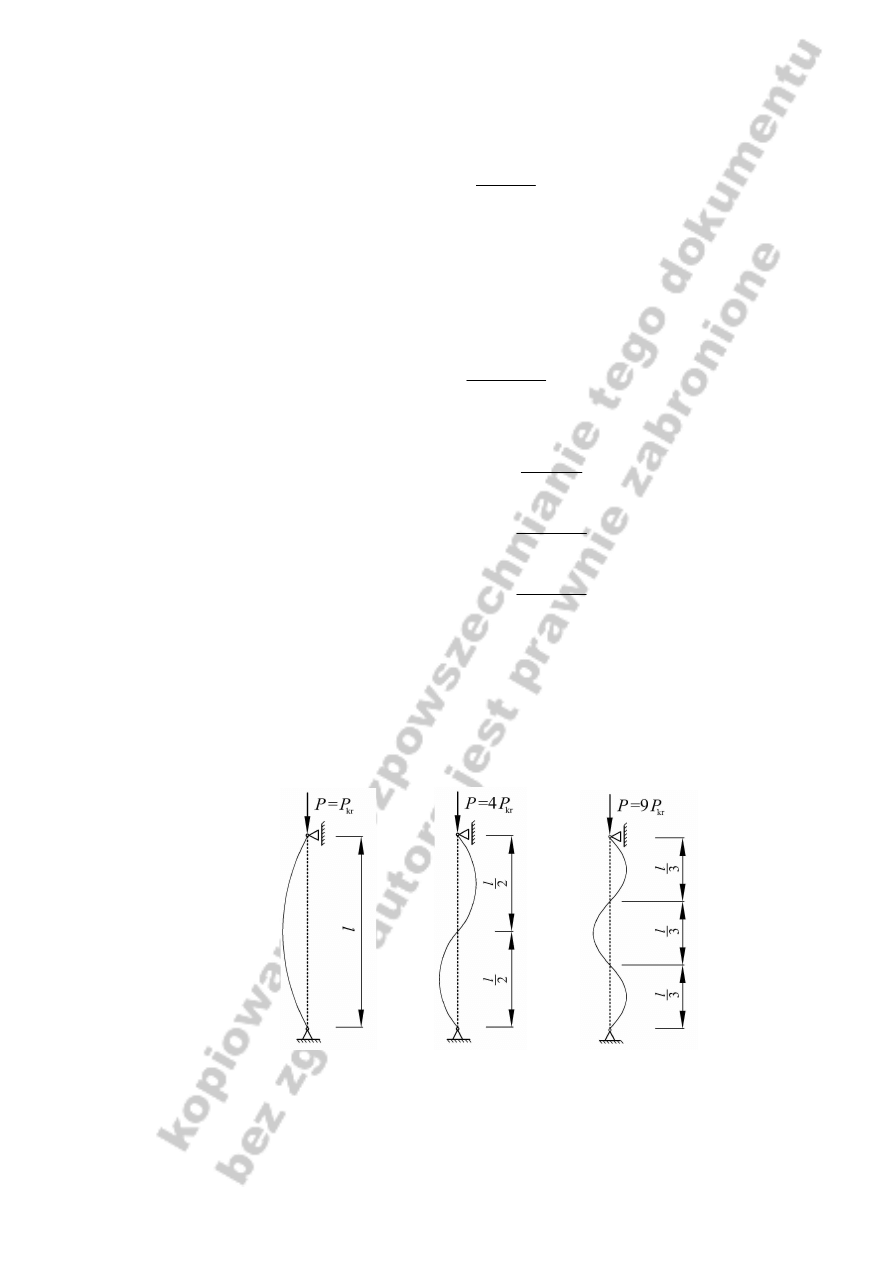
Pojawia się zatem pytanie jak fizycznie interpretować te różne wartości n oraz którą
uwzględniać w obliczeniach. Otóż przyjęcie n = 2 oznaczałoby fizycznie, że pomimo
przegubowego podparcia na końcach pręt obciążony siłą osiową wyboczy się w sposób
przedstawiony na rysunku 3b.
a)
b)
c)
Rys. 3. Interpretacja graficzna różnych wartości n we wzorze (11): a) n = 1, b) n = 2, c) n = 3
Oczywiście taka sytuacja jest możliwa ale tylko wtedy gdybyśmy „pomogli” przyjąć prętowi
taką właśnie postać linii wyboczenia. Sprawa nie budziłaby wątpliwości gdyby w połowie
5
długości pręta umieścić podporę przesuwną. Podobnie gdy przyjmiemy n = 3 to linia
wyboczenia powinna wyglądać jak na rysunku 3c czyli tak gdyby co 1/3 długości podeprzeć
pręt podporami przesuwnymi. Tak więc w przypadku pręta podpartego przegubowo na
końcach i obciążonego siła osiową jedyną fizycznie uzasadnioną postacią wyboczenia jest
postać przedstawiona na rysunku 3a. A zatem sens fizyczny ma jedynie wartość n = 1.
Powyżej przedstawiono rozwiązanie dla konkretnego przypadku podparcia pręta.
Oczywiście analogiczne rozumowanie możemy przeprowadzić dla różnych przypadków
zamocowania. Będzie to skutkowało przede wszystkim innymi niż tu wykorzystywane
warunkami brzegowymi. Gdybyśmy taką analizę przeprowadzili okazałoby się, że zależność
określająca siłę krytyczną zawsze ma postać:
2
min
kr
2
w
EJ
P
l
π
=
.
(15)
Przy czym wielkość l
w
jest długością wyboczeniową pręta, która nie zawsze pokrywa się z
długością rzeczywistą l i zależy tylko od warunków podparcia:
w
l
l
µ
=
.
(16)
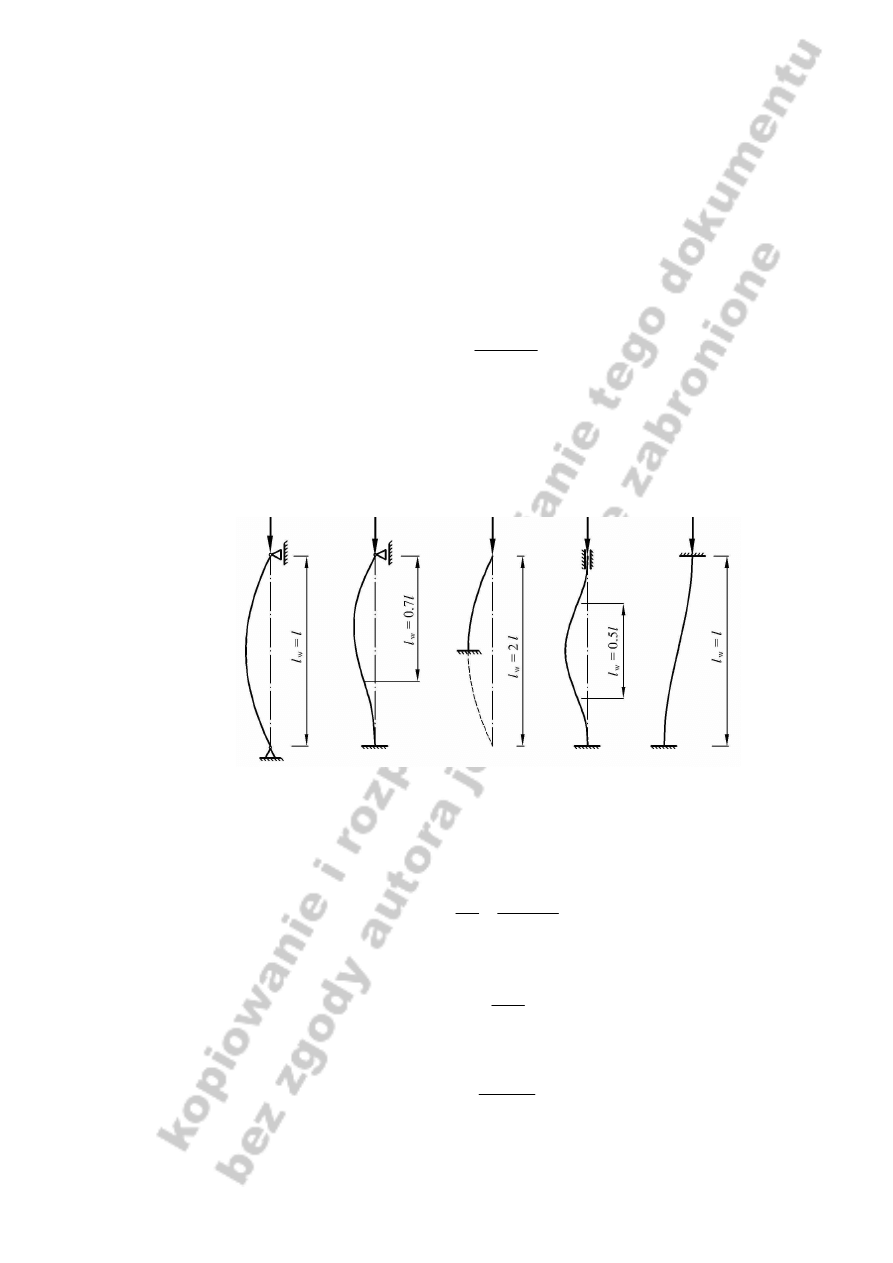
Współczynnik
µ
dla wybranych sposobów podparcia zilustrowano na rysunku 4.
Rys. 4. Współczynniki redukcyjne
µ
dla typowych warunków podparcia
pręta (np.
Niezgodziński T. i Niezgodziński M., 2004
)
Znajomość siły krytycznej pozwala na określenie naprężeń krytycznych panujących w
przekroju w chwili wyboczenia:
kr
min
kr
2
w
P
EJ
A
Al
σ
2
π
=
=
.
(17)
Odnajdując w powyższym wzorze minimalny geometryczny promień bezwładności:
2
min
min
J
i
A
=
,
(18)
możemy go przedstawić w postaci:
2
min
kr
2
w
Ei
l
σ
2
π
=
.
(19)
Pamiętając, że smukłość zdefiniowana jest jako:
6
w
min
l
s
i
=
,
(20)
otrzymujemy ostatecznie:
kr
2
E
s
σ
2
π
=
.
(21)
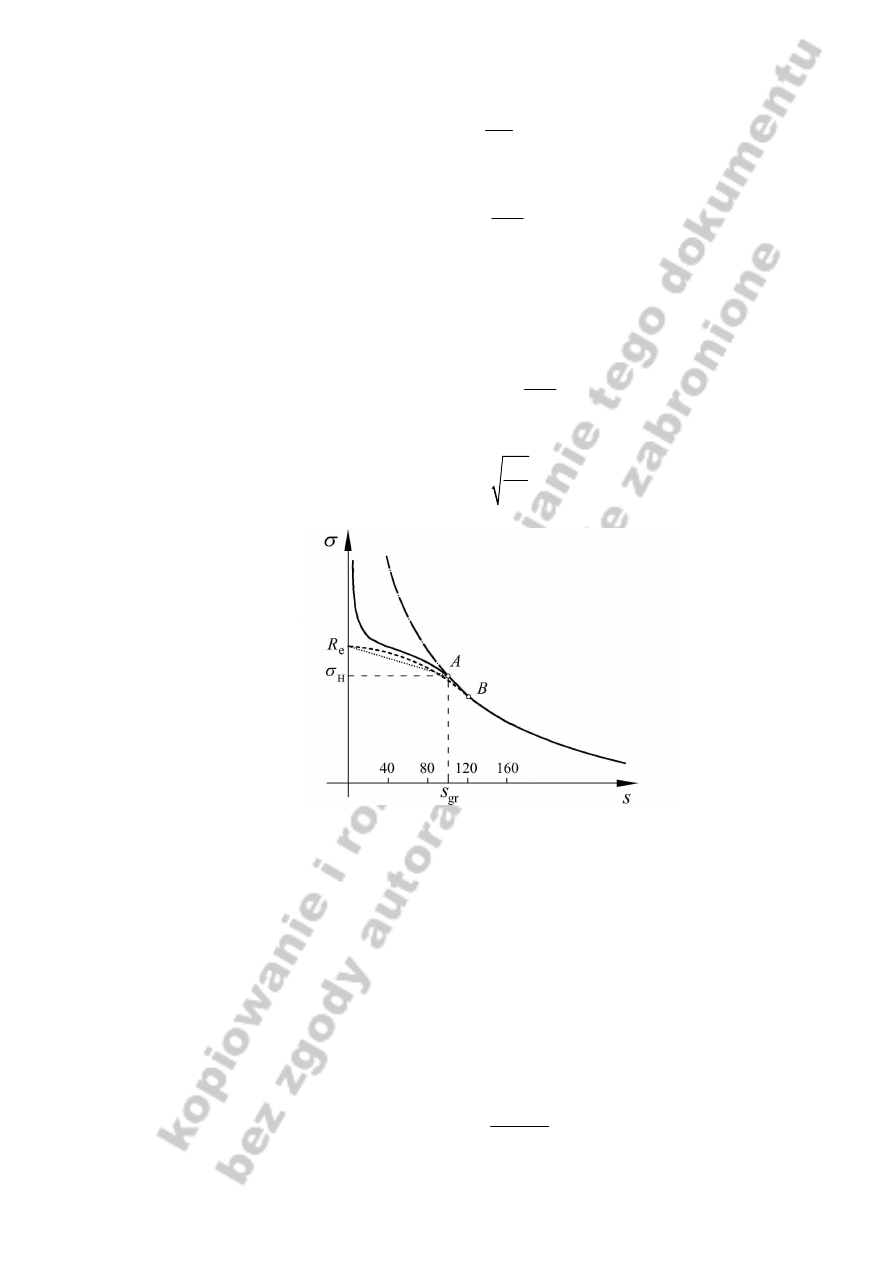
Jak wynika z powyższego wzoru Eulera zależność naprężeń krytycznych od smukłości ma
charakter hiperboliczny (linia kropka-kreska na rysunku 5). Hiperbola ta jednak pokrywa się z
rzeczywistą krzywą
σ
(s) jedynie od pewnej charakterystycznej wartości smukłości zwanej
smukłością graniczną s
gr
. Wartość smukłości granicznej zależy jedynie od rodzaju materiału i
odpowiada ona granicy proporcjonalności zatem:
( )
kr
gr
2
gr
E
s
s
σ
σ
2
π
=
=
.
(22)
Smukłość graniczną określimy więc ze wzoru:
gr
H
E
s
σ
= π
.
(23)
Rys. 5. Interpretacja graficzna naprężenia krytycznego
w zakresie sprężystym i sprężysto-plastycznym
(np.
Niezgodziński T. i Niezgodziński M., 2004
)
Jeżeli smukłość rzeczywista pręta określona z zależności (20) będzie większa od
granicznej, wówczas wyboczenie następuje w zakresie liniowo-sprężystym i możemy
stosować zależności (15) i (17). Z chwilą gdy smukłość rzeczywista jest mniejsza od
granicznej mamy do czynienia z wyboczeniem sprężysto-plastycznym i musimy korzystać z
innych zależności. Najczęściej w zagadnieniach wyboczenia sprężysto-plastycznego stosuje
się teorie Tetmajera-Jasińskiego lub Johnsona-Ostenfelda (zob.
Niezgodziński T. i
Niezgodziński M., 2004
). Zależność Tetmajera-Jasińskiego sugeruje by opisywać sprężysto-
plastyczny odcinek na krzywej
σ
(s) linią prostą (linia kropkowa na rys. 5). Linia ta łączy
punkt odpowiadający granicy plastyczności R
e
oraz punkt A odpowiadający granicy
proporcjonalności
σ
H
:
e
H
kr
e
gr
R
R
s
s
σ
σ
−
=
−
.
(24)
7
1
6
Inną propozycją opisu zakresu sprężysto-plastycznego wyboczenia jest propozycja Johnsona-
Ostenfelda przybliżająca ten zakres parabolą (linia kreskowa na rys. 5). Wierzchołek tej
paraboli przechodzi przez punkt wytyczający granicę plastyczności zaś sama parabola jest
styczna do hiperboli Eulera w pewnym punkcie B:
2
2
e
kr
e
2
4
R
R
s
E
σ
π
=
−
.
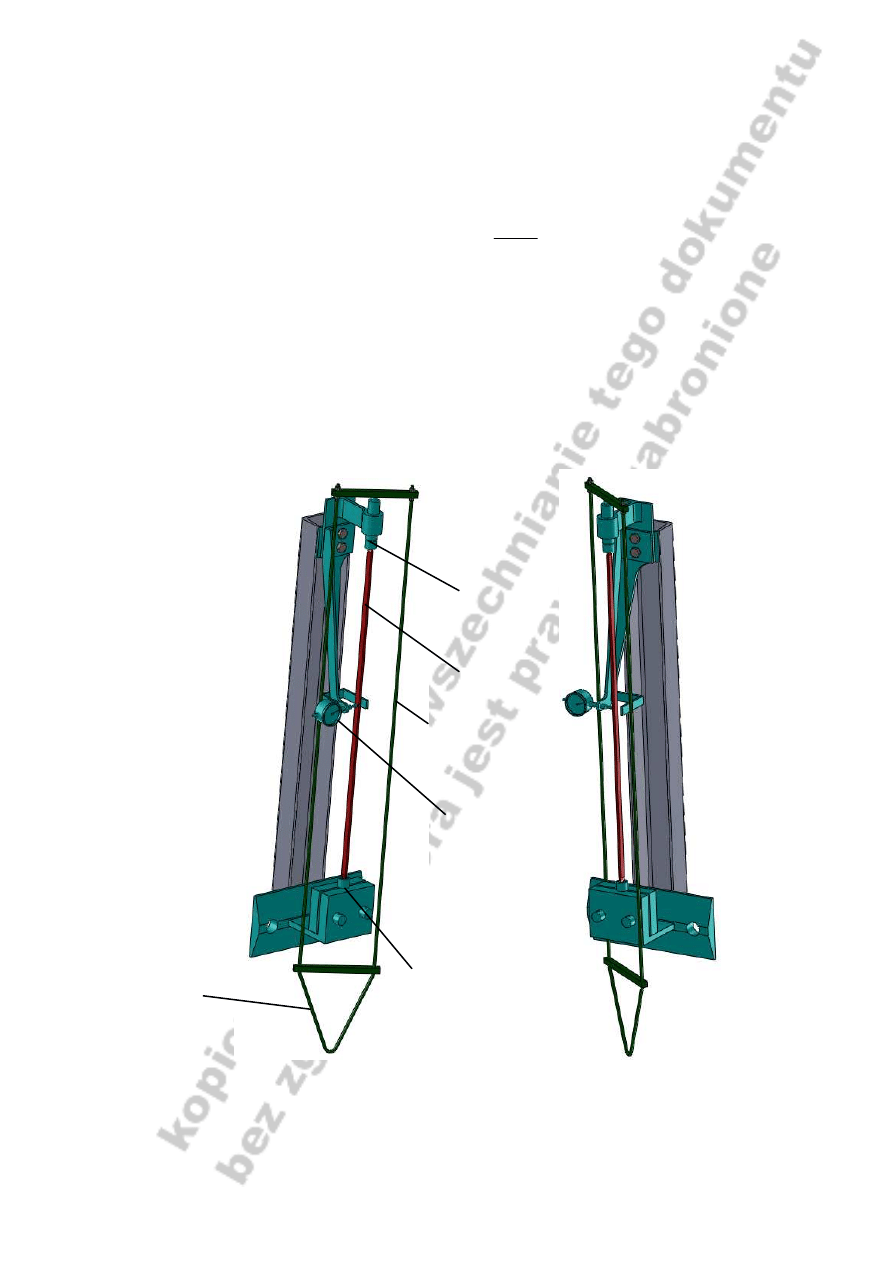
Stanowisko do badań
Przedmiotem badań są pręty pryzmatyczne 1 wykonane z dwóch różnych materiałów.
Pręt montowany jest w podporze stałej 2 i ruchomej 3 w sposób przegubowy. Obciążanie
pręta siła osiową odbywa się za pośrednictwem ramy 6 poprzez umieszczanie na szalce
uchwytu 5 ciężarków. Pomiaru przemieszczenia (wyboczenia) należy dokonać za pomocą
czujnika zegarowego 4.
Rys. 6. Dwa różne widoki stanowiska pomiarowego: 1 – badany pręt, 2 – przegubowa
podpora nieruchoma, 3 – przegubowa podpora przesuwna, 4 czujnik zegarowy, 5 – uchwyt
do montażu szalki z ciężarkami, 6 – rama układu obciążającego
3
4
2
5
8
Przebieg ćwiczenia
1)
określić wymiary przekroju poprzecznego pręta oraz jego długość rzeczywistą,
2)
zamocować pręt w uchwytach (podporach) przyrządu umożliwiającego realizację
osiowego ściskania pręta,
3)
sprawdzić prawidłowość podparcia oraz działanie czujnika zegarowego,
4)
określić długość wyboczeniową pręta,
5)
obciążać pręt umieszczając kolejne ciężarki na szalce przyrządu notując wskazania
czujnika,
6)
zaprzestać dalszego obciążania z chwilą gdy pręt zacznie się wybaczać nieprzerwanie
bez dalszego zwiększania obciążenia (utraci stateczność),
7)
wyniki pomiarów w postaci siły P
d
oraz ugięcia f zestawić w tabeli 1.
Opracowanie wyników pomiarów
Tab. 1. Zestawienie wyników pomiarów
materiał 1
Materiał 2
Nr
pomiaru
P
d
[N]
f [m]
P
d
[N]
f [m]
1
2
3
…
…..
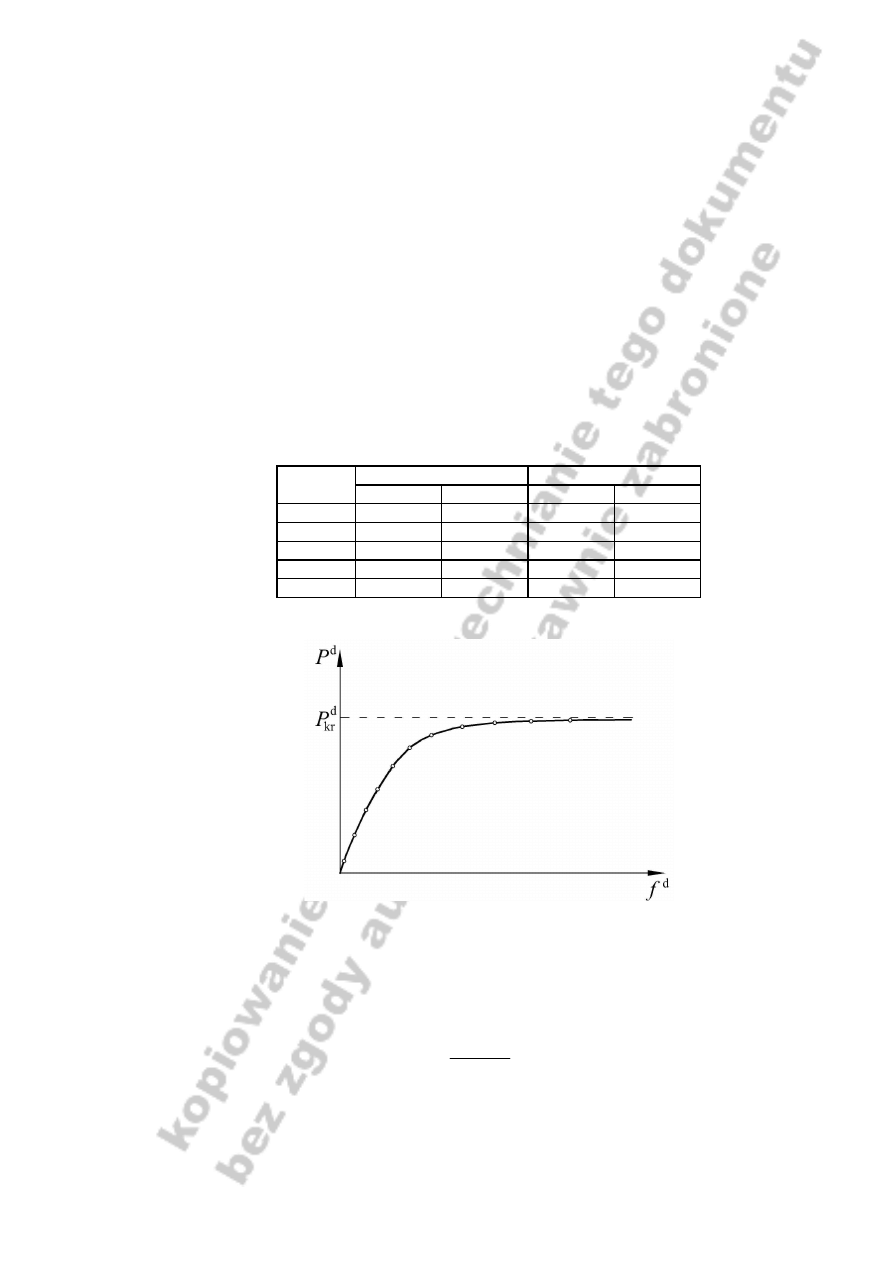
Rys. 7. Orientacyjny charakter wykres zależności siła
– przemieszczenie uzyskanych w doświadczeniu
Na postawie wyników z tabeli 1 sporządzić wykresy zależności siła doświadczalna P
d
– przemieszczenie f dla prętów wykonanych z dwóch materiałów. Określić błąd pomiędzy
siłą wyznaczoną na drodze badań doświadczalnych a siłą określoną teoretycznie:
d
kr
kr
kr
100%
P
P
P
∆
−
=
.
(17)
9
Tab. 2. Wartości siły krytycznej dla prętów wykonanych z
dwóch różnych materiałów
Materiał
kr
[N]
P
d
kr
[N]
P
∆∆∆∆
[%]
materiał 1
materiał 2
Wnioski
We wnioskach przedyskutować między innymi ewentualne przyczyny powstawania
różnic w wartościach siły teoretycznej i doświadczalnej.
Literatura
1.
Niezgodziński M.E., Niezgodziński T., Wytrzymałość Materiałów, PWN, Warszawa
2004.
2.
Brzoska Z., Wytrzymałość materiałów, PWN, W-wa 1983.
3.
Dyląg Z., Jakubowicz A., Orłoś Z., Wytrzymałość Materiałów t. I, II, WNT, W-wa 1997.
4.
Walczak J., Wytrzymałość materiałów oraz podstawy teorii sprężystości i plastyczności,
t. 1, 2, 3, WNT, W-wa 1977.
5.
Zielenica J., Wytrzymałość materiałów, Wydaw. Polit. Poznańskiej, 1996.
6.
Rajfert T., Rżysko J., Zbiór zadań ze statyki i wytrzymałości materiałów, PWN,
Warszawa1979.
7.
Banasiak M., Grossman K., Trombski M., Zbiór zadań z wytrzymałości materiałów,
PWN, Warszawa 1992.
Przykładowe pytania sprawdzające
1.
Wyprowadzić zależność opisującą linię wyboczenia sprężystego pręta smukłego o
długości rzeczywistej l dla dowolnego schematu podparcia pręta.
2.
Zdefiniować pojęcia minimalnego promienia bezwładności, smukłości rzeczywistej i
smukłości granicznej pręta.
3.
Scharakteryzować wyboczenie pręta w zakresie sprężysto-plastycznym.
4.
Jak zmieni się smukłość pręta o długości
rzeczywistej l jeżeli warunki jego
podparcia zmienimy z A na B zaś
wymiary
przekroju
poprzecznego
wzrosną dwukrotnie.
5. Pręt podparty jak na rysunku obciążono
siłą P. Który z podanych obok
przekrojów należałoby dobrać (i dla-
czego) aby pręt przeniósł większe
obciążenie. Smukłość pręta jest większa
od granicznej.