Elementyopracowywaniadanychpomiarowychdlaćwiczenia28

Pomiar stałej siatki dyfrakcyjnej za pomocą mikroskopu 

 

W celu pomiaru stałej siatki dyfrakcyjnej musimy policzyć liczbę odstępów między rysami siatki dy-

frakcyjnej na możliwie długim odcinku. Jeśli przez   oznaczymy liczbę tych odstępów, a przez   długość tego 
odcinka, to stała siatki   wynosi 

= . 

 
Liczba   w powyższym wzorze ma wartość dokładną (nie jest obarczona niepewnością). Jednak w przypadku 
małych powiększeń mikroskopu zliczenie liczby odstępów między rysami może być bardzo kłopotliwe. Dla-
tego najlepiej dokonać tego pomiaru na dużym powiększeniu (z obiektywem. x100). Niepewność wyznacze-
nia stałej siatki dyfrakcyjnej będzie w tym przypadku związana jedynie z niepewnością pomiaru długości   i 
będzie równa 
 

=

. 

 
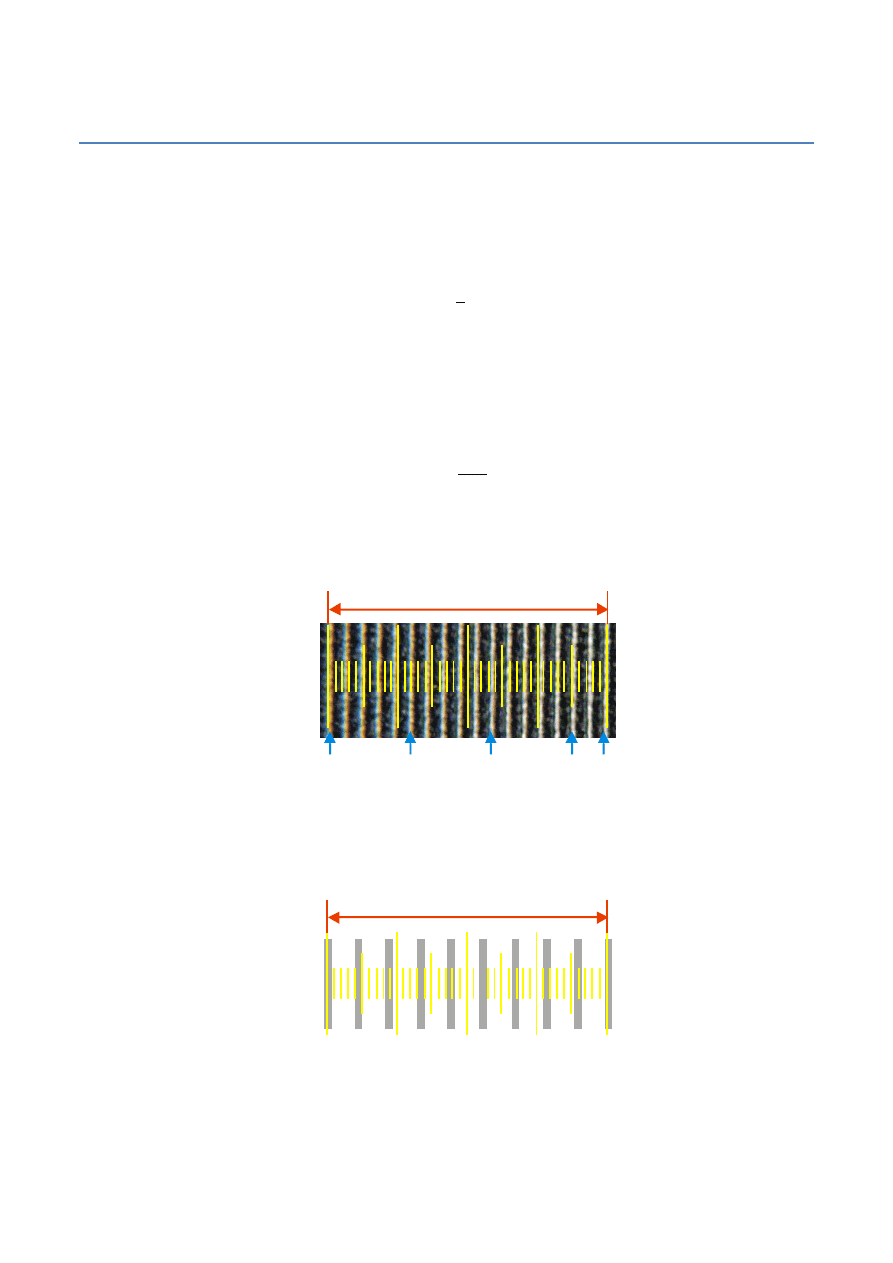
Na poniższym rysunku pokazano obraz siatki dyfrakcyjnej widziany pod mikroskopem wraz ze skalą okularu. 
Na odcinku o długości   (równym 40 działkom skali okularu) widzimy 17 odstępów pomiędzy rysami siatki 
dyfrakcyjnej. 
 

0

5

10

15 17

k =

l

 

 
Długości   naszego odcinka nie znamy,  gdyż nie znamy odstępów między działkami skali okularu. Musimy 
zatem  wykonać  pomiar  długości  tego  odcinka.  W  tym  celu  pod  obiektyw  mikroskopu  podkładamy  skalę 
wzorcową stosując to same powiększenie, którego użyliśmy podczas liczenia rys siatki. Przykładowy obraz tej 
sytuacji pokazuje poniższy rysunek. 

 

0

5

9

k’ =

l

 

 
Na przykładowym rysunku widzimy, że interesujący nas odcinek   (40 działek skali okularu) ma długość ok. 

= 9 działek skali wzorcowej. Jeśli przez   oznaczymy odległość między działkami skali wzorcowej (u 

nas 

= 0,01mm) to 

= ∙

. 

Niepewność pomiaru długości   naszego odcinka możemy wyliczyć przyjmując, że połowa szerokości prze-
działu granicznego jest równa połowie najmniejszej działki skali wzorcowej 

Δ =

/2, a rozkładem statycz-

nym zmiennej losowej jest rozkład trójkątny, czyli 
 

=

2√6

. 

 
Ostatecznie stałą siatki i niepewność jej wyznaczenia wyliczymy ze wzorów 
 

=

∙

,

=

2 √6

. 

 

Pomiar długości fali 

 
Długość fali wyliczamy ze wzoru 
 

=

+

 

 
Niepewność standardową pomiaru pośredniego długości fali liczymy ze wzoru.  
 

=   

! + " 

! +  

! #   + !  

 
Jeśli pomiary wykonaliśmy dla trzech rzędów ugięcia, to średnia ważona długość fali wyniesie 
 

=

$

$

+

+

%

%

1

$

+ 1 + 1

%

, 

 
a średnia ważona niepewność 

=

1

1

$

+ 1 + 1

%

. 

 
W przypadku pomiarów dla dwóch rzędów ugięcia w powyższych wzorach nie będzie wyrazów z indeksem 3, 
czyli 
 

=

$

$

+

1

$

+ 1

,

=

1

1

$

+ 1

.