
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
POLITECHNIKI WARSZAWSKIEJ
Zakład Teorii Maszyn i Robotów
Laboratorium Podstaw Automatyki i Sterowania IV
Instrukcja do ćwiczenie nr 6
Regulacja impulsowa
2
I. Cel ćwiczenia
Celem ćwiczenia jest poznanie typowych własności liniowych układów regulacji impulsowej oraz
poznanie i wypróbowanie prostej metody doboru optymalnych nastaw linowego regulatora
impulsowego P oraz PI.
II. Wprowadzenie
II.1. WSTĘP
Coraz częściej w technice znajdują zastosowanie układy sterowania i regulacji, w których występują
sygnały dyskretne
. Istnienie sygnałów dyskretnych wynika niekiedy z fizycznych zasad
działania urządzeń (np. radiolokacja), a ostatnio z coraz powszechniejszego stosowania maszyn
cyfrowych (komputery) w technice sterowania.
Współpraca urządzeń, w których sygnały mają charakter ciągły z urządzeniami cyfrowymi, wymaga
dyskretyzacji
sygnałów ciągłych. Dyskretyzacja może dotyczyć zarówno wartości sygnału jak i
czasu.
Sygnał y(t) nazywamy impulsem, jeśli spełnia warunek: y(t) = c w przedziale czasu ∆t oraz y(t) ≠
c poza tym przedziałem, przy czym c = const. Zakłada się, że przedział ∆t jest mały w porównaniu z
czasem trwania procesów przejściowych w danym układzie automatyki. Przetworzenie sygnału
ciągłego w sygnał impulsowy może się odbywać w różny sposób, w zależności od kształtu impulsów
oraz sposobu ich modulacji
. Przez modulację rozumie się uzależnienie parametrów opisujących
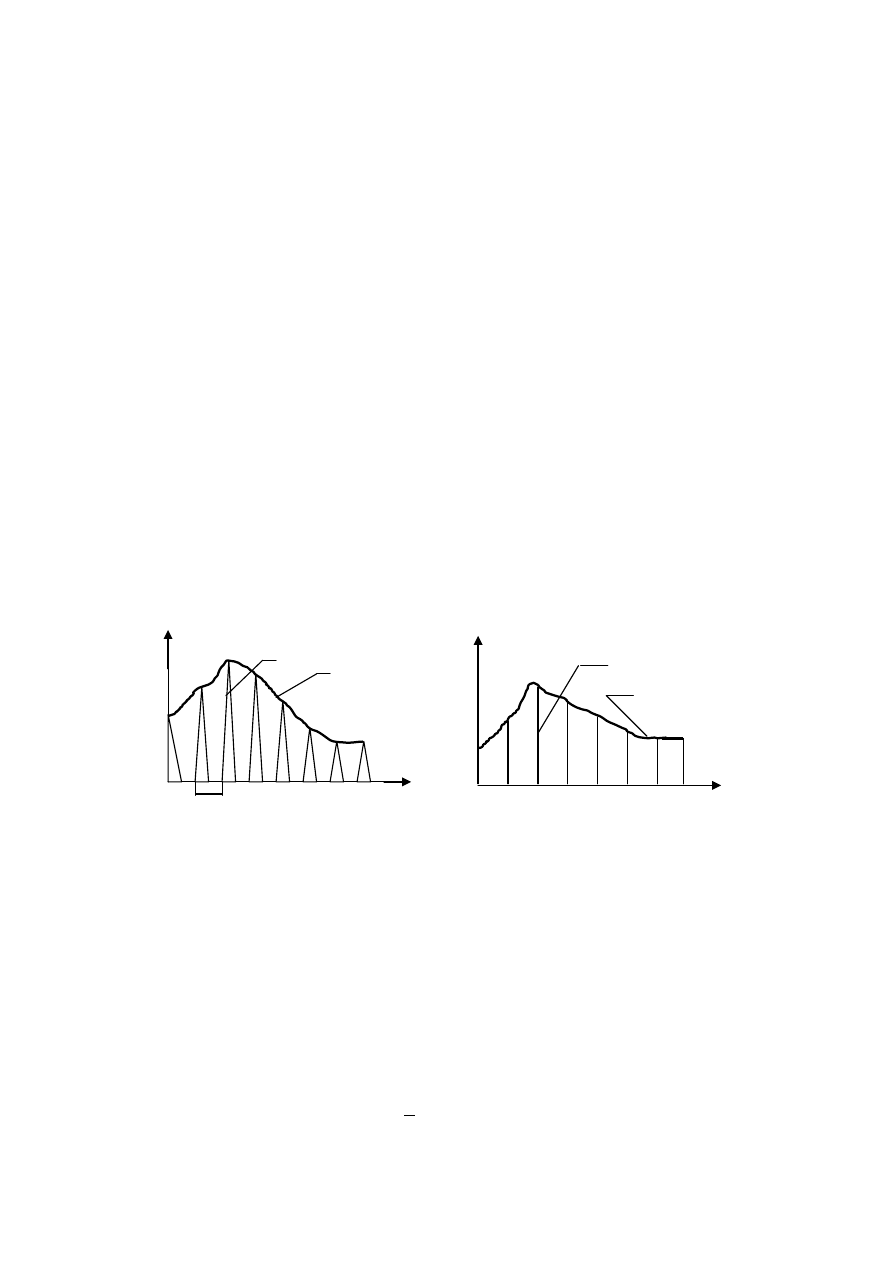
impuls od przebiegu ciągłego, który jest przetwarzany na ciąg impulsów. Na rys. 1 pokazano sygnał
impulsowy y
*
(t), w którym wartości sygnału ciągłego y(t) w chwilach 0, T
p
, 2T
p
, ... modulują
amplitudy impulsów trójkątnych. Przedział czasu między chwilami pojawienia się kolejnych
impulsów nazywa się czasem (okresem) impulsowania T
p
, a urządzenie realizujące
modulację impulsową – impulsatorem.
Rys.1. Modulacja impulsów trójkątnych Rys. 2. Modulacja impulsów „szpilkowych”
Na ogół T
p
jest ustalony, a
le bywają też układy, w których okres impulsowania jest zmienny.
Szczególne znaczenie w teorii układów impulsowych ma modulacja (rys.2) polegająca na
przetworzeniu sygnału ciągłego y(t) na ciąg impulsów „szpilkowych” y(kTp) o amplitudzie równej
wartości sygnału w chwilach impulsowania. Są one ze sobą powiązane relacją:
y(t) = y(kT
p
), gdy t = kT
p
, przy czym k = 1, 2, ...
( 1.1 )
Każdy impulsator oprócz elementu realizującego modulację pokazaną na rys. 2 posiada element ciągły
nazywany ekstrapolatorem
, dla którego sygnał y
1
*
(t) jest sygnałem wejściowym (rys. 3). W
omawianym laboratoryjnym układzie regulacji zastosowano ekstrapolator zerowego
rzędu
, który zapamiętuje w chwilach t = kT
p
wartość sygnału y(kT
p
) przez cały okres impulsowania
T
p
. Taki
ekstrapolator jest zwykle członem liniowym o transmitancji operatorowej:
( )
(
)
s
T
p
p
e
s
s
G
−
−
= 1
1
( 1.2 )
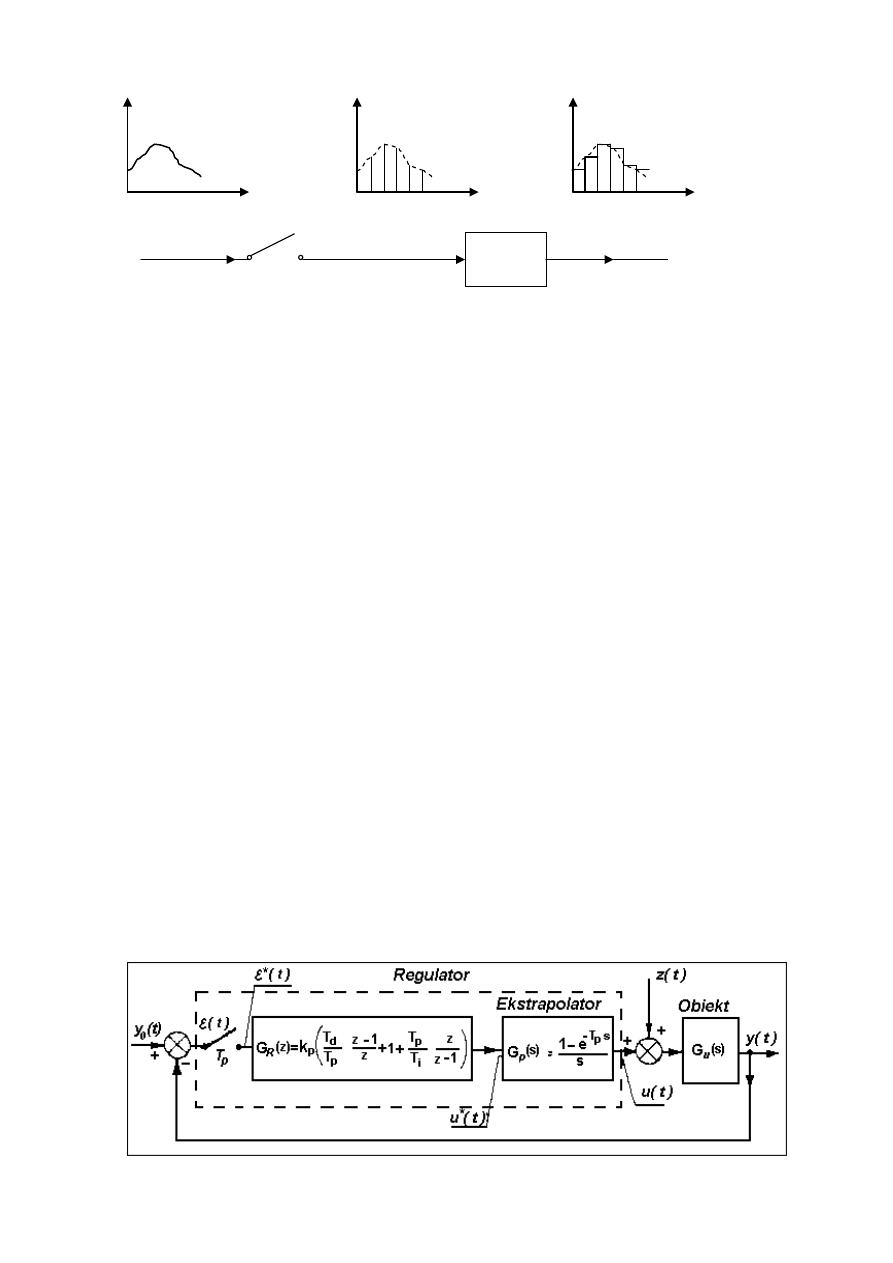
Na rys. 3 pokazano schemat blokowy impulsatora wraz z ekstrapolatorem oraz przebieg sygnałów.
Element impulsujący oznaczono symbolem przełącznika.
y(t)
y
*
(t)
y(t)
y
*
(t)
y(t)
y
1*
(t)
y(t)
y
1
*
(t)
t
t
T
p
2T
p
...
T
p
3
Rys. 3. Schemat blokowy impulsatora oraz przebieg sygnałów
Podobnie jak dla układów ciągłych, w celu uproszczenia analizy układów dyskretnych, wprowadza się
transformację przebiegów czasowych sygnałów. Najbardziej rozpowszechniona jest
transformacja Z
. Przekształcenie Z, nazywane dyskretnym przekształceniem
Laplace’a
jest analogiczne do ciągłego przekształcenia L Laplace’a i zdefiniowane następująco:
( )
[ ]
( )
( )
,
*
0
z
F
z
kT
f
t
f
Z
k
k
p
=
=
−
∞
=
∑
( 1.3 )
gdzie:
p
sT
e
z
−
=
oraz s –
parametr przekształcenia Laplace’a.
Warunki istnienia przekształcenia Z są takie same jak dla przekształcenia L, lecz dotyczą tylko
wartości funkcji f(t) w chwilach t = kT
p
, k = 1, 2, ... . Istnieje także przekształcenie odwrotne
względem (1.3). Jest ono jednoznaczne względem ciągu wartości f(kT
p
Warto tu podkreślić, że przekształcenie Z transformuje do dziedziny zmiennej zespolonej z ciąg
impulsów „szpilkowych” utworzonych z funkcji f(t) w chwilach odległych w czasie o T
) funkcji f(t), a nie jest
jednoznaczne względem tej funkcji.
p
, począwszy
od t = 0.
II.2. REGULACJA IMPULSOWA
Jednym ze sposobów poprawienia (korekcji) własności statycznych i dynamicznych układu jest
doda
nie elementu korekcyjnego w gałęzi głównej układu regulacji. Elementy takie są standaryzowane
i noszą nazwę regulatorów. W badanym w ćwiczeniu układzie regulacji impulsowej (rys.4)
zastosowano regulator impulsowy, który jest szeregowym połączeniem dwóch członów:
-
impulsowego liniowego o przepustowości G
R
*
-
ciągłego ekstrapolatora zerowego rzędu o przepustowości G
(z);
P
Regulator przekształca ciągły sygnał uchybu ε(t) na ciąg impulsów „szpilkowych” ε
(s);
*
(t) o amplitudzie
równej wartości sygnału ε(t) w chwilach będących wielokrotnościami okresu T
p
. Następnie sygnał ten
jest przekształcany na inny ciąg impulsów „szpilkowych” u
*
(t), zgodnie z funkcją przejścia G
R
(z).
Sygnał u
*
Re
gulator połączono szeregowo z ciągłym członem liniowym o przepustowości G
(t) po przejściu przez ekstrapolator jest przetwarzany na sygnał schodkowy u(t).
u
Na wejściu układu jest podawany sygnał sterujący y
(s).
0
(t), sygnałem wyjściowym (regulowanym) jest
y
(t). Sygnał zakłócający z(t) został zredukowany do sygnału wejściowego do obiektu.
Rys. 4. Schemat badanego układu regulacji
t
t
t
y
y
*
y
1
*
y(t)
T
p
y
1
*
(t)
y
*
(t)
G
p
(s)
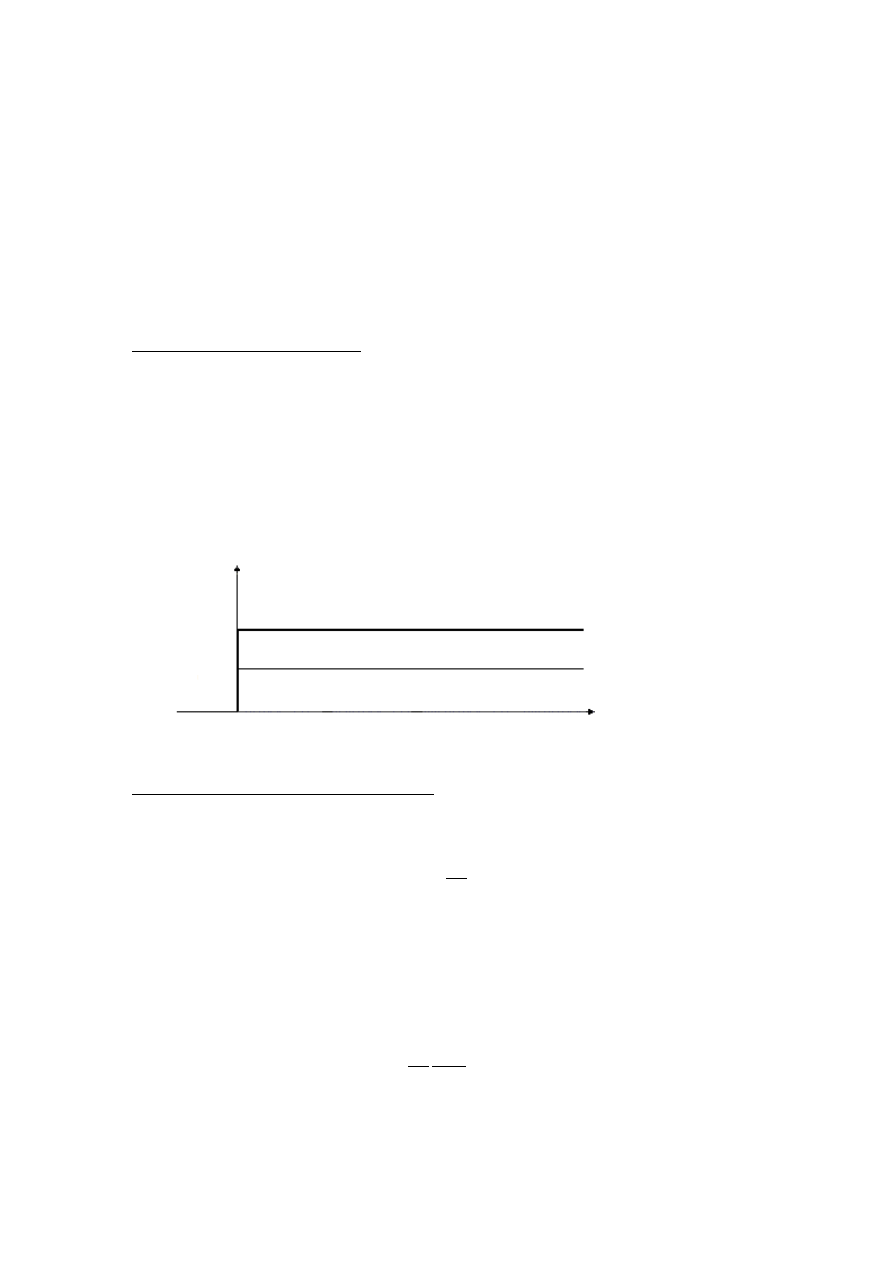
4
II.3. LINIOWE REGULATORY IMPULSOWE
Najbardziej rozpowszechnione są regulatory liniowe, realizujące działania proporcjonalne (regulator
P), całkujące (regulator I), różniczkujące (regulator D). Praktycznie są realizowane regulatory typu P,
I, PI, PD, PID, działające w sposób ciągły lub dyskretny.
W wersji dyskretnej operacje całkowania i różniczkowania są zastąpione przez operacje dodawania i
odejmowania dyskretnych wartości sygnału.
W dalszej części omówione zostanie pokrótce działanie regulatorów impulsowych typu P, PI,
PD, PID, poprzez podanie zależności między dyskretnym ciągiem sygnałów (szpilkowych)
wejściowych ε(kT
p
), a sygnałem wyjściowym (szpilkowym) u(kT
p
) w chwili t = kT
p
oraz
charakterystyk skok
owych regulatorów połączonych z ekstrapolatorem zerowego rzędu.
REGULATOR P (proporcjonalny)
Równanie regulatora ma postać:
( )
( )
p
p
p
kT
k
kT
u
ε
⋅
=
, k = 0, 1, 2, ...
( 1.4 )
k
p
Transmitancję impulsową regulatora P opisuje zależność (1.5) natomiast jego
–
współczynnik proporcjonalności.
( )
p
R
k
z
G
=
*
( 1.5 )
charakterystykę skokową (odpowiedź na sygnał ε = 1(t)) pokazano rys. 5.
Rys. 5. Charakterystyka skokowa regulatora P
REGULATOR PI (proporcjonalno całkujący)
Równanie regulatora ma postać:
( )
( )
( )
+
=
∑
=
k
j
p
i
p
p
p
p
jT
T
T
kT
k
kT
u
0
ε
ε
( 1.6 )
T
i
– czas zdwojenia
Drugi człon prawej strony równości (1.6) jest sumą wszystkich dyskretnych wartości sygnału
wejściowego w chwilach impulsowania, począwszy od t = 0 do t = kT
p
Transmitancję impulsową regulatora PI opisuje zależność (1.7),
, p
omnożoną przez
odpowiednią stałą.
( )
−
+
=
1
1
*
z
z
T
T
k
z
G
i
p
p
R
( 1.7 )
natomiast jego
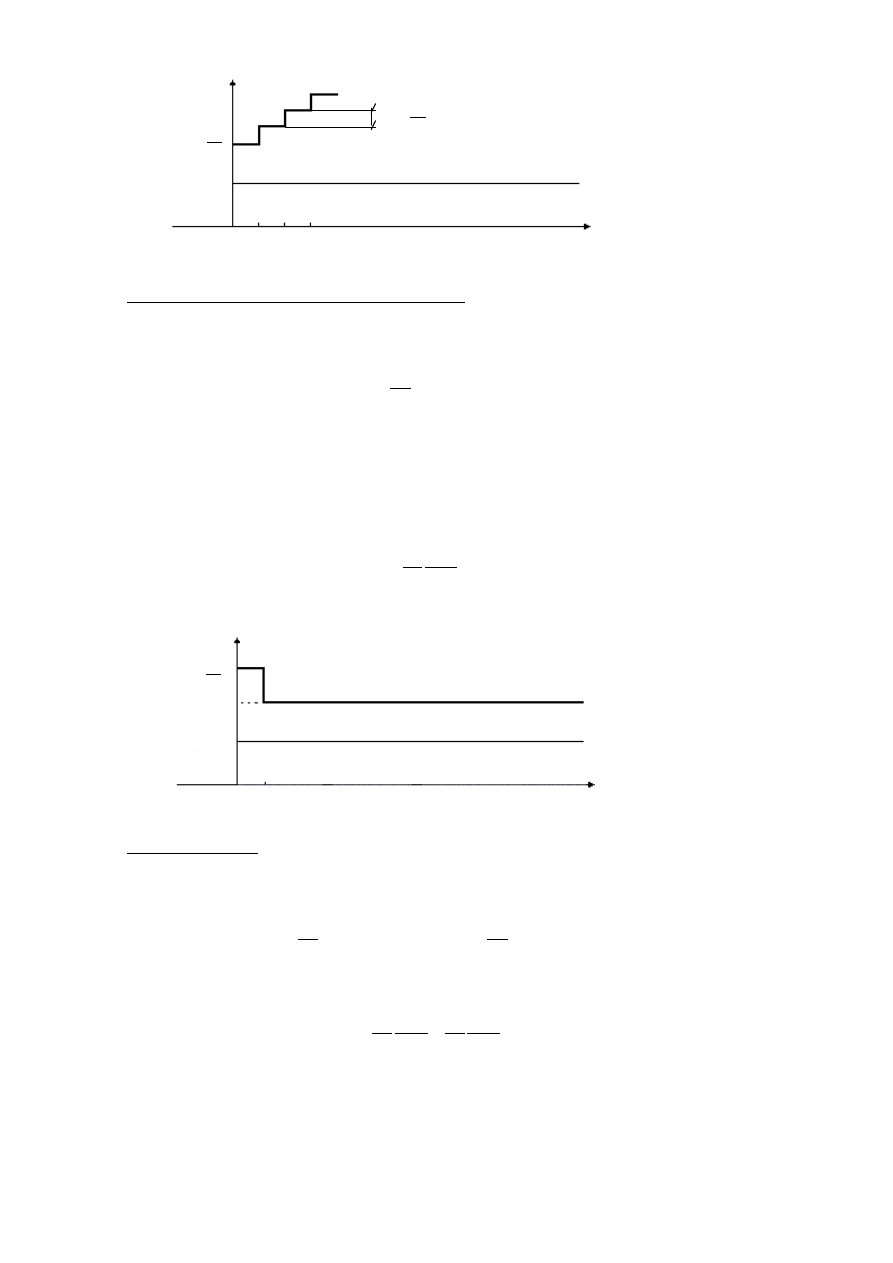
charakterystykę skokową (odpowiedź na sygnał ε = 1(t)) pokazano na rys. 6.
u(t)
u(t)
t
1
ε(t) = 1(t)
ε(t)
p
k
⋅
ε
5
Rys. 6. Charakterystyka skokowa regulatora PI
REGULATOR PD (proporcjonalno różniczkujący)
Równanie regulatora ma postać:
( )
(
)
[
]
( )
+
−
∆
=
p
p
p
d
p
p
kT
T
k
T
T
k
kT
u
ε
ε
1
( 1.8 )
T
d
– czas wyprzedzenia
Przez
(
)
[
]
( )
(
)
[
]
p
p
p
T
k
kT
T
k
1
1
−
−
=
−
∆
ε
ε
ε
oznaczono różnicę dwóch kolejnych wartości
dys
kretnego sygnału wejściowego.
Transmitancja impulsowa opisana jest zależnością (1.9)
( )
−
+
=
z
z
T
T
k
z
G
p
d
p
R
1
1
*
( 1.9 )
a charakterystyka skokowa (odpowiedź na sygnał ε = 1(t)) pokazana jest na rys. 7.
Rys. 7. Charakterystyka skokowa regulatora PD
REGULATOR PID
Równanie regulatora ma postać:
( )
(
)
[
]
( )
( )
+
+
−
∆
=
∑
=
k
j
p
i
p
p
p
p
d
p
p
jT
T
T
kT
T
k
T
T
k
kT
u
0
1
ε
ε
ε
( 1.10 )
Transmitancję impulsową regulatora PID opisuje zależność (1.11)
( )
−
+
−
+
=
z
z
T
T
z
z
T
T
k
z
G
p
d
i
p
p
R
1
1
1
*
( 1.11 )
a charakterystykę skokową (odpowiedź na sygnał ε = 1(t)) pokazano na rys. 8.
ε(t) = 1(t)
u(t)
ε(t)
u(t)
1
t
T
p
2T
p
3T
p
i
p
p
T
T
k
⋅
ε
+
⋅
i
p
p
T
T
k 1
ε
T
p
t
ε(t) = 1(t)
u(t)
1
+
⋅
p
d
p
T
T
k
1
ε
u(t)
ε(t)
p
k
⋅
ε

6
Rys. 8. Charakterystyka skokowa regulatora PID
II.4. JAKOŚĆ REGULACJI
Wymagania stawiane układom regulacji są różne – zależą od ich celu technicznego i od
specyfiki procesu regulowanego.
Podstawowym wymaganiem s
tawianym każdemu układowi regulacji jest, aby badany układ był
stabilny
. Układ impulsowy będziemy nazywać niestabilnym, jeśli przy ograniczonym
sygnale wejściowym jego sygnał wyjściowy jest nieograniczony.
Można wykazać, że liniowy układ impulsowy jest stabilny, jeśli pierwiastki z
1
, z
2
, ..., z
n
równania charakterystycznego utworzonego przez przyrównanie mianownika transmitancji do zera
(bieguny transmitancji) leżą wewnątrz okręgu jednostkowego na płaszczyźnie zmiennej z, czyli:
1
<
i
z
i = 1, 2, ..., n,
( 1. 12 )
gdzie n –
stopień równania charakterystycznego.
Istnieją również inne sposoby badania stabilności, np. przez odwzorowanie okręgu
jednostkowego na płaszczyźnie z na półpłaszczyznę innej zmiennej u i zastosowanie kryterium
Hu
rwitza, jednak nie będą tutaj szerzej opisywane.
Dążenie do optymalizacji procesu regulacji narzuca konieczność przyjęcia kryteriów jakości
regulacji. Spośród wielu sposobów oceny jakości, przyjęto ocenę na podstawie wartości pewnych
wskaźników. Wartości tych wskaźników, osiągane przez układy regulacji, są porównywane z
wartościami umownymi, przyjętymi na podstawie doświadczenia.
Dokładność statyczna
regulacji określa wartość odchylenia wielkości regulowanej w
stanie ustalonym od wielkości zadanej przy różnych standardowych wymuszeniach. Miarą tej
dokładności jest uchyb statyczny, odniesiony do ustalonej wartości wielkości regulowanej, wyrażony
najczęściej w procentach.
Oznaczając uchyb statyczny przez ε
st
(
)
( )
t
y
y
t
t
st
ε
ε
∞
→
∞
→
=
−
=
lim
lim
0
:
Uchyb
ε
st
y
st
ε
ma dwie składowe:
-
składowa wywołana wymuszeniem y
0
z
st
ε
(t),
-
składowa wywołana zakłóceniem z(t).
Układ, dla którego
y
st
ε
= 0 nazywa się astatycznym względem sterowania. Jeśli
z
st
ε
= 0 to układ nazywa się astatycznym względem zakłócenia.
Ostatecznie jakość statyczną regulacji ocenia się jako zadowalającą, jeśli spełnione są
nierówności:
1
0
e
y
y
st
≤
ε
( 1.13 )
2
e
z
z
st
≤
ε
( 1.14 )
gdzie e
1
i e
2
Oprócz wymagań dotyczących stabilności i dokładności statycznej żąda się od układów
regulacji dobrej jakości dynamicznej
. Jest to pojęcie dość szerokie, które obejmuje m. in.:
charakter i czas zanikania procesów przejściowych, wartości maksymalnych uchybów, a także pasma
częstotliwości, w których zachodzi wystarczająco dokładne odtwarzanie sygnałów wymuszających lub
tłumienie zakłóceń. Jakość dynamiczną określa się zwykle za pomocą wskaźników liczbowych
mieszczą się w przedziale: 5% - 10%.
t
T
p
2T
p
...
ε(t) = 1(t)
u(t)
ε(t) u(t)
i
p
p
T
T
k
⋅
ε
+
⋅
i
p
p
T
T
k
2
1
ε
+
+
⋅
i
p
p
d
p
T
T
T
T
k
1
ε
7
odnoszących się do niektórych cech charakterystyki skokowej lub charakterystyk częstotliwościowych
układu zamkniętego. Zostało to szerzej omówione w instrukcji do ćwiczenia nr 5.
Zastosowanie konkretnego typu regulatora zależy od obiektu regulacji. Dla obiektów
astatycznych, rzeczywistych regulator P
może być wystarczający. Pożądane jest wówczas możliwie
duże wzmocnienie k
p
Wprowadzenie akcji sumowania I
wpływa niekorzystnie na czas regulacji t
, jednak ze względu na stabilność nie może być ono zwiększane w sposób
dowolny. Natomiast dla obiektów statycznych ze względu na bardzo małą dokładność statyczną
stosowanie samego regulatora P
jest niepożądane. Uchyby można sprowadzić do zera dzięki akcji
sumowania regulatora PI
. Można to sprawdzić obliczając wartości dyskretne uchybów przy liczbie k
impulsowania dążącej do nieskończoności.
r
Nie istnieją optymalne nastawy regulatora PID, minimalizujące równocześnie
wszystkie
wskaźniki jakości regulacji. Na ogół, dla danego obiektu regulacji, nastawy te dobiera
się w sposób doświadczalny, tak aby regulator minimalizował wybrane wskaźniki lub według „recept”
wynikających z doświadczenia inżynierskiego.
i na wielkość
przeregulowania. Wskaźniki te można zmniejszyć, zachowując zerowe uchyby, przez wprowadzenie
akcji różnicowania D, stosując regulator PID.
II.5. REGUŁA ZIEGLERA-NICHOLSA DLA REGULACJI IMPULSOWEJ
Dobór nastaw regulatora dyskretnego przeprowadza się tak, żeby uzyskać określone cechy
procesu regulacji. Chodzi o takie dobranie nastaw, które zapewni regulację możliwie bliską
optymalnej, choć niekiedy żąda się aby tylko jeden ze wskaźników regulacji spełniał określone
wymagania, np. aby czas regulacji t
r
Nastawy regulatorów dobiera się przeważnie metodą prób i błędów, ponieważ rzeczywiste
obiekty zazwyczaj odbiegają od stosowanych do ich opisów modeli matematycznych. Opracowano
różne empiryczne metody doboru odpowiednich nastaw. Jedną z najbardziej rozpowszechnionych
jest stosowana zarówno w regulacji ciągłej jak i dyskretnej reguła Zieglera-Nicholsa, dzięki
której osiąga się przeregulowanie κ=(30-50%) i t
był minimalny.
r
1.
regulator w badanym dyskretnym układzie należy nastawić na działanie proporcjonalne P
(wyłączyć działanie różniczkujące i sumujące) i zwiększać stopniowo współczynnik wzmocnienia
k
zbliżony do minimum. Algorytm postępowania jest
następujący:
p
aż do wartości granicznej k
pg
2.
Należy zmierzyć okres tych oscylacji T
, przy której wystąpią oscylacje niegasnące (granica stabilności).
g
i zanotować k
pg
3.
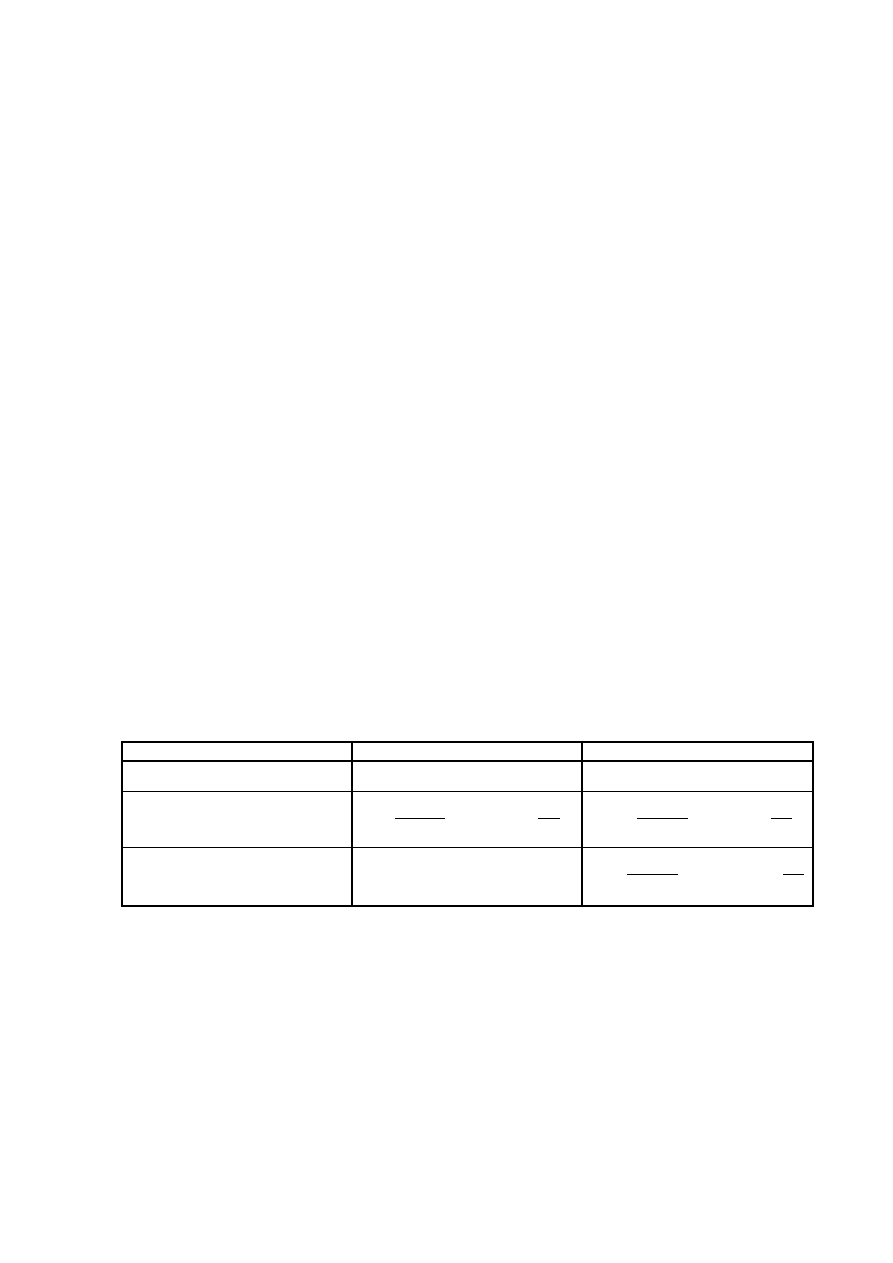
Zależnie od typu regulatora przyjąć:
.
W regulacji ciągłej algorytm Zieglera-Nicholsa jest podobny, lecz zalecane wartości nastaw
inne.
W przypadku regulatora PD pojawiają się duże problemy z uchybami od wartości zadanej,
dlatego też nie daje się sformułować prostej i przejrzystej reguły dotyczącej doboru optymalnych
nastaw. Reguła Zieglera-Nicholsa nie jest dla tego przypadku określona!
III. Opis stanowiska laboratoryjnego
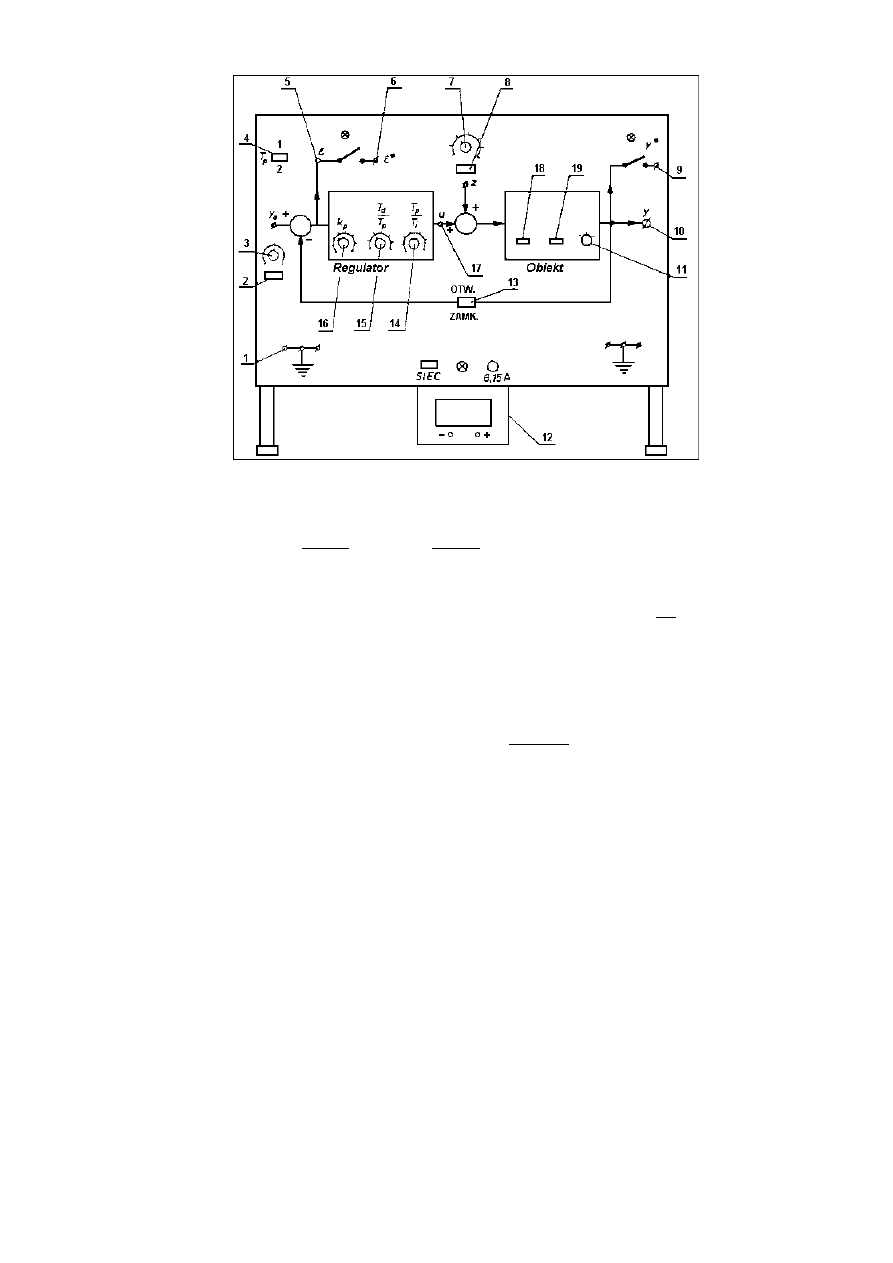
Ćwiczenie wykonuje się na elektronicznym modelu układu regulacji impulsowej, pokazanym na rys. 9.
Stanowisko wyposażone jest ponadto w komputer PC pełniący rolę wielokanałowego oscyloskopu
(program SC
OPE), umożliwiającego rejestrację przebiegów czasowych badanych sygnałów.
P
PI
PID
pg
p
k
k
⋅
= 5
,
0
i
pg
p
k
k
k
⋅
−
⋅
=
5
,
0
45
,
0
i
pg
p
k
k
k
⋅
−
⋅
=
6
,
0
6
,
0
_______________
g
p
pg
i
p
p
i
T
T
k
T
T
k
k
⋅
⋅
=
⋅
=
54
,
0
g
p
pg
i
p
p
i
T
T
k
T
T
k
k
⋅
⋅
=
⋅
=
2
,
1
_______________
_______________
p
g
pg
p
d
p
d
T
T
k
T
T
k
k
⋅
⋅
=
⋅
=
075
,
0
8
Rys. 9. Model układu regulacji wykorzystany w ćwiczeniu
Obiekt ciągły może mieć przepustowość operatorową G
u
( )
p
sT
e
s
G
−
=
1
(s) będącą iloczynem przepustowości
,
( )
1
1
1
2
+
=
s
T
s
G
,
( )
1
1
2
3
+
=
s
T
s
G
, przy czym stałe czasowe mogą przyjmować
wartości: T
1
=0,4 s lub T
1
=0 ; T
2
=2 s lub T
2
=0. Ponadto można wyłączyć element opóźniający
(wówczas G
1
( )
s
s
G
2
1
3
=
(s)=1) oraz włączyć efekt całkowania (wówczas
). Do otrzymania
odpowiedniej transmitancji obiektu służą przyciski (18) i (19) oraz pokrętło (11).
Regulator jest typu PID. Działania składowe regulatora I oraz D można wyłączyć lub ustawić z
odpowiednim współczynnikiem. Służą do tego pokrętła (14) i (15). Podobnie można zmieniać
wzmocnienie k
p
s
e
G
p
sT
p
−
−
=
1
regulatora (pokrętło 16). Regulator jest połączony z obiektem za pośrednictwem
ekstrapolatora zerowego rzędu o transmitancji
. Okres impulsowania T
p
Sygnałami w układzie są przebiegi napięć elektrycznych. Sygnał sterujący y
można
nastawić na wartość 1 lub 2 sekundy za pomocą przycisku (4).
0
Sygnały ε, y
można włączać
skokowo za pomocą przycisku (2) a jego amplitudę ustala się pokrętłem (3). Sygnał zakłócający z jest
włączany przyciskiem (8). Wartość tego sygnału można zmieniać pokrętłem (7).
0
, y
są ciągłe i można je mierzyć jako napięcia między gniazdkami (5) i (10) a (1)
(masa). Sygnały ε
*
, u, y
są dyskretne (o postaci schodkowej). Do pomiaru napięć służy woltomierz
cyfrowy (12). Największe lub najmniejsze napięcie występujące w gniazdach płyty czołowej
względem masy (1) może mieć wartość ± 15 V. Napięcie nasycenia sygnału u na wyjściu regulatora
zależy od jego nastaw.
IV. Przebieg ćwiczenia
W trakcie ćwiczenia przeprowadza się badanie układu regulacji stałowartościowej zawierającego
obiekt inercyjny drugiego rzędu z opóźnieniem T
p
Badanie układu ma na celu dobór nastaw metodą Zieglera-Nicholsa dla kolejnych typów
regulatorów w dwóch przypadkach:
=2s. W badanym układzie regulacji stosuje się
kolejno regulatory impulsowe typu P, PI.
-
po zadziałaniu wymuszenia skokowego na wejściu układu regulacji,
-
po zadziałaniu wymuszeń skokowych na wejściu układu i na wejściu obiektu (zakłócenie).

9
Podczas przeprowadzania ćwiczenia rejestrowane są przy użyciu programu komputerowego
SCOPE przebiegi badanych wielkości. Wszelkich wskazówek niezbędnych do poprawnej obsługi
programu udziela prowadzący.
Kolejność czynności przy wykonywaniu ćwiczenia jest następująca:
1. Badanie odpowiedzi obiektu inercyjnego I-
rzędu z opóźnieniem na skok jednostkowy
-
otworzyć pętlę sprzężenia zwrotnego (przycisk 13);
-
ustawić wzmocnienie (pokrętło 16) na piątą nastawę i wyłączyć nastawy akcji D (skrajna lewa
pozycja pokrętła 15) oraz I (skrajna prawa pozycja pokrętła 14) regulatora;
-
w obiekc
ie ustawić odpowiednio opóźnienie (przycisk 18) oraz inercyjność (pokrętło 11 na
T=2 s) i wyłączyć przycisk 19;
-
załączyć SIEĆ oraz sygnał wejściowy (przycisk 2) i na woltomierzu cyfrowym (12) ustawić
na wejściu do obiektu (gniazdo 17) wartość wskazaną przez prowadzącego;
-
wtyczki kanałów rejestratora wetknąć odpowiednio: kanał B na wejściu obiektu (gniazdo 17),
kanał A na wyjściu (gniazdo 10);
-
wyłączyć sygnał wejściowy i sieć oraz ustawić w programie SCOPE: T/div=4 s, scale*5 oraz
pomiar na dwóch kanałach;
-
w
łączyć rejestrację, włączyć SIEĆ i chwilę odczekać na ustabilizowanie sygnału, włączyć
sygnał wejściowy;
-
po zarejestrowaniu przebiegów wyłączyć sygnał wejściowy i SIEĆ;
2. Identyfikacja nastaw
Nastawa P
-
wyłączyć wzmocnienie (skrajna lewa pozycja pokrętła 16) i pozostawić wyłączone sprzężenie
zwrotne i nastawy dla D oraz I;
-
włączyć SIEĆ oraz sygnał wejściowy (przycisk 2) i ustawić napięcie na wejściu do regulatora
(gniazdo 5) wg wskazań prowadzącego ćwiczenie;
-
po zanotowaniu wartości podczepić kabelek pomiarowy na wyjście regulatora (gniazdo 17);
-
przekręcając pokrętło 16 odczytywać dla każdej nastawy wartość napięcia na wyjściu;
-
wyłączyć sygnał wejściowy i SIEĆ i policzyć wartości nastaw jako stosunek U
wy
/U
we
Nastawa D
;
-
ustawić wzmocnienie na piątą nastawę (pokrętło 16) i przy wyłączonych nastawach D oraz I
ustawić na wyjściu regulatora wartość napięcia wg wskazań prowadzącego;
-
na wyjście regulatora podłączyć wybrany kanał rejestratora (A lub B) a w programie SCOPE
ustawić: T/div=10 s, scale*1 oraz rejestrację na jednym kanale;
-
włączyć pierwszą wartość nastawy D (pokrętło 15); włączyć rejestrację przebiegu, włączyć
SIEĆ po czym wprowadzić sygnał wejściowy (przycisk 2);
-
po uzyskaniu przebiegu odpowiedzi wyłączyć SIEĆ i sygnał wejściowy (w celu rozładowania
elemen
tów elektronicznych tablicy) i przełączyć na kolejną wartość nastawy D;
-
podaną sekwencję czynności powtórzyć dla wszystkich wartości nastaw D; całość należy
przeprowadzić w oparciu o wskazówki prowadzącego;
-
za pomocą kursora odczytać wartości „schodka” dla wszystkich nastaw i korzystając z
zależności
+
⋅
=
p
d
p
T
T
k
U
1
max
ε
obliczyć wartości wszystkich nastaw części D regulatora;
Nastawa I
-
ustawić wzmocnienie na piątą nastawę (pokrętło 16) i przy wyłączonych nastawach D oraz I
ustawić na wyjściu regulatora wartość napięcia wskazaną przez prowadzącego;
-
na wyjście regulatora podłączyć wybrany kanał rejestratora (A lub B) a w programie SCOPE
ustawić: T/div=20 s, scale*2 oraz rejestrację na jednym kanale;
-
włączyć pierwszą wartość nastawy I (pokrętło 14); włączyć rejestrację przebiegu, włączyć
SIEĆ po czym wprowadzić sygnał wejściowy (przycisk 2);
-
po uzyskaniu przebiegu odpowiedzi (minimum 3-
4 „schodki”) wyłączyć SIEĆ i sygnał
wejściowy (w celu rozładowania elementów elektronicznych tablicy) i przełączyć kolejną
w
artość nastawy I;
-
podaną sekwencję czynności powtórzyć dla wszystkich wartości nastaw I; całość należy
przeprowadzić w oparciu o wskazówki prowadzącego;

10
-
za pomocą kursora odczytać dla każdej nastawy wysokość wybranego schodka i korzystając z
zależności
i
p
p
T
T
k
U
⋅
⋅
=
∆
ε
obliczyć wartości wszystkich nastaw części I regulatora;
3.
Określenie okresu drgań niegasnących T
g
i wzmocnienia k
pgr
-
przy otwartej pętli sprzężenia zwrotnego ustawić sygnał wejściowy na ok.1,5 V;
-
ustawić w programie SCOPE: T/div=10 s, scale*2 oraz rejestrację na jednym kanale;
-
wyłączyć SIEĆ i sygnał wejściowy oraz akcje P, D, I;
-
podłączyć rejestrację na wyjście za obiektem (gniazdo 10) i zamknąć pętlę sprzężenia
zwrotnego (wcisnąć przycisk 13);
-
włączyć SIEĆ i sygnał wejściowy i przełączając kolejne nastawy wzmocnienia obserwować
przebieg sygnału aż do uzyskania drgań niegasnących (wartość nastawy potraktować jako
k
pgr
-
odczytać okres T
)
g
4.
Wyznaczenie optymalnych nastaw regulatorów P, PI, PID przy użyciu reguły Zieglera-
Nicholsa
drgań niegasnących
-
ze wzorów podanych w punkcie II.5. wyznaczyć optymalne wartości nastaw dla regulatorów:
P, PI, PID;
-
sprawdzić, które wartości nastaw dla regulatorów badanych w ćwiczeniu są najbliższe
optymalnym;
5. Badanie regulacji P, PI
-
przy wyłączonej pętli sprzężenia zwrotnego (wyciśnięty przycisk 13) przy pomocy kabelka
pomiarowego odmierzyć sygnał wejściowy (gniazdo 5) Y
0
-
wyłączyć sygnał wejściowy i przepiąć kabelek pomiarowy na wyjście (gniazdo 10) i
odmierzyć sygnał zakłóceniowy Z=2 V (włączyć przycisk 8 i regulować pokrętłem 7);
=3 V korzystając z przycisku 2 i
pokrętła 3;
-
wpiąć kanał rejestratora na wyjście układu (gniazdo 10);
Dla regulatora P
-
wyłączyć zakłócenie i SIEĆ a w programie SCOPE ustawić T/div=20 s, scale*2 oraz
rejestrację na jeden kanał;
-
zamk
nąć pętlę sprzężenia zwrotnego;
-
ustawić wzmocnienie regulatora k
p
-
włączyć rejestrację, włączyć SIEĆ i odczekać chwilę (na ustanie drobnych zakłóceń) po czym
włączyć sygnał wejściowy (przycisk 2);
na nastawie odpowiadającej wyznaczonemu z reguły Z-N
optimum (pokrętło 16);
-
odczekać na zarejestrowanie przebiegu;
Dla regulatora PI
-
wyłączyć zakłócenie i SIEĆ a w programie SCOPE ustawić T/div=20 s, scale*2 oraz
rejestrację na jeden kanał;
-
ustawić wzmocnienie regulatora k
p
-
włączyć rejestrację, włączyć SIEĆ i odczekać chwilę (na ustanie drobnych zakłóceń) po czym
włączyć sygnał wejściowy (przycisk 2);
(pokrętło 16) oraz akcję sumowania I (pokrętło 14) na
nastawach odpowiadających wyznaczonemu z reguły Z-N optimum;
-
odczekać na zarejestrowanie przebiegu;
V. Sprawozdanie
W sprawozdaniu z ćwiczenia należy zamieścić następujące elementy:
-
starannie wykonany protokół z ćwiczenia (wraz z wykonanymi obliczeniami) podpisany
przez prowadzącego!;
-
zarejestrowane wykresy badanych przebiegów czasowych sygnałów z naniesionymi
wi
elkościami, które mają być wyznaczone na podstawie wykresów;

11
-
na wykresie odpowiedzi obiektu inercyjnego I-
szego rzędu wyznaczyć stałą czasową jako:
T(stała czasowa)= czas dla wartości odpowiadającej 0,632*Y
ustalone
-
wyznaczenie uchybów ustalonych od wartości zadanej i od zakłócenia dla regulatorów P i
PI oraz ocena jakości na podstawie wzorów 1.13 oraz 1.14;
;
-
wyznaczenie wskaźników jakości regulacji dla regulacji P, PI: czasu regulacji t
r
-
wnioski z przeprowadzonego ćwiczenia;
i
przeregulowania
κ;
Document Outline
- Zakład Teorii Maszyn i Robotów
- Laboratorium Podstaw Automatyki i Sterowania IV
Wyszukiwarka
Podobne podstrony:
06 Regulacja impulsowa
Laboratorium automatyki Regulacja impulsowa
Regulacia impulsowa 9, Politechnika Lubelska
85 Nw 06 Regulator obrotow
02.Tyrystorowe regulatory impulsowe napięcia stałego, Semestr VII, Semestr VII od Grzesia, Elektroni
Tyrystorowe regulatory impulsowe napięcia stałego, Semestr VII, Semestr VII od Grzesia, Elektronika
Regulacja impulsowa, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, Elektryczny, TEO
Regulacja impulsowa nr5, UTP Bydgoszcz Elektrotechnika, automatyka
Tranzystorowe regulatory impulsowe napięcia stałegoa, Semestr VII, Semestr VII od Grzesia, Elektroni
Regulator impulsowy
Tyrystorowe regulatory impulsowe napięcia stałego KOŁEK, POLITECHNIKA POZNAŃSKA
2005 03 Regulator impulsowy DC, Nieznany
5 Regulacja impulsowa
Regulacja impulsowal
Tranzystorowe regulatory impulsowe napięcia stałego, studia, sem 5, Lab. Energoelektronika, regulato
2002 06 Generator impulsów
Tranzystorowe regulatory impulsowe napięcia stałego
Tranzystorowe regulatory impulsowe napięcia stałegoc
więcej podobnych podstron