ROZDZIAŁ V
5
ROZWIĄZYWANIE UKŁADÓW
RÓWNAŃ LINIOWYCH
5.1 PRZYKŁAD ZADANIA INŻYNIERSKIEGO
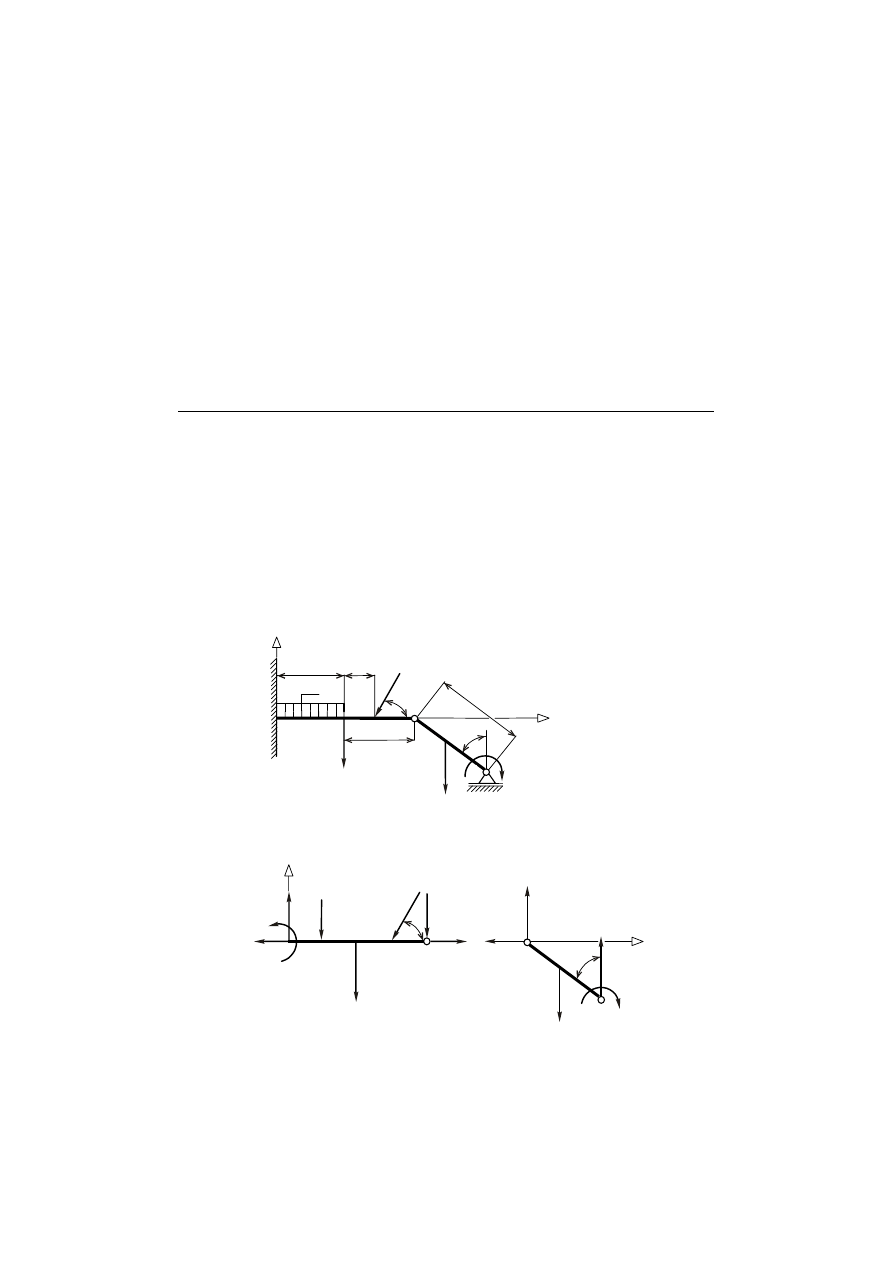
Przykład 5.1. Wyznaczenie reakcji
Oblicz reakcje w przegubach B i C oraz w utwierdzeniu A, układu belek
pokazanego na rys. 5.1.
P=30N
G=300N
M=200Nm
q=100Nm
l=3m
α=45°
β=60°
α
G
B
l
β
l
C
M
l
q
2G
½l
P
A
x
y
Rys. 5.1. Układ dwóch belek
Rozdzielony i oswobodzony z więzów układ belek przedstawia rys. 5.2.
R
By
R
Ax
R
Bx
Mu
R
Ax
A
Q
2G
P
α
β
R
By
B
B
C
M
R
C
G
x
y
Rys. 5.2. Belki oswobodzone z więzów

Układ belek jest statycznie wyznaczalny. W pierwszej kolejności należy z
układu równań warunków równowagi dla belki BC, wyznaczyć reakcje
, a następnie z układu równań warunków równowagi dla belki
AB, należy wyznaczyć reakcje
oraz moment utwierdzenia M
By
Bx
C
i R
, R
R
Ay
Ax
, R
R
u
.
Obciążenie ciągłe q zastępujemy siłą skupioną
ql
Q
=
zaczepioną w środku
długości tego obciążenia.
=
−
−
−
−
=
−
−
−
−
=
−
=
+
−
−
=
+
−
=
0
2
2
0
2
0
0
0
0
3
2
2
1
2
1
l
R
sin
l
P
Gl
l
Q
M
R
sin
P
G
Q
R
cos
P
R
sin
l
R
M
sin
l
G
R
G
R
R
By
u
By
Ay
Ax
C
C
By
Bx
β
β
β
α
α
(5.1)
Rozwiązanie układu równań liniowych (5.1) jest zagadnieniem stosunkowo
prostym, lecz już czasochłonnym. Opracowano wiele metod numerycznych
rozwiązywania tego typu zagadnień. Większość z nich znajduje zastosowanie
tam, gdzie istnieje potrzeba rozwiązywania układów dla dużej lub bardzo
dużej liczby niewiadomych.
5.2 CHARAKTERYSTYKA ZAGADNIENIA NUMERYCZNEGO
Przez układ równań liniowych rozumie się koniunkcje pewnej liczby równań
algebraicznych, które spełniane są przez te same wartości niewiadomych danych w
równaniach w pierwszej potędze. Przez rozwiązanie układu równań rozumiemy
znalezienie takich liczb, które po podstawieniu w miejsce niewiadomych spełniają
układ równań.
Układy równań liniowych algebraicznych pojawiają się bardzo często w technice, są
np.: podstawową formą opisu zagadnień fizycznych modelujących zagadnienia statyki,
termodynamiki oraz elektrotechniki.
Ponadto, konieczność rozwiązania układu równań liniowych pojawia się często w
innych algorytmach numerycznych, np. interpolacji, aproksymacji lub w wielu
metodach bazujących na linearyzacji równań nieliniowych, np. przy rozwiązywaniu
układów równań nieliniowych.
5.2.1 Przekształcanie układu równań do zapisu macierzowego
Układ równań liniowych można zapisać w postaci macierzowej, w której A jest
macierzą główną układu o m wierszach i n kolumnach (m – odpowiada liczbie równań
w układzie, n – odpowiada liczbie niewiadomych), b jest wektorem wyrazów wolnych o
m elementach, x wektorem n niewiadomych.
78

b
Ax
=
(5.2)
Procedura formowania macierzy i wektorów w zapisie (5.2) składa się z etapów:
1. Zapisanie równań w formie układu na podstawie modelu.
2. Identyfikacja niewiadomych i ich uporządkowanie.
3. Przeniesienie elementów równań związanych z niewiadomymi na lewą stronę
znaku równości w ustalonym porządku.
4. Przeniesienie elementów równań związanych z danymi na prawą stronę znaku
równości.
5. Zapisanie elementów układu równań w postaci macierzy.
Przykład 5.2. Przekształcenie układu równań do zapisu macierzowego
Przekształcić układ równań z przykładu 5.1 do zapisu macierzowego.
Identyfikujemy niewiadome i porządkujemy je. Niewiadome to
stąd otrzymujemy wektor niewiadomych:
u
C
By
Bx
Ay
Ax
, M
, R
, R
, R
, R
R
(5.3)
=
u
C
By
Bx
Ay
Ax
M
R
R
R
R
R
x
Przenosimy elementy równań związane z niewiadomymi na lewą stronę
znaku równości porządkując je zgodnie z przyjętą kolejnością. Elementy
równań związane z danymi przenosimy na prawą stronę znaku równości.
+
+
=
+
−
+
+
=
−
=
+
=
=
+
=
β
β
β
α
α
sin
l
P
Gl
l
Q
M
l
R
sin
P
G
Q
R
R
cos
P
R
M
sin
l
G
sin
l
R
G
R
R
R
u
By
By
Ay
Ax
C
C
By
Bx
3
2
2
1
2
1
2
2
2
0
(5.4)
W każdym z równań dopisujemy element zawierający brakujące niewiadome
z ustalonej listy ze współczynnikiem zero. Przenosimy wartości w
składnikach równań zawierających niewiadome przed symbol niewiadomej:
79

+
+
=
+
+
−
+
+
+
+
=
+
+
−
+
+
=
+
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
β
β
β
α
α
sin
l
P
Gl
l
Q
M
R
lR
R
R
R
sin
P
G
Q
M
R
R
R
R
R
cos
P
M
R
R
R
R
R
M
sin
l
G
M
R
sin
l
R
R
R
R
G
M
R
R
R
R
R
M
R
R
R
R
R
u
C
By
Bx
Ay
Ax
u
C
By
Bx
Ay
Ax
u
C
By
Bx
Ay
Ax
u
C
By
Bx
Ay
Ax
u
C
By
Bx
Ay
Ax
u
C
By
Bx
Ay
Ax
3
2
2
1
2
1
2
1
0
2
0
0
0
2
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
0
0
(5.5)
Zapisujemy współczynniki stojące przy niewiadomych w formie
macierzy. Otrzymujemy stąd macierz główną układu A. Zapisując
wartości znajdujące się za znakiem równości otrzymujemy wektor
wyrazów wolnych układu b.
−
−
−
=
1
0
2
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
l
sin
l
α
A
+
+
+
+
+
=
β
β
β
α
sin
l
P
Gl
l
Q
sin
P
G
Q
cos
P
M
sin
l
G
G
3
2
2
1
2
1
2
2
0
b
(5.6)
Kompletny układ równań posiada postać zgodną z zależnością (5.2)
+
+
+
+
+
=
×
−
−
−
β
β
β
α
α
sin
l
P
Gl
l
Q
sin
P
G
Q
cos
P
M
sin
l
G
G
M
R
R
R
R
R
l
sin
l
u
C
By
Bx
Ay
Ax
3
2
2
1
2
1
2
2
0
1
0
2
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
(5.7)
Macierz główna A posiada więcej elementów o wartościach zerowych niż
nie-zerowych. Jest to przykład tzw. macierzy rzadkiej.
5.2.2 Warunki istnienia rozwiązania
Macierz główna układu A nie musi być kwadratowa. W ogólnym przypadku A jest
macierzą o m-wierszach (równaniach) i n-kolumnach (niewiadomych), co prowadzi do
trzech typów układów równań liniowych. Jeżeli m=n, liczba równań i niewiadomych
jest zgodna, a macierz A jest kwadratowa. Jeżeli m>n, liczba równań jest większa od
liczby niewiadomych. Jeżeli m<n, liczba równań jest mniejsza od liczby niewiadomych.
Dla dowolnej postaci macierzy A warunki rozwiązywalności układów równań
liniowych rozstrzyga twierdzenie Croneckera-Capelli, w którym bada się rząd macierzy
głównej A i rząd macierzy głównej uzupełnionej kolumną wyrazów wolnych b. W
przypadku interesującej nas kwadratowej macierzy głównej A układu równań, rząd
macierzy równy liczbie kolumn automatycznie gwarantuje, że układ równań posiada
80

jednoznaczne rozwiązanie. Rzędem macierzy nazywamy liczbę jej niezależnych
liniowo kolumn lub wierszy.
Przykład 5.3. Rząd macierzy
Wyznaczyć w Matlabie rząd macierzy głównej A dla zagadnienia z
przykładu 5.1 dla danych l=3m;
α=45°.
Wprowadzamy macierz A do obszaru zmiennych Matlaba.
>> A=[0 0 1 0 0 0;0 0 0 1 1 0; 0 0 0 0 -
3*sin(45*pi/180) 0;...
1 0 0 0 0 0;0 1 0 -1 0 0;0 0 0 -2*3 0 1]
A =
0 0 1.0000 0 0 0
0 0 0 1.0000 1.0000 0
0 0 0 0 -2.1213 0
1.0000 0 0 0 0 0
0 1.0000 0 -1.0000 0 0
0 0 0 -6.0000 0 1.0000
Obliczamy rząd macierzy A korzystając z polecenia
rank()
.
>> r=rank(A)
r =
6
W zagadnieniach technicznych utworzenie układu równań liniowych o
niejednoznacznym rozwiązaniu świadczy z reguły o błędnie sformułowanym
matematycznym opisie zjawiska, np. błędach popełnionych przy formułowaniu równań.
Dlatego też pominiemy dalsze rozważania nad twierdzeniem Croneckera-Capelli.
5.2.3 Układy równań liniowych – formalne metody rozwiązywania
Dla układów równań, w których macierz główna A jest macierzą kwadratową m=n
rozwiązanie formalne polega na znalezieniu odwrotności macierzy A, czyli A
-1
a
następnie wyznaczeniu iloczynu wektorowego. Czyli:
(5.8)
b
A
x
b
Ax
1
−
=
⇒
=
Równanie (5.8) jest macierzowym zapisem wzorów Cramera. Numeryczne
wyznaczanie odwrotności macierzy nie jest powszechnie wykorzystywane, ponieważ
jest czasochłonne i mniej dokładne niż metody alternatywne. Warto sobie uzmysłowić,
że liczba mnożeń potrzebnych do obliczania wyznacznika n-tego stopnia za pomocą
rozwijania względem wiersza wynosi n!. Policzmy w poniższym przykładzie czas
potrzebny na obliczenie wyznacznika.
Przykład 5.4. Obliczanie wyznacznika za pomocą reguł rozwijania
Liczba mnożeń dla macierzy 15x15 i 20x20 wynosi odpowiednio:
>> factorial(15)
ans =
1.3077e+012
>> factorial(20)
ans =
81

2.4329e+018
Czas potrzebny na wykonanie 10
6
mnożeń, wynosi:
>> tic; for i=1:10^6, pi*pi; end; czas=toc
czas =
3.1880
Czas potrzebny na wyliczenie wyznacznika z macierzy 15x15:
>> factorial(15)*czas/10e6/60/60/24
ans =
4.8251
Czyli prawie 5 dni. Dla macierzy 20x20:
>> factorial(20)*czas/10e6/60/60/24/365
ans =
2.4594e+004
Czyli prawie 25 tysięcy lat.
W Matlabie istnieją narzędzia umożliwiające uzyskanie rozwiązania na drodze
wyznaczania odwrotności macierzy. Nie są to oczywiście metody oparte na rozwijaniu
względem kolumny lub wiersza.
Przykład 5.5. Odwracanie macierzy
Wyznaczyć rozwiązanie zadania z przykładu 5.1 zgodnie z zależnością (5.8).
Na bazie danych z przykładu 5.2 wprowadźmy wektor b do obszaru
zmiennych Matlaba
>> b = [ 0; 300; 300*0.5*3*sin(45*pi/180)+200;
30*cos(60*pi/180);...
3*100+2*300+30*sin(60*pi/180);...
3*100*0.5*3+2*300*3+30*(2/3)*3*sin(60*pi/180)]
b =
1.0e+003 *
0
0.3000
0.5182
0.0150
0.9260
2.3020
Korzystając z polecenia
inv()
obliczamy odwrotność macierzy A, a
korzystając z zależności (8.2) wyznaczamy rozwiązanie układu równań.
>> format short e
>> x=inv(A)*b
x =
1.5000e+001
1.4703e+003
0
5.4428e+002
-2.4428e+002
5.5676e+003
82

Kolejne elementy wektora rozwiązań x to wartości kolejnych
niewiadomych układu równań, uporządkowane w kolejności przyjętej
podczas formowania macierzy układu:
−
=
=
Nm
,
N
,
N
,
N
N
,
N
M
R
R
R
R
R
u
C
By
Bx
Ay
Ax
6
5567
28
244
28
544
0
3
1470
15
x
5.2.4 Dokładność rozwiązania
Zgodnie z zależnością (5.8) rozwiązanie układu równań liniowych istnieje, kiedy
istnieje odwrotność macierzy głównej A. Jednocześnie należy zauważyć, że są
macierze, dla których nie można wyznaczyć macierzy odwrotnej. Macierze tego typu
nazywamy osobliwymi. Macierz o wymiarach n
×n jest macierzą osobliwą, gdy: jej
kolumny lub wiersze macierzy są liniowo zależne (rząd macierzy jest mniejszy od
liczby kolumn lub wierszy) lub wyznacznik macierzy jest równy zero. Osobliwość
macierzy głównej układu równań powoduje, że rozwiązanie tego układu może nie
istnieć, a jeżeli istnieje to nie jest jednoznaczne.
Na skutek występowania błędów zaokrągleń w arytmetyce zmiennopozycyjnej istnieją
macierze nieosobliwe, które stają się macierzami osobliwymi lub bliskimi osobliwej.
5.2.4.1 Wskaźnik uwarunkowania
Udowodniono, że wpływ błędów zaokrągleń w zapisie elementów macierzy głównej A
lub wektora wyrazów wolnych b na rozwiązanie układów równań liniowych jest mały
tylko wtedy, gdy mała jest wartość
1
−
A
A
. Wartość tego iloczynu nazywana jest
wskaźnikiem uwarunkowania i zapisywana jako:
|
( )
1
−
A
=
A
A
κ
(5.9)
Wskaźnik uwarunkowania jest liczbą z zakresu od 1 do
∞. Charakteryzuje on własności
macierzy A. Duża wartość
κ(A) oznacza, że każdy algorytm numerycznego
rozwiązywania układu równań jest wrażliwy na błędy zaokrągleń. Układ równań z
macierzą główną A o dużej wartości wskaźnika uwarunkowania, nazywamy źle
uwarunkowanym. W arytmetyce, w której nie występują błędy zaokrągleń, dowolna
macierz jest osobliwa dla
κ(A)=∞ i nieosobliwa dla κ(A)=1.
Jeżeli macierz główna A i wektor wyrazów wolnych b są zapisane z dokładnością
obliczeniową maszyny
ε
m
, numeryczne rozwiązanie jest dane do d cyfr znaczących
(zależność dotyczy metod dokładnych):
( )
( )
(
)
A
κ
log
ε
log
d
m
10
10
−
=
(5.10)
Przykład 5.6. Współczynnik uwarunkowania
83

Wyznaczyć współczynnik uwarunkowania macierzy A z przykładu 5.1 przy
pomocy polecenia
cond()
. Ustalić liczbę cyfr znaczących w rozwiązaniu.
>> cond(A)
ans =
43.0237
>> d=abs(log10(eps))-log10(cond(A))
d =
14.0199
W wyniku uzyskano wskaźnik uwarunkowania
( )
A
κ
o niewielkiej wartości.
Daje to aż 14 cyfr znaczących w wyniku.
5.2.4.2 Wektor reszt
Jeśli jest przybliżonym (numerycznym) rozwiązaniem układu równań liniowych gdzie
x jest rozwiązaniem dokładnym. Wektor reszt r określa, jaki popełniamy błąd w
rozwiązaniu dokładnym x.
x
ˆ
x
A
b
r
ˆ
−
=
(5.11)
Przy czym wykazano, że:
( )
b
r
A
x
x
x
κ
≤
−
ˆ
ˆ
(5.12)
Niewielka wartość normy wektora reszt
r
nie gwarantuje istnienia małej normy
różnicy
x
x
−
ˆ
. Jeśli bowiem wartość κ jest duża, nie ma gwarancji, że wyznaczone
przez algorytm numeryczny rozwiązanie jest zbliżone do rozwiązania dokładnego x.
x
ˆ
5.3 METODY NUMERYCZNE ROZWIĄZYWANIA UKŁADÓW
RÓWNAŃ LINIOWYCH
5.3.1 Metody dokładne
Jeżeli rozwiązanie układu równań Ax=b polega na takim przekształceniu macierzy A i
wektora b, że przy założeniu dokładnie obliczanych wyrażeniach
arytmetycznych, po
skończonej liczbie działań, otrzymujemy rozwiązanie, to taką metodę rozwiązywania
nazywamy metodą dokładną. Jednakże pamiętać należy, że metody dokładne dla zadań
źle uwarunkowanych numerycznie mogą dawać rozwiązanie obarczone dużym błędem.
Metody te nie dają błędu metody, lecz mogą być niestabilne ze względu na błędy
zaokrągleń.
5.3.1.1 Uprzywilejowane postacie macierzy głównej układu
Niektóre postacie macierzy głównej układu A z punktu widzenia rozwiązywania układu
równań metodami numerycznymi są postaciami uprzywilejowanymi ze względu na
prostotę wyznaczenia rozwiązania.
Przykład 5.7. Macierz diagonalna
84

Rozważmy układ równań:
(5.13)
−
−
=
=
15
6
1
5
0
0
0
3
0
0
0
1
b
A
;
Jest on równoznaczny z następującym układem równań:
(5.14)
−
=
=
−
=
15
5
6
3
1
3
2
1
x
x
x
Jego rozwiązanie to:
−
=
−
=
=
=
−
=
3
5
15
5
2
3
6
1
3
2
1
x
x
x
(5.15)
Rozwiązanie układu równań z diagonalną macierzą główną A sprowadza się do
podzielenia kolejnych elementów wektora wyrazów wolnych b przez kolejne elementy
na głównej przekątnej macierzy A.
Układy równań, w których macierz główna A jest macierzą trójkątną górną lub dolną
mogą być rozwiązane przez postępowanie wprost lub przez postępowanie odwrotne.
Przykład 5.8. Macierz trójkątna górna
Układu równań, w którym A jest górną macierzą trójkątną:
(5.16)
−
=
−
−
=
8
1
9
4
0
0
2
3
0
2
1
2
b
A
;
Jest równoznaczny z układem:
(5.17)
=
−
=
−
=
+
+
−
8
4
1
2
3
9
2
1
2
3
3
2
3
2
1
x
x
x
x
x
x
Rozwiązując ostatnie równanie otrzymujemy:
2
4
8
3
=
=
x
(5.18)
Następnie drugie równanie:
(
)
1
3
3
2
1
3
1
3
2
=
=
+
−
=
x
x
(5.19)
85

A na końcu równanie pierwsze:
(
)
2
2
4
2
9
2
1
3
2
1
−
=
−
=
−
−
−
=
x
x
x
(5.20)
W ogólnym przypadku dla ostatniego równania w układzie:
nn
n
n
a
b
x
=
(5.21)
gdzie:
n – liczba wierszy macierzy A.
Dla pozostałych równań obowiązuje zależność (dla każdego i
≠1,...,n).
ii
n
i
k
k
ik
i
i
u
x
a
b
x
∑
+
=
−
−
=
1
1
(5.22)
gdzie:
i – indeks wiersza w macierzy A,
k – indeks kolumny w macierzy A.
Proces obliczania kolejnych niewiadomych począwszy od x
n
do x
1
dla górnej macierzy
trójkątnej A nazywany jest postępowaniem odwrotnym. Podobna procedura obliczania
kolejnych niewiadomych od x
1
do x
n
, dla dolnej macierzy trójkątnej A nazywana jest
postępowaniem wprost.
5.3.1.2 Metoda eliminacji Gaussa
Najczęściej stosowaną metodą numerycznego rozwiązywania układów równań
liniowych jest metoda eliminacji Gaussa. Polega ona na przekształceniu kwadratowej
macierzy głównej A do macierzy górnej trójkątnej. Eliminacja realizowana jest przez
elementarne działania na wierszach macierzy A i b.
Przykład 5.9. Metoda eliminacji Gaussa
Wykorzystując elementarne działania na wierszach macierzy rozwiązać układ
równań liniowych:
(5.23)
−
=
+
+
−
=
+
+
=
−
+
1
4
2
4
2
1
3
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Przekształcenie układu równań do zapisu macierzowego:
(5.24)
b
Ax
=
−
=
×
−
−
=
2
2
1
1
4
1
4
1
2
3
2
1
3
2
1
x
x
x
Utworzenie rozszerzonej o wektor b macierzy A:
86

[
]
−
−
−
=
2
2
1
1
4
1
4
1
2
3
2
1
b
A
(5.25)
Redukcja elementów macierzy pod główną przekątną w pierwszej kolumnie.
Redukcja następuje przez pomnożenie pierwszego wiersza macierzy A przez
2 i odjęcie go od drugiego wiersza oraz pomnożenie pierwszego wiersza
przez –1 i odjęcie go od wiersza trzeciego. Wynikiem tych działań jest:
[
]
−
−
−
−
=
1
0
1
2
6
0
10
3
0
3
2
1
b
A
(5.26)
Redukcja elementów pod główną przekątną w kolumnie drugiej następuje
przez odjęcie drugiego wiersza pomnożonego przez –2 od wiersza trzeciego.
Wynikiem jest górna macierz trójkątną A:
[
]
−
−
−
=
1
0
1
18
0
0
10
3
0
3
2
1
b
A
(5.27)
Powrót z zapisu macierzowego do układu równań:
(5.28)
−
=
=
+
−
=
−
+
1
18
0
10
3
1
3
2
3
3
2
3
2
1
x
x
x
x
x
x
Rozwiązanie układu równań w postępowaniu odwrotnym:
=
−
+
−
−
=
−
=
−
−
−
=
−
=
54
65
1
18
1
3
27
5
2
1
27
5
3
18
1
10
0
18
1
3
2
3
x
x
x
(5.29)
Metoda eliminacji Gaussa jest podstawową metodą rozwiązywania układów równań
liniowych, zdarza się jednak, że zawodzi.
Przykład 5.10. Problem występujący w metodzie eliminacji Gaussa
Rozwiązać układ równań składający się z macierz A i wektora b w postaci.
87
(5.30)
−
=
−
−
−
−
−
−
−
−
=
7
7
5
4
3
6
1
1
2
8
3
3
3
4
2
1
2
2
4
2
b
A
;
Po rozszerzeniu macierzy A o wektor b mamy:
[
]
−
−
−
−
−
−
−
−
−
=
7
7
5
4
3
6
1
1
2
8
3
3
3
4
2
1
2
2
4
2
b
A
(5.31)
Redukując elementy pod główna przekątną w pierwszej kolumnie należy:
odjąć pierwszy wiersz pomnożony przez 1/2 od drugiego; odjąć pierwszy
wiersz pomnożony przez 3/2 od trzeciego oraz odjąć pierwszy wiersz
pomnożony przez 1/2 od czwartego:
[
]
[ ]
−
−
−
−
−
−
=
5
1
7
4
4
5
3
0
5
5
3
0
2
5
0
0
2
2
4
2
b
A
(5.32)
W tym miejscu eliminacja Gaussa zawodzi, ponieważ w drugim wierszu na
głównej przekątnej znajduje się zero, co powoduje, że nie można tego
elementu macierzy wykorzystać do redukowania elementów drugiej
kolumny.
W sytuacjach jak powyżej stosuje się modyfikację metody Gaussa polegającą na
częściowym wyborze elementu podstawowego. Elementem podstawowym nazywamy
ten element macierzy A, za pomocą którego redukuje się inne elementy macierzy.
Dotychczas podstawowymi elementami macierzy A były elementy leżące na głównej
przekątnej macierzy. Stosując częściowy wybór elementu podstawowego należy wybrać
ten z elementów k-tej kolumny, która charakteryzuje się największą wartością
bezwzględną. Zmieniając kolejności wierszy przenosi się wybrany element tak, aby
znalazł się on na głównej przekątnej macierzy.
Przykład 5.11. Częściowy wybór elementu podstawowego
Zadanie polega na dokończeniu rozwiązania przykładu 5.9.
Stosując częściowy wybór elementu podstawowego wiersze drugi i czwarty
zostają zamienione wierszami.
[
]
−
−
−
−
−
−
=
7
1
5
4
2
5
0
0
5
5
3
0
4
5
3
0
2
2
4
2
b
A
(5.33)
88

Redukcja elementów drugiej kolumny: odejmujemy wiersz drugi od
trzeciego.
[
]
[ ]
−
−
−
−
−
−
−
=
7
4
5
4
2
5
0
0
1
0
0
0
4
5
3
0
2
2
4
2
b
A
(5.34)
Kolejne zero pojawia się jako element podstawowy, dokonując wyboru
elementu podstawowego zmieniamy miejscami wiersz trzeci i czwarty.
[
]
−
−
−
−
−
−
−
=
4
7
5
4
1
0
0
0
2
5
0
0
4
5
3
0
2
2
4
2
b
A
(5.35)
Uzyskano układ z trójkątną macierzą A.
W wyborze częściowym poszukuje się elementu wyłącznie poniżej głównej przekątnej
w kolumnie, której elementy mają być redukowane. Częściowy wybór elementu
podstawowego jest zwykle wystarczający do uzyskania poprawnego rozwiązania.
Jednakże stabilność numeryczna eliminacji Gaussa z częściowym wyborem elementu
podstawowego jest uzależniona od wyboru elementu o maksymalnej wartości
bezwzględnej.
Drugą metodą jest pełny wybór elementu podstawowego, w którym zamianie podlegają
zarówno wiersze jak i kolumny macierzy. Pełny wybór elementu podstawowy jest
mniej wrażliwy na błędy zaokrągleń, podnosząc jednocześnie poziom stabilności
algorytmu rozwiązywania układu równań. Zabieg ten jest jednak okupiony znacznym
skomplikowaniem algorytmu i wydłużeniem czasu obliczeń.
5.3.1.3 Rozkład LU
Rozwiązanie Ax=b z wykorzystaniem rozkładu LU polega na wykonaniu podziału
macierzy A na macierz górną U i dolną L trójkątną, takich, że A=LU. Podział ten,
zwany rozkładem LU, umożliwia uniezależnienie rozwiązania układu równań od
wartości wektora wyrazów wolnych b. Dzięki temu możliwe staje się uzyskanie
rozwiązania układu równań liniowych, jednocześnie dla wielu różnych wektorów
wyrazów wolnych b.
Rozwiązanie Ax=b z wykorzystaniem rozkładu LU realizowane jest w trzech krokach:
1. Znajdź korzystając z rozkładu LU macierzy A, dolną trójkątną macierz L,
górną trójkątną macierz U oraz macierz permutacji P takie aby:
PA
LU
=
(5.36)
Ponieważ rozkład LU nie musi zachowywać oryginalnej kolejności wierszy
macierzy A (tzn. równań w układzie), konieczne jest natomiast zastosowanie
dodatkowej macierzy permutacji P, która przywraca poprawną kolejność.
2. Rozwiąż układ równań:
89

Pb
Ly
=
gdzie
Ux
y
=
(5.37)
3. Rozwiąż układ równań:
y
Ux
=
(5.38)
Dokładne wyjaśnienie przebiegu poszczególnych etapów rozwiązywania układu równań
z zastosowaniem rozkładu LU prezentuje poniższy przykład.
Przykład 5.12. Rozkład LU
Rozwiąż układ równań z wykorzystaniem rozkładu LU:
(5.39)
−
=
+
+
−
=
+
+
=
−
+
2
4
2
4
2
1
3
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Krok pierwszy: Realizacja rozkładu LU.
Definiujmy wektor n
p
w postaci [1 2 3]
T
. Wektor ten posłuży do
zapamiętania zmian położenia wierszy macierzy A. Redukujmy drugi i trzeci
element pierwszej kolumny oraz trzeci element drugiej kolumny macierzy A
korzystając z metody eliminacji Gaussa. Wykorzystujemy jedynie macierz A,
a nie macierz rozszerzoną [A b]. Postać macierzy A to:
(5.40)
[ ]
−
−
1
4
1
4
1
2
3
2
1
Przeszukujemy pierwszą kolumnę od przekątnej w dół w poszukiwaniu
elementu o największej wartości bezwzględnej – jest to drugi element w
drugim wierszu. Zamieniamy miejscami pierwszy i drugi wiersz, co daje:
[ ]
−
−
1
4
1
3
2
1
4
1
2
(5.41)
Zmieniamy miejscami pierwszy i drugi element wektora n
p
, zapisując w ten
sposób, że pierwszy i drugi wiersz macierzy A zostały zamienione. Wektor n
p
ma teraz postać [2 1 3]
T
.
Mnożymy pierwszy wiersz macierzy przez współczynnik 1/2 i odejmujemy
od wiersza drugiego. Mnożymy pierwszy wiersz przez współczynnik –1/2 i
odejmujemy od wiersza trzeciego. Kiedy wykonamy tą operacje macierzy
przyjmie postać:
90

−
3
0
5
0
4
1
2
2
9
2
3
(5.42)
W celu zaoszczędzenia pamięci w miejsce zer wpisujemy wykorzystane do
redukcji elementów macierzy współczynniki. I tak współczynnik 1/2, który
był mnożnikiem pierwszego wiersza, wykorzystanym do redukcji elementu
w pierwszej kolumnie i drugim wierszu macierzy, wpisujemy do pierwszej
kolumny i drugiego wiersza, itd.
−
−
⇒
−
3
5
4
1
2
3
0
5
0
4
1
2
2
9
2
1
2
3
2
1
2
9
2
3
(5.43)
Przeszukujemy drugą kolumnę macierzy A od głównej przekątnej w dół w
poszukiwaniu elementów o największej wartości bezwzględnej – jest nim
element w trzecim wierszu. Zmieniamy drugi i trzeci wiersz miejscami.
−
−
5
3
4
1
2
2
3
2
1
2
9
2
1
(5.44)
Zmieniamy miejscami drugi i trzeci element wektora n
p
co zmienia jego
postać do następującej [2 3 1]
T
. Redukujemy element w trzecim wierszu i
drugiej kolumnie przez pomnożenie drugiego wiersza przez współczynnik
1/3 i odjęcie od wiersza trzeciego. Co daje w wyniku macierz (z
współczynnikiem 1/3 zapisanym w miejscu 0):
−
−
6
3
4
1
2
3
1
2
1
2
9
2
1
(5.45)
Dokonujemy rozdzielenia uzyskanej macierzy na dolną macierz trójkątną L
oraz górną macierz trójkątną U.
−
=
−
=
6
0
0
3
0
4
1
2
1
0
1
0
0
1
2
9
3
1
2
1
2
1
U
L
;
(5.46)
Główną przekątną dolnej macierzy trójkątnej uzupełniono jedynkami.
Uzyskano w ten sposób dwie macierzy spełniające zależność:
91

−
=
−
×
−
=
3
2
1
1
4
1
4
1
2
6
0
0
3
0
4
1
2
1
0
1
0
0
1
2
9
3
1
2
1
2
1
LU
(5.47)
LU jest macierzą A z zmieniona kolejnością wierszy. Aby wyznaczyć
macierz P, która określi w jaki sposób została zmieniona wykorzystujemy
informacje znajdujące się w wektorze n
p
o elementach [2 3 1]
T
. Znaczenie
elementów tego wektora jest następujące: pierwszy wiersz staje się drugim,
drugi wiersz trzecim a trzeci pierwszym. Zmianę kolejności macierzy można
zaprezentować z wykorzystaniem macierzy permutacji. Jest to macierz z
pojedynczą jedynką w każdym wierszu i kolumnie i z pozostałymi
elementami równymi 0. W naszym przykładzie kolejne elementy wektora n
p
wskazują jednocześnie numery kolumny i wiersza elementu macierzy P,
którego wartość wynosi 1.:
[ ]
[ ]
[ ]
P
=
⇒
=
0
0
1
1
0
0
0
1
0
1
3
2
p
n
(5.48)
Spełniona jest zależność.
(5.49)
LU
PA
=
−
−
=
−
−
×
=
3
2
1
1
4
1
4
1
2
1
4
1
4
1
2
3
2
1
0
0
1
1
0
0
0
1
0
Krok drugi: Rozwiązanie układu równań Ly=Pb
Ponieważ:
Pb
LUx
Pb
PAx
b
Ax
=
⇒
=
⇒
=
(5.50)
można wprowadzić zapis y=Ux wtedy Ly=Pb.
Poszukujemy y rozwiązując równania poczynając od pierwszego. Wynik
iloczynu Pb oznacza wektor kolumnowy b ze zmienionymi miejscami
wierszami.
(5.51)
−
=
−
×
=
1
2
2
2
2
1
0
0
1
1
0
0
0
1
0
Pb
Mamy do rozwiązania.
(5.52)
−
=
×
−
1
2
2
1
3
1
2
1
0
1
2
1
0
0
1
3
2
1
y
y
y
/
/
/
Z pierwszego równania:
2
1
=
y
(5.53)
Z drugiego równania:
92

1
2
1
2
2
2
−
=
−
−
−
=
y
(5.54)
Z równania trzeciego:
( )
3
1
1
3
1
2
1
2
1
3
=
−
−
−
=
y
(5.55)
Krok trzeci: Rozwiązanie układu równań Ux=y.
Ponieważ dysponujemy wektorem y możemy rozwiązać układ.
y
Ux
=
(5.56)
Stąd:
(5.57)
−
=
×
−
3
1
1
2
6
0
0
3
2
9
0
4
1
2
3
2
1
/
x
x
x
/
Z trzeciego równania:
18
1
3
−
=
x
(5.58)
Z drugiego równania:
27
5
18
1
9
2
−
−
−
1
3
2
−
=
=
x
(5.59)
Z pierwszego równania:
54
27
18
2
2
−
−
−
65
5
1
4
1
1
=
−
=
x
(5.60)
Rozwiązaniem układu jest:
−
−
=
=
=
=
18
1
27
5
54
65
Pb
LUx
b
Ax
(5.61)
5.3.1.4 Przykład innych rozkładów – rozkład Cholesky’ego
(Banachiewicza)
Oprócz rozkładu LU, dla pewnych szczególnych postaci macierzy głównej układu
równań, opracowano inne rodzaje przekształceń. Na przykład, jeśli macierz A jest
dodatnio określoną macierzą symetryczną tzn. wszystkie elementy leżące na przekątnej
są większe od 0, a pozostałe elementy spełniają warunek:
dla każdego
ji
ij
a
a
=
j
i
i każdego
gdzie: k=1,2,...,n
≥
k
j
≥
(5.62)
To możliwy jest jej rozkład na iloczyn macierzy trójkątnych zwany rozkładem
Cholesky’ego:
T
LL
A
=
(5.63)
gdzie macierz L jest macierzą trójkątną dolną przy czym na przekątnej mogą znajdować
się elementy niekoniecznie równe 1. Rozkład Cholesky’ego zachowuje podstawową
93

zaletę rozkładu LU tj. możliwości rozwiązania Ax=b dla wielu różnych b przy
jednokrotnym rozkładzie macierzy A. W stosunku do rozkładu LU, realizacja rozkładu
Cholesky’ego wymaga dwukrotnie mniejszej liczby działań.
5.3.2 Metody iteracyjne
Metody iteracyjne polegają na wyznaczaniu kolejnych, przybliżonych wartości wektora
niewiadomych x będącego rozwiązaniem układu Ax=b. Kolejne przybliżenia zmierzają
od rozwiązania dokładnego. Rozwiązaniem jest to przybliżenie, które przybliża
rozwiązanie dokładne z założoną dokładnością. Obliczenia polegające na wyznaczeniu
kolejnych przybliżeń na bazie wyznaczonego wcześniej nazywamy iteracjami.
Przykład 5.13. Iteracyjne rozwiązanie układu równań
Wyznaczyć metodą iteracyjną przybliżone rozwiązanie równania:
(5.64)
=
+
−
−
=
−
+
−
=
+
+
1
6
2
2
1
2
4
1
5
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
Przyjmujemy rozwiązanie początkowe: x
1
=1, x
2
=1, x
3
=1.
Przekształcamy pierwsze równanie do postaci x
1
=...; x
2
=...; x
3
=... . W
wyniku otrzymujemy układ równań:
+
+
=
+
+
=
−
−
=
6
2
2
1
4
2
1
5
1
2
1
3
3
1
2
3
2
1
x
x
x
x
x
x
x
x
x
(5.65)
Iteracja 1. Ponieważ przyjęto x
1
=1, x
2
=1, x
3
=1, umożliwia to podstawienie
tych wartości po prawej stronie równań w układzie. Co prowadzi do
pierwszego, przybliżonego rozwiązania:
=
+
+
=
=
+
+
=
−
=
−
−
=
8333
0
6
2
2
1
0000
1
4
2
1
1
2000
0
5
1
1
1
3
2
1
.
x
.
x
.
x
(5.66)
Iteracja 2. Po prawej stronie równań w układzie wstawiamy wartości x
1
, x
2
, x
3
uzyskane w pierwszej iteracji. Co daje następne rozwiązanie:
94

=
×
+
−
=
=
×
+
−
=
−
=
−
−
=
4667
0
6
0000
1
2
2000
0
1
6167
0
4
8333
0
2
2000
0
1
1667
0
5
8333
0
1
1
3
2
1
.
.
.
x
.
.
.
x
.
.
x
(5.67)
W kolejnych iteracjach – proces jest kontynuowany.
Przykład powyższy można uogólnić na dowolny układ równań Ax=b. Dowolne i-te
równanie układu równań z kwadratową macierzą główną A o liczbie kolumn i wierszy
równej n można zapisać jako:
(5.68)
∑
=
=
n
j
i
j
ij
b
x
a
1
Równanie to można przekształcić przenosząc wszystkie czynniki a
ij
x
j
na prawą stronę, a
następnie dzieląc równanie przez a
ii
, co daje:
,...,n
,
, gdzie: i
a
b
x
a
x
ii
i
n
i
j
j
j
ij
i
2
1
1
=
+
−
=
∑
≠
=
(5.69)
Indeks j przyjmuje wartości 1,2, ..., n za wyjątkiem j=i, ponieważ x
i
pozostawiono po
lewej stronie równania.
Numer iteracji oznacza indeks górny umieszczony w nawiasach, x
(k-1)
= [x
1
(k-1)
, x
2
(k-
1)
, ... ,x
n
(k-1)
]
T
oznacza rozwiązanie po (k-1) iteracji. Indeks dolny oznacza numer
niewiadomej. Zgodnie z powyższymi oznaczeniami k-ta iteracja może być zapisana
jako:
,...,n
,
;gdzie: i
a
b
x
a
x
ii
i
i
j
j
)
(k
j
ij
(k)
i
2
1
1
1
=
+
−
=
∑
≠
=
−
(5.70)
Równanie to może zostać zapisane w formie macierzowej, przy założeniu, że dowolna
macierz główna A może zostać zapisana w postaci.
U
L
D
A
+
+
=
(5.71)
gdzie: D główna przekątna, L dolna trójkątna, U górna trójkątna część macierzy A.
Przykład 5.14. Rozkład A na L, U i D
Wyznaczyć macierze L, U i D macierzy głównej układu z przykładu 5.12,
czyli:
95

(5.72)
−
−
−
−
=
6
2
2
2
4
1
1
1
5
A
Podział ten realizuje się w Matlabie poleceniami
diag
,
tril
oraz
triu
.
>> A=[5 1 1;-1 4 -2;-2 -2 6]
A =
5 1 1
-1 4 -2
-2 -2 6
>> D=diag(diag(A))
D =
5 0 0
0 4 0
0 0 6
>> L=tril(A,-1)
L =
0 0 0
-1 0 0
-2 -2 0
>> U=triu(A,1)
U =
0 1 1
0 0 -2
0 0 0
Polecenie
tril
odczytuje dolną trójkątną cześć macierzy A. Drugi parametr
tego polecenia równy –1 oznacza, że odczytywana jest dolna macierz
trójkątna począwszy od przekątnej, której elementy leżą o jeden wiersz
poniżej elementów głównej przekątnej macierzy A. Polecenie
triu
odczytuje górną trójkątną część macierzy A, a drugi parametr równy 1
oznacza, że odczytywana jest górna macierz trójkątna począwszy od
przekątnej, której elementy leżą o jeden wiersz powyżej elementów głównej
przekątnej macierzy A.
5.3.2.1 Metoda Jaccobiego
Dysponując rozkładem DLU macierzy głównej, układ równań Ax=b można zapisać
jako:
(
)
b
x
U
L
D
=
+
+
(5.73)
To równanie można dalej przekształcić do postaci:
(
)
b
x
U
L
Dx
+
+
−
=
(5.74)
A następnie znając odwrotność macierzy D:
(
)
b
D
x
U
L
D
x
1
1
−
−
+
+
−
=
(5.75)
Po dodaniu indeksów z numerem iteracji otrzymamy:
(
)
b
D
x
U
L
D
x
1
1
1
−
−
−
+
+
−
=
)
k
(
)
k
(
(5.76)
96

Jest to równanie opisujące metodę iteracyjną Jacobiego rozwiązywania układu równań.
Przykład 5.15. Metoda Jacobiego
Rozwiązać układ równań z przykładu 5.12, stosując zapis macierzowy
iteracyjnej metody Jacobiego. Zrealizować 20 iteracji, przyjmując jako
wektor rozwiązań początkowych x=[1 1 1]
T
. Przybliżenia rozwiązania z
kolejnych iteracji przechować w kolejnych kolumnach macierzy x.
Wprowadzamy do obszaru zmiennych macierz A, wektor b.
>> A=[5 1 1;-1 4 -2;-2 -2 6];
>> b=[1 1 1]'
Tworzymy macierz rozwiązań x o liczbie kolumn równej liczbie iteracji i
liczbie wierszy równej liczbie niewiadomych, a następnie do pierwszej
kolumny macierzy wpisujemy przyjęty wektor rozwiązań początkowych.
>> x=zeros(3,20);
>> x(:,1)=[1 1 1]';
Jak w poprzednim przykładzie, dokonujemy podziału macierzy A na
macierze L, U oraz D.
>> L=tril(A,-1);
>> U=triu(A,1);
>> D=diag(diag(A));
Stosując w pętli zależność iteracyjną (5.76) obliczamy kolejne przybliżenia
wektora rozwiązań.
>> for i=1:20,
x(:,i+1)=-1*inv(D)*(L+U)*x(:,i)+inv(D)*b;
end
>> x
x =
Columns 1 through 6
1.0000 -0.2000 -0.1667 -0.0100 0.0517 0.0578
1.0000 1.0000 0.6167 0.4250 0.4058 0.4154
1.0000 0.8333 0.4333 0.3167 0.3050 0.3192
Columns 7 through 12
0.0531 0.0503 0.0498 0.0499 0.0500 0.0500
0.4240 0.4255 0.4254 0.4251 0.4250 0.4250
0.3244 0.3257 0.3253 0.3251 0.3250 0.3250
Columns 13 through 18
0.0500 0.0500 0.0500 0.0500 0.0500 0.0500
0.4250 0.4250 0.4250 0.4250 0.4250 0.4250
0.3250 0.3250 0.3250 0.3250 0.3250 0.3250
Columns 19 through 21
0.0500 0.0500 0.0500
0.4250 0.4250 0.4250
0.3250 0.3250 0.3250
Iteracyjny proces dochodzenia do rozwiązania przedstawiono na rys. 5.3
Równania układu równań tworzą płaszczyzny przecinające się w punkcie
x=[0.05 0.425 0.325], który jest jego rozwiązaniem. Wierzchołki linii
łamanej, począwszy od punktu [1 1 1] odpowiadają kolejnym rozwiązaniom.
97
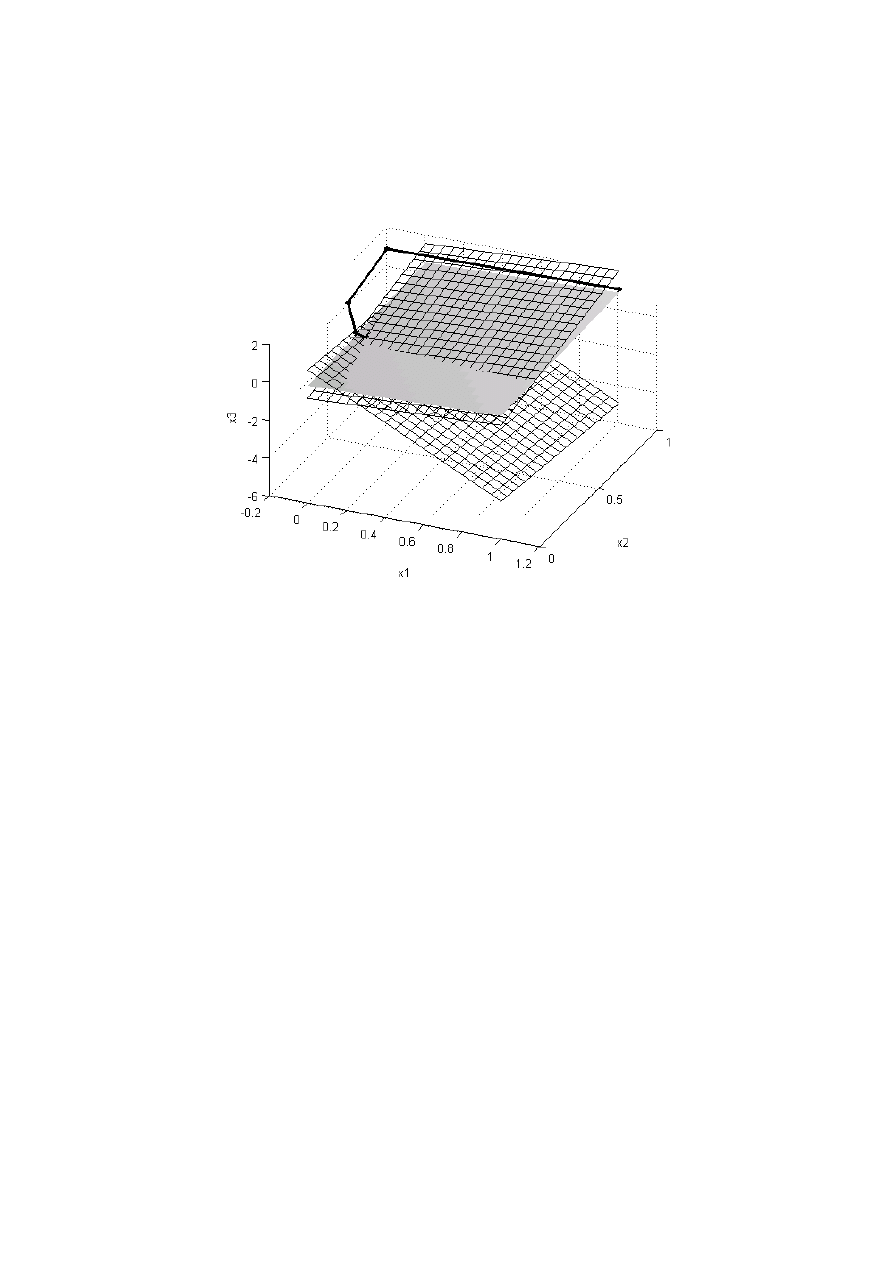
Rys. 5.3. Iteracyjny proces rozwiązywania układu równań metodą Jacobiego
Oznaczając:
oraz
otrzymamy uogólnioną zależność
opisującą metodę iteracyjną w postaci:
U)
(L
-D
M
-
+
=
1
b
D
c
1
−
=
(5.77)
c
Mx
x
)
k
(
)
k
(
+
=
−1
Jeśli w zależności (5.77) M oraz c nie zależy od numeru iteracji k to taką metod
iteracyjną nazywamy stacjonarną. Metody iteracyjne niestacjonarne zmieniają macierz
M oraz wektor c w każdej iteracji.
Przykład 5.16. Metoda Jacobiego – zapis uogólniony
Znaleźć macierz iteracji M oraz wektor c w metodzie Jacobiego dla danych z
przykładu 5.14. Zakładamy, że zmienne A, L, U, D i b znajdują się w
obszarze zmiennych Matlaba.
>> M=-1*inv(D)*(L+U)
M =
0 -0.2000 -0.2000
0.2500 0 0.5000
0.3333 0.3333 0
>> c=inv(D)*b
c =
0.2000
0.2500
0.1667
98
5.3.2.2 Metoda Gaussa-Seidla
Metoda Gaussa-Seidla jest modyfikacją metody Jaccobiego polegającą na
wykorzystaniu obliczonych n-pierwszych składowych wektora niewiadomych k-1-szej
iteracji. Porównajmy układy równań. Korzystając z danych z przykładu 5.15, dla
metody Jaccobiego, mamy:
(5.78)
+
=
−
−
−
1667
0
25
0
2
0
0
3333
0
3333
0
5
0
0
25
0
2
0
2
0
0
1
3
1
2
1
1
3
2
1
.
.
.
x
x
x
.
.
.
.
.
-
.
-
x
x
x
)
(k
)
(k
)
(k
(k)
(k)
(k)
Dla metody Gaussa-Seidla, układ równań będzie wyglądał następująco:
(5.79)
+
+
=
−
−
−
1667
0
25
0
2
0
0
3333
0
3333
0
0
0
25
0
0
0
0
0
0
0
5
0
0
0
2
0
2
0
0
3
2
1
1
3
1
2
1
1
3
2
1
.
.
.
x
x
x
.
.
.
x
x
x
.
.
-
.
-
x
x
x
(k)
(k)
(k)
)
(k
)
(k
)
(k
(k)
(k)
(k)
Wartość
jest wyliczana na podstawie następnej składowej wektora z poprzedniej
iteracji
. Ale w przypadku poprzednich składowych wektora niewiadomych,
korzystamy z wartości obliczonych w bieżącej iteracji tzn.
. W zapisie
uogólnionym:
)
k
(
x
2
)
k
(
x
1
3
−
)
k
(
x
1
(5.80)
c
x
M
x
M
x
)
k
(
l
)
k
(
u
)
k
(
+
+
=
−1
5.3.2.3 Zbieżność metod iteracyjnych
W metodach iteracyjnych obliczenia prowadzone są z reguły do chwili, w którym
zmiany wartości rozwiązania w dwóch kolejnych iteracjach są wystarczające małe. W
zapisie matematycznym obliczenia powinny zostać zatrzymane gdy:
TOL
≤
1)
-
(k
(k)
x
-
x
(5.81)
Ta nierówność nazywana jest testem zbieżności. Jeśli jest spełniona można powiedzieć,
że iteracje są zbieżne i prowadzą do uzyskania rozwiązania o założonej dokładności.
Wartość TOL w teście zbieżności jest małą dodatnią liczbą i nazywana jest
dokładnością.
Przykład 5.17. Test zbieżności
Wyznaczyć wartość różnicy między kolejnymi rozwiązaniem układu równań
z przykładu 5.15. Wyniki przedstawić w formie wykresu.
>> for i=2:20, test_zb(i)=norm(x(:,i)-x(:,i-1)); end
>> plot(test_zb(2:20))
>> xlabel('Numer iteracji')
>> ylabel('Test zbieznosci')
Na wykresie widać, że wartość błąd w rozwiązaniu od 7 iteracji praktycznie
nie ulega zmianie, a więc w tej iteracji należałoby przerwać obliczenia.
Polecenie norm oblicza normę euklidesową macierzy.
99
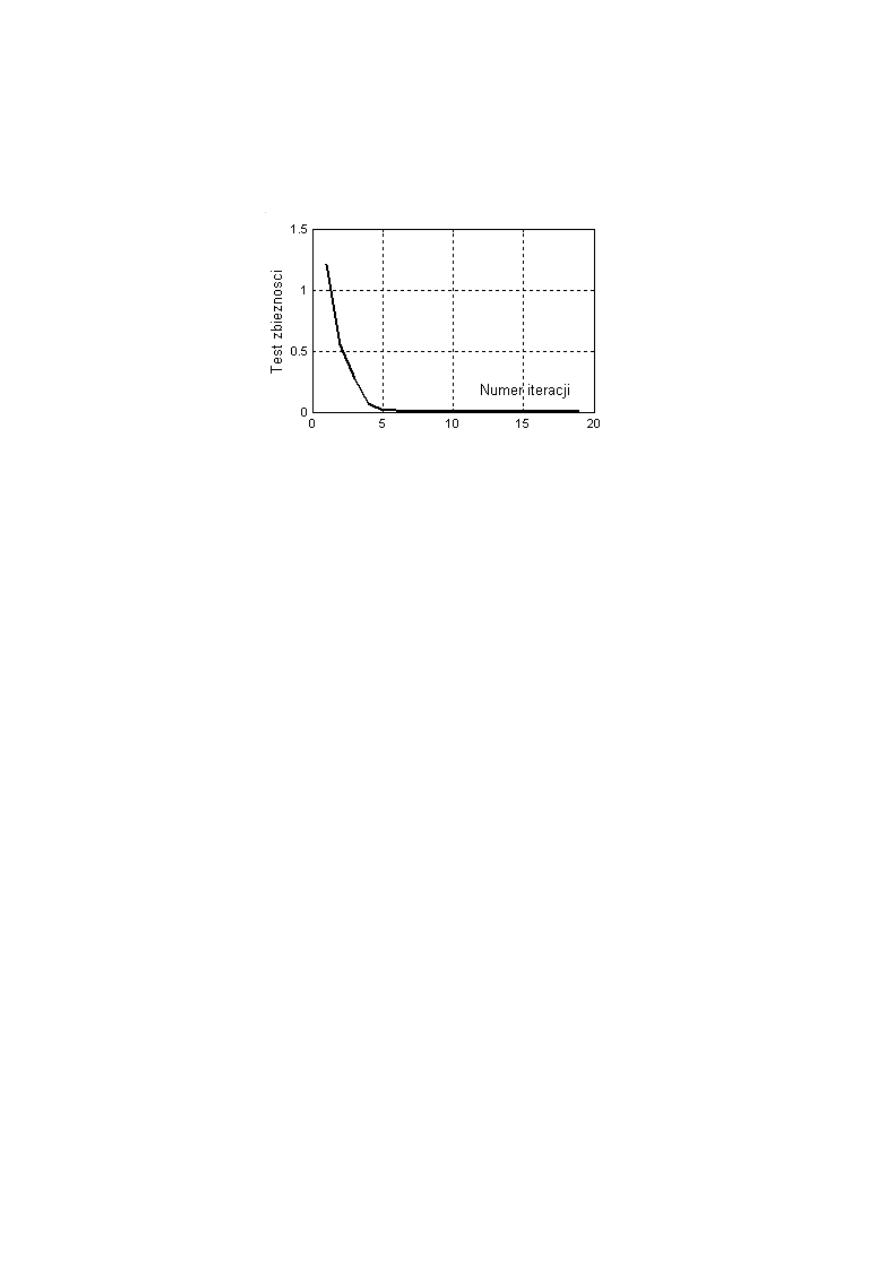
Rys. 5.4. Test zbieżności dla kolejnych iteracji w przykładzie 5.15
Dokładność metody iteracyjnej w teście zbieżności jest określana z reguły przez
użytkownika algorytmu i jej wartość ogranicza jedynie dokładność obliczeniowa
wykorzystywanej maszyny cyfrowej
m
ε . Należy przy tym pamiętać, że zmniejszanie
wartości TOL prowadzi z reguły do lepszego przybliżenia rozwiązania ale oznacza
jednocześnie konieczność zrealizowania większej liczby iteracji, co wydłuża czas
obliczeń.
Metody iteracyjne nie zawsze są zbieżne, czyli nie zawsze pozwalają na uzyskanie
wystarczająco dokładnego rozwiązania (lub rozwiązania w ogóle). Ponadto, nawet gdy
zbieżność jest możliwa, proces jej uzyskiwania nie koniecznie przebiega w sposób
monotoniczny.
Warunek konieczny i wystarczający zbieżności dowolnej metody iteracyjnej określono
z warunku Couchego. W warunku tym, ciąg kolejnych przybliżeń
jest zbieżny do
rozwiązania dokładnego
, dla dowolnego rozwiązania początkowego
wtedy i
tylko wtedy, gdy promień spektralny macierzy iteracji
)
k
(
x
x
)
( 0
x
( )
M
ρ
jest mniejszy od 1.
( )
1
<
M
ρ
(5.82)
Promień spektralny to wartość własna macierzy M o maksymalnej wartości
bezwzględnej.
Przykład 5.18. Test zbieżności
Wyznaczyć promień spektralny macierzy iteracji M z przykładu 5.15.
>> ro=max(abs(eigs(M)))
ro =
0.4134
Ponieważ promień spektralny macierzy jest mniejszy od 1, metoda iteracyjna
Jacobiego z macierzą iteracji M wyznaczoną dla danej macierzy głównej
układu A będzie zbieżna.
100

Wyznaczenia promienia spektralnego macierzy iteracji M w trakcie rozwiązywania
układów równań liniowych metodami iteracyjnymi nie jest regułą. Dla metod
niestacjonarnych musiałoby być przeprowadzane osobno w każdej iteracji. Oznacza to,
że w trakcie realizacji obliczeń nie wiemy, czy zastosowana metoda iteracyjna będzie
zbieżna. Dlatego w metodach iteracyjnych wprowadza się dodatkowy parametr
określający po ilu iteracjach, w przypadku nie osiągnięcia zbieżności, należy
bezwzględnie przerwać obliczenia.
5.4 PRZYKŁADY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ
LINIOWYCH
5.4.1 Metody dokładne
Za rozwiązywanie układów równań liniowych w Matlabie odpowiedzialny jest symbol
\, czyli operator lewostronnego dzielenia. Wykorzystuje on metody dokładne. Wybór
konkretnej metody bazuje na automatycznej analizie struktury macierzy głównej układu
A wykonywanej w następujący sposób:
1. Jeśli macierz A jest macierzą diagonalną rozwiązanie uzyskiwane jest jak w
przykładzie 5.7.
2. Jeśli macierz A jest macierzą trójkątną górną lub dolną wykorzystywane jest
postępowanie odwrotne lub postępowanie wprost.
3. Jeśli macierz A jest macierzą, z której można utworzyć macierz trójkątną przez
proste przestawienie wierszy lub kolumn to wykorzystywane jest postępowanie
odwrotne po uprzednim przestawieniu wierszy lub kolumn.
4. Jeśli macierz A jest symetryczna, dodatnio zorientowana, wykorzystywany jest
rozkład Cholesky’ego.
5. Jeśli macierz A jest kwadratowa i nie zaszły przypadki od 1 do 4 do
rozwiązania układu równań wykorzystywany jest rozkład LU.
Przykład 5.19. Rozwiązanie układu równań za pomocą dzielenia \
Rozwiązać układ równań dla zadania z przykładu 5.1. Zakładamy, że do
obszaru zmiennych Matlaba wprowadzono już macierz A oraz wektor b.
>> format long e
>> x=A\b
x =
1.500000000000000e+001
1.470261666271740e+003
0
5.442809041582063e+002
-2.442809041582063e+002
5.567646949176304e+003
Wektor wyrazów wolnych b może składać się z wielu kolumn. Pozwala skorzystać to z
zalet rozkładów Cholesky’ego i LU, czyli rozwiązywać układy równań przy
101

jednokrotnym rozkładzie macierzy głównej dla wielu różnych wektorów wyrazów
wolnych.
Przykład 5.20. Rozwiązanie układu równań dla dwóch zestawów danych
Ustalić wartości reakcji dla przykładu 5.19, dodatkowo definiując drugi
wektor wyrazów wolnych, w którym zwiększono dwukrotnie wartość sił.
Wprowadzamy oba wektory wyrazów wolnych do Matlaba.
>> b1=[0; 300; 300*0.5*3*sin(45*pi/180)+200;
30*cos(60*pi/180);...
3*100+2*300+30*sin(60*pi/180);...
3*100*0.5*3+2*300*3+30*(2/3)*3*sin(60*pi/180)]
>> b2=[0; 2*300;
2*300*0.5*3*sin(45*pi/180)+2*200;...
2*30*cos(60*pi/180);
2*3*100+4*300+2*30*sin(60*pi/180);...
2*3*100*0.5*3+4*300*3+2*30*(2/3)*3*sin(60*pi/180)]
b1 =
1.0e+003 *
0
0.3000
0.5182
0.0150
0.9260
2.3020
b2 =
1.0e+003 *
0
0.6000
1.0364
0.0300
1.8520
4.6039
Tworzymy macierz wyrazów wolnych przez “sklejenie” obu wektorów.
>> b=[b1 b2]
Rozwiązujemy układ równań:
>> format long e
>> x=A\b
x =
1.500000000000000e+001 3.000000000000001e+001
1.470261666271740e+003 2.940523332543479e+003
0 0
5.442809041582063e+002 1.088561808316413e+003
-2.442809041582063e+002 -4.885618083164127e+002
5.567646949176304e+003 1.113529389835261e+004
Pierwsza kolumna macierzy niewiadomych x zawiera rozwiązanie dla
pierwszej kolumny macierzy wyrazów wolnych, druga – dla drugiej.
102

5.4.2 Metody iteracyjne
W podstawowej konfiguracji Matlab dysponuje dziewięcioma metodami iteracyjnym
(niestacjonarnymi) do rozwiązywania układów równań liniowych. Polecenia
odpowiedzialne za realizację obliczeń dowolną metod posiadają identyczną składnię:
x=metoda(A,b,TOL,MaxIT)
gdzie:
x
– zmienna, w której zostanie umieszczony wektor rozwiązań,
A
– macierz
główna układu równań,
b
– wektor wyrazów wolnych,
TOL
– oczekiwana dokładność w
teście zbieżności, jeśli parametr zostanie pominięty Matlab przyjmie wartość 1
×10
-6
,
MaxIT
– maksymalna liczba iteracji, po której w przypadku nie osiągnięcia zbieżności
obliczenia mają zostać przerwane, jeśli parametr zostanie pominięty maksymalna liczba
iteracji wynosi 20.
Metody dostępne w pakiecie Matlab to:
Bicg
Biconjugate gradient
Bicgstab
Biconjugate gradient stabilized
Cgs
Conjugate gradient squared
gmres
Generalized minimum residual
Lsqr
Conjugate Gradients on the Normal Equations
minres
Minimum residual
Pcg
Preconditioned conjugate gradient
Qmr
Quasiminimal residual
symmlq
Symmetric LQ
Podstawowym kryterium wyboru metody iteracyjnej jest znajomość własności macierzy
głównej układu A. Np. metoda
pcg
wymaga, aby macierz A była symetryczna dodatnio
zorientowana. Metody
minres
oraz
symmlq
mogą być wykorzystane dla macierzy
symetrycznej niezorientowanej. Metoda
lsqr
umożliwia rozwiązanie układów równań
o nie kwadratowej macierzy A. Natomiast pozostałych pięć metod można zastosować
dla kwadratowych macierzy A dowolnego typu.
Przykład 5.21. Rozwiązanie układu równań metodami iteracyjnymi
Rozwiązać zadanie z przykładu 5.1 stosując wszystkie dziewięć metod
iteracyjnych. Określić, która z metod prowadzi do uzyskania
najdokładniejszego rozwiązania oraz umożliwia uzyskanie rozwiązania w
najmniejszej liczbie iteracji. W poleceniach Matlaba pominąć parametry
TOL oraz MaxIT (przyjąć domyślne). Zakładamy, że macierz A i wektor b
zostały wprowadzone do Matlaba, jak w przykładach 5.3 i 5.5.
Wykorzystujemy kolejno wszystkie dziewięć metod do uzyskania
rozwiązania. Polecenie zostały wydane w taki sposób, aby móc określić
wektor rozwiązań (x), fakt osiągnięcie zbieżności (test), uzyskaną dokładność
(tol), numer iteracji w którym osiągnięto zbieżność (iter) oraz wektor reszt w
każdej iteracji (blad).
>> x=zeros(6,9); test=zeros(9,1); tol=zeros(9,1);
>> [x(:,1),test(1),tol(1),iter1,blad1]=bicg(A,b);
>> [x(:,2),test(2),tol(2),iter2,blad2]=bicgstab(A,b);
>> [x(:,3),test(3),tol(3),iter3,blad3]=cgs(A,b);
>> [x(:,4),test(4),tol(4),iter4,blad4]=gmres(A,b);
>> [x(:,5),test(5),tol(5),iter5,blad5]=lsqr(A,b);
103

>> [x(:,6),test(6),tol(6),iter6,blad6]=minres(A,b);
>> [x(:,7),test(7),tol(7),iter7,blad7]=pcg(A,b);
>> [x(:,8),test(8),tol(8),iter8,blad8]=qmr(A,b);
>> [x(:,9),test(9),tol(9),iter9,blad9]=symmlq(A,b);
Tworzymy wykres prezentujący zmiany względnej wartości błędu w
kolejnych iteracjach.
figure
hold on
plot(blad1/norm(b),'k-')
plot(blad2/norm(b),'k--')
plot(blad3/norm(b),'k:')
plot(blad4/norm(b),'k-.')
plot(blad5/norm(b),'k-+')
plot(blad6/norm(b),'k--*')
plot(blad7/norm(b),'k:o')
plot(blad8/norm(b),'k-.s')
plot(blad9/norm(b),'k-x')
axis([1 12 0 4])
xlabel('Numer iteracji')
ylabel('Blad wzgledny [%]')
Rys. 5.5. Błąd względny analizowanych metod iteracyjnych
Dla danej macierzy głównej A układu równań najszybszą zbieżnością
charakteryzuje się metoda QMR. Metody SymmLQ, PCG oraz Minres nie
osiągają zbieżności (macierz A nie jest symetryczna). Wyświetlając wektor
tol możemy odczytać uzyskaną w każdej metodzie dokładność
>> tol'
ans =
2.2152e-013
1.7764e-010
5.4093e-012
1.0859e-015
104
6.7741e-011
3.8872e-001
1.0000e+000
3.3401e-013
7.0988e-001
Największą dokładność uzyskano w metodzie GmRes, lecz dopiero w 12
iteracji
5.5 ZADANIA
Zadanie 5.1.
Jednorodna płyta prostopadłościenna o ciężarze G=20000 N spoczywa na sześciu
przegubowo połączonych lekkich prętach.
a
y
M
A
D
G
B
S
1
S
2
P
1
P
2
b
S
4
S
3
S
6
S
5
γ
β
β
α
x
C
z
Rys. 5.6. Płyta podparta na prętach
Na płytę działają w płaszczyźnie poziomej dwie siły: P
1
= 40000 N pod kątem
α = 30°
do krawędzi AB i P
2
= 30000 N wzdłuż krawędzi BC oraz para sił o momencie
M=60 kNm. Wyznaczyć siły w prętach. Dodatkowe dane: a=2m, b=h=1m,
β=45°,
γ=arctg(0,5rad).
Pręty są lekkie, zakończone przegubami, więc siły działają wzdłuż ich osi. Dla układu
osi współrzędnych jak na rysunku równania warunków równowagi są:
(
)
(
)
=
−
+
+
=
+
+
+
−
=
−
+
=
−
+
+
+
+
+
=
−
+
−
=
−
−
−
0
0
0
0
0
0
4
6
2
2
4
5
3
2
6
5
6
5
4
3
2
1
4
2
1
6
2
1
γ
β
γ
β
β
γ
β
γ
α
β
β
α
cos
b
S
sin
a
S
b
P
M
G
b
sin
S
S
S
G
a
cos
S
S
G
cos
S
S
sin
S
S
cos
S
S
cos
S
P
sin
P
sin
S
sin
S
cos
P
b
a
(5.83)
Obliczyć:
-
Rząd macierzy głównej układu równań.
105

-
Współczynnik uwarunkowania macierzy głównej układu równań.
-
Rozwiązanie układu równań z określeniem jednostek fizycznych. Układ równań
rozwiązać metodą dokładną oraz dowolną metodą iteracyjną.
Zadanie 5.2.
Poniższy rysunek przedstawia kratownicę płaską składającą się z 13 prętów
połączonych w 8 węzłach. Obciążenie w postaci sił skupionych o wartościach
wyrażonych w kN przyłożono w węzłach 2, 5 i 6. Kąt nachylenia prętów ukośnych
α = 45°. Należy wyznaczyć siły w każdym z prętów kratownicy.
10 kN
15 kN
20 kN
1
2
3
4
5
6
7
8
9
10
11
12
13
1
3
2
4
5
6
8
7
Rys. 5.7. Kratownica
Aby kratownica znajdowała się w równowadze statycznej suma sił w każdym węźle
powinna być równa 0. Otrzymujemy układ równań.
(5.84)
=
+
=
+
+
=
+
=
=
=
+
+
+
=
+
=
=
=
+
+
+
=
=
=
0
0
20000
15000
0
0
10000
12
13
12
11
9
12
9
8
11
13
10
9
7
5
10
9
6
5
7
8
4
5
3
1
5
4
1
3
6
2
f
cos
f
f
sin
f
f
sin
f
cos
f
cos
f
N
f
f
f
N
f
sin
f
f
sin
f
f
cos
f
f
cos
f
f
f
f
sin
f
f
sin
f
cos
f
f
cos
N
f
f
f
α
α
α
α
Obliczyć:
-
Rząd macierzy głównej układu równań.
-
Współczynnik uwarunkowania macierzy głównej układu równań.
-
Rozwiązanie układu równań z określeniem jednostek fizycznych. Układ równań
rozwiązać metodą dokładną oraz dowolną metodą iteracyjną.
106

5.6 PYTANIA
1. Podaj zależność formalnego rozwiązania układu równań liniowych Ax = b.
2. Podaj powody, dla których nie wykorzystuje się rozwiązania formalnego.
3. Podaj nazwy metod dokładnych rozwiązywania układu równań liniowych.
4. Opisz znaczenie współczynnika uwarunkowania
κ(A) na dokładność rozwiązania.
5. Podaj powód częściowego wyboru elementu podstawowego.
6. Opisz procedurę rozwiązywania układu równań liniowych mając dany rozkład LU
macierzy głównej układu.
7. Podaj warunek zbieżności dowolnej metody iteracyjnego rozwiązywania układu
równań liniowych.
8. Czym są tolerancja i maksymalna liczba iteracji w metodach iteracyjnych.
5.7 LITERATURA
1. Banachowski L., Diks K., Rytter W.: Algorytmy i struktury danych, Wydawnictwa
Naukowo-Techniczne, Warszawa 1999
2. Fortuna Z., Macukow B., Wąsoski J.: Metody numeryczne, Wydawnictwa
Naukowo-Techniczne, Warszawa 1993
3. Moler C.: Numerical Computing with MATLAB, SIAM, 2004.
4. Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P.: Numerical Recipes in
C. The Art of Scientific Computing, Cambridge University Press, 1992
5. Recktenwald G.: Numerical Methods with MATLAB. Implementations and
Applications, Prentice Hall, 2000
6. Zalewski A., Cegieła R.: Matlab – obliczenia numeryczne i ich zastosowania,
Wydawnictwo NAKOM, Poznań 1997
7. Praca zbiorowa: Introductory tutorial for the Advanced Computing Laboratory.
Materiały kursu Numerical computation (445.270), University of Auckalnd, 1998
8. Siołkowski B., Holka H., Malec M.: Zbiór zadań ze statyki i wytrzymałości
materiałów, Wydawnictwo Uczelniane Akademii Techniczno-Rolniczej w
Bydgoszczy, Bydgoszcz 1988.
107
Wyszukiwarka
Podobne podstrony:
Metody rozwiązywania układów równań liniowych
Rozwiazywanie ukladow rownan liniowych
Rozwiązywanie układów równań liniowych
rozwiązywanie układów równań liniowych spr, Politechnika Lubelska, Studia, Studia, sem III, sprawka,
sciaga rozwiazywanie ukladow rownan liniowych za pomoca wzorow cramera, Matematyka
Rozwiazywanie ukladów rownan liniowych W11
Metody rozwiązywania układów równań liniowych
Rozwiązywanie układów równań liniowych algebraicznych
100 ukladow rownan liniowych z pelnymi rozwiazaniami krok po kroku (2)
100 układów równań liniowych z pełnymi rozwiązaniami krok po kroku
Rozwiązywanie układów równań
Rozwiązywanie układów równań metodą wyznaczników
4 Metody numeryczne rozwiązywania układów równań2
M[1] 7 Rozwiazywanie ukladow rownan typu Cramera
matematyka, Roz uk równań wyznaczników m, Rozwiązywanie układów równań metodą wyznaczników
Macierzowe metody rozwiązywania układów równań, t2d
więcej podobnych podstron