w w w. e l e k t r o . i n f o . p l

n r 1 0 / 2 0 0 4

47

i n s t a l a c j e e l e k t r o e n e r g e t y c z n e

W

poprzednich artykułach [4] i [7]
opisano metody projektowania

pasywnych filtrów prostych. Metody te
mają swoje wady i zalety. Cechą wspól-
ną jest to, że wymagają założenia, iż fil-
try te są pozbawione części rzeczywi-
stej impedancji, R

Fn

= 0. Wymagają

także znajomości pewnych wzorów,
z których należy skorzystać przy pro-
jektowaniu filtrów.

Algorytmy Genetyczne umożliwiają

uwzględnienie rezystancji filtrów, ich
wzajemnego wpływu na siebie, oraz
dają możliwość optymalizacji wielokry-
terialnej. Wystarczy znać tylko podsta-
wowe wzory analityczne oraz skonstru-
ować funkcję celu, a Algorytm Gene-
tyczny sam znajdzie rozwiązanie pro-
blemu. Podkreślić należy, że Algorytmy
Genetyczne należą do grupy metod pro-
babilistycznych, przez co mogą znajdo-
wać rozwiązanie bliskie optymalnemu,
ale niekoniecznie optymalne.

algorytmy genetyczne

Jak większość prostych metod po-

wstały na bazie obserwacji przyrody.
Osobnik, który jest lepszy, silniejszy
szybszy, dłużej przeżyje i będzie miał
więcej potomków, które odziedziczą
po nim te cechy. Algorytmy Genetycz-
ne różnią się od tradycyjnych metod
optymalizacyjnych kilkoma podsta-
wowymi cechami:



nie przetwarzają bezpośrednio

parametrów zadania, lecz ich za-
kodowaną postać,



prowadzą przeszukiwanie, wy-

chodząc nie z pojedynczego punk-
tu, lecz z pewnej ich populacji,



korzystają tylko z funkcji celu, nie

korzystają zaś z pochodnych lub
innych pomocniczych informacji,



stosują probabilistyczne, a nie de-

terministyczne reguły wyboru,



umożliwiają dowolne kształtowa-

niu funkcji celu, co umożliwia wy-
korzystanie AG do optymalizacji
wielokryterialnej.
W skład podstawowego Algorytmu

Genetycznego wchodzą:



inicjalizacja populacji początko-

wej,



dekodowanie chromosomów do

przestrzeni parametrów zadania,



wyznaczenie wartości funkcji celu

dla każdego osobnika,



sprawdzenie warunku kończące-

go pracę algorytmu,



operator selekcji,



operator krzyżowania i mutacji.

Ważne jest, by zauważyć, że AG

dostarczają potencjalnych rozwiązań
danego problemu, a wybór rozwiąza-
nia ostatecznego pozostawiają użyt-
kownikowi. W przypadku, gdy szcze-
gólny problem nie ma jednego roz-
wiązania, np. rodzina pareto-opty-
malnych rozwiązań jak w przypad-
ku wielokryterialnej optymalizacji,
wtedy AG są potencjalnie użytecz-
ne do identyfikacji tych alternatyw-
nych rozwiązań.

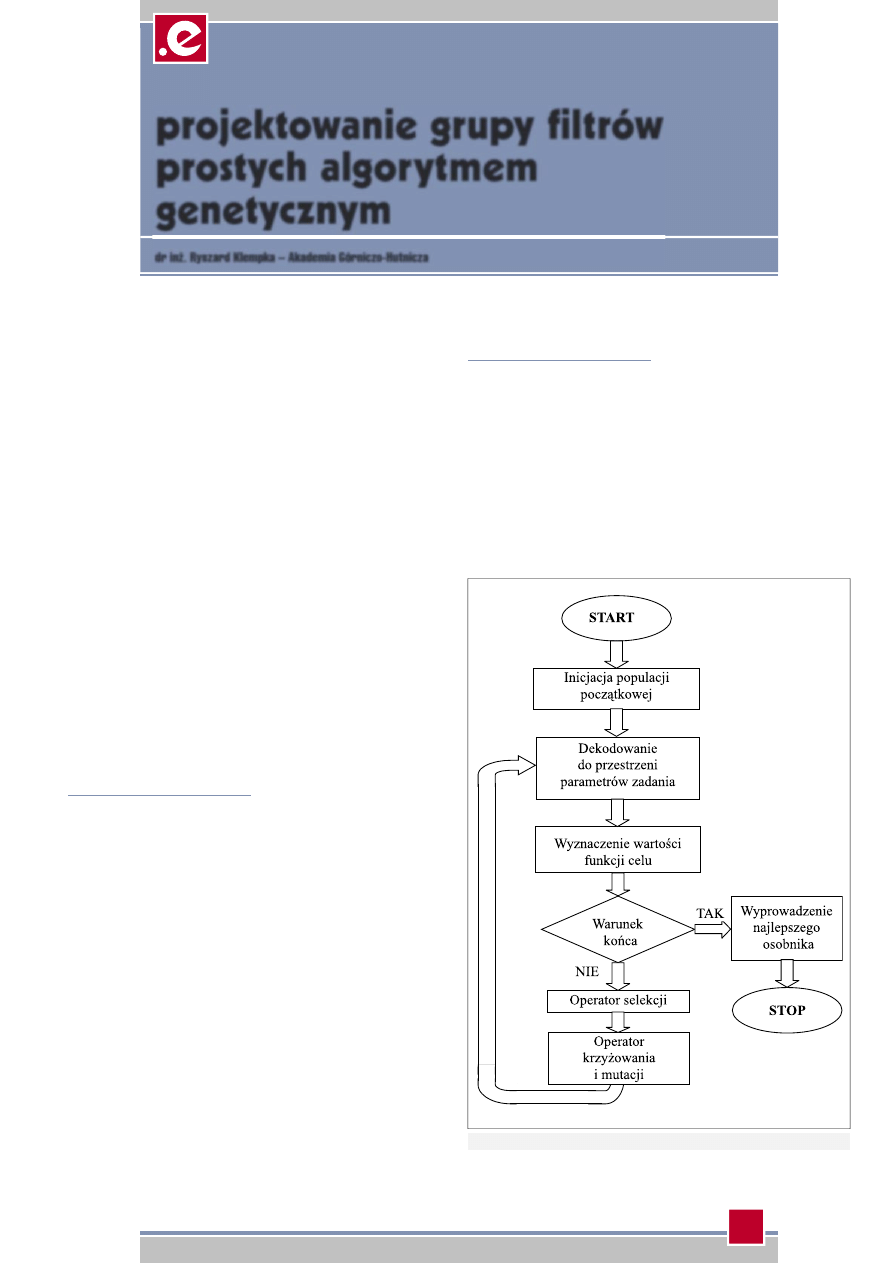
Schemat blokowy podstawowe-

go Algorytmu Genetycznego został
przedstawiony na

rysunku 1. W za-

stosowaniach praktycznych sche-
mat ten jest bardziej rozbudowany,
np. o przekształcenie funkcji celu
w funkcję przystosowania oraz do-
datkowe operatory. Również podsta-
wowe operatory jak selekcja, krzyżo-
wanie i mutacja mogą wyglądać ina-
czej niż podaje to literatura opisując
zasadę działania AG. Różnice te wy-
nikają z adaptacji AG do postawione-
go zadania.

inicjacja populacji

początkowej

W tej części należy określić pod-

stawowe parametry Algorytmu Ge-
netycznego, takie jak: liczność popu-
lacji (liczba chromosomów w popu-
lacji), ilość parametrów zadania, jak
długi będzie chromosom, jaki alfabet
zostanie użyty. Po określeniu tych pa-
rametrów, losowo generuje się popu-
lację początkową. Algorytm Gene-
tyczny zazwyczaj startuje z zupełnie

losowego punktu (losowej populacji
początkowej). Osobniki są kodowane
jako ciągi (chromosomy) odpowied-
niego alfabetu. W większości zasto-
sowań używa się reprezentacji alfa-
betu binarnego {0, 1} lub Gray ’a, acz-
kolwiek w niektórych przypadkach
można użyć np. alfabetu trójkowego,
liczb całkowitych lub rzeczywistych,
itp. Ciągi kodowe nie zawierają in-
formacji o problemie, który rozwią-
zujemy. Proces przeszukiwania dzia-
ła na zakodowanych zmiennych de-

projektowanie grupy filtrów

prostych algorytmem

genetycznym

dr inż. Ryszard Klempka – Akademia Górniczo-Hutnicza

Rys. 1 Schemat blokowy podstawowego Algorytmu Genetycznego

w w w. e l e k t r o . i n f o . p l

n r 1 0 / 2 0 0 4

48

i n s t a l a c j e e l e k t r o e n e r g e t y c z n e

cyzyjnych, a nie na zmiennych decy-
zyjnych bezpośrednio.

Przykładowo, jeżeli mamy dwie

zmienne decyzyjne, które będziemy
kodować kodem binarnym odpowied-
nio o długości 10 i 15 bitów, to chro-
mosom (osobnik) będzie wyglądał na-
stępująco:

Cała zaś populacja osobników jest

macierzą o wymiarach zdefiniowa-
nych jako:

1 0

1 1

1 1

0 0

0 1

1 0

1 1

0 1

L
L

M

M O M

M

L
L

1

2

444

3

444

































chromosom

m

chromosom

chromosom N

1
2

















liczność
populacji = N

długość chromosomu

Σ długości kodu dla każdego

z paramerów

dekodowanie

Dekodowanie chromosomów do

przestrzeni parametrów zadania –
aby Algorytmy Genetyczne mogły
poprawnie pracować, jest koniecz-
ne dekodowanie genotypów (chro-
mosomów) do fenotypów, czyli do
przestrzeni parametrów zadania.
Pierwszym etapem jest dekodowa-
nie z n-kodu do postaci dziesiętnej,
a następnie wartości te należy prze-
skalować do zakresu zmienności da-
nego parametru zadania.

x a y

b a

m

= +

−

−

2

1

gdzie:
x – wartość parametru,
a, b – zakres zmienności parametru,
y – zdekodowana wartość binarna,
m – długość ciągu binarnego.

Czasami przy dużych zakresach

zmienności parametru stosuje się
logarytmiczny zapis wartości, dzię-
ki czemu uzyskuje się krótsze chro-
mosomy.

funkcja celu

Mając zdekodowaną reprezentację

chromosomu jest możliwe ocenienie
poszczególnych członków populacji.
Dokonuje się to przez funkcję celu lub
funkcję przystosowania. Funkcja celu
jest pojęciem podstawowym wynika-

jącym z postawionego problemu. Jed-
nak Algorytmy Genetyczne stawiają
pewne ograniczenia na funkcję oce-
niającą osobniki. Funkcja ta ma być
nieujemna. Z właściwości AG wyni-
ka dążenie do maksymalizacji funk-
cji oceniającej. A jeżeli chcemy zna-
leźć minimum systemu? W wielu za-
stosowaniach wymagane jest złoże-
nie wielu kryteriów pożądanych w za-
daniu optymalizacyjnym z różnymi
wagami ważności do jednej funkcji
oceniającej populację. Dlatego funkcja
celu przekształcana jest i skalowana,
a wynik tych operacji nazwany jest
funkcją przystosowania. Na podsta-
wie tej funkcji dokonywana jest se-
lekcja do puli rodzicielskiej.

Do skalowania funkcji celu zasto-

sować można skalowanie liniowe
lub ranking. Obie metody zapobiega-
ją zbyt szybkiej zbieżności (domina-
cji lepszego osobnika), jak też ślepe-
mu błądzeniu AG.

zakończenie pracy

algorytmu genetycznego

Warunek zakończenia pracy AG za-

leży od konkretnego zadania optyma-
lizacyjnego. Algorytm może zakończyć
pracę, gdy funkcja celu (przystosowa-
nia) osiągnie wartość maksymalną
(pod warunkiem, że wartość ta jest
znana). Innym sposobem jest licze-
nie odchyłki funkcji celu w populacji.
Jeżeli jest ona mała, algorytm kończy
działanie. Najczęściej stosowanym wa-
runkiem zakończenia pracy Algoryt-
mu Genetycznego jest określenie ilości
pokoleń, czyli liczby iteracji pętli głów-
nej. Możliwe jest też zakończenie AG,
gdy po pewnej ilości iteracji nie znaj-
dzie się lepszego osobnika.

selekcja

Najważniejszy operator w AG pole-

ga na wybraniu na podstawie warto-
ści funkcji przystosowania tych chro-
mosomów, które będą brały udział
w tworzeniu nowego pokolenia. Wy-
bór ten odbywa się zgodnie z zasadą
naturalnej selekcji, tzn. najbardziej
przystosowany ma największą szan-

sę na udział w tworzeniu nowej po-
pulacji. Istnieje wiele metod selek-
cji, np.:



wybór deterministyczny,



wybór losowy z powtórzeniami –

ruletka,



wybór losowy bez powtórzeń,



wybór losowy według reszt z po-

wtórzeniami,



wybór losowy według reszt bez

powtórzeń,



uniwersalne losowanie,



turnieje losowe.

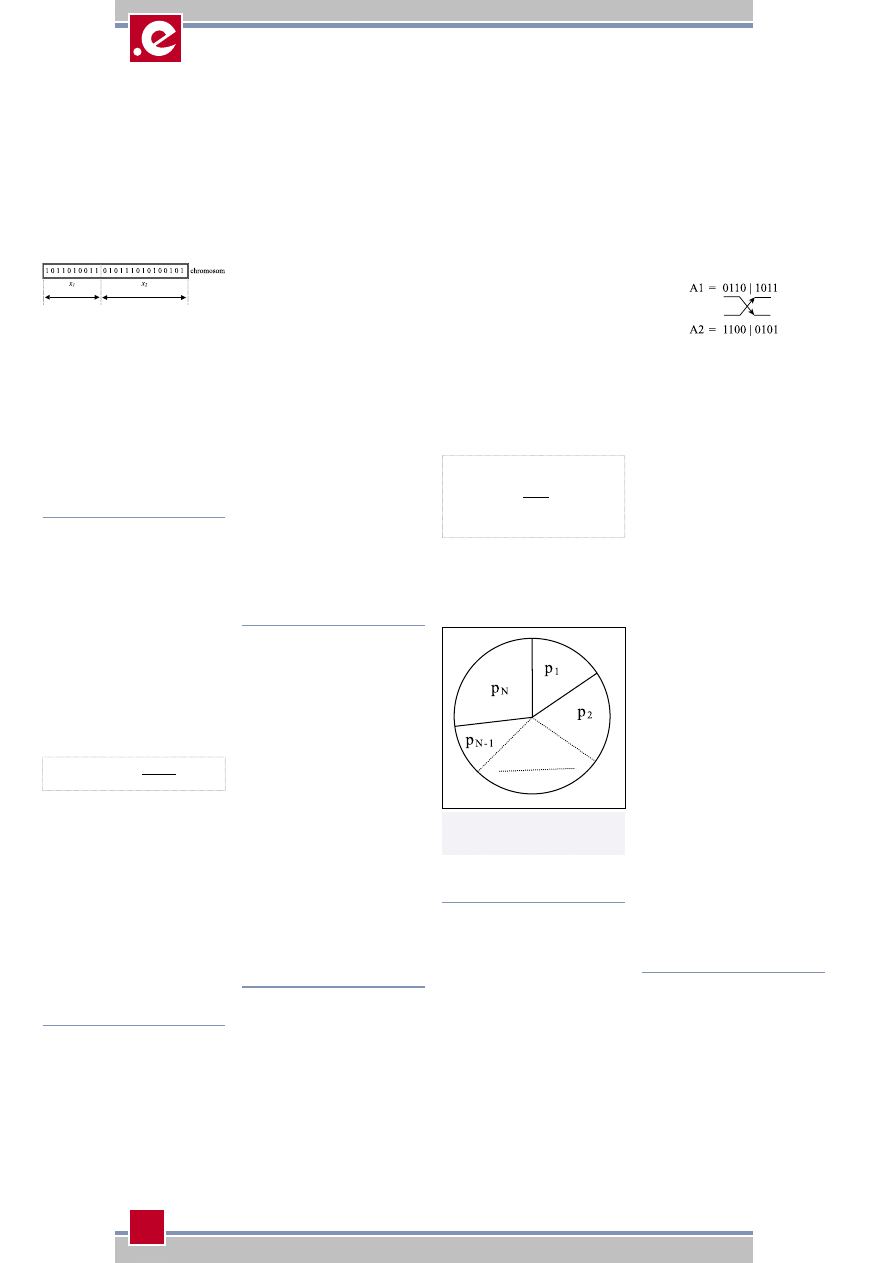
Koło ruletki jest dobrą metodą do

zobrazowania zasady AG (lepszy osob-
nik otrzymuje większy obszar koła,
przez co ma większe szanse na dosta-
nie się do puli rodzicielskiej).

v

p

p

f

f

i

i

i

i

i

i

N

= ⋅

=

=

∑

100

1

%

gdzie:
v

i

– wielkość wycinka koła przyzna-

nego i-temu osobnikowi w %,
p

i

– prawdopodobieństwo selekcji.

Rys. 2 Przykładowe koło ruletki z przy-

dzielonymi obszarami dla osob-

ników populacji

krzyżowanie i mutacja

Operator ten ma za zadanie wy-

mieniać miedzy osobnikami informa-
cje przez nich niesione. Dzięki temu
operatorowi Algorytm Genetyczny
przeszukuje przestrzeń parametrów
zadania. Przeszukiwanie to jest ukie-
runkowane przez statystycznie lepsze
osobniki z populacji wybrane pod-
czas selekcji. Krzyżowanie polega na
wymianie między osobnikami rodzi-
cielskimi podciągów kodowych. Krzy-
żowanie można podzielić na:



jednopunktowe,



wielopunktowe,



tasowanie.

Różnice pomiędzy tymi krzyżowa-

niami wynikają z gęstości wymienia-
nych informacji.

Krzyżowanie jednopunktowe moż-

na zobrazować na przykładzie dwóch
osobników wybranych z puli rodzi-
cielskiej:

Przypuśćmy, że wybierając losowo

jedną z liczb od 1 do 7, otrzymaliśmy
lk=4. Operacja krzyżowania daje dwa
nowe ciągi wchodzące w skład nowe-
go pokolenia:

A’1 = 01100101

A’2 = 11001011

Operator mutacji ma ograniczone

działanie. Statystycznie rzadko doko-
nuje modyfikacji jakiegoś osobnika.
Jego zadaniem jest losowa zmiana lo-
sowej informacji w losowym osobni-
ku. Jeżeli jakiś osobnik ulega mutacji,
losuje się gen podlegający temu pro-
cesowi. Następnie zamienia się dany
gen na przeciwny tzn. 0 zamieniane
jest na 1, a 1 na 0.

Przedstawiony opis Algorytmu Ge-

netycznego dotyczy jego wersji pod-
stawowej. W praktycznych zastoso-
waniach stosuje się, w zależności od
sposobu zapisu chromosomu, zmody-
fikowane operatory genetyczne (se-
lekcja, krzyżowanie i mutacja), jak
również stosuje się inne dodatkowe
operatory, przyśpieszające działanie
AG. Wiele informacji na ten temat
można znaleźć w [2].

Algorytmy Genetyczne

w projektowaniu

zespołu filtrów

Dla porównania wyników, uży-

jemy AG do zadania postawione-
go w [7], czyli należy zaprojektować
cztery filtry proste jednogałęziowe
o sumarycznej mocy 1 MVAr, pracu-
jące na napęciu 6 kV (założeni R

F

=

0 jest zbędne). Filtry mają za zadanie
eliminację harmonicznych o nume-
rach 5, 7, 11 i 13.

w w w. e l e k t r o . i n f o . p l

n r 1 0 / 2 0 0 4

49

U = 6 kV
Q

F

= 1 MVAr

n

r

5

7

11

13

ω

(n)

500

π

700

π

1100

π

1300

π

Pamiętamy z poprzednich artyku-

łów, że znaczącym problemem było
dokonanie podziału mocy na po-
szczególne filtry. W przypadku AG
ten problem nie istnieje. Należy za-
łożyć, w jakich granicach wartości
mogą się zmieniać wartości poszcze-
gólnych kondensatorów. Decyduje-
my, że wszystkie cztery kondensa-
tory będą miały wartość w zakresie
C

min

= 1 µF, C

max

= 100 µF.

Zgodnie z teorią AG należy ustalić

pewne parametry:



liczność populacji N = 100,



każdy z parametrów kodowany

będzie w kod binarny o długości
8 bitów,



prawdopodobieństwo krzyżowa-

nia p

k

= 0,8,



prawdopodobieństwo mutacji

p

m

= 0,01,



zastosowano krzyżowanie przez

tasowanie (wymiana informacji
co jeden bit),



selekcja SUS (za jednym obrotem

koła ruletki losujemy całą pulę ro-
dzicielską),



warunek końca AG – 100 pokoleń.

Pozostaje określić funkcję celu. Jak

pamiętamy wykres modułu impedan-
cji zespołu czterech równoległych fil-
trów prostych, wykres ten posiada
cztery minima (cztery eliminowane
harmoniczne), trzy maksima dla har-
monicznych rzędu 6., 9. i 12. (tak sta-
wiamy cel projektowy) oraz koniecz-
ne jest, aby cały zespół filtrów kom-
pensował zadaną moc bierną. Z te-
go opisu wynika 8 kryteriów (czte-
ry minima, 3 maksima oraz określo-
na moc filtrów).

Minima zapewnimy sobie poprzez

wyznaczanie indukcyjności poszcze-
gólnych filtrów ze wzorów na pulsa-
cję rezonansową:

L

C

Fn

rn Fn

=

1

2

ω

Konieczne jest wyznaczenie impe-

dancji całego zespołu filtrów dla pul-
sacji podstawowej oraz dla 6., 9. i 12.
harmonicznej.

Z

R

j L

j

C

Fn

Fn

Fn

Fn

=

+

−

ω

ω

1

Dla filtrów powietrznych tej mocy

prawdziwy jest wzór empiryczny:

R

X

X

Fn

L

Hz

C

Hz

=

+

(

)

(

)

50

50

100

5000

1

1

Z

Z

Fn

n

=

∑

Dla pulsacji podstawowej prawdzi-

wa jest zależność:

imag Z

j

U

Q

( )

= −

2

czyli dla danych z zadania
X = –j36 Ω.

Algorytm Genetyczny będzie dą-

żył, aby różnica wartości X i wyzna-
czonej reaktancji zespołu filtrów była
jak najmniejsza oraz w żadnym razie
nie spadła poniżej tej wartości (war-
tość bezwzględna), gdyż spowodu-
je to przekompensowanie. Pozostaje
zapewnić maksymalizację impedan-

nr

5

7

11

13

Klasycznie

C

Fn

[

µ

F]

33,24

24,23

15,61

13,24

L

Fn

[mH]

12,2

8,5

5,4

4,5

Q

Fn

[kVar]

391,63

279,73

178,01

150,63

Macierze

C

Fn

[

µ

F]

45,33

19,95

10

10,7

L

Fn

[mH]

8,9

10,4

8,4

5,6

Q

Fn

[kVar]

533,94

230,3

113,93

121,79

GA

C

Fn

[

µ

F]

45,17

19,88

10,67

9,95

L

Fn

[mH]

9

10,4

7,8

6

Q

Fn

[kVar]

532,1

229,5

121,7

113,3

Tab. 2 Parametry filtrów wyznaczone obiema metodami

reklama

w w w. e l e k t r o . i n f o . p l

n r 1 0 / 2 0 0 4

50

i n s t a l a c j e e l e k t r o e n e r g e t y c z n e

3. Hanzelka Z., Klempka R., Filtry

wyższych harmonicznych – wy-
brane zagadnienia. Napędy i Ste-
rowanie, 3, 9, 2000.

4. Hanzelka Z., Klempka R., Pasywne

filtry wyższych harmonicznych,
„elektro.info” 6 / 2003.

5. Klempka R., Hanzelka Z., Applica-

tion of Genetic Algorithm in Do-
uble Tuned Filters Design, EPE
2001, Graz.

6. Klempka R., Designing a group of

single-branch filters, Electrical
Power Quality and Utilisation
2003, Kraków.

7. Klempka R., Projektowanie grupy

filtrów prostych z uwzględnie-
niem ich wzajemnych wpływów,
„elektro.info” 7 / 8 / 2004.

8. Klempka R., Hanzelka Z., Filtr pa-

sywny podwójnie nastrojony, za-
projektowany Algorytmem Gene-
tycznym. SENE’01, Łódź, 2001.

9. Klempka R., Hanzelka Z., Filtering

Properties of the Selected Do-
uble Tuned Passive Filter Struc-
tures Designed Using Genetic Al-
gorithm, EPE PEMC 2002, Dubro-
vnik.

10. Harder J.E., AC filter arrester ap-

plication. IEEE Trans. on Power
Delivery, 11, 3, 1996.

11. Xiao Yao, Algorithm for the para-

meters of double tuned filter. 8th
Int. Conf. on Harmonics and Qu-
ality of Power, Oct. 14-16, 1998,
Athens.

sku, że Algorytmy Genetyczne prawi-
dłowo dobrały parametry filtrów.

Pokazana metoda jest przykładem

zastosowania AG pokazującym, że są
one użytecznym narzędziem optyma-
lizacyjnym. Jednak należy pamiętać,
że jeżeli można otrzymać prawidłowe
wyniki metodą analityczną, wtedy
nie powinno się stosować AG. W tym
przypadku, uwzględnienie rezystan-
cji filtrów pozwoliło zastosować AG.

Uwzględniono podczas projekto-

wania filtrów ich wzajemny wpływ
oraz ich rezystancję. To jednak może
nie być wystarczające. W systemach
energetycznych każdy element sys-
temu będzie wywierał wzajemny
wpływ (impedancja sieci, transforma-
tor, odbiornik, itd.). Dopiero uwzględ-
nienie tych elementów pozwoli na
prawidłowe projektowanie grupy fil-
trów. Algorytmy Genetyczny mogą
być użytecznym narzędziem w ta-
kiej optymalizacji.

literatura

1. Chi-Jui Wu, Jung-Chen Chiang

etc., Investigation and mitigation
of harmonic amplification cau-
sed by single-tuned filters. IEEE
Trans. on Power Delivery, 13, 3,
1998.

2. Goldberg D. Genetic Algorithms

in Search, Optimization, and Ma-
chine Learning, WNT (in polish)
1995.

cji dla harmonicznych 6., 9. i 12. Za-
pewnione to zostanie poprzez dzie-
lenie obliczonej impedancji zespołu
filtrów przez iloczyn impedancji dla
odpowiednich harmonicznych. Ce-
chą naturalną AG jest maksymaliza-
cja funkcji celu. W tym zagadnieniu
wykorzystamy nadawanie rang osob-
nikom w kolejności rosnącej. Nadawa-
nie rang jest to przekształcenie funk-
cji przystosowania w funkcję celu,
przez co zapewnia się wartości dodat-
nie funkcji celu, chroni się populację
przed dominacją jednego superosob-
nika oraz przed przedwczesną zbież-
nością do optimum lokalnego. W za-
leżności od potrzeby sortujemy osob-
niki ze względu na funkcję celu rosną-
co lub malejąco i przypisujemy im ran-
gi z zakresu od 0 do 2, co umożliwi naj-
lepszemu osobnikowi mieć dwóch po-
tomków, średniemu jednego potom-
ka, a najsłabszego wyeliminuje (sta-
tystycznie rzecz biorąc). Możliwe są
oczywiście inne zakresy rang.

F

U

imag Z

Z

Z

Z

dla im

przyst

Hz

Hz

Hz

Hz

=

−

(

)

10

6

2

50

300

450

600

(

)

(

)

(

)

(

)

*

*

aag Z

Hz

50

36

(

)

( )

>

Dla pozostałych przypadków
F

przyst

= 10

10

.

Dla tak skonstruowanego AG uru-

chomiono program, który po ok. 2 mi-
nutach podał rozwiązanie przedsta-

wione w

tabeli 1, a wykres impedan-

cji zespołu filtrów na

rysunku 3.

nr

5

7

11

13

C

Fn

[

µ

F]

45,17 19,88 10,67 9,95

L

Fn

[mH]

9

10,4

7,8

6

Q

Fn

[kVar] 532,1 229,5 121,7 113,3

Tab. 1 Parametry filtrów wyznaczone

przez AG

wnioski

Jak widać na wykresie 3, Algorytm

Genetyczny prawidłowo zaprojekto-
wał zespół filtrów prostych. Problem
podziału mocy na poszczególne filtry
został rozwiązany przez AG bez udzia-
łu projektanta. Uwzględniono wza-
jemne wpływy filtrów oraz ich rezy-
stancje. Trzecie maksimum jest prze-
sunięte trochę na prawo i nie pokry-
wa się z 12. harmoniczną, lecz jest jej
bliskie. Dla przypomnienia AG nale-
żą do grupy metod probabilistycznych
stąd możliwość znalezienia rozwiąza-
nia prawie optymalnego zamiast do-
kładnie jego.

W

tabeli 2 zestawiono wyniki

otrzymane w artykule [2] oraz otrzy-
mane za pomocą AG.

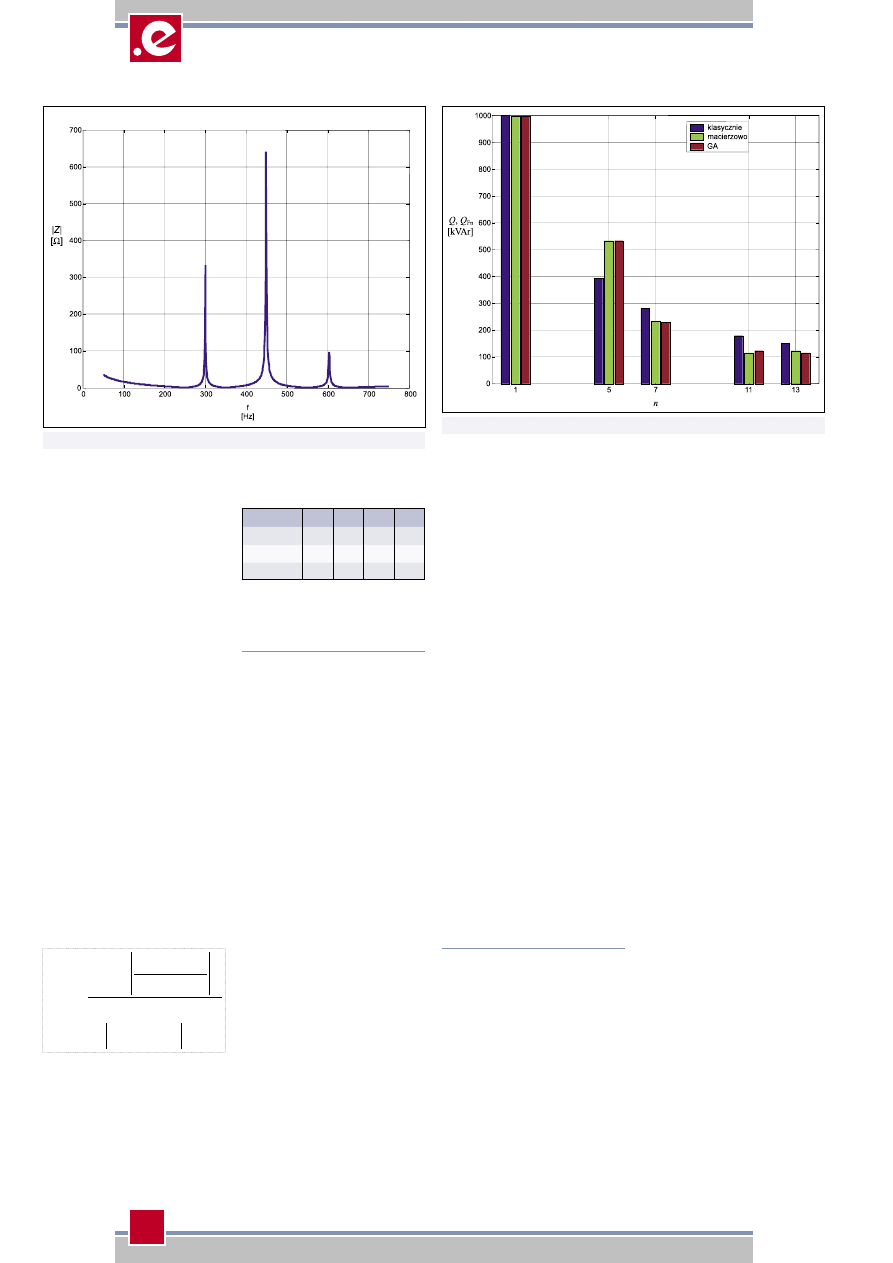
Na

rysunku 4 zestawiono wartości

mocy poszczególnych filtrów otrzy-
manych metodami opisanymi w ar-
tykule [2] oraz za pomocą Algorytmu
Genetycznego. Jak widać, filtry otrzy-
mane za pomocą AG są bardzo zbli-
żone do filtrów otrzymanych metodą
macierzową, co uprawnia do wnio-

Rys. 4 Zestawienie mocy poszczególnych filtrów otrzymanych różnymi metodami

Rys. 3 Impedancja zespołu filtrów wyznaczona Algorytmem Genetycznym