www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
POZIOM ROZSZERZONY
7
MARCA
2008
C
ZAS PRACY
: 150(180?)
MINUT
Z
ADANIE
1
(5
PKT
.)
Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy wi˛eksza
od pierwszej. Wyznacz trzy liczby spełniaj ˛
ace podane warunki tak, aby suma ich kwadratów
była najmniejsza.
R
OZWI ˛
AZANIE
Mamy układ
(
a
+
b
+
c
=
13
b
=
3a
(
4a
+
c
=
13
b
=
3a
(
c
=
13
−
4a
b
=
3a
i chcemy znale´z´c rozwi ˛
azanie z minimalnym a
2
+
b
2
+
c
2
. Z układu mamy
a
2
+
b
2
+
c
2
=
a
2
+ (
3a
)
2
+ (
13
−
4a
)
2
=
=
a
2
+
9a
2
+
169
−
104a
+
16a
2
=
=
26a
2
−
104a
+
169
=
=
13
(
2a
2
−
8a
+
13
)
.
Aby znale´z´c warto´s´c najmniejsz ˛
a tego wyra ˙zenia, szukamy warto´sci najmniejszej funkcji
f
(
a
) =
2a
2
−
8a
+
13. W tym miejscu jest jednak pewien delikatny szczegół. Poniewa ˙z liczby
maj ˛
a by´c dodatnie, a nie mo ˙ze by´c zupełnie dowolne. Dokładniej:
a
>
0
b
=
3a
>
0
c
=
13
−
4a
>
0
⇒
a
<
13
4
.
Szukamy zatem minimum funkcji f na przedziale
0,
13
4
. Liczymy pierwsz ˛
a współrz˛edn ˛
a
wierzchołka paraboli b˛ed ˛
acej wykresem tej funkcji:
x
w
=
2.
Materiał pobrany z serwisu
1
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Poniewa ˙z punkt ten le ˙zy w przedziale
0,
13
4
, to wła´snie w nim funkcja osi ˛
aga minimum.
Otrzymujemy st ˛
ad a
=
2, b
=
6, c
=
5.
Odpowied´z: a
=
2, b
=
6, c
=
5
Z
ADANIE
2
(4
PKT
.)
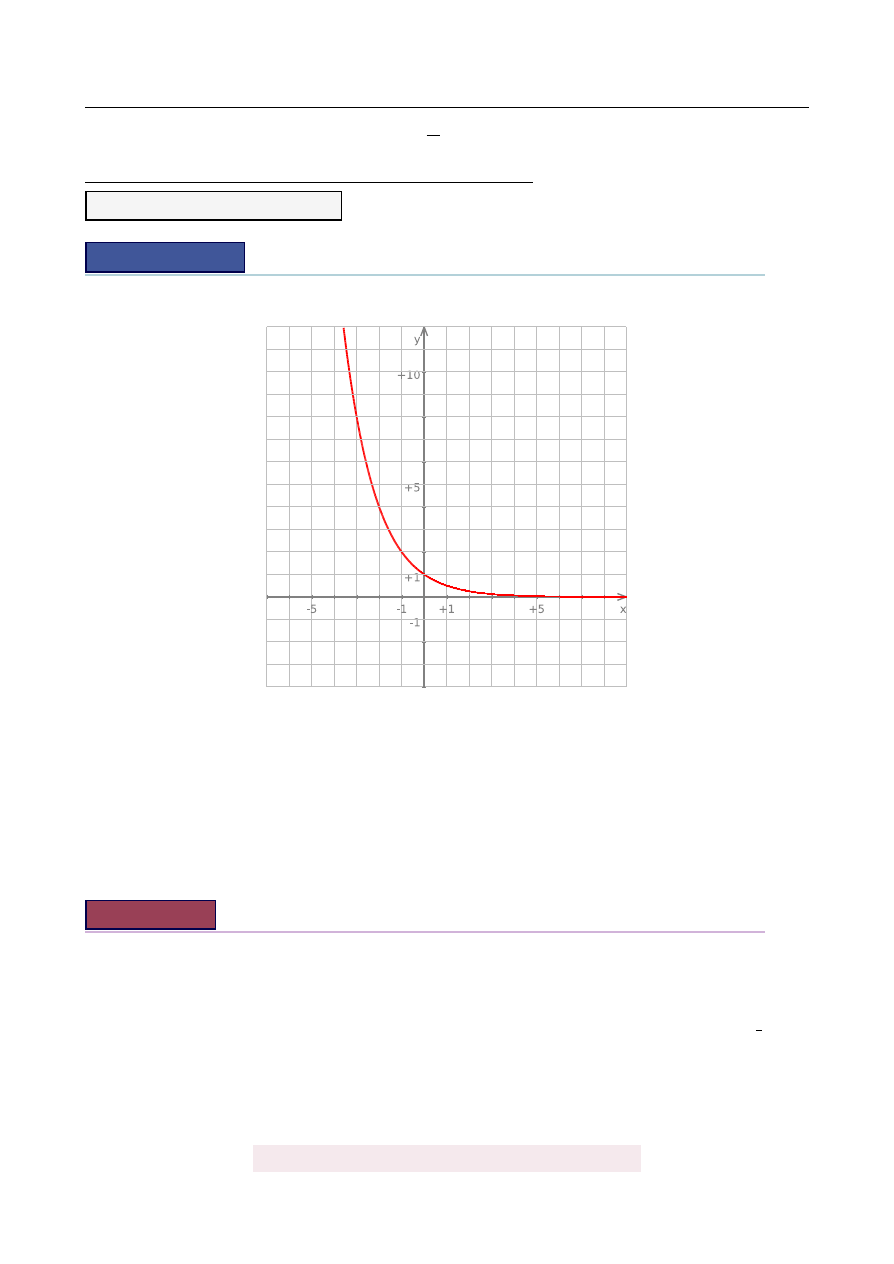
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej f
(
x
) =
a
x
dla x
∈
R
a) Narysuj wykres funkcji g, który jest obrazem wykresu funkcji f w przesuni˛eciu o wek-
tor
→
u
= [
2,
−
1
]
.
b) Wyznacz a i zapisz wzór funkcji g otrzymanej w wyniku tego przesuni˛ecia.
c) Odczytaj z wykresu zbiór wszystkich argumentów, dla których g
(
x
) >
0.
R
OZWI ˛
AZANIE
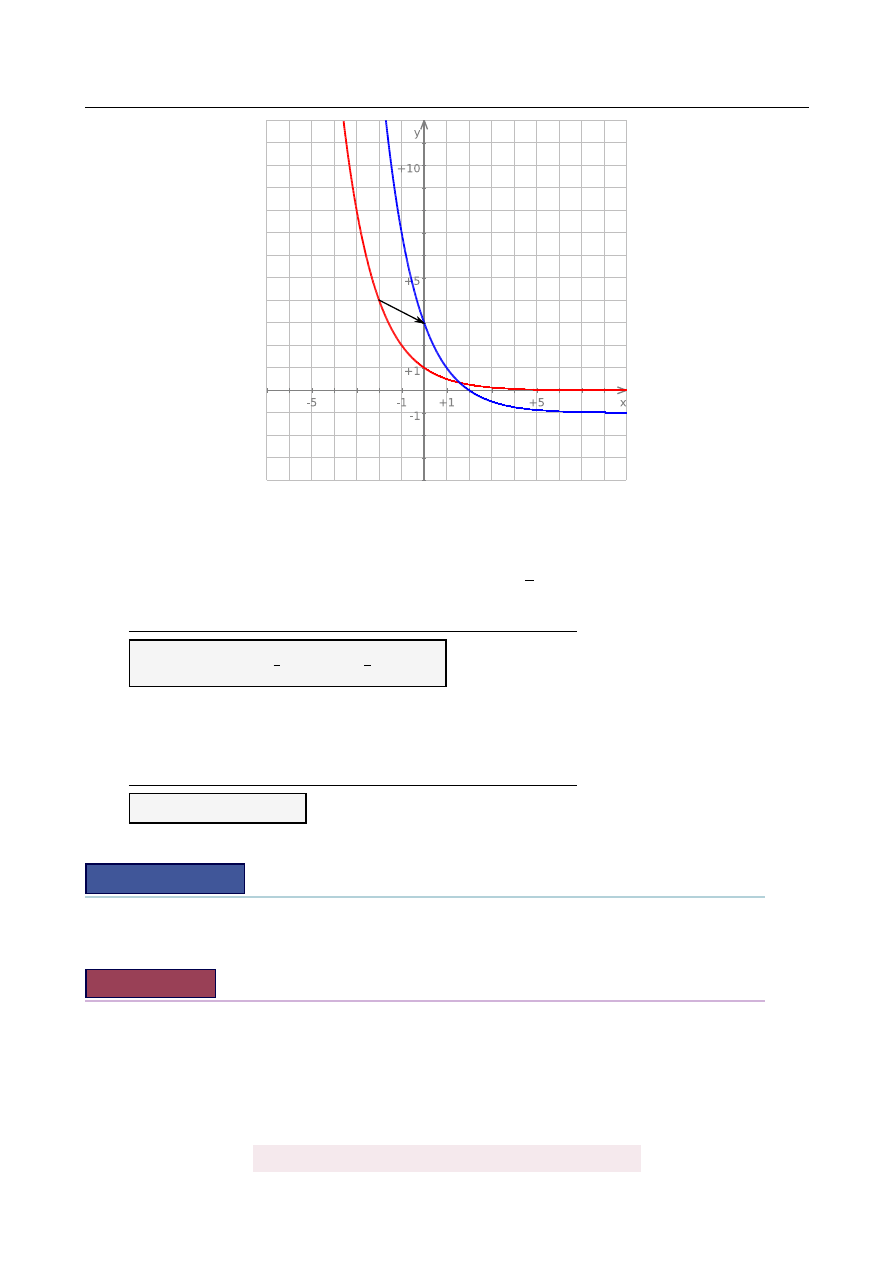
a) Wykres funkcji g powstaje z f przez przesuni˛ecie o dwie jednostki w prawo i jedn ˛
a w
dół – niebieski wykres na rysunku.
b) Na wykresie w tre´sci zadania wida´c, ˙ze f
(−
1
) =
2, tzn. a
−
1
=
2. St ˛
ad a
=
1
2
. Aby
napisa´c wzór funkcji g korzystamy ze wzoru na przesuni˛ecie funkcji y
=
f
(
x
)
o wektor
→
v
= [
a, b
]
:
y
=
f
(
x
−
a
) +
b.
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
W naszej sytuacji
g
(
x
) =
f
(
x
−
2
) −
1
=
1
2
x
−
2
−
1.
Odpowied´z: a
=
1
2
, g
(
x
) =
1
2
x
−
2
−
1
c) Odczytujemy z wykresu:
x
∈ (−
∞, 2
)
.
Odpowied´z:
(−
∞, 2
)
Z
ADANIE
3
(4
PKT
.)
Wyznacz wszystkie warto´sci parametru m, dla których jedynym rozwi ˛
azaniem rzeczywi-
stym równania x
3
+
m
3
x
2
−
m
2
x
−
1
=
0 jest liczba 1.
R
OZWI ˛
AZANIE
Sposob I
Po pierwsze sprawdzamy, kiedy x
=
1 jest rzeczywi´scie pierwiastkiem podanego wielomia-
nu.
1
+
m
3
−
m
2
−
1
=
0
⇒
m
(
m
−
1
) =
0.
Materiał pobrany z serwisu
3

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Widzimy zatem, ˙ze m
=
0 lub m
=
1. Dla m
=
0 mamy wielomian
x
3
−
1
= (
x
−
1
)(
x
2
+
x
+
1
)
.
Łatwo sprawdzi´c (z
∆-y), ˙ze wielomian w nawiasie nie ma pierwiastków, czyli m
=
0 jest
ok.
Dla m
=
1 mamy wielomian
x
3
+
x
2
−
x
−
1.
W tym miejscu mamy wiele mo ˙zliwo´sci, mo ˙zemy go podzieli´c przez
(
x
−
1
)
, mo ˙zemy spraw-
dzi´c, ˙ze drugi dzielnik wyrazu wolnego, czyli -1 te ˙z jest pierwiastkiem, mo ˙zemy wreszcie
rozło ˙zy´c wielomian bezpo´srednio
x
3
+
x
2
−
x
−
1
=
=
x
2
(
x
+
1
) − (
x
+
1
) = (
x
2
−
1
)(
x
+
1
) =
= (
x
−
1
)(
x
+
1
)(
x
+
1
) = (
x
−
1
)(
x
+
1
)
2
Tak czy inaczej, x
=
1 nie jest jedynym pierwiastkiem.
Sposób II
Dzielimy z reszt ˛
a podany wielomian przez
(
x
−
1
)
(na razie nie nale ˙zy przejmowa´c si˛e pa-
rametrem m). Tak jak poprzednio robimy to grupuj ˛
ac wyrazy (chocia ˙z najpro´sciej byłoby
schematem Hornera):
x
3
+
m
3
x
2
−
m
2
x
−
1
=
= (
x
3
−
x
2
) +
x
2
+
m
3
x
2
−
m
2
x
−
1
=
=
x
2
(
x
−
1
) + (
m
3
+
1
)(
x
2
−
x
) + (
m
3
+
1
)
x
−
m
2
x
−
1
=
=
x
2
(
x
−
1
) + (
m
3
+
1
)
x
(
x
−
1
) + (
m
3
+
1
−
m
2
)(
x
−
1
) +
m
3
+
1
−
m
2
−
1
= (
x
−
1
)(
x
2
+ (
m
3
+
1
)
x
+
m
3
+
1
−
m
2
) +
m
3
−
m
2
.
Wida´c teraz, ˙ze x
=
1 jest pierwiastkiem tylko wtedy, gdy reszta m
3
−
m
2
jest równa 0, czyli
dla m
=
0 lub m
=
1.
Dla m
=
0, z powy ˙zszego dzielenia mamy:
x
3
−
1
= (
x
−
1
)(
x
2
+
x
+
1
)
i wielomian x
2
+
x
+
1 nie ma pierwisatków.
Dla m
=
1 mamy
x
3
+
x
2
−
x
−
1
= (
x
−
1
)(
x
2
+
2x
+
1
) = (
x
−
1
)(
x
+
1
)
2
i x
=
1 nie jest jedynym pierwiastkiem.
Odpowied´z: m
=
0
Z
ADANIE
4
(5
PKT
.)
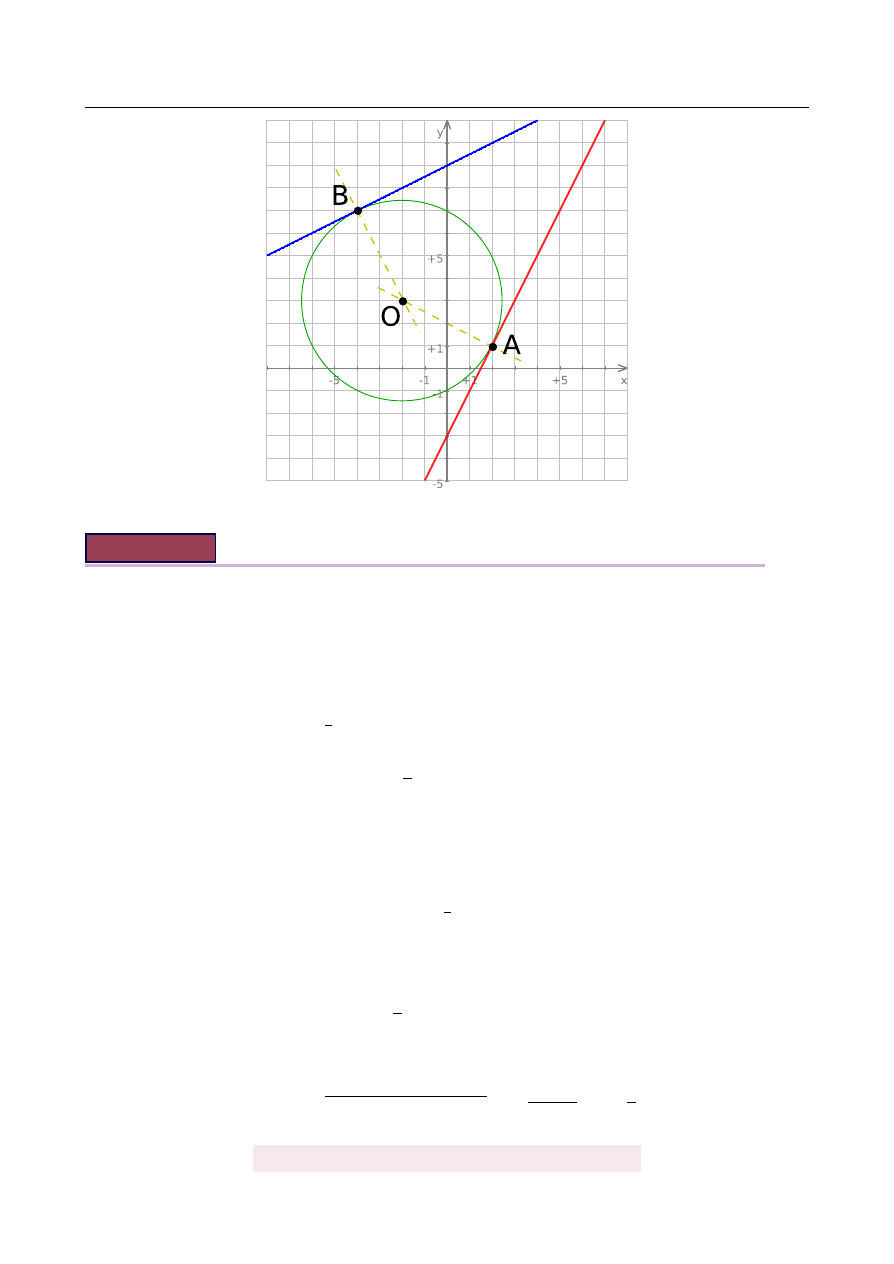
Wiadomo, ˙ze okr ˛
ag jest styczny do prostej o równaniu y
=
2x
−
3 w punkcie A
= (
2, 1
)
i styczny do prostej o równaniu y
=
1
2
x
+
9 w punkcie B
= (−
4, 7
)
. Oblicz promie ´n tego
okr˛egu.
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zacznijmy od schematycznego rysunku. Jak zwykle w przypadku zadania z geometrii ana-
litycznej jest wiele sposobów rozwi ˛
azania. My poka ˙zemy dwa z nich.
Sposób I
Spróbujemy znale´z´c współrz˛edne ´srodka O
= (
x, y
)
okr˛egu, o którym mowa w tre´sci za-
dania. W tym celu napiszemy równania prostych prostopadłych do podanych prostych w
punktach styczno´sci z okr˛egiem i znajdziemy ich punkt wspólny. Prosta prostopadła do
y
=
2x
−
3 jest postaci y
= −
1
2
x
+
b. Ponadto szukamy prostej przechodz ˛
acej przez punkt
A
= (
2, 1
)
, czyli
1
= −
1
2
·
2
+
b
⇒
b
=
2.
Podobnie znajdujemy drug ˛
a prost ˛
a. Ma on posta´c y
= −
2x
+
b oraz
7
= (−
2
) · (−
4
) +
b
⇒
b
= −
1.
Aby wyznaczy´c O, musimy znale´z´c punkt wspólny tych dwóch prostych
(
y
= −
1
2
x
+
2
y
= −
2x
−
1.
Odejmuj ˛
ac od pierwszego równania drugie ( ˙zeby skróci´c y), otrzymujemy
0
=
3
2
x
+
3
⇒
x
= −
2.
Zatem y
=
3 i O
= (−
2, 3
)
.
Pozostało wyliczy´c promie ´n okr˛egu, czyli długo´s´c odcinka AO:
AO
=
q
(−
2
−
2
)
2
+ (
3
−
1
)
2
=
√
16
+
4
=
2
√
5.
Materiał pobrany z serwisu
5
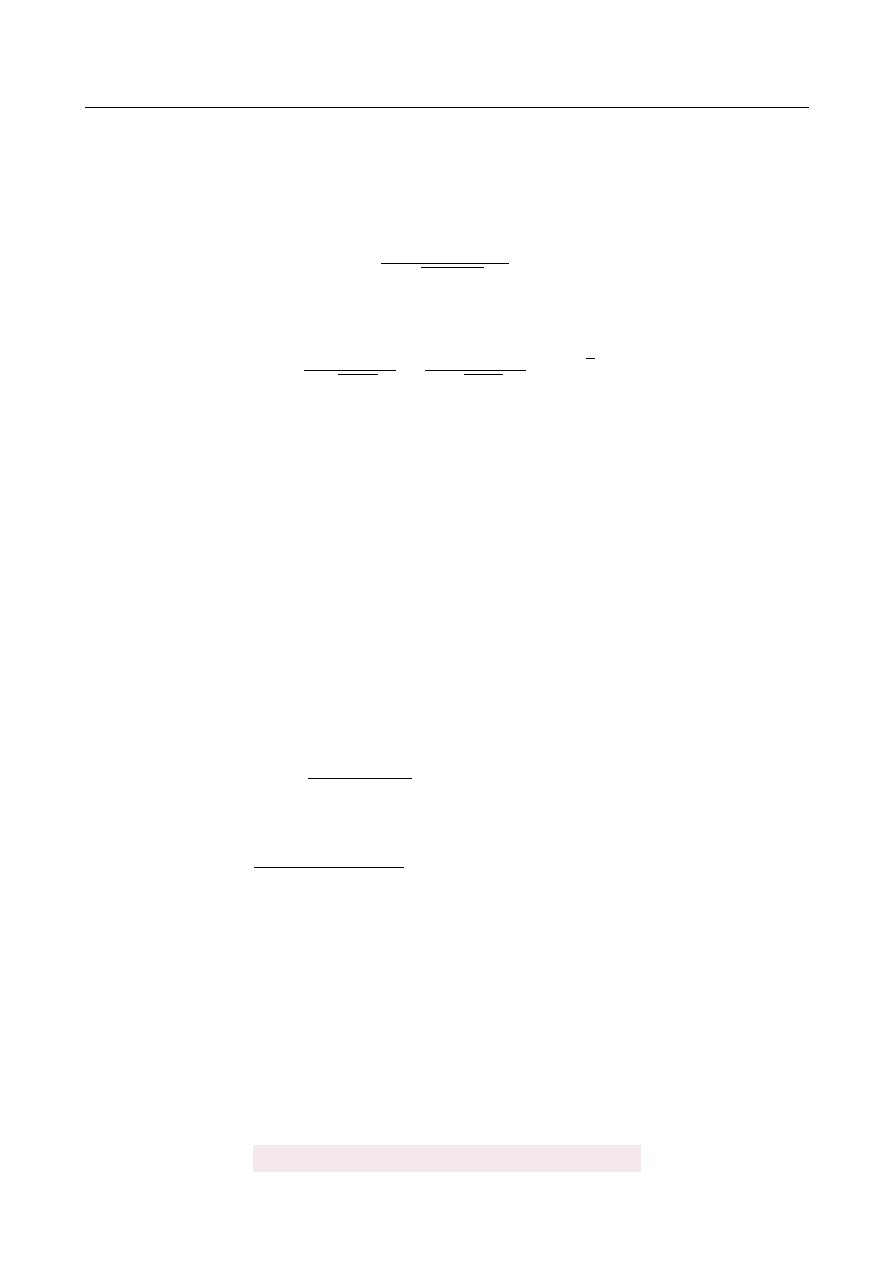
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Sposób II
Podobnie jak poprzednio, znajdziemy współrz˛edne punktu O
= (
x, y
)
. Jakie ten punkt ma
własno´sci? Po pierwsze jest równoodległy od podanych prostych. Jak to zapisa´c? – trzeba
skorzysta´c ze wzoru na odległo´s´c punktu P
= (
x
0
, y
0
)
od prostej Ax
+
By
+
C
=
0.
|
Ax
0
+
By
0
+
C
|
√
A
2
+
B
2
.
˙Zeby nie mie´c ułamków, równanie drugiej prostej zamie ´nmy na x
−
2y
+
18
=
0 i mamy
wtedy:
|
2x
−
y
−
3
|
√
4
+
1
=
|
x
−
2y
+
18
|
√
1
+
4
/
·
√
5
|
2x
−
y
−
3
| = |
x
−
2y
+
18
|
.
Jak teraz opu´sci´c warto´sci bezwgl˛edne? Do tego potrzebna jest informacja o poło ˙zeniu punk-
tu O wzgl˛edem danych prostych. Dla punktu na prostej wyra ˙zenie, które znajduje si˛e pod
warto´sci ˛
a bezwzgl˛edn ˛
a jest 0. Je ˙zeli punkt jest na lewo od prostej, to ma x-a mniejszego,
czyli wyra ˙zenie jest ujemne. Gdy jest na prawo, to x jest wi˛ekszy, wi˛ec jest dodatnie. Nasz
punkt O jest na prawo od pierwszej prostej i na lewo od drugiej, zatem
2x
−
y
−
3
= −(
x
−
2y
+
18
)
3x
=
3y
−
15
x
=
y
−
5.
Dobrze, ale mamy jedno równanie a dwie niewiadome (nic w tym dziwnego, na razie wyli-
czyli´smy tylko równanie dwusiecznej podanego k ˛
ata). Drugie równanie to fakt, ˙ze odległo´s´c
punktu O od danych prostych to ma by´c dokładnie jego odległos´c od punktu A. Od razu
porównamy kwadraty odległo´sci i wykorzystamy poprzednie wyliczenie odległo´sci O od
pierwszej prostej
(
2x
−
y
−
3
)
2
5
= (
x
−
2
)
2
+ (
y
−
1
)
2
Zanim przkształcimy to dalej podstawmy wyliczone ju ˙z x
=
y
−
5
(
2
(
y
−
5
) −
y
−
3
)
2
5
= ((
y
−
5
) −
2
)
2
+ (
y
−
1
)
2
(
y
−
13
)
2
=
5
((
y
−
7
)
2
+ (
y
−
1
)
2
)
y
2
−
26y
+
169
=
5
(
y
2
−
14y
+
49
+
y
2
−
2y
+
1
)
y
2
−
26y
+
169
=
5y
2
−
70y
+
245
+
5y
2
−
10y
+
5
9y
2
−
54y
+
81
=
0
y
2
−
6y
+
9
=
0
(
y
−
3
)
2
=
0
y
=
3.
Tak wi˛ec x
= −
2 i promie ´n wyliczamy jak w poprzednim sposobie.
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
5
(3
PKT
.)
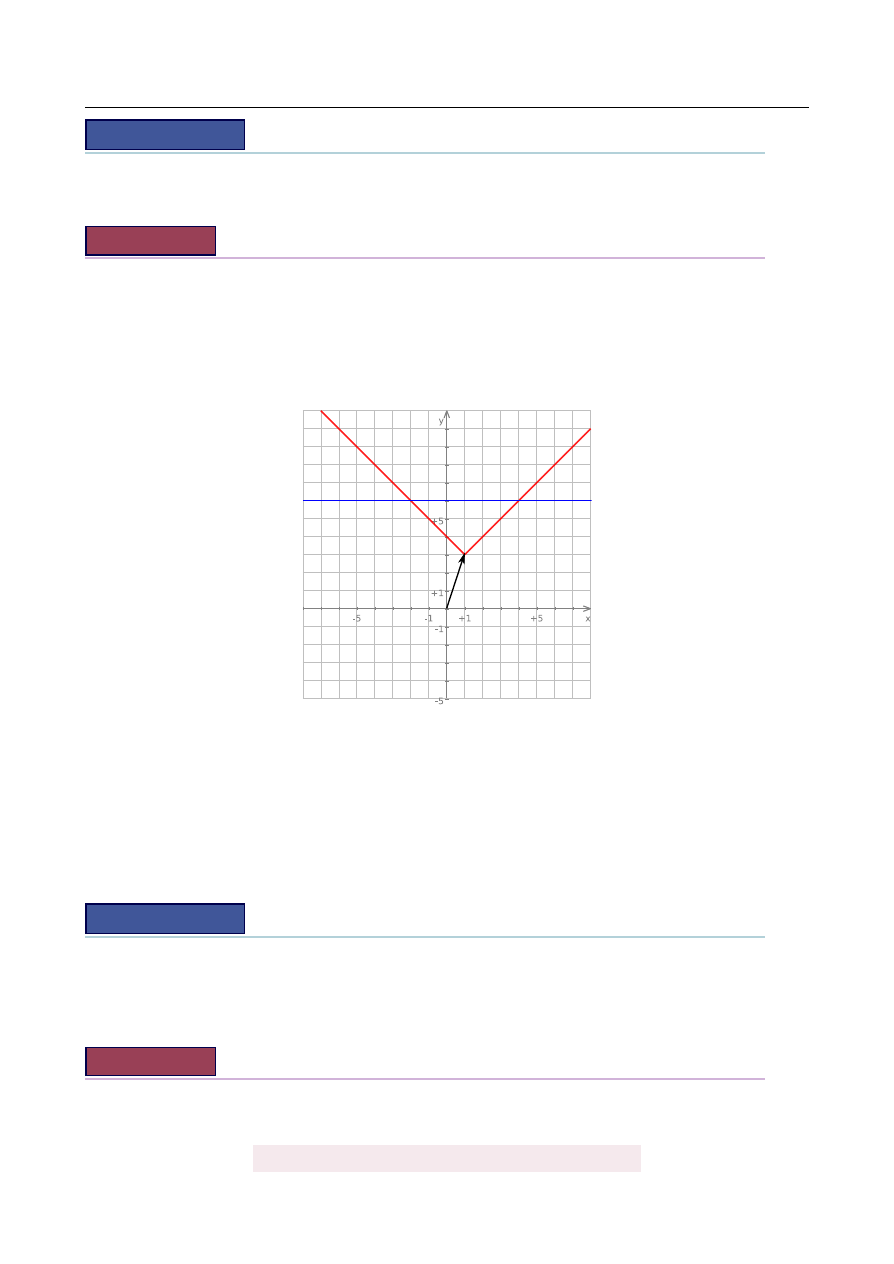
Narysuj wykres funkcji f
(
x
) = |
x
−
1
| +
3 okre´slonej dla x
∈
R, a nast˛epnie na jego podsta-
wie podaj liczb˛e rozwi ˛
aza ´n równania f
(
x
) =
m w zale ˙zno´sci od parametru m
∈
R.
R
OZWI ˛
AZANIE
Korzystamy ze wzoru na przesuni˛ecie funkcji y
=
f
(
x
)
o wektor
→
v
= [
a, b
]
:
y
=
f
(
x
−
a
) +
b.
W naszej sytuacji wykres f powstaje z wykresu y
= |
x
|
przez przesuni˛ecie o wektor
[
1, 3
]
–
rysunek.
Z rysunku bez trudu odczytujemy, ˙ze f
(
x
) =
m ma
0 rozwi ˛
aza ´n
dla m
<
3
1 rozwi ˛
azanie
dla m
=
3
2 rozwi ˛
azania
dla m
>
3.
Z
ADANIE
6
(5
PKT
.)
Wła´sciciel sklepu z odzie ˙z ˛
a kupił w hurtowni koszulki, płac ˛
ac za nie 720 zł. Gdyby ka ˙zda
koszulka kosztowała o 2 złote mniej, to za t˛e sam ˛
a kwot˛e mógłby kupi´c o 5 koszulek wi˛ecej.
Oblicz, ile koszulek kupił w tej hurtowni wspomniany wła´sciciel sklepu. Podaj cen˛e jednej
koszulki.
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Oznaczmy liczb˛e koszulek przez k, a cen˛e pojedy ´nczej koszulki przez c. Mamy wtedy
(
kc
=
720
(
k
+
5
)(
c
−
2
) =
720
(
kc
=
720
kc
+
5c
−
2k
−
10
=
720.
Odejmuj ˛
ac od drugiego równania pierwsze ( ˙zeby skróci´c kc), dostajemy
5c
−
2k
−
10
=
0
⇒
k
=
5
2
c
−
5.
Wstawiaj ˛
ac to do równania kc
=
720, dostajemy
5
2
c
−
5
c
=
720
5
2
c
2
−
5c
−
720
=
0
/ : 5
1
2
c
2
−
c
−
144
=
0.
Rozwi ˛
azujemy to standardowo,
∆
=
1
+
144
·
2
=
289
=
17
2
.
Otrzymujemy st ˛
ad c
1
=
1
−
17
= −
16, c
2
=
1
+
17
=
18. Oczywi´scie pierwsze rozwi ˛
azanie
odrzucamy.
Odpowied´z: 18 zł
Z
ADANIE
7
(4
PKT
.)
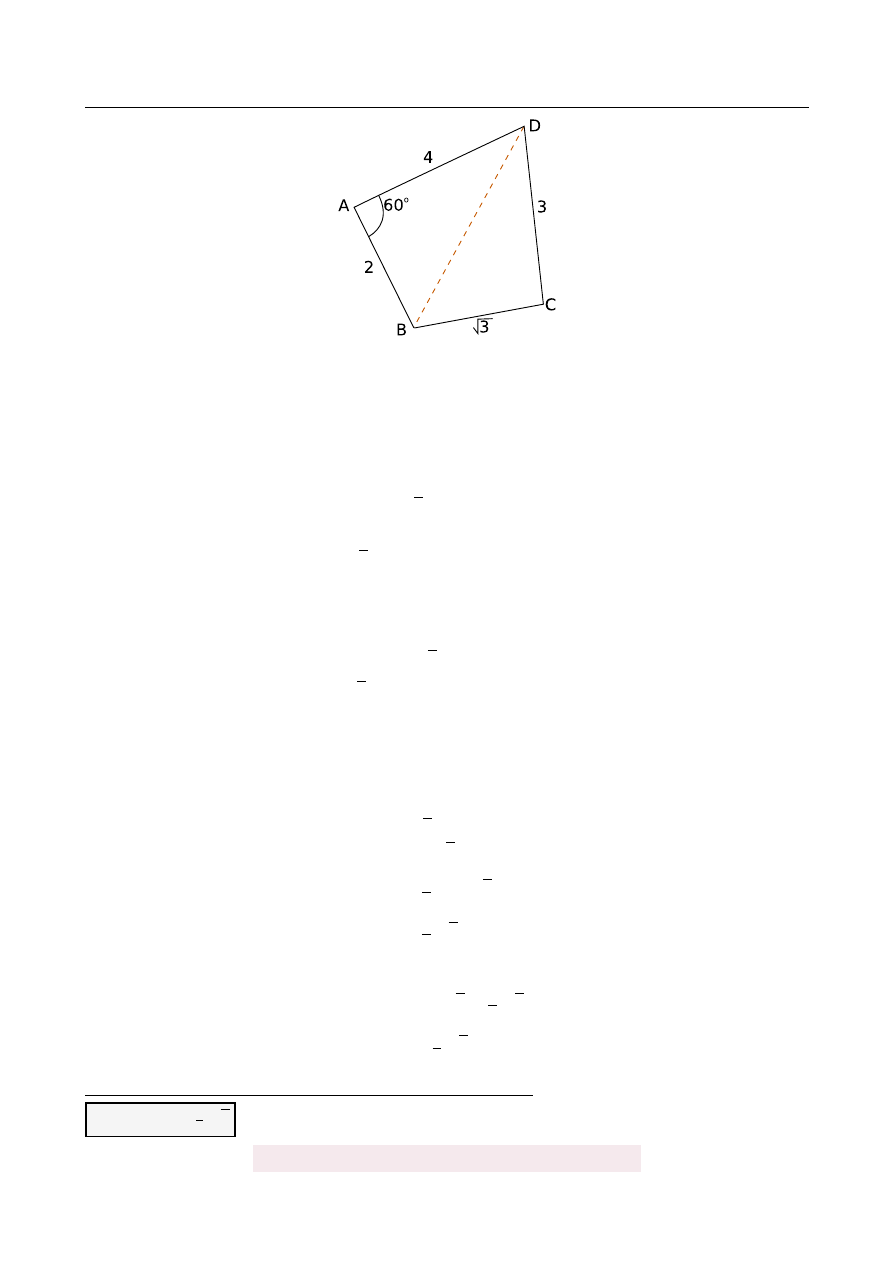
W czworok ˛
acie wypukłym ABCD dane s ˛
a:
|
AB
| =
2,
|
BC
| =
√
3,
|
CD
| =
3,
|
DA
| =
4 i
|]
DAB
| =
60
◦
. Oblicz pole tego czworok ˛
ata.
R
OZWI ˛
AZANIE
Jak zwykle, zacznijmy od schematycznego rysunku.
Plan rozwi ˛
azania zadania jest nast˛epuj ˛
acy. Aby obliczy´c pole czworok ˛
ata, podzielimy go
na dwa trójk ˛
aty (przek ˛
atn ˛
a DB). Pole ka ˙zdego z nich obliczymy ze wzoru
P
∆
=
1
2
ab sin γ,
gdzie γ – k ˛
at mi˛edzy bokami a i b. Jedyna rzecz, której nam brakuje, to miara k ˛
ata przy
wierzchołku C. B˛edziemy mogli go wyliczy´c z twierdzenia kosinusów, je ˙zeli b˛edziemy znali
długo´s´c BD, a t˛e mo ˙zemy wyliczy´c znowu z twierdzenia kosinusów, ale w trójk ˛
acie ABD.
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
No dobrze, skoro wszystko ju ˙z wiemy, to do dzieła. Liczymy BD:
BD
2
=
AD
2
+
AB
2
−
2
·
AD
·
AB
·
cos
]
A
BD
2
=
16
+
4
−
16 cos 60
◦
BD
2
=
20
−
16
·
1
2
BD
2
=
12
BD
=
2
√
3.
Liczymy teraz cos
]
C:
BD
2
=
CB
2
+
CD
2
−
2CB
·
CD cos
]
C
12
=
3
+
9
−
6
√
3 cos
]
C
0
=
6
√
3 cos
]
C
]
C
=
90
◦
.
Jak ju ˙z wiemy co wyszło, to wiemy, ˙ze mo ˙zna było to wyliczy´c z twierdzenia Pitagorasa, ale
to przegapili´smy, trudno. Teraz bez trudu liczymy szukane pola
P
ABD
=
1
2
·
4
·
2
·
sin 60
◦
P
ABD
=
2
√
3
P
BCD
=
1
2
·
3
·
√
3
P
BCD
=
3
2
√
3
P
ABCD
=
P
ABD
+
P
BCD
P
ABCD
=
2
√
3
+
3
2
√
3
P
ABCD
=
7
2
√
3.
Odpowied´z:
7
2
√
3
Materiał pobrany z serwisu
9
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
8
(5
PKT
.)
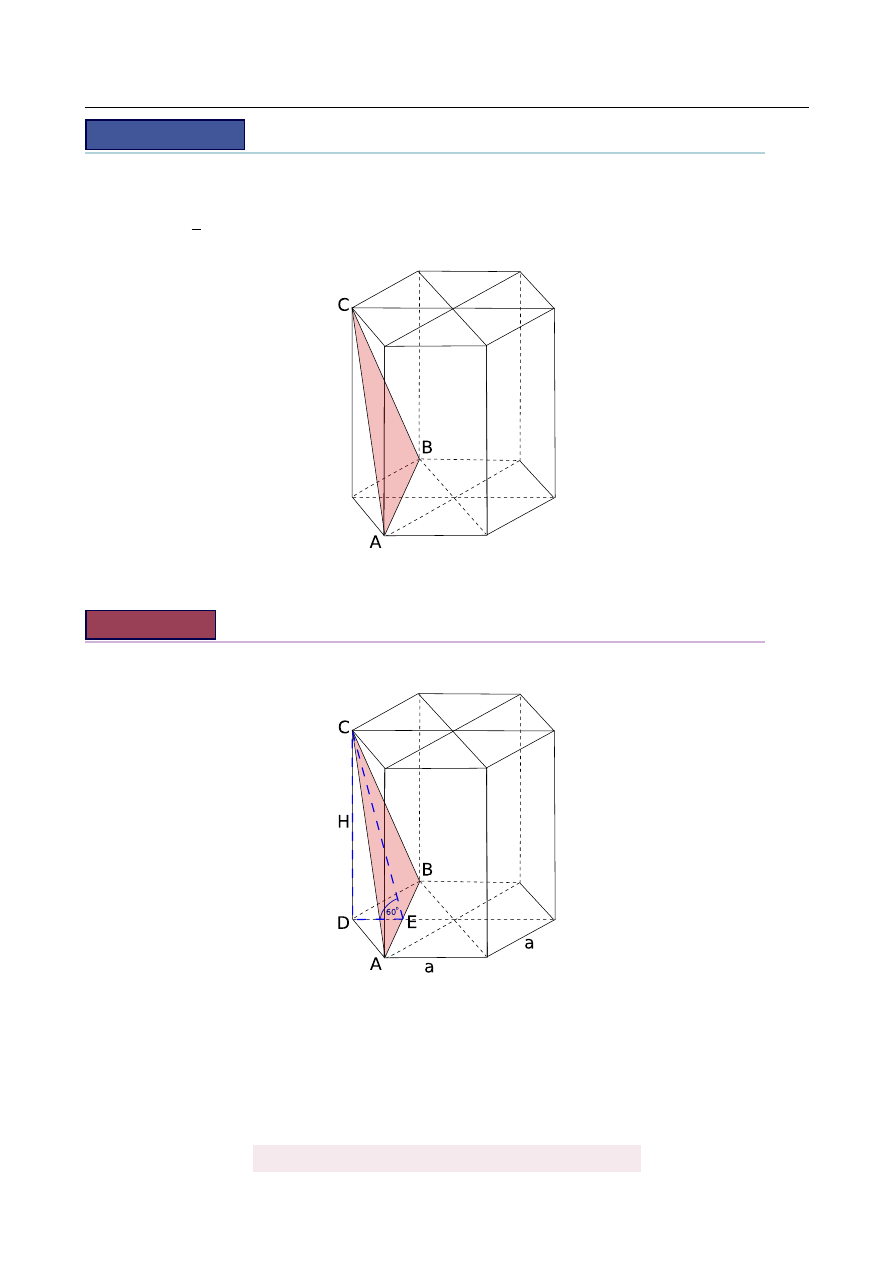
W graniastosłupie prawidłowym sze´sciok ˛
atnym płaszczyzna ABC zawieraj ˛
aca przek ˛
atne
s ˛
asiednich ´scian bocznych, wychodz ˛
acych z tego samego wierzchołka, jest nachylona do
podstawy graniastosłupa pod k ˛
atem α
=
60
◦
. Pole przekroju graniastosłupa t ˛
a płaszczyzn ˛
a
równa si˛e 8
√
3. Zaznacz na poni ˙zszym rysunku k ˛
at α. Oblicz obj˛eto´s´c tego graniastosłupa.
R
OZWI ˛
AZANIE
Zacznijmy od zazanczenia podanego k ˛
ata.
Aby obliczy´c obj˛eto´s´c graniastosłupa potrzebujemy zna´c jego wysoko´s´c H i pole podsta-
wy. Podstawa składa si˛e z 6 trójk ˛
atów równobocznych, oznaczmy długo´s´c ich boku przez a.
Spróbujmy najpierw jako´s wykorzysta´c podan ˛
a informacj˛e o polu trójk ˛
ata ABC. W tym celu
wyrazimy to pole w zale ˙zno´sci od a i H.
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zauwa ˙zmy, ˙ze odcinek AB jest dwa razy dłu ˙zszy ni ˙z wysoko´s´c trojk ˛
atów równobocz-
nych, które s ˛
a w podstawie. Zatem (ze wzoru na wysoko´s´c w trójk ˛
acie równobocznym
h
=
a
√
3
2
)
AB
=
a
√
3.
Natomiast wysyko´s´c CE trójk ˛
ata ABC wyliczamy z trójk ˛
ata prostok ˛
atnego CDE:
CD
CE
=
sin 60
◦
H
CE
=
√
3
2
CE
=
2H
√
3
CE
=
2
√
3H
3
.
Mo ˙zemy zatem zapisa´c warunek z polem:
1
2
a
√
3
·
2
√
3H
3
=
8
√
3
aH
=
8
√
3.
Sk ˛
ad wzi ˛
a´c jeszcze jedno równanie? – jeszcze raz korzystamy z trójk ˛
ata CDE oraz z faktu,
˙ze DE
=
1
2
a
DE
DC
=
ctg 60
◦
a
2
H
=
√
3
3
a
=
2
√
3
3
H.
Z obu otrzymanych zwi ˛
azków dostajemy
2
√
3
3
H
·
H
=
8
√
3
H
2
=
12
H
=
2
√
3
a
=
2
√
3
3
H
=
4.
Teraz bez problemu liczymy obj˛eto´s´c (korzystamy ze wzoru na pole trójk ˛
ata równobocznego
P
=
a
2
√
3
4
)
V
=
6
·
a
2
√
3
4
·
H
=
=
6
·
4
√
3
·
2
√
3
=
144.
Odpowied´z: 144
Materiał pobrany z serwisu
11
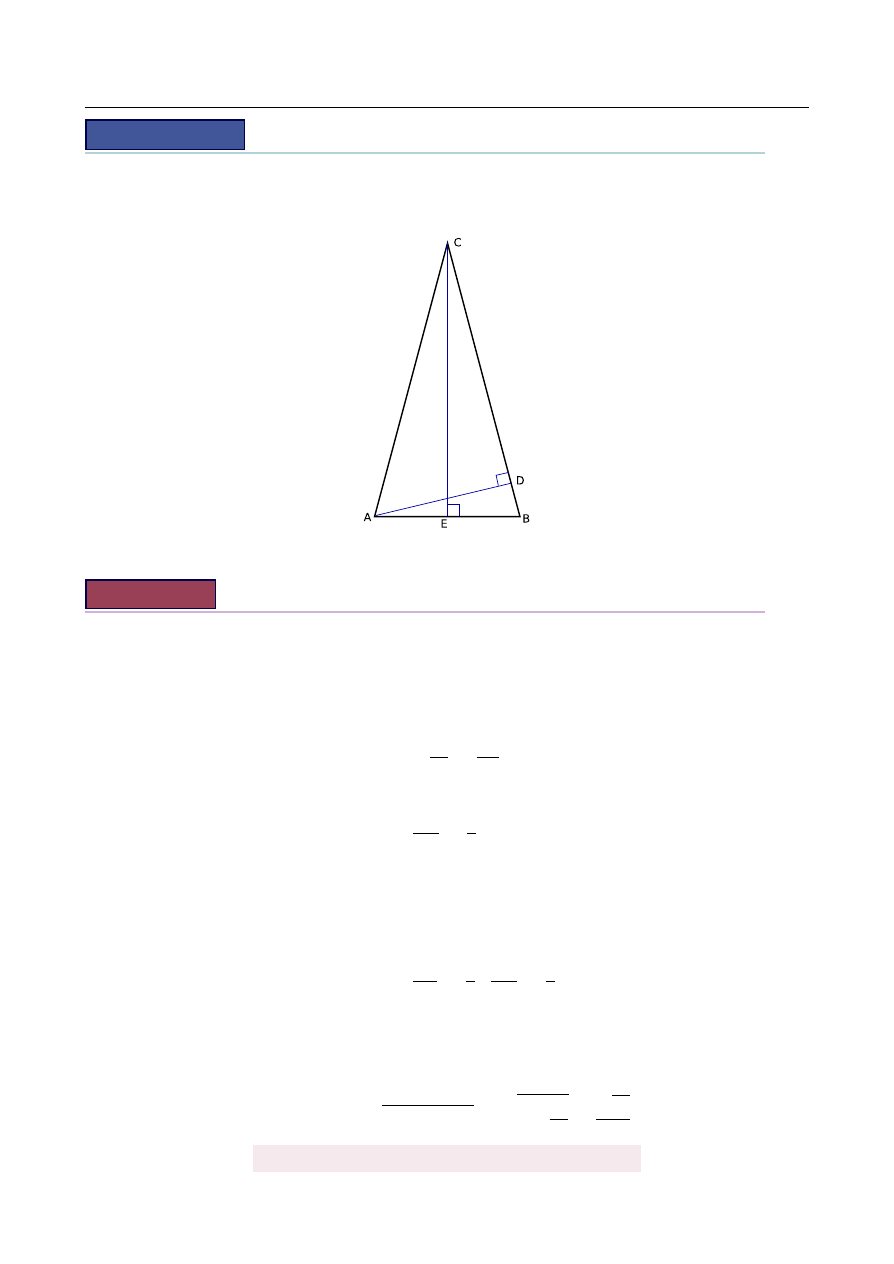
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
9
(5
PKT
.)
W trójk ˛
acie równoramiennym ABC, w którym
|
AC
| = |
BC
|
wysoko´s´c CE jest dwa razy
dłu ˙zsza od wysoko´sci AD (patrz rysunek). Oblicz kosinusy wszystkich k ˛
atów wewn˛etrz-
nych trójk ˛
ata ABC.
R
OZWI ˛
AZANIE
Ogólnie, to to co chcemy zrobi´c, to zamieni´c podan ˛
a infomacj˛e o stosunku wysoko´sci na
informacj˛e o stosunku boków trójk ˛
ata – bo to, mniej wi˛ecej, daje funkcje trygonometryczne
jego k ˛
atów. Najwa ˙zniejsze to znale´z´c jak ˛
a´s równo´s´c w danym trójk ˛
acie, w której wystepuj ˛
a
jednocze´snie obie wysoko´sci. Mo ˙zliwo´sci jest wiele, ale dwie najprostsze to
- dwa wzory na pole: AB
·
CE
=
CB
·
AD,
- podobie ´nstwo trójk ˛
atów CEB i ADB:
CE
CB
=
AD
AB
.
Ka ˙zda z tych równo´sci prowadzi do wniosku
AB
CB
=
1
2
.
I to w zasadzie prawie koniec, zostało jeszcze sporo rachunków, ale s ˛
a one do´s´c oczywiste
– jest ju ˙z jasne, ˙ze kształt (a wi˛ec k ˛
aty) trójk ˛
ata ABC jest przez ten warunek jednoznacznie
wyznaczony (z warunku z wysoko´sciami nie było to całkiem jasne).
No to liczymy. Najpierw cos
]
B
=
cos
]
A:
cos
]
B
=
EB
CB
=
1
2
·
AB
CB
=
1
4
.
Na wyliczenie cos
]
C znowu jest wiele ró ˙znych sposobów, ale najmniej trickowy to wyli-
czenie cos
]
ECB
=
cos
(
90
◦
− ]
B
)
, a potem ze wzoru cos 2α
=
2 cos
2
α
−
1. Liczymy:
cos
]
ECB
=
cos
(
90
◦
− ]
B
) =
sin
]
B
=
=
p
1
−
cos
2
]
B
=
r
1
−
1
16
=
√
15
4
.
Materiał pobrany z serwisu
12

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
I dalej
cos
]
C
=
cos 2
]
ECB
=
2 cos
2
]
ECB
−
1
=
=
2
·
15
16
−
1
=
7
8
.
Odpowied´z: cos
]
A
=
cos
]
A
=
1
4
,
cos
]
C
=
7
8
Z
ADANIE
10
(5
PKT
.)
Ci ˛
ag geometryczny
(
a
n
)
jest okre´slony wzorem a
n
=
3
1
−
n
dla n
>
1.
a) Oblicz iloraz tego ci ˛
agu.
b) Oblicz log
3
a
1
+
log
3
a
2
+
log
3
a
3
+ · · · +
log
3
a
100
czyli sum˛e logarytmów, o podstawie
3, stu pocz ˛
atkowych, kolejnych wyrazów tego ci ˛
agu.
R
OZWI ˛
AZANIE
• Iloraz to iloraz dwóch s ˛
asiednich wyrazów:
q
=
a
2
a
1
=
3
−
1
3
0
=
3
−
1
=
1
3
.
Odpowied´z:
1
3
• Prosty rachunek (pod warunkiem znajmo´sci wzoru log
a
a
c
=
c):
log
3
3
0
+
log
3
3
−
1
+
log
3
3
−
2
+ · · · +
log
3
3
−
99
=
=
0
+ (−
1
) + (−
2
) + · · · + (−
99
) =
= −(
1
+
2
+ · · · +
99
) = −
1
+
99
2
·
99
=
= −
50
·
99
= −
4950.
Pod koniec wykorzystali´smy wzór na sum˛e wyrazów ci ˛
agu arytmetycznego.
Odpowied´z: -4950
Z
ADANIE
11
(5
PKT
.)
Rzucamy trzykrotnie symetryczn ˛
a kostk ˛
a sze´scienn ˛
a do gry. Oblicz prawdopodobie ´nstwa
nast˛epuj ˛
acych zdarze ´n:
A -– na ka ˙zdej kostce wypadnie nieparzysta liczba oczek,
B — suma kwadratów liczb wyrzuconych oczek b˛edzie podzielna przez 3.
Materiał pobrany z serwisu
13

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Jak zwykle zaczynamy od wyboru odpowiedniej przestrzeni zdarze ´n elementarnych. Ustal-
my, ˙ze
Ω to wszystkie mo˙zliwe wyniki z uwzgl˛ednion ˛a kolejno´sci ˛a, czyli np. odró˙zniamy
(
1, 2, 3
)
od
(
2, 1, 3
)
. W takim modelu wszystkich zdarze ´n jest 6
·
6
·
6
=
6
3
.
Pierwsza cz˛e´s´c zadania jest łatwa, zdarzenia sprzyjaj ˛
ace A to takie, ˙ze wylosowane liczby
s ˛
a ze zbioru 1, 3, 5. Mamy zatem 3
·
3
·
3
=
3
3
mo ˙zliwo´sci, sk ˛
ad
P
(
A
) =
3
3
6
3
=
1
8
.
Co do drugiego prawdopodobie ´nstwa, to trzeba najpierw zrozumie´c kiedy suma kwadra-
tów trzech liczb dzieli sie przez 3. Nie ma na to lepszego sposobu ni ˙z powypisywa´c sobie
troch˛e mo ˙zliwych wyników i poszuka´c jakiej´s prawidłowo´sci. My pominiemy ten krok i od
razu podamy odpowied´z. Ka ˙zda liczba przy dzieleniu przez trzy daje reszt˛e 0, 1 lub 2. Licz-
ba jest podzielna przez 3, gdy reszta jest 0. Mamy zatem trzy liczby a, b, c i zastanawiamy si˛e
kiedy a
2
+
b
2
+
c
2
daje reszt˛e 0 z dzielenia przez trzy. Sprawd´zmy jak ˛
a reszt˛e daje a
2
:
je ˙zeli a
=
3k to reszta jest 0
je ˙zeli a
=
3k
+
1 to a
2
= (
3k
+
1
)
2
=
9k
2
+
6k
+
1, czyli reszta jest 1
je ˙zeli a
=
3k
+
2 to a
2
= (
3k
+
2
)
2
=
9k
2
+
12k
+
3
+
1, czyli reszta jest 1
Widzimy zatem, ˙ze a
2
ma zawsze reszt˛e 0 lub 1 z dzielenia przez 3. W ko ´ncu rozumiemy
kiedy a
2
+
b
2
+
c
2
dzieli si˛e przez trzy: albo a, b, c s ˛
a wszystkie podzielne przez 3 (reszta
0+0+0) albo ˙zadna z nich (reszta 1+1+1). Innych mo ˙zliwo´sci nie ma.
Pozostało policzy´c ile jest takich wyników. Układów z liczbami podzielnymi przez 3 jest
2
·
2
·
2
=
2
3
(bo do wyboru jest 3 i 6). Układów z liczbami, które nie s ˛
a podzielne przez 3
jest 4
3
(do wyboru mamy 1,2,4 lub 5). Mamy zatem
P
(
B
) =
2
3
+
4
3
6
3
=
1
+
2
3
3
3
=
1
3
.
Odpowied´z: P
(
A
) =
1
8
, P
(
B
) =
1
3
Materiał pobrany z serwisu
14
Wyszukiwarka
Podobne podstrony:
Zestaw1 PR rozwiazania id 58873 Nieznany
Zestaw 2 PR rozwiązania
Zestaw 2 PR rozwiązania
zestaw 07 rozwiazania
4R ruch obrotowy bryly PR rozwiazania id 39410 (2)
Zestaw 2 PP rozwiązania
zestaw 05 rozwiazania
zestaw 06 rozwiazania
zestaw 10 rozwiązania
zestaw 08 rozwiazania
2013 02 CEN PR rozwiązania
MJA 1 PR rozwiazania id 303664 Nieznany
zestaw 04 rozwiazania
zestaw 03 rozwiazania
Zestaw 1 PP rozwiązania
Chemia Ćwiczenia zestawy rozwiązane, Zestaw nr 7 rozwiazany, Zestaw 7
więcej podobnych podstron