
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
Wykład 4
Modelowanie predykcyjne
– sieci neuronowe

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
2
Struktura wykładu:
• Podstawowy model neuronu i sieci neuronowej
• Działanie sieci neuronowej i jej uczenie
• Zalety i wady sieci neuronowych

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
3
Biologiczne inspiracje sztucznych sieci neuronowych
Skomplikowane systemy uczące w mózgach zwierząt składają się
z połączonych między sobą grup neuronów.
Sztuczne sieci neuronowe (sieci neuronowe (neural networks))
stanowią próbę odwzorowania uczenia nieliniowego występującego
w biologicznych systemach nerwowych.
• Sieci neuronowe składają się z określonych grup elementów
naśladujących działanie neuronu jako jednostki biologicznej.
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
4
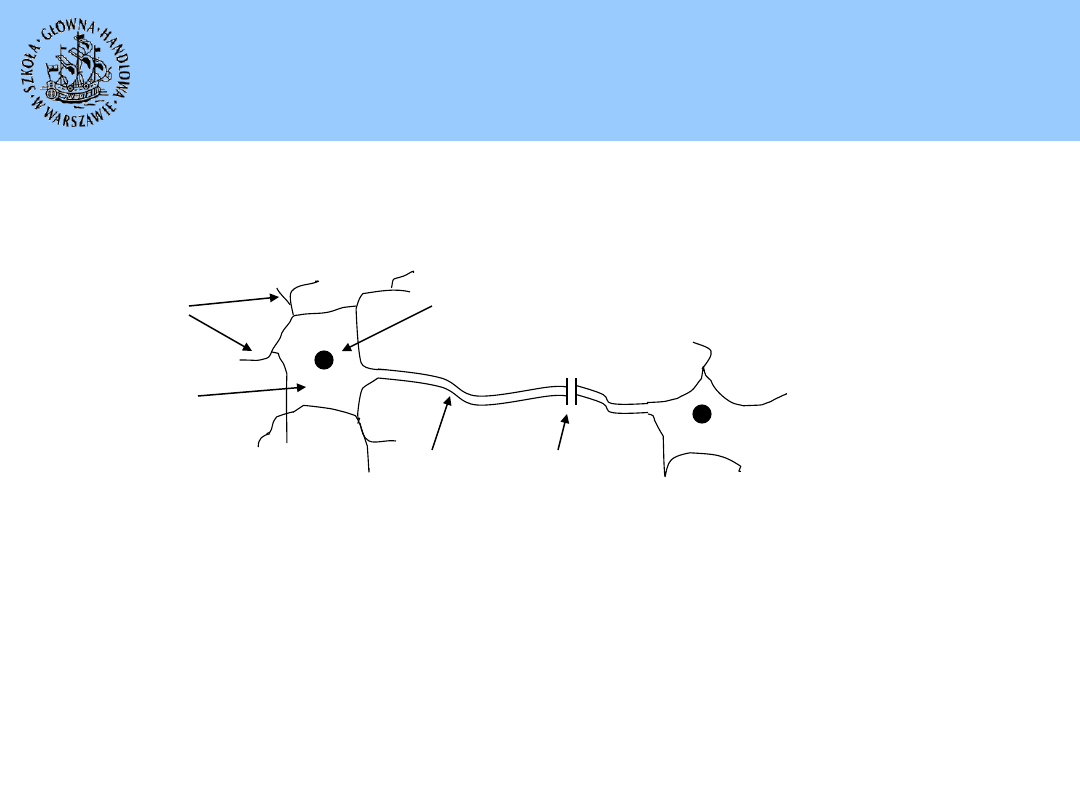
Biologiczne inspiracje sztucznych sieci neuronowych
Budowa biologicznej komórki nerwowej (neuronu)
• Dendryty – rozgałęziona struktura wielu wejść informacyjnych
zbierająca sygnały z innych komórek i receptorów
• Akson – wyprowadza sygnał wyjściowy i przekazuje go
do odbiorników informacji
• Synapsa – przekazuje sygnał od neuronu do neuronu
• Korpus komórki nerwowej – agreguje sygnały wejściowe i wyznacza
sygnał wyjściowy
dendryty
ciało komórki
jądro
akson
synapsa
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
5
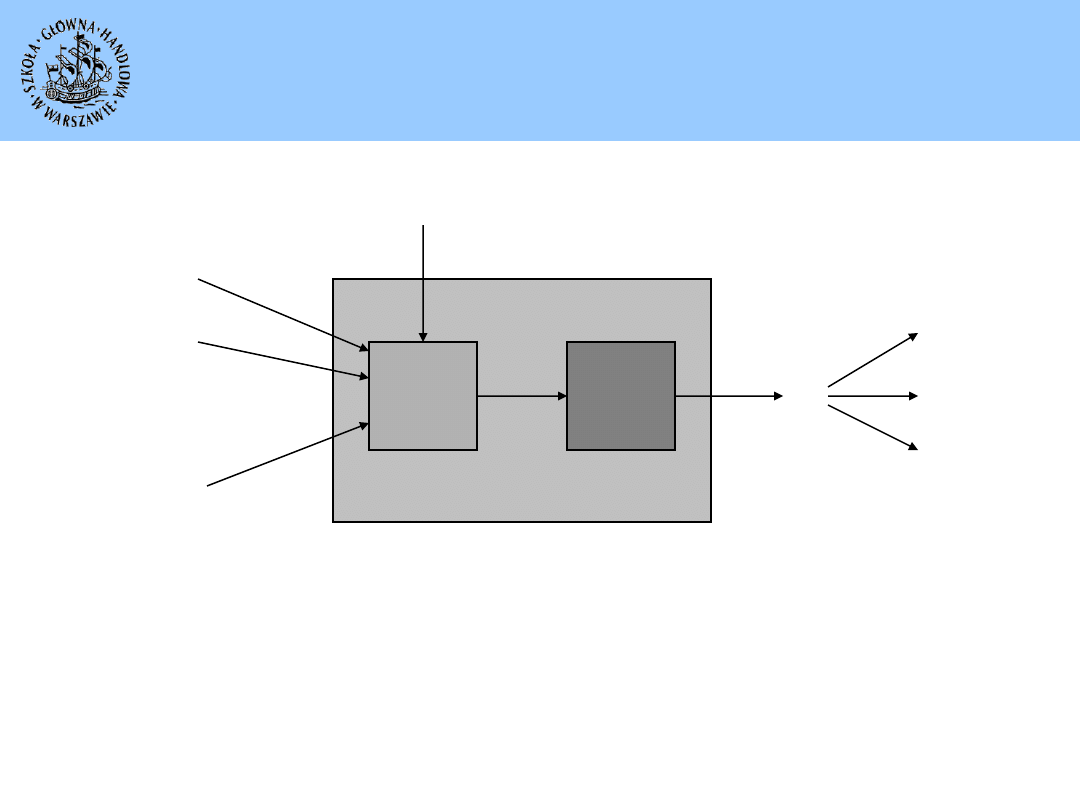
Model sztucznego neuronu
Sztuczny neuron
• Zbiera sygnały (dane) wejściowe ( ) z poprzedzających go neuronów.
• Sumuje otrzymane sygnały z odpowiednimi wagami ( ) i tworzy z nich
jedną wartość (np. za pomocą funkcji Σ).
• Otrzymany wynik jest wejściem dla funkcji aktywacji (φ).
• Funkcja aktywacji zwraca sygnał wyjściowy (dane wyjściowe) (y).
• Sygnał wyjściowy przekazywany jest do następnych neuronów.
1
x
2
x
n
x
1
w
2
w
n
w
y
i
x
1
0
x
0
w
i
w
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
6
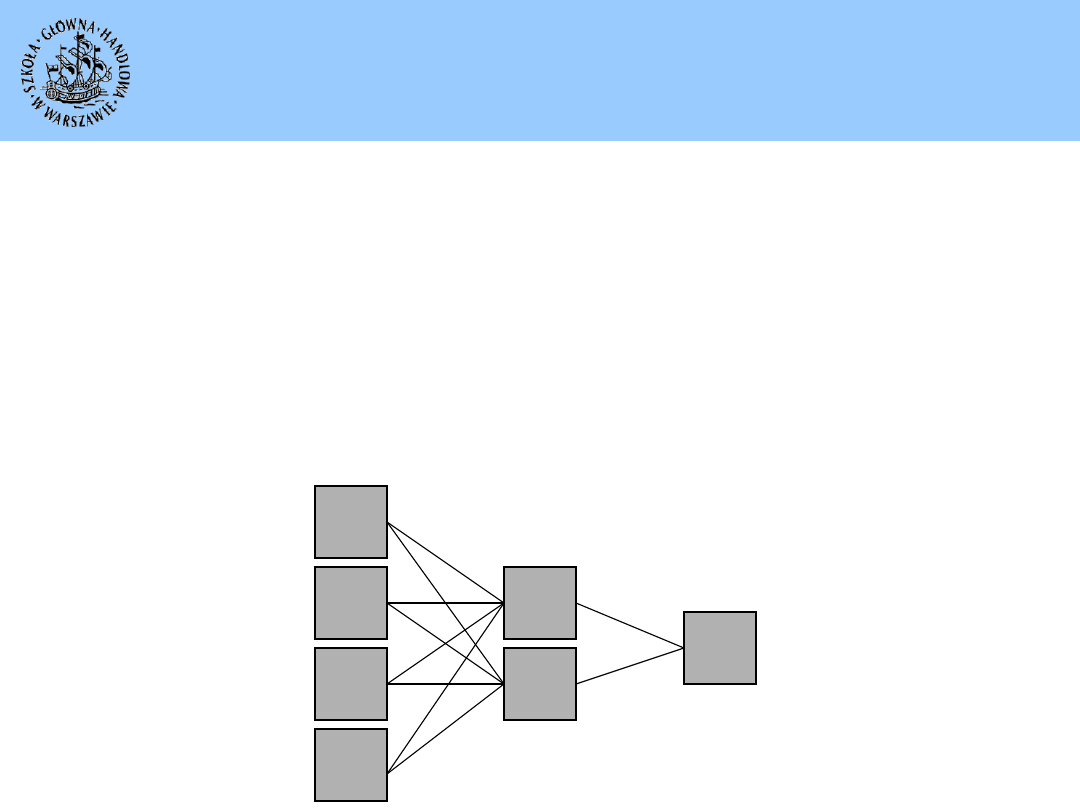
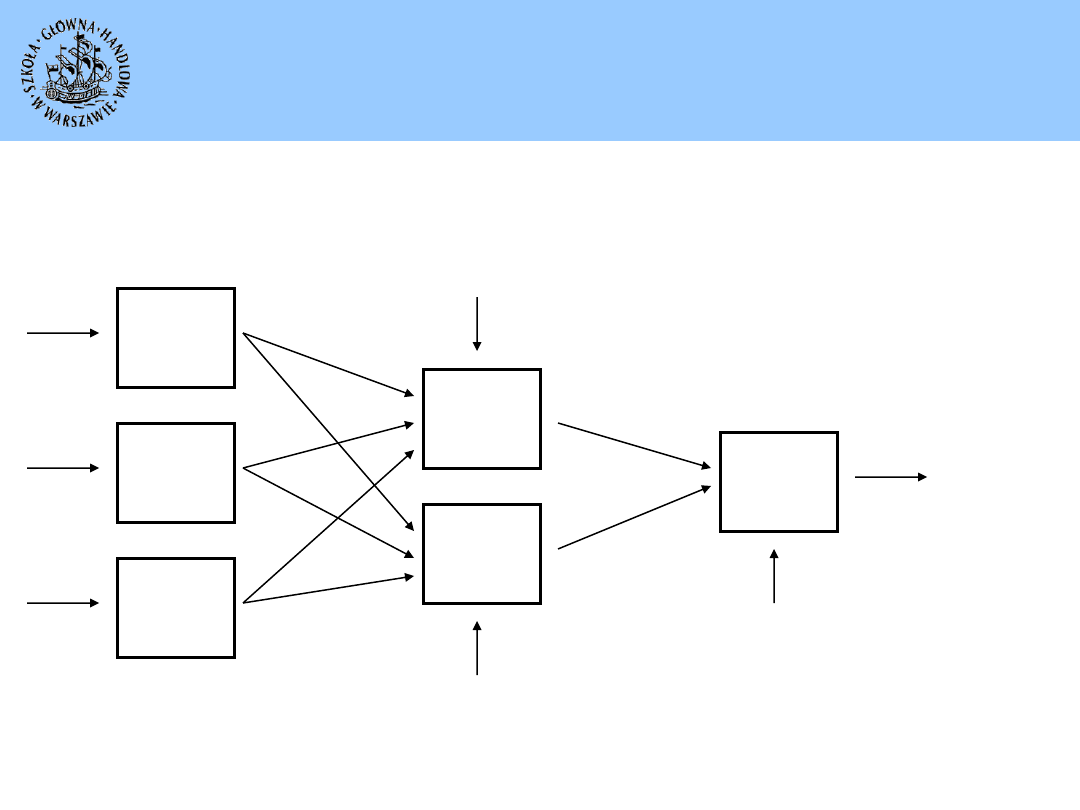
Przykładowy model sieci neuronowej
Sieć neuronowa jest zbiorem prostych jednostek (neuronów) połączonych
w określony sposób.
Sygnały (wartości) wejściowe sieci mają przypisane wagi, których wartość
mogą podlegać zmianom w trakcie uczenia.
Sygnały wyjściowe sieci powstające jako odpowiedzi na sygnały wejściowe
wyznaczają rozwiązanie stawianego sieci zadania.
Warstwa wejściowa Warstwa ukryta Warstwa wyjściowa
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
7
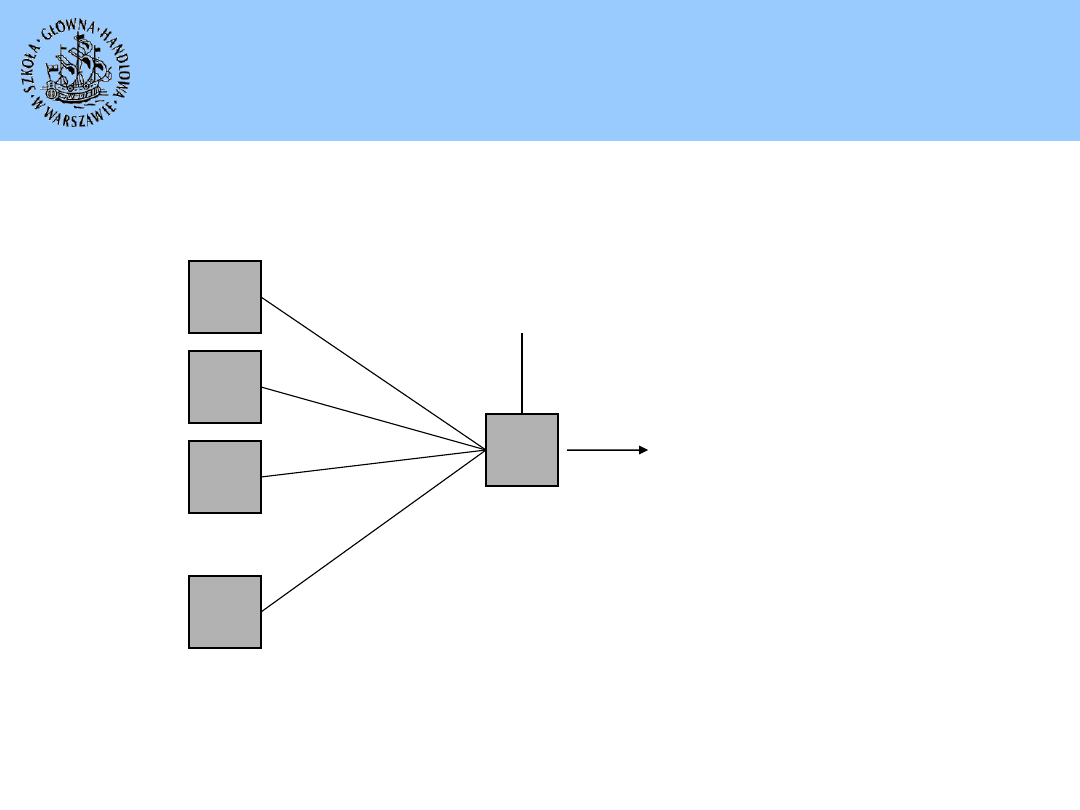
Model regresji liniowej
– przykład prostej sieci
neuronowej
)
(
)
(
1
0
n
i
i
i
x
w
w
y
E
Warstwa
wejściowa
Warstwa
wyjściowa
n
i
i
i
x
w
w
y
E
1
0
1
))
(
(
1
x
2
x
3
x
n
x
1
w
2
w
3
w
n
w
0
w

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
8
Kodowanie sygnałów wejściowych oraz wyjściowych
Zaleca się kodowanie danych wejściowych tak, aby przyjmowały wartości
z przedziału od 0 do 1.
• Zmienne ciągłe – normalizacja min-max
• Zmienne jakościowe – znaczniki (flagi) informujące o wartości atrybutu.
Zmienne jakościowe o k wartościach zamieniamy na k-1 znaczników.
Neurony wyjściowe najczęściej zwracają wartości z przedziału od 0 do 1.
X
X
X
X
X
X
X
X
min
max
min
zakres
min
*

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
9
Sieci neuronowe
– klasyfikacja
• Dwudzielny problem klasyfikacyjny:
„Czy klient spłaci kredyt?”
„Czy klient zrezygnuje z usług firmy?”
Przypadek pojedynczego neuronu wyjściowego z uprzednio
ustawioną wartością progową oddzielającą dwie klasy.
• Wielodzielny problem klasyfikacyjny:
„Jakiej jakości jest produkt: złej, średniej, dobrej?”
Przypadek pojedynczego neuronu wyjściowego dla kilku kategorii
jednoznacznie uporządkowanych.
• Wielodzielny problem klasyfikacyjny:
„Od jakiego producenta pochodzi produkt: XX, YY, ZZ”
Przypadek wielu neuronów wyjściowych – kodowanie 1 z n (każdej
kategorii przypisywany jest dokładnie jeden neuron wyjściowy).

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
10
Sieci neuronowe
– szacowanie, przewidywanie
• Dane wejściowe kodowanie np. normalizacja min-max
• Dane wyjściowe denormalizacja
wartość przewidywana = wynik * zakres + minimum
wynik
– wartość zwracana przez sieć
zakres
– zakres wartości początkowych atrybutu przed skalowaniem
minimum
– minimalna wartość atrybutu przed skalowaniem
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
11
Prosta sieć neuronowa – przykład
Warstwa wejściowa
Warstwa wyjściowa
Warstwa ukryta
neuron 1
neuron 2
neuron 3
neuron B
neuron A
neuron Z
A
w
1
B
w
1
A
w
2
B
w
2
A
w
3
B
w
3
A
w
0
B
w
0
Z
A
w
Z
B
w
Z
w
0
Sieć warstwowa, jednokierunkowa i pełna.

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
12
Prosta sieć neuronowa
Funkcja
łącząca (kombinacji) oblicza kombinacje liniową sygnałów
wejściowych z odpowiednimi wagami połączeń. Funkcja liniowa
(LINEAR
) dla węzła j:
– sygnał przekazywany z i-tego wejścia do j-tego neuronu
– waga połączenia pomiędzy i-tym wejściem a j-tym neuronem
(j-ty neuron ma I
+1 wejść)
– sygnały wejściowe pochodzące z warstwy poprzedniej
– stałe w czasie wymuszenie zewnętrzne
Przykład c.d.
Dla neuronu A w warstwie ukrytej:
j
I
j
I
j
j
j
j
i
j
i
j
i
j
x
w
x
w
x
w
x
w
net
1
1
0
0
j
i
x
j
i
w
i
x
0
x
A
A
A
A
A
A
A
i
A
i
A
i
A
x
w
x
w
x
w
w
x
w
net
3
3
2
2
1
1
0
1

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
Inne funkcje kombinacji
Niech będą wartościami standaryzowanymi, a , b, , będą
obliczane w sposób interaktywny, wówczas:
ADD
EQSLOPES
EQRADIAL
EHRADIAL
p
i
i
i
j
j
x
w
w
net
1
1
01
p
i
i
ij
j
x
w
b
net
1
2
2
)
(
p
i
i
j
x
net
1
p
i
i
ij
j
j
x
w
b
net
2
2
)
(
p
x
x
x
,
,
,
2
1
j
a
j
b
ij
w
13

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
Inne funkcje kombinacji
Niech f
oznacza liczbę połączeń z neuronem, w Enterprise Miner f nazywane
jest fan-in.
EWRADIAL
EVRADIAL
XRADIAL
p
i
i
ij
j
j
j
x
w
b
a
abs
f
net
2
2
)
(
))
(
log(
p
i
i
ij
j
j
j
x
w
b
b
abs
f
net
2
2
)
(
))
(
log(
p
i
i
ij
j
j
x
w
b
a
abs
f
net
2
2
)
(
))
(
log(
14

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
15
Prosta sieć neuronowa – funkcja aktywacji
• Wyznaczona kombinacja liniowa jest następnie wejściem
dla funkcji aktywacji.
Funkcja aktywacji
przekształca wyjście z funkcji kombinacji i przesyła
je dalej.
Przykładowa sigmoidalna funkcja aktywacji:
x
e
x
1
1
0
0,5
1
j
net
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
16
Inne funkcje aktywacji
Funkcjami aktywacji mogą być dowolne funkcje ciągłe generujące
w neuronie wyjściowym wartość z odpowiedniej skali.
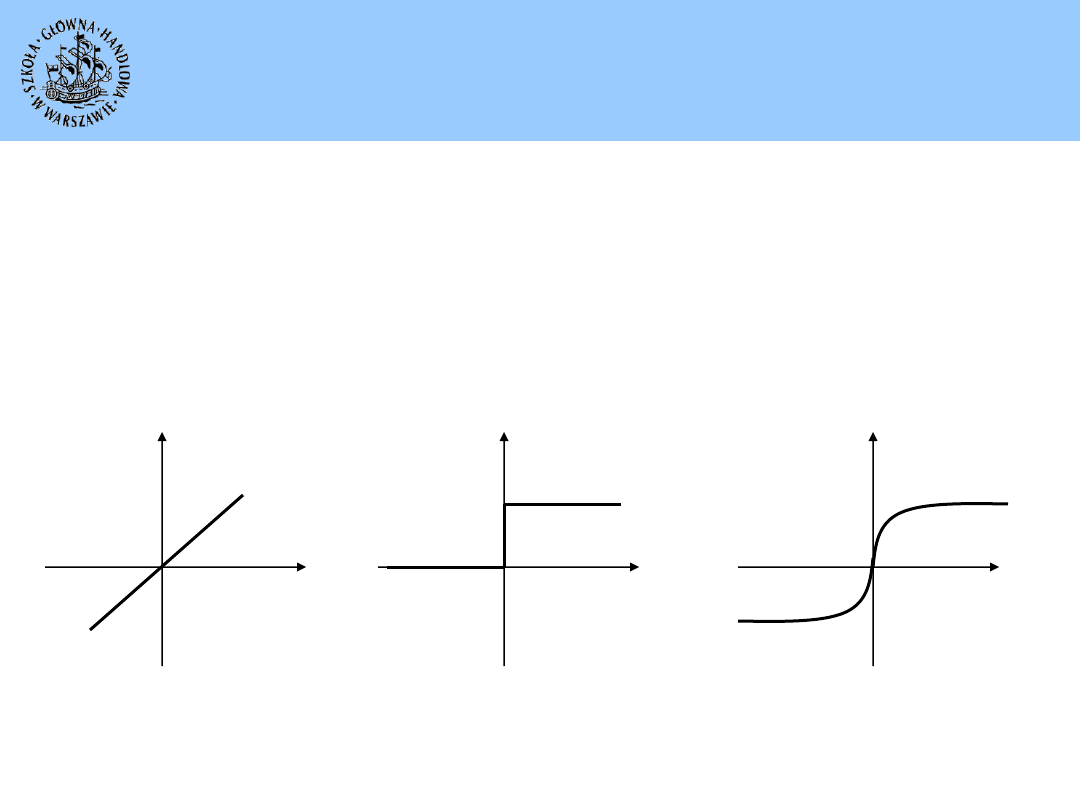
Trzy inne podstawowe rodzaje funkcji aktywacji stosowane w sieciach
neuronowych:
Funkcja liniowa
Funkcja tangens
hiperboliczny
Funkcja skoku
jednostkowego

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
Funkcje aktywacji
Arc Tan
Elliot
Hyperbolic Tangent
Logistic
Gauss
Sine
Cosine
Exponential
Square
Reciprocal
Softmax
j
j
net
H
1
tan
2
j
j
net
H
tanh
j
j
j
net
net
H
1
j
j
net
H
exp
1
1
2
5
.
0
exp
j
j
net
H
j
j
net
H
sin
j
j
net
H
cos
j
j
net
H
exp
2
j
j
net
H
j
j
net
H
1
3
1
exp
exp
k
k
j
j
net
net
H
3
,
2
,
1
j
3
,
2
,
1
j
17

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
18
Prosta sieć neuronowa
Przykład c.d.
Dla neuronu A
funkcja aktywacji przyjmuje jako wejście i wyznacza wartość
wyjściową neuronu A:
Analogicznie wyznaczamy wartość wyjściową dla neuronu B:
Neuron Z
łączy wartości wyjściowe pochodzące z neuronów A i B wyznaczając
ważoną sumę sygnałów wejściowych dla neuronu Z, oznaczając
mamy:
Wartość funkcji aktywacji neuronu Z:
A
A
A
net
net
y
exp
1
1
A
net
B
B
B
net
net
y
exp
1
1
Z
B
Z
B
Z
A
Z
A
Z
i
Z
i
Z
i
Z
x
w
x
w
w
x
w
net
1
0
Z
Z
Z
net
net
y
exp
1
1
A
AZ
y
x
B
BZ
y
x
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
19
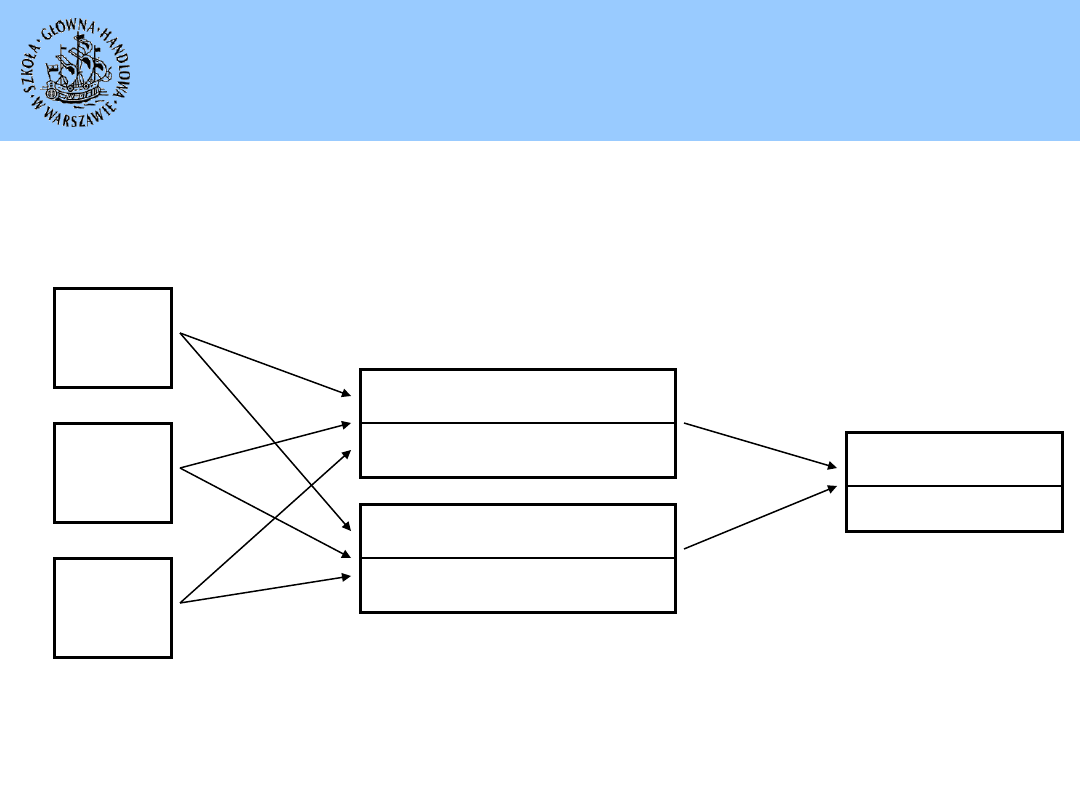
Przepływ informacji w sieci neuronowej
Warstwa wejściowa
Warstwa wyjściowa
Warstwa ukryta
wiek
płeć
dochód
dochód
eć
pł
wiek
4
3
2
1
A
dochód
eć
pł
wiek
4
3
2
1
dochód
eć
pł
wiek
8
7
6
5
B
dochód
eć
pł
wiek
8
7
6
5
B
A
13
12
11
B
A
13
12
11

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
20
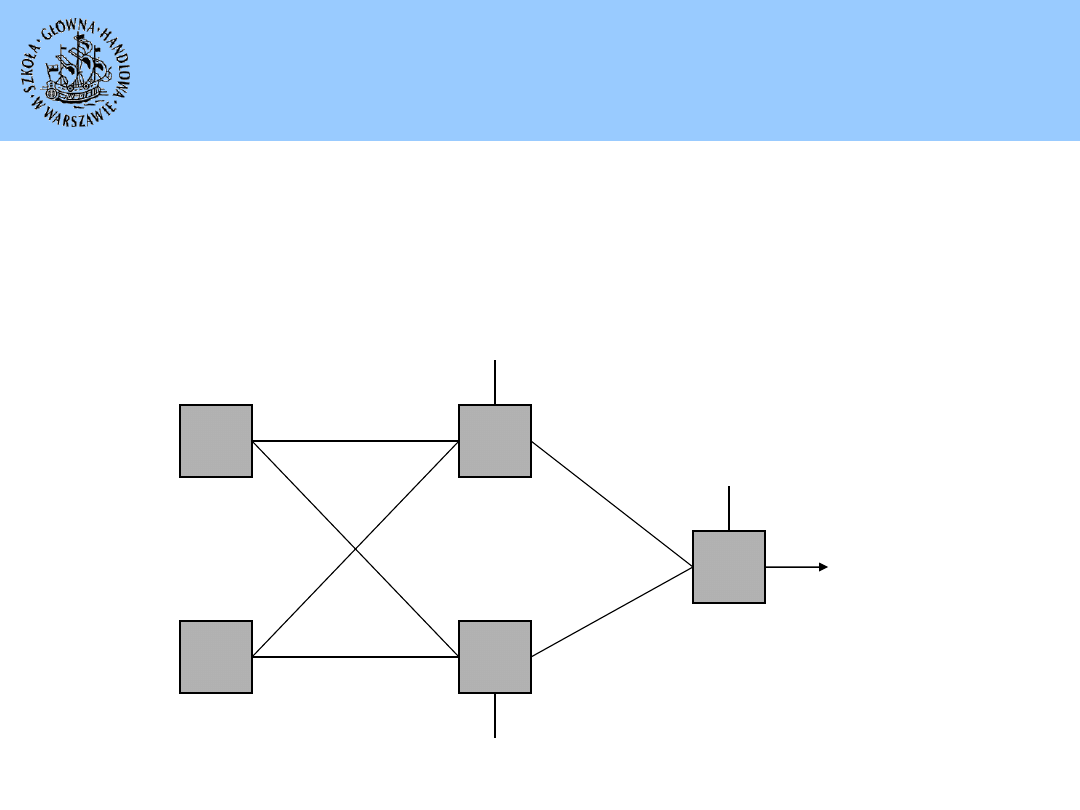
Perceptron wielowarstwowy (MLP
– Multi Layer Perceptron)
Warstwy MLP:
Wejściowa
zawiera co najmniej tyle neuronów, ile jest zmiennych objaśniających
(co najmniej jeden neuron dla każdej zmiennej objaśniającej)
Ukryta lub kilka warstw ukrytych
nieliniowo przekształca sygnał wejściowy (ważoną kombinację liniową
wejść)
Wyjściowa
zbiera i łączy wyniki z warstwy ukrytej w celu otrzymania ostatecznej
predykcji (otrzymany wynik można porównać z wartością rzeczywistą)
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
21
Model perceptronu wielowarstwowego
n
i
m
j
j
ji
oi
i
i
x
w
w
w
w
y
E
1
1
0
)
(
)
(
0
w
1
w
n
w
01
w
n
w
0
11
w
mn
w
1
m
w
n
w
1

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
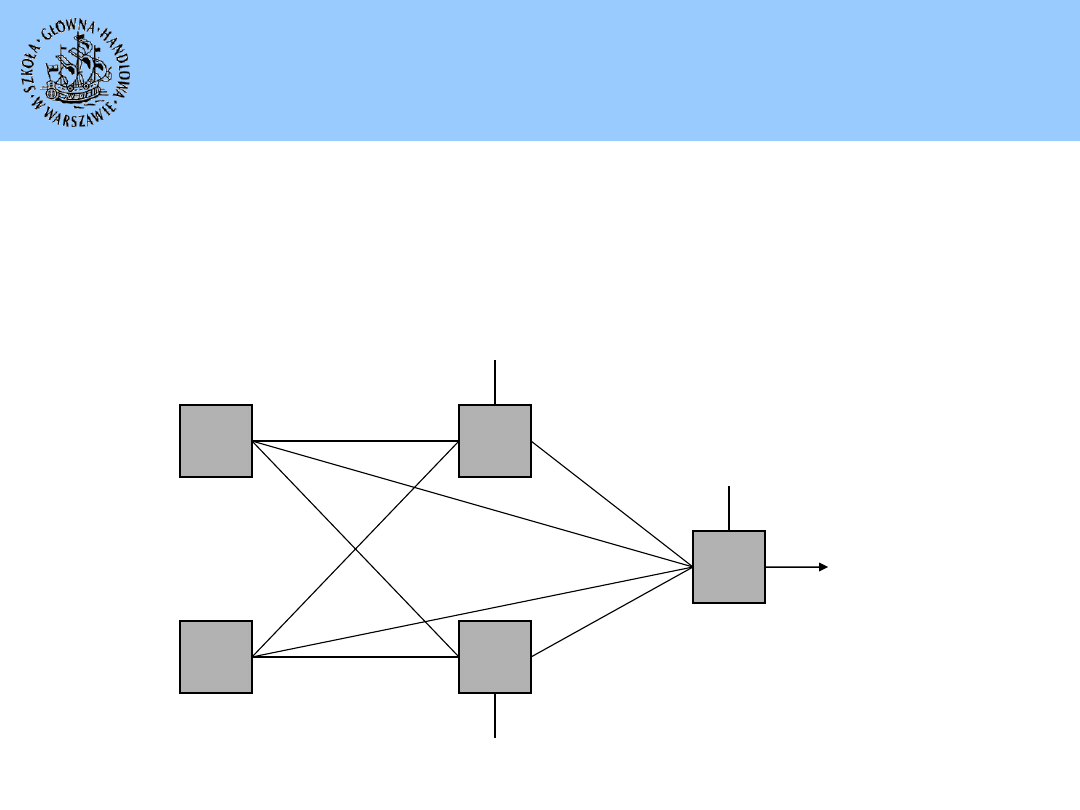
22
Liczba neuronów
Większa liczba neuronów w warstwie ukrytej:
• większa moc obliczeniowa i elastyczność sieci neuronowej;
• przeuczenie – zbyt dobre dopasowanie sieci do zbioru uczącego oraz
mniejsza zdolność do uogólniania.
Przeuczenie mniejsza liczba neuronów w warstwie ukrytej
Mała dokładność klasyfikacji większa liczba neuronów w warstwie
ukrytej
• Brak jednoznacznych zasad określających liczbę neuronów w warstwie
ukrytej.
• Np. według jednej z zasad zaleca się umieszczenie ~2*k (k - liczba
zmiennych objaśniających) neuronów w pierwszej warstwie ukrytej.
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
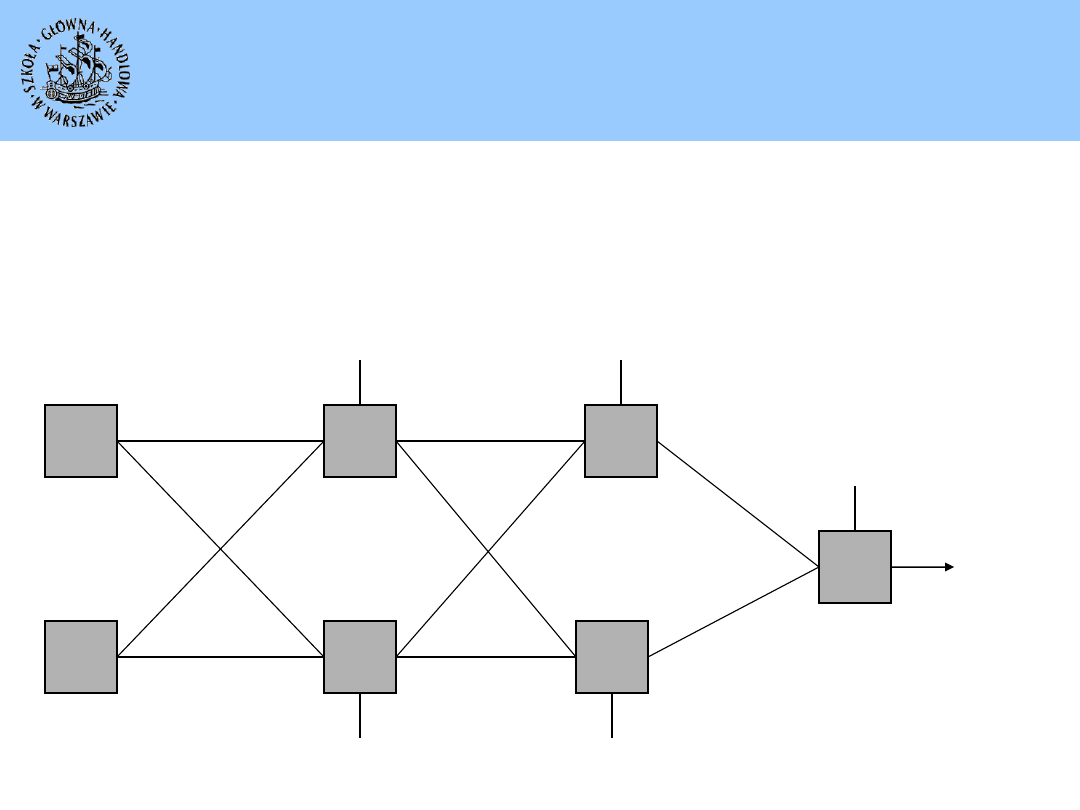
23
Model sieci z bezpośrednimi połączeniami
0
w
1
w
n
w
01
w
n
w
0
11
w
mn
w
1
m
w
n
w
1
n
i
m
k
k
k
m
j
j
ji
oi
i
i
x
d
x
w
w
w
w
y
E
1
1
1
0
)
(
)
(
1
d
m
d
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
24
MLP z dwiema warstwami ukrytymi
0
w
1
w
n
w
101
w
n
w
10
11
w
mn
w
1
m
w
n
w
1
)
)
(
(
)
(
1
1
10
1
1
1
20
2
0
k
i
m
h
j
hj
j
i
n
j
ji
i
i
i
x
w
w
w
w
w
w
y
E
111
w
k
w
11
1
1n
w
nk
w
1
201
w
k
w
20

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
25
Sieci radialne
Sieci radialne
•
oparte są na radialnych funkcjach bazowych (Radial Basis Functions)
•
aproksymują odwzorowania prowadzące z jednej przestrzeni wielowymiarowej
w inną przestrzeń wielowymiarową
•
posiadają jedną warstwę ukrytą, która składa się z neuronów radialnych
•
warstwa wyjściowa składa się z neuronów liniowych
•
każdy neuron posiada parametr, który steruje „szerokością” dzwonu Gaussa
Funkcje radialne (RBF)
– klasa funkcji aktywacji, których wartości maleją
lub rosną monotonicznie wraz z odległością od centrum neuronu.
Parametrami funkcji radialnej są: centrum neuronu i współczynnik skalowania
(wyznacza szerokość oddziaływania neuronu).
Funkcje ORBF (Ordinary RBF)
– wykładnicze funkcje aktywacji, tworzące zbiór
dzwonów Gaussa.
Funkcje NRBF (Normalized RBF)
– funkcje aktywacji tworzone w oparciu
o normalizowaną kombinację dzwonów Gaussa.

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
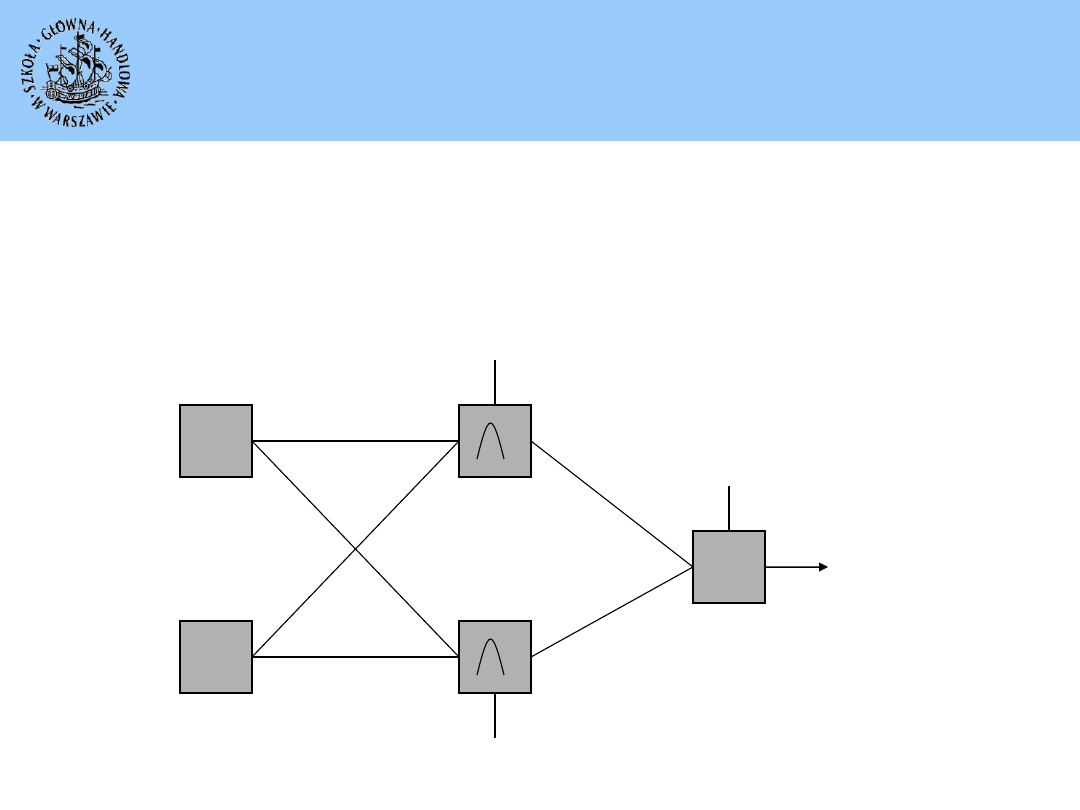
Funkcje ORBF
XRADIAL
– nierówne wysokości i szerokości
EQRADIAL
– równe wysokości i szerokości
EWRADIAL
– równe szerokości
EHRADIAL
– równe wysokości
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
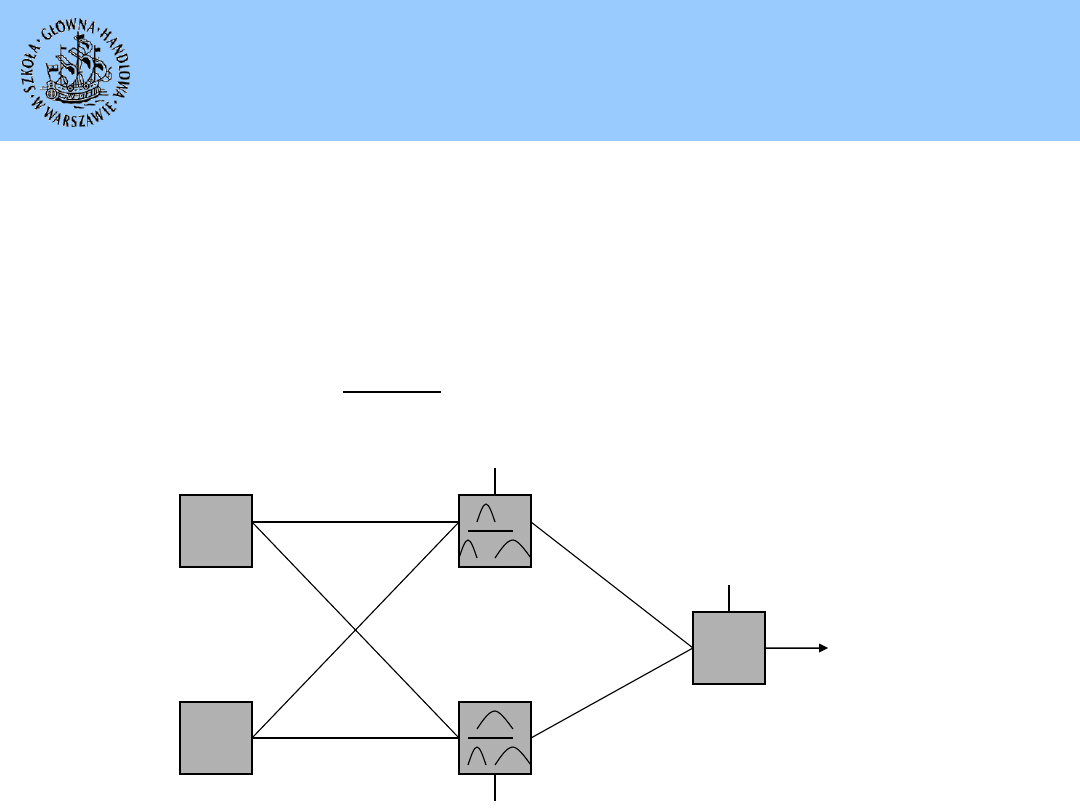
27
Model sieci ORBF
0
w
1
w
n
w
01
w
n
w
0
11
w
mn
w
1
m
w
n
w
1
n
i
m
j
ji
j
i
i
w
x
w
w
w
y
E
1
1
2
0
0
exp
)
(
DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
28
Model sieci NRBF
n
i
k
j
j
i
i
e
e
w
w
y
E
1
1
0
)
(
0
w
1
w
n
w
01
w
n
w
0
11
w
mn
w
1
m
w
n
w
1
Problem
: stosowanie funkcji ORBF może spowodować, że otrzymana
hiperpłaszczyzna nie będzie gładka (zbiór uwypukleń będzie miał charakter lokalny).
Rozwiązanie: zastosowanie normalizowanych funkcji RBF (NRBF)
m
j
ji
j
i
i
i
w
x
w
a
l
e
1
2
2
0
ln
exp
l
– liczba połączeń
poprzedzających neuron
– wysokość najwyższego
z „dzwonów”
i
a
+
+

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
29
Proces uczenia sieci neuronowej
Jak uczy się sieci neuronowe typu wielowarstwowy perceptron?
1.
Ustalane są wagi początkowe (losowanie lub uczenie wstępne).
2.
Każda obserwacja ze zbioru uczącego jest przetwarzana przez sieć.
3.
Następnie korygowane są wagi przez odpowiedni algorytm
optymalizacyjny.
4.
Uczenie kontynuowane jest aż do osiągnięcia zadanego warunku
przerwania uczenia.

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
30
Sieć ze wsteczną propagacją błędów
Algorytm propagacji wstecznej
• Zbiór danych wejściowych przetwarzany jest przez sieć neuronową.
• Otrzymana wartość wyjściowa jest porównywana z wartością
oczekiwaną (wejściową) – wyznaczany jest błąd dla danego rekordu.
• Różnice pomiędzy wartościami wyjściowymi a wejściowymi stanowią
podstawę zmian wag neuronów.
• Szukamy zbioru wag minimalizujących SSE.
• Podstawową metodą minimalizacji SSE jest gradientowa metoda
największego spadku, dająca zależność na zmianę wartości wag
w kolejnych krokach iteracji (reguła delta).
• Regułę tą można bezpośrednio stosować dla sieci jednowarstwowych.
W przypadku sieci wielowarstwowych, konieczne jest wprowadzenie
dodatkowego algorytmu pozwalającego na równoczesną zmianę wag
neuronów we wszystkich warstwach.
2
SSE
oczekiwana
wyjście
rekord
neuron
wyjściowy

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
31
Miary błędu dla zmiennej binarnej
Kryterium maksymalnej wiarogodności
Dla zmiennej objaśnianej zero-jedynkowej:
n
i
i
i
i
i
p
y
p
y
1
1
ln
1
ln
i
i
i
i
p
p
1
ln
ln

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
32
Miary błędu dla zmiennej ciągłej
Rozkład zmiennej objaśnianej Miara błędu
• NORMALNY
• POISSON
• GAMMA
2
SSE
w
f
y
w
f
y
w
f
y
ln
2
1
ln
2
w
f
y
w
f
y

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
33
Warunki stopu
Sieć neuronowa kontynuuje uczenie się na zbiorze uczącym, rekord
po rekordzie, stale dopasowując wagi.
Algorytm uczenia może potrzebować wielu przebiegów przez zbiór
danych.
Warunki przerwania uczenia sieci:
• osiągnięto zamierzoną liczbę powtórzeń uczenia
• wykorzystano rzeczywistą ilość czasu na uczenie
• wartość błędu na zbiorze walidacyjnym stabilizuje się lub zaczyna
wzrastać
• wartości otrzymanych wag nie zmieniają się
Niezależnie od użytego kryterium stopu algorytmy uczenia sieci
nie gwarantują znalezienia rozwiązania optymalnego – globalnego
minimum SSE.

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
34
Zalety sieci neuronowych
• Otrzymane wyniki są zmienną ciągłą
• Analiza wielu zmiennych jednocześnie
• Możliwości stworzenia modelu gdy rozwiązanie ma dużą złożoność
• Odporność na zaszumione dane

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
35
Wady sieci neuronowych
• Trudności w ustaleniu parametrów architektury sieci
• Wpadanie w minima lokalne
• Potencjalnie długi czas uczenia sieci
• Problemy braków danych i obserwacji odstających
• Brak jasnej interpretacji

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
36
Zastosowania sieci neuronowych
• Predykcja
• Klasyfikacja i rozpoznawanie
• Analiza danych
• Kojarzenie danych
• Optymalizacja
• Filtracja sygnałów

DATA MINING – nr przedmiotu 233100-0997
Zakład Analizy Historii Zdarzeń i Analiz Wielopoziomowych ISiD SGH
dr Wioletta Grzenda
37
Dziękuję za uwagę !
Wyszukiwarka
Podobne podstrony:
04 Wyklad4 predykcja sieci neuronoweid 523 (2)
04 Wyklad4 predykcja sieci neuronoweid 523 (2)
Sieci logistyczne 09.04.2011 kopia wykład 1, studia, sieci logistyczne
Wykłady Sieci Neuronowe(1), uczenie maszynowe, sieci neuronowe
sztuczne sieci neuronowe wykłady
Wykład 7 Drgania sieci krystalicznej
MSI-program-stacjonarne-15h-2011, logistyka, semestr IV, sieci neuronowe w log (metody sztucznej int
Ontogeniczne sieci neuronowe skrypt(1)
04 wykład ped
Pytania egz AGiSN, SiMR - st. mgr, Alg. i Sieci Neuronowe
MSI-ściaga, SiMR - st. mgr, Alg. i Sieci Neuronowe
32 Sieci neuronowe
04 Wyklad SystemPlikowv2
Identyfikacja Procesów Technologicznych, Identyfikacja charakterystyki statycznej obiektu dynamiczne
więcej podobnych podstron