Projekt „Informatyka – inwestycją w przyszłość”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Biuro Projektu:

Politechnika Radomska im. Kazimierza Pułaskiego

26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. [phone]

www.zamawiane.pr.radom.pl; e-mail: [e-mail]

Zajęcia wyrównawcze z fizyki -Zestaw 8

dr M.Gzik-Szumiata

Oddziaływania elektrostatyczne. Siła elektrostatyczna, natężenie pola elektrostatycznego, zasada
superpozycji pól. Pole elektrostatyczne jednorodne i centralne. Potencjał elektrostatyczny. Ruch
ładunków w polu elektrostatycznym.

Zadanie 1. Cząsteczka soli kuchennej zbudowana jest z dodatniego jonu sodu i ujemnego jonu chloru.
W odległości równej 2,8·10

-10

m siła oddziaływania elektrostatycznego ma wartość 2,93·10

-9

N. W

odległości dwa razy większej jony te będą się przyciągały siłą, której wartość jest równa:

a) 2,93·10

-9

N,

b) 1,47·10

-9

N, c) 0,73·10

-9

N,

d) 0,37·10

-9

N.

Zadanie 2. Dwa ujemnie naładowane pyłki znajdujące się w odległości 10

-3

m od siebie odpychają się

siłą 2·10

-5

N. Ładunek elementarny ma wartość 1,6·10

-19

C. Oblicz, ile dodatkowych elektronów

znajduje się na każdym pyłku, jeżeli wartości ładunków zgromadzonych na obu pyłkach są
jednakowe.

Zadanie 3. W doświadczeniu Millikana w pionowym polu elektrycznym obserwowano ruch ujemnie
naładowanej kropelki oleju o masie 3,8·10

-9

kg. Kropelka pozostawała w spoczynku, gdy natężenie

pola elektrycznego miało wartość 5·10

3

V/m. Zakładamy, że ruch odbywał się w próżni.

1.Oblicz ładunek kropelki.
2.Z jaką wartością przyspieszenia poruszałaby się ta kropelka, gdyby jej ładunek ujemny zwiększono
dwukrotnie, nie zmieniając natężenia pola elektrycznego?

Zadanie 4. Na rysunku przedstawiono trzy małe, identyczne kulki metalowe o masie 10 g każda.
Jedna z nich zawieszono na jedwabnej nitce, a dwie pozostałe spoczywają na plastikowym stoliku
poniżej. Przed rozmieszczeniem kulek jedną z nich naelektryzowano, a
następnie wszystkie ze sobą zetknięto i rozmieszczono jak na rysunku.

a) Narysuj wektory wszystkich sił działających na wiszącą kulkę.

b) Oblicz wartość ładunku zgromadzonego na widzącej kulce, jeżeli

wiadomo, że siła, którą nic działa na kulkę ma wartość o 10%
mniejszą od wartości ciężaru kulki, a = 10 cm, g = 10 m/s

2

, k =

9·10

9

N·m

2

/C

2

.

Zadanie 5. W polu elektrycznym wytwarzanym przez dwa ładunki
różnoimienne przemieszczano mały ładunek elektryczny q wzdłuż linii
pola elektrostatycznego. Przy którym przemieszczeniu A, B czy C
wykonano największą pracę? Odpowiedź uzasadnij.


Zadanie 6. W trzech wierzchołkach kwadratu o boku a umieszczono
ładunki elektryczne, każdy o takiej samej wartości bezwzględnej q. Dwa z nich są ujemne, a trzeci
dodatki, przy czym ładunki jednoimienne nie znajdują się w sąsiednich wierzchołkach.

Projekt „Informatyka – inwestycją w przyszłość”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Biuro Projektu:

Politechnika Radomska im. Kazimierza Pułaskiego

26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. [phone]

www.zamawiane.pr.radom.pl; e-mail: [e-mail]

a)Wykorzystując zasadę superpozycji narysuj wektor natężenia pola
elektrostatycznego w czwartym, pustym wierzchołku kwadratu. Zachowaj
odpowiednie proporcje długości wektorów.
b)Oblicz wartość natężenia pola elektrostatycznego w czwartym, pustym
wierzchołku kwadratu.
c)Oblicz potencjał pola w czwartym, pustym wierzchołku kwadratu.
d)Oblicz pracę wykonaną przez siłę pola elektrostatycznego podczas przenoszenia ładunku dodatniego
o wartości 2q umieszczonego w czwartym wierzchołku kwadratu do jego środka.

Zadanie 7. Cztery ładunki elektrostatyczne zostały umieszczone w
narożnikach kwadratu o boku b w sposób następujący: ładunki
dodatnie o wartości Q umieszczono w górnych narożnikach a ładunki
ujemne o wartości 2Q w dolnych narożnikach kwadratu. Obliczyć siłę
wypadkową działającą na punktowy ładunek dodatni o wartości q
umieszczony w środku kwadratu i energię potencjalną , jaką posiada
ładunek elektryczny q w polu wytwarzanym przez pozostałe ładunki.

Zadanie 8. Cząstka α o początkowej energii kinetycznej 5,4·10

-13

J

ulega rozproszeniu na jadrze atomu złota

Au

197

79

. W najmniejszej

odległości od jadra cząstka α zachowała połowę swojej energii
kinetycznej. Zakładamy, że początkowa energia potencjalna cząstki
była równa zero.
1.Oblicz energię potencjalną tej cząstki w najmniejszej odległości od jadra atomu złota.
2.Oblicz, na jaką najmniejszą odległość zbliżyła się cząstka α do jądra atomu złota.

Zadanie 9. Elektron, o początkowej energii kinetycznej wynoszącej zero, w jednorodnym polu
elektrycznym w czasie 10

-8

s osiągnął prędkość 1,6·10

7

m/s. Oblicz wartość natężenia pola

elektrycznego przyspieszającego elektron.

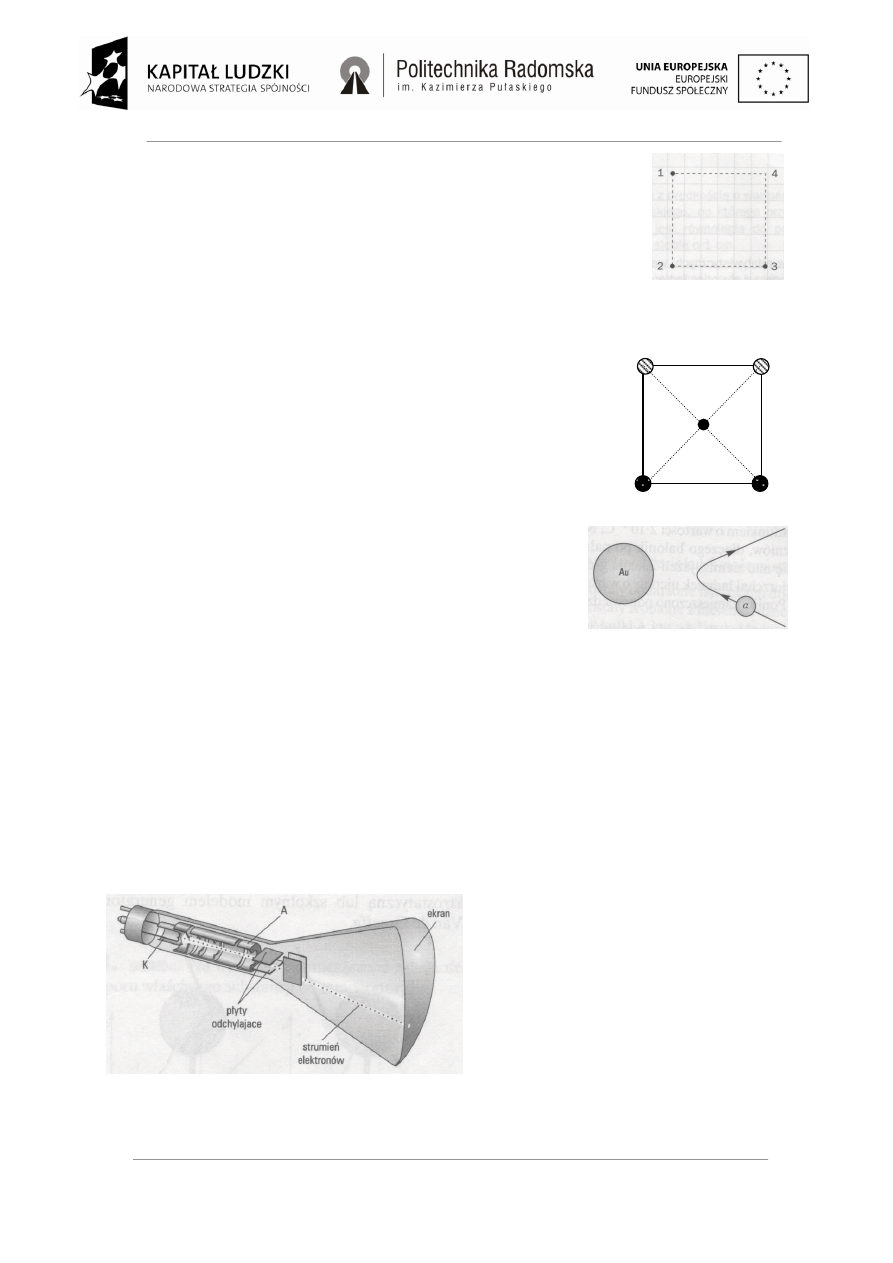
Zadanie 10.W lampie oscyloskopowej elektrony emitowane przez katodę K zostają przyspieszone w
polu elektrycznym pomiędzy katodą K i anodą A, następnie wpadają w obszar, gdzie istnieje pole
elektryczne o natężeniu E = 6·10

4

V/m wytworzone przez dwie kwadratowe poziome płyty tworzące

kondensator próżniowy. Płytki te są odległe od siebie o 1 cm, a ich bok ma długość 3 cm.

Wykaż, że dla elektronu wpadającego miedzy
płytki odchylające z prędkością 1,36·10

7

m/s,

prostopadłą do linii pola, odchylenie toru przy
wyjściu wynosić będzie około 60

o

.

+Q

+Q

-2Q

-2Q

+q