
dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
1
5. Rozkład funkcji zmiennej losowej
i dwuwymiarowe zmienne losowe
5.1. Rozkład funkcji zmiennej losowej
•
Mówimy, że
g
jest funkcją borelowską, jeśli dla każdego a∈ℝ zbiór
{
x : g ( x)<a
}
jest zbiorem borelowskim (elementem σ -ciała generowanego przez
zbiory otwarte).
•
W szczególności każda funkcja ciągła na pewnym przedziale jest w tym
przedziale funkcją borelowską.
•
Niech zmienna losowa Y będzie pewną funkcją zmiennej losowej X, tzn. dla każdego
ω∈Ω
mamy Y (ω)=g ( X (ω)) , gdzie
g
jest funkcją borelowską.
•
Znając rozkład prawdopodobieństwa zmiennej losowej X, możemy wyznaczyć
rozkład prawdopodobieństwa zmiennej losowej Y.
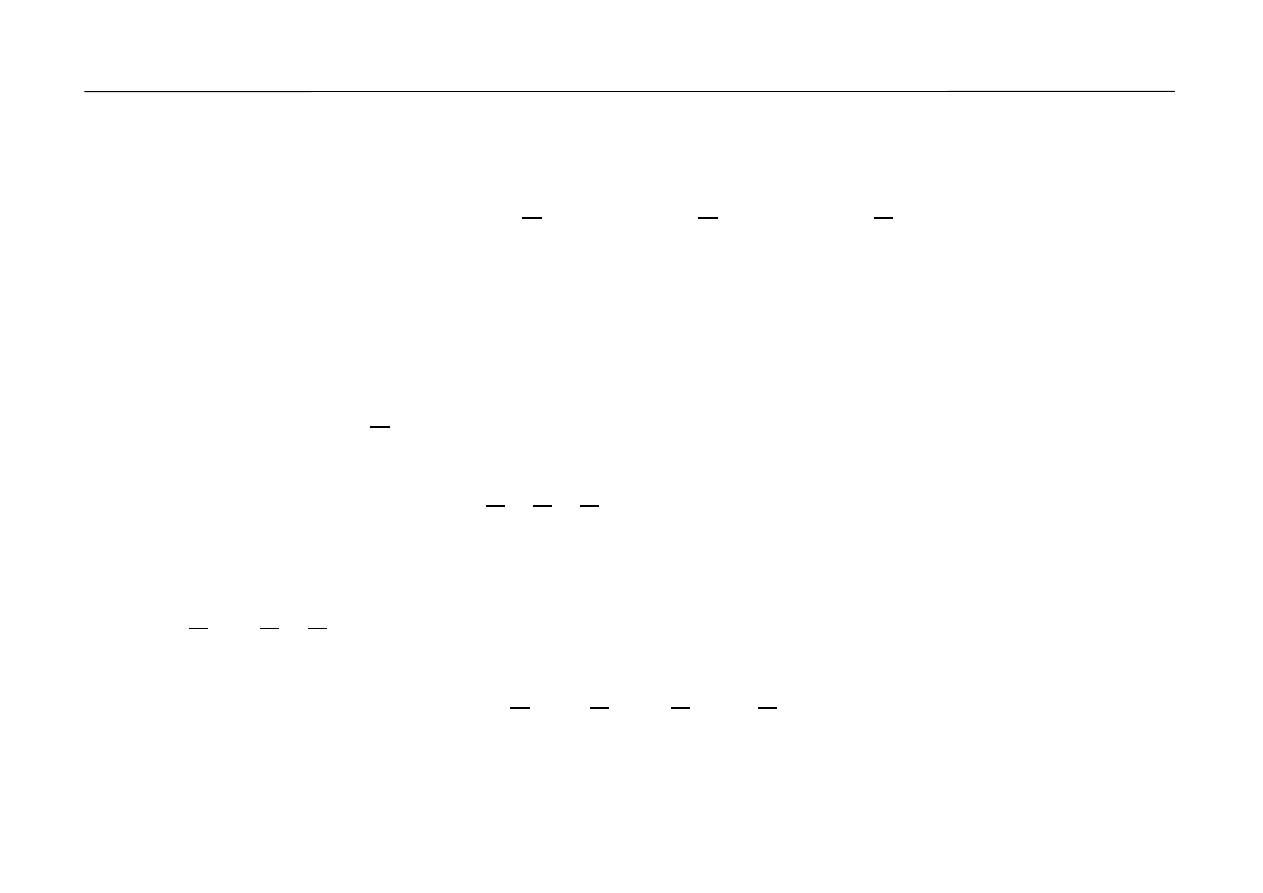
dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
2
Przykład 5.1.
Niech
Y = X
2
+
1,
gdzie X jest zmienną losową o rozkładzie
P( X =−1)=
1
4
, P ( X =0)=
1
4
, P ( X =1)=
1
2
.
Znaleźć rozkład zmiennej losowej Y i obliczyć EY.
Rozkład zmiennej losowej Y:
P(Y =1)=P ( X =0)=
1
4
,
P(Y =2)=P( X =−1∨ X =1)=
1
4
+
1
2
=
3
4
.
EY =1⋅
1
4
+
2⋅
3
4
=
7
4
lub
EY =E ( X
2
+
1)=EX
2
+
1=(−1)
2
⋅
1
4
+
0
2
⋅
1
4
+
1
2
⋅
1
2
+
1=
7
4
.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
3
Twierdzenie 5.1.
Jeżeli X jest zmienną losową ciągłą o gęstości f
X
skoncentrowanej na przedziale
(
a , b)
oraz
y=g ( x)
jest funkcją ściśle monotoniczną klasy
C
1
o pochodnej
g ' (x)≠0
w tym przedziale, przy czym x=h( y) jest funkcją odwrotną do funkcji
y=g ( x)
, to gęstość f
Y
zmiennej losowej ciągłej Y =g ( X ) wyraża się wzorem
f
Y
(
y )= f
X
(
h( y)
)
∣
h ' ( y)
∣
dla
y∈(c , d )
oraz f
Y
(
y )=0 dla pozostałych y,
gdzie c=min(c
1,
d
1
)
, d=max(c
1,
d
1
)
, c
1
=
lim
x → a
+
g ( x) , d
1
=
lim
x → b
-
g (x).
Przykład 5.2.
Niech X będzie zmienną losową typu ciągłego o gęstości
f
X
przyjmującą wartości
z przedziału
(−∞
,+∞).
Wyznaczyć gęstość zmiennej losowej
Y =aX +b , a≠0.
Funkcja liniowa
y=g ( x)=ax+b
spełnia założenia twierdzenia 5.1. (dla a > 0 funkcja
jest rosnąca, dla a < 0 funkcja jest malejąca).
Funkcja odwrotna x=h( y)=
1
a
(
y−b) , x ' =h' ( y)=
1
a
Zatem f
Y
(
y )= f
X
(
y−b
a
)
1
∣
a
∣
, y∈ℝ .
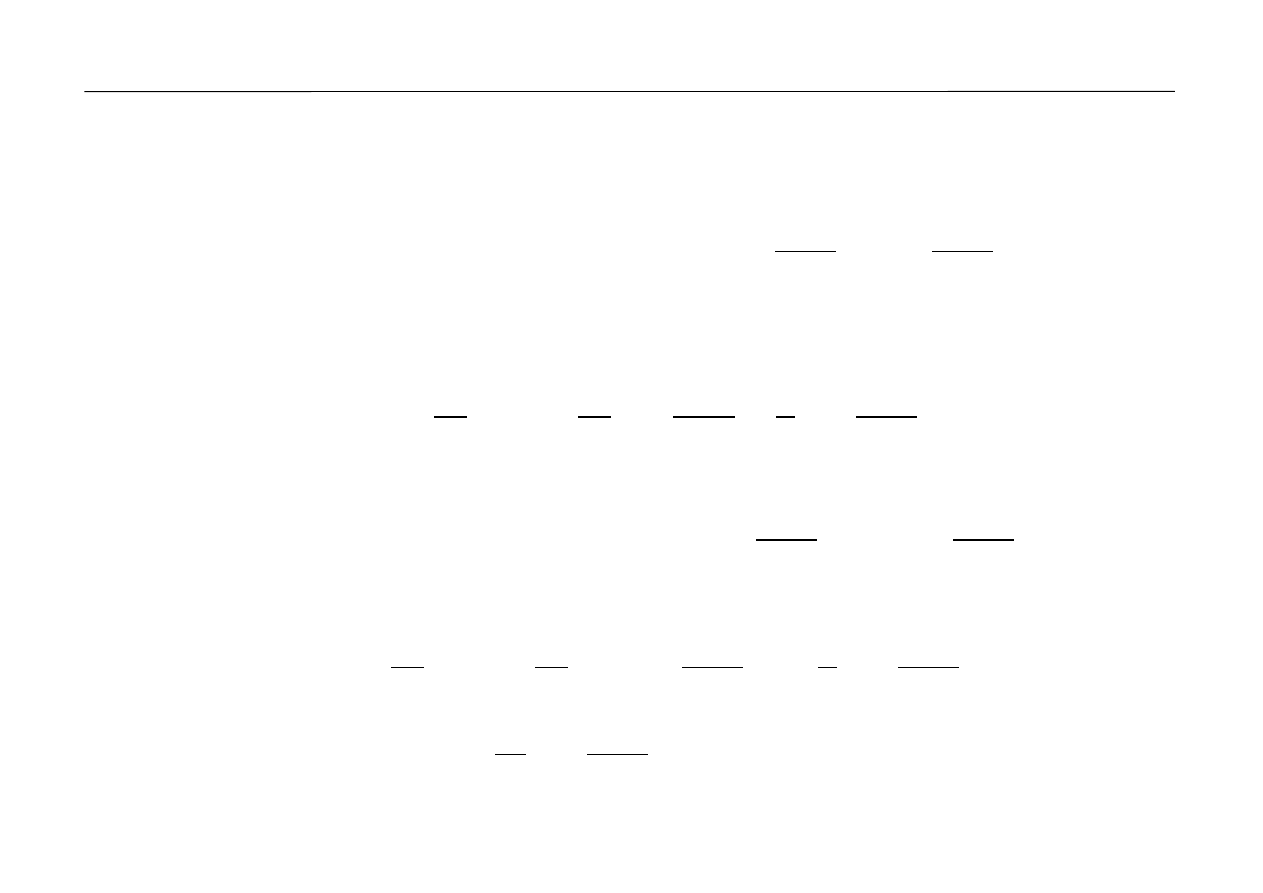
dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
4
Zauważmy, że wzór ten możemy także uzyskać w następujący sposób.
W przypadku a > 0 mamy
F
Y
(
y)=P(Y ≤ y)=P (aX +b≤ y)=P
(
X ≤
y−b
a
)
=
F
X
(
y−b
a
)
Ponieważ funkcja
F
X
jest różniczkowalna w punktach ciągłości f
X
, więc w tych
punktach
f
Y
(
y )=
d
dy
F
Y
(
y)=
d
dy
F
X
(
y−b
a
)
=
1
a
f
X
(
y−b
a
)
W przypadku a < 0 mamy
F
Y
(
y)=P (Y ≤y )=P (aX +b≤y)=P
(
X ≥
y−b
a
)
=
1−F
X
(
y−b
a
)
f
Y
(
y )=
d
dy
F
Y
(
y)=
d
dy
(
1−F
X
(
y−b
a
)
)
=−
1
a
f
X
(
y−b
a
)
Zatem otrzymujemy, że f
Y
(
y )=
1
∣
a
∣
f
X
(
y−b
a
)
.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
5
5.2. Dwuwymiarowe zmienne losowe
•
Niech (Ω ,
Α
, P) będzie przestrzenią probabilistyczną, w której jest określonych n
zmiennych losowych
X
1,
X
2,
, X
n
X
i
:Ω → R ,
i=1, 2, , n
.
•
Wówczas dla każdego ∈ możemy rozpatrywać układ
X = X
1
, X
2
,, X
n
•
Układ ten nazywamy wektorem losowym (n-wymiarowym).
•
Dystrybuantą wektora losowego
X = X
1,
X
2,
, X
n
nazywamy funkcję
F : R
n
R daną wzorem:
F x
1,
x
2,
, x
n
=
P
{
∈
: X
1
x
1
, X
2
x
2
,, X
n
x
n
}
.
•
Wektor losowy X = X
1,
X
2,
, X
n
nazywamy wektorem losowym o rozkładzie
dyskretnym jeśli przyjmuje skończoną bądź przeliczalną liczbę wartości.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
6
•
Wektor losowy X = X
1,
X
2,
, X
n
nazywamy wektorem losowym o rozkładzie
(absolutnie) ciągłym, jeśli istnieje nieujemna funkcja n zmiennych
f x
1
, x
2,
, x
n
taka, że
F x
1,
x
2,
, x
n
=
∫
−∞
x
1
∫
−∞
x
2
∫
−∞
x
n
f t
1
, t
2
,,t
n
dt
1
dt
2
dt
n
.
•
Niech X , Y będzie dwuwymiarową zmienną losową dyskretną (skokową),
czyli zmienne losowe X i Y mają skończony lub przeliczalny zbiór wartości.
•
Rozkładem łącznym dyskretnej zmiennej dwuwymiarowej X , Y nazywa się
zbiór prawdopodobieństw:
P X =x
i
,Y = y
j
=
p
ij
dla i=1, 2,…(r) , , j=1,2,…( s).
•
Prawdopodobieństwa
p
ij
spełniają warunek:
∑
i
∑
j
p
ij
=
1 .
•
Dystrybuantę dwuwymiarowej zmiennej losowej dyskretnej określa się wówczas
wzorem:
F x , y=P X x ,Y y=
∑
x
i
x
∑
y
j
y
p
ij
.
dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
7
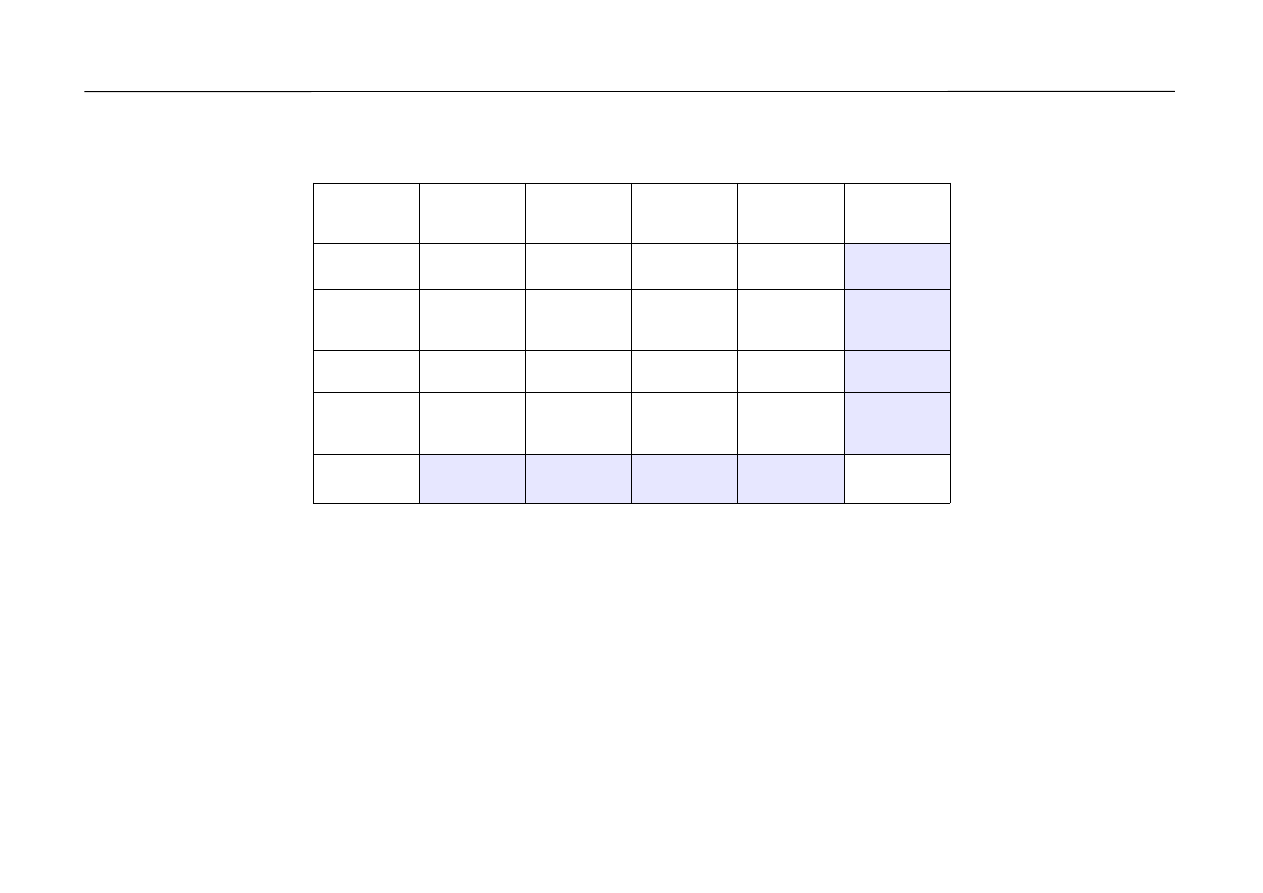
•
Rozkład dwuwymiarowej zmiennej losowej dyskretnej zwykle jest zapisywany
w postaci tablicy, nazywanej tablicą korelacyjną.
y
1
y
2
y
s
∑
x
1
p
11
p
12
p
1s
p
1⋅
x
2
p
21
p
22
p
2s
p
2⋅
⋮
⋮
⋮
⋮
⋮
⋮
x
r
p
r1
p
r2
p
rs
p
r⋅
∑
p
⋅
1
p
⋅
2
p
⋅
s
1
•
Rozkładem brzegowym dyskretnej zmiennej losowej X nazywamy rozkład
prawdopodobieństwa : P( X =x
i
)=
p
i⋅
=
∑
j=1
s
p
ij
, dla
i=1, 2,, r
.
•
Podobnie rozkładem brzegowym dyskretnej zmiennej losowej Y nazywamy rozkład
prawdopodobieństwa: P Y = y
j
=
p
⋅
j
=
∑
i=1
r
p
ij
dla j=1,2,, s .

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
8
•
Rozkładem warunkowym zmiennej losowej dyskretnej X pod warunkiem Y = y
j
,
j=1, 2,…, s , nazywamy rozkład prawdopodobieństwa:
P( X =x
i
∣
Y = y
j
)=
P( X =x
i
,Y = y
j
)
P (Y = y
j
)
=
p
ij
p
⋅
j
, dla
i=1, 2,… , r
.
•
Rozkładem warunkowym zmiennej losowej dyskretnej Y pod warunkiem X =x
i
,
i=1, 2,… , r , nazywamy rozkład prawdopodobieństwa:
P(Y = y
j
∣
X =x
i
)=
P( X =x
i
,Y = y
j
)
P ( X = x
i
)
=
p
ij
p
i⋅
, dla j=1,2,…, s .
•
Zmienne losowe dyskretne X i Y są niezależne jeżeli
P X =x
i
,Y = y
j
=
P X =x
i
⋅
P Y = y
j
, czyli p
ij
=
p
i⋅
⋅
p
⋅
j
,
dla wszystkich
i=1, 2,, r
,
j=1,2,, s
.
•
Jeżeli zmienne losowe X i Y są niezależne, to oczywiście
P X =x
i
∣
Y = y
j
=
P X =x
i
=
p
i⋅
, dla
i=1, 2,, r
.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
9
•
Niech teraz dwuwymiarowa zmienna losowa X , Y będzie zmienną losową
ciągłą.
•
Funkcja gęstości f x , y dwuwymiarowej zmiennej losowej ciągłej X , Y
łącznego rozkładu jest funkcją spełniającą warunki:
f x , y0 ,
∫
−∞
∞
∫
−∞
∞
f (x , y)dxdy=1 .
•
Dystrybuantą dwuwymiarowej zmiennej losowej ciągłej
X , Y
nazywamy
funkcję określoną za pomocą wzoru:
F x , y=P X x ,Y y =
∫
−∞
x
∫
−∞
y
f s ,t dsdt .
•
Rozkładami brzegowymi f
1
x , f
2
y ciągłych zmiennych losowych X i Y
nazywa się następujące funkcje: f
1
x=
∫
−∞
∞
f x , y dy , f
2
y=
∫
−∞
∞
f x , y dx .

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
10
•
Warunkowe funkcje gęstości zmiennych losowych ciągłych X i Y są określone
wzorami: f ( x
∣
y )=
f ( x , y)
f
2
(
y)
, dla f
2
(
y)>0
oraz f ( y
∣
x )=
f ( x , y)
f
1
(
x)
, dla f
1
(
x)>0 .
•
Zmienne losowe ciągłe X i Y są niezależne jeżeli:
f x , y= f
1
x⋅f
2
y , dla każdej pary liczb rzeczywistych x , y .
•
Oczywiście dla dowolnych niezależnych zmiennych losowych X i Y mamy:
F
X ,Y
x , y =P X x , Y y =P X x ⋅P Y y =F
X
x⋅F
Y
y
.
•
Momenty zwykłe dwuwymiarowej zmiennej losowej X , Y definiujemy
następująco:
α
rs
=
E ( X
r
Y
s
)
,
gdzie liczby
r , s∈ℕ.
•
Jeżeli
X , Y
jest zmienną losową dyskretną, to: α
rs
=
∑
i
∑
j
x
i
r
y
j
s
p
ij
.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
11
•
Jeżeli
X , Y
jest zmienną losową ciągłą o funkcji gęstości prawdopodobieństwa
f ( x , y) , to α
rs
=
∫
−∞
∞
∫
−∞
∞
x
r
y
s
f ( x , y)dxdy .
•
Najczęściej wykorzystuje się momenty zwykłe rzędu pierwszego
(α
10
=
E ( X
1
Y
0
)=
EX ,α
01
=
E ( X
0
Y
1
)=
EY )
oraz momenty zwykłe rzędu drugiego
(α
20
=
E ( X
2
Y
0
)=
EX
2
,α
11
=
E ( X
1
Y
1
)=
E ( XY ) , α
02
=
E ( X
0
Y
2
)=
EY
2
)
•
Momenty centralne definiujemy w następujący sposób:
μ
rs
=
E( X −EX )
r
(
Y −EY )
s
.
•
W szczególności μ
20
=
E ( X −EX )
2
=
D
2
X ,μ
02
=
E (Y −EY )
2
=
D
2
Y.
•
Kowariancja zmiennych losowych X , Y jest określona za pomocą wzoru:
Cov ( X , Y )=μ
11
=
E
(
(
X −EX )(Y −EY )
)
=
E ( XY )−EX⋅EY
.
•
Zauważmy, ze dla niezależnych zmiennych losowych X i Y kowariancja wynosi 0.

dr Tomasz Walczyński –
Statystyka (I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 5. (19.03.2014 r.)
12
•
Ponadto Cov X , X =VarX ,
Var X Y =VarX VarY 2Cov X , Y
.
•
Współczynnik korelacji liniowej między zmiennymi X i Y jest określony wzorem:
ρ=ρ(
X , Y )=
Cov ( X , Y )
σ
X σ Y
.
•
Zachodzi nierówność: −1 X , Y 1
•
Współczynnik korelacji mierzy „siłę” zależności liniowej między zmiennymi
losowymi X i Y.
•
Jeżeli ρ( X ,Y )=0, czyli gdy
Cov ( X ,Y )=0,
to zmienne losowe X i Y nazywamy
nieskorelowanymi.
•
Oczywiście zmienne losowe niezależne są nieskorelowane (nie są skorelowane).
•
Jeżeli ρ( X ,Y )=1, to zmienne losowe X i Y związane są funkcyjnie, a zależność
między nimi ma charakter liniowej funkcji rosnącej.
•
Jeżeli ρ( X ,Y )=−1, to zmienne losowe X i Y związane są funkcyjnie, a zależność
między nimi ma charakter liniowej funkcji malejącej.
•
Jeżeli 0<
∣
ρ(
X ,Y )
∣
<
1, to istnieje współzależność między zmiennymi losowymi
X i Y, ale nie ma ona charakteru funkcyjnego. Im współzależność ta jest silniejsza,
tym ρ( X ,Y ) bardziej odbiega od zera.
Wyszukiwarka
Podobne podstrony:
05 Wyklad 5. Rozkład funkcji zmiennej losowej i dwuwymiarowe zmienn e losowe
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
rachunek prawdopodobieństwa, rachl5, Rozkłady, funkcje, parametry zmiennych losowych jedno i dwuwymi
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Zadania
C Wyklady Wskazniki Do Funkcji I Zmienna Dlugosc List Argumentow
Konspekt wykładu r różniczkowy funkcji jednej zmiennej(1)
Matematyka III (Ćw) Lista 05 Rachunek rózniczkowy funkcji wielu zmiennych Odpowiedzi
6 funkcje zmiennej zespolonej, holomorficzność
Analiza matematyczna Wykłady, GRANICE FUNKCJI
wyklad Mes funkcje ksztaltu, Budownictwo, Semestr V, Budownictwo komunikacyjne 1, most5
M.Walczak - wyklad 4 - rachunek kosztów zmiennych a rachunek kosztów pełnych, Zarządzanie, rachunkow
Zadania dr Marty Kuc, zadania2, Poniżej mamy podany skumulowany rozkład częstości zmiennej Z do dane
FUNKCJA WYKŁADNICZA I LOGARYTMICZNA, FUNKCJA WYKŁADNICZA I LOGARYTMICZNA
Rozkład funkcji wymiernej na ułamki proste
M.Walczak - wyklad 5 - rachunek kosztów zmiennych a rachunek kosztów pełnych ciąg dalszy, Zarządzani
06 funkcje zmiennej rzeczywistej 3 1 funkcje elementarne
więcej podobnych podstron