Rozkłady, funkcje, parametry zmiennych losowych jedno i dwuwymiarowych

Zadanie 1.

Gęstością prawdopodobieństwa dwuwymiarowej zmiennej losowej (X, Y) jest

e -
[x² +
].

Obliczyć prawdopodobieństwo p tego, że zmienna (X, Y) przyjmuje wartość z obszaru określonego nierównością x ≥ y, x ≥ 0 i y ≥ 0.

Zadanie 2.

Wiemy, że dla wektora losowego (X, Y) gęstość prawdopodobieństwa

f(x, y) =
e [-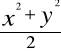
].

Znaleźć prawdopodobieństwo tego, że ta zmienna przyjmuje wartość z wnętrza obszaru o wierzchołkach (-2, 0), (2, 0), (0, -2), (0, 2).

Zadanie 3.

Zmienne losowe X₁ i X₂ są niezależne i mają jednakowe rozkłady normalne N(0, 1). Wykazać, że zmienne losowe Y₁ = X₁ + X₂ i Y₂ = X₁ - X₂ są niezależne.

Zadanie 4.^(*)

Zmienne X i Y mają rozkłady normalne: N(m_x, ∂_x), N(m_y, ∂_y). U = X + Y, V = X - Y. Kiedy U i V są niezależne?

Zadanie 5.

Zmienne losowe X i Y są niezależne i mają rozkłady normalne odpowiednio N(1, 2) i N(-1, 2). Znaleźć E(Z) i D²(Z), jeśli Z = 2X - 3Y.

Zadanie 6.

Dwuwymiarowa zmienna losowa (X, Y) ma gęstość prawdopodobieństwa określoną wzorem

f(x, y) =
exp [^-
(
+
) ].

Znaleźć wartość oczekiwaną i wariancje odległości R punktu (X, Y) od punktu (0, 0) układu współrzędnych.

Zadanie 7.

Odbywa się strzelanie do celu, którym jest położony na płaszczyźnie x 0 y punkt P (0, 0). Współrzędne (X, Y) punktu, w który pada strzał, są dwuwymiarową zmienną losową o gęstości

(*) zadanie nieobowiązujące

f(x, y) =
exp [^-
(
+
) ].

Zmienna losowa Z jest funkcją X i Y o postaci

Z = 2 X - 3 Y.

Znaleźć E(Z) i D²(Z).

Zadanie 8.

Dwuwymiarowa zmienna losowa (X, Y) ma własności: E(X) = 0, E(Y) = 1, D²(X) = 2, D²(Y) = 1, a współczynnik korelacji ρ = 1/
. Znaleźć E (Z ) i D² (Z) dla Z = 2 X - 3 Y.

Zadanie 9.

Kiedy dla wektora losowego (X, Y):

a). D² (X + Y) = D² (X) + D² (Y)?

b). D² (X - Y) = D² (X) + D² (Y)?

Zadanie 10.

Wektor losowy (X, Y) ma rozkład jednostajny w kole o promieniu r i środku w początku układu współrzędnych. Znaleźć wartość oczekiwaną i wariancję odległości R punktu losowego (X, Y) od punktu P (0, 0).

Zadanie 11. ^(*)

Zmienna losowa X ma rozkład gamma o p₁ = 2, b₁ = 3, zmienna losowa Y ma również rozkład gamma o p₂ = 2 i b₂ = 6. Dobrać tak współczynniki A i B, by gęstość zmiennej Z miała rozkład gamma, gdy zmienna Z jest funkcją liniową postaci

Z = A ∗ X + B ∗ Y.

Zadanie 12.

Zmienna losowa X ma rozkład normalny N (4, 2), zmienna losowa Y ma rozkład Bernoulliego, gdzie liczba wykonanych niezależnie doświadczeń wyniosła n = 10 o prawdopodobieństwie sukcesu p = 0,05. Obie zmienne realizują swoje wartości niezależnie. Obliczyć E(Z) i D²(Z), gdy Z = 2 X - 3 Y.

Zadanie 13.

Zmienne losowe wektora (X, Y) są niezależne i obie mają rozkład normalny N (0, 1). U = X + Y, a V = X - Y. Pokazać, że wektor losowy (U, V) składa się ze zmiennych losowych U i V niezależnych.

Zadanie 14.

Wiemy, że współczynnik korelacji ρ (X, Y) = 0,5. Zmienna losowa Z = 3 Y - 1. Obliczyć ρ (X, Z).

Zadanie 15.

P(X = -1) = P(X = 0) = P(X = 1) =

Y = X². Obliczyć kowariancję zmiennych losowych X i Y.

Zadanie 16.

Zmienna losowa X podlega rozkładowi Poissona, tzn.

P (X = k) = e ^{- λ} ∗
,

gdzie k = 0, 1, 2, … i λ > 0. Obliczyć E(X) tej zmiennej losowej X.

Zadanie 17.

Zmienna losowa X podlega rozkładowi:

P (X = k) =

k = 1, 2, 3, …

Obliczyć E(X).

Zadanie 18.

Obliczyć wartość przeciętną i wariancję zmiennej losowej X standaryzowanej, gdy X ma dowolny rozkład o E(X) < ∞ i 0 < D²(X) < ∞.

Zadanie 19.

Rzucamy dwiema kostkami do gry. Niech X będzie zmienną losową przyjmującą wartości równe liczbie oczek na pierwszej kostce, Y - liczbą oczek na drugiej kostce. Niech dalej U = X + Y, V = X - Y. Wykazać, że zmienne losowe U i V są nieskorelowane.

Wskazówka. Dla wykazania zależności zmiennych U i V wziąć np. U = 2, V = 2.

Zadanie 20.

Wiemy, że zmienna losowa X ma skończoną wariancję, Y - również. Z = a X ± b Y. Obliczyć D²(Z).

2

---