
POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ ELEKTRYCZNY
___________________________________________________________
Laboratorium M iernictwa Elektrycznego
Graficzna prezentacja wyników pomiarów
Instrukcja do
ć
wiczenia
Nr 15
Opracował dr in
ż
. R. Piotrowski
___________________________________________________
Białystok 1999

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
2
1. Wprowadzenie
raficzna forma wyników pomiaru, znana najcz
ęś
ciej jako tzw. wykres,
posiada istotne zalety, dla których jest powszechnie stosowana. Tak
wi
ę
c pozwala ona szybko oceni
ć
charakter badanego zjawiska, układu,
elementu elektrycznego, itp. Pod tym wzgl
ę
dem jest wprost niezast
ą
piona.
Umo
ż
liwia dalej łatwe wychwycenie punktów szczególnych charakterystyki, tzn.
punktów zerowych, ekstremalnych, itp.
Wa
ż
ne znaczenie ma równie
ż
fakt, i
ż
dysponuj
ą
c sko
ń
czon
ą
liczb
ą
wyników pomiaru, mo
ż
na przez sporz
ą
dzenie wykresu uzyska
ć
informacje
o charakterystyce obiektu dla dowolnego jej punktu z okre
ś
lonego przedziału.
Charakteryzowanie wła
ś
ciwo
ś
ci obiektów przy pomocy ró
ż
norodnych
form graficznych stosowane jest w nauce i technice powszechnie. Nale
ż
y przy
tym podkre
ś
li
ć
,
ż
e spotykane w dokumentacjach, katalogach i innych
opracowaniach wykresy, maj
ą
znaczenie nie tylko pogl
ą
dowe. Bardzo cz
ę
sto
bowiem s
ą
wykorzystywane w praktyce projektowej, eksploatacyjnej, a tak
ż
e
w badaniach naukowych jako
ź
ródła
ś
cisłych informacji o wła
ś
ciwo
ś
ciach
obiektów.
Studenci powinni to sobie u
ś
wiadomi
ć
by nie traktowa
ć
sporz
ą
dzanych
przez siebie wykresów jako czego
ś
drugorz
ę
dnego wobec pomiaru, lub co
gorsza, jako oderwanej od laboratoryjnej rzeczywisto
ś
ci pracy artystycznej, co
niestety zdarza si
ę
nad wyraz cz
ę
sto.
Budowa układu współrz
ę
dnych prostok
ą
tnych
Przewa
ż
aj
ą
ca wi
ę
kszo
ść
wielko
ś
ci fizycznych ma charakter ci
ą
gły, a ich
obrazem graficznym jest linia ci
ą
gła wyst
ę
puj
ą
ca w układzie współrz
ę
dnych
prostok
ą
tnych.
Układ taki tworz
ą
dwie osie liczbowe wzajemnie do siebie prostopadłe,
o wspólnym punkcie pocz
ą
tkowym.
O
ś
liczbowa jest obrazem graficznym uporz
ą
dkowanego zbioru
liczbowego
z
okre
ś
lonego
przedziału.
Ka
ż
demu
punktowi
prostej
przyporz
ą
dkowana jest tu jedna i tylko jedna liczba. Wobec tego ka
ż
dej liczbie
odpowiada jedna i tylko jedna długo
ść
odcinka prostej, b
ę
d
ą
ca odległo
ś
ci
ą
danego punktu od punktu zerowego (pocz
ą
tkowego) osi. Okre
ś
lanie długo
ś
ci
G

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
3
odcinków odwzorowuj
ą
cych poszczególne liczby danego zbioru odbywa si
ę
w wi
ę
kszo
ś
ci wypadków według nast
ę
puj
ą
cej formuły.
l
a x
l
b y
x
y
= ⋅
= ⋅
(1)
gdzie:
x y
, - liczby ze zbiorów
X Y
,
l l
x
y
, - długo
ś
ci odcinków odpowiadaj
ą
ce liczbom x, y odpowiednio na
osi poziomej (odci
ę
tych) oraz pionowej (rz
ę
dnych)
a b
,
- współczynniki proporcjonalno
ś
ci, wyra
ż
aj
ą
ce długo
ś
ci odcinków
jednostkowych na ka
ż
dej z osi
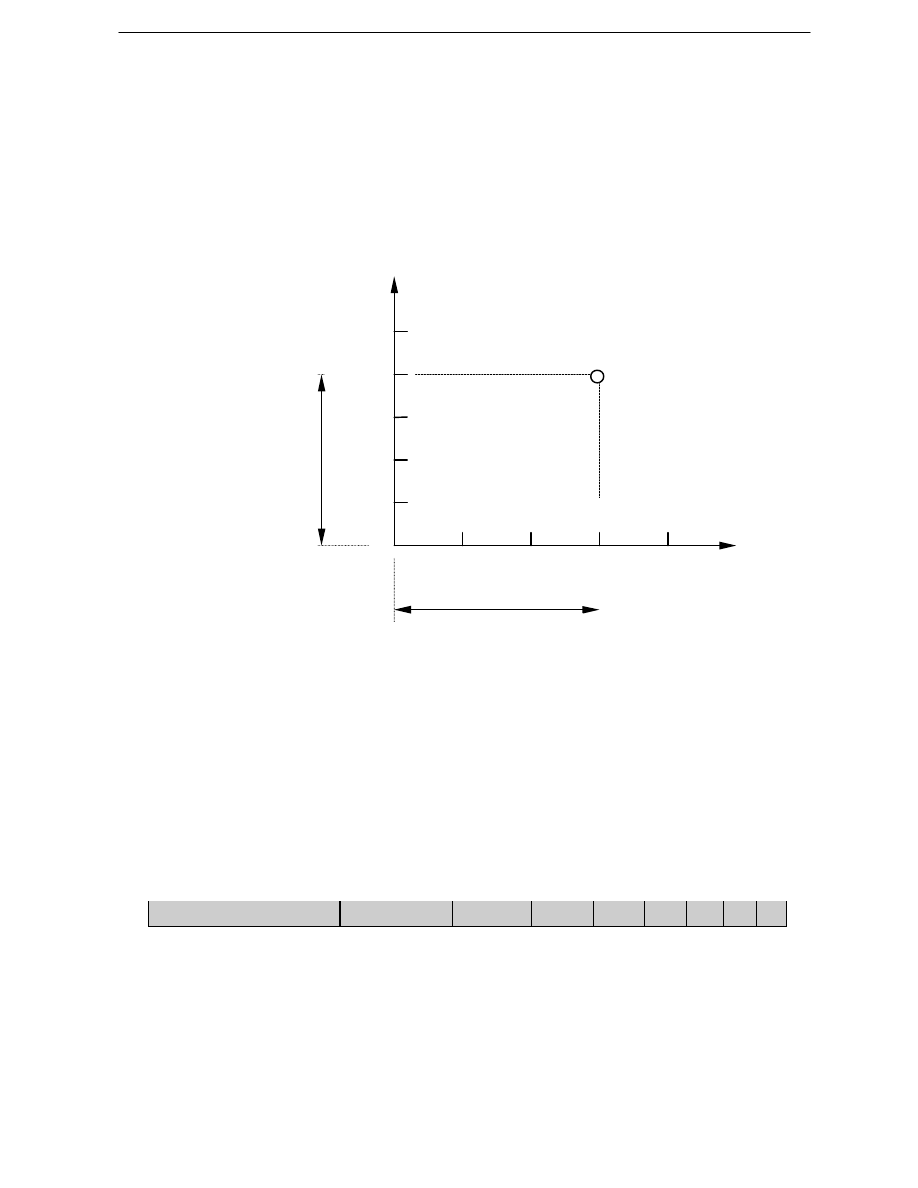
Zasady wyło
ż
one wy
ż
ej ilustruje rys.1.
x
y
5
4
3
2
1
4
3
2
1
0
P(3,4)
x = 3
y = 4
l
y
= 4 cm
(b= 1cm)
l
x
= 6 cm (a = 2cm)
Rys.1. Zasada tworzenia układu współrz
ę
dnych prostok
ą
tnych
Tworzenie układu współrz
ę
dnych prostok
ą
tnych polega wi
ę
c na obliczaniu
długo
ś
ci stosowanych odcinków prostej, a nast
ę
pnie przez ich odkładanie od
punktu zerowego ka
ż
dej osi znajdowanie interesuj
ą
cych nas punktów tej osi.
Jest oczywiste,
ż
e tak znalezione punkty opisuje si
ę
liczbami
przedstawianymi graficznie a nie długo
ś
ciami odcinków (rys.1).

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
4
Papier milimetrowy
Do sporz
ą
dzania układu współrz
ę
dnych prostok
ą
tnych bardzo przydatny
jest tzw. papier milimetrowy. Zawiera on g
ę
st
ą
siatk
ę
utworzon
ą
przez dwie
rodziny prostych równoległych, wzajemnie do siebie prostopadłych. Linie
prowadzone s
ą
w odst
ę
pach milimetrowych, a co pi
ą
ta i co dziesi
ą
ta z nich jest
wyró
ż
niona wi
ę
ksz
ą
grubo
ś
ci
ą
.
Podziałka logarytmiczna
Podziałka logarytmiczna znajduje zastosowanie w przypadkach, gdy
przedział zmienno
ś
ci wielko
ś
ci x, y jest bardzo szeroki (rys.2). Gdyby w takich
razach konstruowa
ć
podziałk
ę
według formuły (1), tzn. liniow
ą
, punkty
odpowiadaj
ą
ce małym liczbom byłyby trudne do zidentyfikowania na osi. Na
przykład punkt odpowiadaj
ą
cy liczbie 10 musiałby le
ż
e
ć
1000 razy bli
ż
ej
pocz
ą
tku układu współrz
ę
dnych ni
ż
punkt odpowiadaj
ą
cy liczbie 10 000. Je
ś
li
wi
ę
c liczbie 10 000 przyporz
ą
dkowaliby
ś
my odcinek długo
ś
ci 15 cm, to liczbie
10 odpowiada
ć
musiałby odcinek 0,015 cm, czyli tylko nieco dłu
ż
szy od 0,1 mm.
Podziałk
ę
logarytmiczn
ą
tworzy si
ę
przez przyporz
ą
dkowanie liczbom
odcinków prostej według formuły (2).
l
x
= a
∗
log x
(2)
l
y
= b
∗
log y
gdzie:
x y
, - liczby ze zbiorów
X Y
,
l l
x
y
, - długo
ś
ci odcinków odpowiadaj
ą
ce logarytmom liczb x, y
odpowiednio na osi poziomej (odci
ę
tych) oraz pionowej
(rz
ę
dnych)
a b
,
- współczynniki proporcjonalno
ś
ci, wyra
ż
aj
ą
ce długo
ś
ci odcinków
jednostkowych na ka
ż
dej z osi
Podobnie jak poprzednio, równie
ż
tym przypadku wyznaczone na osi
punkty opisuje si
ę
przedstawianymi graficznie liczbami. Zasad
ę
takiego
odwzorowywania liczb na osiach układu współrz
ę
dnych prostok
ą
tnych ilustruje
rys.2.
Zauwa
ż
my,
ż
e na osiach liczbowych nie znajduj
ą
swego obrazu liczby
z przedziału 0
≤
x <1. Logarytm zera równy jest -
∞
, za
ś
liczbom ułamkowym
odpowiadaj
ą
ujemne warto
ś
ci logarytmów. Liczb ułamkowych nie odwzorowuje
si
ę
w tym przypadku, to znaczy w przypadku gdy operuje si
ę
warto
ś
ciami bardzo
du
ż
ymi, dla których podziałka logarytmiczna została stworzona.
Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
5
Wobec tego za punkt pocz
ą
tkowy ka
ż
dej z osi, a wi
ę
c i układu
współrz
ę
dnych przyjmuje si
ę
punkt odpowiadaj
ą
cy liczbie 1 (log1 = 0).
Konstruowanie podziałki logarytmicznej jest do
ś ć
ż
mudne, gdy konieczne
staje si
ę
wyznaczenie na osiach liczb innych ni
ż
10, 100, 1000 itp. Dlatego
najcz
ę ś
ciej korzysta si
ę
z gotowego papieru logarytmicznego. Na papierze takim
na obydwu osiach naniesione s
ą
punkty wg formuły (2) dodatkowo prowadzone
proste prostopadłe, tworz
ą
ce g
ę
st
ą
nieregularn
ą
siatk
ę
.
x
y
100000
1000
100
10
10000
1000
100
10
1
P(10
3
,10
4
)
x = 10
3
y = 10
4
l
y
= b
∗
log(10
4
)=
= 4 cm
(b= 1cm
)
l
x
= a
∗
log(10
3
)= 6cm
(a= 2 cm)
10000
Rys.2. Zasada konstruowania podziałek logarytmicznych na osiach układu
współrz
ę
dnych prostok
ą
tnych.
Na rys.3 przedstawiono układ punktów podstawowej sekwencji (1,10)
podziałki logarytmicznej. Odległo
ś
ci mi
ę
dzy punktami w pozostałych
sekwencjach (rys. 4) s
ą
identyczne, lecz opisywane liczbami 10, 100, 1000 razy
wi
ę
kszymi. Jest to zrozumiałe, bowiem
log c - log d = log 10c - log 10d
1 2 3 4 5 6 7 8 9
10
Rys. 3. Rozmieszczenie punktów podstawowej sekcji podziałki logarytmicznej
Tablica 1 zawiera warto
ś
ci logarytmów liczb z przedziału (1, 10) i ma na
celu ułatwienie
ć
wicz
ą
cym sporz
ą
dzanie własnych podziałek logarytmicznych.

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
6
Poniewa
ż
opisywanie punktów du
ż
ymi liczbami prowadziłoby do
pogorszenia czytelno
ś
ci opisu, w ka
ż
dej sekwencji stosowany jest opis przy
u
ż
yciu liczb z przedziału (1,10). Ilustruje to rys. 4. W ka
ż
dym kolejnym
przedziale liczbom tym nale
ż
y przypisywa
ć
warto
ś
ci dziesi
ę
ciokrotnie wi
ę
ksze
ni
ż
w przedziale poprzednim.
Punktem pocz
ą
tkowym osi niekoniecznie musi by
ć
liczba 1. Ka
ż
da z osi
mo
ż
e zaczyna
ć
si
ę
liczb
ą
10, 100. itd., w zale
ż
no
ś
ci od konkretnych potrzeb.
Tablica 1
log 1 = 0,0000
log 2 = 0,3010
log 3 = 0,4771
log 4 = 0,6021
log 5 = 0,6990
log 6 = 0,7782
log 7 = 0,8451
log 8 = 0,9031
log 9 = 0,9542
log 10 = 1,0000
W u
ż
yciu jest tak
ż
e tzw. papier półlogarytmiczny, na którym na jednej osi
(zwykle osi rz
ę
dnych) naniesiona jest podziałka liniowa, na drugiej za
ś
logarytmiczna Papier taki stosowany jest w przypadkach, gdy tylko jedna ze
zmiennych funkcji y = f(x) przybiera warto
ś
ci z bardzo szerokiego przedziału.
Samodzielne sporz
ą
dzanie podziałki logarytmicznej
Przyst
ę
puj
ą
c do sporz
ą
dzania podziałki logarytmicznej, nale
ż
y zna
ć
najwi
ę
ksz
ą
warto
ś ć
wielko
ś
ci, która ma by
ć
odwzorowana na osi. Na tej
podstawie okre
ś
li
ć
mo
ż
na potrzebn
ą
liczb
ę
n sekwencji podziałki (patrz rys.4),
zgodnie z warunkiem
X
max
≤
10
n
sk
ą
d
log X
max
≤
n
(3)
gdzie n - liczba naturalna
Najlepiej przy tym zaokr
ą
gli
ć
liczb
ę
X
max
do całkowitej pot
ę
gi dziesi
ę
ciu,
a nast
ę
pnie obliczy
ć
zgodnie z (3) liczb
ę
sekwencji podziałki.
Je
ż
eli np. X
max
= 86 000 Hz, to zaokr
ą
glaj
ą
c t
ę
warto
ś ć
do 100 000 Hz,
otrzymujemy zgodnie z (3) n = 5.

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
7
1 2 3 4 5 6 7 8 10
2 3 4 5 6 7 8 10
2
2 3 4 5 6 7 8 10
3
sekwencja I
sekwencja II
sekwencja III
Rys. 4. Przykład opisu osi zawieraj
ą
cej trzy sekwencje podziałki logarytmicznej
Nie zawsze jednak tak du
ż
a liczba sekwencji jest potrzebna. Je
ś
li na osi
nie musz
ą
by
ć
odwzorowywane np. pojedyncze herce, to wystarczy przyj
ąć
n = 4, a gdy dodatkowo nie musz
ą
by
ć
tak
ż
e zaznaczane dziesi
ą
tki herców,
wtedy n = 3. Kwestia ta zostanie wyja
ś
niona bli
ż
ej w dalszej cz
ę ś
ci instrukcji.
Po ustaleniu liczby n, nale
ż
y zorientowa
ć
si
ę
, jaka długo
ś ć
na osi mo
ż
e by
ć
przeznaczona na jedn
ą
sekwencj
ę
. Zale
ż
y to od formatu posiadanego arkusza
papieru.
Niech długo
ś ć
odpowiadaj
ą
ca jednej sekwencji wynosi L, wtedy długo
ś
ci
odpowiadaj
ą
ce liczbom z przedziału (1, 10) okre
ś
lone s
ą
zale
ż
no
ś
ci
ą
,
l
x
= L log x
(4)
Sporz
ą
dzaj
ą
c samodzielnie podziałk
ę
logarytmiczn
ą
, mo
ż
emy nanie
ś ć
na
osi te punkty, które s
ą
nam potrzebne do sporz
ą
dzenia wykresu, ale oprócz tego
powinni
ś
my tak
ż
e oznaczy
ć
te punkty „standardowe”, tzn. spotykane na
produkowanym fabrycznie papierze logarytmicznym.
Odległo
ś
ci l
x
obliczone i naniesione dla pierwszej sekwencji, mog
ą
by
ć
przeniesione cyrklem lub specjalnym przeno
ś
nikiem na pozostałe sekwencje osi,
jak wiadomo bowiem, układ punktów dla ka
ż
dej sekwencji jest taki sam.
Formuła (4) pozwala tak
ż
e znale
ź ć
na papierze fabrycznym te punkty,
które nie s
ą
oznaczone. Nale
ż
y w tym celu zmierzy
ć
długo
ś ć
L pojedynczej
sekwencji.
Szczegółowe zasady sporz
ą
dzania wykresów
Niech dane b
ę
d
ą
dwa zbiory wyników pomiaru wielko
ś
ci y, x, o których
wiadomo,
ż
e istnieje mi
ę
dzy nimi zwi
ą
zek y = f(x). Nale
ż
y na podstawie tej
ograniczonej liczby danych pomiarowych wykre
ś
li
ć
lini
ę
ci
ą
gł
ą
, która
stanowiłaby obraz graficzny funkcji y = f(x). Zadanie to nale
ż
y wykona
ć
według
nast
ę
puj
ą
cych zasad.

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
8
1. Dokona
ć
analizy otrzymanych z pomiaru wyników i zdecydowa
ć
o wyborze
potrzebnego papieru (milimetrowego, logarytmicznego, czy półlogaryt-
micznego).
2. Zarysowa
ć
lekko ołówkiem na posiadanym arkuszu papieru ramy wykresu,
pami
ę
taj
ą
c o konieczno
ś
ci pozostawienia z jego lewej strony marginesu
o szeroko
ś
ci 3 cm., z prawej za
ś
- ok. 1,5 cm, jak te
ż
pozostawieniu wolnego
miejsca u góry (tytuł) i u dołu wykresu (podpisy, obja
ś
nienia). Mo
ż
na np.
zaplanowa
ć
wykres na planie kwadratu, albowiem wskazane jest aby obie osie
układu współrz
ę
dnych miały zbli
ż
one do siebie długo
ś
ci. Okre
ś
lanie obydwu
współrz
ę
dnych punktów wykresu jest wtedy obarczone jednakowymi bł
ę
dami
wzgl
ę
dnymi.
3. Narysowa
ć
obydwie osie układu i oznaczy
ć
na nich tak
ą
ilo
ś ć
punktów równo
od siebie odległych, jaka si
ę
zmie
ś
ci. Je
ż
eli posługujemy si
ę
papierem
milimetrowym, to niezale
ż
nie od jego formatu, poleca si
ę
oznaczenie punktów
co 5 , 10 lub 20 mm. Mniej korzystne s
ą
odległo
ś
ci 15 mm, ze wzgl
ę
du na
pó
ź
niejsze trudno
ś
ci przy interpolowaniu (nieprzyjemne dzielenie przez 15).
Wybrane punkty oznaczamy krótkimi (2mm), prostopadłymi od osi kreskami
skierowanymi ku wn
ę
trzu układu współrz
ę
dnych.
4. Opisa
ć
liczbami oznaczone punkty osi. Zadanie to wymaga wyczucia
i do
ś
wiadczenia. Mo
ż
na poleci
ć
tu nast
ę
puj
ą
ce zasady:
a) nie wszystkie oznaczone punkty osi musz
ą
by
ć
wykorzystane.
b) nie wszystkie punkty oznaczone na osi musz
ą
by
ć
opisane liczbami, mo
ż
na np.
opisa
ć
co drugi oznaczony punkt, unikaj
ą
c w ten sposób nadmiernego
zag
ę
szczenia liczb.
c) opis powinien zapewnia
ć
łatwo
ś ć
interpolacji, tzn. okre
ś
lania liczb dla
punktów poło
ż
onych mi
ę
dzy dwoma s
ą
siednimi punktami opisanymi.
d) warto
ś ć
ostatniego opisanego punktu powinna nieznacznie przekracza
ć
maksymalny wynik pomiaru.
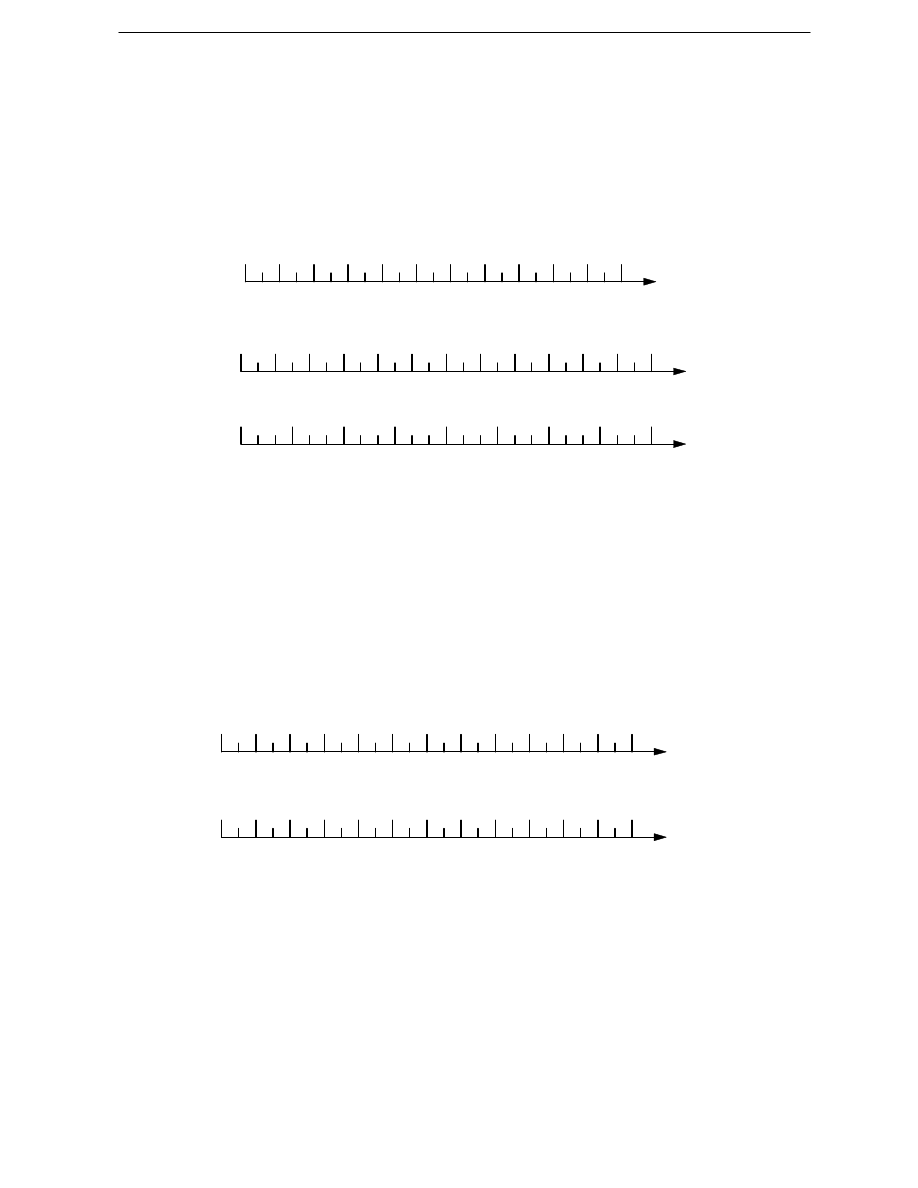
Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
9
Przykład 1
Je
ż
eli przy zdejmowaniu pewnej charakterystyki, zmieniano napi
ę
cie do zera
do 220V, to o
ś
napi
ę ć
mo
ż
e by
ć
przykładowo opisana tak, jak pokazuje rys. 5.
160
220
200
180
14
0
120
100
80
60
0
20
40
V
U
U
U
160
240
200
120
80
0
40
V
150
120
240
210
180
90
60
0
30
V
Rys.5. Mo
ż
liwe warianty opisu osi układu współrz
ę
dnych.
5. Je
ż
eli liczby opisuj
ą
ce o
ś
s
ą
zbyt du
ż
e (np. 1500) lub zbyt małe (np. 0,0002),
co mo
ż
e pogorszy
ć
czytelno
ś ć
opisu, wskazane jest dziesi
ę
cio-, stu- lub
tysi
ą
ckrotne (najwła
ś
ciwsze) zmniejszenie ich lub zwi
ę
kszenie, a w
ś
lad za
tym umieszczenie na ko
ń
cu osi stosownego mno
ż
nika, albo zmiana jednostki
miary danej wielko
ś
ci, tak jak to pokazano na rys.6.
I
1,6
2,4
2,0
1,2
0,8
0
0,4
x10
-3
A
I
1,6
2,4
2,0
1,2
0,8
0
0,4
mA
Rys. 6. Przykład opisu osi z zastosowaniem mno
ż
nika
6. Pocz
ą
tkowy punkt osi nie musi by
ć
koniecznie opisany zerem. Je
ż
eli wyniki
pomiarów zawieraj
ą
si
ę
w przedziale liczbowym nie zawieraj
ą
cym zera
i odległym od niego, to pocz
ą
tek osi mo
ż
e by
ć
opisany liczb
ą
blisk
ą
naj-
mniejszemu wynikowi pomiaru.

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
10
7. W koniecznych przypadkach dopuszczalne jest stosowanie innej skali na
półosi dodatniej, innej za
ś
na półosi ujemnej. Jest to na przykład konieczne
przy wykre
ś
laniu charakterystyki pr
ą
dowo-napi
ę
ciowej diody Zenera.
8. Obowi
ą
zuje zasada, i
ż
nad osi
ą
odci
ę
tych ( na jej ko
ń
cu) umieszcza si
ę
symbol wielko
ś
ci, pod osi
ą
za
ś
- symbol jednostki (patrz rys.5 i rys. 6).
Dla osi rz
ę
dnych zasada ta brzmi - z lewej strony osi symbol jednostki - z
prawej - symbol wielko
ś
ci. Liczby umieszcza si
ę
z lewej strony osi
rz
ę
dnych i pod osi
ą
odci
ę
tych.
9. W przypadku papieru logarytmicznego lub półlogarytmicznego, jeste
ś
my
bardziej ograniczeni w wyborze, jako
ż
e punkty osi układu zastajemy ju
ż
opisane. Jak ju
ż
wyja
ś
niano, na papierze takim znajduje si
ę
kilka identycznych
sekwencji
punktów
(rys.4).
U
ż
ytkownik
korzysta
ć
mo
ż
e
z jednej lub wi
ę
cej sekwencji, przypisuj
ą
c ponadto zastanym liczbom warto
ś
ci
10
k
krotnie wi
ę
ksze (k = 1,2,3,...). Kwesti
ę
t
ę
wyja
ś
niaj
ą
podane ni
ż
ej
przykłady.
Przykład 2
Podczas bada
ń
pewnego obiektu, zmieniano cz
ę
stotliwo
ść
napi
ę
cia
podawanego na jego wej
ś
cie. Zanotowano przy tym nast
ę
puj
ą
ce cz
ę
stotliwo
ś
ci:
5, 10, 20, 40, 60, 80,100, 200, 400, 600, 800, 1000 Hz.
Sposób wykorzystania podziałki logarytmicznej jest tu jasny. Pojedynczym
hercom przypisa
ć
nale
ż
y punkty z I sekwencji, dziesi
ą
tkom herców punkty z II
sekwencji, za
ś
setkom herców - z III sekwencji. W tej ostatniej znajdzie
odwzorowanie tak
ż
e cz
ę
stotliwo
ść
1000 Hz (jako ostatni punkt).
Przykład 3
W podobnym do opisanego do
ś
wiadczeniu zanotowano nast
ę
puj
ą
ce
cz
ę
stotliwo
ś
ci: 500, 1000, 5000, 10 000, 50 000, 100 000 Hz. Je
ż
eli do
dyspozycji mamy podziałk
ę
logarytmiczn
ą
z rys. 4 (jest tu wystarczaj
ą
ca), to
liczbom z I sekwencji nale
ż
y przypisa
ć
warto
ś
ci 100 razy wi
ę
ksze od podanych,
za
ś
liczbom z ka
ż
dej nast
ę
pnej sekwencji dziesi
ę
ciokrotnie wi
ę
ksze od warto
ś
ci
liczb z sekwencji poprzedniej (pierwszy punkt osi oznaczy
ć
trzeba wtedy liczb
ą
100).

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
11
Sposób nanoszenia punktów i kre
ś
lenia krzywej
Punkty wykresu nanosi si
ę
ostrym, niezbyt mi
ę
kkim ołówkiem, odciskaj
ą
c
najpierw jego
ś
lad punktowy, a nast
ę
pnie przekre
ś
laj
ą
c go niewielkim
krzy
ż
ykiem.
Przez naniesione punkty prowadzi si
ę
lini
ę
ci
ą
gł
ą
, prowadz
ą
c ołówek przy
krzywiku. Krzywik (jeden z trzech wyst
ę
puj
ą
cych zwykle w komplecie)
powinien obejmowa
ć
co najmniej trzy punkty, za
ś
kre
ś
lona krzywa powinna
by
ć
doprowadzona do połowy odległo
ś
ci mi
ę
dzy dwoma s
ą
siednimi punktami.
Jej dalszy odcinek mo
ż
e by
ć
kre
ś
lony przy innym poło
ż
eniu krzywika.
Poszczególne odcinki powinny tworzy
ć
ł
ą
cznie gładk
ą
, pozbawion
ą
jakichkolwiek załama
ń
lini
ę
ci
ą
gł
ą
.
Gdyby obj
ę
cie krzywikiem trzech punktów było niemo
ż
liwe, nale
ż
y
prowadzi
ć
krzyw
ą
mi
ę
dzy punktami tak, aby w ko
ń
cowym rezultacie po obu
stronach wykre
ś
lonej linii znajdowała si
ę
w przybli
ż
eniu taka sama liczba
punktów.
Mo
ż
na w tym przypadku stosowa
ć
technik
ę
polegaj
ą
c
ą
na ł
ą
czeniu
s
ą
siednich punktów pomocniczymi odcinkami prostej, a nast
ę
pnie prowadzeniu
krzywej przez
ś
rodki tych odcinków.
Wszystkie pomocnicze linie musz
ą
by
ć
znacznie słabiej widoczne ni
ż
krzywa wykresu.
Je
ż
eli we wspólnym układzie współrz
ę
dnych ma by
ć
wykre
ś
lonych kilka
krzywych, mo
ż
na je wyró
ż
ni
ć
kolorami, nie zakrywaj
ą
c jednak obrazu
kre
ś
lonego ostrym ołówkiem..
Poza tym poszczególne krzywe mo
ż
na odró
ż
ni
ć
stosownymi przepisami
prowadzonymi równolegle do tych krzywych lub w inny czytelny sposób.
Pod wykresami powinien znale
ź ć
si
ę
stosowny podpis oraz dodatkowe
obja
ś
nienia, je
ś
li potrzebne to jest do wła
ś
ciwego zrozumienia wykresów.
Przedstawione w tej instrukcji zasady, nie wyczerpuj
ą
wszystkich
zagadnie
ń
zwi
ą
zanych z graficznym przedstawianiem wyników pomiarów.
Wynika to m.in. z mnogo
ś
ci przypadków, z jakimi mo
ż
na si
ę
spotka
ć
w prak-
tyce pomiarowej.
Swoje umiej
ę
tno
ś
ci w tej dziedzinie nale
ż
y doskonali
ć
przez uwa
ż
ne
ś
ledzenie wykresów zamieszczonych w dobrych wydawnictwach naukowych
i technicznych.
Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
12
2. Przebieg
ć
wiczenia
Studenci wykre
ś
laj
ą
, zgodnie z poznanymi zasadami, krzywe wynikaj
ą
ce z
przedstawionych ni
ż
ej wyników pomiarów zawartych w Tablicy 2 oraz
Tablicy 3. Wykonane prace podlegaj
ą
ocenie i decyduj
ą
o zaliczeniu
ć
wiczenia.
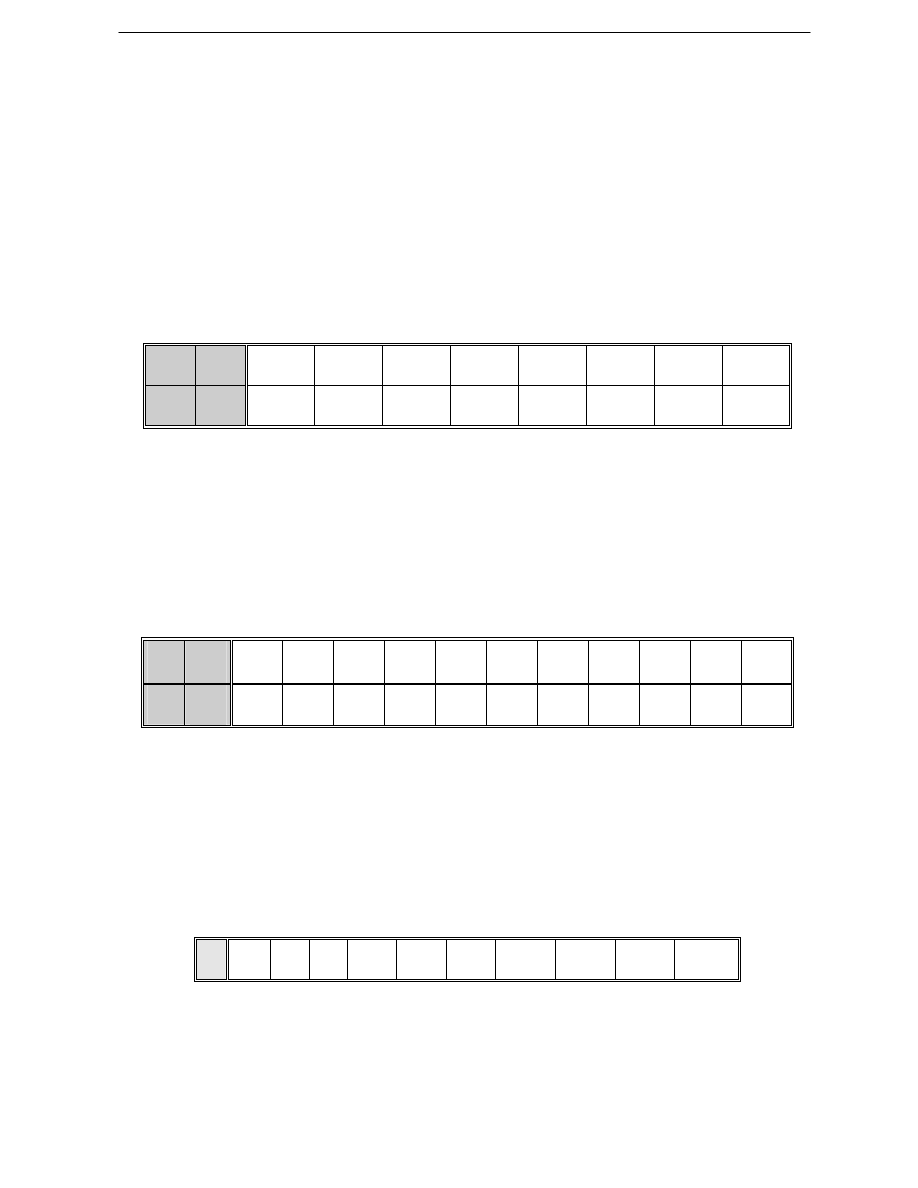
Zadanie 1
Wykre
ś
l charakterystyk
ę
I = f(U) na podstawie wyników pomiaru
zawartych w Tablicy 2.
Tablica 2
U
V
0
1,5
3,0
4,5
6,0
7,5
9,0
10,5
I
mA
0
2,3
3,6
5,9
6,6
8,4
8,3
9,3
Zadanie 2
Wykre
ś
l charakterystyk
ę
R = f(I) na podstawie wyników pomiaru
zawartych w Tablicy 3.
Tablica 3
I
mA
0
1
2
3
4
5
6
7
8
9
10
R
Ω
95
81
67,5 54,5 43,5 33,8 25,5 19,1 14,3 11,2
10
Zadanie 3
(studenci samodzielnie sporz
ą
dzaj
ą
podziałk
ę
logarytmiczn
ą
)
Wykre
ś
l funkcj
ę
y = x
2
dla nast
ę
puj
ą
cych warto
ś
ci argumentu x:
Tablica 4
x
1 2
5
10
20
50
100
200
500
1000
Ka
ż
dy z trzech wykresów nale
ż
y zamie
ś
ci
ć
na oddzielnym arkuszu papieru
milimetrowego, opisa
ć
zale
ż
no
ś
ci
ą
funkcyjn
ą
, której jest on obrazem,
a tak
ż
e poda
ć
nazwisko i imi
ę
autora.

Ć
wicz. Nr15 Graficzna prezentacja wyników pomiarów
13
3. Literatura
Jako literatur
ę
poleca si
ę
wszelkie techniczne wydawnictwa ksi
ą ż
kowe
oraz czasopisma, w których zwróci
ć
nale
ż
y uwag
ą
na zamieszczone tam
przykłady graficznego przedstawiania zale
ż
no
ś
ci funkcyjnych.
Wyszukiwarka
Podobne podstrony:
Graficzna prezentacja wyników pomiarów
15 Graficzna prezentacja wynikow pomiarow
Graficzna prezentacja wyników pomiarów
3 Opracowanie wyników pomiaru metodą analityczno graficzną (Langa)
Cwiczenie 4 Statystyczna obróbka wyników pomiarowych
ocena dokładności wyników pomiar
B Kamys Statystyczne metody opracowania wyników pomiarów
graficzna analiza wynikow Nieznany
Analiza błędów Statystyczne opracowanie wyników pomiarów
Opracowanie wyników pomiaru
Zestawienie wyników pomiarów
Opracowanie wyników pomiarowych - błędy, bledy, Gęstość jest cechą substancji określającą masę jedno
C - Statystyczna analiza wyników pomiarów, spraw.
Test sprawdzający Z. Hak, VII, VII Analizy ilościowe i graficzne przedstawienie wyników
METODYKA OPRACOWYWANIA WYNIKÓW POMIAROWYCH, MET0DYKA-spr., POLITECHNIKA RADOMSKA
Zastosowanie programów statycznych do opracowania wyników pomiarów
Instrukcja do prezentacji wyników ankiety, metody badawcze-ćw
więcej podobnych podstron