
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
PODSTAWY AUTOMATYKI
część 5
Charakterystyki częstotliwościowe

2
Transmitancja widmowa
∫
∞
−
=
)
(
)
(
dt
e
t
f
j
F
t
j
ω
ω
∫
∞
∝
−
−
=
dt
e
t
f
j
F
t
j
ω
ω
)
(
)
(
dla t>0
Przekształcenie Fouriera
∫
=
0
)
(
)
(
dt
e
t
f
j
F
ω
ω
ω
j
s
s
G
j
G
=
=
)
(
)
(
3
Charakterystyki częstotliwościowe
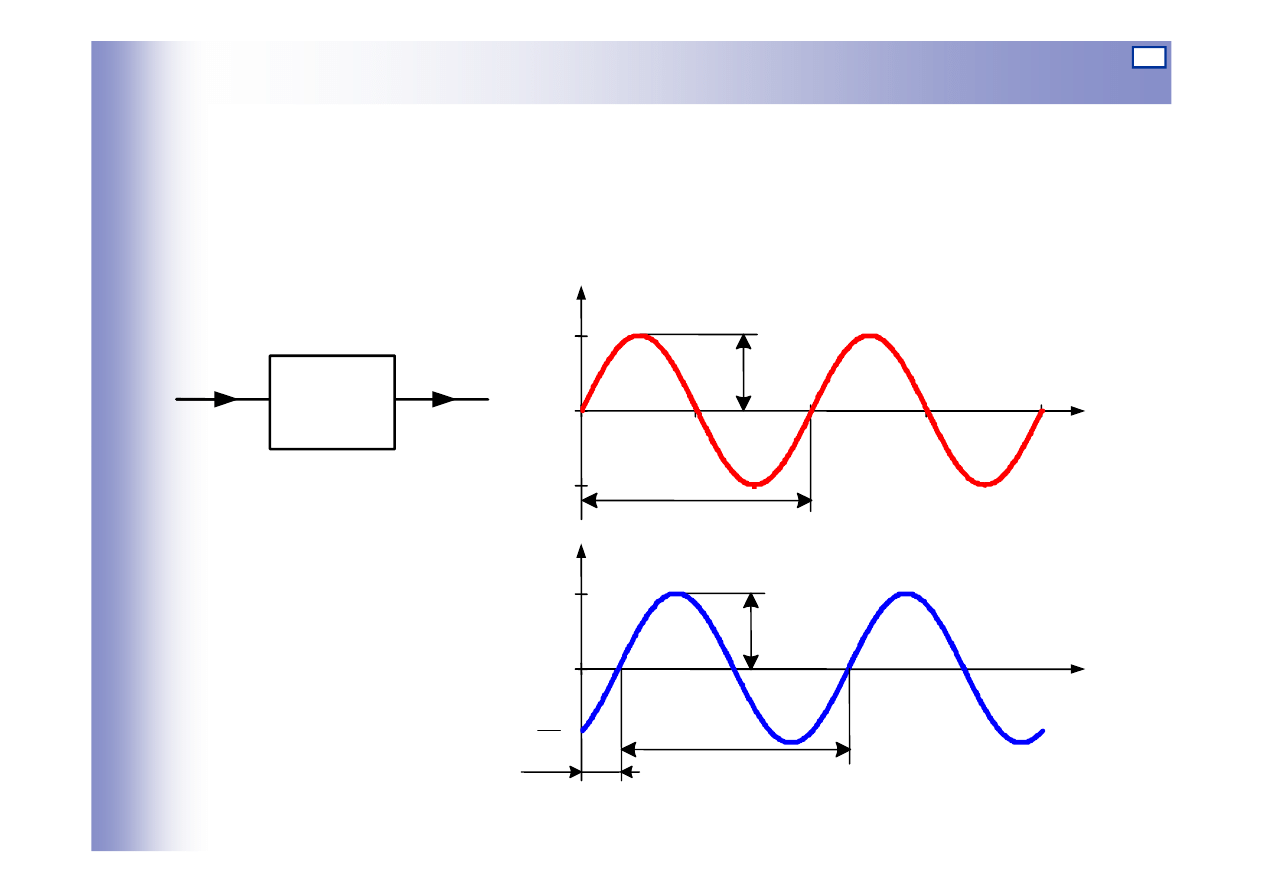
Jeżeli na wejście elementu lub układu liniowego stabilnego wprowadzone zostanie
wymuszenie sinusoidalne o stałej częstotliwości, to na wyjściu, po zaniknięciu
przebiegu przejściowego, ustali się odpowiedź sinusoidalna o tej samej
częstotliwości, ale w ogólnym przypadku, o innej amplitudzie i fazie niż wymuszenie
u
0
A
1
( ω)
t
u
y
ω
ϕ
T=2 π/ω
A
2
( ω)
0
t
y
T=2 π/ω
]
sin[
)
(
sin
2
1
ϕ
ω
ω
ω
+
=
=
t
A
y
t
A
u

4
Charakterystyki częstotliwościowe
Charakterystyki cz
ę
stotliwo
ś
ciowe -
określają zachowanie się elementu
lub układu przy wszystkich częstotliwościach wymuszenia
Określają w funkcji częstotliwości:
•
stosunek amplitud odpowiedzi do wymuszenia
•
przesunięcie fazowe między odpowiedzią a wymuszeniem

5
Podstawy teoretyczne
s
s
s
e
A
e
t
L
A
s
G
t
L
e
t
L
t
L
t
L
A
A
t
A
L
t
A
L
s
G
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ϕ
ω
ω
ϕ
ω
ω
ϕ
ω
2
2
1
2
1
2
)]
[sin(
)
(
)]
[sin(
)]
[sin(
)]
[sin(
)]
[sin(
)]
sin(
[
)]
sin(
[
)
(
=
=
=
+
=
+
=
+
=
Wejście:
Wyjście:
)
sin(
)
(
2
ϕ
ω
ω
+
t
A
)
sin(
1
t
A
ω
)]
(
[
)]
(
[
t
f
L
e
t
f
L
s
τ
τ
−
=
−
Gdzie:
- moduł charakterystyki częstotliwościowej
(stosunek amplitud odpowiedzi do wymuszenia)
1
2
)
(
)
(
A
A
M
ω
ω
=
s
s
e
A
A
e
t
L
t
L
A
A
s
G
ω
ω
ω
ω
1
2
1
2
)]
[sin(
)]
[sin(
)
(
=
=
)
(
1
)
(
2
)
(
)
(
)
(
ω
ϕ
ω
ϕ
ω
ω
ω
⋅
⋅
⋅
=
⋅
=
j
j
e
M
A
e
A
j
G
6
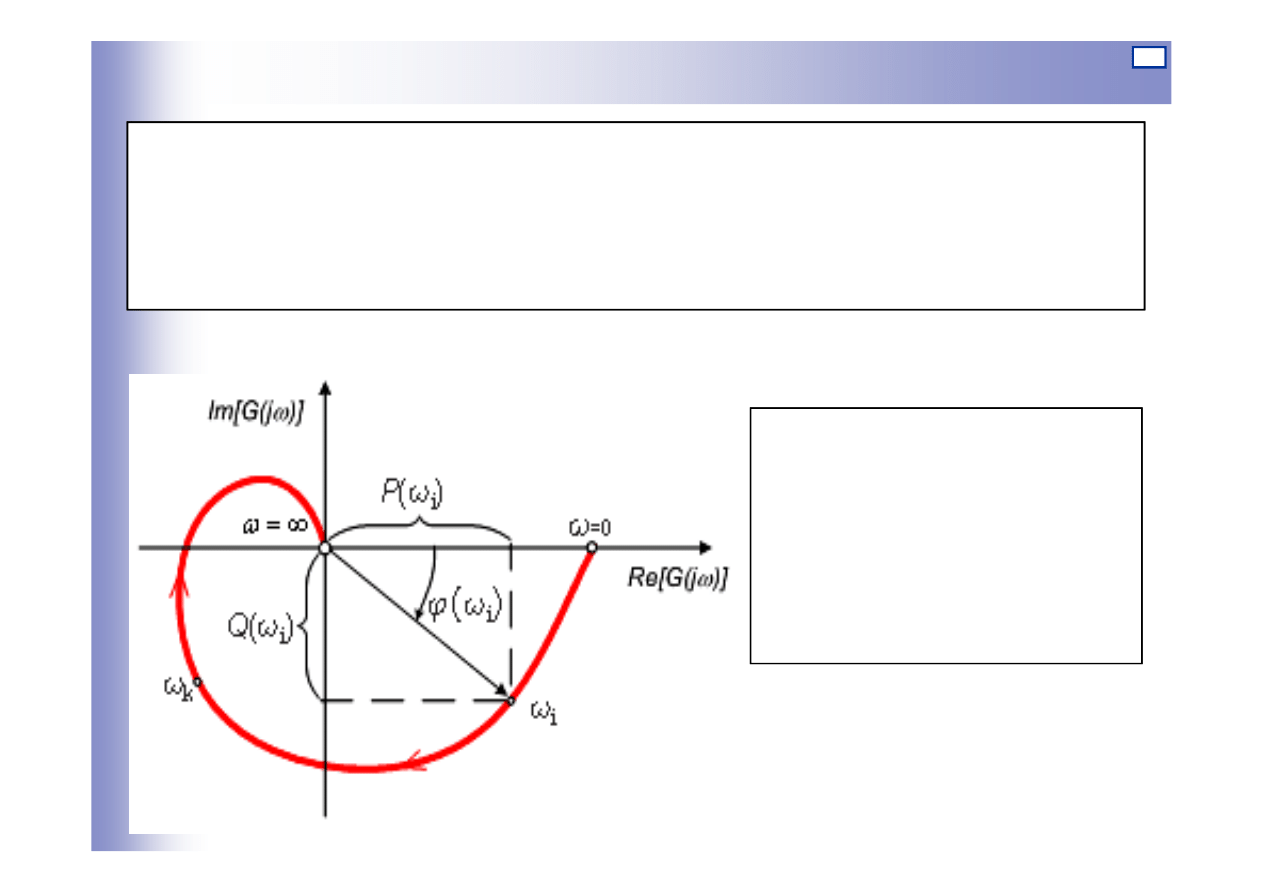
Charakterystyka amplitudowo-fazowa
Charakterystyka amplitudowo-fazowa - wykres końców wektorów,
których:
•
długość reprezentuje stosunek amplitud odpowiedzi do wymuszenia
•
kąt przesunięcie fazowe między odpowiedzią a wymuszeniem
Definiowana cz
ę
sto jako:
Definiowana cz
ę
sto jako:
Wykres transmitancji
widmowej G(jω)
Zespolona charakterystyka
częstotliwościowa
G(jω)
7
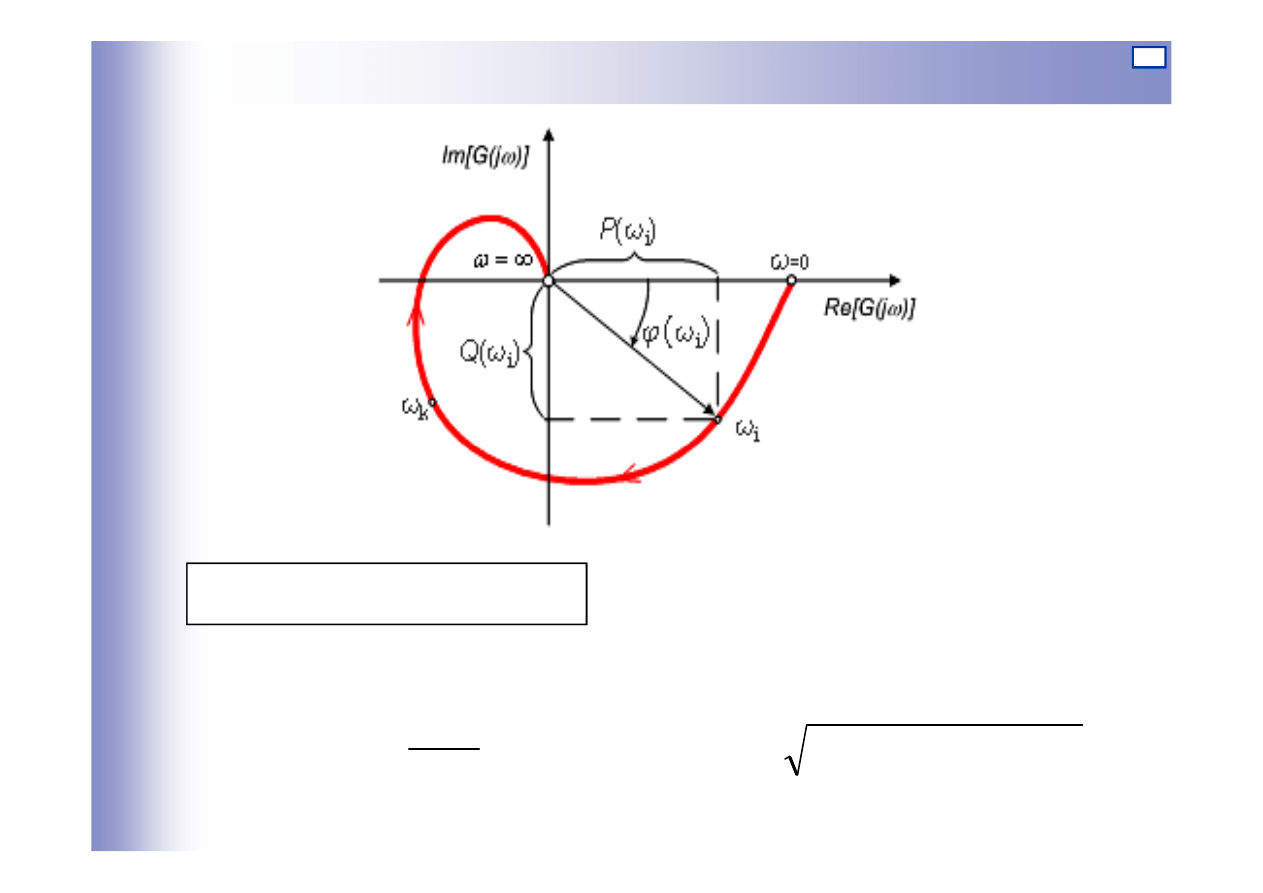
Charakterystyka amplitudowo-fazowa
G(jω)
związki:
Charakterystyczne
związki:
2
2
)]
(
[
)]
(
[
)
(
ω
ω
ω
Q
P
j
M
+
=
)
(
)
(
)
(
ω
ω
ω
ϕ
P
Q
arctg
=
)
(
cos
)
(
)
(
ω
ϕ
ω
ω
M
P
=
)
(
sin
)
(
)
(
ω
ϕ
ω
ω
M
Q
=
8
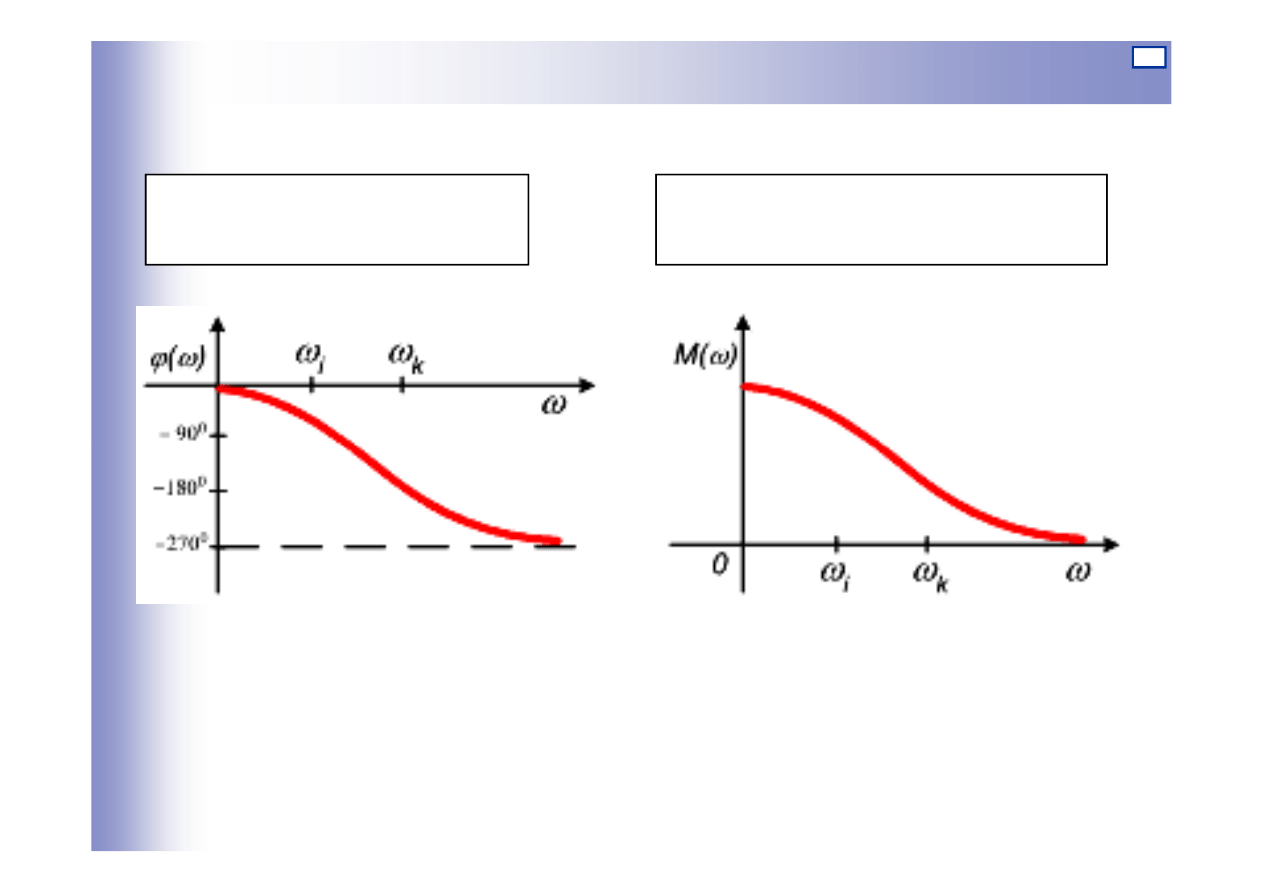
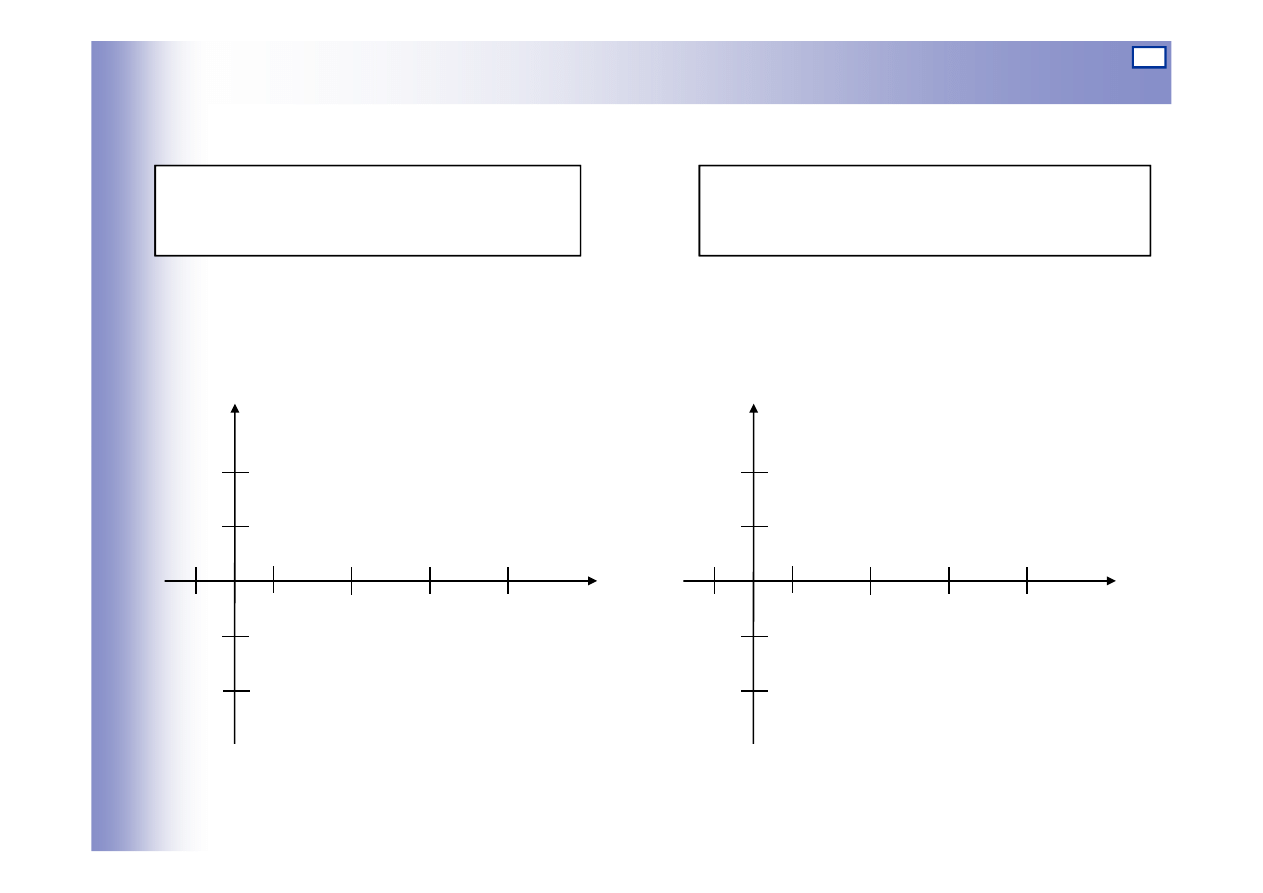
Charakterystyki częstotliwościowe
amplitudowa charakterystyka
częstotliwościowa
fazowa charakterystyka
częstotliwościowa
9
Charakterystyka amplitudowo-fazowa
ϕ
(ω)
M(ω)
L(ω)
Logarytmiczna
charakterystyka amplitudowa
Logarytmiczna
charakterystyka
fazowa
)
(
log
20
)
(
ω
ω
M
L
=
)
(
ω
ϕ
0,1
1
10
100
0,01
90
0
180
0
-90
0
-180
0
π
-π
π
/2
-π/2
ω
0,1
1
10
100
0,01
20dB
40dB
-20dB
-40dB
100
0,01
10
0,1
ω
10
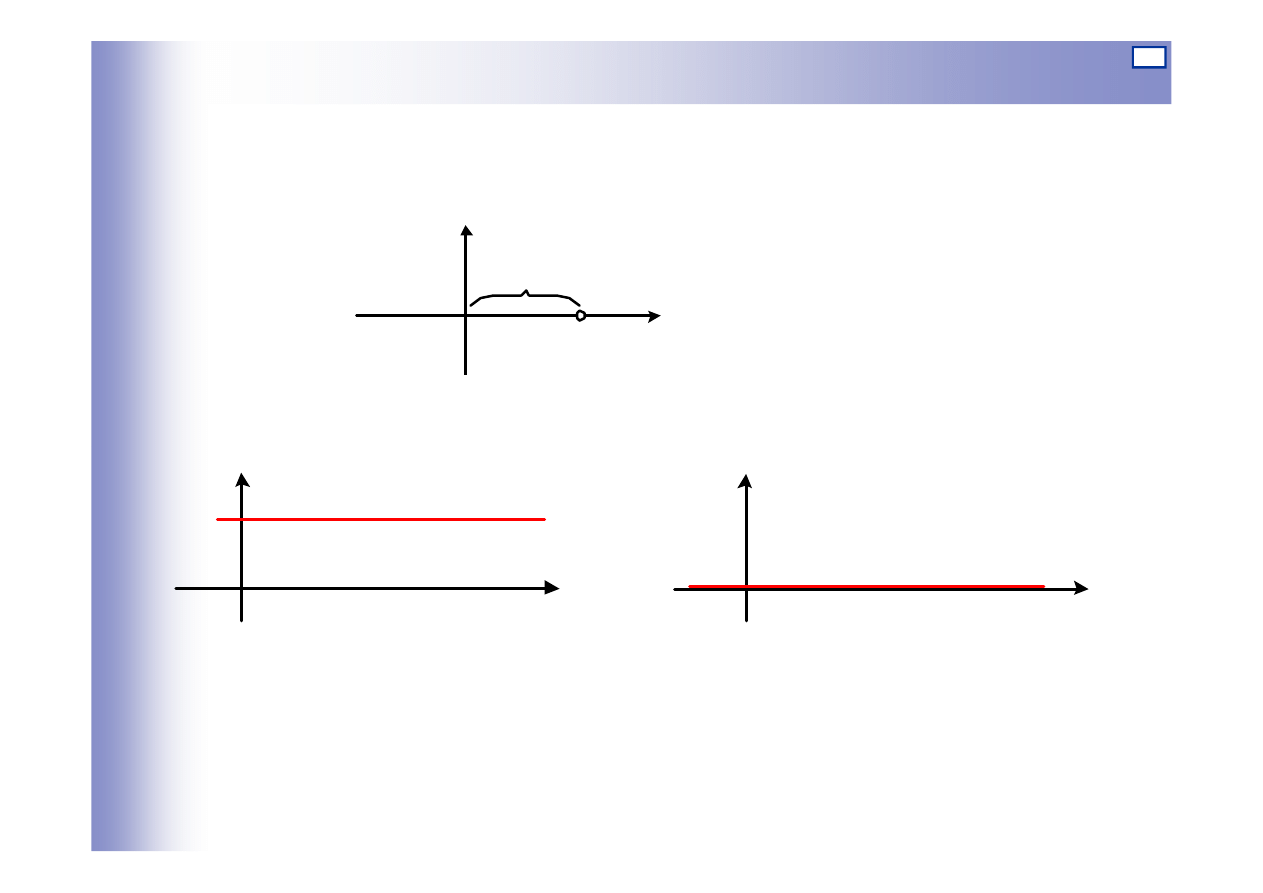
Charakterystyki elementu proporcjonalnego
jQ(
ω
)
P(
ω
)
G( j
ω
)
k
0
)
(
)
(
=
=
ω
ω
Q
k
P
L(
ω
)
dB
ω
20 log k
ω
0
0
ϕ
(
ω
)
11
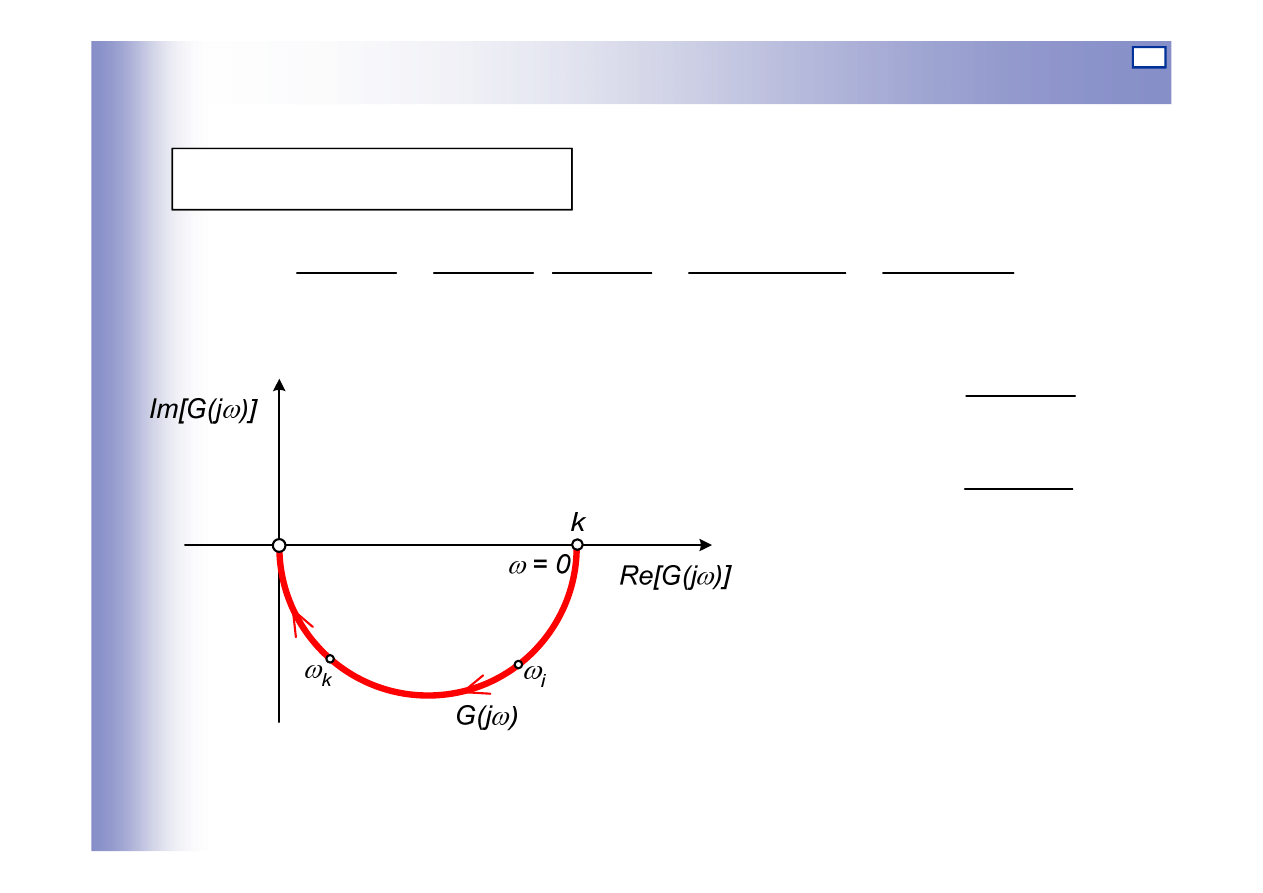
Charakterystyki elementu inercyjnego I rzędu
Transmitancja widmowa:
1
1
1
1
1
1
)
(
2
2
2
2
+
−
=
−
−
+
−
=
−
−
⋅
+
=
+
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
T
jkT
k
T
jkT
k
Tj
Tj
Tj
k
Tj
k
j
G
1
)
(
2
2
+
−
=
ω
ω
ω
T
kT
Q
∞
=
ω
1
)
(
2
2
+
=
ω
ω
T
k
P
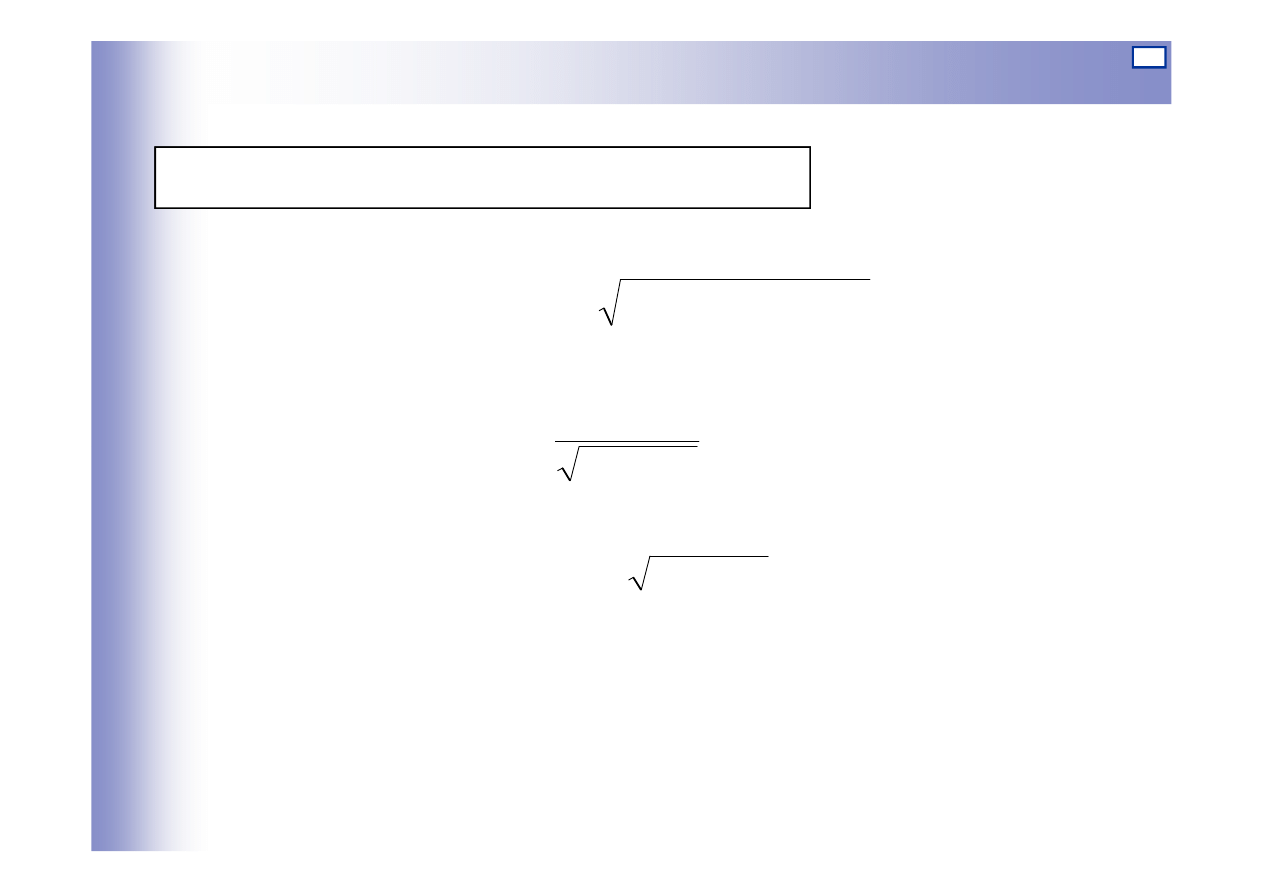
12
Charakterystyki elementu inercyjnego I rzędu
[
] [
]
log
20
)
(
)
(
)
(
log
20
)
(
log
20
)
(
2
2
+
=
+
=
=
ω
ω
ω
ω
ω
ω
k
L
Q
P
M
L
c
Logarytmiczna charakterystyka amplitudowa:
1
log
20
log
20
)
(
1
log
20
)
(
2
2
2
2
+
−
=
+
=
ω
ω
ω
ω
T
k
L
T
L
c
13
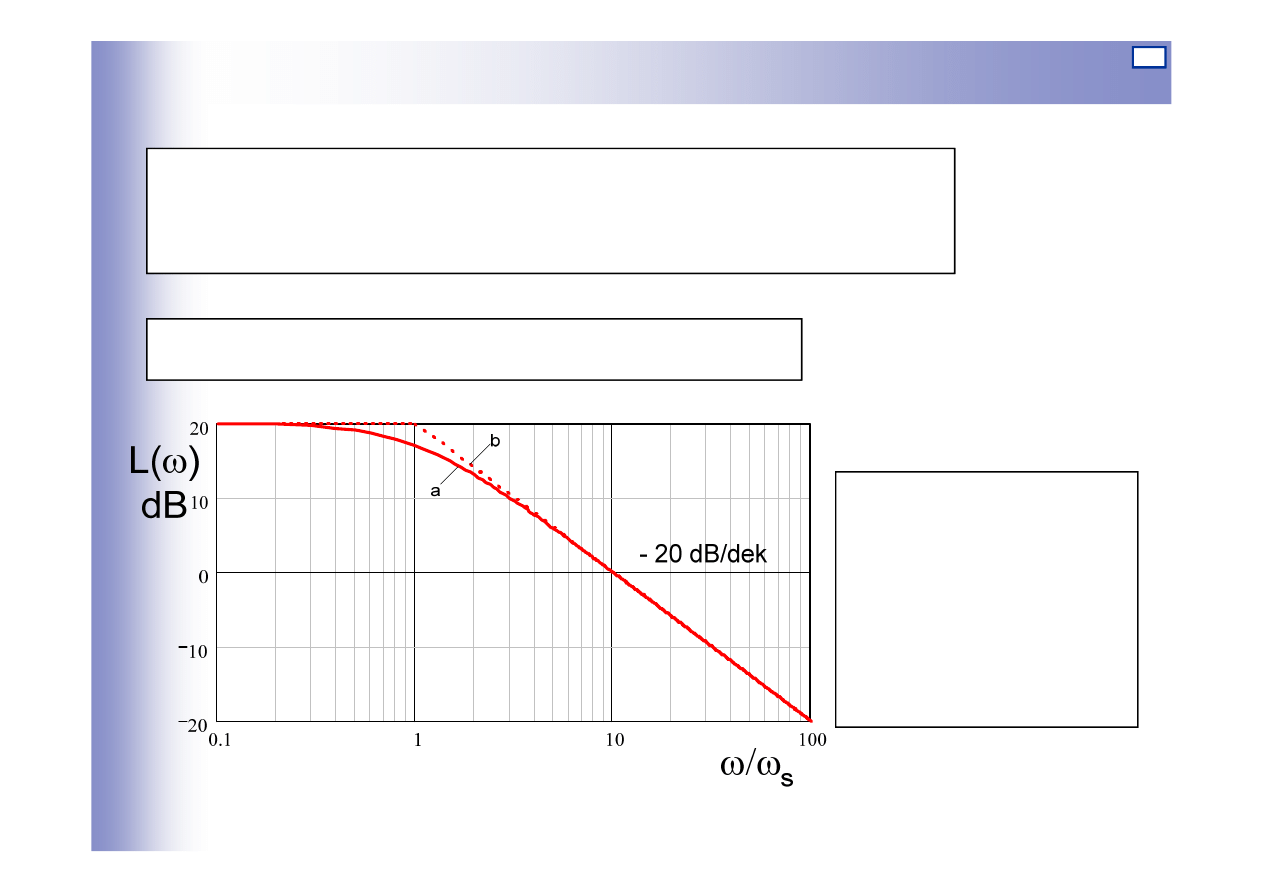
Charakterystyki elementu inercyjnego I rzędu
Dla:
T
/
1
<
ω
k
L
log
20
)
(
=
ω
T
/
1
>
ω
ω
ω
T
k
L
log
20
log
20
)
(
−
=
Logarytmiczna charakterystyka amplitudowa:
Dla: k=10
a – charakterystyka
rzeczywista
b – charakterystyka
asymptotyczna
T
s
/
1
=
ω
14
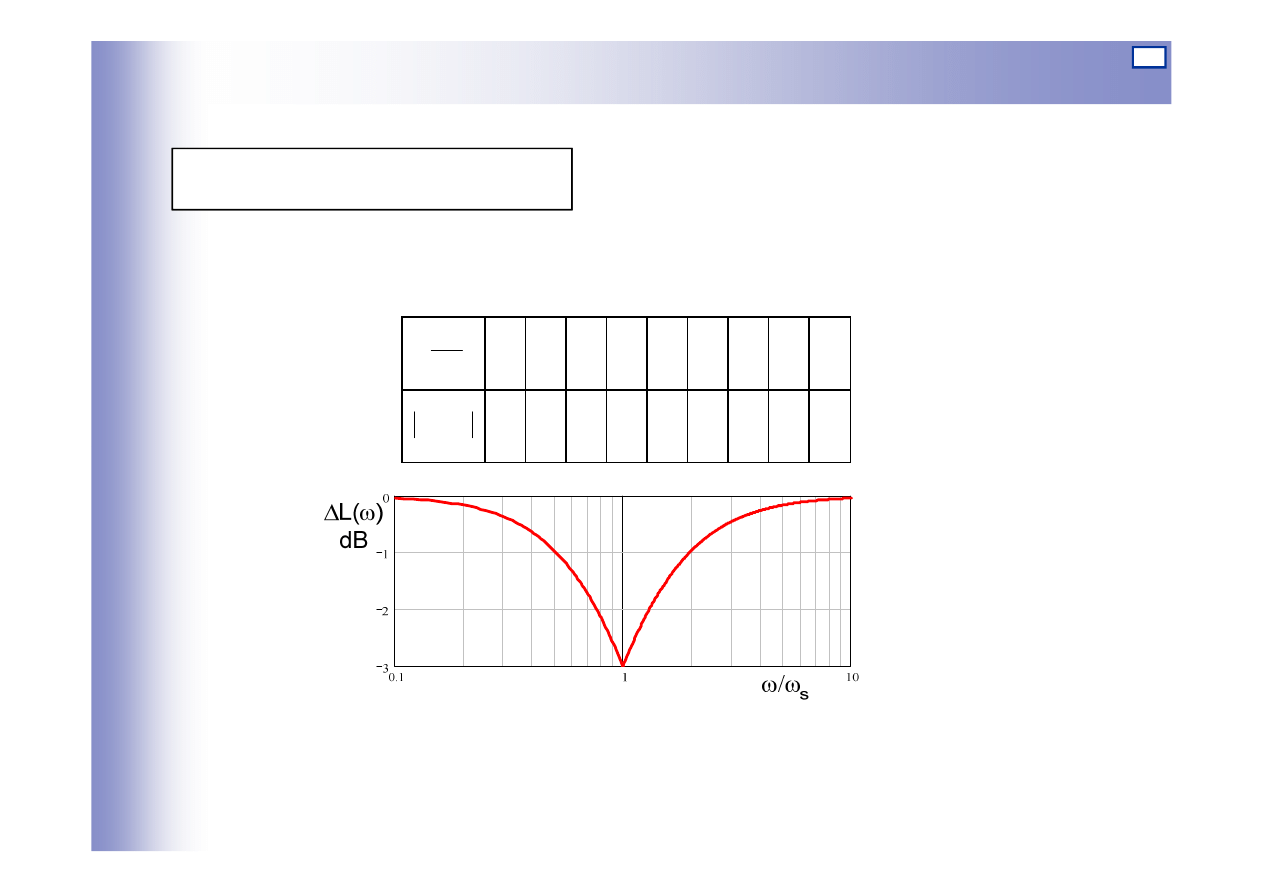
Charakterystyki elementu inercyjnego I rzędu
Tablica 4.1
0,1 0,25 0,4 0,5 1,0
10
2,5 4,0 10,0
0,04 0,32 0,65 1,0 3,01 1,0 0,65 0,32 0,04
S
ω
ω
)
(
ω
L
∆
Wykres błędu:
15
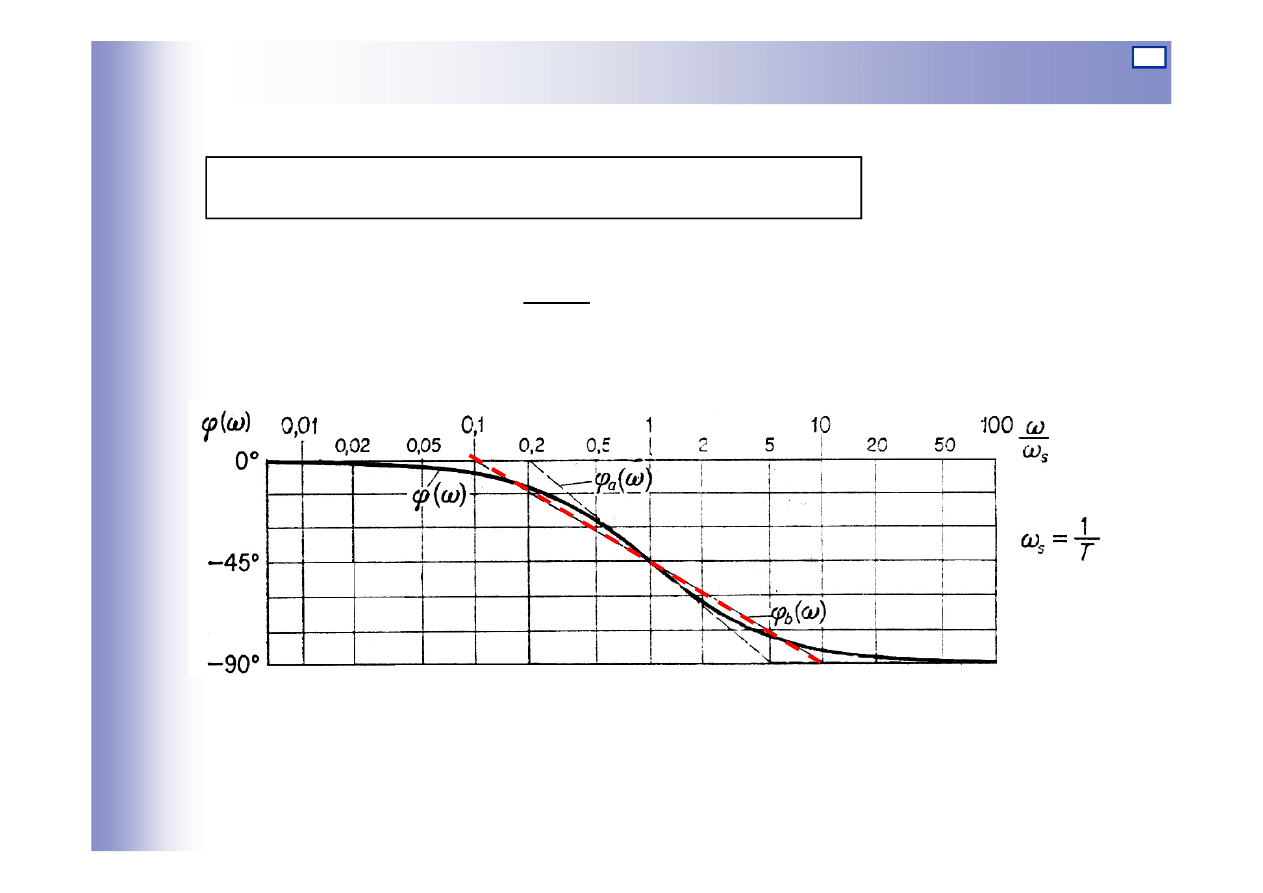
Charakterystyki elementu inercyjnego I rzędu
)
(
)
(
)
(
)
(
)
(
ω
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
−
=
=
Logarytmiczna charakterystyka fazowa:
16
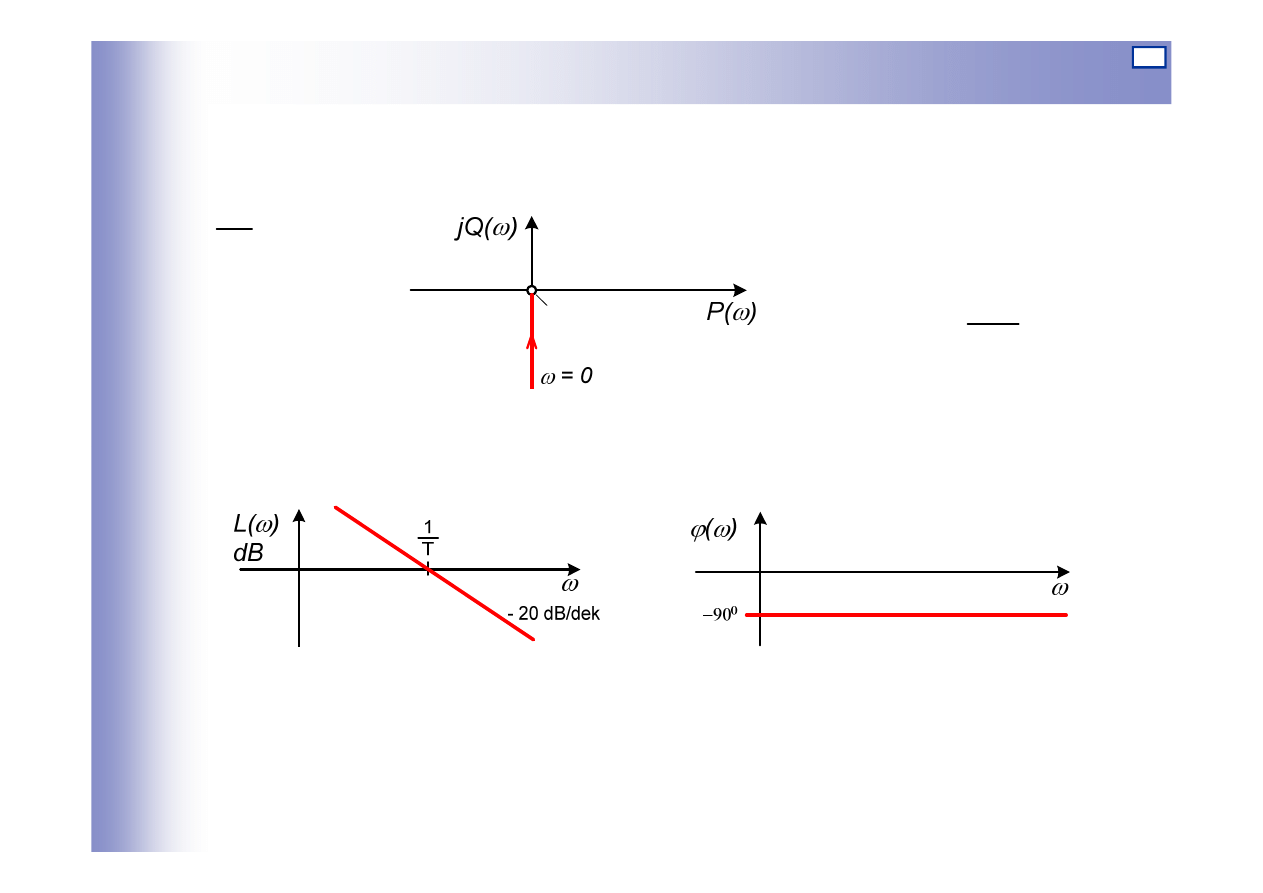
Charakterystyki elementu całkującego
∞
=
ω
ω
ω
ω
T
Q
P
1
)
(
0
)
(
−
=
=
Ts
1
17
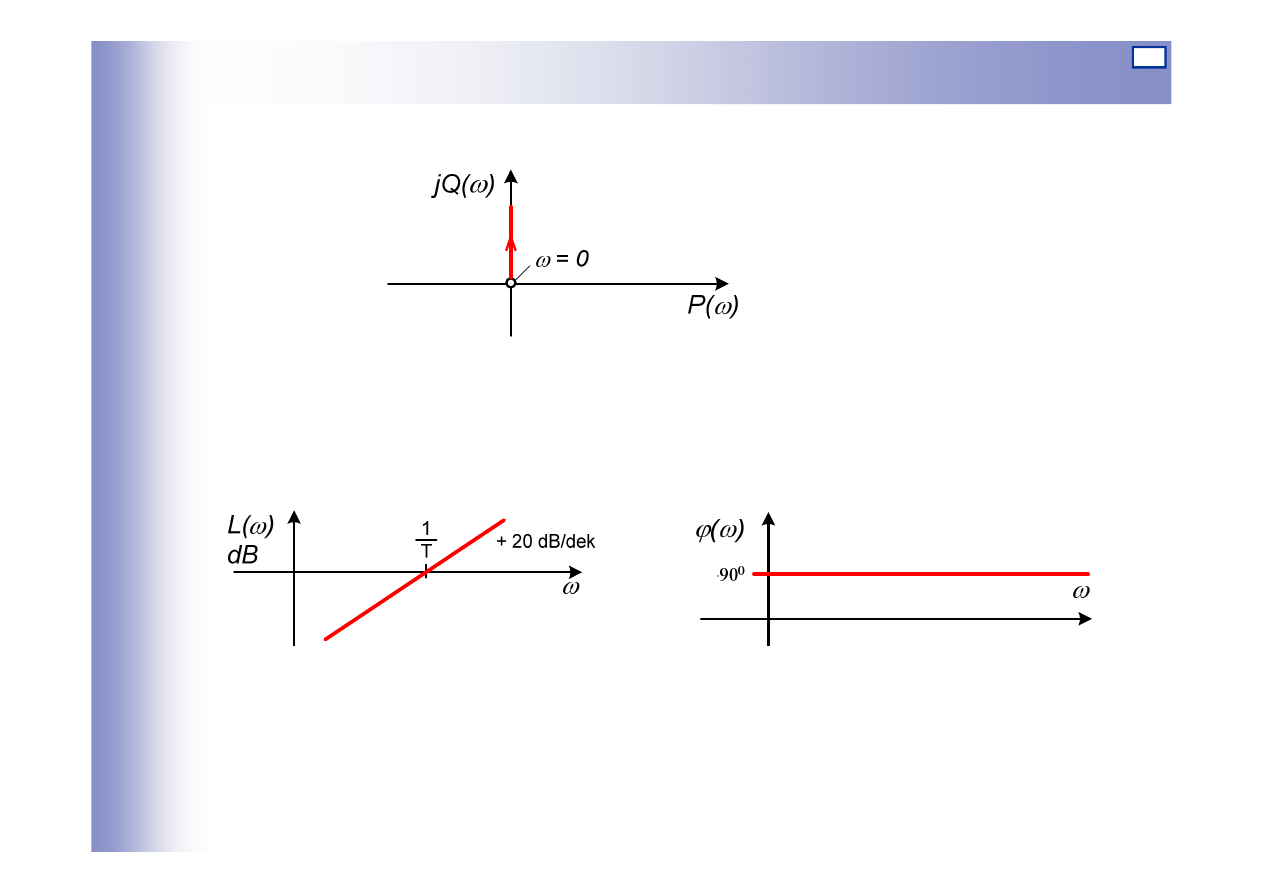
Charakterystyki elementu różniczkującego
∞
=
ω
ω
ω
ω
T
Q
P
=
=
)
(
0
)
(
Ts
18
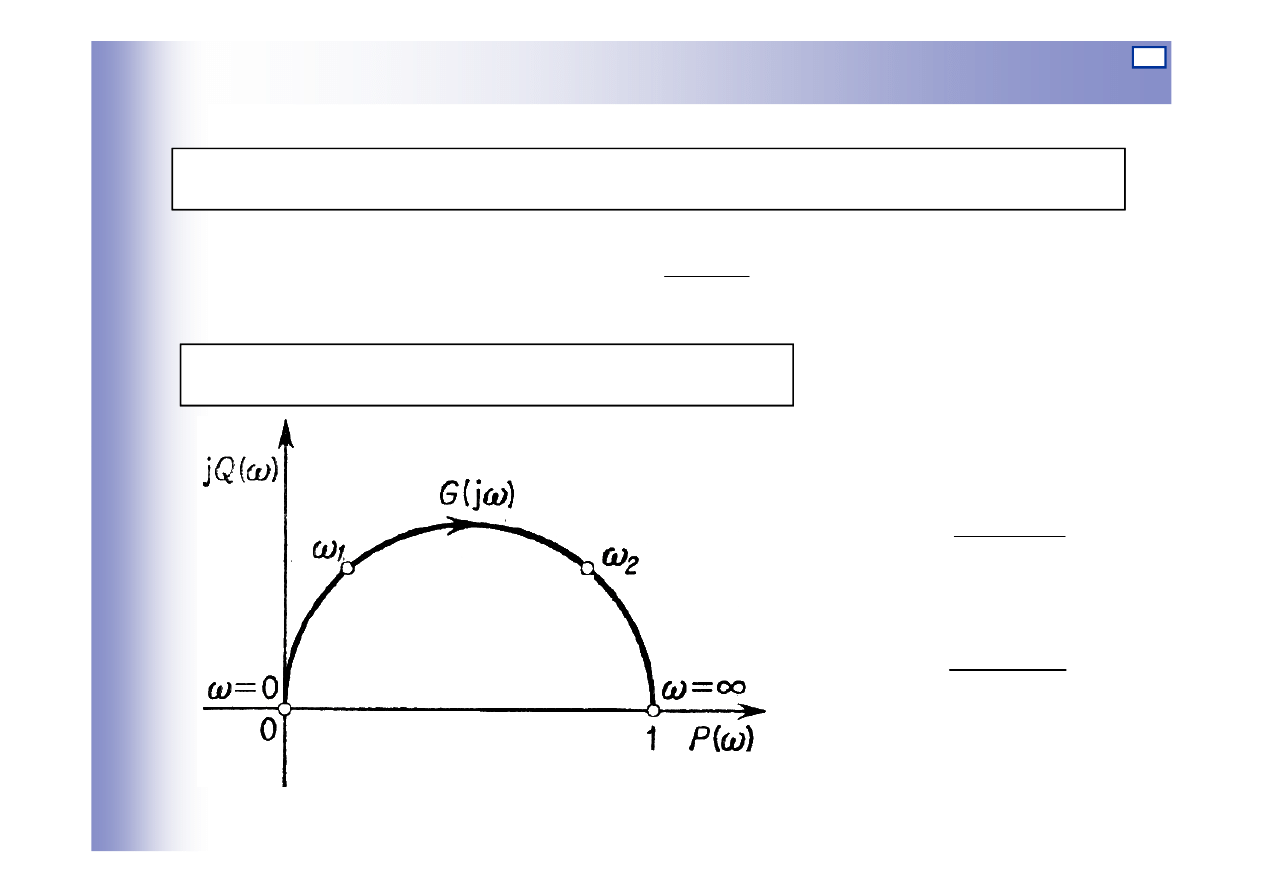
Charakterystyki elementu różniczkującego
Transmitancja widmowa elementu różniczkującego rzeczywistego:
1
)
(
+
=
ω
ω
ω
Tj
Tj
j
G
Charakterystyka amplitudowo-fazowa:
1
)
(
2
2
2
2
+
=
ω
ω
ω
T
T
P
1
)
(
2
2
+
=
ω
ω
ω
T
T
Q
19
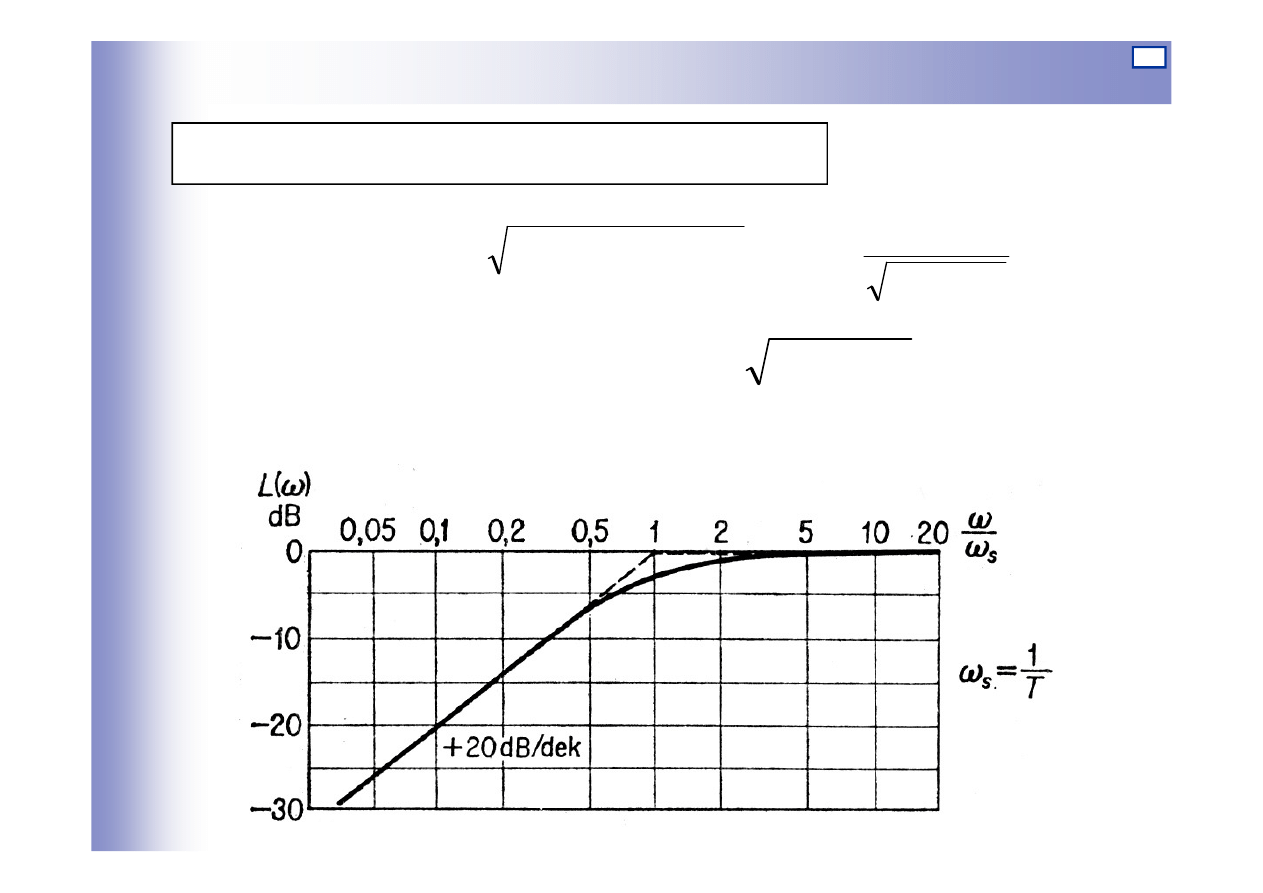
Charakterystyki elementu różniczkującego
[
] [
]
1
log
20
)
(
)
(
log
20
)
(
2
2
2
2
+
=
+
=
ω
ω
ω
ω
ω
T
T
Q
P
L
1
log
20
log
20
)
(
2
2
+
−
=
ω
ω
ω
T
T
L
Logarytmiczna charakterystyka amplitudowa:
20
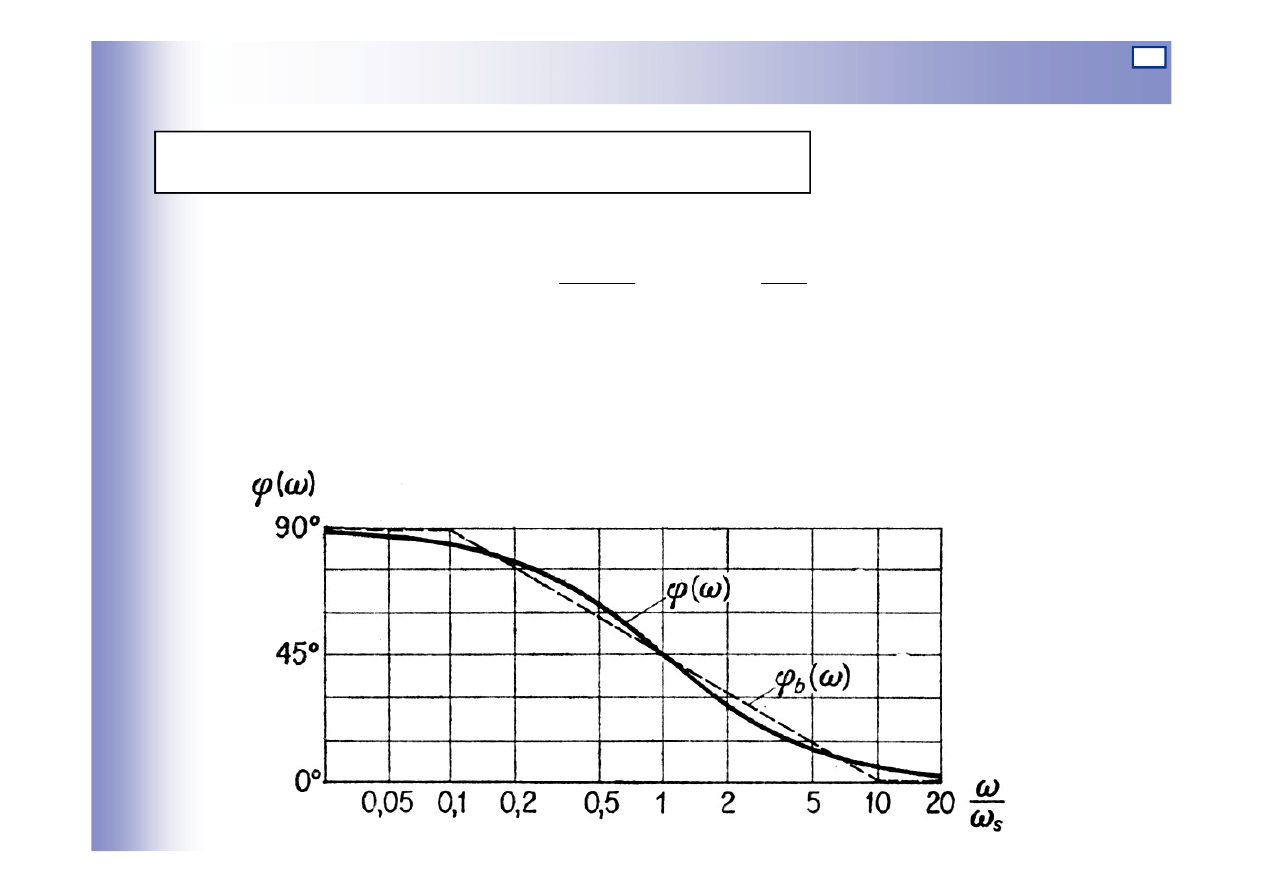
Charakterystyki elementu różniczkującego
)
(
90
)
(
)
1
(
)
(
)
(
)
(
0
ω
ω
ϕ
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
=
=
c
Logarytmiczna charakterystyka fazowa:

21
Charakterystyki elementu oscylacyjnego
Transmitancja widmowa:
( )
( ) ( )
0
2
2
0
2
0
2
0
0
2
2
0
2
2
)
(
ζωω
ω
ω
ω
ω
ω
ζω
ω
ω
ω
⋅
+
−
=
+
+
=
j
k
j
j
k
j
G
Gdzie:
k — współczynnik proporcjonalności
ω
0
— pulsacja oscylacji własnych elementu
ω
0
— pulsacja oscylacji własnych elementu
ζ — zredukowany (względny) współczynnik tłumienia
2
0
2
2
2
0
2
2
0
2
0
)
2
(
)
(
)
(
)
(
ω
ζω
ω
ω
ω
ω
ω
ω
+
−
−
=
k
P
2
0
2
2
2
0
3
0
)
2
(
)
(
2
)
(
ω
ζω
ω
ω
ω
ζω
ω
+
−
=
k
Q
22
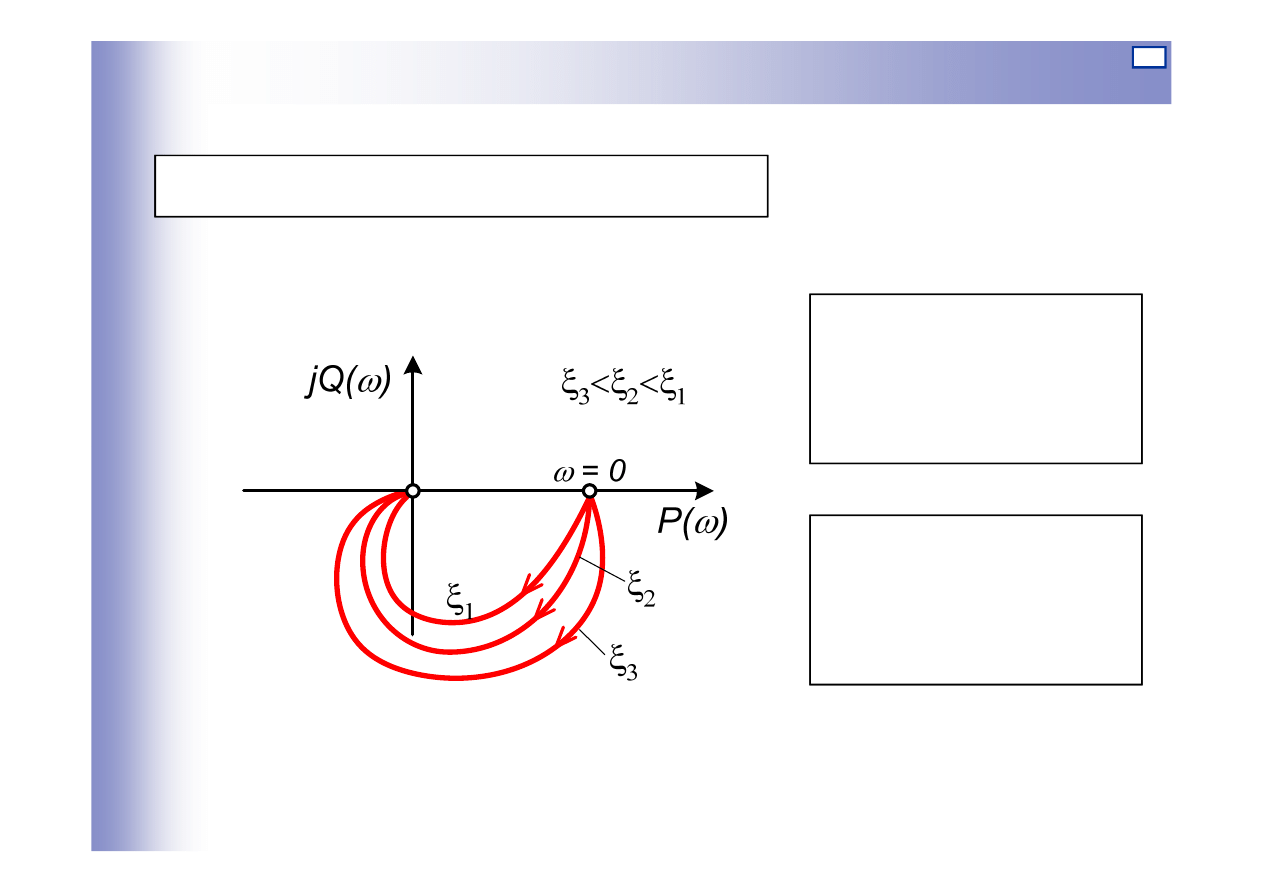
Charakterystyki elementu oscylacyjnego
Charakterystyka amplitudowo-fazowa:
Dla: ω=0
k
P
=
)
0
(
0
)
0
(
=
Q
,
∞
=
ω
Dla: ω=∞
0
)
(
=
∞
P
0
)
(
=
∞
Q
,

23
Charakterystyki elementu oscylacyjnego
(
) (
)
2
0
2
2
2
0
2
0
2
2
)
2
(
)
(
log
20
)
(
)
(
)
(
+
−
=
+
=
ω
ζω
ω
ω
ω
ω
ω
ω
k
Q
P
L
c
Logarytmiczna charakterystyka amplitudowa:
2
0
2
2
0
2
1
log
20
log
20
)
(
+
−
−
=
ω
ω
ζ
ω
ω
ω
k
L
c
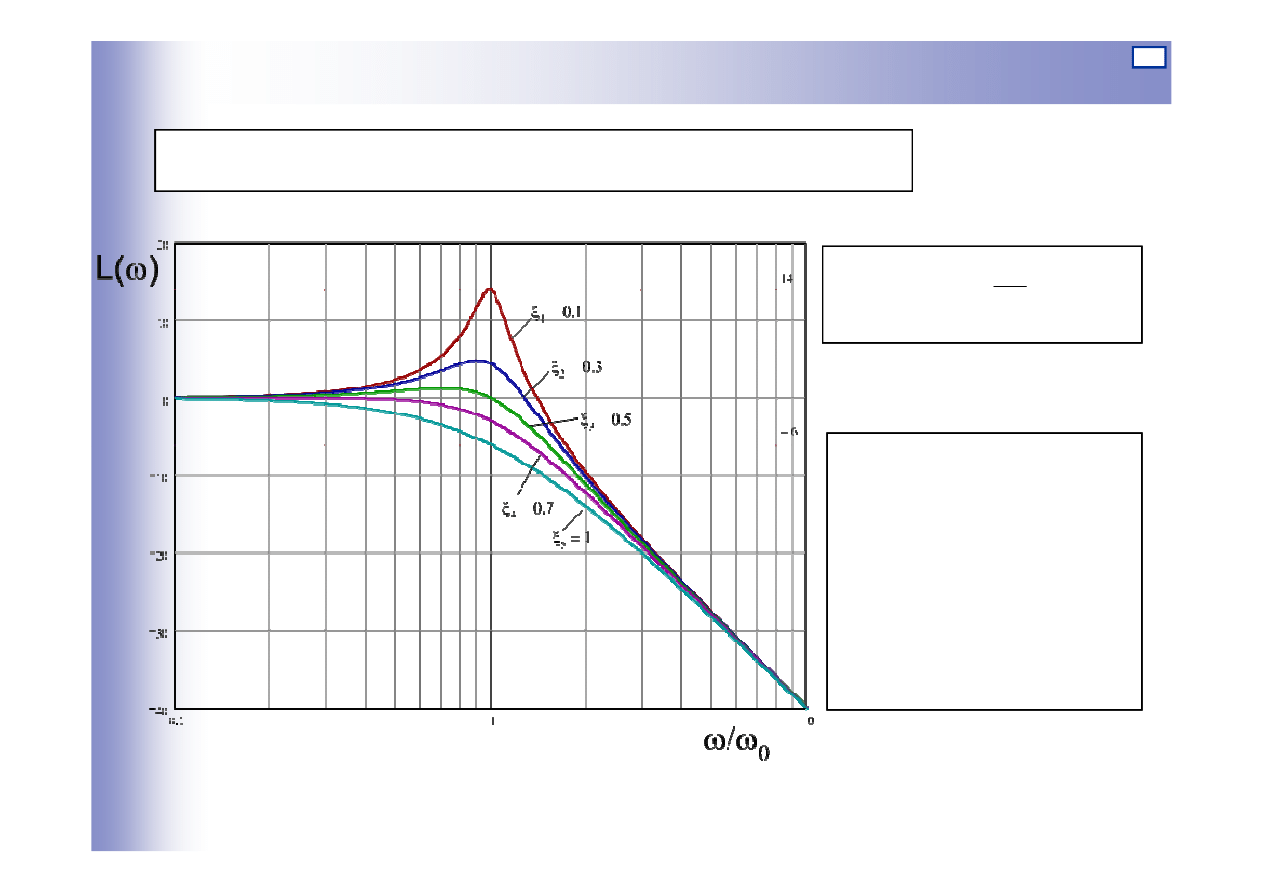
24
Charakterystyki elementu oscylacyjnego
Dla:
ξ
ξξ
ξ=0
∞
=
= )
1
(
0
ω
ω
L
ξ
ξξ
ξ
Logarytmiczna charakterystyka amplitudowa dla k=1:
Dla:
ξ
ξξ
ξ=1 – wartość
graniczna,
przebieg
aperiodyczny
(najkrócej
trwający)
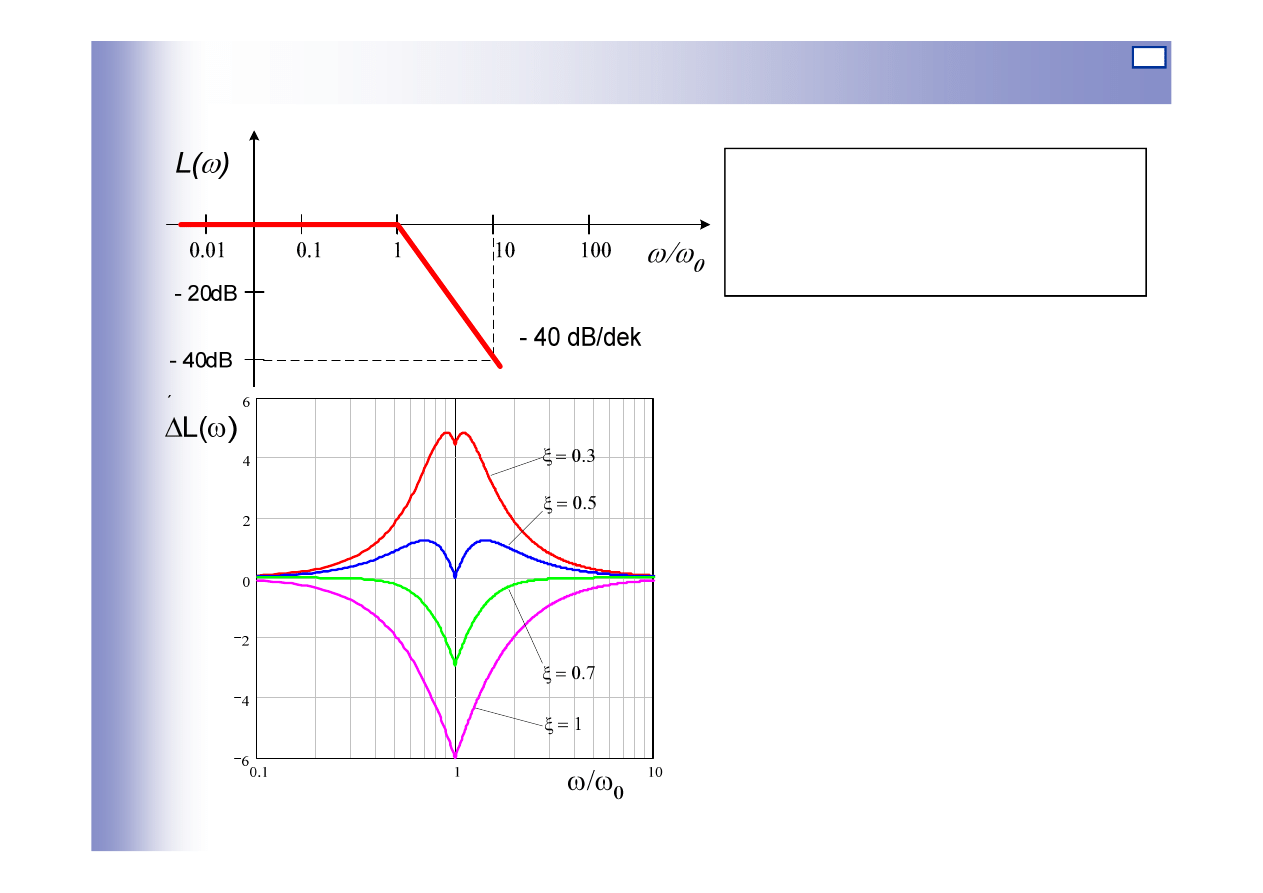
25
Charakterystyki elementu oscylacyjnego
Asymptotyczna
charakterystyka amplitudowa
dla:
1
3
,
0
≤
≤
ξ
Wykres błędu
dB
L
6
)
(
<
∆
ω
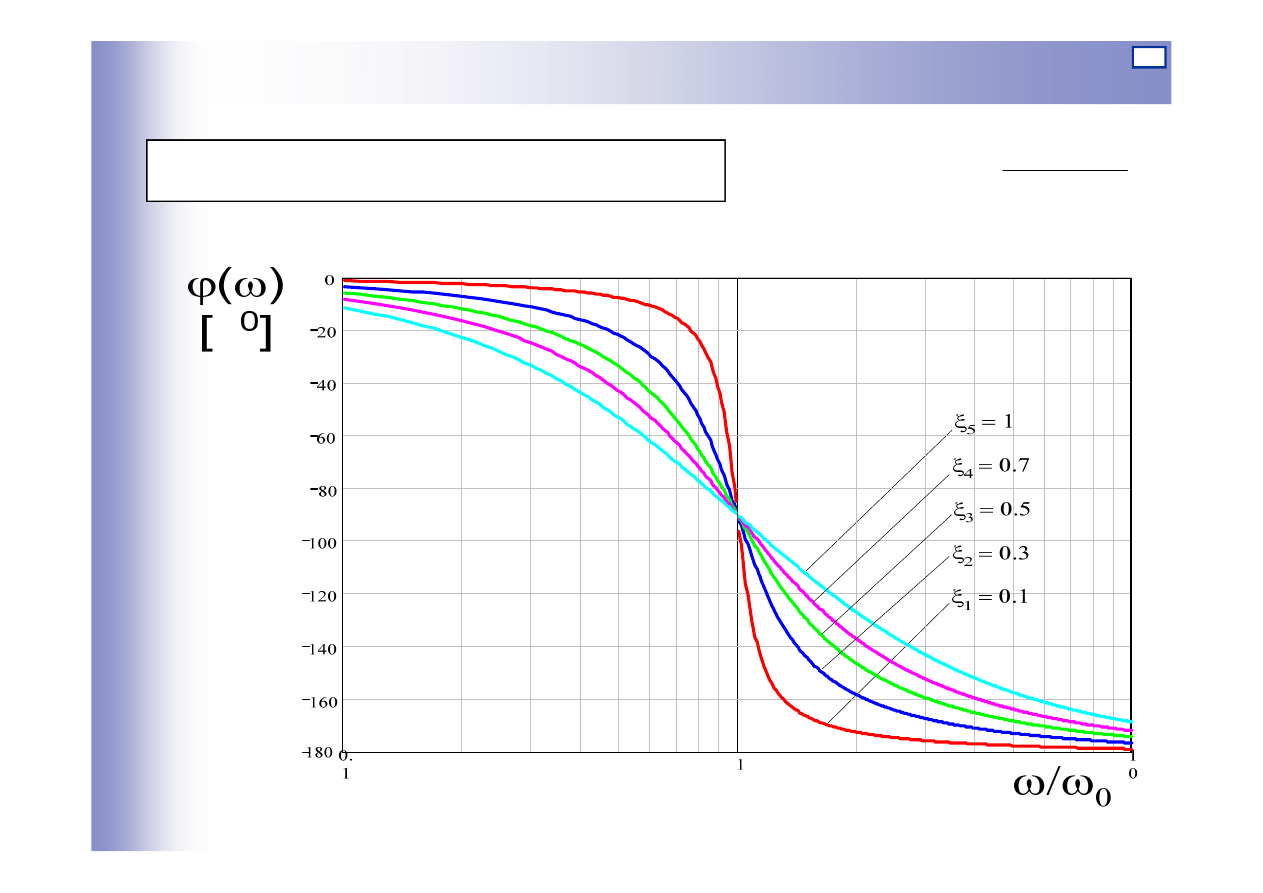
26
Charakterystyki elementu oscylacyjnego
Logarytmiczna charakterystyka fazowa:
−
−
=
2
2
0
0
2
)
(
ω
ω
ω
ζω
ω
ϕ
arctg
27
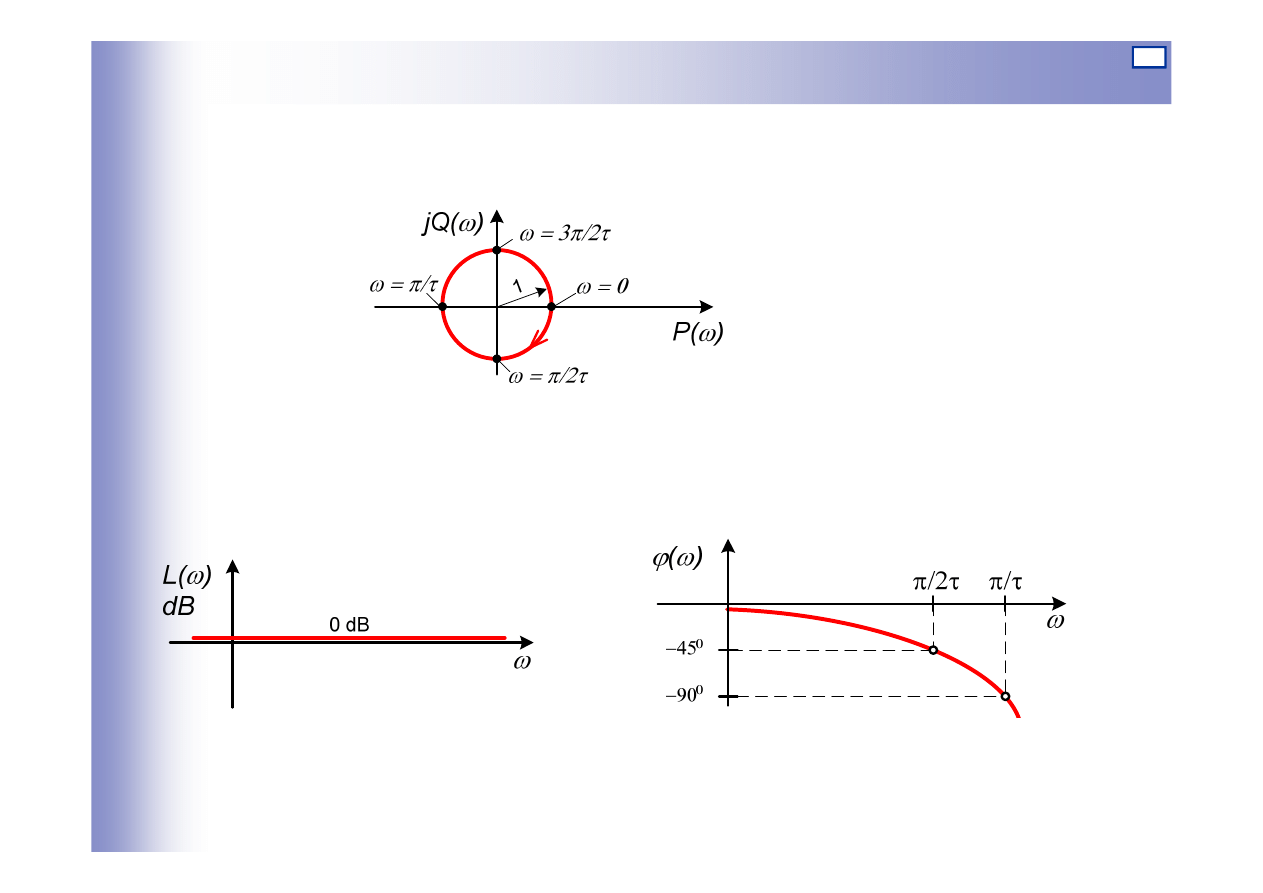
Charakterystyki elementu opóźniającego
ωτ
ω
ωτ
ω
sin
)
(
cos
)
(
−
=
=
Q
P
s
e
τ
−
28
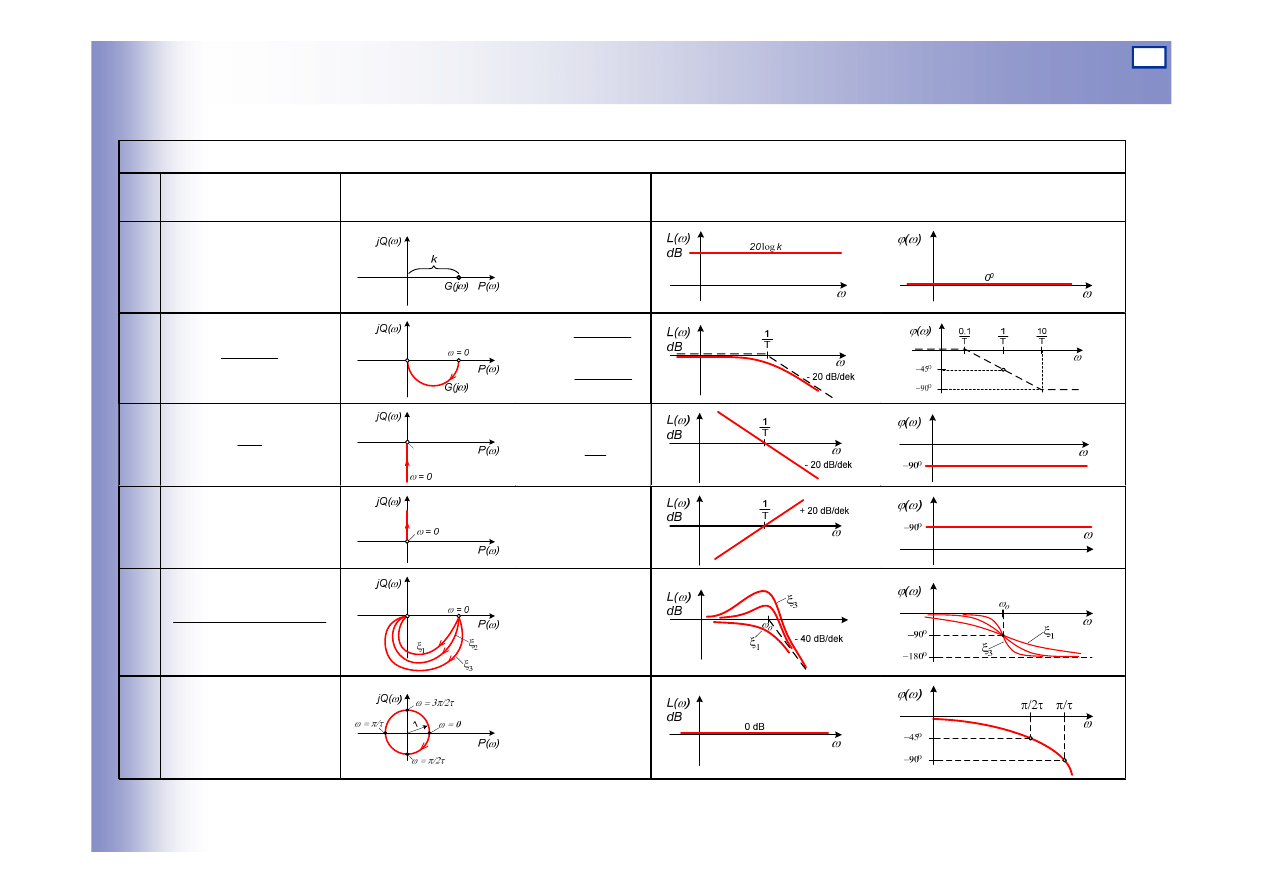
Charakterystyki częstotliwościowe podst. elementów
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE ELEMENTÓW PODSTAWOWYCH
L.p.
Transmitancja
operatorowa
)
(s
G
Wykres charakterystyki amplitudowo-fazowej
)
(
ω
j
G
(transmitancji widmowej)
Wykresy logarytmicznych charakterystyk amplitudowej
)
(
ω
L
i fazowej
)
(
ω
ϕ
1
k
0
)
(
)
(
=
=
ω
ω
Q
k
P
2
1
1
+
Ts
∞
=
ω
1
)
(
1
1
)
(
2
2
2
2
+
−
=
+
=
ω
ω
ω
ω
ω
T
T
Q
T
P
3
1
ω
ω
Q
P
1
)
(
0
)
(
−
=
=
3
Ts
∞
=
ω
ω
ω
T
Q
1
)
(
−
=
4
Ts
∞
=
ω
ω
ω
ω
T
Q
P
=
=
)
(
0
)
(
5
2
0
0
2
2
0
2
ω
ξω
ω
+
+
s
s
k
∞
=
ω
1
2
3
ξ
ξ
ξ
<
<
6
s
e
τ
−
ωτ
ω
ωτ
ω
sin
)
(
cos
)
(
−
=
=
Q
P
29
Charakterystyki elementów szeregowo połączonych
)
(
)
(
2
2
)
(
1
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
ω
n
j
j
j
e
M
j
G
e
M
j
G
e
M
j
G
=
=
=
K
K
K
K
)
(
)
(
)
(
ω
ϕ
ω
ω
n
j
n
n
e
M
j
G
=
)
(
)]
(
)
(
)
(
[
2
1
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
j
j
n
e
M
e
M
M
M
j
G
n
c
K
K+
+
+
=

30
Charakterystyki elementów szeregowo połączonych
Logarytmiczna charakterystyka amplitudowa:
)
(
log
20
)
(
log
20
)
(
log
20
)
(
log
20
)
(
2
1
ω
ω
ω
ω
ω
n
M
M
M
M
L
+
+
+
=
=
K
∑
=
=
n
i
i
L
L
1
)
(
)
(
ω
ω
)
(
)
(
)
(
)
(
2
1
ω
ω
ω
ω
n
M
M
M
M
⋅
⋅
⋅
=
K
=
i
1
∑
=
=
n
i
i
1
)
(
)
(
ω
ϕ
ω
ϕ
Logarytmiczna charakterystyka fazowa:

31
Charakterystyki elementów szeregowo połączonych
Przykład 1:
(
) (
)
{ {
3
2
1
3
2
1
c
3
2
2
1
1
3
2
1
1
1
1
1
)
(
1
1
)
(
+
⋅
+
⋅
⋅
⋅
=
+
⋅
+
⋅
⋅
=
s
T
s
T
s
T
k
s
G
s
T
s
T
s
T
k
s
G
Dla: k=2;
T
1
=1;
T
2
=10;
T
3
=100;
3
2
1
3
2
1
4
3
2
)
(
ω
jQ
)
(
ω
P
32
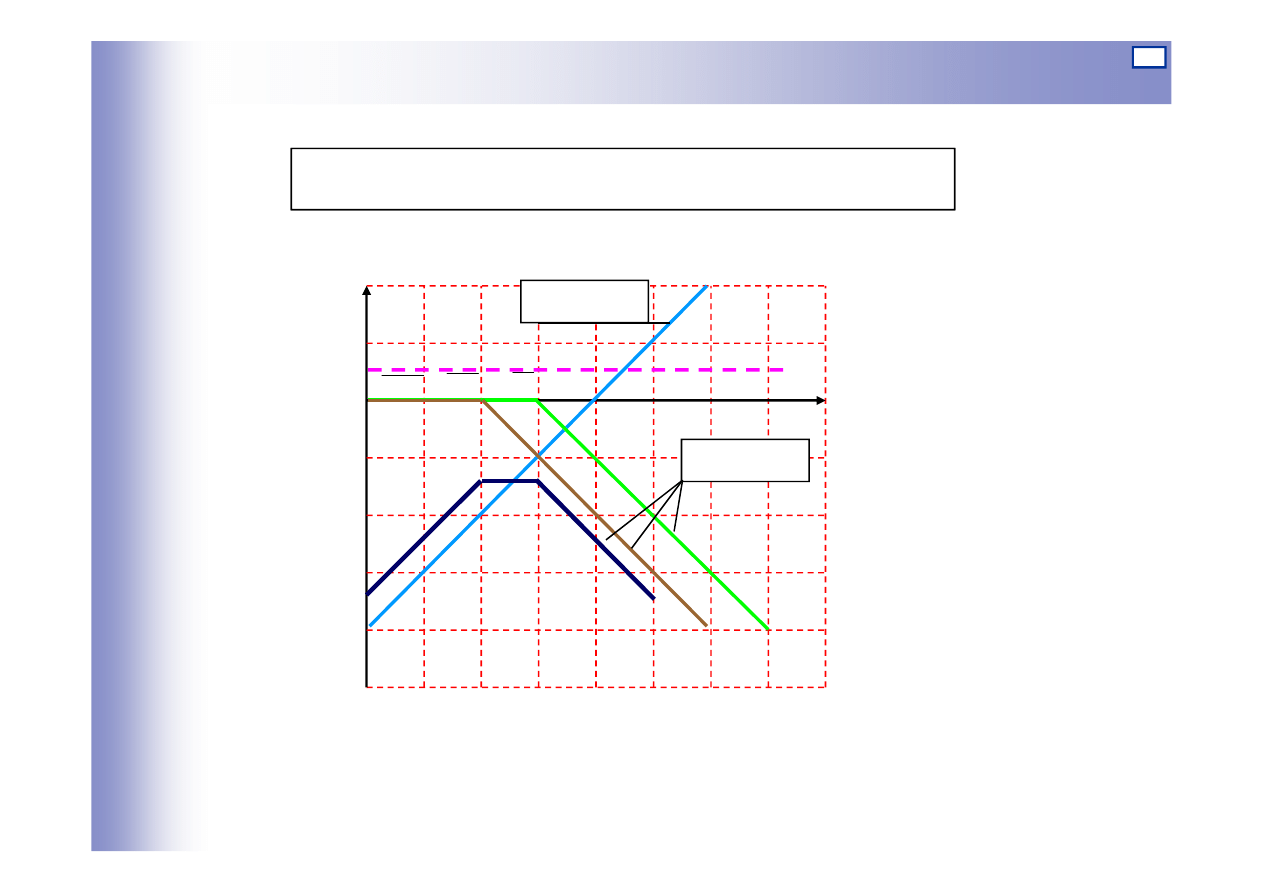
Charakterystyki elementów szeregowo połączonych
1000
1
100
1
10
1
1
10
100 1000
ω
2
1
L(ω)
Logarytmiczna charakterystyka amplitudowa:
-20dB/dek
20dB/dek
6dB
20dB
3
4
c
-20dB/dek
-20dB
-40dB
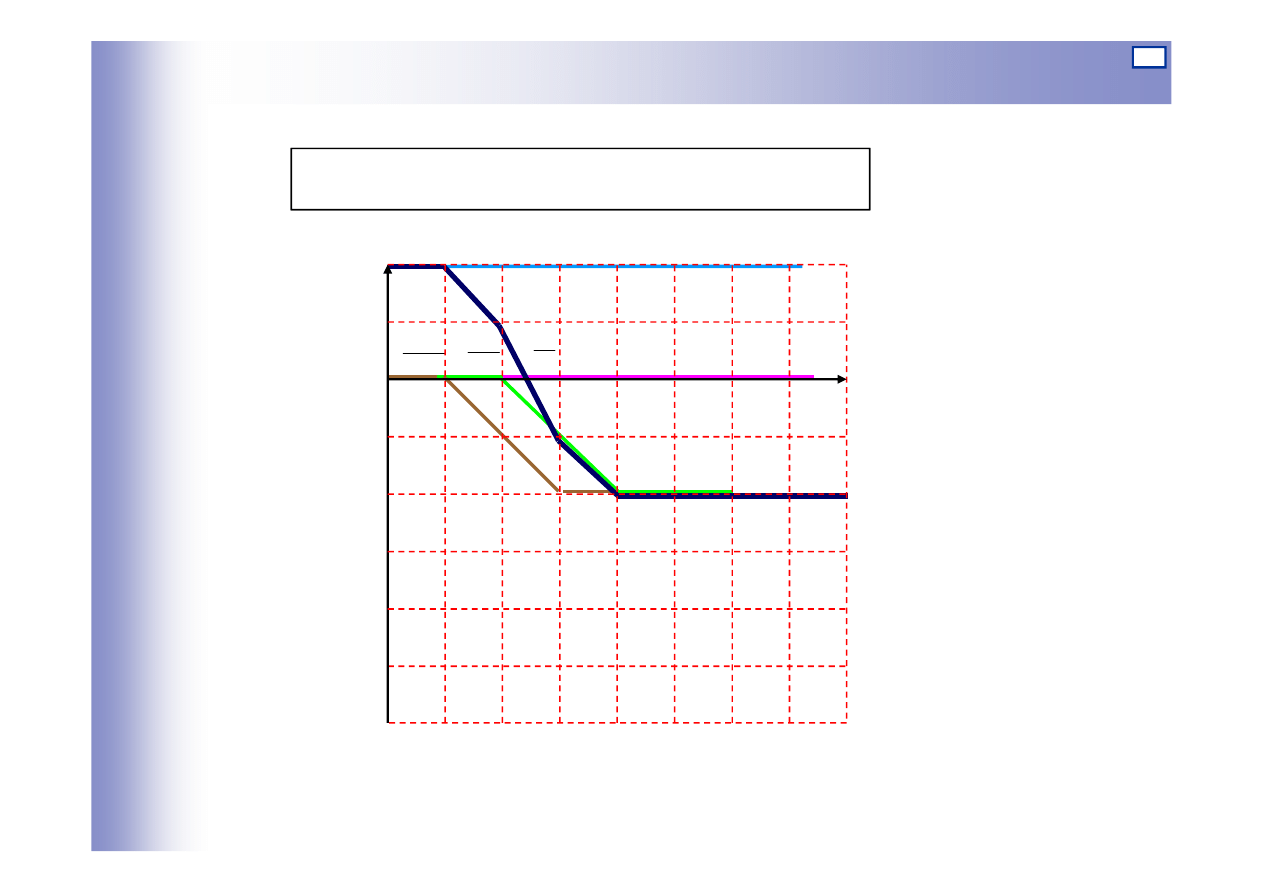
33
Charakterystyki elementów szeregowo połączonych
Logarytmiczna charakterystyka fazowa:
2
4
1
1000
1
100
1
10
1
1
10
100 1000
ω
ϕ
(ω)
-45
0
45
0
3
c
-45
-90
0
-180
0
-270
0

34

35
Podstawy teoretyczne
t
j
e
A
u
ω
ω
)
(
_
=
)]
(
[
_
)
(
ω
ϕ
ω
ω
+
=
t
j
e
A
y
Podstawiając za: x i y parę odpowiadających sobie funkcji harmonicznych
zapisanych w postaci wykładniczej
]
sin
)[cos
(
)
(
1
1
t
j
t
A
e
A
t
j
ω
ω
ω
ω
ω
+
=
)]}
(
sin[
)]
(
){cos[
(
)
(
2
)]
(
[
2
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ϕ
ω
+
+
+
=
+
t
j
t
A
e
A
t
j
Wejście:
Wyjście:
t
j
e
A
u
ω
ω
)
(
1
=
)]
(
[
2
)
(
ω
ϕ
ω
ω
+
=
t
j
e
A
y
)
(
1
)
(
2
)
(
)
(
)
(
)
(
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ω
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
=
j
t
j
j
t
j
e
M
e
A
e
e
A
j
G
Wyszukiwarka
Podobne podstrony:
05 Charakterystyki czestotliwoscio
05 Charakterystyki częstotliwościowe
05 Charakterystyki częstotliwościowe
Ćw 11 Czwórniki bierne charakterystyki częstotliwościowedocx
Charakterystyki czestotliwosciowe
Charakterystyki czestosciowe
Cw Charakterystyki częstotliwościowe, Semestr III PK, Semestr Zimowy 2012-2013 (III), Automatyka, Au
Miernictwo- Zdejmowanie charakterystyk częstotliwościowych przebiegów odkształconych, ?w._
Badanie częstotliwości i charakterystyk częstotliwościowych
Charakterystyki czestotliwosciowe
Charakterystyki częstotliwościowe podstawowych członów dynamicznych v4
05 Charakteryzowanie funkcji narządów organizmu człowieka 2
Charakterystyki czestotliwosciowe
Charakterystyki czestotliwo ciowe wybranych elementow liniowych
PA5 charakterystyki czestotliwosciowe [tryb zgodności]
PROJEKT I?DANIE CZWÓRNIKÓW RC?LEM WYZNACZENIA NAPIĘCIOWEJ CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWEJ
05 Charakteryzowanie funkcji narządów organizmu człowieka
druk, Poziom dźwięku A -poziom ciś akust skorygowanego wg charakterystyki częstotliwościowej A
więcej podobnych podstron