J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
1
Zastosowanie szeregów Fouriera do rozwiązywania tarcz
Ćwiczenie 8
Przypomnienie z teorii szeregów Fouriera:
Jeżeli
( )
f x
– to dowolna funkcja s
pełniająca warunki Dirichleta
w przedziale
( ; )
l l
−
→
( )
0
1
1
cos
sin
2
n
n
n
n x
n x
f x
a
a
b
l
l
π
π
∞
=
=
+
+
∑
to
w każdym przedziale ciągłości funkcji
( )
f x
zachodzi:
0
1
( )
l
l
a
f x dx
l
−
= ⋅
∫
1
( ) cos
l
n
l
n x
a
f x
dx
l
l
π
−
= ⋅
⋅
∫
;
1
( ) sin
l
n
l
n x
b
f x
dx
l
l
π
−
= ⋅
⋅
∫
x
2l
2l
l
l
( )
f x

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
2
Jeżeli funkcja
( )
f x
jest parzysta, to zachodzi
0
n
b
= , natomiast
jeżeli
( )
f x
jest nieparzysta, to zachodzi
0
0
n
a
a
=
= .
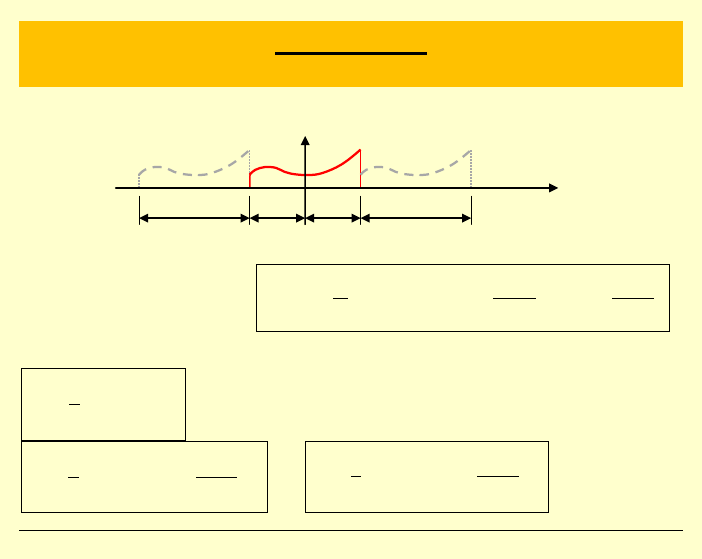
Ze względu na periodyczność
( )
sin
funkcji
i
( )
cos
dla dowolnych
wartości x otrzymujemy powtarzanie się wartości funkcji
( )
f x
,
jak
pokazano to na powyższym rysunku.
( )
f x
Uwagi:
1.
Mówimy, że funkcja
spełnia warunek Dirichleta
w pewnym
przedziale, jeżeli przedział ten można rozłożyć
na
skończoną liczbę podprzedziałów, w taki sposób, że w każdym
podprzedziale funkcja ta jest monotoniczna i ograniczona.
2.
Ważną zaletą szeregów Fouriera jest to, że mogą reprezentować
funkcje nieciągłe (szeregi Taylora reprezentują tylko funkcje, które
posiadają pochodne wszystkich rzędów
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
3
3.
W punktach nieciągłości funkcji
( )
f x
jej szereg Fouriera jest
zbieżny do wartości
(
)
(
)
1
0
0
2
f x
f x
⋅
+
+
−
(patrz: rysunek)
4.
Motywacja współczynnika
1
2
przy
0
a : dla
0
n
= wzór na
n
a
pokrywa się ze wzorem na
0
a (
regularność notacji)
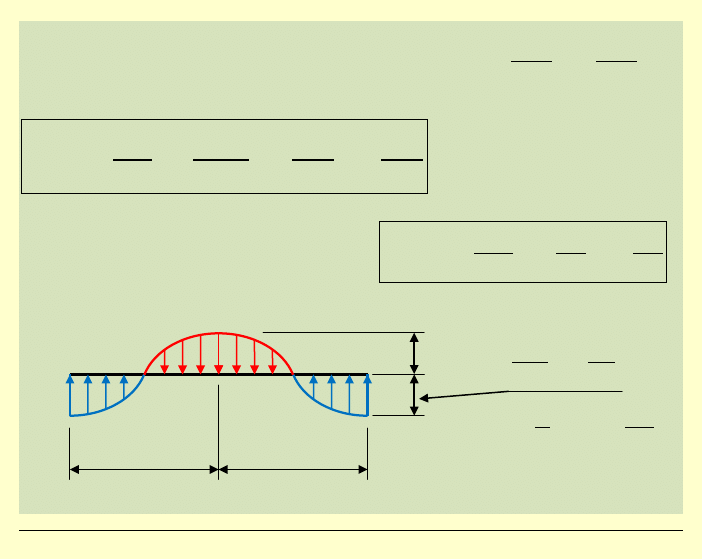
Przykład:
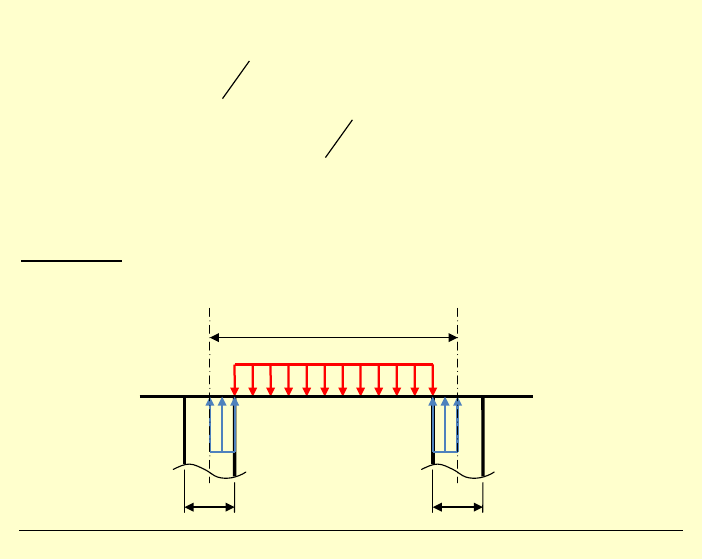
Rozwinięcie obciążenia odcinkowego stałego w szereg
Fouriera
(częsty przypadek w praktyce inżynierskiej)
2l
2c
2c
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
4
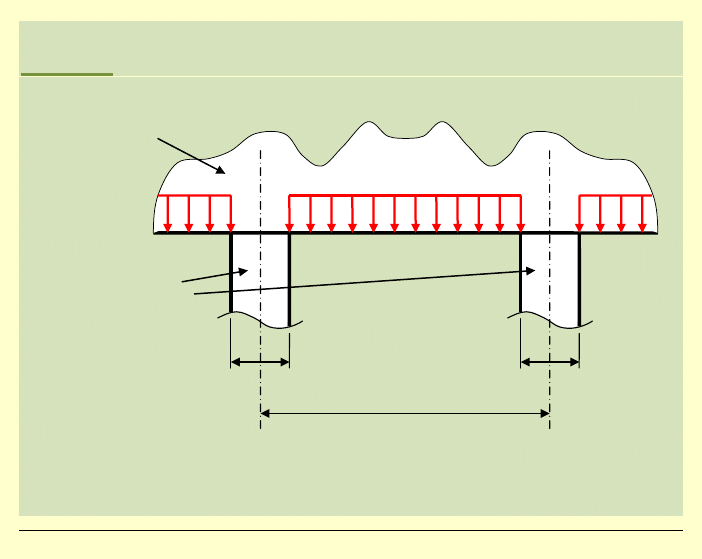
Zadanie:
Rozwinąć funkcję odcinkowo stałą w szereg Fouriera.
(jest to
częsty przypadek w zagadnieniach obciążeń tarcz)
tarcza
2l
2c
2c
g
×
podpory
o szerokości
2c
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
5
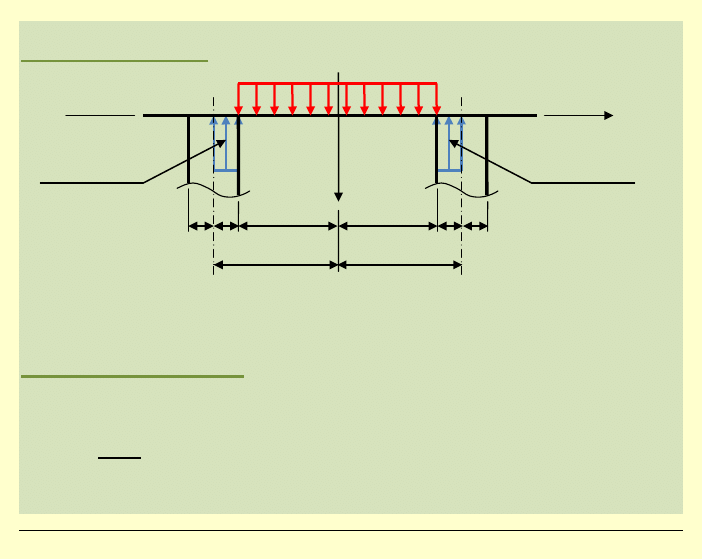
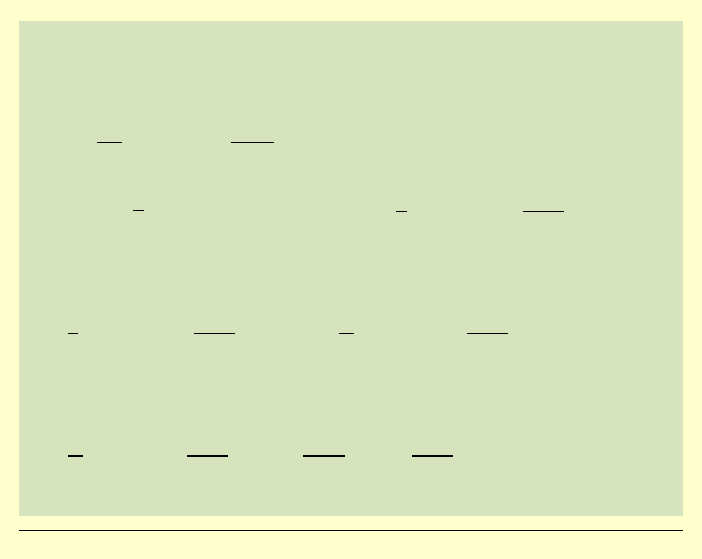
Model obciążenia:
( )
p x
– funkcja
nieciągła, spełnia warunki Dirichleta w
( ; )
l l
−
Rozwiązanie zadania:
Z warunku równowagi rzutów na oś poziomą wynika:
1
l
c
p
p
c
−
= ⋅
( )
p x
l
c
−
c
c
c
c
l
c
−
l
l
x
p
const
=
1
p
const
=
1
p
const
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
6
Zauwa
żmy, iż
( )
p x
jest funkcją parzystą, a zatem:
0
n
b
= !
Rozw
ija się w szereg cosinusowy:
( )
0
1
cos
2
n
n
a
n x
p x
a
l
π
∞
=
+
∑
,
gdzie:
0
1
( )
0
l
l
a
p x dx
l
−
= ⋅
=
∫
oraz:
1
( ) cos
l
n
l
n x
a
p x
dx
l
l
π
−
= ⋅
⋅
∫
Przekształcając, mamy:
1
( ) cos
l
n
l
n x
a
p x
dx
l
l
π
−
= ⋅
⋅
∫
0
2
( ) cos
l
n
n x
a
p x
dx
l
l
π
→
= ⋅
⋅
∫
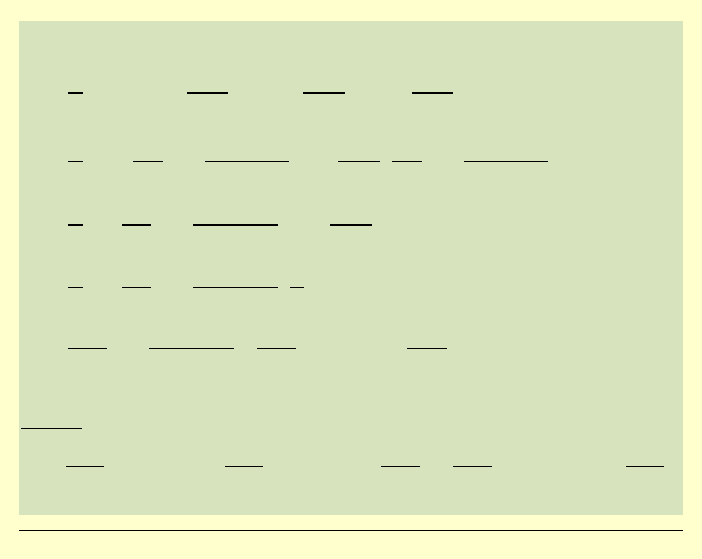
Rozbijając na odpowiednie składniki, otrzymujemy:
0
2
cos
cos
l c
l
n
l c
n x
l
c
n x
a
p
dx
p
dx
l
l
c
l
π
π
−
−
−
= ⋅
⋅
− ⋅
⋅
∫
∫
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
7
Rozwiązując całki, otrzymujemy:
0
2
cos
cos
l c
l
n
l c
n x
l
c
n x
a
p
dx
p
dx
l
l
c
l
π
π
−
−
−
= ⋅
⋅
− ⋅
⋅
∫
∫
2
(
)
(
)
sin
sin
n
l
n
l
c
l
c
l
n
l
c
a
p
p
l
n
l
c
n
l
π
π
π
π
−
−
−
= ⋅
⋅
⋅
+ ⋅
⋅
⋅
2
(
)
sin
1
n
l
n
l
c
l
c
a
p
l
n
l
c
π
π
−
−
= ⋅ ⋅
⋅
⋅ +
2
(
)
sin
n
l
n
l
c
l
a
p
l
n
l
c
π
π
−
= ⋅ ⋅
⋅
⋅
2
(
)
sin
n
pl
n
l
c
a
n c
l
π
π
−
=
⋅
2
sin
pl
n c
n
n c
l
π
π
π
=
⋅
−
Jeżeli: sin(
)
sin
cos
cos
sin
α β
α
β
α
β
−
=
⋅
−
⋅
, to:
2
sin
cos
cos
sin
n
pl
n c
n c
a
n
n
n c
l
l
π
π
π
π
π
=
⋅
⋅
−
⋅
2
cos
sin
pl
n c
n
n c
l
π
π
π
=
⋅ −
⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 8 • KMBiM WILiŚ PG
8
Zauważmy, iż:
( )
cos
1
n
n
π
= −
, więc:
( )
2
1
sin
n
n
pl
n c
a
n c
l
π
π
= − −
⋅
⋅
Podstawiając, otrzymujemy zatem:
( )
( )
1
1
2
sin
cos
n
n
pl
n c
n x
p x
c
n
l
l
π
π
π
∞
=
−
= −
⋅
⋅
⋅
∑
Pierwszy wyraz szeregu, (dla
1
n
= ):
( )
(1)
2
sin
cos
pl
c
x
p
x
c
l
l
π
π
π
=
⋅
⋅
l
l
2
sin
pl
c
c
l
π
π
⋅
4
2
l
p
dla c
równe
l
=
Document Outline
Wyszukiwarka
Podobne podstrony:
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
35) TSiP 2010 11 ćw11
36) TSiP 2010 11 ćw12
24) TSiP 2010 11 ćw06
31) TSiP 2010 11 ćw10
37) TSiP 2010 11 ćw14
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
więcej podobnych podstron