L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
L
INIE WPŁYWOWE SIŁ W BELKACH CIĄGŁYCH
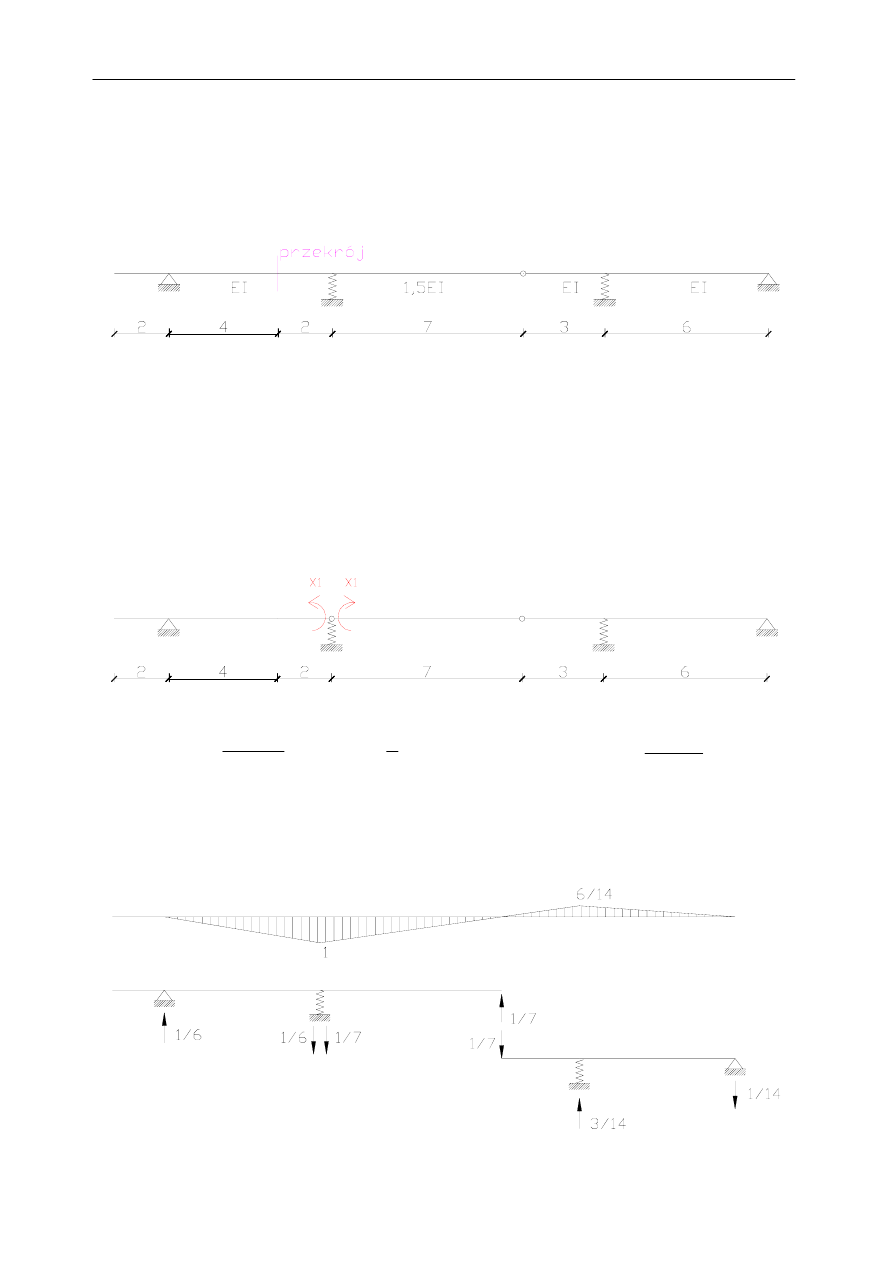
Dla zadanej belki wyznaczyć linie wpływowe momentów i reakcji podporowych oraz
momentów zginających i sił poprzecznych w zaznaczonych przekrojach.
Zadana belka:
Linie wpływowe sił z belkach ciągłych statycznie niewyznaczalnych oblicza się zgodnie ze
wzorem superpozycyjnym:
n
x
x
x
n
x
x
x
n
x
x
x
X
Lw
R
X
Lw
R
X
Lw
R
R
Lw
R
Lw
X
Lw
T
X
Lw
T
X
Lw
T
T
Lw
T
Lw
X
Lw
M
X
Lw
M
X
Lw
M
M
Lw
M
Lw
n
n
n
1
2
2
1
2
1
1
2
0
2
2
1
2
1
1
1
0
1
2
1
1
1
0
...
...
...
2
1
2
1
2
1
=
=
=
=
=
=
=
=
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
=
α
α
α
α
α
α
α
α
α
α
Układ jest statycznie niewyznaczalny więc należy dobrać układ podstawowy i zapisać układ
równań kanonicznych:
{
0
1
1
11
=
+
⋅
P
X
δ
δ
0
8
,
0
1
EI
k
gdzie
k
R
R
ds
EI
M
M
k
i
ik
⋅
=
⋅
⋅
+
⋅
=
∑
∫
δ
∫
⋅
=
∆
ds
EI
M
M
i
P
iP
Obciążenie P jest jedynkowe dlatego zgodnie z konwencją oznaczamy je jako δ
.
Rysuję wykresy momentów od poszczególnych sił jednostkowych:
M
1
[-]
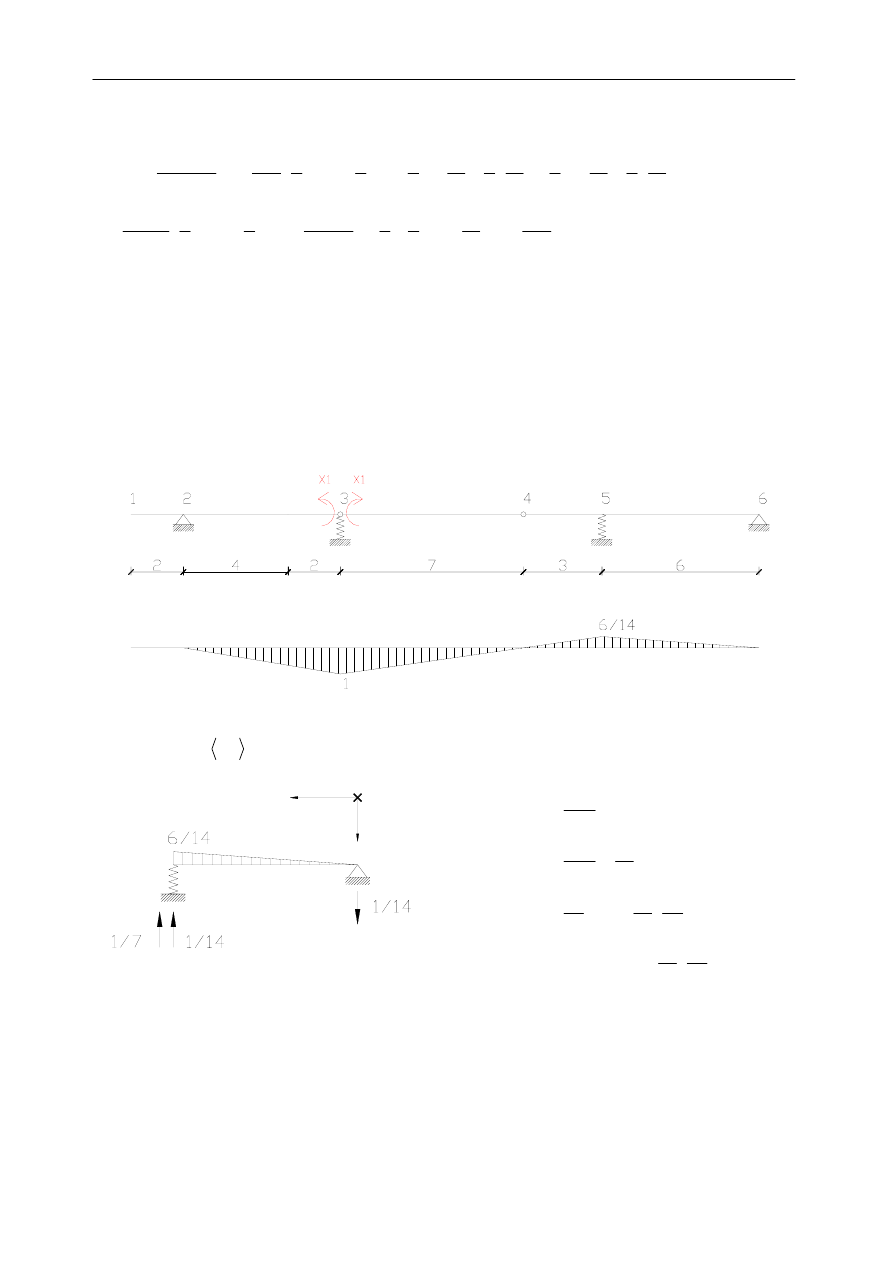
L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
Korzystając z metody Wereszczegina- Mohra całkowania iloczynu dwóch funkcji (w tym
jednej prostoliniowej) otrzymuje się:
21995
,
4
1
14
3
7
1
6
1
8
,
0
1
1
3
2
1
7
2
1
5
,
1
1
14
6
3
2
14
6
6
2
1
14
6
3
2
14
6
3
2
1
1
3
2
1
6
2
1
1
0
2
2
0
0
0
1
1
11
⋅
=
+
+
⋅
+
⋅
⋅
⋅
⋅
+
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
⋅
=
∫
EI
EI
EI
EI
ds
EI
M
M
δ
Należy wykorzystać twierdzenie Maxwella:
)
(
)
(
1
1
x
x
P
P
δ
δ
=
Zamiast obliczać przemieszczenie w danym punkcie od poruszającej się siły P, obliczamy
przemieszczenia wszystkich punktów nad którymi stanie siła P (czyli linię ugięcia) od
założonej siły jedynkowej X
1
=1
Aby obliczyć linię wpływu X
1
należy obliczyć linie ugięcia w każdym z przedziałów
wykorzystując równanie różniczkowe linii ugięcia.
O
DCINEK
6
,
5
∈
x
x
y
( )
6
14
1
2
14
1
14
1
3
0
2
0
2
2
0
2
2
0
x
Cx
D
y
EI
x
C
dx
dy
EI
x
dx
y
d
EI
x
M
dx
y
d
EI
⋅
+
+
=
⋅
+
=
⋅
=
−
=

L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
Warunki brzegowe:
112
43
14
36
6
8
10
14
3
6
14
1
8
,
0
1
14
3
8
,
0
1
14
3
1
14
3
1
6
0
0
0
3
0
0
0
−
=
→
+
⋅
=
⋅
⋅
+
+
=
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
=
=
=
→
=
=
C
C
x
Cx
D
EI
EI
EI
k
y
x
D
y
x
Znając stałe można napisać równanie różniczkowe linii ugięcia:
+
⋅
−
=
84
112
43
1
3
0
x
x
EI
y
O
DCINEK
5
,
4
∈
x
x
y
( )
6
7
1
2
7
3
2
7
1
7
3
7
1
7
3
3
2
0
2
0
2
2
0
2
2
0
x
x
x
C
D
y
EI
x
x
C
x
d
y
d
EI
x
x
d
y
d
EI
x
M
x
d
y
d
EI
⋅
−
⋅
+
+
=
⋅
+
⋅
+
=
⋅
−
=
−
=
Warunki brzegowe:
( )
(
)
112
101
2
6
14
1
112
43
6
0
0
112
30
8
,
0
1
14
3
8
,
0
1
14
3
0
2
0
0
0
=
→
⋅
+
−
=
=
=
=
=
=
⋅
⋅
⋅
=
→
⋅
⋅
=
=
C
C
x
x
x
EI
EI
D
EI
y
x
ϕ
ϕ
Znając stałe można napisać równanie różniczkowe linii ugięcia:
⋅
−
⋅
+
⋅
+
=
3
2
0
42
1
14
3
112
101
112
30
1
x
x
x
EI
y

L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
O
DCINEK
4
,
3
∈
x
x'
y'
( )
3
)
'
(
14
1
'
'
5
,
1
)
'
(
14
1
'
'
5
,
1
)
'
(
7
1
)
'
(
'
5
,
1
'
)
'
(
'
2
0
2
0
2
2
2
0
2
2
0
x
Cx
D
y
EI
x
C
dx
dy
EI
x
x
d
y
d
EI
x
M
x
d
y
d
EI
⋅
−
+
=
⋅
⋅
+
=
⋅
⋅
=
⋅
−
=
Warunki brzegowe:
(
)
( )
672
115
3
343
14
1
7
224
1431
8
,
0
1
42
13
5
,
1
8
,
0
1
42
13
'
7
'
224
1431
3
42
1
3
14
3
3
112
101
112
30
1
5
,
1
1
3
0
'
0
'
0
0
0
3
2
0
0
=
→
⋅
−
⋅
+
=
⋅
⋅
−
⋅
⋅
⋅
⋅
−
=
=
=
→
⋅
−
⋅
+
⋅
+
=
⋅
=
=
=
=
C
C
EI
EI
EI
y
x
D
EI
D
EI
x
y
x
y
x
Znając stałe można napisać równanie różniczkowe linii ugięcia:
⋅
−
⋅
+
⋅
=
3
'
14
1
'
672
115
224
1431
5
,
1
1
'
3
0
x
x
EI
y
O
DCINEK
3
,
2
∈
x
x
y
( )
36
2
2
6
1
1
6
1
1
3
2
0
2
0
2
2
0
2
2
0
x
x
x
C
D
y
EI
x
x
C
x
d
y
d
EI
x
x
d
y
d
EI
x
M
x
d
y
d
EI
+
−
+
=
⋅
+
⋅
−
=
⋅
+
−
=
−
=
Warunki brzegowe:
1008
2081
6
2
36
6
336
130
0
0
6
336
130
8
,
0
1
42
13
0
0
=
→
+
−
⋅
+
−
=
=
=
−
=
→
⋅
⋅
−
=
=
C
C
y
x
D
EI
y
x
Znając stałe można napisać równanie różniczkowe linii ugięcia:
+
−
⋅
+
−
=
36
2
1008
2081
336
130
1
3
2
0
x
x
x
EI
y
L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
O
DCINEK
2
,
1
∈
x
x
y
( )
x
C
D
y
EI
C
x
d
y
d
EI
x
d
y
d
EI
x
M
x
d
y
d
EI
+
=
=
=
−
=
0
0
2
2
0
2
2
0
0
Warunki brzegowe:
( )
(
)
1008
943
3
6
1008
2081
6
0
0
0
0
0
−
=
→
+
−
=
=
=
=
=
=
→
=
=
C
C
x
x
x
D
y
x
ϕ
ϕ
Znając stałe można napisać równanie różniczkowe linii ugięcia:
⋅
−
=
x
EI
y
1008
943
1
0
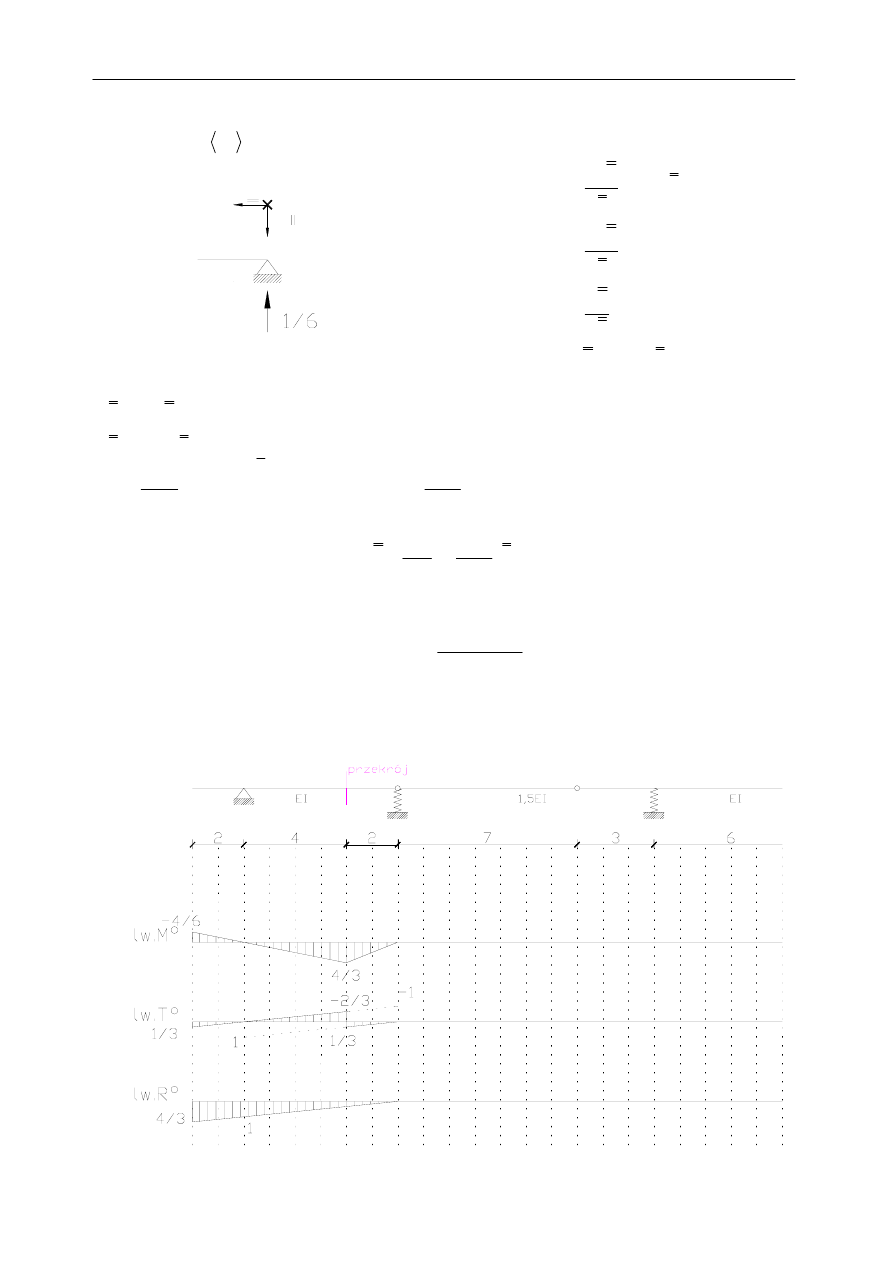
Znając równania linii ugięcia belki można obliczyć linię wpływu X
1
zgodnie z zależnością:
11
0
1
1
)
(
δ
δ
EI
x
lwX
P
⋅
−
=
Do obliczenia linii wpływu potrzebne są jeszcze linie wpływu M
0
, R
0
, T
0
w układzie
statycznie wyznaczalnym i wartości M, R, T w przekroju od wprowadzonej siły X
1
=1. Całość
na końcu zostanie zestawiona w tabeli.
Linie wpływu w układzie statycznie wyznaczalnym:
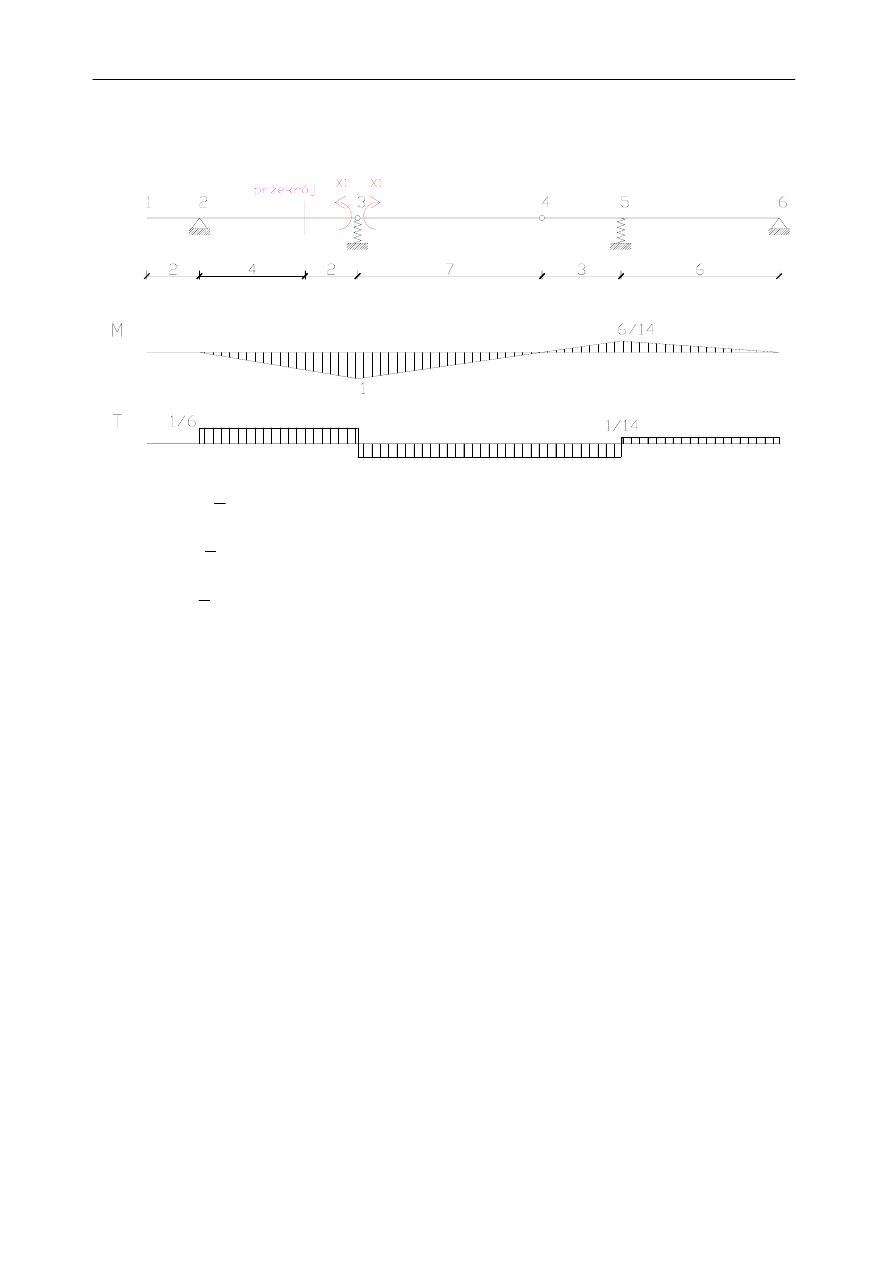
L
INIE WPŁYWOWE W BELKACH
Politechnika Poznańska
Adam Łodygowski ®
Wartości M, T i R od wprowadzonej siły X
1
=1:
6
1
)
1
(
6
1
)
1
(
3
2
)
1
(
1
1
1
=
=
=
=
=
=
X
R
X
T
X
M
α
α
L
INIE
WP
Ł
YWOW
E W BEL
K
A
C
H
Pol
itechni
ka P
ozna
ńs
ka
Adam
Ł
od
ygow
sk
i ®
8
M
0
T
0
R
0
M od X=1
T 0d X=1
R od X=1
Lw. X
1
Lw. M
Lw. T
Lw. R
0
-0,667
0,33
333
3
1,33
333
3 0,66
666
7 0,16
666
7 0,16
666
7
2
0,44
692
5
-0,368
72
0,40
782
1 1,40
782
1
1
-0,334
0,16
666
7
1,16
666
7 0,66
666
7 0,16
666
7 0,16
666
7
1
0,22
346
2
-0,184
36
0,20
391
1,20
391
2
0
0
1
0,66
666
7
0,16
666
7
0,16
666
7
0 0
0 0 1
3
0,33
4
-0,166
67
0,83
333
3 0,66
666
7 0,16
666
7 0,16
666
7
5
-0,215
11
0,18
992
9
-0,202
52
0,79
748
2
4
0,66
7
-0,333
33
0,66
666
7 0,66
666
7 0,16
666
7 0,16
666
7
4
-0,390
72
0,40
618
8
-0,398
45
0,60
154
7
5
1
-0,5
0,5
0,66
666
7 0,16
666
7 0,16
666
7
3
-0,487
34
0,67
510
7
-0,581
22
0,41
877
7
6
1,33
4
-0,666
67
0,33
333
3 0,66
666
7 0,16
666
7 0,16
666
7
2
-0,465
48
1,02
301
6
-0,744
25
0,25
575
4
1,33
4
0,33
333
3
0,33
333
3 0,66
666
7 0,16
666
7 0,16
666
7
2
-0,465
48
1,02
301
6
0,25
575
4
0,25
575
4
7
0,66
7
0,16
666
7
0,16
666
7 0,66
666
7 0,16
666
7 0,16
666
7
1
-0,285
63
0,47
624
5 0,11
906
1 0,11
906
1
8
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
0
0,09
168
5
0,06
112
3 0,01
528
1 0,01
528
1
9
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
6
-0,358
98
-0,239
32
-0,059
83
-0,059
83
10
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
5
-0,674
24
-0,449
49
-0,112
37
-0,112
37
11
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
4
-0,876
65
-0,584
43
-0,146
11
-0,146
11
12
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
3
-0,988
78
-0,659
19
-0,164
8
-0,164
8
13
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
2
-1,033
22
-0,688
81
-0,172
2
-0,172
2
14
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
1
-1,032
51
-0,688
34
-0,172
09
-0,172
09
15
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
0
-1,009
24
-0,672
82
-0,168
21
-0,168
21
16
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
2
-0,648
85
-0,432
56
-0,108
14
-0,108
14
17
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
1
-0,322
31
-0,214
87
-0,053
72
-0,053
72
18
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
0
-0,063
47
-0,042
32
-0,010
58
-0,010
58
19
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
5
0,10
226
4
0,06
817
6 0,01
704
4 0,01
704
4
20
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
4
0,18
336
9
0,12
224
6 0,03
056
2 0,03
056
2
21
0
0
0 0,66
666
7
0,16
666
7
0,16
666
7 3 0,19
676
9
0,13
118
0,03
279
5
0,03
279
5
22
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
2
0,15
939
0,10
626
0,02
656
5 0,02
656
5
23
0
0
0
0,66
666
7 0,16
666
7 0,16
666
7
1
0,08
815
8
0,05
877
2 0,01
469
3 0,01
469
3
24
0
0
0
0,66
666
7
0,16
666
7
0,16
666
7
0 0
0 0 0


L
INIE
WP
Ł
YWOW
E W BEL
K
A
C
H
Pol
itechni
ka P
ozna
ńs
ka
Adam
Ł
od
ygow
sk
i ®
8
L
INIE W
PŁ
YW
O
W
E W
UK
Ł
ADZIE STATYCZNIE NIEW
Y
Z
NACZAL
NYM ZGO
DNI
E Z
W
A
RTO
Ś
CIAMI NA ST
RONIE
7:
Wyszukiwarka
Podobne podstrony:
Linie wpływowe sił w belkach ciągłych
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil krata
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil luk
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil rama
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil luk
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil krata
Mechanika Budowli - Linie wpływu, BUDOWNICTWO, Mechanika budowli
cwicz mechanika budowli metoda przemieszczen rama ugiecie
Linie wpływowe sił w układach statycznie wyznaczalnych
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli metoda przemieszczen rama
Mechanika Budowli - Linie wpływu, BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika Budowli
cwicz mechanika budowli metoda przemieszczen rama temperatura
cwicz mechanika budowli metoda przemieszczen rama osiadanie
więcej podobnych podstron