Zintegrowane Systemy Zarządzania
1
Ocena opłacalności
decyzji inwestycyjnych
dr Robert Piechota
Finansowanie usług turystycznych
Decyzje inwestycyjne przedsiębiorstw
1.
Działania mające na celu poszukiwanie efektywnych projektów
inwestycyjnych
- wybór tych, które maksymalizują wartość firmy -
decyzje dotyczące rodzaju inwestycji (rzeczowe – finansowe), a
także wielkości i struktury aktywów
2.
Decyzje dotyczące źródeł finansowania
przyjętego programu
inwestycyjnego – struktury kapitału firmy
Zintegrowane Systemy Zarządzania
2
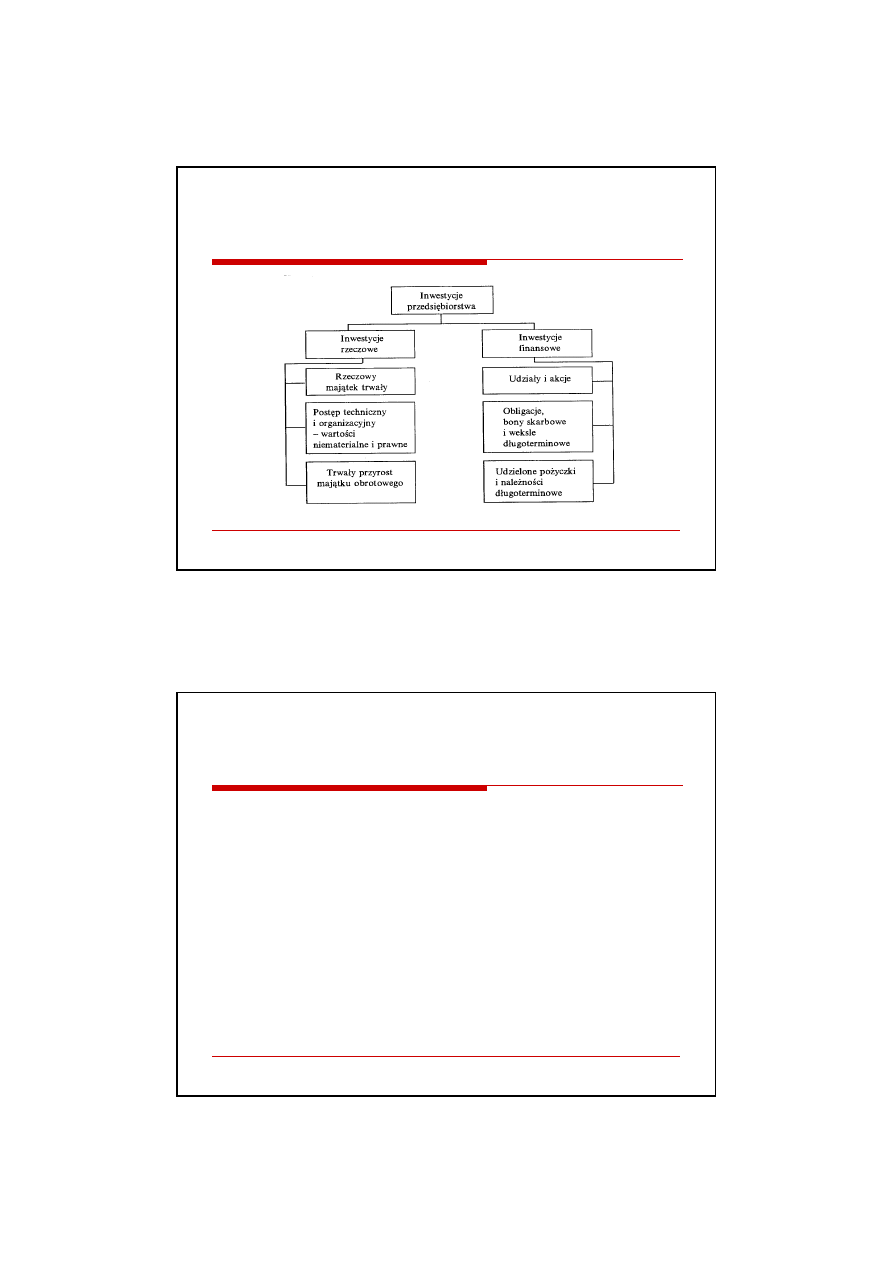
Rodzaje przedsięwzięć inwestycyjnych
Źródło: D.Krzemińska, Finanse przedsiębiorstwa. Wyd. WSB, Warszawa
2000, s.176.
Analiza finansowej efektywności
przedsięwzięcia
Analiza finansowa jest stosowana od samego początku procesu
formułowania koncepcji przedsięwzięcia, pełniąc rolę weryfikatora
rozważanych rozwiązań.
Analiza
ta
stanowi
prezentację
oczekiwanych
rezultatów
finansowych,
wynikających
z
podjęcia
przedsięwzięcia,
posiadającego ostatecznie wybrane rozwiązania.
Zintegrowane Systemy Zarządzania
3
Cele analizy finansowej:
1.
Ocena alternatywnych rozwiązań przedsięwzięcia, w celu wyboru najbardziej
uzasadnionego
2.
Sprawdzenie
i
udowodnienie,
że
przedsięwzięcie
będzie
generowało
zysk
odpowiedni w stosunku do zainwestowanego kapitału oraz ryzyka
3.
Przedstawienie potrzeb finansowych, które występują w kolejnych okresach
wdrażania i funkcjonowania przedsięwzięcia oraz sposobu ich pokrycia
4.
Sprawdzenie finansowanej efektywności przedsięwzięcia w warunkach innych od
zakładanych
5.
Oszacowanie minimalnego poziomu aktywności gospodarczej przedsięwzięcia,
warunkującego osiągnięcie jego finansowej opłacalności
6.
Oszacowanie finansowej efektywności przedsięwzięcia w warunkach inflacji.
Inwestycyjne przepływy pieniężne
netto
Oszacowanie przepływów pieniężnych jest podstawową czynnością w
trakcie analizy finansowej.
W większości decyzji dotyczących planowania przedsięwzięć
inwestycyjnych dla zarządzającego istotniejsze znaczenie odgrywa Cash
Flow, a więc przewidywany przepływ pieniężny, niż wykazany zysk
przedsięwzięcia.
Cash Flow jest kategorią znacznie realniej oddającą wielkość nakładów i
efektów związanych z inwestycją, a więc w rezultacie uzyskany dochód.
Przepływy pieniężne (CF) są to strumienie różnic (sald) pomiędzy
wpływami i wydatkami (strumienie netto), jakie zgodnie z dokonanymi
prognozami wystąpią w poszczególnych okresach (najczęściej latach)
realizacji, a następnie eksploatacji przedsięwzięcia.
Zintegrowane Systemy Zarządzania
4
W praktyce oznacza to, że:
1.
Wydatki inwestycyjne, finansowane ze środków własnych
inwestora, uwzględnia się w kalkulacji opłacalności
przedsięwzięcia w tych okresach, w których rzeczywiście są
ponoszone
2.
Wydatki inwestycyjne, finansowanie środkami obcymi, np.
kredytem bankowym uwzględnia się w okresach spłaty rat
kredytu i odsetek, a więc w latach faktycznego wypływu
pieniądza z przedsiębiorstwa.
Dochody również odzwierciedlają faktyczne wpływy pieniądza do
przedsiębiorstwa, a nie wyniki wynikające z ewidencji księgowej,
tzn. wyniki bilansowe.
Strumienie finansowe przedsięwzięcia
1. Strumień inwestycji
a) wydatki przedrealizacyjne (koszty związane z uzyskaniem kredytu,
koszty prac studialnych, koszty nadzoru inwestycyjnego, koszty
zaplecza budowy, koszty uruchomienia budowy i przekazywania do
eksploatacji),
b) wydatki na rzeczowe składniki majątku trwałego (koszty: zakupu
ziemi, przygotowania terenu, wznoszenia budynków, zakupu maszyn
i urządzeń, cła, ubezpieczenia, montażu oraz wyposażenia
pomocniczego),
c) nakłady na inwestycje (wymiana obiektów o krótszym okresie
eksploatacji np. samochodów, nakłady na inwestycje towarzyszące)
d) rezerwy – nieprzewidziane wydatki spowodowane zmianą zakresu
rzeczowego inwestowania, zmianą sposobu realizacji inwestycji,
rezerwy na wzrost cen.
Zintegrowane Systemy Zarządzania
5
f) nakłady na stworzenie kapitału obrotowego –nakłady niezbędne do
sfinansowania przyrostu zapotrzebowania na środki obrotowe
(zapasy surowców, półwyrobów, należności), które zwiększają się
wraz ze wzrostem poziomu aktywności gospodarczej
przedsięwzięcia.
Prawidłowe oszacowanie środków obrotowych ma szczególne
znaczenie w analizie przedsięwzięć produkcyjnych, gdyż w tym
przypadku udział kapitału obrotowego w całości bywa znaczący.
Niedoszacowanie tego składnika może być przyczyną utraty
płynności finansowej, szczególnie w początkowym okresie
funkcjonowania obiektu.
2. Strumień eksploatacyjny:
a) strumień przychodów – wynikających z ostatecznie przyjętych w
studium wykonalności prognozy sprzedaży towarów i usług. Strumień
ten opracowuje się przynajmniej dla całego okresu objętego analizą, a
więc począwszy od rozpoczęcia eksploatacji, aż do ostatniego roku
okresu obliczeniowego,
b) strumień kosztów operacyjnych –bieżące funkcjonowanie obiektu
(surowce, materiały podstawowe, media, robocizna bezpośrednia,
części zamienne, opakowania, koszty marketingu, koszty
ogólnowydziałowe).
Zintegrowane Systemy Zarządzania
6
3. Wartość likwidacyjna netto - wartość majątku, jaką posiada
przedsiębiorstwo w ostatnim roku objętym analizą finansową
przedsięwzięcia. Przy jej obliczaniu uwzględnia się:
a) kapitał trwały,
b) koszty likwidacji majątku,
c) wartość odzyskanego kapitału obrotowego.
Jako wartość likwidacyjną majątku trwałego można przyjąć hipotetyczny
przychód z jego sprzedaży pomniejszony o koszty likwidacji i podatek.
Wartość likwidacyjna powiększa (lub pomniejsza) wartość przepływów
finansowych w ostatnim roku eksploatacji objętym analizą.
Roczne przepływy gotówki netto
w okresie eksploatacji
CF = S – K – (S – K –Am)T
gdzie: CF - przepływy gotówki w danym roku
S - przychód ze sprzedaży
K - koszty bieżące (bez amortyzacji)
Am - amortyzacja
T - stopa podatku dochodowego
Ponieważ amortyzacja nie stanowi wypływu pieniądza inwestora a
uwzględniana jest w kalkulacji zysku (i w wyliczaniu płaconego od zysku
podatku), jest ona dodawana do zysku po opodatkowaniu, przy szacowaniu
strumienia pieniężnego generowanego przez podmiot gospodarczy.
Zintegrowane Systemy Zarządzania
7
Przepływy pieniężne stanowią podstawę do dokonania syntetycznej
oceny
finansowej efektywności przedsięwzięcia.
W tym celu stosuje się następujące metody:
1)
prostego okresu zwrotu,
2)
księgowej stopy zwrotu,
3)
wartości bieżącej netto,
4)
wewnętrznej stopy zwrotu.
Prosty okres zwrotu (payback period)
Przez okres zwrotu rozumie się czas niezbędny do odzyskania
początkowych nakładów na realizację przedsięwzięcia z osiąganych
nadwyżek finansowych (zysk netto + amortyzacja).
Okres zwrotu jest miarą, która określa ile czasu potrzeba, aby suma
przepływów pieniężnych z inwestycji pokryła poniesione na nią
wydatki.
Nadwyżki te obejmują zysk netto oraz amortyzację i są obliczane dla
kolejnych lat funkcjonowania przedsięwzięcia.
W przypadku, gdy źródłem finansowania części nakładów jest kredyt
bankowy, zaleca się uwzględnienie w obliczeniach również kosztów
finansowych ponoszonych przez inwestora z tego tytułu.
Zintegrowane Systemy Zarządzania
8
W przypadku zastosowania kryterium okresu zwrotu, projekt
inwestycyjny należy zaakceptować, jeżeli okres zwrotu projektu jest
niższy od dopuszczalnego okresu przyjętego przez decydenta.
W przypadku zastosowania tego kryterium do porównania efektywności
dwóch projektów, za lepszy uznaje się projekt o krótszym okresie zwrotu.
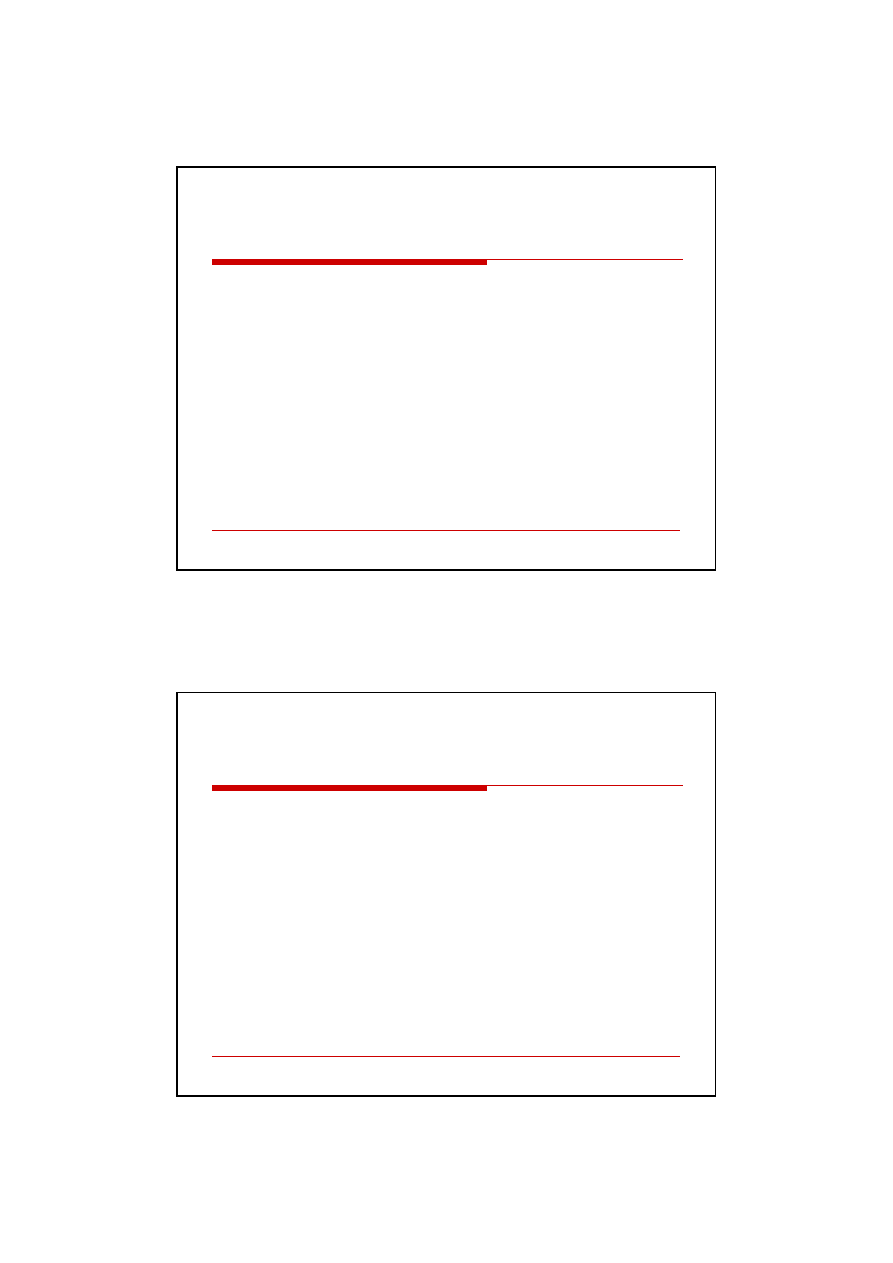
gdzie:
P - okres zwrotu
t - ostatni rok, na koniec którego nakłady pozostają niezwrócone,
N
o
- nakłady niezwrócone na koniec roku t
PT -
przychody
netto (wpływy) w roku następnym
PT
N
t
P
o
Przykład
Dysponując następującymi danymi obliczyć prosty okres zwrotu.
Maksymalny wymagany okres zwrotu nakładów wynosi 3 lata.
PROSTY OKRES ZWROTU;
Lata: 0, 1, 2, 3, 4,
Przepływy
pieniężne
: - 4 000, 1 700, 2 200, 2 400, 1 600
No = 4 000 - (1 700+2 200) = 100,
PT = 2 400, t = 2
T = t + No/PT
T = 2 + 100 / 2 400 = 2,042
0,042 * 365 dni = 15 dni
W 15 dniu trzeciego roku wpływy wyrównają nakłady inicjujące.
Zintegrowane Systemy Zarządzania
9
Zalety i wady
Zalety:
1)
wskaźnik jest łatwy do wyliczenia,
2)
daje obraz płynności projektu,
3)
pozwala wyeliminować przedsięwzięcia najbardziej ryzykowne,
o długim okresie zwrotu.
Wady:
1)
nie uwzględnia wartości pieniądza w czasie,
2)
brak informacji, co stanie się z realizowanym projektem po
upływie okresu zwrotu, jaką efektywnością będzie się on
charakteryzował,
3)
brak informacji o tak podstawowym parametrze projektu,
jakim jest jego rentowność.
Metoda księgowej stopy zwrotu
(Accounting rate of return ARR)
Księgową stopę zwrotu określa się jako przeciętną stopę zwrotu z
inwestycji z całego okresu eksploatacji obiektu powstałego z
inwestycji.
Projekt powinien zostać zaakceptowany, jeżeli wyliczona dla niego
stopa zwrotu jest wyższa od stopy zwrotu wymaganej przez
decydenta.
Spośród dwóch projektów porównywanych przy zastosowaniu tego
kryterium lepszy jest ten, który charakteryzuje się wyższą stopą
zwrotu
Zintegrowane Systemy Zarządzania
10
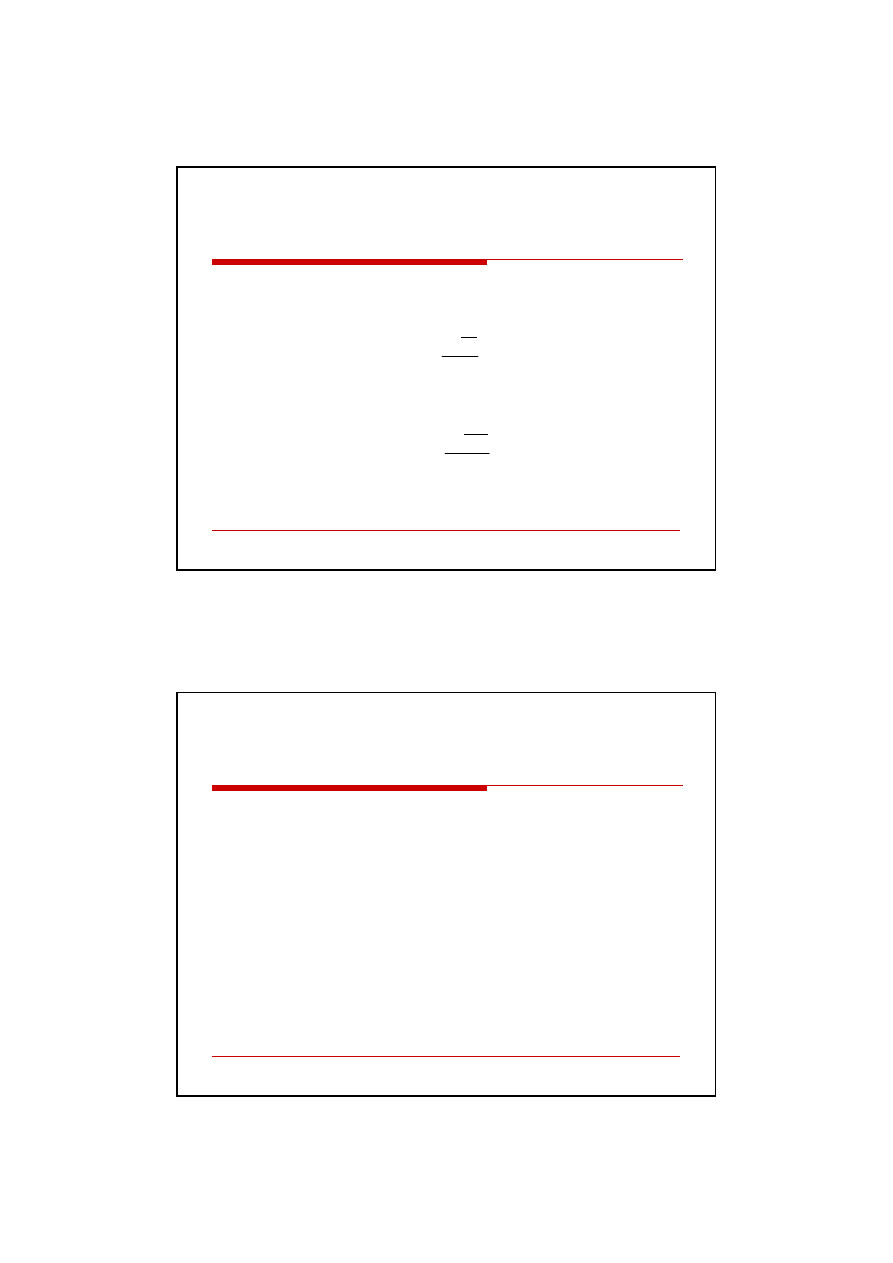
Można obliczać według dwóch wariantów:
1) na podstawie zysków:
2) na podstawie przepływów pieniężnych
Gdzie:
n – liczba okresów eksploatacji projektu
Io – początkowy wydatek inwestycyjny
o
n
i
i
Z
I
n
Z
ARR
0
o
n
i
i
CF
I
n
CF
ARR
0
Zalety i wady
Zalety:
1)
wskaźnik jest łatwy do wyliczenia,
2)
pozwala wyeliminować przedsięwzięcia nierentowne
Wady:
1)
nie uwzględnia zmiennej wartości pieniądza w czasie,
2)
posługuje się wielkościami średnimi, czyli nie bierze pod uwagę
rozkładu strumienia pieniądza w czasie,
3)
wykorzystuje kategorię zysku księgowego, a nie preferowane w
finansach przepływy pieniężne
Zintegrowane Systemy Zarządzania
11
Metody dyskontowe
Najbardziej precyzyjnym narzędziem oceny opłacalności
przedsięwzięć rozwojowych są dyskontowe metody rachunku
ekonomicznego.
Uwzględniają one, w przeciwieństwie do prostych metod oceny,
rozłożenie w czasie przewidywanych wpływów i wydatków
związanych z badaną inwestycją.
Metoda dyskonta pozwala sprowadzić do porównywalności
nakłady i efekty realizowane w różnych okresach czasu.
Wartość bieżąca netto
(Net Present Value NPV)
Metoda NPV pozwala określić obecną wartość wpływów i wydatków
pieniężnych związanych z realizacją ocenianego
przedsięwzięcia rozwojowego.
Wartość zaktualizowana netto projektu jest równa sumie
zdyskontowanych przepływów pieniężnych w kolejnych latach
objętych rachunkiem efektywności inwestycji
Inaczej mówiąc NPV wyraża zdyskontowaną, czyli zaktualizowaną
na dany moment (najczęściej pierwszy rok), wielkość
przepływów pieniężnych, jaką dane przedsięwzięcie przyniesie
przedsiębiorstwu
Zintegrowane Systemy Zarządzania
12
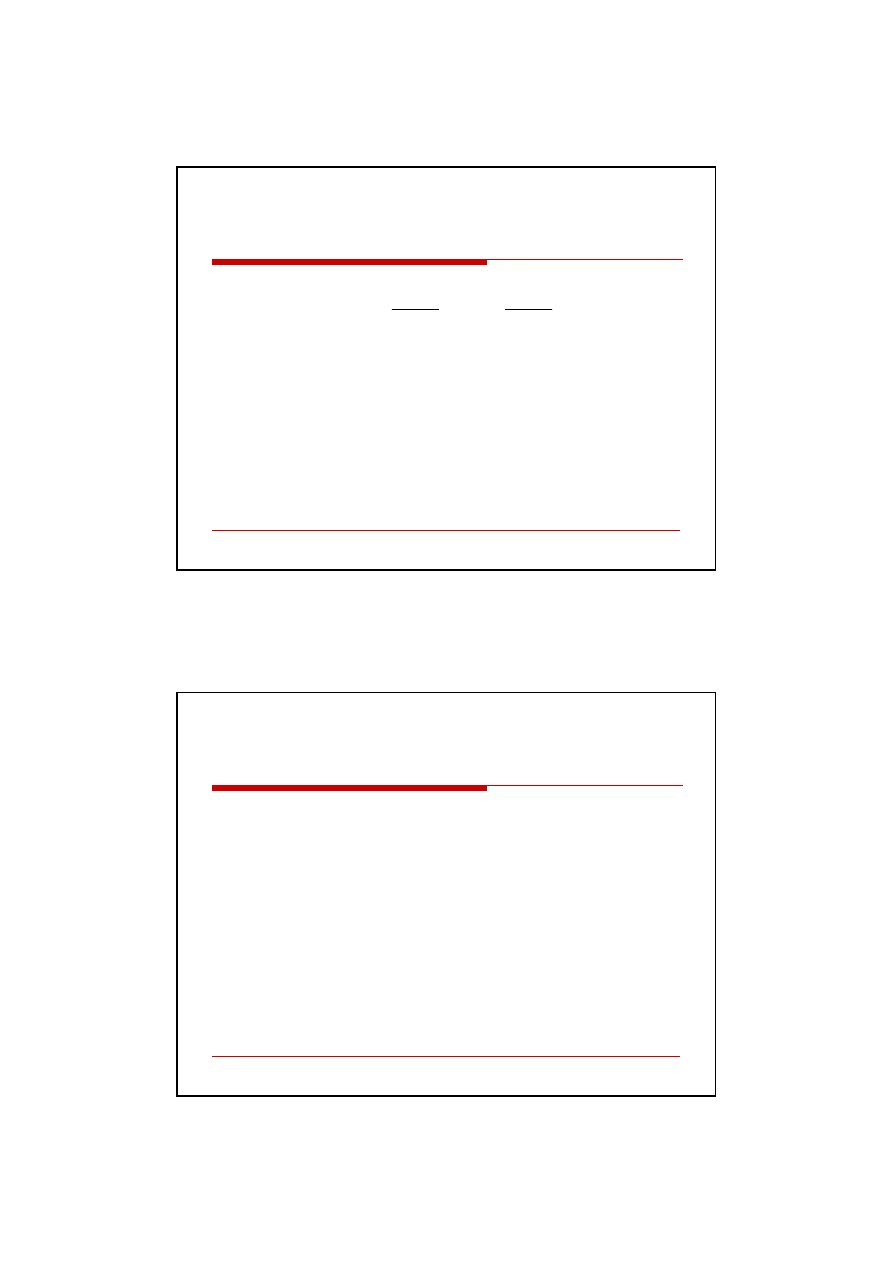
gdzie:
NPV - wartość bieżąca netto,
CF - przepływy pieniężne (bez nakładów inwestycyjnych) w kolejnych latach
okresu obliczeniowego,
Io - nakłady inwestycyjne w kolejnych latach okresu obliczeniowego,
r - stopa procentowa (koszt kapitału),
i - liczba okresów w danym horyzoncie inwestycyjnym.
n
i
i
o
n
i
i
i
r
CF
I
r
CF
NPV
0
0
1
)
1
(
)
1
(
Zasady wyboru projektu
Decyzja o podjęciu projektu zapada na podstawie NPV w następujący
sposób:
NPV > 0 – realizacja, projekt zwiększa zasoby przedsiębiorstwa
NPV < 0 – odrzucone, projekt zmniejsza zasoby przedsiębiorstwa
NPV = 0 - nie ma znaczenia.
Jak wynika z powyższych formuł, im wyższa jest stopa dyskontowa przyjęta
do obliczeń, tym niższe jest NPV.
Przy wykorzystaniu tego kryterium do porównania efektywności dwóch
projektów, za lepszy uznaje się ten o większej wartości NPV.
Zintegrowane Systemy Zarządzania
13
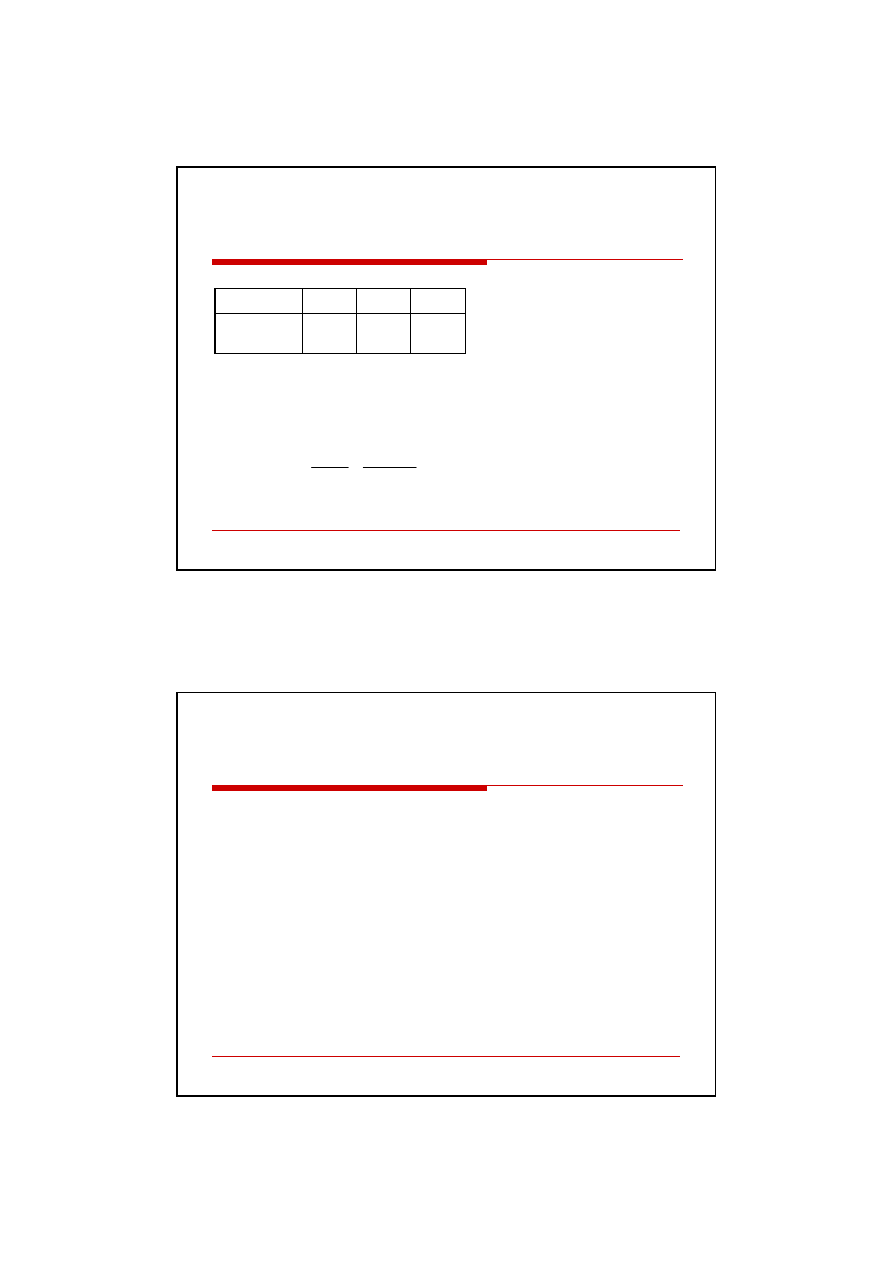
Przykład
Okres
0
1
2
Przepływy
pieniężne (CF
i)
(2000)
1700
1800
Źródło: Opracowanie własne.
Stopa dyskontowa właściwa dla projektu wynosi 20%.
Mając takie dane możemy obliczyć wartość NPV dla danego projektu inwestycyjnego.
67
,
666
)
2
,
0
1
(
1800
0,2
1
1700
-2000
NPV
2
Poziom NPV uzależniony jest z jednej strony od wielkości i
rozłożenia w czasie przepływów pieniężnych netto, z drugiej
strony natomiast od przyjętej do obliczeń stopy procentowej.
Podniesienie stopy procentowej prowadzi do obniżenia
zaktualizowanej wartości przepływów pieniężnych w kolejnych
latach okresu obliczeniowego.
W przypadku inwestycji charakteryzujących się ujemnymi
przepływami pieniężnymi w początkowych latach tego okresu,
a dodatnimi w dalszych latach, wielkość NPV ulega obniżeniu.
Zintegrowane Systemy Zarządzania
14
Cechy metody NPV
1.
Uwzględnia zmianę wartości pieniądza w czasie.
2.
Uwzględnia wszystkie przepływy pieniężne związane z danym
przedsięwzięciem.
3.
Mierzy wzrost wartości przedsiębiorstwa, wywołany przez dane
przedsięwzięcie.
4.
W przypadku kilku przedsiębiorstw umożliwia sumowanie
poszczególnych wartości NPV.
5.
Daje niezawodną wskazówkę, umożliwiającą akceptację
przedsięwzięcia.
6.
W przypadku porównywalnych przedsięwzięć (np. jednakowy okres
eksploatacji) pozwala dokonać jednoznacznej hierarchizacji.
Ścisła zależność występująca pomiędzy omawianymi wielkościami
ekonomicznymi wskazuje, że wybór poziomu stopy procentowej ma
istotne znaczenie dla racjonalności wyników rachunku ekonomicznego.
Stopa ta odzwierciedla w tym przypadku graniczną, wymaganą przez
inwestora, rentowność przedsięwzięcia rozwojowego.
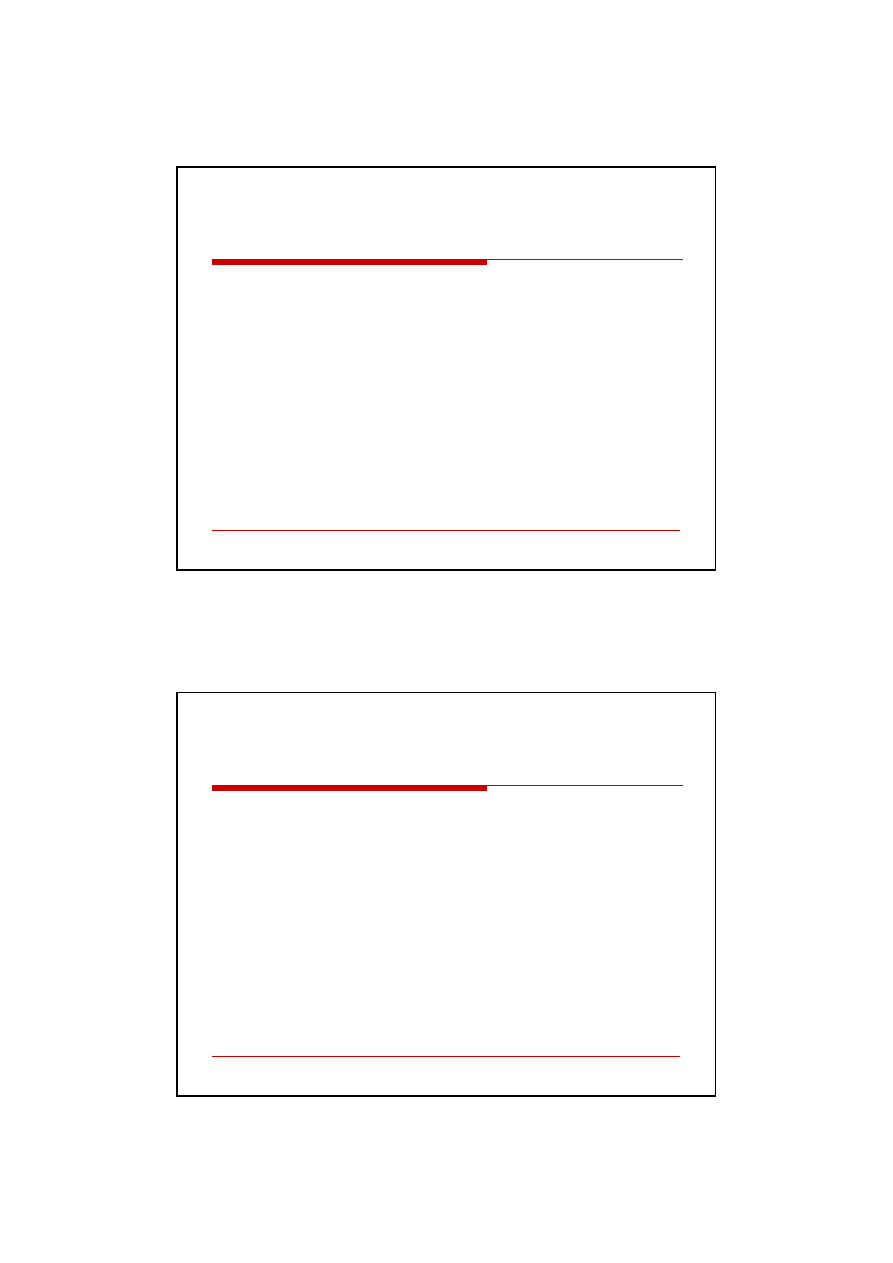
Ocena opłacalności projektów A i B
Okres
Współczynnik
dyskonta (1+r)
t
dla r = 18%
Projekt A
Projekt B
Przepływy pieniężne netto
Nominalne
Zdyskontowane
Nominalne
zdyskontowane
0
1
- 28000
- 28000
- 35000
- 35000
1
0,847458
8000
6780
8000
6780
2
0,718184
8000
5745
8000
5745
3
0,608631
8000
4869
9000
5478
4
0,515789
8000
4126
10000
5158
5
0,437109
8000
3497
18000
7868
6
0,370432
-
-
11000
4075
7
0,313925
-
-
4000
1256
NPV = 6780 + 5745 + 4869 +
4126 + 3497 – 28000 = - 2983
NPV = 6780 + 5745 + 5478
+ 5158 + 7868 + 4075
+1256 – 35000 = 1360
NPV A < 0, projekt jest
nieopłacalny
NPV B > 0, projekt nadaje się do
realizacji
Zintegrowane Systemy Zarządzania
15
Najwięcej trudności sprawia określenie wielkości stopy
dyskontowej. Od niej głównie zależy NPV przedsięwzięcia.
Trudno jest określić precyzyjnie wielkość, jaką powinna przyjąć.
Określa się ją najczęściej porównując z innymi stopami
procentowymi, występującymi na rynku kapitałowym.
Jeżeli przyszły dochód jest absolutnie pewny, to stopa dyskontowa
(inaczej nazywana jako „okazyjny koszt kapitału”) jest stopą
procentową bezpiecznych obligacji rządowych.
Zalety NPV:
1. Wartość przedsięwzięcia zależy od przyszłych strumieni
przepływów pieniężnych, strumienie pieniężne generowane w
przeszłości są bez znaczenia dla oceny opłacalności
inwestycji
2. NPV opiera się jedynie na prognozowanych przepływach
pieniężnych z danego przedsięwzięcia oraz na alternatywnym
koszcie kapitału. Nie jest uzależniona od gustów
kierownictwa, doboru metod księgowania – jest obiektywna
3. Uwzględnia fakt, że każda złotówka dzisiaj jest warta więcej
niż złotówka jutro, gdyż można ją dzisiaj zainwestować i
otrzymać dochód z odsetek
4. Wartości zaktualizowane można sumować, gdyż są mierzone w
wartościach odniesionych do tego samego momentu w czasie
Zintegrowane Systemy Zarządzania
16
Wewnętrzna stopa zwrotu
(Internal rate of return IRR)
IRR to stopa procentowa, przy której obecna wartość strumieni wydatków
pieniężnych jest równa obecnej wartości strumieni wpływów pieniężnych.
Jest to więc taka stopa procentowa, przy której wartość zaktualizowana
netto ocenianego przedsięwzięcia rozwojowego jest równa zero (NPV = 0).
Miernik NPV wyraża efektywność inwestycji w określonej kwocie pieniężnej,
a miernik wewnętrznej stopy zwrotu wyraża tę samą efektywność inwestycji
w formie procentu
IRR jest oczekiwaną stopą dochodu danego projektu
inwestycyjnego
Jeśli wewnętrzna stopa zwrotu jest wyższa od kosztu środków
wykorzystanych do sfinansowania projektu, pozostaje
nadwyżka po opłaceniu kapitału i nadwyżka ta stanowi korzyść
akcjonariuszy firmy
Podejmując projekt, którego IRR jest wyższa od kosztu kapitału,
zwiększa się wartość majątku akcjonariuszy. Gdy zaś
wewnętrzna stopa zwrotu jest mniejsza od kosztu kapitału,
wówczas podjęcie projektu narzuca koszty na obecnych
akcjonariuszy
Zintegrowane Systemy Zarządzania
17
Aby obliczyć wewnętrzną stopę zwrotu należy przyrównać równanie
na NPV do zera. Przy założeniu, że znane są przepływy
pieniężne (CF
i
) realizowane w kolejnych okresach, otrzymamy
równanie n-tego stopnia z jedną niewiadomą w postaci IRR
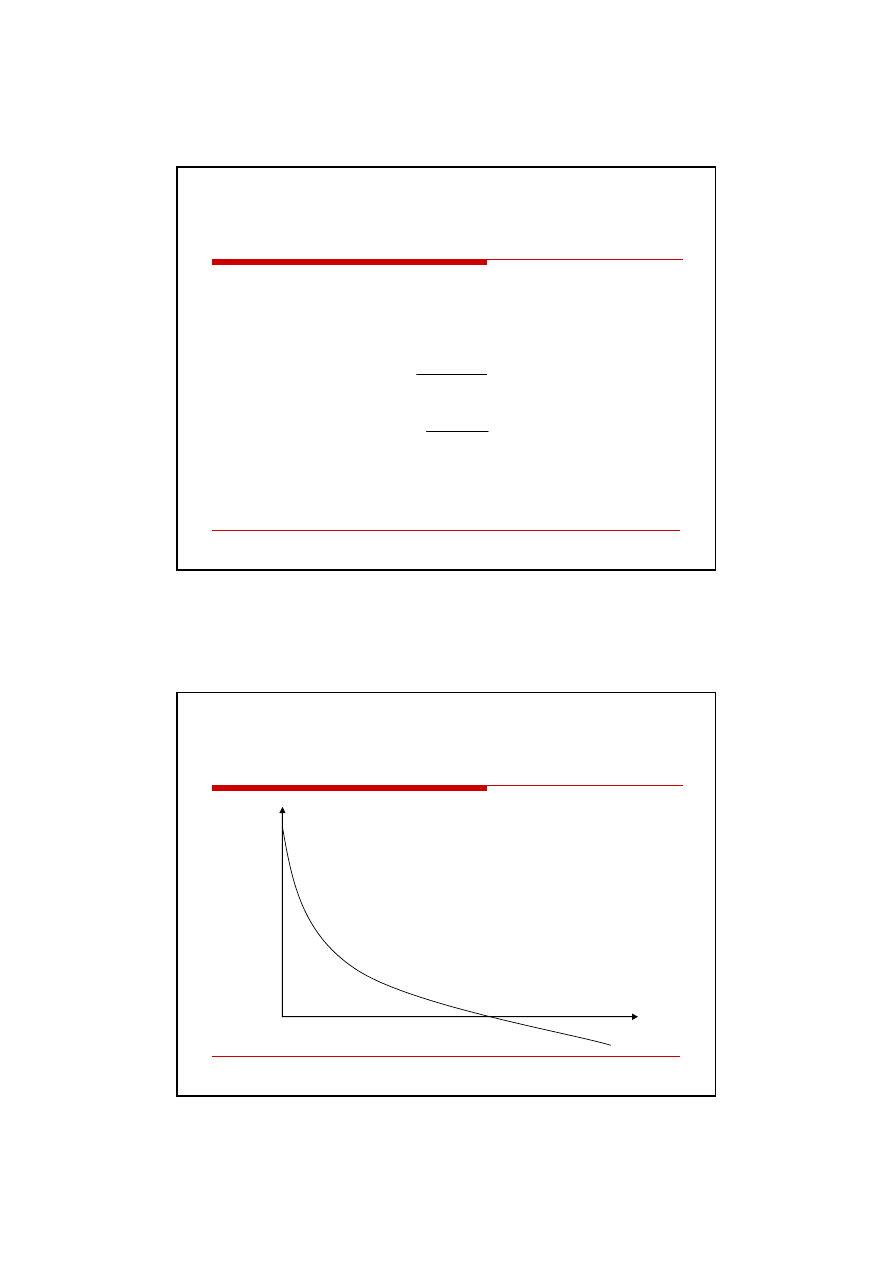
Wewnętrzna stopa zwrotu (IRR) oznacza taki punkt równowagi, dla
którego suma zdyskontowanych wpływów równa się sumie
zdyskontowanych wydatków.
0
IRR)
(1
CF
I
1
i
i
0
n
i
0
IRR
1
Cf
n
0
i
i
i
r
IRR
NPV
r – bieżący koszt kapitału
Zintegrowane Systemy Zarządzania
18
1)
r < IRR Oznacza to, że przy danym koszcie kapitału (r)
inwestycja generuje dodatnią wartość bieżącą netto. Projekt
można wstępnie zaakceptować. Jest on źródłem nadwyżki
finansowej dla firmy.
2)
r = IRR Wewnętrzna stopa zwrotu równa kosztom kapitału
oznacza, że projekt inwestycyjny jest neutralny. Nie zmniejsza
ani nie zwiększa zasobów gotówkowych. Innymi słowy
generuje zerową wartość bieżącą netto.
3)
r > IRR Oznacza to, że przy danym koszcie kapitału (r)
projektowana inwestycja pochłania środki finansowe, nie
tworząc wystarczająco dużych wpływów. Projekt tworzy
ujemną wartość bieżącą netto i dlatego należy go odrzucić
Przykład
Okres
0
1
2
Przepływy
pieniężne (CF
i)
(2000)
1500
1500
Źródło: Opracowanie własne.
Zakładając że koszt kapitału kształtuje się na poziomie 15%, aby obliczyć wewnętrzną
stopę zwrotu, rozwiązujemy równanie:
0
IRR)
1
(
1500
IRR
1
1500
2000
2
IRR = 62%
Taka wartość wewnętrznej stopy zwrotu oznacza, iż projekt w ciągu dwóch lat zapewni
średnią roczną stopę zwrotu równą 62%. A jak wynika z założeń koszt kapitału dla projektu
kształtuje się na poziomie 15%, co za tym idzie projekt inwestycyjny zapewnia stopę zwrotu
wyższą od założonego kosztu kapitału.
Zintegrowane Systemy Zarządzania
19
Cechy metody IRR
1.
Uwzględnia zmianę wartości pieniądza w czasie
2.
Uwzględnia wszystkie przepływy pieniężne, związane z danym
przedsięwzięciem
3.
Pozwala obliczyć ekonomiczną stopę zwrotu przedsięwzięcia, która jest
bezpośrednio porównywalna z kosztem kapitału
4.
Niezbędna przy podejmowaniu decyzji o akceptacji lub odrzuceniu w
przypadku przedsięwzięć pojedynczych
5.
Jest zawodna w hierarchizowaniu przedsięwzięć, szczególnie gdy różnią
się one skalą wielkości lub okresem eksploatacji
6.
Nie powinna być stosowana w przypadku przedsięwzięć o
niekonwencjonalnym strumieniu przepływów
Zasady postępowania z IRR
1.
Akceptuj przedsięwzięcie, dla którego IRR > żądanej
(granicznej) stopy zwrotu r
2.
Zaniechaj inwestycji, dla której IRR < r
3.
Jeżeli IRR = r to badana inwestycja i projekt alternatywny są
jednakowo opłacalne
Obliczone dla powyższych projektów A i B IRR wynoszą
odpowiednio: 13,202% oraz 19,291%, czyli projekt A jest
nieopłacalny, projekt B można realizować.
Zintegrowane Systemy Zarządzania
20
Porównanie NPV i IRR
IRR
B
NPV
NPV
A
NPV
B
Punkt Fishera
B
r
1
r
3
r
2
IRR
A
r
A
Punkt Fishera
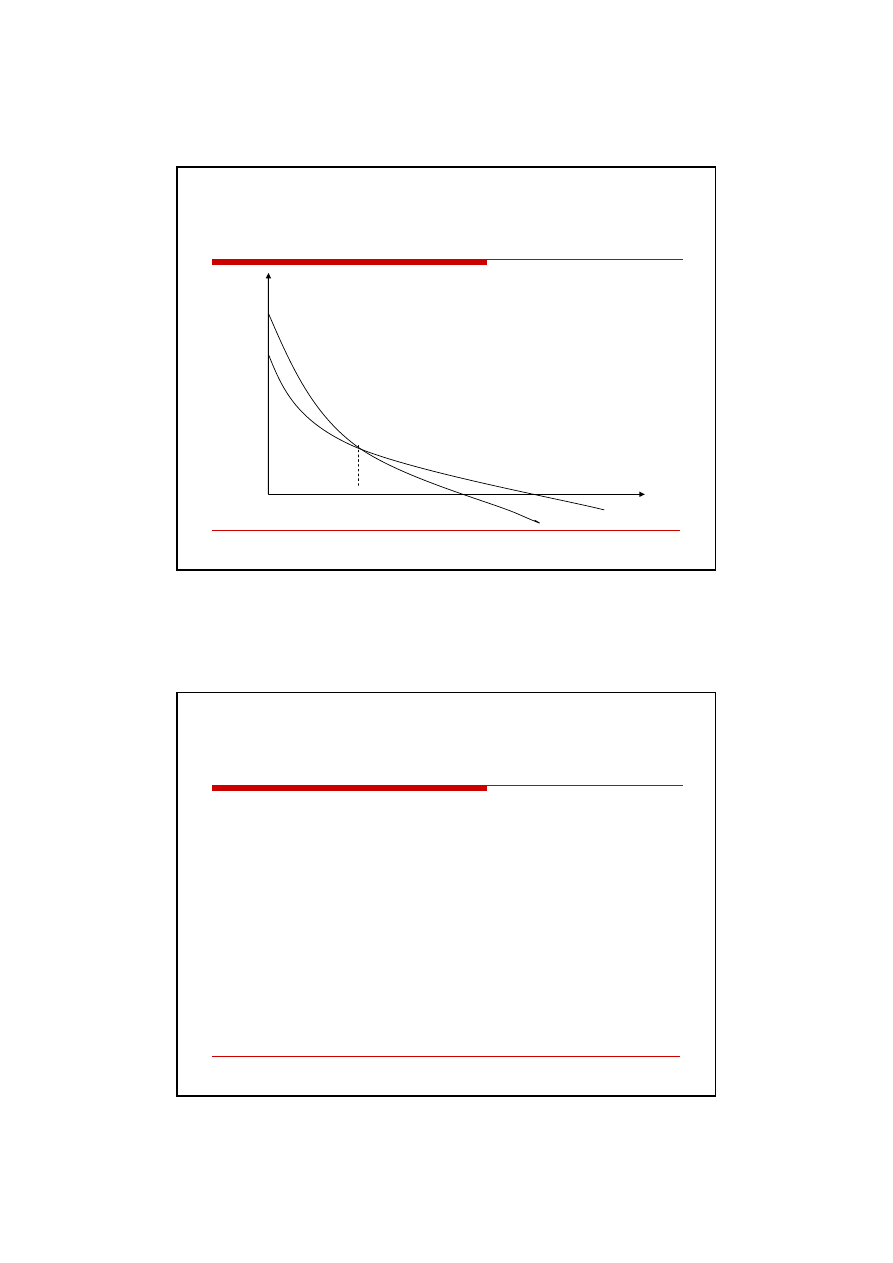
Przedstawiony wykres dwóch projektów inwestycyjnych
pokazuje, że projekt A jest bardziej wrażliwy na zmiany
stopy dyskontowej, tj. kosztu kapitału (bardziej stromy).
Przy porównaniu obu projektów podstawowego znaczenia
nabiera wyznaczenie punktu przecięcia wykresów NPV
dla przykładowych projektów. Punkt ten nazywamy
punktem Fishera.
Zintegrowane Systemy Zarządzania
21
Stopa dyskontowa: 0 < r < r
1
Przy wartości stopy dyskontowej w przedziale od 0 do r
1
, należy
wybrać projekt A, ponieważ osiąga większą wartość NPV w
porównaniu z projektem B.
Stopa dyskontowa: r
1
< r < r
3
Przy wartości stopy dyskontowej w przedziale od r
1
do r
3,
należy
wybrać projekt B, ponieważ to on osiąga wyższą wartość NPV
w porównaniu z projektem B.
Stopa dyskontowa: r > r
3
Wartość stopy dyskontowej dla przedziału powyżej r
3
, mówi nam o
odrzuceniu obydwu projektów ponieważ, zarówno projekt A jak
i B wiązałby się ze stratami. NPV obydwu jest mniejszy od zera
Rodzaje projektów inwestycyjnych
Istnieją dwa rodzaje projektów inwestycyjnych:
a) projekty niezależne – wówczas kryteria NPV i IRR prowadzą
do tych samych wniosków decyzyjnych. Co za tym idzie jeżeli
NPV mówi nam o przyjęciu projektu do realizacji (NPV>0) to
IRR mówi nam dokładnie to samo (r<IRR).
b) projekty wzajemnie się wykluczające – oznacza to dla
inwestora, że do realizacji może przyjąć tylko jeden z
wybieranych projektów albo może wszystkie odrzucić.
I tutaj szczególnego znaczenia nabiera punkt Fishera, ponieważ
kiedy koszt kapitału jest wyższy od stopy w punkcie równowagi
to inwestor patrząc na rysunek wybrałby projekt B ponieważ
NPV
B
> NPV
A
, a także IRR
B
> IRR
A
. Natomiast w sytuacji gdy
koszt kapitału kształtowałby się na poziomie poniżej stopy
równowagi, to: NPV
A
> NPV
B
, oraz IRR
B
> IRR
A
i ta sytuacja
pokazuje konflikt kryteriów wyboru.
Wyszukiwarka
Podobne podstrony:
Ocena efektywności projektów inwestycyjnych 2014 01 12 zadania
Ocena efektywności projektów inwestycyjnych 2013 12 22 zadania
Ocena Efektywności Projektów Inwestycyjnych (2)
Ocena efektywności projektów inwestycyjnych 2014 01 12 zadania
Ocena Efektywności Projektów Inwestycyjnych ebook
Ocena efektywności projektów inwestycyjnych 2014 01 12 zadania
Ocena Efektywności Projektów Inwestycyjnych Paweł Pabianiak
Ocena Efektywności Projektów Inwestycyjnych
OCENA EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH
Ocena Efektywności Projektów Inwestycyjnych ebook
Analiza ekonomiczna ocena efektywności inwestycji
Zarządzanie Finansami Ocena Efektywności Inwestycji
Ocena efektywności inwestycji
ocena efektywności inwestycji (6 str), Ekonomia
Wykład 10 Ocena efektywności inwestycji, Notatki UTP - Zarządzanie, Semestr IV, Zarządzanie finansam
Analiza ekonomiczna ocena efektywności inwestycji
Pabianiak Pawel Ocena efektywnosci inwestycji 2
więcej podobnych podstron