Politechnika Wrocławska, Wydział Mechaniczny  

LABOTRATORIUM 

 

 Ćwiczenie nr 12: Własności mechaniczne tworzyw sztucznych 

dr inż. Andrzej Bełzowski, dr inż. Agnieszka Szust 

 

1.

Wprowadzenie 

 

Własności  mechaniczne  tworzyw  termoplastycznych  zależą  od  wielu  czynników:  struktury 

molekularnej, temperatury, zawartości wody, prędkości obciążania, czasu działanie obciążenia. Wiele 
z  wymienionych  zależności  w  materiałach  metalicznych  nie  występuje  lub  jest  znacznie  słabsza. 
Przykładem  tego  może  być  absorpcja  wody  (wchłanianie  do  wnętrza  elementu):  w  metalach 
praktycznie  nieobecna,  w  tworzywach  niekiedy  osiągająca  w  stanie  nasycenia  nawet  kilka  procent 
(np. w poliamidach jest to 2,5‐7,5 %, dla PET około 0,8%). Zaabsorbowana woda uszkadza wiązania 
chemiczne  cząstek  polimeru,  co  powoduje  degradację  materiału  przejawiającą  się  w  pogarszaniu 
własności  mechanicznych  i  fizycznych.  W  stalach  i  innych  stopach  metali  kontakt  z  wodą  może 
wywołać korozję na powierzchni, ale trudno byłoby mówić o nasiąkliwości tych materiałów.  

Cechą  specyficzną  polimerów  jest  zależność  ich  właściwości  mechanicznych  od  czasu  działania 

obciążenia. Zagadnienie to jest omówione w dalszej części opracowania.  

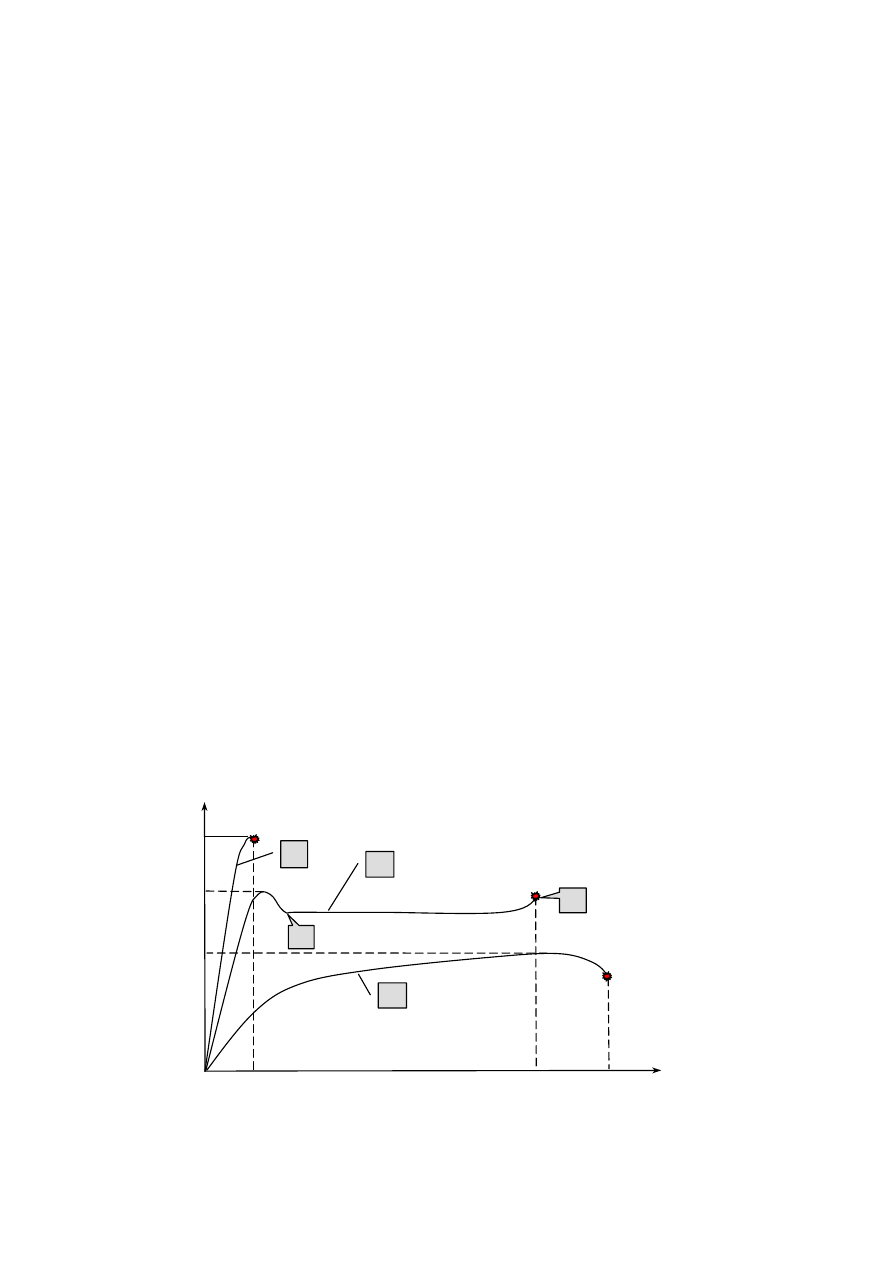
Podczas  prób  wytrzymałości  tworzywa  termoplastyczne  mogą  wykazać  zachowanie  kruche  lub 

ciągliwe.  Te  właściwości  można  wstępnie  ocenić  na  podstawie  zarejestrowanych  wykresów  prób 
rozciągania  (rys. 1.1).  Krzywa  typu  1  na  rys. 1.1  przedstawia  zachowanie  materiału  kruchego.  W 
praktyce w temperaturach otoczenia takie zachowanie mogą wykazywać:  

• niektóre termoplasty ‐  PS (polistyren), poli (sulfid fenylenu) (PPS), 
• liczne  duroplasty  używane  jako  osnowy  polimerowych  kompozytów  konstrukcyjnych  – 

żywice poliestrowe nienasycone (UP), żywice epoksydowe (EP) i żywice vinyloestrowe (VE). 

Charakterystyczną  cechą  tworzyw  kruchych  zauważalną  na  wykresach  obciążania  jest  niewielka 
wartość odkształcenia w momencie zerwania ε

B

, na ogół  ε

B 

≤5%.  

Krzywe  2  i  3  przedstawione  na  rys. 1.1  reprezentują  materiały  ciągliwe.  Przy  wydłużeniach  rzędu 
kilkunastu  procent  jest  to  ciągliwość  raczej  umiarkowana.  Wiele  tworzyw  termoplastycznych 
wykazuje  wartość  ε

B 

  rzędu  50‐1000%,  co  kwalifikuje  je  do  materiałów  ciągliwych  lub  bardzo 

ciągliwych. Do takich materiałów zaliczają się między innymi takie popularne tworzywa jak polietylen, 
polipropylen, poliamid. Ciągliwość jest ważną cechą materiałów używanych do produkcji opakowań, 
ponieważ jest ona miarą odporności na uderzenia. 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Rys. 1.1. Typowe wykresy rozciągania tworzyw sztucznych. 

ε

B

ε

B

σ

M

σ

y

σ

M

3

1

2

C

D

2

 
Mechanizmy odkształcania polimerów termoplastycznych pod wpływem przyłożonego obciążenia 

polegają na rozluźnieniu wiązań między łańcuchami cząstek i względnym ruchu łańcuchów. Obecność 
w  materiale  fazy  krystalicznej  wpływa  na  jego  właściwości.  Wzrost  stopnia  krystaliczności  zwiększa 
wytrzymałość,  sztywność,  twardość,  odporność  chemiczną.  Krystaliczność  może  sprzyjać  kruchemu 
pękaniu i obniża odporność na obciążenia udarowe.  

W polietylenie o niskiej gęstości (jest to tzw. polietylen wysokociśnieniowy) stopień krystaliczności 

wynosi 40‐50%. W polietylenie o wysokiej gęstości PE‐HD (tzw. polietylen niskociśnieniowy) stopień 
krystaliczności  osiąga  60‐80%.  Stopień  krystaliczności  polipropylenu  izotaktycznego  może  osiągać 
65%.  

 

2.

Badania tworzyw sztucznych ‐ informacje ogólne 

Celem badań własności mechanicznych tworzyw sztucznych może być: 

•

kontrola jakości produkcji, 

•

kontrola jakości dostarczonej partii produktu, 

•

uzyskanie danych potrzebnych do projektowania wytrzymałościowego, 

•

sprawdzenie  własności  materiału  nowego  lub  powstałego  w  wyniku  badań  nad 
ulepszeniem istniejących tworzyw. 

Ze  względu  na  stosunkowo  dużą  zależność  własności  polimerów  od  temperatury,  zawartości 

wody,  szybkości  obciążania  itd.,  badania  własności  mechanicznych  tworzyw  sztucznych  są  z  reguły 
trudniejsze  technicznie  w  porównaniu  do  analogicznych  prób  materiałów  metalicznych.  Tworzywa 
sztuczne  wymagają  stosowania  znormalizowanych  sposobów  pobierania  materiału  na  próbki,  ich 
wykonywania,  klimatyzacji  próbek.  Badania  wymagają  ścisłego  respektowania  wymagań  odnośnie 
warunków przeprowadzania prób, w szczególności wilgotności i temperatury badania. 

Na ogół trudniejszy technicznie (w porównaniu do metali) jest pomiar odkształceń. W tworzywach 

kruchych  montowanie  na  próbkach  ekstensometrów  mechaniczno‐elektrycznych  do  określania 
wydłużeń i przemieszczeń wymaga szczególnej ostrożności w celu uniknięcia uszkodzeń powierzchni 
próbki  w  miejscu  styku  z  czujnikiem.  Ryzyko  uszkodzeń  próbki  przez  zamontowanie  układu  do 
pomiaru odkształceń może być zminimalizowane dzięki użyciu nowoczesnych  czujników optycznych 
(kamery wideo, czujniki laserowe).  

 
 

3. Próba rozciągania tworzyw sztucznych 

Warunki  i  sposób  przeprowadzania  próby  rozciągania  tworzyw  sztucznych  są  opisane  w  normie 

PN‐EN  ISO 527:  1998,  Tworzywa  sztuczne.  Oznaczanie  właściwości  mechanicznych  przy  statycznym 
rozciąganiu.  

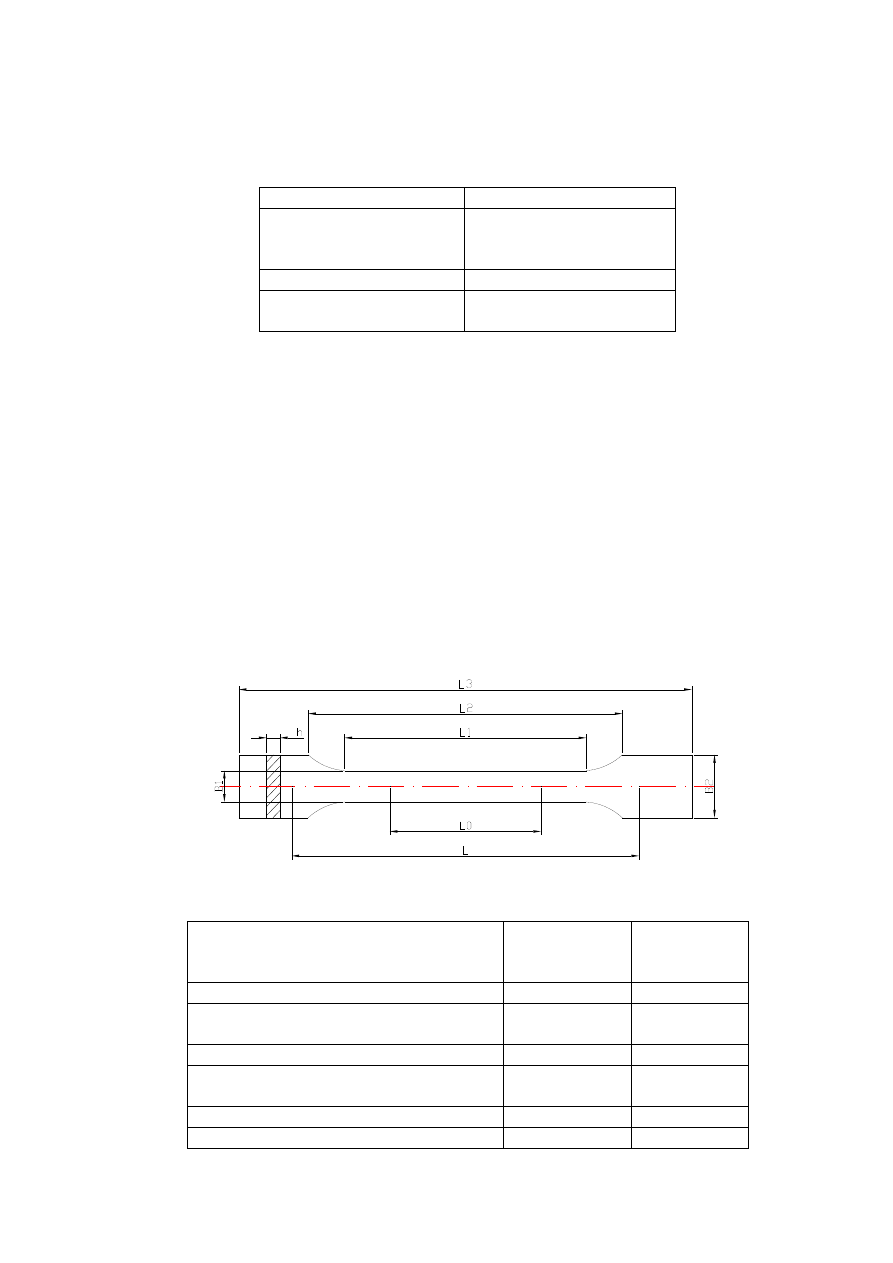
Typowa  próbka  (nazywana  w  normie  kształtką)  jest  płaska  i  ma  kształt  „wiosełkowy”  (rys. 3.1). 

Przy grubości 4,0±0,2 mm, szerokość części pomiarowej wynosi 10±0,2 mm a długość 80 lub 60 mm.  

Wielkość  σ

y

  określono  w  normie  jako  granicę  plastyczności  materiału,  chociaż  jest  ona  bliższa 

pojęciu  wytrzymałości  na  rozciąganie  w  rozumieniu  normy  do  badania  metali.  Tworzywa  sztuczne 
wykazujące  w  próbie  rozciągania  zachowanie  opisane  krzywą  typu  2  cechuje  utworzenie  się 
widocznego  stosunkowo  dużego  przewężenia,  które  w  zakresie  odkształceń  odpowiadających 
odciętym  punktów  C  i  D  obejmuje  stopniowo  całą  długość  części  pomiarowej.  W  zakresie  C‐D 
uszkodzenie próbki widoczne gołym okiem przeważnie jest na tyle poważne, że materiał można uznać 
za w zasadzie zniszczony. Gdyby w takim przypadku wartość naprężenia w punkcie D była wyższa od 
granicy plastyczności σ

y 

, to niedoświadczony inżynier mógłby przyjąć wartość wytrzymałości σ

M

=σ(D) 

i  zaprojektować  element  na  podstawie  tak  określonej  wytrzymałości.  Stanowiłoby  to  pominięcie 
faktu,  że  uszkodzenie  dyskwalifikujące  materiał  elementu  do  dalszego  bezpiecznego  użytkowania 
pojawiło  się  wcześniej,  przy  wartości  naprężenia  σ

y

<σ

M

.

 

Należy  mieć  świadomość,  że  wielkości 

określane  podobnymi  terminami  w  badaniach  metali  i  tworzyw  sztucznych  mogą  mieć  inny  sens 
fizyczny.  

3

Wydłużenie ε

B

 jest określane jako wydłużenie całkowite tuż przed wystąpieniem zniszczenia próbki. 

W  badaniach  stali  i  innych  ciągliwych  stopów  metali  przeważnie  określa  się  wydłużenie  względne 
próbki po jej zerwaniu (w przeszłości oznaczane symbolem A

5

, obecnie A

C

). Jest to odkształceni trwałe 

a  nie  całkowite  materiału  (odkształcenie  całkowite  jest  sumą  składowej  sprężystej  (zanikającej  po 
odciążeniu) i składowej trwałej, pozostającej w materiale nie obciążonym.         

 

Rys. 3.1. Próbka wiosełkowa z żywicy poliestrowej wzmocnionej tkaniną szklaną z zamontowanym 

ekstensometrem do pomiaru wydłużeń. W przypadku takiego materiału ‐ o podwyższonej  

wytrzymałości i sztywności ‐ można mieć nadzieję na uniknięcie istotnego wpływu zamocowania 

ekstensometru bezpośrednio na próbce na wynik próby. Inne zagrożenie stanowi możliwość poślizgu 
w miejscu połączenia czujnika z próbką (przy zbyt delikatnym mocowaniu), co spowodowałoby uskok 

wykresu obciążania dyskwalifikujący taką próbę. W metalach możliwość zakłócenia przebiegu próby 

przez wpływ zamocowania takiego czujnika jest znacznie mniejszy. 

 
 
 
 

4. Określanie własności tworzyw sztucznych przy statycznym zginaniu 

 

4.1. Wiadomości ogólne o próbach zginania tworzyw sztucznych 

Próby  zginania  są  stosowane  przede  wszystkim  w  celu  określenia  własności  tworzyw  sztywnych, 

które charakteryzują się stosunkowo dużym modułem sprężystości wzdłużnej E. Stosowanie obciążeń 
zginających  jest  szczególnie  przydatne  w  przypadku  badania  materiałów  kruchych.  Jest  to  ważna 
grupa  tworzyw  sztucznych  szeroko  stosowanych  w  technice,  których  charakterystyczną  cechą  są 
niewielkie  wartości  wydłużenia  względnego  przy  zerwaniu,  wynoszące  najczęściej   

ε

r

  =  1–5  %. 

Określenie  odkształceń  o  takich  wartościach  z  wymaganą  dokładnością  względną  rzędu  1%,  jest  w 
próbie  rozciągania  dość  trudne  w  przeciętnie  wyposażonym  laboratorium  wytrzymałościowym. 
Wynika to między innymi z następujących okoliczności: 
• przy  najczęściej  spotykanych  długościach  baz  pomiarowych,  wynoszących  kilkadziesiąt 

milimetrów, dokładność bezwzględna pomiaru wydłużeń powinna wynosić około 1–5 μm, 

• stosowany  system  mocowania  czujnika  do  pomiaru  wydłużeń  powinien  wykluczać  możliwość 

powstania w miejscu mocowania uszkodzeń powierzchni próbki, co mogłoby mieć istotny wpływ 
na wynik próby. 
Wymienione  trudności  można  w  dużej  mierze  ominąć,  określając  własności  tworzywa  na 

podstawie  przeprowadzonej  próby  zginania.  Jedną  z  zalet  prób  zginania  jest  łatwość  pomiaru 

4

wielkości  charakteryzującej  odkształcenie  próbki,  którą  jest  jej  największe  ugięcie  zwane  strzałką 
ugięcia.  

Próby  zginania  są  szeroko  stosowane  w  laboratoriach  zajmujących  się  udoskonalaniem 

istniejących  oraz  opracowywaniem  nowych  tworzyw.  Decyduje  o  tym  względna  łatwość  oraz 
szybkość  ich  przeprowadzania.  W  tym  przypadku  celem  badań  jest  często  dokonanie  oceny 
porównawczej różnych materiałów.  

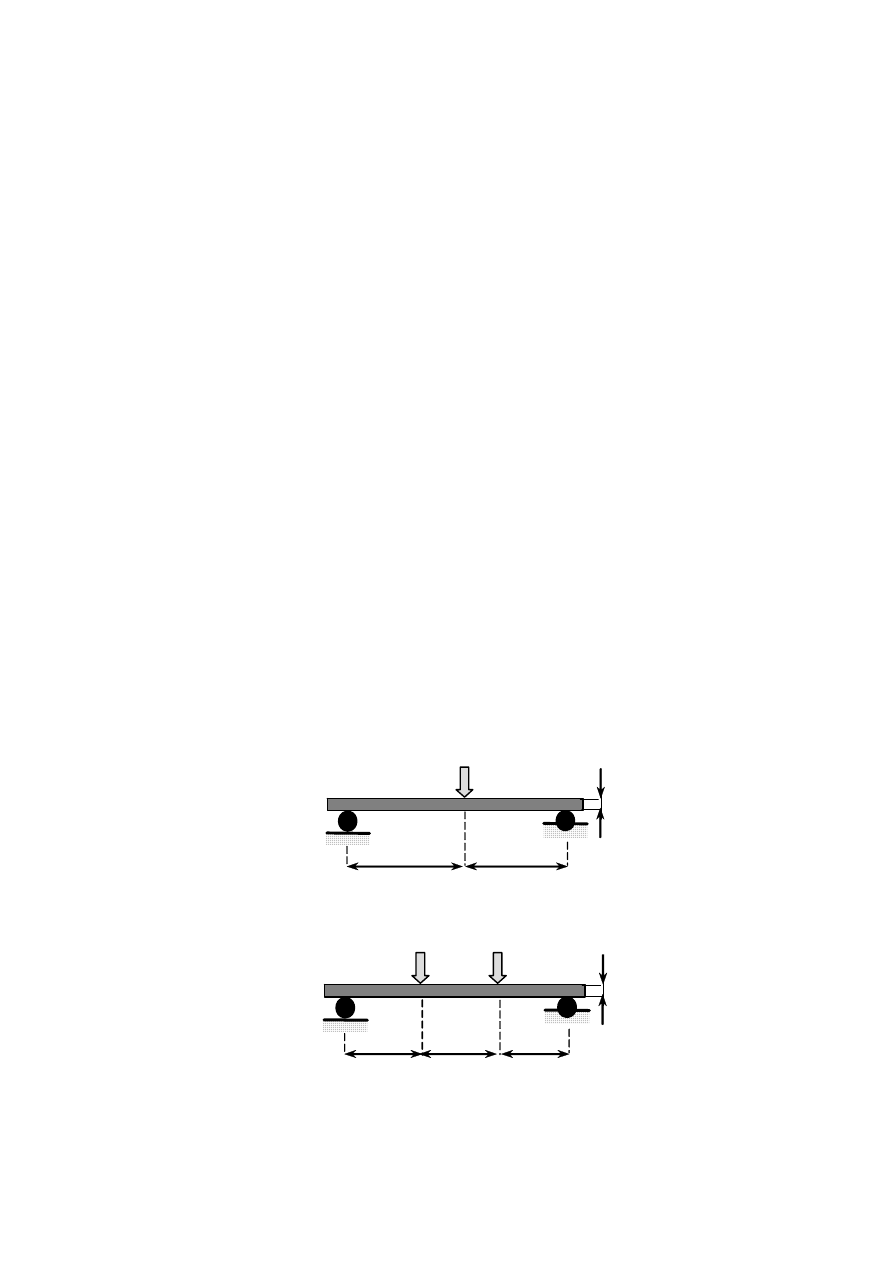
W  praktyce  najczęściej  stosuje  się  schemat  zginania  trójpunktowego  (rys. 4.1.a).  W  przypadku 

tworzyw  nie  wzmocnionych  włóknami  próbę  prowadzi  się  aż  do  zniszczenia  próbki,  które  powinno 
być spowodowane przez naprężenia normalne związane z działaniem momentu zginającego.  

Badanie  podczas  zginania  polega  na  tym,  że  próbkę  pomiarową  z  tworzywa  w  postaci  beleczki 

prostopadłościennej, podpartą w określony sposób, obciąża się prostopadle do jej osi wzdłużnej. Na 
rys. 4.1‐2 pokazano niektóre stosowane sposoby obciążania.  

Próba  zginania  tworzyw  sztucznych  nie  wzmocnionych  jest  opisana  w  normie  PN‐

EN ISO 178: 1998 Tworzywa  sztuczne.  Oznaczanie  właściwości  podczas  zginania.  W  przeszłości 
norma ta była stosowana również do przeprowadzania prób kompozytów polimerowych tj. tworzyw 
wzmocnionych włóknami. Obecnie próby zginania kompozytów polimerowych są opisane w normie 
PN‐EN ISO 14125: 2001 Kompozyty  tworzywowe  wzmocnione  włóknem.  Oznaczanie  właściwości 
przy zginaniu.  

Oprzyrządowanie 

do 

prób 

zginania 

stanowi 

standardowe 

wyposażenie 

maszyn 

wytrzymałościowych.  Wzajemne  usytuowanie  punktów  podparcia  i  przyłożenia  obciążenia  jest 
zwykle ściśle określone w obowiązujących normach. Obciążenie zwiększa się powoli, jednostajnie, aż 
do  zniszczenia  próbki  lub  do  osiągnięcia  określonej  umownej  strzałki  ugięcia.  Prędkości  obciążania 
podane  w  PN‐EN ISO 178  w  mm/min  wynoszą:  1,  2,  5,  10,  20,  50,  100,  200,  500.  W  praktyce 
najczęściej stosuje się prędkości nie przewyższające 10 mm/min.  

W  obowiązującej  w  Polsce  normie  PN−EN

 

ISO

 

178 przewiduje  się  stosowanie  zginania 

trzypunktowego (rys. 4.1)  próbek prostopadłościennych o stosunku wysokości do odległości podpór 
wynoszącym  l/h=16.  Zalecanym  kształtem  próbki  jest  prostopadłościan  o  wymiarach  przekroju 
poprzecznego  b×h=10×4 mm  i  długości  całkowitej  l=80 mm.  W  uzasadnionych  przypadkach  są 
możliwe  odstępstwa  wymiarowe  w  granicach  określonych  w  normie.  Rozstaw  podpór  powinien 
spełniać  warunek  l

r

=16h,  co  w  materiałach  kruchych  zapewnia  zniszczenie  wskutek  osiągnięcia 

naprężeń normalnych σ związanych z momentem zginającym.  

 

h

F

l

r

/2

l

r

/2

 

 

Rys. 4.1. Schemat sposobu obciążania próbki w próbie zginania tzw. „trzypunktowego”. 

 

h

F

F

l

r

/3

l

r

/3

l

r

/3

 

 

. 

Rys. 4.2. Schemat próby zginania czteropunktowego opisanej w niektórych normach 

zagranicznych (np. amerykańskich). 

5

 

Wartości naprężenia obliczamy wg znanej zależności  
 

W

M

g

=

σ

 

 

 

4.2. Wyznaczanie modułu sprężystości wzdłużnej 

Strzałkę  ugięcia  f  pręta  prostopadłościennego  o  szerokości  b  i  wysokości  przekroju  h,  zginanego 

trzypunktowo siłą o wartości F możemy obliczyć z zależności  

postępowania jest następująca: 

1. Przeprowadzając  próbę  zginania  (niszczącą  lub  do  osiągnięcia  tylko  pewnej  wymaganej 

strzałki ugięcia zarejestrować krzywą obciążenie – ugięcie lub tylko wartości siły i ugięcia 
odpowiadające  odkształceniom  ε

f1

=0,0005  i  ε

f2

=0,0025.  Wartości  ugięć  f

1

  i  f

2

  należy 

obliczyć ze wzoru    
 

       

 

                

)

2

;

1

(

6

2

=

=

i

h

l

f

fi

i

ε

 

 

 
podstawiając kolejno ε

f1

=0,0005 i ε

f2

=0,0025.  

2. Określić wartości siły F obciążającej próbkę w chwilach osiągnięcia wartości odkształceń 

ε

f1 

 i  ε

f2 

 oraz odpowiadające wartości największego naprężenia normalnego σ

f1 

 i  σ

f2 

. 

3. Obliczyć moduł Younga materiału   

 

       

 

 

 

1

2

1

2

f

f

f

f

f

E

ε

ε

σ

σ

−

−

=

 

 
Ponieważ  odkształcenie  zerwania  tworzyw  sztucznych  stosowanych  w  technice  z  reguły 

przekracza  wartość  1%  jest  oczywiste,  że  zakres  wartości  odkształceń  0,0005≤

 

ε  ≤  0,0025 

wykorzystany do wyznaczenia modułu należy do zakresu liniowo sprężystego. 

 
 

5.1 Cel i zakres ćwiczenia. 

Ćwiczenie ma na celu zapoznanie studentów z inżynierskimi podstawami badania i doboru 
tworzyw sztucznych.  
W zakres ćwiczenia wchodzi: 
a/  samodzielne  wykonanie  znormalizowanych  prób  rozciągania  i    zginania      wybranych 
tworzyw sztucznych, 

b/  określenie  własności  wytrzymałościowych  badanych  próbek  przez  wyznaczenie 

zdefiniowanych w     normach wskaźników wytrzymałościowych, 

c/  przeprowadzenie krótkiej zbiorczej analizy otrzymanych wyników, mającej na celu 

porównanie     mechanicznego zachowania się różnych tworzyw sztucznych przy danym 
sposobie obciążania oraz     danego tworzywa sztucznego przy różnych sposobach 
obciążania. 

Podczas przeprowadzonych, wymienionych prób wytrzymałościowych, wyznaczone zostaną 
następujące charakterystyki mechaniczne: 
‐ granica plastyczności, 
‐ wydłużenie, 
‐ moduł elastyczności, 
‐ wytrzymałość na zginanie 

6

Szczególne, oczekiwane wartości omawianych charakterystyk mechanicznych powinny być 
zgodne z odpowiednimi normami i zawierać swe wartości w następujących granicach: 
 
Tab. 5.1 

WŁAŚCIWOŚCI 

WYMAGANIA 

Granica plastyczności ‐ σS 
Wydłużenie σS i εR 

σS ≥24 N/mm

2

 

εS ≥ 8% 

εR≥ 100% 

Moduł elastyczności E 

Et≥ 1200 N/mm

2

Wytrzymałość na zginanie 
3,5%  σb 3,5 

σb 3,5 ≥ 22 N/mm

2 

 
Wymienione próby powinny być przeprowadzone zgodnie z zaleceniami norm:  
‐

PN‐EN ISO 527‐1/1998, PN‐EN ISO 527‐2/1998 – rozciąganie; 

‐

PN‐EN ISO 187:2003+A1:2005 – zginanie; 

 
5.2 Oznaczenie  właściwości  mechanicznych  tworzyw  sztucznych  przy  statycznym 

rozciąganiu. 

 
Cel, zakres i szczegółowe wytyczne dotyczące przeprowadzenia próby rozciągania 
statycznego oraz wyznaczanych na podstawie wyników z przeprowadzenia tej próby cech 
wytrzymałościowych tworzyw sztucznych określają normy: PN‐EN ISO 527‐1/1998, PN‐EN ISO 
527‐2/1998.  

Przeprowadzenie próby statycznego rozciągania pozwala na wyznaczenie takich cech 
wytrzymałościowych jak, maksymalne naprężenie rozciągające, moduł sprężystości oraz 
zależności naprężenie/wydłużenie w określonych warunkach.  

 

Aby przeprowadzić omawiane badanie potrzebujemy próbkę o określonej geometrii. (Rys1) 

 

 

 

Rys. 5.2 Uniwersalna kształtka do badań typu A1 i  B1. 

 

Wymiary kształtek 

Typ A1 

Bezpośrednio 

formowalna. 

Typ B1 

Obrabiana 

mechanicznie. 

L3 – długość całkowita 

≥150 mm 

≥150 mm 

L1 – długość części ograniczonej liniami 
równoległymi 

80±2mm 

60±0,5mm 

R  – promień (20‐25 mm) 

20‐25 mm 

≥60 mm 

L2 – odległość między szerokimi równolegle 
usytuowanymi częściami 

104‐113mm 

106‐120mm 

B2 ‐ szerokość na końcach 

20,0±0,2mm 

20,0±0,2mm 

B1 – szerokość wąskiej części 

10,0 ±0,2mm 

10,0 ±0,2mm 

7

H – zalecana grubość 

4,0±0,2mm 

4,0±0,2mm 

L0 – długość pomiarowa 

50,0±0,5mm 

50,0±0,5mm 

L – początkowa odległość między uchwytami 

115 ±1mm 

115 ±1mm 

 

W przypadku niektórych materiałów może zaistnieć potrzeba zwiększenia długości całkowitej.  W 
celu zabezpieczenia przed zerwaniem lub ślizganiem się w szczękach maszyny wytrzymałościowej. 
Wszystkie  powierzchnie  kształtek  powinny  być  wolne  od  pęknięć,  rys  i  innych  niedoskonałości.  Z 
kształtek  otrzymanych  przez  formowanie  wszystkie  wypływki,  jeśli  istnieją,  powinny  być  usunięte 
ostrożnie, by nie uszkodzić formowanej powierzchni. 
Kształtka do badań rozciąga się wzdłuż jej głównej osi wzdłużnej, przy stałej prędkości, aż do zerwania 
kształtki lub do określonej wartości naprężenia(lub zadanego obciążenia) lub odkształcenia 
(wydłużenia). W czasie tej próby mierzy się trwałe obciążenie kształtki i jej wydłużenie.   
 
 

5.3 Wyznaczane własności wytrzymałościowe w próbie rozciągania statycznego. 

 
Naprężenia: [MPa]  
Naprężenie  rozciągające  σ  (konstrukcyjne)  –  siła  rozciągająca  na  jednostkę  powierzchni 
początkowego  przekroju  kształtki  wewnątrz  odcinka  pomiarowego  przenoszona  przez  kształtkę  w 
każdej określonej chwili. 

(A) Wytrzymałość na rozciąganie σ

M

 (maksymalne naprężenie rozciągające przenoszone przez 

kształtkę  w  czasie  próby  rozciągania  –  tj.  siła  rozciągająca  na  jednostkę  powierzchni  początkowego 
przekroju kształtki wewnątrz odcinka pomiarowego przenoszona przez kształtkę w każdej określonej 
chwili.) 
‐  naprężenie przy zerwaniu σ

B 

(naprężenie rozciągające przy którym próbka ulega zerwaniu) 

‐  granica  plastyczności  σ

y

  (pierwsze  naprężenie,  przy  którym  wzrost  wydłużenia  nie  powoduje 

wzrostu naprężenia; może być mniejsze niż osiągane naprężenie maksymalne) 

(B)  Wydłużenia  względne:  ε  (Wzrost  długości  na  jednostkę  długości  początkowej  odcinka 

pomiarowego. Wyraża się jako stosunek bezwymiarowy lub w procentach (%)) 
‐  wydłużenie  względne  przy  maksymalnym  naprężeniu  rozciągającym  ε

M

  (Wydłużenie  w  punkcie 

odpowiadającym  wytrzymałości  na  rozciąganie,  jeśli  występuje  bez  lub  na  granicy  plastyczności  – 
rys.1 krzywe a i d); 
‐  wydłużenie  względne  przy  zerwaniu  ε

B

  (wydłużenie  względne  przy  zerwaniu,  jeśli  zerwaniu  nie 

towarzyszy 
‐  wydłużenie  względne  przy  granicy  plastyczności  ε

y

  (Wydłużenie  względne  przy  naprężeniu  przy 

granicy plastyczności. ) 

(C) Moduł sprężystości przy rozciąganiu E

t

 

 

(D) Pozostałe definicje: 

Długość  odcinka  pomiarowego  L

0

  –  początkowa  odległość  między  znakami  pomiarowymi  na 

środkowej części kształtki do badań. Wyraża się w milimetrach (mm). 
Prędkość  badania  v  –  szybkość  przesuwu  szczęk  maszyny  wytrzymałościowej  podczas  badania. 
Wyraża się w milimetrach na minutę (mm/min). 
Naprężenie  rozciągające  σ  (konstrukcyjne)  –  siła  rozciągająca  na  jednostkę  powierzchni 
początkowego  przekroju  kształtki  wewnątrz  odcinka  pomiarowego  przenoszona  przez  kształtkę  w 
każdej określonej chwili. Wyraża się w megapaskalach (MPa). 
Naprężenie  rozciągające  przy  x%  odkształcenia  σ

x

  –  maksymalne  naprężenie  rozciągające 

przenoszone prze kształtkę w czasie badania rozciągania. Wyraża się w megapaskalach (MPa). Może 
być  mierzone  na  przykład  wtedy,  gdy  krzywa  naprężenie/wydłużenie  nie  wykazuje  granicy 
plastyczności. W takim przypadku x  należy przyjąć  z  określonej normy wyrobu lub uzgodnić między 
zainteresowanymi  stronami.  Jednak  w  każdym  przypadku  wartość  x  powinna  być  mniejsza  niż 

wartość odkształcenia odpowiadającego wytrzymałości na rozciąganie.

8

Wydłużenie  względne  nominalne  ε

ts

  –  wydłużenie    względne  nominalne  przy  naprężeniu 

zrywającym, jeśli badana kształtka zerwie się po przekroczeniu granicy plastyczności.  
Wyraża się jako stosunek bezwymiarowy lub w procentach (%). 
Wydłużenie  względne  nominalne  przy  maksymalnym  naprężeniu  rozciągającym  ε

ts

  –  wydłużenie 

względne  nominalne  przy  maksymalnym  naprężeniu  rozciągającym,  jeśli  naprężenie  to  wystąpi 
powyżej granicy plastyczności. Wyraża się jako stosunek bezwymiarowy lub w procentach (%).  
Moduł  sprężystości  przy  rozciąganiu  E

t

  –  stosunek  różnicy  naprężeń  σ

1

  i  σ

2

,  do  różnicy  wartości 

odkształceń ε

2

 = 0,0025 i ε

1

 = 0,0005. Wyraża się w megapaskalach (MPa).  

Definicji nie stosuje się w przypadku folii i gumy. 
Współczynnik Poissona µ ‐ ujemny stosunek wydłużenia względnego ε

n

 z jednego z dwóch kierunków 

prostopadłych do kierunku rozciągania, do odpowiadającego mu wydłużenia względnego w kierunku 
rozciągania, w zakresie początkowej zależności liniowej krzywej odkształcenia podłużnego względem 
prostopadłego.  Wyraża  się  jako  stosunek  bezwymiarowy.  Współczynnik  Poissona  jest  w  pierwszym 
rzędzie oznaczany dla tworzyw wzmocnionych długimi włóknami. 
 

 

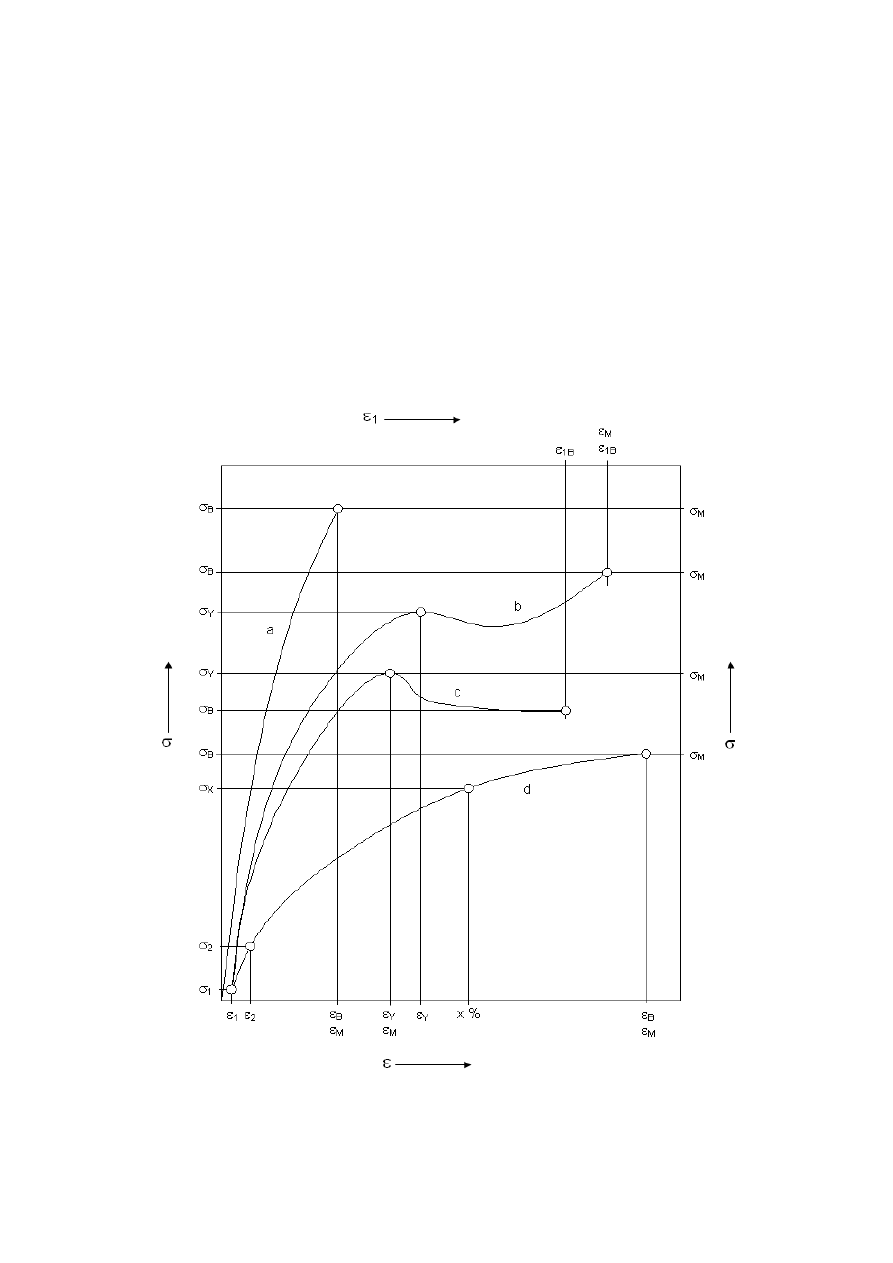
Rys. 5.3. Typowe krzywe naprężenie/wydłużenie uzyskane w próbie rozciągania statycznego.  
 

 

Krzywa a  

– tworzywa kruche; 

 

 

Krzywa b 

‐ tworzywa wzmocnione z granicą plastyczności 

 

 

Krzywa c 

‐ tworzywa wzmocnione bez granicy plastyczności 

9

5.4 Obliczanie i przedstawianie wyników. 

A) Obliczanie naprężeń. Wszystkie wartości naprężeń w odniesieniu do początkowego 

przekroju, należy obliczać w odniesieniu do przekroju początkowego. 

A

F

=

σ

  

Gdzie:  

σ – jest określoną wartością naprężenia, wyrażona w MPa, 

 

 

F – jest odpowiadającą siłą przypadającą na przekrój.  

A‐ Jest początkowym przekrojem poprzecznym kształtki, wyrażonym w milimetrach 

kwadratowych. 

 

5.5 Wytrzymałość na zginanie. 

Według  cytowanej  normy  PN‐EN ISO 178,  właściwości  wytrzymałościowe  tworzyw  wyznacza  się 

stosując  schemat  obciążania  trzypunktowego  (rys. 4.1.),  identyczny  z  używanym  w  próbie 
wyznaczania  modułu  sprężystości  E

f   

(l

r

/  h=16).  Próbę  przeprowadza  się  do  osiągnięcia  określonej 

umownej strzałki ugięcia, wynoszącej  s

c

=1,5

⋅

h. Jeżeli próbka ulegnie złamaniu przed osiągnięciem tej 

strzałki,  to  wielkością  charakteryzującą  materiał  jest  wytrzymałość  na  zginanie 

σ

fM

,  określona  jako 

największe naprężenie zginające przeniesione przez próbkę, obliczone wg wzoru 

 

 

 

 

 

    

2

2

2

3

6

4

bh

Fl

bh

l

F

W

M g

r

r

fM

=

⋅

=

=

σ

 

 

 

gdzie F oznacza największą wartość siły zarejestrowaną podczas obciążania próbki. 

 
Wartości  wytrzymałości  na  zginanie  tworzyw  sztucznych  różnią  się  istotnie  od  wytrzymałości  na 

rozciąganie: praktycznie zawsze wytrzymałość na zginanie tworzyw 

σ

fM

 jest większa od wytrzymałości 

na  rozciąganie 

σ

M

.  Różnice  są  niemałe,  często  rzędu  50%  (

σ

fM

  ≈1,50×

σ

M

)  Moduły  sprężystości  nie 

podlegają tej prawidłowości, z reguły ich wartości są zbliżone (E≈E

f

). Wytłumaczenie przyczyny różnic 

wartości 

σ

fM

 i 

σ

M

 wymaga analizy rozkładów naprężeń w kształtkach przy założeniu, że wytrzymałość 

materiału jest opisana statystycznym rozkładem Weibulla, co przekracza zakres tego ćwiczenia.  

Jeżeli  próbka  nie  ulegnie  złamaniu  przed  osiągnięciem  wartości  umownej  strzałki  ugięcia  s

c

,  to 

wielkością charakteryzującą materiał pod względem zdolności do przenoszenia obciążeń zginających 
jest  tzw.  naprężenie  przy  określonej  strzałce  ugięcia   

σ

fC 

.  Jest  to  największe  naprężenie  normalne 

(zginające), występujące w próbce w chwili osiągnięcia ugięcia s

c 

, określone wg wzoru przytoczonego 

wyżej. Wartość F oznacza tym razem siłę zarejestrowaną w momencie osiągnięcia ugięcia s

c

. 

Wielkość 

σ

fC

  jest  pojęciem  umownym,  ponieważ  wiele  tworzyw  w  chwili  osiągnięcia  strzałki 

ugięcia  s

c

 znajduje się już poza granicą stosowalności prawa Hooke’a. Jak wiadomo, wzory używane 

do przeliczania wartości pomiarowych zostały wyprowadzone przy założeniu jego ważności. Sposób 
określenia naprężenia 

σ

fC

 powoduje, że wykorzystanie tej wielkości w obliczeniach jest równoznaczne 

z wprowadzeniem warunku sztywności, często bardziej ostrego, niż warunek wytrzymałości.  

W  celu  określenia  wytrzymałości  na  zginanie 

σ

fM

  lub  naprężenia  zginającego  przy  umownej 

strzałce  ugięcia 

σ

fC

  należy  poddać  próbie  co  najmniej  5  próbek.  Jako  wynik  badania  przyjmuje  się 

średnią  arytmetyczną  wykonanych  oznaczeń.  W  normie  określa  się  dokładnie  sposób  pobrania 
próbek oraz tolerancje wymiarów. Przed badaniem próbki poddaje się tzw. klimatyzacji, trwającej co 
najmniej    16  godzin  w  temperaturze  wynoszącej    23

±

2

0

C    przy  wilgotności  względnej    50

±

5%. 

Prędkość  posuwu  trzpienia  obciążającego  przy  zastosowaniu  zalecanej  kształtki  o  wymiarach 
10×4×80 mm powinna wynosić 2 mm/min .  

 
 

10

 

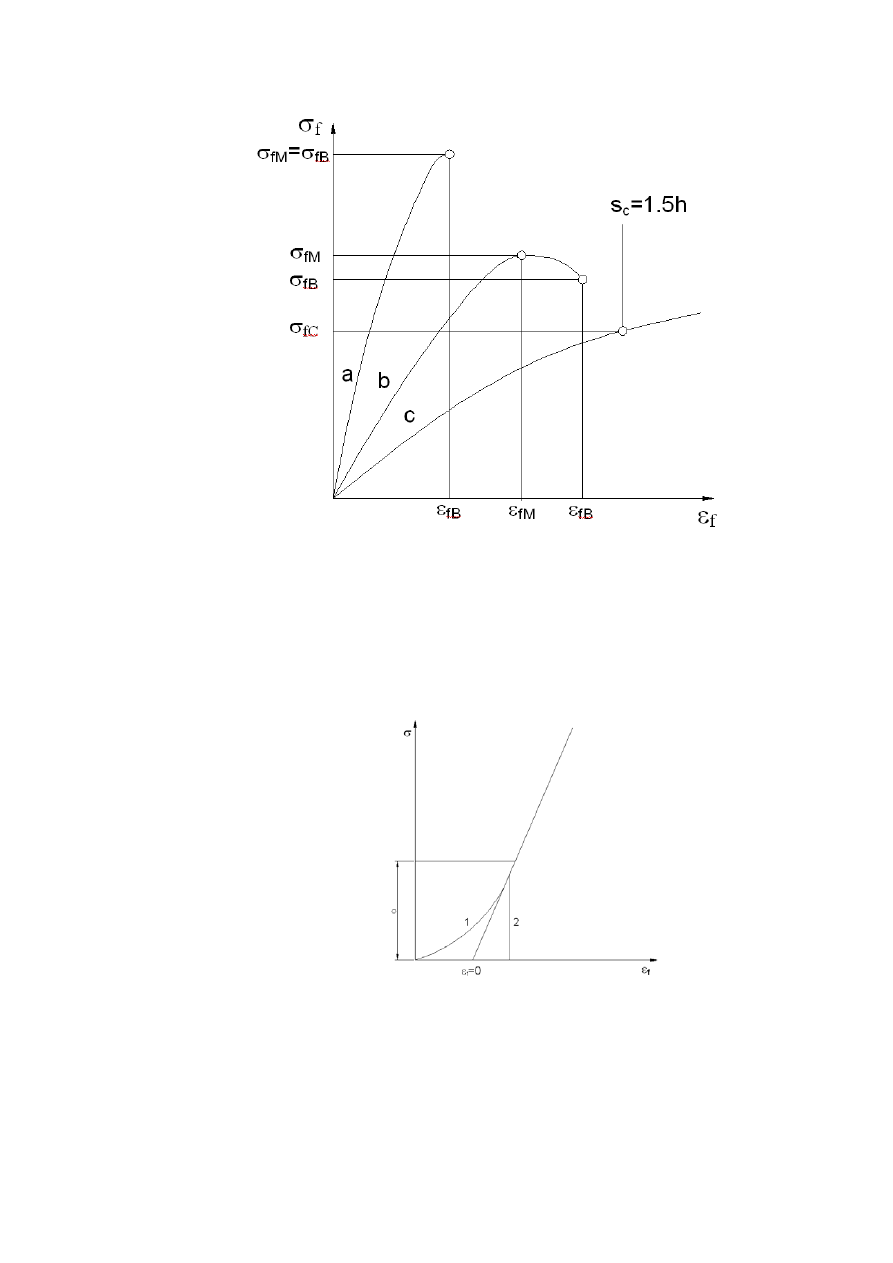
Rys. 5.4 Typowe krzywe naprężenia zginającego 

σ

f

, w zależności do badań   

(a) Kształtka,  która  ulega  zniszczeniu  przed  osiągnięciem  granicy 

plastyczności.   

(b) Kształtka  wykazująca  maksimum,  która  następnie  uległa  złamaniu  przed 

osiągnięciem umownej strzałki ugięcia s

c

. 

(c) Kształtka,  która  nie  wykazuje  maksimum  ani  nie  ulega  złamaniu  przed 

osiągnięciem umownej strzałki ugięcia s

c

. 

 
 

 

Rys.5.5  Przykład  krzywej  naprężenie/odkształcenie  z  początkowym  zakresem 
krzywoliniowym i wyznaczaniem punktu odkształcenia zerowego: 
1  –  początkowa  część  wykresu  naprężenie/odkształcenie  pokazująca  zakres 
krzywoliniowy, 
2  –  początkowa  część  wykresu  naprężenie/odkształcenie  pokazująca  miejsce  od 
którego mierzy się siłę w zakresie prostoliniowym. 
 
 

11

 

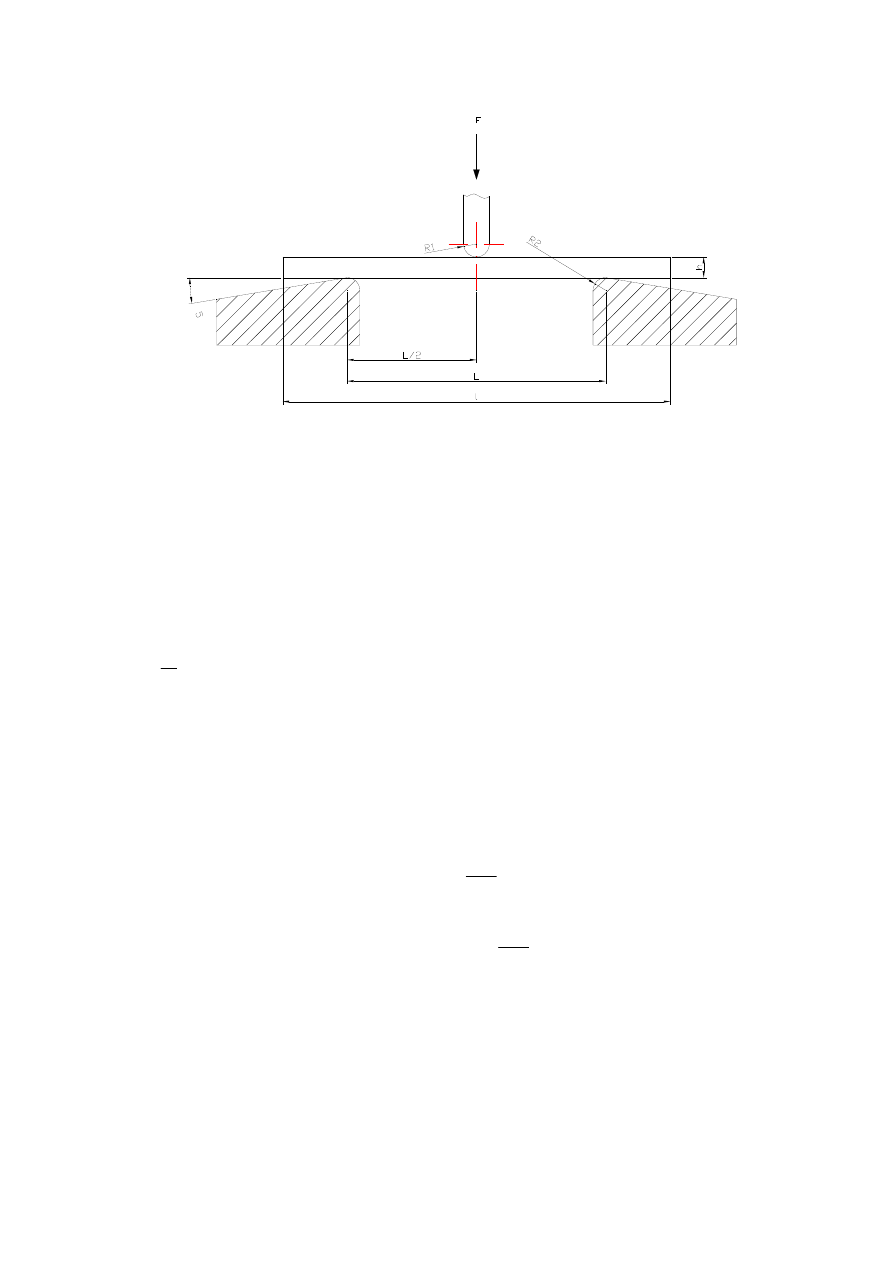
Rys.5.6  Położenie kształtki do badań na początku;  oznaczenia: 1 – kształtka do badań, 

F ‐  przybliżona siła, R

1

– Promień trzpienia obciążającego; R

2

 – Promień podpór; 

h – grubość kształtki; d – długość kształtki; L‐ rozstaw podpór. 

 
 

5.6 Obliczanie i przedstawianie wyników 

 
Obliczanie naprężeń 
Wszystkie wartości naprężeń należy obliczać w odniesieniu do początkowego przekroju poprzecznego 
kształtki: 
 

A

F

=

σ

 

 
gdzie: 

σ

‐ jest określoną wartością naprężenia, wyrażoną w megapaskalach; 

F

‐ jest odpowiadającą siłą, mierzoną w niutonach; 

A

‐ jest początkowych przekrojem poprzecznym kształtki, wyrażonym w milimetrach kwadratowych. 

 
Obliczanie odkształceń 
Wszystkie wartości odkształceń należy obliczać w odniesieniu do odcinka pomiarowego: 

0

0

L

L

Δ

=

ε

 

 

0

0

100

(%)

L

L

Δ

×

=

ε

 

 

gdzie: 

ε

‐ jest określoną wartością wydłużenia względnego, wyrażoną jako wielkość bezwymiarowa lub w 

procentach; 

0

L

‐ jest długością odcinka pomiarowego, wyrażoną w milimetrach; 

0

L

Δ

‐ jest przyrostem długości kształtki do badań między znakami pomiarowymi, wyrażonym w 

milimetrach. 
 

12

Wartość  wydłużenia  względnego  nominalnego  należy  obliczyć  w  odniesieniu  do  początkowej 
odległości między uchwytami do próbek: 
 

L

L

t

Δ

=

ε

 

 

L

L

t

Δ

×

=100

ε

 

gdzie: 

t

ε

‐ jest wydłużeniem względnym nominalnym, wyrażonym jako wielkość bezwymiarowa lub w 

procentach, %; 

L

‐ jest początkową odległością między uchwytami próbek; 

L

Δ

‐ jest przyrostem odległości między uchwytami próbek, wyrażonym w milimetrach. 

 
Obliczanie modułu 
Moduł  sprężystości  przy  rozciąganiu  należy  obliczyć  w  odniesieniu  do  dwóch  określonych  wartości 
wydłużenia względnego: 
 

1

2

1

2

ε

ε

σ

σ

−

−

=

t

E

 

gdzie: 

t

E

‐ jest modułem sprężystości przy rozciąganiu, wyrażonym w megapaskalach; 

1

σ

‐ jest naprężeniem, w megapaskalach, mierzonym przy wartości wydłużenia względnego 

1

ε

=0,0005 

2

σ

‐ jest naprężeniem, w megapaskalach, mierzonym przy wartości wydłużenia względnego 

1

ε

=0,0025 

 
Współczynnik Poissona 
Jeśli  jest  to  wymagane,  należy  obliczyć  współczynnik  Poissona  w  odniesieniu  do  dwóch 
odpowiadających sobie wartości odkształcenia, powstałego prostopadle do siebie: 

ε

ε

μ

n

n

−

=

 

gdzie: 

n

μ

‐  jest  współczynnikiem  Poissona,  wyrażonym  jako  stosunek  bezwymiarowy,  gdy  n=b  (szerokość) 

lub h (grubość), wskazując wybrany kierunek prostopadły; 

ε

‐ jest odkształceniem w kierunku wzdłużnym 

n

ε

‐ jest odkształceniem w kierunku prostopadłym, gdy n=b (szerokość) lub h (długość) 

 
Sprawozdanie z badań 
Sprawozdanie wykonane przez studentów powinno zawierać: 

− wszystkie dane niezbędne do identyfikacji badanego materiału,  
− dane  dotyczące  kształtki  –  typ,  szerokość  i  grubość  przekroju  równoległego,  łącznie 

z wartościami średnimi, minimalnymi i maksymalnymi, sposób wykonania kształtek 

− liczbę badanych kształtek 
− dane dotyczące maszyny wytrzymałościowej 
− dane dotyczące rodzaju miernika wydłużenia lub odkształcenia 
− dane dotyczące rodzaju uchwytu urządzenia i nacisku mocowania 

13

− prędkość badania 
− wyniki badań 
− średnie wartości mierzonych 
− standardowe odchylenie  
− informację,  czy  którąkolwiek  z  kształtek  do  badań  odrzucono  lub  zastąpiono 

i z jakiego powodu 

− datę pomiarów 

 
 
Literatura 
 
1.

PN‐EN  ISO  527‐1.  Oznaczanie  wytrzymałości  mechanicznych  przy  statycznym  rozciąganiu. 
Zasady ogólne 

2.

PN‐EN  ISO  527‐2.  Oznaczanie  wytrzymałości  mechanicznych  przy  statycznym  rozciąganiu. 
Warunki badań tworzyw sztucznych  

3.

PN‐EN  ISO  294.  Tworzywa  sztuczne.  Wtryskiwanie  kształtek  do  badań  z  tworzyw 
termoplastycznych (część 1,2) 

4.

R.  Sikora.  Tworzywa  wielkocząsteczkowe.  Rodzaje,  właściwości  i  struktura.  Politechnika 
Lubelska, Lublin 1991