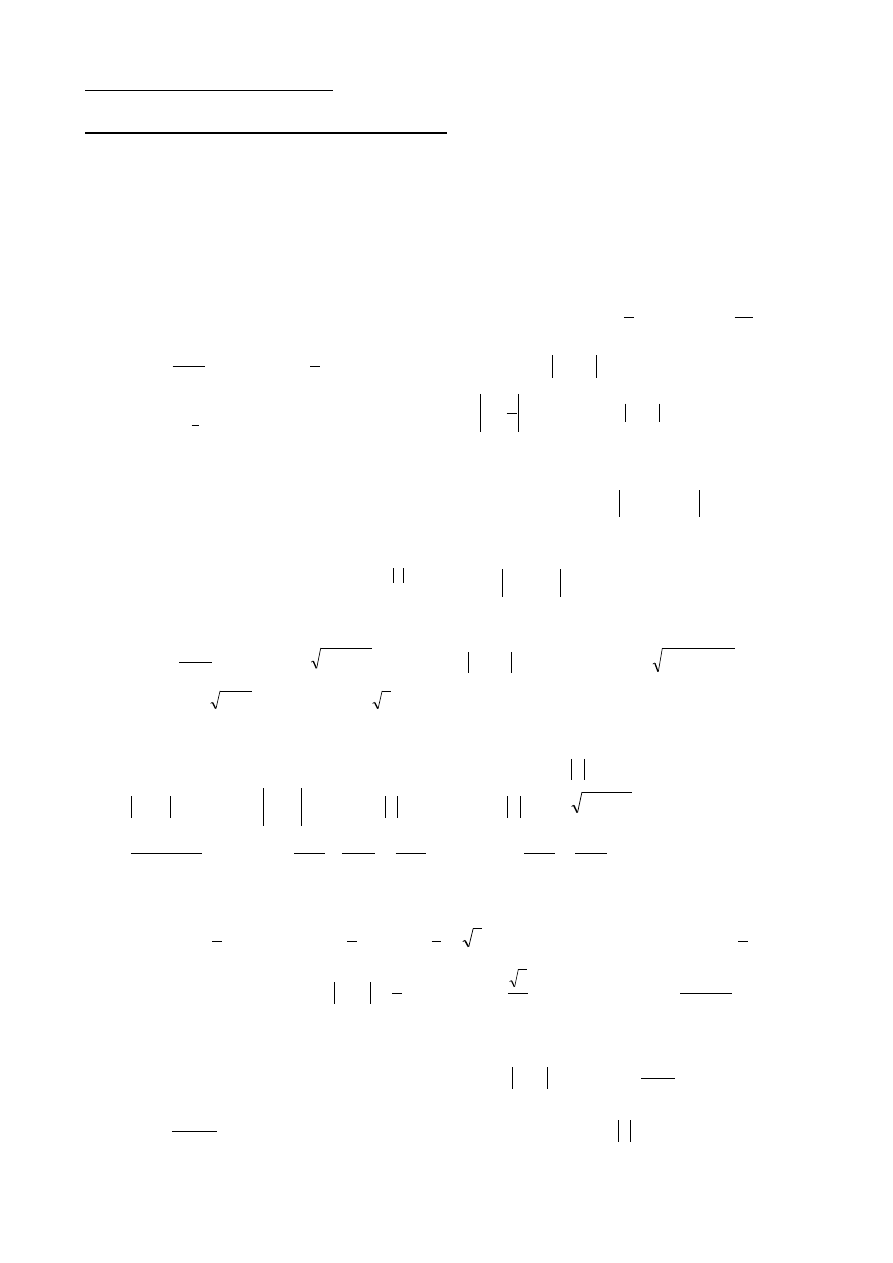
Budownictwo 1 sem (niestacjonarne)

Funkcje jednej zmiennej – repetytorium

1. Przypomnieć pojęcie funkcji, dziedziny funkcji i zbioru jej wartości, definicje funkcji: rosnącej,

malejącej, parzystej, nieparzystej, okresowej, ograniczonej i podać przykłady takich funkcji.

2. Przypomnieć wykresy podstawowych funkcji: liniowa, kwadratowa, potęgowa, wykładnicza,

logarytmiczna, trygonometryczne, a także moduł, signum i podstawowe wymierne.

3. Naszkicować wykresy następujących funkcji i omówić ich własności (wg pojęć z (1)).

,

3

)

(

a)

2



 x

x

f

,

3

2

)

(

b)

2









x

x

x

f

,

3

)

(

c)

x

x

f



,

1

)

(

d)

x

x

f





,

2

1

)

(

e)

x

x

f



,

1

)

(

f)





x

x

x

f

,

2

1

)

(

g)

x

x

f















,

2

2

)

(

h)





x

x

f

,

2

log

)

(

i)

x

x

f







,

3

log

)

(

j)

2

1





x

x

f

,

2

sin

2

)

(

k)

x

x

f



,

2

cos

)

(

l)

x

x

f



.

cot

)

(

m)

x

x

f



4. Przekształcając odpowiednio wykres funkcji

y

x



2

, naszkicować wykresy funkcji:

a) y

x

 

2

2

,





,

3

b)

2



 x

y





,

2

1

c)

2





 x

y

.

3

4

y

d)

2







x

x

5. Przekształcając odpowiednio wykres funkcji

x

y 2



, naszkicować wykresy funkcji:

.

4

2

d)

,

1

2

c)

,

1

2

b)

,

2

a)

2





















x

x

x

x

y

y

y

y

6. Wyznaczyć dziedzinę funkcji oraz zbiór jej wartości (przeciwdziedzinę):

).

tan

3

log(

)

(

f)

,

sin

2

1

)

(

e)

,

)

1

log(

1

)

(

d)

,

1

log

)

(

c)

,

2

)

(

b)

,

1

+

x

x

=

(x)

a)

2

2

2

x

x

f

x

x

f

x

x

f

x

x

f

x

x

x

f

f























7. Rozwiąż równania i nierówności:

5,

2x

x

d)

,

0

c)

,

0

3

2

x

b)

,

0

2

2

a)

5

2

4

2























x

x

x

x

x

,

2

16

x

i)

,

x

x

h)

,

9

g)

,

4

4

f)

,

1

4

2

e)

2

2

2

x

x

x

x

x

x





















3

3

1

1

,

1

6

2

7

1

+

x

3

3

2

1

l)

k)

,

0

j)

2



























x

x

x

x

x

x

x

x

.

8. Rozwiązać równania i nierówności trygonometryczne:

.

1

j)

,

1

cot

i)

,

cos

h)

,

sin

g)

,

sin

cos

sin

f)

,

cos

e)

,

tan

sin

d)

,

tan

c)

,

cos

b)

,

sin

a)

cos

1

cos

2

3

2

1

2

1

2

2

1

2

1

2

2

3

2

3

2

2

2





























x

x

x

x

x

x

x

x

x

x

x

x

x

x

9. Uzasadnić, że podane funkcje są parzyste lub nieparzyste:

.

x

x

=

u(x)

h)

,

x

3

x

3

=

t(x)

g)

x,

sin

=

p(x)

f)

,

x

x

+

2

=

l(x)

e)

,

x

sin x

=

k(x)

d)

,

sin x

=

h(x)

c)

,

x

2

+

x

2

=

g(x)

b)

1,

+

3x

-

x

=

f(x)

a)

3

3

2

3

2

4









10. Czy podane funkcje są ograniczone na wskazanych zbiorach:

R

,

1

+

x

1

=

k(x)

c)

1);

(0;

,

x

log

=

h(x)

b)

;

3)

(1;

,

x

1

=

g(x)

a)

2

2

?

11. Określić złożenie funkcji:

f f f g, g f, g g









,

oraz dziedziny tak złożonych funkcji jeżeli:

a) f(x) = x g(x) = x b) f(x) = 2 g(x) = cos x;

c) f(x) = x g(x) =

1

x

d) f(x) =

x

1 + x

, g(x) =

1
x

.

2

3

3

2

x

,

;

,

,

;

12. Wyznaczyć funkcje odwrotne do danych funkcji oraz określić ich dziedziny i przeciwdziedziny:





f(x)

3x 2, f(x)

x 1

2x 1

, f(x)

2

2, f(x)

log x 3

f(x) = 2 - x +1

f(x)

x

2x dla x

1; )

x 1

2

5

2





























,

,

.

Granica i ciągłość funkcji.

1. Przypomnieć niektóre podstawowe granice ciągów. Wyznaczyć granice danych ciągów:

,

+

=

a

h)

,

=

a

g)

,

=

a

f)

,

n

3

n

=

a

e)

,

=

a

d)

,

+

n

=

a

c)

,

1

n

+

n

n

=

a

b)

,

=

a

)

a

n

n

n

3

+

n

n

2

2

2

4

3

5

2

1

+

3n

4n

+

n

sin

n

+

...

+

3

+

2

+

1

2

3n

+

n

n

5

n

2n

n

n

n

2

n

2

n

n

3

n

n

2

+

n

3













n

 

.

=

a

l)

,

=

a

k)

,

=

a

i)

1

2n

n

3n

n

1

n

1

n

2

+

n

n

2

+

1

n

n

n































2. Wyznaczyć wskazane granice funkcji:

a) lim

b) lim

sin2x

5x

c) lim

tgx

3x

d) lim

e) lim

x 1

4

x 0

x 0

x 0

x 4

x

1

x 1

e

1

e

1

1 2x

3

x

2

3x

x

























,

,

,

,

,





f lim (1 x)

g) lim

x

x

h) lim

x -

x 0

1
x

2 x

3 x

x2

3x 1

x2

x 1

)

,

,







 







 

 









.

3. Podać wartości granic jednostronnych:

lim sgn ,

sgn ,

x

x

x

 



 

 

 



0

lim

lim

1

x

, lim tg x, lim [x], lim [x

x 0+

x 0

3

x 1

2

x 0

x 0+

],



.

e

lim

,

2

lim

,

2

lim

,

2

sgn

1

lim

,

2

sgn

1

lim

,

2

3

lim

1

2

1

x

1

+

0

x

1

0

x

0

+

0

x

2





























x

x

x

x

x

x

x

x

x

4. Zbadać ciągłość funkcji:

.

0

=

x

dla

1

0

x

dla

x

sinx

=

g(x)

b)

,

0

x

dla

1)

-

(x

0

<

x

dla

1

x

f(x)

a)

2























5. Znaleźć rozwiązania przybliżone (z dokładnością do 0,01) równań:

2

x

-

2

ln x

c)

0,

1

x

-

3

x

b)

x,

-

3

=

x

e

a)





