Analiza Funkcjonalna

WPPT IIIr. semestr letni 2011

Twierdzenie Riesza

07/05/2008

ROZKÃLAD FUNKCJONAÃLU NA R ´

O ˙ZNICE

¸ FUNKCJONAÃL ´

OW NIEUJEMNYCH

Definicja. FunckjonaÃl P na przestrzeni funkcyjnej V (na przykÃlad L

p

(µ), C(X))

lub ci¸agowej (np `

p

, c

0

, itp.) nazywa si¸e nieujemny je´sli v ≥ 0 =⇒ P (v) ≥ 0.

Jest oczywiste, ˙ze funkcjonaÃl jest nieujemny wtedy i tylko wtedy dy zachowuje
porz¸adek f ≥ g =⇒ P (f ) ≥ P (g).

Twierdzenie. Ka˙zdy funkcjonaÃl rzeczywisty i ograniczony P na przestrzeni funkcyjnej
lub ci¸agowej przedstawia si¸e jako r´o˙znica dw´och funkcjonaÃl´ow nieujemnych ogranic-
zonych:

P = P

+

− P

−

.

Dow´od. (Wystarczy dla przestrzeni funkcyjnych, bo ci¸agi to funkcje na N.) FunkcjonaÃly
P

+

i P

−

okre´slamy dla funkcji nieujemnej f wzorami

P

+

(f ) = sup{P (g) : 0 ≤ g ≤ f },

P

−

(f ) = − min{P (g) : 0 ≤ g ≤ f }.

Oczywi´scie zawsze dostaniemy warto´sci nieujemne, bo w klamrze jest mi¸edzy in-
nymi funkcja zerowa. Najpierw sprawd´zmy, ˙ze P = P

+

−P

−

. Mamy tak¸a oczywist¸a

r´ownowa˙zno´s´c: 0 ≤ g ≤ f ⇐⇒ 0 ≤ f − g ≤ f . Zatem

sup{P (g) : 0 ≤ g ≤ f } = sup{P (f − g) : 0 ≤ g ≤ f } =

P (f ) + sup{−P (g) : 0 ≤ g ≤ f } = P (f ) − min{P (g) : 0 ≤ g ≤ f }.

Teraz sprawd´zmy liniowo´s´c P

+

: Je´sli g i g

0

realizuj¸a z dokÃladno´sci¸a do epsilona

odpowiednie suprema dla funkcji nieujemnych f i f

0

, to 0 ≤ g + g

0

≤ f + f

0

i

P (g+g

0

) jest z dokÃladno´sci¸a do 2 epsilon r´owna P

+

(f )+P

+

(f

0

). To daje nier´owno´s´c

P

+

(f ) + P

+

(f

0

) ≤ P

+

(f + f

0

). Je´sli teraz 0 ≤ g ≤ f + f

0

, to funkcje (f − g)

+

i

f

0

− (f − g)

−

s¸a nieujemne (dla tej drugiej: tam gdzie f − g ≥ 0 wystarczy wiedzie´c,

˙ze f

0

≥ 0 (a to zaÃlo˙zyli´smy), a w pozostaÃlych punktach (f − g)

−

= −f + g ≤ f

0

),

nie wi¸eksze ni˙z odpowiednio f i f

0

. Zatem

P

+

(f ) + P

+

(f

0

) ≥ P ((f − g)

+

) + P (f

0

− (f − g)

−

) = P (f

0

+ f − g).

Poniewa˙z funkcje f

0

+ f − g reprezentuj¸a wszystkie funkcje mi¸edzy 0 a f

0

+ f ,

otrzymujemy P

+

(f )+P

+

(f

0

) ≥ P

+

(f +f

0

), czyli jest r´owno´s´c. WyÃl¸aczanie skalara

nieujemnego jest natychmiastowe. Dla funkcji znakowanych f = f

+

−f

−

okre´slamy

P

+

(f ) = P

+

(f

+

) − P

+

(f

−

). Liniowo´s´c wynika teraz ze wzor´ow

f

+

+ g

+

= (f + g)

+

+ h, f

−

+ g

−

= (f + g)

−

+ h,

gdzie h jest pewn¸a funkcj¸a nieujemn¸a:

P

+

(f + g) = P

+

((f + g)

+

) − P

+

((f + g)

−

) + P

+

(h) − P

+

(h) =

P

+

(f

+

) + P

+

(g

+

) − P

+

(f

−

) − P

+

(g

−

) = P

+

(f ) + P

+

(g).

Ograniczono´s´c Ãlatwo wida´c z definicji: norma nie przekracza ||P ||. Poniewa˙z P

−

=

P − P

+

, nie musimy ju˙z o P

−

niczego dowodzi´c. ¤

Uwaga. A priori rozkÃlad na r´o˙znic¸e dw´och funkcjonaÃl´ow nieujemnych nie jest jed-
noznaczny, gdy˙z zawsze mo˙zna doda´c jakikolwiek nieujemny fukcjonaÃl jednocze´snie
do P

+

i P

−

. Ale P

+

i P

−

okre´slone w dowodzie lematu s¸a w penym sensie opty-

malne: nie mo˙zna ju˙z ˙zadnego nieujemnego funkcjonaÃlu odj¸a´c od P

+

i od P

−

tak,

aby nieujemno´s´c przynajmniej jedngo z nich nie zostaÃla naruszona (bez dowodu).

Uwaga. Ka˙zdy funkcjonaÃl zespolony rozkÃlada si¸e na kombinacj¸e dw´och funkcjonaÃl´ow
rzeczywistych:

P = P

r

+ iP

i

,

gdzie P

r

i P

i

oznaczaj¸a cz¸e´s rzeczywst¸a i urojon¸a funcjonaÃlu P (zadane wzorami

P

r

(v) = Re(P (v)), P

i

(v) = Im(P (v)). Sprawdzenie tego jest kompletnie trywialne.

TWIERDZENIE RIESZA

Twierdzenie Riesza (o reprezentacji funkcjonaÃlu na C([0, 1])). Niech P b¸edzie
funkcjonaÃlem liniowym ci¸agÃlym na C([0, 1]). Wtedy istnieje sko´

nczona znakowana

(lub zespolona) miara borelowska µ na [0, 1] taka, ˙ze dla ka˙zdej f ∈ C([0, 1])

P (f ) =

Z

f dµ.

Na odwr´ot, dla dowolnej sko´

nczonej znakowanej miary borelowskiej µ powy˙zszy wz´or

zadaje funkcjonaÃl ograniczony P na C([0, 1]). Przyporz¸adkowanie funcjonaÃlowi mi-
ary jest izometrycznym izomorfizmem z C([0, 1]) na M([0, 1]) (zbi´or miar borelows-
kich znakowanych lub zespolonych).

Dow´od. Druga cz¸e´s´c jest oczywista (miara poprzez caÃlk¸e zadaje funkcjonaÃl liniowy
na C([0, 1]) i je´sli miara jest sko´

nczona, to funkcjonaÃl jest ograniczony). Liniow´s

przyporz¸adkowania mierze funkcjonaÃlu i zachowanie normy te˙z s¸a oczywiste.

Przechodzimy do istotnej cz¸e´sci twierdzenia, to znaczy maj¸ac funkcjonaÃl tworzymy
miar¸e. Poniewa˙z P wyra˙za si¸e jako kombinacja dw´och (lub czterech) funkcjonaÃl´ow
nieujemnych

P = P

+

r

− P

−

r

+ i(P

+

i

− P

−

i

),

to wystarczy twierdzenie udowodni´c dla funkcjonaÃl´ow nieujemnych (a potem odpo-
wiednie miary poÃl¸aczy´c t¸a sam¸a kombinacj¸a). Niech wi¸ec P oznacza funcjonaÃl
nieujemny na C([0, 1]). ˙Z¸adan¸a miar¸e zdefiniujemy zadaj¸ac jej dystrybuant¸e. Niech

F

P

(t) = inf{P (f ) : f ≥ 1

[0,t]

}.

Tak zdefiniowana funkcja ma nast¸epuj¸ace, oczywiste wÃlasno´sci: F

P

(0) = 0, F

P

jest niemalej¸aca, F

P

(1) = P (1). Jako funkcja niemalej¸aca, mo˙ze ona mie´c co

najwy˙zej przeliczalnie wiele punkt´ow nieci¸agÃlo´sci. Poka˙zemy prawostronn¸a ci¸agÃlo´s´c
F

P

, tzn. warunek lim

s→t

+

F

P

(s) = F

P

(t). We´zmy ci¸agÃl¸a funkcj¸e f ≥ 1

[0,t]

tak¸a, ˙ze

P (f ) ≤ F

P

(t) + ². Z ci¸agÃlo´sci, ma ona w pewnym przedziale [t, s] warto´sci wi¸eksze

od 1 −

1

n

=

n−1

n

. Tak wi¸ec

n

n−1

f ≥ 1

[0,s]

. To oznacza, ˙ze

F

P

(s) ≤ P (

n

n−1

f ) ≤

n

n−1

(F

P

(t) + ²).

Poniewa˙z s mo˙ze by´c w tym rozumowaniu wzi¸ete dowolnie blisko t, otrzymujemy

lim

s→t

+

F

P

(s) ≤

n

n−1

(F

P

(t) + ²).

Z dowolno´sci n i ² otrzymujemy lim

s→t

+

F

P

(s) ≤ F

P

(t). Odwrotna nier´owno´s´c jest

oczywista z monotoniczno´sci.

Tak wi¸ec F

P

jest dystrybuant¸a pewnej miary nieujemnej µ skupionej na przedziale

[0, 1]. Pozostaje sprawdzi´c, czy faktycznie P (f ) =

R

f dµ dla funkcji ci¸agÃlych.

Poniewa˙z oba funkcjonaÃly s¸a liniowe, i ka˙zda funkcja rozkÃlada si¸e na r´o˙znic¸e funkcji
nieujmnych, wystarczy sprawdza´c t¸e r´owno´s´c dla funkcji nieujemnych. Podobnie,
ka˙zda funkcja nieujemna jest r´o˙znic¸a dw´och funkcji nieujemnych malej¸acych, wi¸ec
mo˙zna ograniczy´c si¸e do funkcji malej¸acych. Najpierw zauwa˙zmy, ˙ze je´sli

1

[0,t]

≤ f ≤ 1

[0,s]

to

µ([0, t]) = F (t) ≤ P (f ) ≤ F (s) = µ([0, s]).

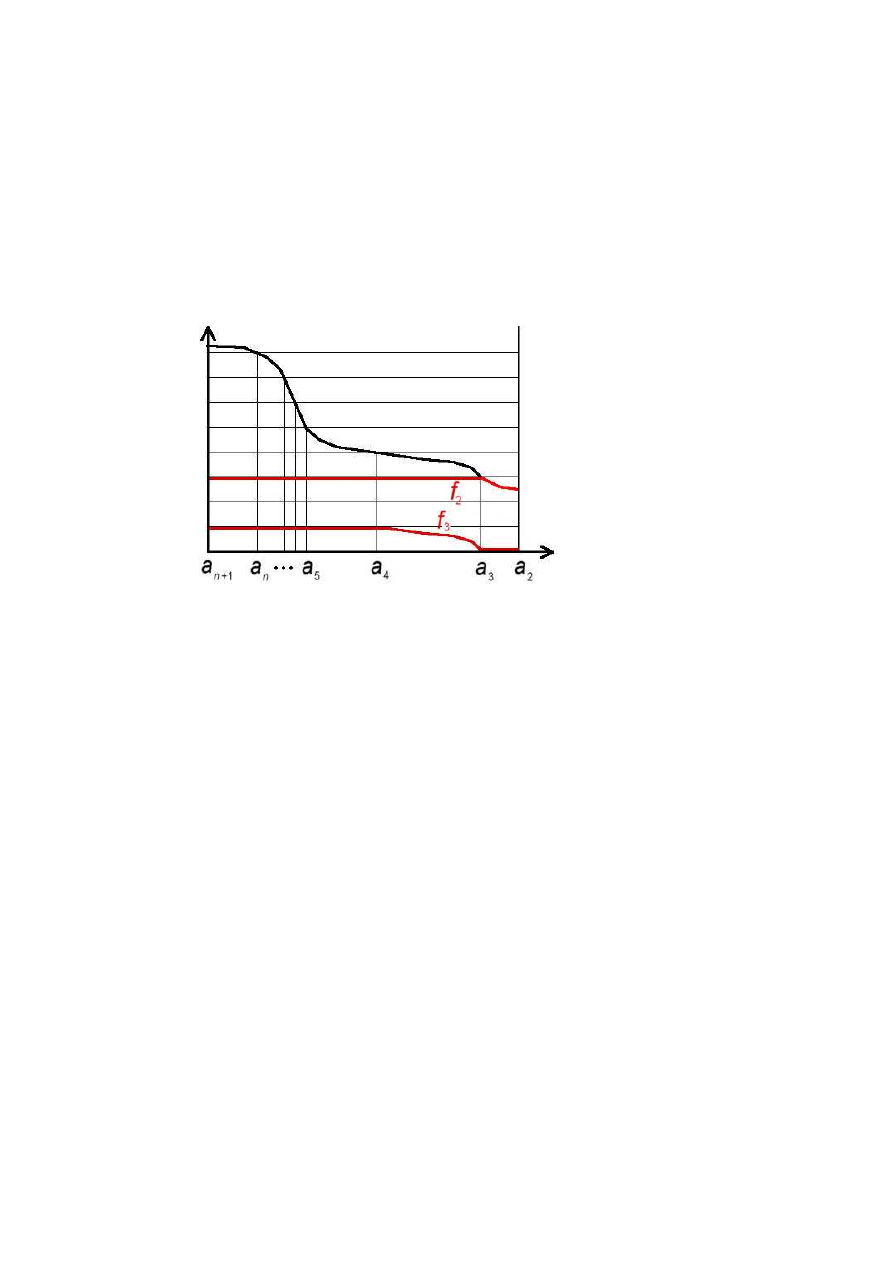
We´zmy teraz dowoln¸a funkcj¸e nieujemn¸a malej¸ac¸a f i ² > 0. Niech a

i

oznaczaj¸a

punkty w kt´orych f przyjmuje warto´sci i². Liczby a

i

oczywi´scie malej¸a i przebiegaj¸a

jakie´s kolejne warto´sci naturalne [m, m + 1, . . . , n]. Dodatkowo przyjmujemy, ˙ze
a

n+1

= 0, a

m−1

= 1. Funkcj¸e f mo˙zna teraz rozÃlo˙zy´c jako f =

P

n
i=m−1

f

i

, gdzie

f

m−1

= min{f, m²}

a dla pozostaÃlych i,

f

i

= max{0, min{f − i², ²}}.

ÃLatwo zauwa˙zy´c, ˙ze ka˙zda z funkcji f

i

speÃlnia warunek

²1

[0,a

i+1

]

≤ f

i

≤ ²1

[0,a

i

]

,

st¸ad

²µ([0, a

i+1

]) ≤ P (f

i

) ≤ ²µ([0, a

i

]).

Sumuj¸ac po i otrzymamy: po lewej stronie caÃlk¸e z funkcji prostej przybli˙zaj¸acej
f od doÃlu (z dokÃladno´sci¸a do ²), w ´srodku P (f ), a po prawej caÃlk¸e z funkcji
prostej przybli˙zaj¸acej f od g´ory. Przechodz¸ac z ² do zera dostajemy r´owno´s´c caÃlki
i funkcjonaÃlu.

¤

TWIERDZENIE RIESZA NA PRZESTRZENI ZWARTEJ

PARE

¸ FAKT ´

OW Z TOPOLOGII

Niech (X, d) oznacza przestrze´

n metryczn¸a.

1) OdlegÃlo´s´c punktu x od (dowolnego) zbioru A ⊂ X okre´slamy wzorem

d(x, A) = inf{d(x, y) : y ∈ A}.

Elementarnie sprawdza si¸e, ˙ze przy ustalonym zbiorze A, d(x, A) jest ci¸agÃl¸a funkcj¸a
zmiennej x. Je´sli A jest zbiorem domkni¸etym, to d(x, A) = 0 ⇐⇒ x ∈ A (dla
zbior´ow niedomkni¸etych d(x, A) = 0 jest r´ownowa´zny temu, ˙ze x nale˙zy do brzegu
zbioru A).

2) Niech U

1

, U

2

b¸ed¸a zbiorami otwartymi i niech f b¸edzie nieujemn¸a funkcj¸a ci¸agÃl¸a

zeruj¸ac¸a si¸e na dopeÃlnieniu sumy U

1

∪ U

2

(m´owimy, ˙ze f ma no´snik w U

1

∪ U

2

).

Wtedy f mo˙zna przedstawi´c jako sum¸e f

1

+ f

2

nieujemnych funkcji ci¸agÃlych o

no´snikach odpowiednio U

1

i U

2

. Dow´od: Na przykÃlad mo˙zna zdefiniowa´c

f

1

(x) =

(

0; x /

∈ U

1

∪ U

2

,

f (x)d(x,U

c

1

)

d(x,U

c

1

)+d(x,U

c

2

)

; x ∈ U

1

∪ U

2

,

f

2

(x) =

(

0; x /

∈ U

1

∪ U

2

,

f (x)d(x,U

c

2

)

d(x,U

c

1

)+d(x,U

c

2

)

; x ∈ U

1

∪ U

2

.

3) ZaÃl´o˙zmy teraz, ˙ze X jest o´srodkowa. Niech F b¸edzie dowoln¸a rodzin¸a funkcji
ci¸agÃlych f : X → [0, 1] i niech sup{f ∈ F} = 1

U

, gdzie U jest pewnym zbiorem

otwartym. Wtedy istnieje ci¸ag f

n

∈ F taki, ˙ze 1

U

= sup

n

f

n

. Dow´od: Ustalmy

² > 0. Dla ka˙zdego x ∈ U istnieje f

x,²

∈ F speÃlniaj¸aca f

x,²

(x) > 1 − ². Nier´owno´s´c

f

x,²

(y) > 1 − ² jest speÃlniona dla y z pewnego otwartego otoczenia V

x

punktu x.

Zbiory V

x

(x ∈ U ) pokrywaj¸a U . Poniewa´z (U, d) jest przestrzeni¸a o´srodkow¸a,

ma ona wÃlasno´s´c Lindel¨ofa, zatem z pokrycia tego mo˙zna wybra´c podpokrycie
przeliczalne {V

x

n

}. Wtedy Ãlatwo wida´c, ˙ze sup

n

f

x

n

,²

≥ 1 − ² na caÃlym zbiorze

U . Dla malej¸acego do zera ci¸agu parametr´ow ²

m

otrzymamy podw´ojnie indek-

sowany ci¸ag funkcji f

x

n

,²

m

o supremum r´ownym 1

U

. Numeruj¸ac ten ci¸ag liczbami

naturalnymi otrzymany ˙z¸adany ci¸ag funkcji f

n

.

4) ZaÃl´o˙zmy teraz, ˙ze X jest zwarta. Je´sli f

n

i f s¸a ci¸agÃlymi funkcjami rzeczywistymi

i f

n

zbiegaj¸a monotonicznie do f w ka˙zdym punkcie x ∈ X, to zbie˙zno´s´c ta jest

jednostajna. Dow´od: Ustalmy ² > 0. Niech F

n

= {x : |f (x) − f

n

(x)| ≥ ²}.

Oczywi´scie jest to zbi´or domkni¸ety. Poniewa˙z f

n

zbiegaj¸a monotonicznie do f ,

zbiory te malej¸a (czyli tworz¸a ci¸ag zst¸epuj¸acy). Gdyby wszystkie one byÃly niepuste,
to tworzyÃly by rodzin¸e scentrowan¸a i ze zwarto´sci ich przekr´oj byÃlby niepusty. Ale
w punkcie z tego przekroju nie byÃloby zbie˙zno´sci. Zatem kt´ory´s zbi´or F

n

0

jest

pusty, a to oznacza, ˙ze od numeru n

0

funkcje f

n

s¸a od funkcji f oddalone mniej ni˙z

² w metryce supremum. Czyli zbie˙zno´s´c jest jednostajna.

TWIERDZENIE RIESZA

Twierdzenie Riesza (o reprezentacji funkcjonaÃlu na C(X)). Niech (X, d) b¸edzie
przestrzeni¸a metryczn¸a zwart¸a i niech C(X) oznacza przestrze´

n Banacha funkcji

ci¸agÃlych rzeczywistych na X z norm¸a supremum. Niech P b¸edzie funkcjonaÃlem li-
niowym ci¸agÃlym (r´ownowa˙znie – ograniczonym) na C(X). Wtedy istnieje sko´

nczona

znakowana miara borelowska µ na X taka, ˙ze dla ka˙zdej f ∈ C(X)

P (f ) =

Z

f dµ.

Na odwr´ot, dla dowolnej sko´

nczonej znakowanej miary borelowskiej µ powy˙zszy wz´or

zadaje funkcjonaÃl ograniczony P na C(X). Przyporz¸adkowanie mierze funckjonaÃlu
jest izometrycznym izomorfizmem.

Dow´od. Ostatnie dwa zdania s¸a oczywiste. GÃl´own¸a cz¸e´s´c twierdzenia udowodnimy
najpierw przy zaÃlo˙zeniu, ˙ze funkcjonaÃl P jest nieujemny.
Niech U b¸edzie zbiorem otwartym. Zadajmy

µ(U ) = sup{P (f ) : 0 ≤ f ≤ 1

U

}.

Oczywi´scie tak zadana funkcja na zbiorach otwartych jest nieujemna i ograniczona.
Poka˙zemy najpierw jej sko´

nczon¸a podaddytywno´s´c. Niech U = U

1

∪ U

2

. Dla

ustalonego ε > 0 istnieje funkcja ci¸agÃla 0 ≤ f ≤ 1

U

taka, ˙ze µ(U ) ≤ P (f ) + ε.

Zgodnie z faktem 2) (patrz cz¸e´s´c tego dokumentu dot. topologii), f = f

1

+ f

2

gdzie

f

1

ma no´snik w U

1

a f

2

ma no´snik w U

2

, obie funkcje s¸a nieujemne i oczywi´scie

ograniczone przez 1. Mamy

µ(U ) ≤ P (f ) + ε = P (f

1

) + P (f

2

) + ε ≤ P (U

1

) + P (U

2

) + ε.

Poniewa˙z ε jest dowolny, µ(U ) ≤ P (U

1

) + P (U

2

). Poka˙zemy teraz ci¸agÃlo´s´c z doÃlu

(dalej tylko na zbiorach otwartych), co da nam przeliczaln¸a podaddytywno´s´c (suma
przeliczalna jest granic¸a wst¸epuj¸ac¸a sum sko´

nczonych). Niech wi¸ec U =

S

n

U

n

b¸edzie sum¸a wst¸epuj¸ac¸a zbior´ow otwartych. Niech x ∈ U . Wtedy x ∈ U

n

dla

pewnego n i funkcja

f (y) = min

½

1,

d(y, U

c

n

)

d(x, U

c

n

)

¾

jest ci¸agÃla, 0 ≤ f ≤ 1

U

n

oraz f (x) = 1. St¸ad bior¸ac

F = {f ci¸agÃla : ∃

n

0 ≤ f ≤ 1

U

n

}

mamy sup{f ∈ F} = 1

U

. Z topologicznego faktu 3) istnieje ci¸ag f

m

∈ F o

supremum 1

U

. Ka˙zda funkcja f

m

ma no´snik w kt´orym´s ze zbior´ow U

n

, powiedzmy

w U

n(m)

. Niech g

m

= sup{f

i

: 1 ≤ i ≤ m}. Wtedy funkcje g

m

s¸a ci¸agÃle, tworz¸a

ci¸ag niemalej¸acy zbie˙zny do 1

U

, ka˙zda z nich ma no´snik w zbiorze U

n

m

, gdzie

n

m

= max{n(i) : 1 ≤ i ≤ m}. Niech znowu f b¸edzie funkcj¸a ci¸agÃl¸a o no´sniku w U

tak¸a, ˙ze µ(U ) ≤ P (f ) + ε. Wtedy f · g

m

jest ci¸agiem zbie˙znym monotonicznie do

f , a zatem z faktu 4) zbie˙znym jednostajnie. Z ci¸agÃlo´sci funkcjonaÃlu (w zbie˙zno´sci
jednostajnej) pozwala to napisa´c

µ(U ) ≤ P (f ) + ε = lim

m

P (g

m

) + ε ≤ lim

m

µ(U

n

m

) + ε.

Poniewa˙z jest jasne, ˙ze µ(U

n

) ro´snie i nie przekracza µ(U ), ostatni¸a granic¸e mo˙zna

zast¸api´c granic¸a po wszystkich n oraz zachodzi ˙z¸adana r´owno´s´c µ(U ) = lim

n

µ(U

n

).

Dla dowolnego zbioru A ⊂ X definiujemy teraz

µ(A) = inf{µ(U ) : U ⊃ A, U otwarty}.

Poka˙zemy przeliczaln¸a podaddytywno´s´c, co da nam, ˙ze µ jest miar¸a zewn¸etrzn¸a.
Niech A =

S

n

A

n

. Ustalmy szereg nieujemnych liczb

P

n

ε

n

= ε. Dla ka˙zdego

n istnieje zbi´or otwarty U

n

⊃ A

n

speÃlniaj¸acy µ(U

n

) ≤ µ(A

n

) + ε

n

. Oczywi´sie

U =

S

n

U

n

jest otwarty i zawiera A. Korzystaj¸ac z przeliczalnej podaddytywno´sci

µ na zbiorach otwartych otrzymujemy

µ(A) ≤ µ(U ) ≤

X

n

µ(U

n

) ≤

X

n

µ(A

n

) + ε.

Poniewa˙z ε jest dowolnie maÃly, mamy przeliczaln¸a podaddytywno´s´c.
Teraz poka˙zemy, ˙ze zbiory otwarte s¸a mierzalne w sensie Caratheodory’ego wzgl¸edem
µ. Czyli mamy pokaza´c, ˙ze je´sli W jest zbiorem otwartym, to dla dowolnego zbioru
A, µ(W ∩ A) + µ(W

c

∩ A) ≤ µ(A). Niech U zawiera A. Rozwa˙zmy par¸e zbior´ow

otwartych V

n

= {x : d(x, W

c

) <

1

n

} i W

n

= {x : d(x, W

c

) >

1

n

}. Para V

n

i W

n

jest rozÃl¸aczna, ponadto V

n

⊃ W

c

oraz W

n

% W . Poniewa˙z U ∩ V

n

i U ∩ U

n

s¸a

rozÃl¸aczne, to dla ka˙zdej pary funkcji ci¸agÃlych 0 ≤ f ≤ 1

U ∩V

n

, 0 ≤ g ≤ 1

U ∩U

n

mamy

f + g ≤ 1

U

. St¸ad, bior¸ac supremum po takich parach funkcji mamy, dla ka˙zdego n,

µ(U ) ≥ µ(U ∩ V

n

) + µ(U ∩ W

n

) ≥ µ(A ∩ W

c

) + µ(U ∩ W

n

).

Przechodz¸ac do granicy (i z ci¸agÃlo´sci z doÃlu µ na zbiorach otwartych) dostajemy
µ(U ) ≥ µ(A ∩ W

c

) + µ(U ∩ W ) ≥ µ(A ∩ W

c

) + µ(A ∩ W ). Bior¸ac infimum po

U , dostajemy µ(A) ≥ µ(A ∩ W

c

) + µ(A ∩ W ), co ko´

nczy dow´od mierzalno´sci.

Ostatecznie wi¸ec µ jest miar¸a (ograniczon¸a) na zbiorach borelowiskich.

Pozostaje sprawdzi´c, czy faktycznie P (f ) =

R

f dµ dla funkcji ci¸agÃlych. Poniewa˙z

oba funkcjonaÃly s¸a liniowe, i ka˙zda funkcja rozkÃlada si¸e na r´o˙znic¸e funkcji nieujm-
nych, wystarczy sprawdza´c t¸e r´owno´s´c dla funkcji nieujemnych. Najpierw zauwa˙zmy,

˙ze je´sli 1

U

≤ f ≤ 1

V

(U, V zbiory otwarte), to µ(U ) ≤ P (f ) ≤ µ(V ). We´zmy teraz

dowoln¸a funkcj¸e nieujemn¸a f i ε > 0. Funkcj¸e f mo˙zna rozÃlo˙zy´c jako f =

P

n
i=0

f

i

,

gdzie

f

i

= max{0, min{f − iε, ε}},

i n nie przekracza

max f

ε

. Ka˙zda z funkcji f

i

ma no´snik w zbiorze

U

i

= {x : f (x) > iε}

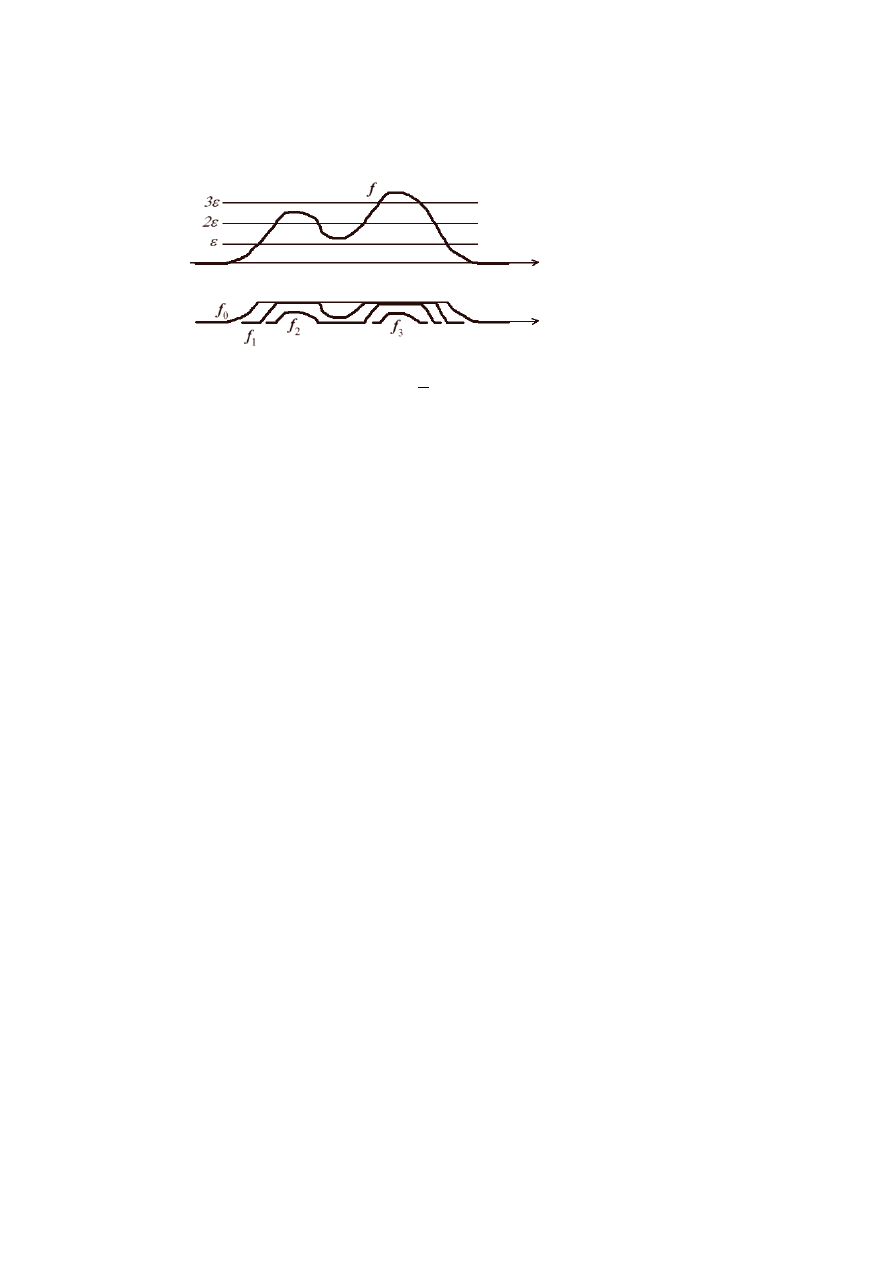
oraz jest r´owna ε na zbiorze U

i+1

(zob. rysunek)

Mamy zatem ε1

U

i+1

≤ f

i

≤ ε1

U

i

, czyli 1

U

i+1

≤

f

i

ε

≤ 1

U

i

, z czego wynika, ˙ze

n

X

i=2

εµ(U

i

) ≤ P (f ) ≤

n

X

i=1

εµ(U

i

).

Oczywi´scie, z monotoniczno´sci caÃlki, r´ownie˙z

n

X

i=2

εµ(U

i

) ≤

Z

f dµ ≤

n

X

i=1

εµ(U

i

).

Prawa i lewa strona r´o˙zni¸a sie co najwy˙zej o εµ(X), zatem co najwy˙zej o tyle
samo mog¸a si¸e r´o˙zni´c P (f ) i

R

f dµ. Poniewa˙z ε jest dowolnie maÃly otrzymujemy

r´owno´s´c. zako´

nczyli´smy dow´od dla funkcjonaÃlu nieujemnego. ¤

Tomasz Downarowicz