WM

Z13/2. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 2

1

Z13/2. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 2

Z13/2.1. Zadanie 2

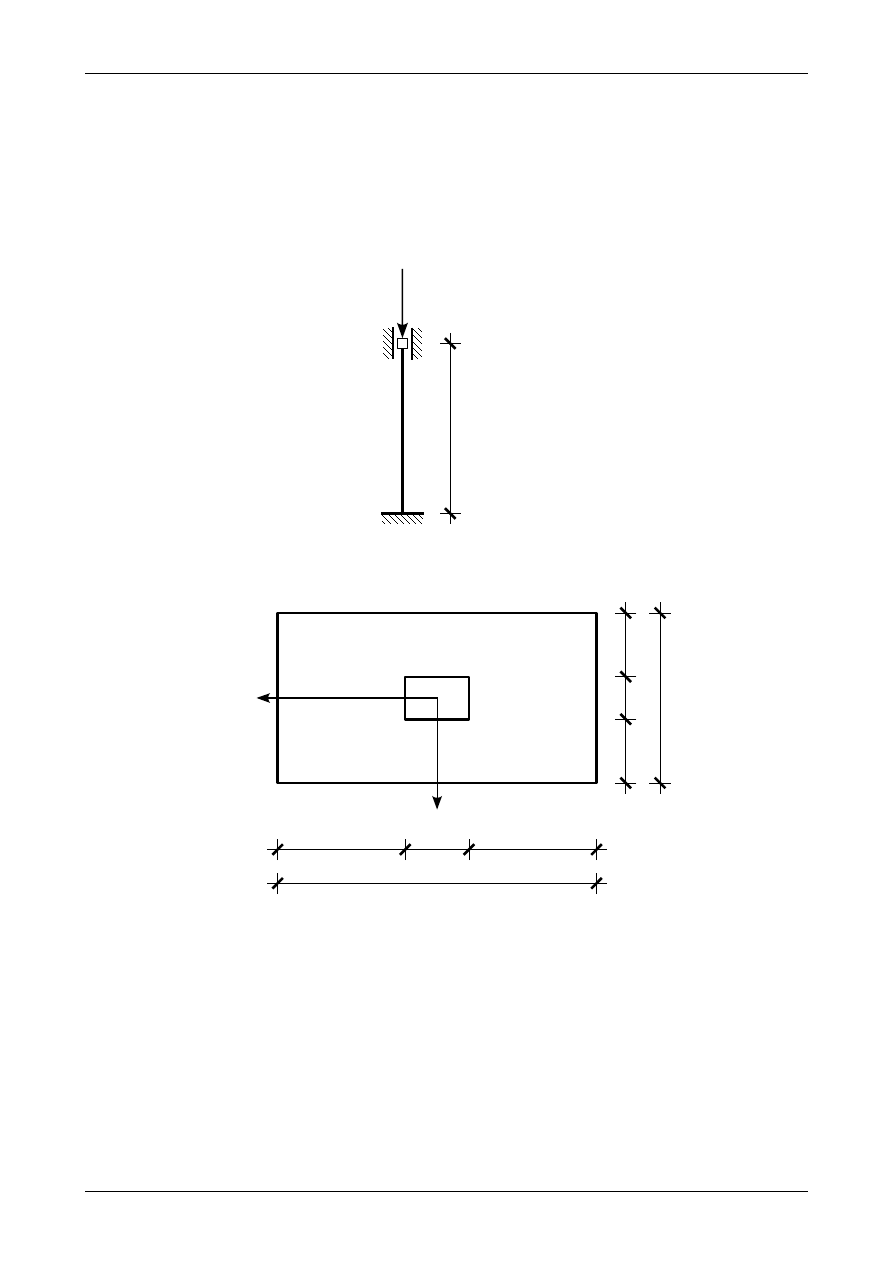
Wyznaczyć siłę krytyczną pręta ściskanego osiowo przedstawionego na rysunku Z13/2.1. Pręt ten jest

zamocowany w obu płaszczyznach pokrywających się z osiami głównymi bezwładności w jednakowy
sposób. Wymiary przekroju pręta podane są w centymetrach natomiast długość pręta podana jest w metrach.
Przekrój pręta przedstawia rysunek Z13/2.2.

4,0

[m]

P

KR

Rys. Z13/2.1. Pręt ściskany osiowo

3,

0

2,

0

3,

0

3,0

6,0

[cm]

Y=Y

gl

Z=Z

gl

6,0

15,0

8,

0

Rys. Z13/2.2. Przekrój pręta ściskanego osiowo

Pręt został wykonany ze stali o granicy proporcjonalności



H

=

205,0 MPa

(Z13/2.1)

oraz granicy plastyczności



P

=

235,0 MPa

.

(Z13/2.2)

Dr inż. Janusz Dębiński

WM

Z13/2. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 2

2

Z13/2.2. Charakterystyki geometryczne przekroju pręta

Główne momenty bezwładności przekroju słupa ściskanego osiowo względem osi Y=Y

gl

oraz Z=Z

gl

wynoszą

J

Y

=

J

Ygl

=

15,0⋅8,0

3

12

−

3,0⋅2,0

3

12

=

638,0 cm

4

,

(Z13/2.3)

J

Z

=

J

Zgl

=

8,0⋅15,0

3

12

−

2,0⋅3,0

3

12

=

2246 cm

4

.

(Z13/2.4)

Pole powierzchni przekroju słupa ściskanego osiowo wynosi

A=15,0⋅8,0 −3,0⋅2,0 =114,0 cm

2

.

(Z13/2.5)

Z13/2.3. Wyznaczenie siły krytycznej pręta ściskanego osiowo

Ponieważ pręt jest zamocowany w obu płaszczyznach pokrywających się z osiami głównymi bez-

władności w jednakowy sposób o wyboczeniu będzie decydował minimalny moment bezwładności. Porów-
nując główne momenty bezwładności (Z13/2.3) i (Z13/2.4) możemy stwierdzić, że będzie to moment
względem osi Y=Y

gl

czyli

J =J

Y

=

638,0 cm

4

.

(Z13/2.6)

Promień bezwładności przekroju wynosi

i=



638,0
114,0

=

2,366 cm

.

(Z13/2.7)

Długość wyboczeniowa pręta wynosi

L

W

=

0,5⋅4,0 m=200,0 cm

.

(Z13/2.8)

Smukłość pręta wynosi

=

200,0
2,366

=

84,53

.

(Z13/2.9)

Moduł Younga dla stali wynosi

E=205GPa=205000 MPa

.

(Z13/2.10)

Dr inż. Janusz Dębiński

WM

Z13/2. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 2

3

50

100

150

200

250

300

0

0

50

100

150

200

250

A

λ

σ

KR

[MPa]

σ

H

=205 MPa

σ

P

=235 MPa

σ

KR

=209,5 MPa

λ

GR

=9

9,3

5

λ

=

84

,53

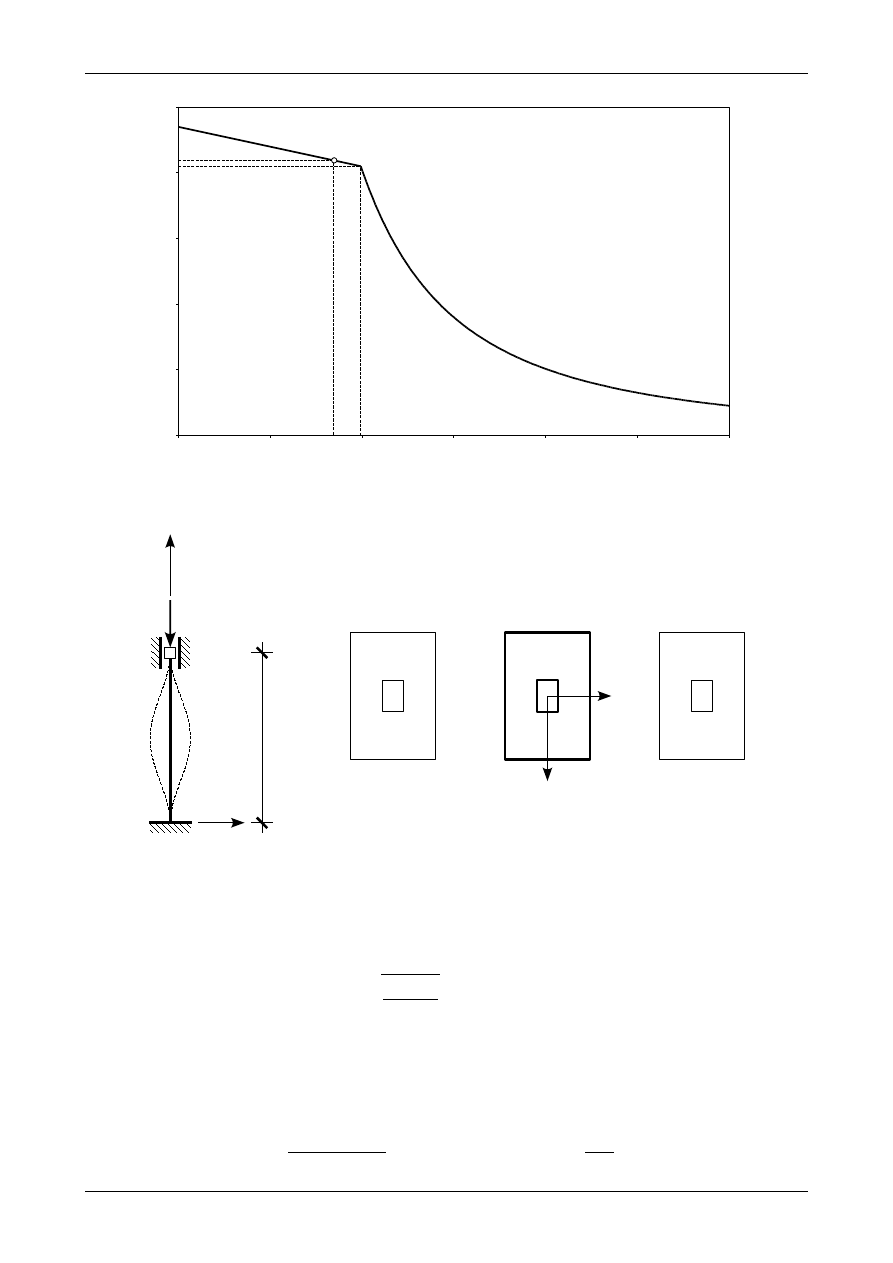
Rys. Z13/2.3. Położenie punktu krytycznego

4,0

[m]

X

Z

P

KR

Y=Y

gl

Z=Z

gl

Rys. Z13/2.4. Postać wyboczeniowa pręta ściskanego osiowo

Smukłość graniczna pręta wynosi



GR

=⋅



205000

205,0

=

99,35

.

(Z13/2.11)

Smukłość (Z13/2.9) jest mniejsza niż smukłość graniczna (Z13/2.11) więc pręt pracuje w zakresie

sprężysto-plastycznym. Normalne naprężenie krytyczne wyznaczamy ze wzoru (13.11) i wynosi ono



KR

=

235,0−

235,0−205,0

99,35

⋅

84,53=209,5 MPa=20,95

kN

cm

2

.

(Z13/2.12)

Dr inż. Janusz Dębiński

WM

Z13/2. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 2

4

Siła krytyczna zgodnie z (13.20) wynosi

P

KR

=

20,95⋅114,0 =2388 kN

.

(Z13/2.13)

Rysunek Z13/2.3 przedstawia położenie punktu krytycznego (A) na wykresie zależności pomiędzy

normalnym naprężeniem krytycznym a smukłością pręta. Rysunek Z13/2.4 przedstawia postać wybocze-
niową pręta. Wyboczenie nastąpi w płaszczyźnie XZ, która to jest prostopadła do osi głównego mini-
malnego momentu bezwładności.

Dr inż. Janusz Dębiński