WM
Z6/2. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 2
1
Z6/2. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 2
Z6/2.1. Zadanie 2
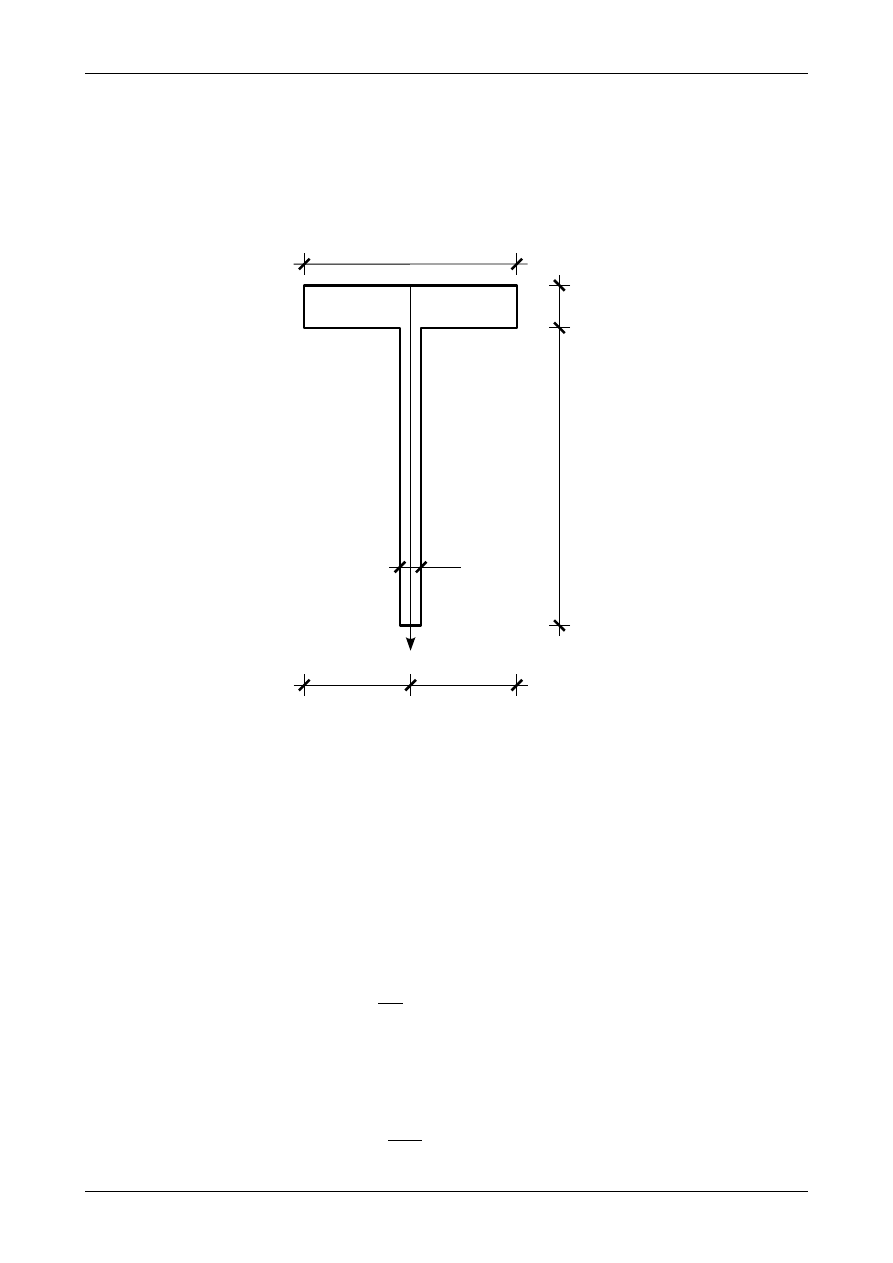
Rysunek Z6/2.1 przedstawia blachownicę o przekroju teowym. Składa się ona z dwóch blach.
Wszystkie wymiary teownika podane są w centymetrach. W przekroju tym wyznaczymy wartości głównych
momentów bezwładności.
4,0
Z
0
=Z
P
20,0
10,0
10,0
28
,0
2,0
[cm]
Rys. Z6/2.1. Przekrój teowy
Z6/2.2. Położenie środka ciężkości
Ponieważ przekrój teowy posiada jedną oś symetrii środek ciężkości znajduje się na tej osi. W celu
wyznaczenia położenia środka ciężkości teownika obieramy początkowy układ współrzędnych Y
P
Z
P
. Oś Z
P
jest osią symetrii przekroju teowego. Współrzędna y
C
środka ciężkości przekroju teowego wynosi więc zero.
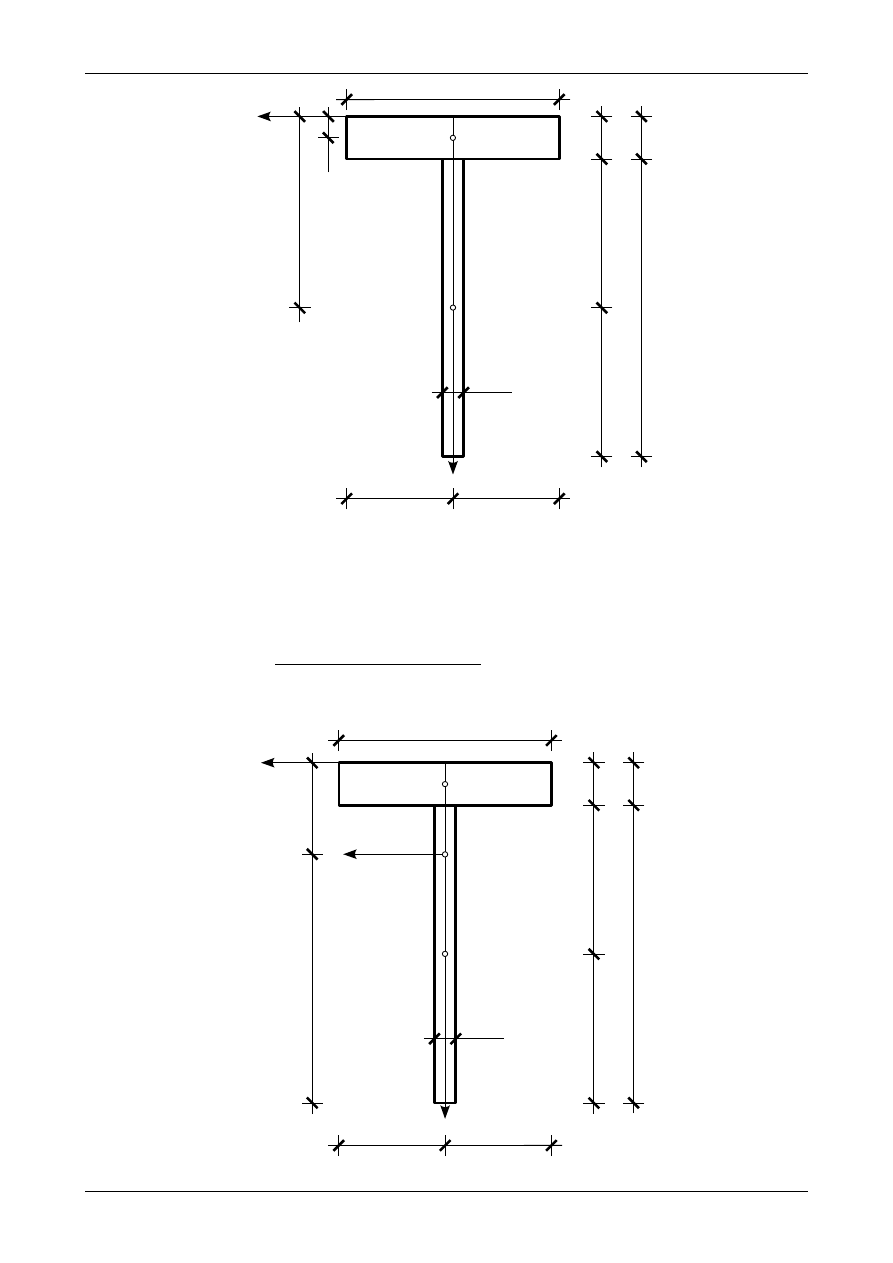
Przekrój teowy dzielimy na dwa prostokąty: półkę o wymiarach 20,0 cm na 4,0 cm oraz środnik o wymia-
rach 28,0 cm na 2,0 cm. Rysunek Z6/2.2 przedstawia położenie środków ciężkości poszczególnych figur
składowych w układzie Y
P
Z
P
.
Środek ciężkości figury numer 1 posiada współrzędną z równą
z
P1
=
4,0
2
=
2,0 cm
.
(Z6/2.1)
Środek ciężkości figury numer 2 posiada współrzędną z równą
z
P2
=
4,0
28,0
2
=
18,0 cm
.
(Z6/2.2)
Dr inż. Janusz Dębiński
WM
Z6/2. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 2
2
10,0
10,0
20,0
4,
0
14
,0
14
,0
18
,0
Y
P
Z
0
=Z
P
[cm]
4,
0
28
,0
2,0
2,0
sc
2
sc
1
Rys. Z6/2.2. Podział przekroju teowego na figury składowe
Zgodnie ze wzorem (6.14) współrzędna z
C
środka ciężkości wynosi
z
C
=
20,0⋅4,0⋅2,028,0⋅2,0⋅18,0
20,0⋅4,028,0⋅2,0
=
8,588 cm
.
(Z6/2.3)
10,0
10,0
20,0
4,0
14
,0
14
,0
8,5
88
Y
P
Z
0
=Z
P
[cm]
4,
0
28
,0
2,0
Y
0
23
,4
1
sc
2
sc
sc
1
Rys. Z6/2.3. Położenie środka ciężkości przekroju teowego
Dr inż. Janusz Dębiński
WM
Z6/2. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 2
3
Rysunek Z6/2.3 przedstawia położenie środka ciężkości przekroju teowego w początkowym układzie
współrzędnych.
Z6/2.3. Główne momenty bezwładności
W celu wyznaczenia współrzędnych środków ciężkości w układzie osi środkowych wykorzystamy
wzory transformacyjne
y
oi
=
y
Pi
−
y
C
,
(Z6/2.4)
z
oi
=
z
Pi
−
z
C
.
(Z6/2.5)
Współrzędne środka ciężkości figury numer 1 w układzie osi środkowych wynoszą
z
01
=
2,0−8,588=−6,588 cm y
01
=
0,0 cm
.
(Z6/2.6)
Współrzędne środka ciężkości figury numer 2 w układzie osi środkowych wynoszą
z
02
=
18,0−8,588=9,412 cm y
02
=
0,0 cm
.
(Z6/2.7)
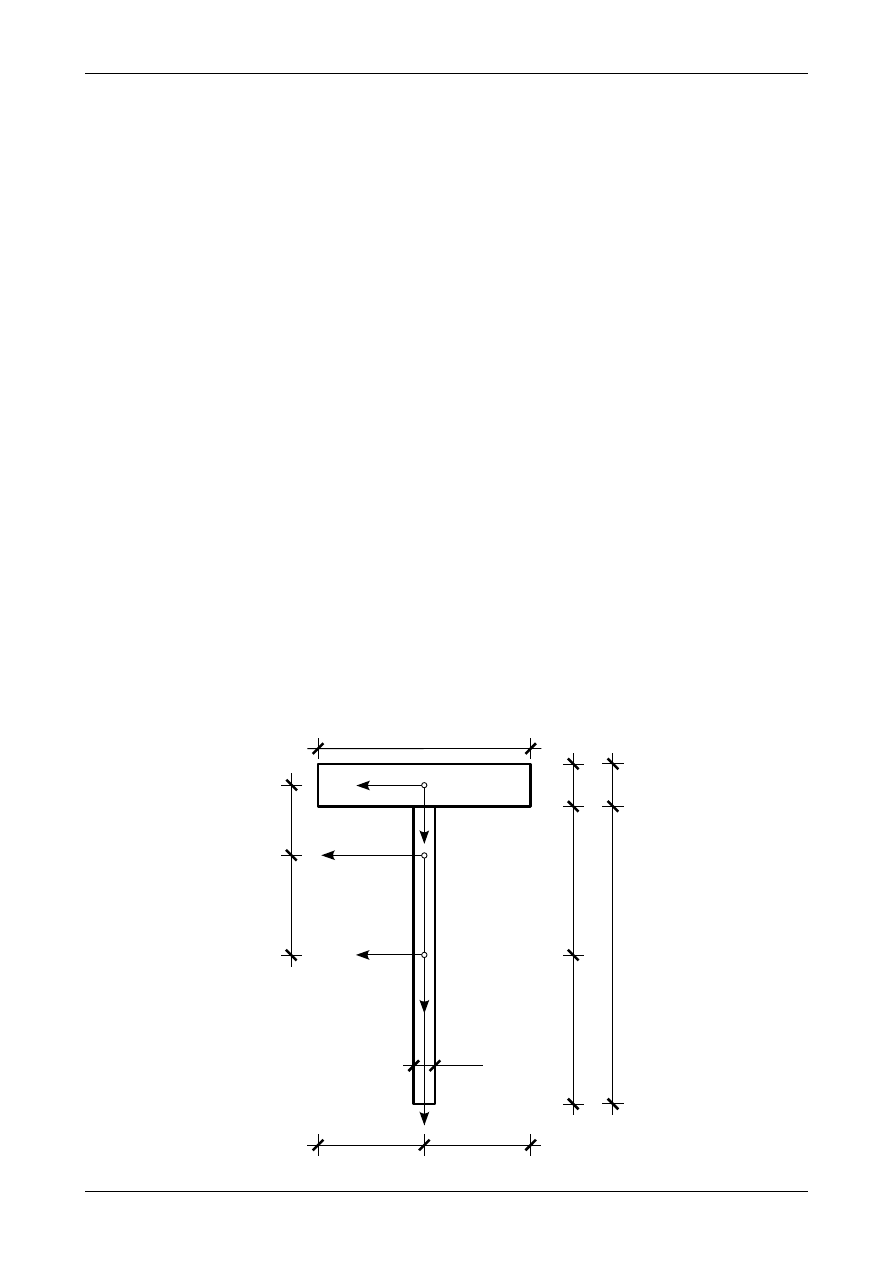
Współrzędne (Z6/2.6) i (Z6/2.7) zostały pokazane na rysunku Z6/2.4. Na rysunku tym zaznaczono także
fakt, że osie środkowe Y
0
i Z
0
są także osiami głównymi, ponieważ oś Z
0
jest osią symetrii przekroju
teowego, a jak wiadomo dewiacyjny moment bezwładności w układzie, w którym jedna z osi jest osią
symetrii wynosi zero. Jest on także równy zero w układzie osi głównych.
10,0
10,0
20,0
4,0
14
,0
14
,0
6,
588
Y
0
=Y
gl
sc
1
[cm]
4,0
28
,0
2,0
9,
412
Z
0
=Z
gl
Z
01
Y
01
Z
02
Y
02
sc
sc
2
Rys. Z6/2.4. Współrzędne środków ciężkości figur składowych w układzie osi głównych
Dr inż. Janusz Dębiński
WM
Z6/2. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 2
4
Zgodnie ze wzorem (6.31) moment bezwładności względem osi Y
0
=Y
gl
wynosi
J
Y0
=
J
Ygl
=
20,0⋅4,0
3
12
−
6,588
2
⋅
20,0⋅4,0
2,0⋅28,0
3
12
9,412
2
⋅
28,0⋅2,0=12200 cm
4
.
(Z6/2.8)
Zgodnie ze wzorem (6.32) moment bezwładności względem osi Z
0
=Z
gl
wynosi
J
Z0
=
J
Zgl
=
4,0⋅20,0
3
12
0,0
2
⋅
20,0⋅4,0
28,0⋅2,0
3
12
0,0
2
⋅
28,0⋅2,0=2685 cm
4
.
(Z6/2.9)
Dr inż. Janusz Dębiński