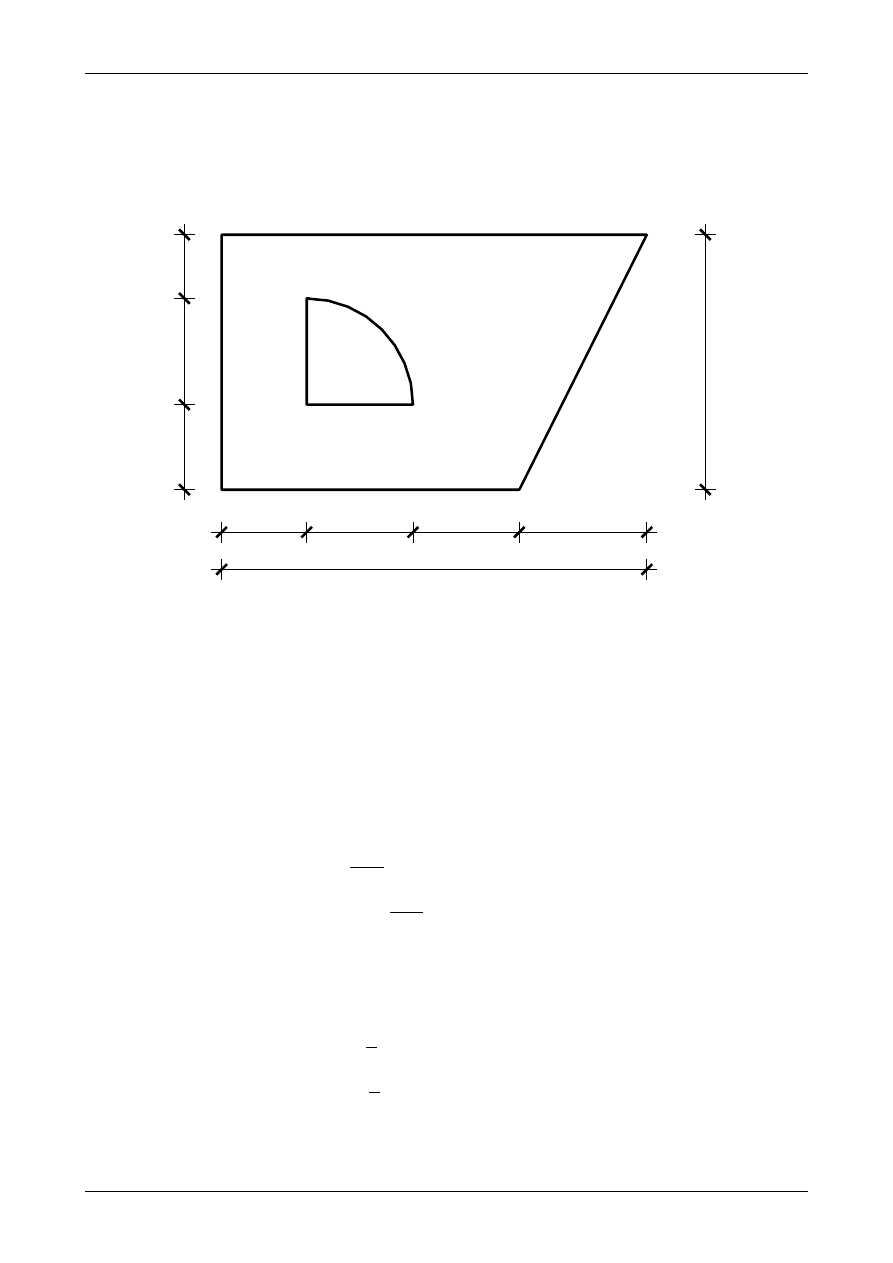
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
1
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
Z6/3.1 Zadanie 3
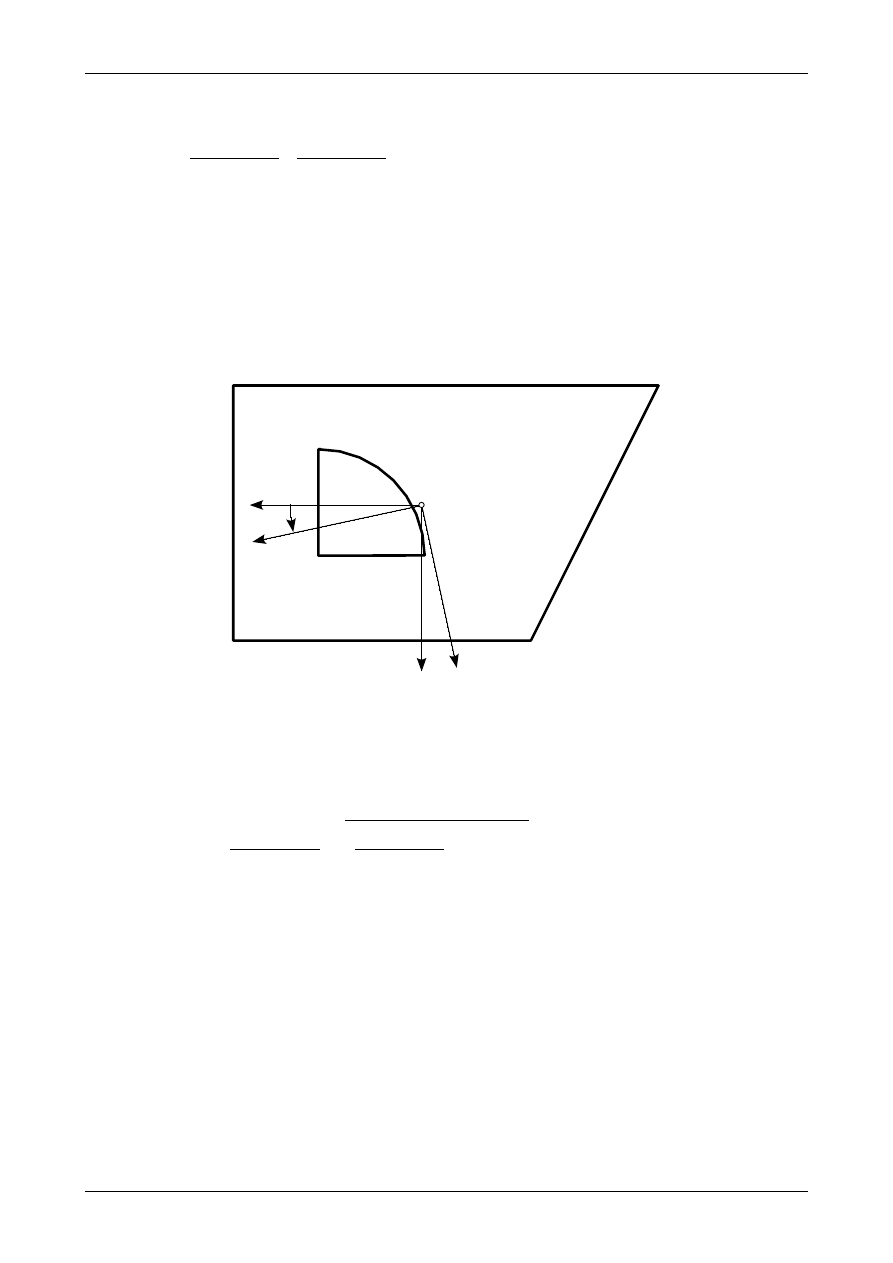
Wyznaczyć główne momenty bezwładności przekroju na rysunku Z6/3.1. Wszystkie wymiary na tym
rysunku są podane w centymetrach. Ćwiartka koła jest figurą wyciętą z przekroju i stanowi „dziurę”.
4,0
5,0
5,0
6,0
20,0
12
,0
4,0
5,0
3,0
[cm]
Rys. Z6/3.1. Przekrój złożony
Z6/3.2 Środek ciężkości przekroju
W celu wyznaczenia położenia środka ciężkości obieramy początkowy układ współrzędnych Y
P
Z
P
tak
aby cały przekrój znalazł się w pierwszej ćwiartce układu. Początkowy układ współrzędnych przedstawia
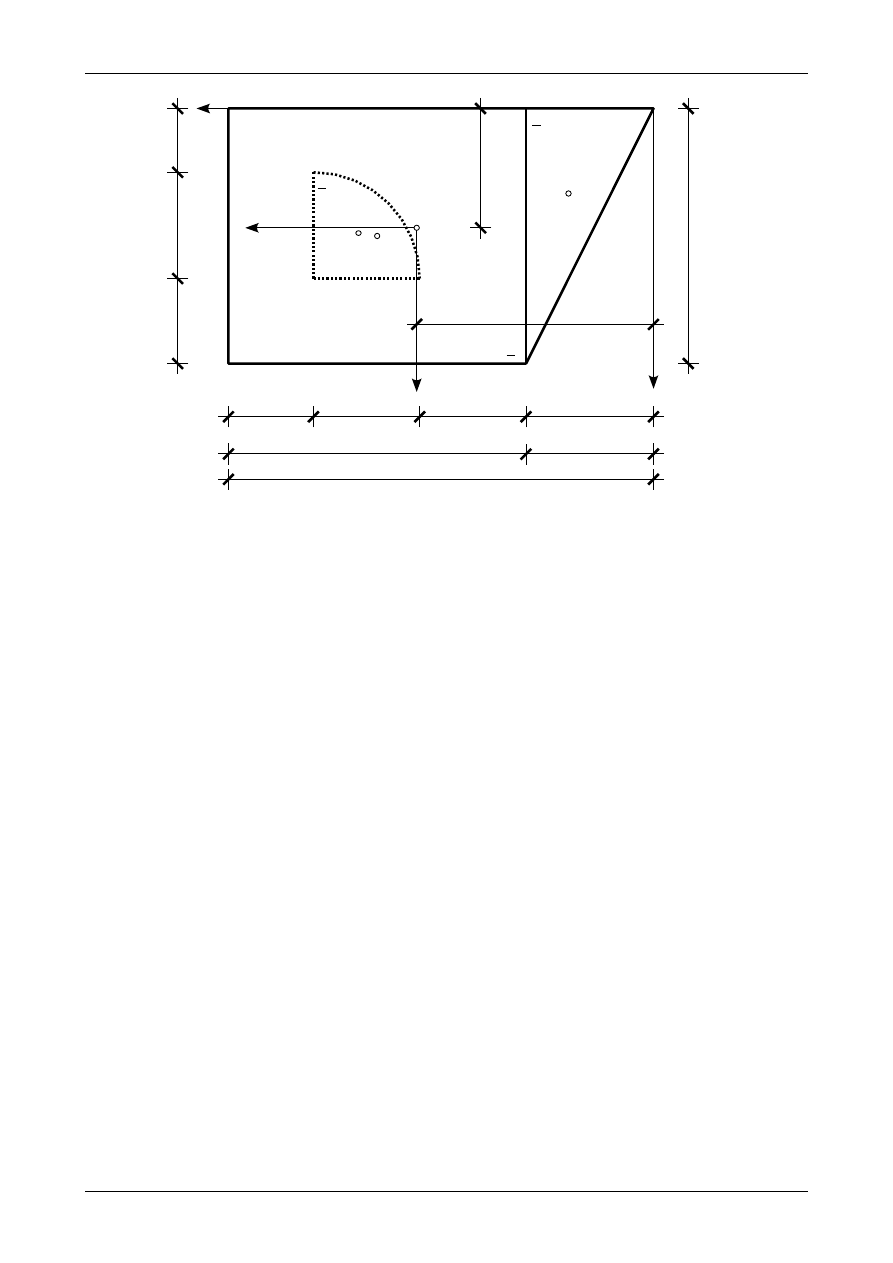
rysunek Z6/3.2. Przekrój został podzielony na: prostokąt o wymiarach 14,0 cm na 12,0 cm, trójkąt
prostokątny o wymiarach 6,0 cm na 12,0 cm oraz ćwiartkę koła o promieniu 5,0 cm. Podział ten przedstawia
także rysunek Z2/1.2.
Współrzędne środka ciężkości figury numer 1 (prostokąta) wynoszą
z
P1
=
12,0
2
=
6,0 cm
y
P1
=
6,0
14,0
2
=
13,0 cm
.
(Z6/3.1)
Współrzędne środka ciężkości figury numer 2 (trójkąta prostokątnego) wynoszą
z
P2
=
1
3
⋅
12,0=4,0 cm
y
P2
=
2
3
⋅
6,0=4,0 cm
.
(Z6/3.2)
Współrzędne środka ciężkości figury numer 3 (ćwiartki koła) wynoszą
Dr inż. Janusz Dębiński
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
2
4,0
5,0
5,0
6,0
14,0
12
,0
4,0
5,0
3,0
[cm]
2
3
1
sc
1
sc
2
sc
3
Y
P
Z
P
4,
0
6,0
5,
87
8
13,0
4,0
13,88
20,0
6,0
Rys. Z6/3.2. Podział przekroju pręta na figury składowe
z
P3
=
3,05,0−
4⋅5,0
3⋅
=
5,878 cm
y
P3
=
6,05,05,0−
4⋅5,0
3⋅
=
13,88 cm
.
(Z6/3.3)
Położenie środków ciężkości poszczególnych figur składowych w początkowym układzie współrzędnych
przedstawia rysunek Z6/3.2.
Zgodnie ze wzorem (6.13) współrzędna y
C
środka ciężkości przekroju wynosi
y
C
=
14,0⋅12,0⋅13,0
1
2
⋅
6,0⋅12,0⋅4,0−
⋅
5,0
2
4
⋅
13,88
14,0⋅12,0
1
2
⋅
6,0⋅12,0−
⋅
5,0
2
4
=
11,15 cm
.
(Z6/3.4)
Zgodnie ze wzorem (6.13) współrzędna z
C
środka ciężkości przekroju wynosi
z
C
=
14,0⋅12,0⋅6,0
1
2
⋅
6,0⋅12,0⋅4,0−
⋅
5,0
2
4
⋅
5,878
14,0⋅12,0
1
2
⋅
6,0⋅12,0−
⋅
5,0
2
4
=
5,622 cm
.
(Z6/3.5)
Położenie środka ciężkości całego przekroju w początkowym układzie współrzędnych przedstawia rysunek
Z6/3.3.
Dr inż. Janusz Dębiński
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
3
4,0
5,0
5,0
6,0
14,0
12
,0
4,0
5,0
3,0
[cm]
2
3
1
sc
1
sc
2
sc
3
Y
P
Z
P
20,0
6,0
sc
Z
0
Y
0
5,
62
2
11,15
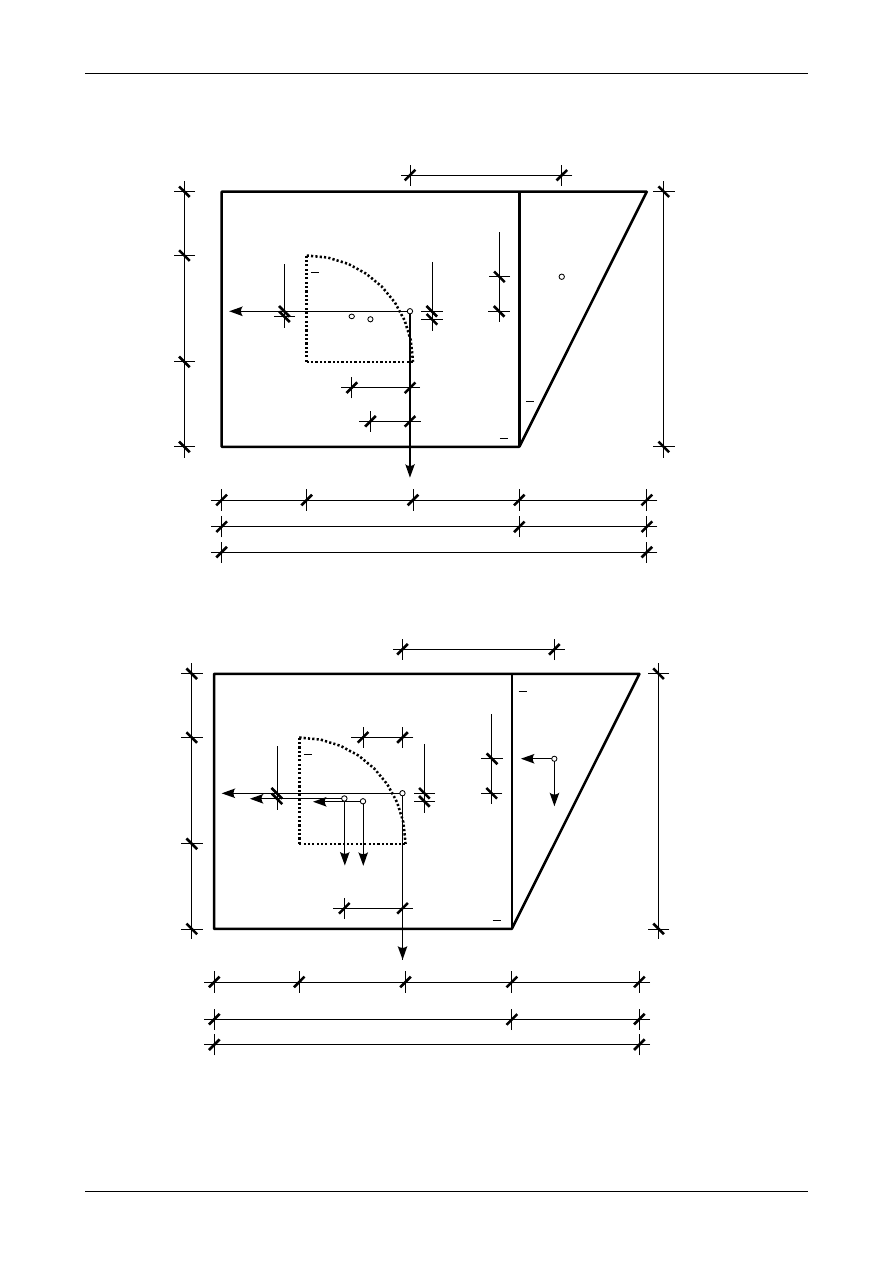
Rys. Z6/3.3. Położenie środka ciężkości przekroju pręta
Z6/3.3 Momenty bezwładności w układzie osi środkowych
W celu wyznaczenia współrzędnych środków ciężkości w układzie osi środkowych wykorzystamy
wzory transformacyjne
y
oi
=
y
Pi
−
y
C
,
(Z6/3.6)
z
oi
=
z
Pi
−
z
C
.
(Z6/3.7)
Współrzędne środka ciężkości figury numer 1 (prostokąta) w układzie osi środkowych wynoszą
z
01
=
6,0−5,622 =0,378 cm
y
01
=
13,0−11,15 =1,85 cm
.
(Z6/3.8)
Współrzędne środka ciężkości figury numer 2 (trójkąta prostokątnego) w układzie osi środkowych wynoszą
z
02
=
4,0−5,622=−1,622 cm
y
02
=
4,0−11,15=−7,15 cm
.
(Z6/3.9)
Współrzędne środka ciężkości figury numer 3 (ćwiartki koła) w układzie osi środkowych wynoszą
z
03
=
5,878−5,622 =0,256 cm
y
03
=
13,88−11,15 =2,73 cm
.
(Z6/3.10)
Dr inż. Janusz Dębiński
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
4
Położenie środków ciężkości poszczególnych figur składowych w układzie osi środkowych przedstawia
rysunek Z6/3.4. Rysunek Z6/3.5 przedstawia osie środkowe wszystkich figur składowych przekroju.
4,0
5,0
5,0
6,0
14,0
12
,0
4,0
5,0
3,0
[cm]
2
3
1
sc
1
sc
2
sc
3
1,6
22
0,
37
8
0,2
56
1,85
7,15
2,73
20,0
6,0
sc
Z
0
Y
0
Rys. Z6/3.4. Położenie środków ciężkości figur składowych w układzie osi środkowych
4,0
5,0
5,0
6,0
14,0
12
,0
4,0
5,0
3,0
[cm]
2
3
1
sc
1
sc
2
sc
3
1,
622
0,3
78
0,
256
1,85
7,15
2,73
20,0
6,0
sc
Z
0
Y
0
Z
02
Y
02
Y
01
Z
01
Y
03
Z
03
Rys. Z6/3.5. Osie środkowe poszczególnych figur składowych
Mając wyznaczone położenie środków ciężkości poszczególnych figur w układzie osi środkowych
możemy przystąpić do wyznaczenia momentów bezwładności w układzie osi środkowych Y
0
Z
0
. Zgodnie ze
wzorem (6.31) moment bezwładności względem osi Y
0
wynosi
Dr inż. Janusz Dębiński
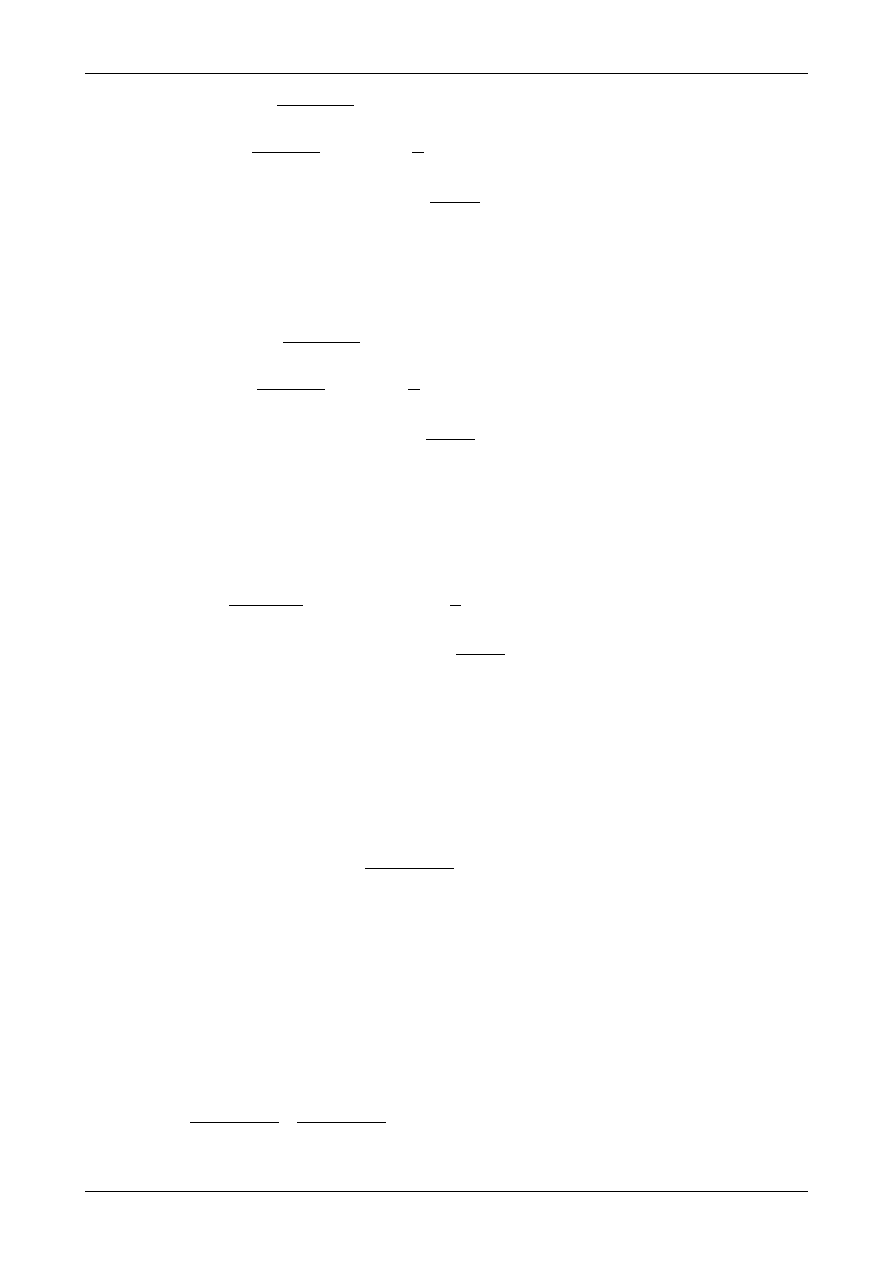
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
5
J
Y0
=
14,0⋅12,0
3
12
0,378
2
⋅
12,0⋅14,0
6,0⋅12,0
3
36
−
1,622
2
⋅
1
2
⋅
12,0⋅6,0
−
0,05488⋅5,0
4
0,256
2
⋅
⋅
5,0
2
4
=
2387 cm
4
.
(Z6/3.11)
Zgodnie ze wzorem (6.32) moment bezwładności względem osi Z
0
wynosi
J
Z0
=
12,0⋅14,0
3
12
1,85
2
⋅
12,0⋅14,0
12,0⋅6,0
3
36
−
7,15
2
⋅
1
2
⋅
12,0⋅6,0
−
0,05488⋅5,0
4
2,73
2
⋅
⋅
5,0
2
4
=
5051 cm
4
.
(Z6/3.12)
Zgodnie ze wzorem (6.33) dewiacyjny moment bezwładności w układzie Y
0
Z
0
wynosi
J
Y0Z0
=
0,0
0,378
⋅
1,85
⋅
12,0⋅14,0
6,0
2
⋅
12,0
2
72
−
1,622
⋅
−
7,15
⋅
1
2
⋅
12,0⋅6,0
−
−
0,01647⋅5,0
4
0,256
⋅
2,73
⋅
⋅
5,0
2
4
=
603,6 cm
4
.
(Z6/3.13)
Z6/3.4 Główne momenty bezwładności
Znając wartości momentów bezwładności w układzie osi środkowych możemy wyznaczyć momenty
główne i kierunek główny. Tangens podwójnego kąta nachylenia osi głównych zgodnie z wzorem (6.43)
będzie miał wartość
tg2⋅
gl
=
−
2⋅
603,6
2387−5051
=
0,4532
.
(Z6/3.14)
Kąt nachylenia osi głównych wynosi
gl
=
12,19
o
.
(Z6/3.15)
Główny moment bezwładności I
ygl
zgodnie z (6.44) wynosi
J
Ygl
=
23875051
2
2387−5051
2
⋅
cos
2⋅12,19
o
−
603,6
⋅
sin
2⋅12,19
o
J
Ygl
=
2257 cm
4
.
(Z6/3.16)
Dr inż. Janusz Dębiński
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
6
Główny moment bezwładności I
Zgl
zgodnie z (6.45) wynosi
J
Ygl
=
23875051
2
−
2387−5051
2
⋅
cos
2⋅12,19
o
603,6
⋅
sin
2⋅12,19
o
J
Ygl
=
5181 cm
4
.
(Z6/3.17)
Uporządkowane momenty bezwładności wynoszą
J
1
=
5181 cm
4
J
2
=
2257 cm
4
.
(Z6/3.18)
sc
Z
0
Y
0
Y
gl
=2
Z
gl
=1
12,19
o
Rys. Z6/3.6. Położenie głównych osi bezwładności
W celu sprawdzenia obliczeń zastosujemy wzór (6.48). Główne momenty bezwładności wynoszą
J
1/ 2
=
23875051
2
±
2387−5051
2
2
603,6
2
=
{
5181 cm
4
2257 cm
4
.
(Z6/3.19)
Pierwszy niezmiennik w układzie osi środkowych wynosi
I
1
=
50512387=7438 cm
4
.
(Z6/3.20)
Pierwszy niezmiennik w układzie osi głównych wynosi
I
1
=
51812257=7438 cm
4
.
(Z6/3.21)
Jak widać niezmienniki (Z6/3.20) i (Z6/3.21) są równe. Drugi niezmiennik w układzie osi środkowych
wynosi
Dr inż. Janusz Dębiński
WM
Z6/3. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 3
7
I
2
=
5051⋅2387−
−
603,6
2
=
11690000 cm
8
.
(Z6/3.22)
Drugi niezmiennik w układzie osi głównych wynosi
I
2
=
5181⋅2257=11690000 cm
8
.
(Z6/3.23)
Jak widać niezmienniki (Z6/3.22) i (Z6/3.23) są równe. Położenie głównych osi bezwładności przedstawia
rysunek Z6/3.6.
Dr inż. Janusz Dębiński
Document Outline