WM

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

1

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

Z6/5.1 Zadanie 5

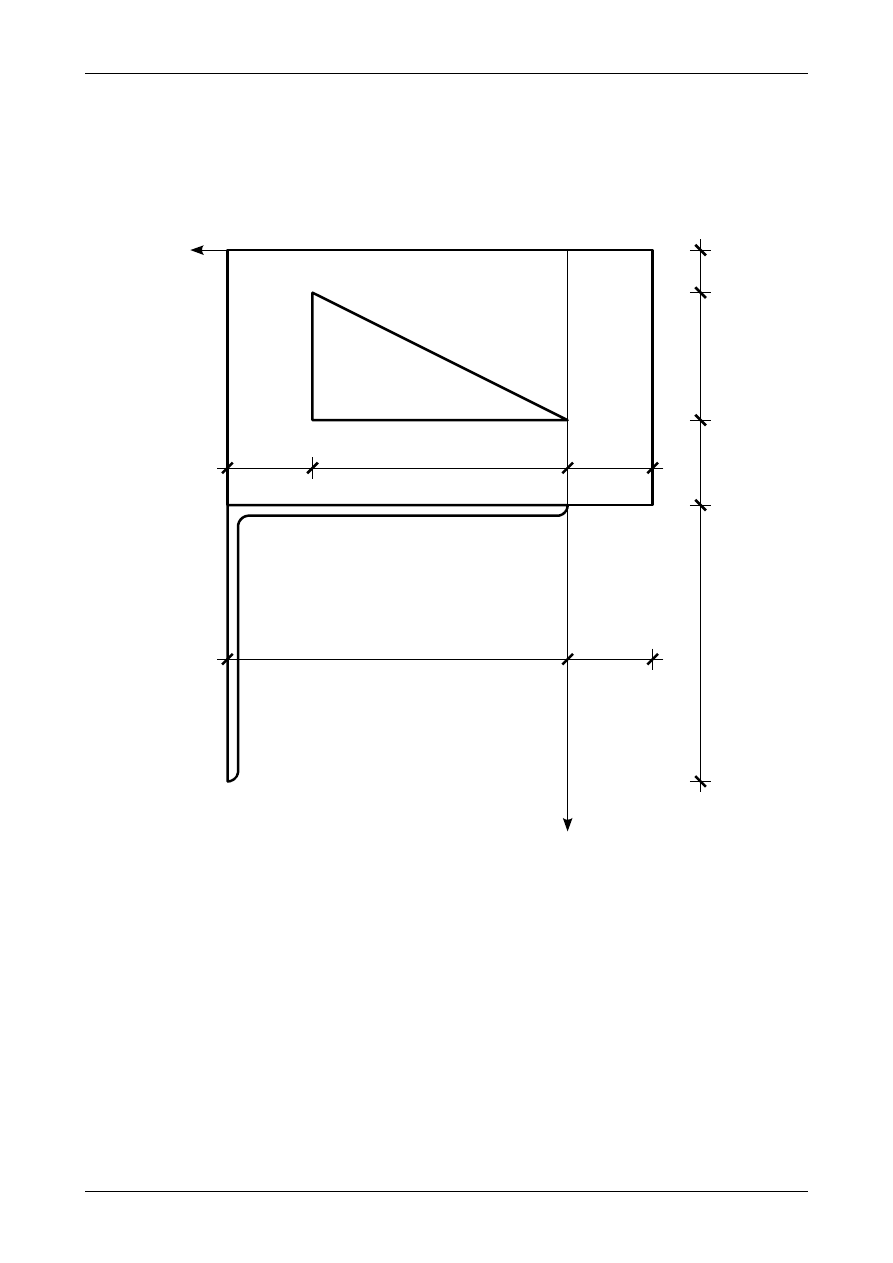
Dany jest przekrój pokazany na rysunku Z6/5.1. Wyznaczyć momenty bezwładności w zadanym

układzie współrzędnych YZ.

2,0

6,0

2,0

8,0

2,0

1,0

3,0

2,0

6,5

[cm]

Z

Y

L 80x65x10

Rys. Z6/5.1. Przekrój pręta

Z6/5.2 Charakterystyki geometryczne kątownika nierównoramiennego

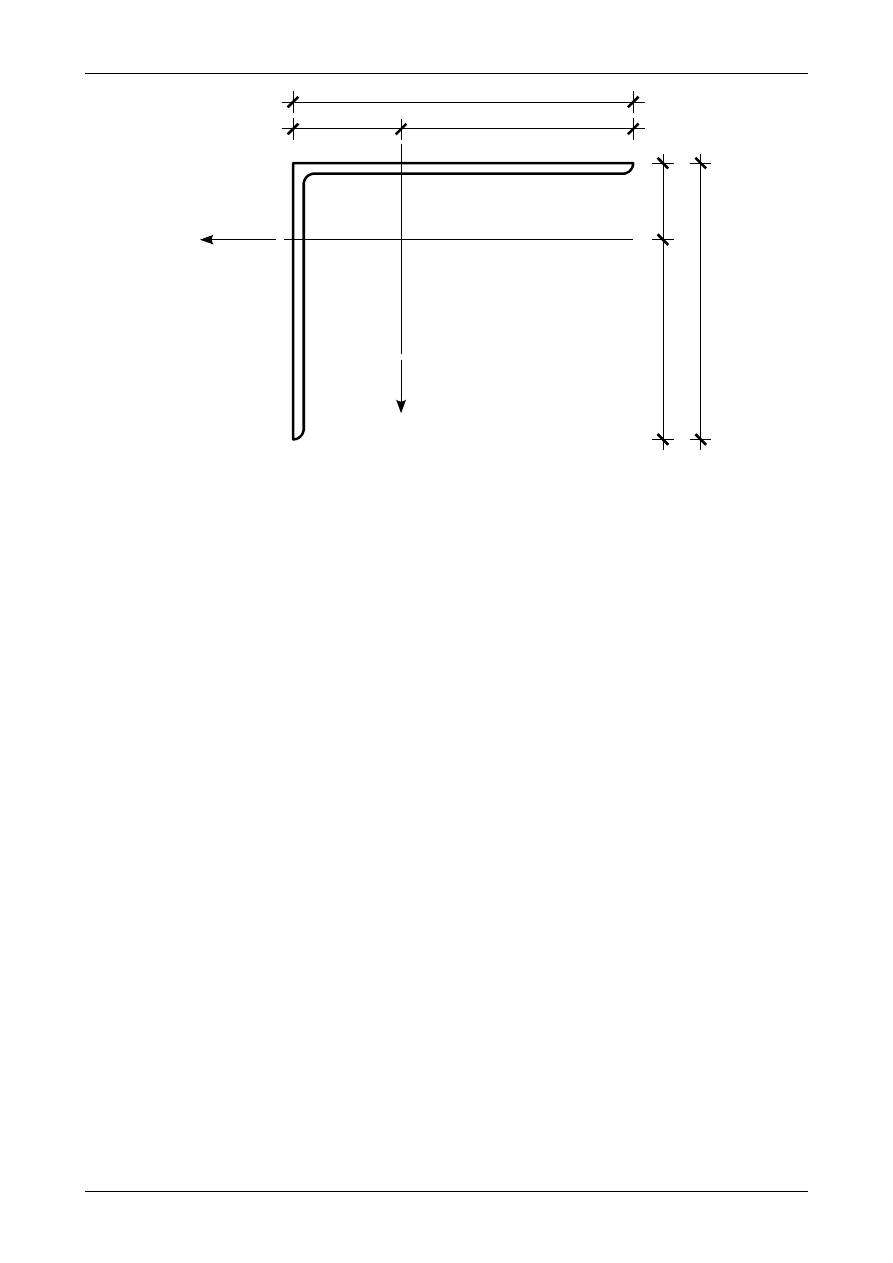
Rysunek Z6/5.2 przedstawia położenie kątownika w jego układzie osi środkowych oraz położenie osi

X i Y, które są stosowane w tablicach. Osiowe momenty bezwładności wynoszą

J

Y03

=

J

Y



T

=

48,3 cm

4

,

(Z6/5.1)

J

Z03

=

J

X



T 

=

82,2 cm

4

.

(Z6/5.2)

Pole powierzchni kątownika nierównoramiennego 80x65x10 wynosi 13,6 cm

2

. Minimalny moment bezwład-

ności kątownika wynosi

Dr inż. Janusz Dębiński

WM

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

2

8,0

[cm]

5,45

2,55

4,6

9

1,8

1

Y

03

Z

03

X

X

Y

Y

6,

5

Rys. Z6/5.2. Kątownik nierównoramienny

J

2



3

=

24,8 cm

4

.

(Z6/5.3)

Pierwszy niezmiennik dla kątownika wynosi

I

1



3

=

48,382,2=130,5 cm

4

.

(Z6/5.4)

Maksymalny moment bezwładności dla kątownika nierównoramiennego wynosi

J

1



3

=

130,5−24,8=105,7 cm

4

.

(Z6/5.5)

Drugi niezmiennik dla głównych momentów bezwładności dla kątownika nierównoramiennego wynosi

I

2



3

=

24,8⋅105,7=2621 cm

8

.

(Z6/5.6)

Drugi niezmiennik dla momentów bezwładności w układzie osi środkowych kątownika nierównora-
miennego wynosi

I

2



3

=

48,3⋅82,2−J

Y03Z03

2

=

2621 cm

8

.

(Z6/5.7)

Kwadrat dewiacyjnego momentu bezwładności w osiach środkowych kątownika nierównoramiennego
wynosi

J

Y03Z03

2

=

1349 cm

8

.

(Z6/5.8)

Dr inż. Janusz Dębiński

WM

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

3

Wartość bezwzględna dewiacyjnego momentu bezwładności w osiach środkowych kątownika nierów-
noramiennego wynosi

∣

J

Y03Z03

∣

=

36,73 cm

4

.

(Z6/5.9)

8,0

[cm]

5,45

2,55

4,

69

1,

81

Y

03

Z

03

6,5

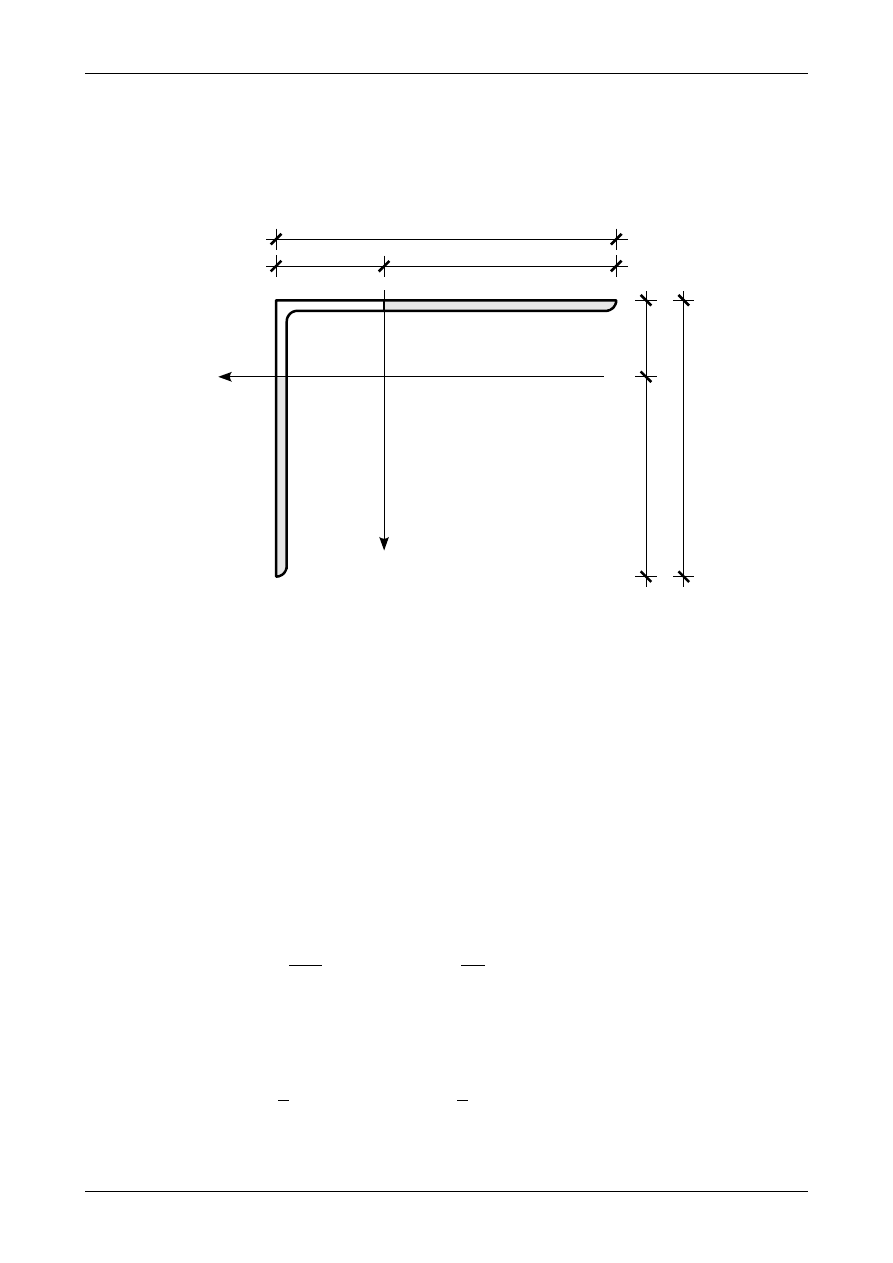
Rys. Z6/5.3. Większa część kątownika nierównoramiennego

Zgodnie z rysunkiem Z6/5.3 większa część kątownika nierównoramiennego znajduje się w ćwiartkach
dodatnich więc dewiacyjny moment bezwładności w układzie osi środkowych kątownika wynosi

J

Y03Z03

=

36,73 cm

4

.

(Z6/5.10)

Z6/5.3 Wyznaczenie współrzędnych środków ciężkości w układzie YZ

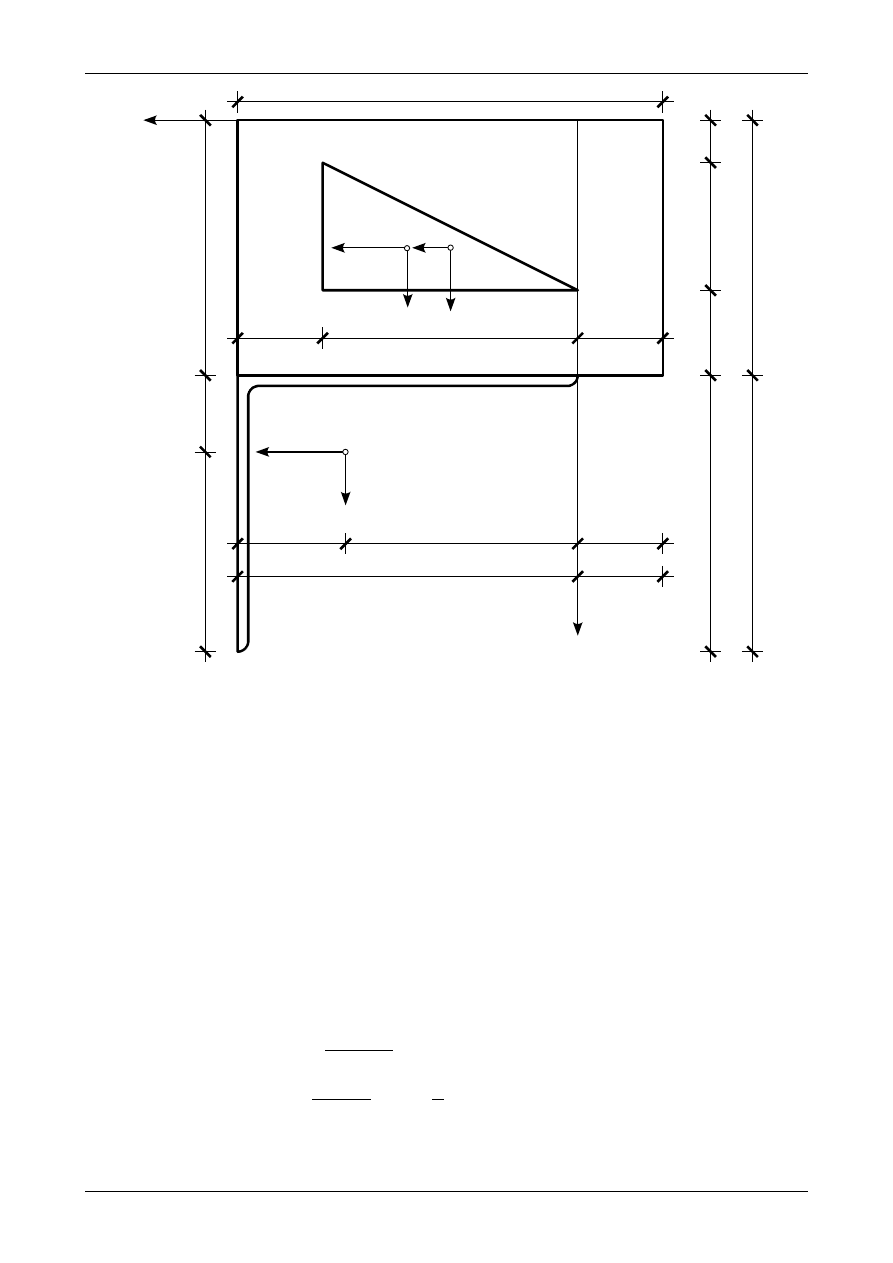
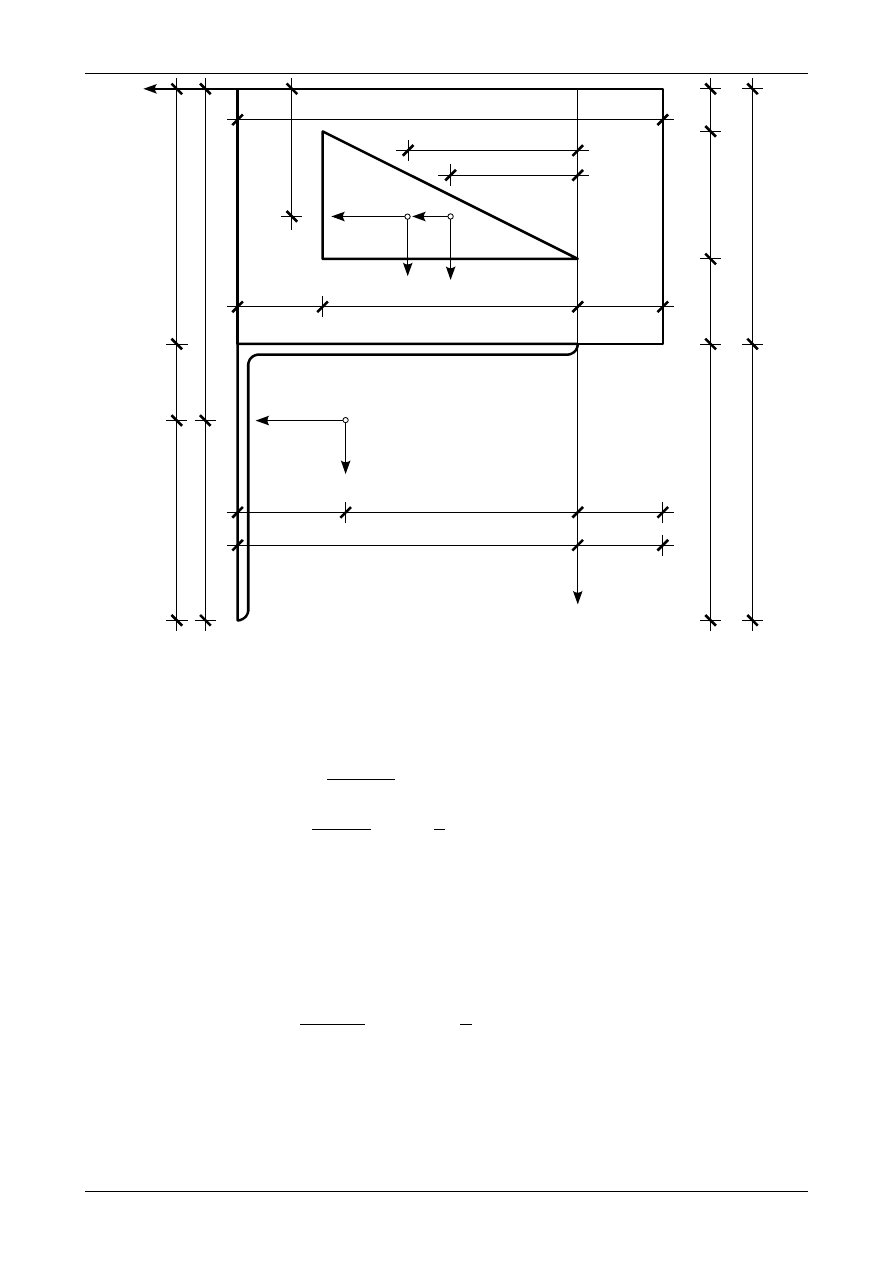
Rysunek Z6/5.4 przedstawia położenie układów osi środkowych dla poszczególnych figur składowych

w układzie współrzędnych YZ. Pierwszą figurą jest prostokąt o wymiarach 10,0 cm na 6,0 cm. Drugą figurą
jest trójkąt prostokątny o wymiarach 6,0 na 3,0 cm. Trzecią figurą jest kątownik nierównoramienny
80x65x10. Współrzędne środka ciężkości prostokąta w układzie YZ wynoszą

y

1

=

10,0

2

−

2,0=3,0 cm z

1

=

6,0

2

=

3,0 cm

.

(Z6/5.11)

Współrzędne środka ciężkości trójkąta prostokątnego w układzie YZ wynoszą

y

2

=

2
3

⋅

6,0=4,0 cm z

2

=

1,0 

2
3

⋅

3,0 =3,0 cm

.

(Z6/5.12)

Współrzędne środka ciężkości kątownika nierównoramiennego w układzie YZ wynoszą

Dr inż. Janusz Dębiński

WM

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

4

2,0

6,0

2,0

8,0

2,0

1,

0

3,

0

2,

0

6,

5

[cm]

Z

Y

5,45

2,0

6,0

6,5

10,0

2,55

6,0

4,6

9

1,8

1

Y

01

Z

01

Y

02

Z

02

Y

03

Z

03

sc

1

sc

2

sc

3

Rys. Z6/5.4. Położenie osi środkowych poszczególnych figur składowych

y

3

=

8,0−2,55=5,45 cm z

3

=

6,01,81=7,81 cm

.

(Z6/5.13)

Rysunek Z6/5.5 przedstawia współrzędne środków ciężkości poszczególnych figur składowych w układzie
YZ.

Z6/5.4 Wyznaczenie momentów bezwładności w układzie YZ

Mając już wyznaczone charakterystyki geometryczne w układzie osi środkowych kątownika

nierównoramiennego oraz współrzędne środków ciężkości poszczególnych figur składowych w układzie YZ
możemy wyznaczyć wartości momentów bezwładności w tym układzie.

Zgodnie ze wzorem (6.22) osiowy moment bezwładności względem osi Y będzie miał wartość

J

Y

=

10,0⋅6,0

3

12





3,0



2

⋅

10,0⋅6,0

−



6,0⋅3,0

3

36





3,0



2

⋅

1

2

⋅

6,0⋅3,0





48,3



7,81



2

⋅

13,6=1512 cm

4

.

(Z6/5.14)

Dr inż. Janusz Dębiński

WM

Z6/5. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 5

5

2,0

6,0

2,0

8,0

2,0

1,

0

3,

0

2,

0

6,

5

[cm]

Z

Y

5,45

2,0

6,0

6,5

10,0

2,55

4,6

9

7,8

1

Y

01

Z

01

Y

02

Z

02

Y

03

Z

03

3,0

4,0

6,

0

4,

69

1,

81

3,

0

sc

2

sc

1

sc

3

Rys. Z6/5.5. Współrzędne środków ciężkości poszczególnych figur składowych

Zgodnie ze wzorem (6.23) osiowy moment bezwładności względem osi Z będzie miał wartość

J

Z

=

6,0⋅10,0

3

12





3,0



2

⋅

10,0⋅6,0

−



3,0⋅6,0

3

36





4,0



2

⋅

1
2

⋅

6,0⋅3,0





82,2



5,45



2

⋅

13,6=1364 cm

4

.

(Z6/5.15)

Zgodnie ze wzorem (6.24) dewiacyjny moment bezwładności w układzie YZ będzie miał wartość

J

YZ

=

0,0



3,0



⋅



3,0



⋅

10,0⋅6,0

−



−

3,0

2

⋅

6,0

2

72





4,0



⋅



3,0



⋅

1
2

⋅

6,0⋅3,0





36,73



5,45



⋅



7,81



⋅

13,6=1052 cm

4

.

(Z6/5.16)

Dr inż. Janusz Dębiński