WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
1
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
Z12/5.1. Zadanie 5
Dana jest belka złożona z zadania Z12/2 przedstawiona na rysunku Z12/5.1. Wykresy sił przekro-
jowych dla tej belki przedstawia rysunek Z15/4.2. Zaprojektować dwa przekroje belki będące dwuteow-
nikami walcowanymi zgodnie z rysunkiem Z15/4.1. Następnie metodą obciążeń krzywiznami wyznaczyć
kąty obrotu w punktach A, B, C (z lewej i prawej strony), D i E oraz ugięcia w punktach C i E.
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
E∙J
Y
(1)
E∙J
Y
(2)
Rys. Z12/5.1. Belka złożona
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
29,5 kN
34,25 kN
7,25 kN
0,9063
1,056
3,094
1,944
T [kN]
12,0
17
,5
9,5
24
,7
5
7,
25
0,9063
3,094
1,056
1,944
16
,0
19
,29
19
,0
0,0
5,0
14
12
,0
0,0
M [kNm]
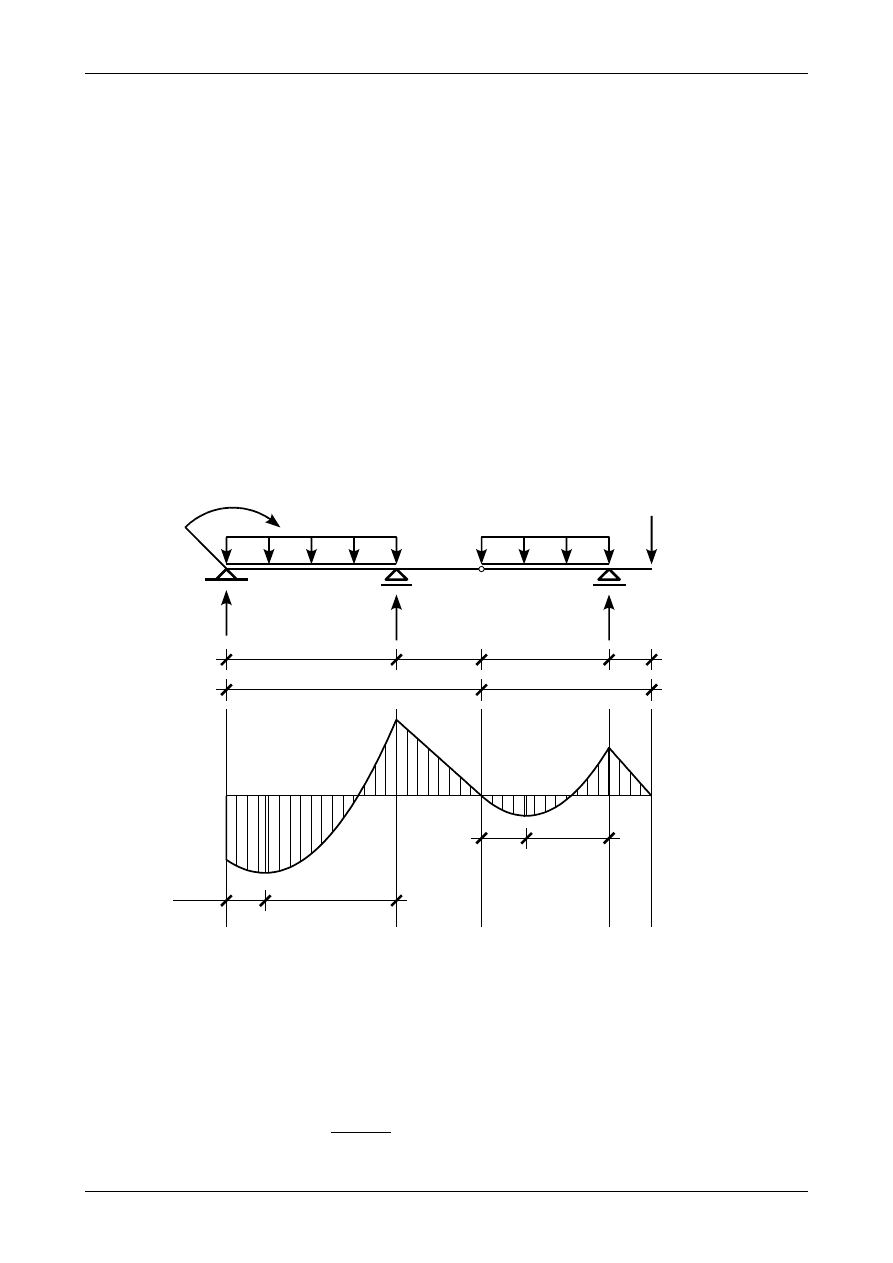
Rys. Z12/5.2. Wykresy sił przekrojowych w belce złożonej.
Z12/5.2. Przyjęcie przekrojów belki
Przekroje pręta przyjmiemy na podstawie wartości ekstremalnej momentu zginającego. Jak widać na
rysunku Z12/5.2 ekstremalny moment dla belki AC wynosi
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
2
M
Y
EXT 1
=
19,29 kNm=1929 kNcm
.
(Z12/5.1)
Wytrzymałość materiału, z którego wykonana jest belka czyli stali wynosi
R=215 MPa=21,5
kN
cm
2
.
(Z12/5.2)
Wskaźnik wytrzymałości przekroju na zginanie powinien być większy niż
W
Y
1
1929
21,5
=
89,72 cm
3
.
(Z12/5.3)
Przyjmiemy walcowany dwuteownik 160 o wskaźniku wytrzymałości na zginanie równym
117 cm
3
(Z12/5.4)
i momencie bezwładności względem osi Y równym
J
Y
1
=
J
Ygl
1
=
935,0 cm
4
.
(Z12/5.5)
Moduł Younga stali wynosi
E=205 GPa=205⋅10
6
kPa
.
(Z12/5.6)
Sztywność przekroju na zginanie dla belki AC wynosi więc
E⋅J
Y
1
=
205⋅10
6
⋅
935⋅10
−
8
=
1917 kNm
2
.
(Z12/5.7)
Jak widać na rysunku Z12/5.2 ekstremalny moment dla belki CE wynosi
M
Y
EXT 2
=
12,0 kNm=1200 kNcm
.
(Z12/5.8)
Wskaźnik wytrzymałości przekroju na zginanie powinien być większy niż
W
Y
2
1200
21,5
=
55,81 cm
3
.
(Z12/5.9)
Przyjmiemy walcowany dwuteownik 140 o wskaźniku wytrzymałości na zginanie równym
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
3
81,9 cm
3
(Z12/5.10)
i momencie bezwładności względem osi Y równym
J
Y
2
=
J
Ygl
2
=
573 cm
4
.
(Z12/5.11)
Sztywność przekroju na zginanie dla belki CE wynosi więc
E⋅J
Y
2
=
205⋅10
6
⋅
573⋅10
−
8
=
1175 kNm
2
.
(Z12/5.12)
Z12/5.3. Przygotowanie wykresu momentu zginającego i obliczenie krzywizn
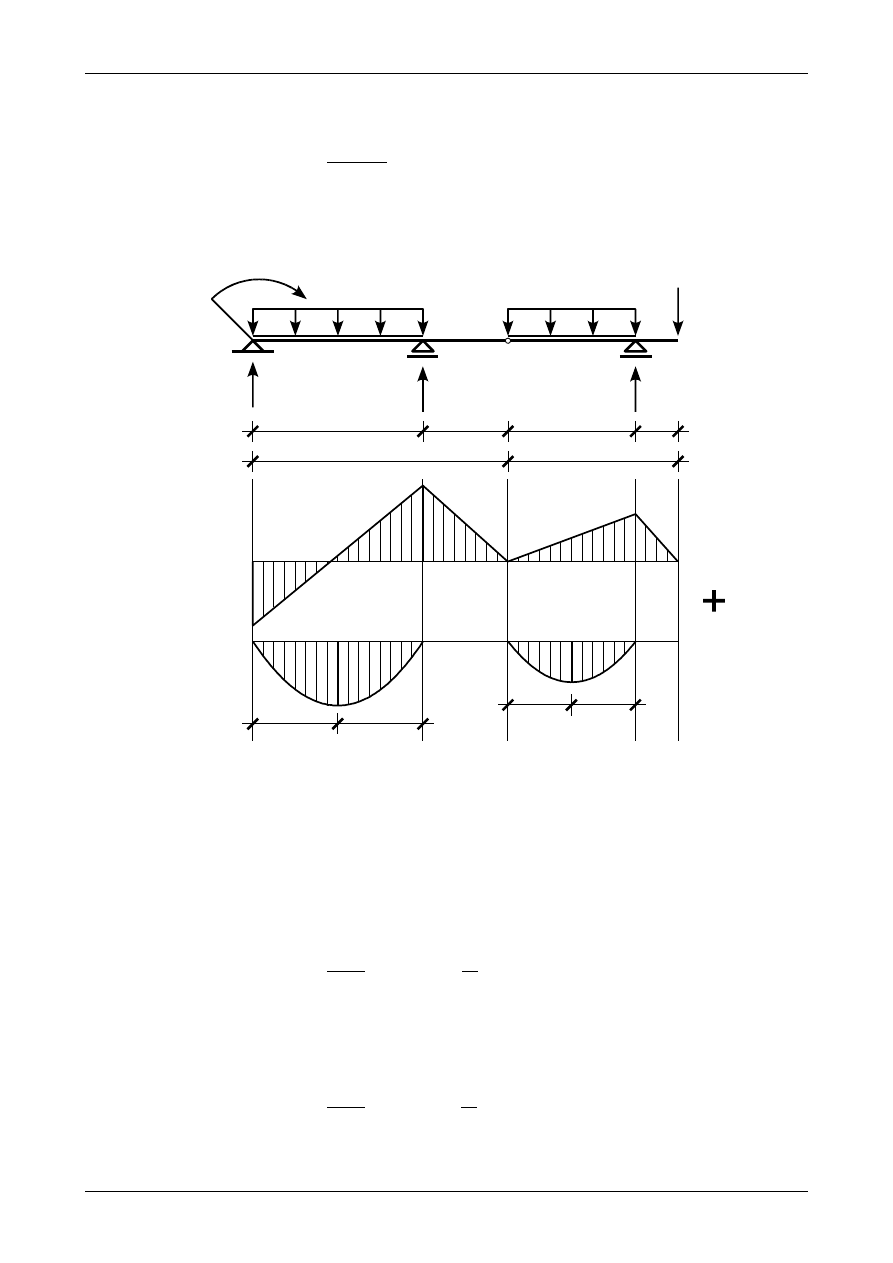
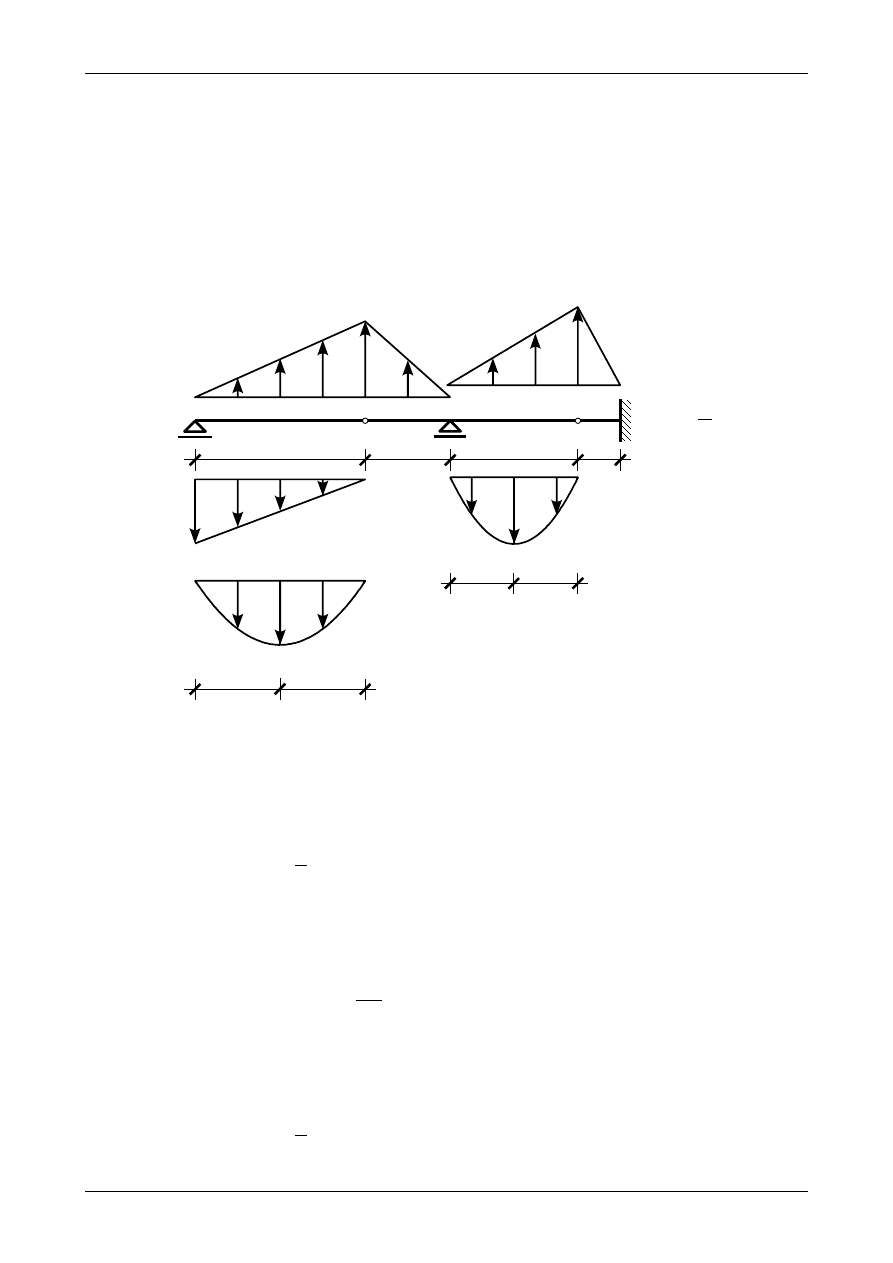
Rysunek Z12/5.3 przedstawia wykres momentu zginającego. Na rysunku tym zaznaczone są także
odpowiednie sztywności na zginanie dla poszczególnych belek prostych.
1917 kNm
2
1175 kNm
2
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
29,5 kN
34,25 kN
7,25 kN
0,9063
3,094
1,056
1,944
16
,0
19
,2
9
19
,0
0,
0
5,
01
4
12
,0
0,0
M [kNm]
Rys. Z12/5.3. Wykres momentu zginającego oraz sztywności przekrojów belki na zginanie
Na belce mamy dwa przedziały, w których działa obciążenie ciągłe równomiernie rozłożone czyli AB
i CD. W przedziałach tych łączymy rzędne wykresu na początku i końcu przedziału linią prostą oraz
dodajemy parabolę jak dla belki swobodnie podpartej z takim samym obciążeniem ciągłym równomiernie
rozłożonym i takiej samej długości jak dany przedział. Rzędna w środku paraboli w przedziale AB wynosi
8,0⋅4,0
2
8
=
16,0 kNm
.
(Z12/5.13)
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
4
Rzędna w środku paraboli w przedziale CD wynosi
9,0⋅3,0
2
8
=
10,13 kNm
.
(Z12/5.14)
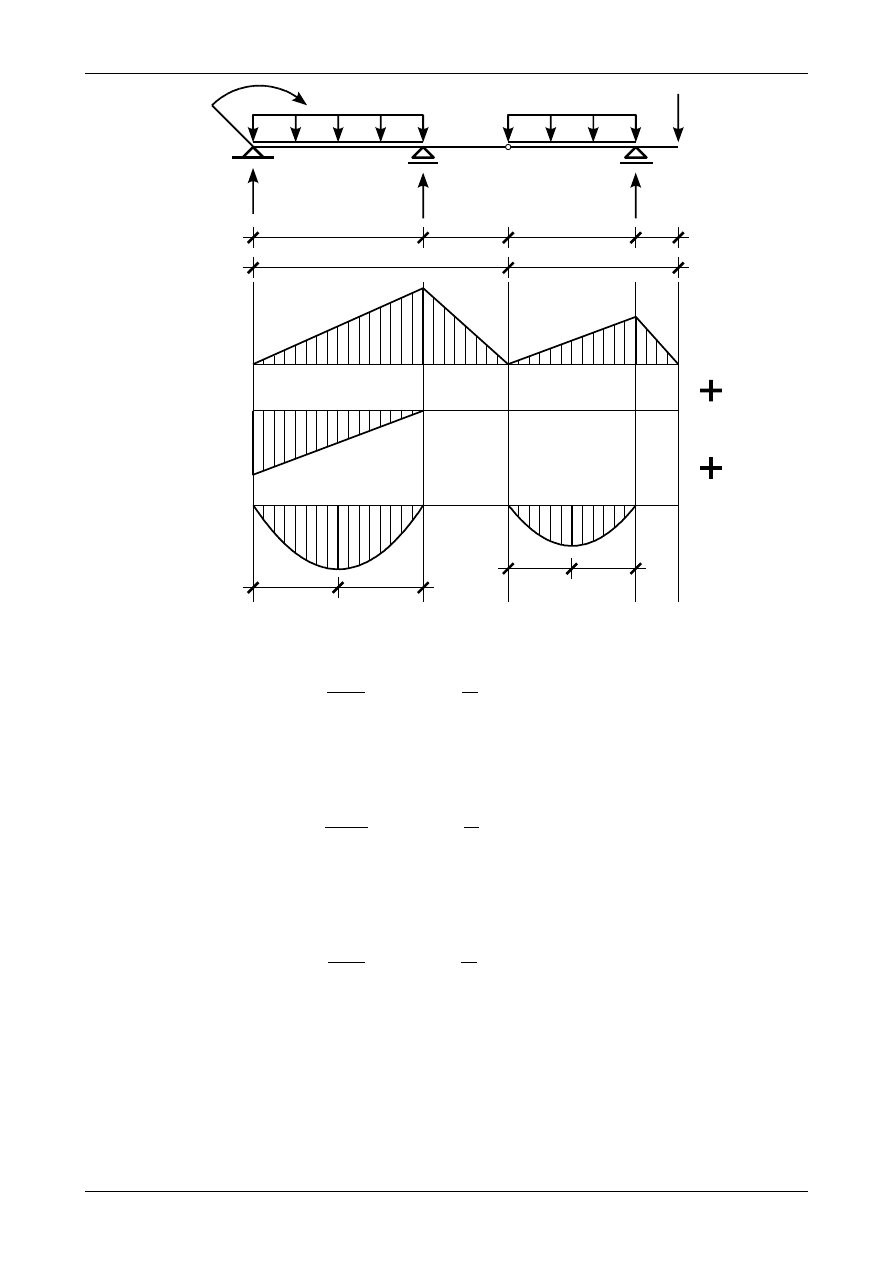
Rysunek Z12/5.4 przedstawia tak przerobiony wykres momentu zginającego.
16
,0
19
,0
0,0
12
,0
0,0
M [kNm]
2,0
1,5
1,5
2,0
16
,0
10
,13
M [kNm]
0,0
0,
0
0,0
0,0
1917 kNm
2
1175 kNm
2
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
29,5 kN
34,25 kN
7,25 kN
Rys. Z12/5.4. Przerobiony wykres momentów zginających w belce
Jak widać na rysunku Z12/5.4 w przedziale AB mamy przewinięty wykres liniowy, który dla ułat-
wienia obliczeń możemy przerobić na dwa wykresy liniowe. Przedstawia to rysunek Z12/5.5. Rysunek ten
jest już ostatecznym wykresem momentów zginających, które posłużą nam do metody obciążeń krzy-
wiznami.
Krzywizna w punkcie A wynosi
16,0
1917
=
8,346⋅10
−
3
1
m
.
(Z12/5.15)
Krzywizna w środku paraboli w przedziale AB wynosi
16,0
1917
=
8,346⋅10
−
3
1
m
.
(Z12/5.16)
Krzywizna w punkcie B wynosi
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
5
16
,0
19
,0
0,
0
12
,0
0,0
M [kNm]
2,0
1,5
1,5
2,0
16
,0
10
,13
0,0
0,0
M [kNm]
M [kNm]
0,
0
0,0
0,0
0,0
1917 kNm
2
1175 kNm
2
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
29,5 kN
34,25 kN
7,25 kN
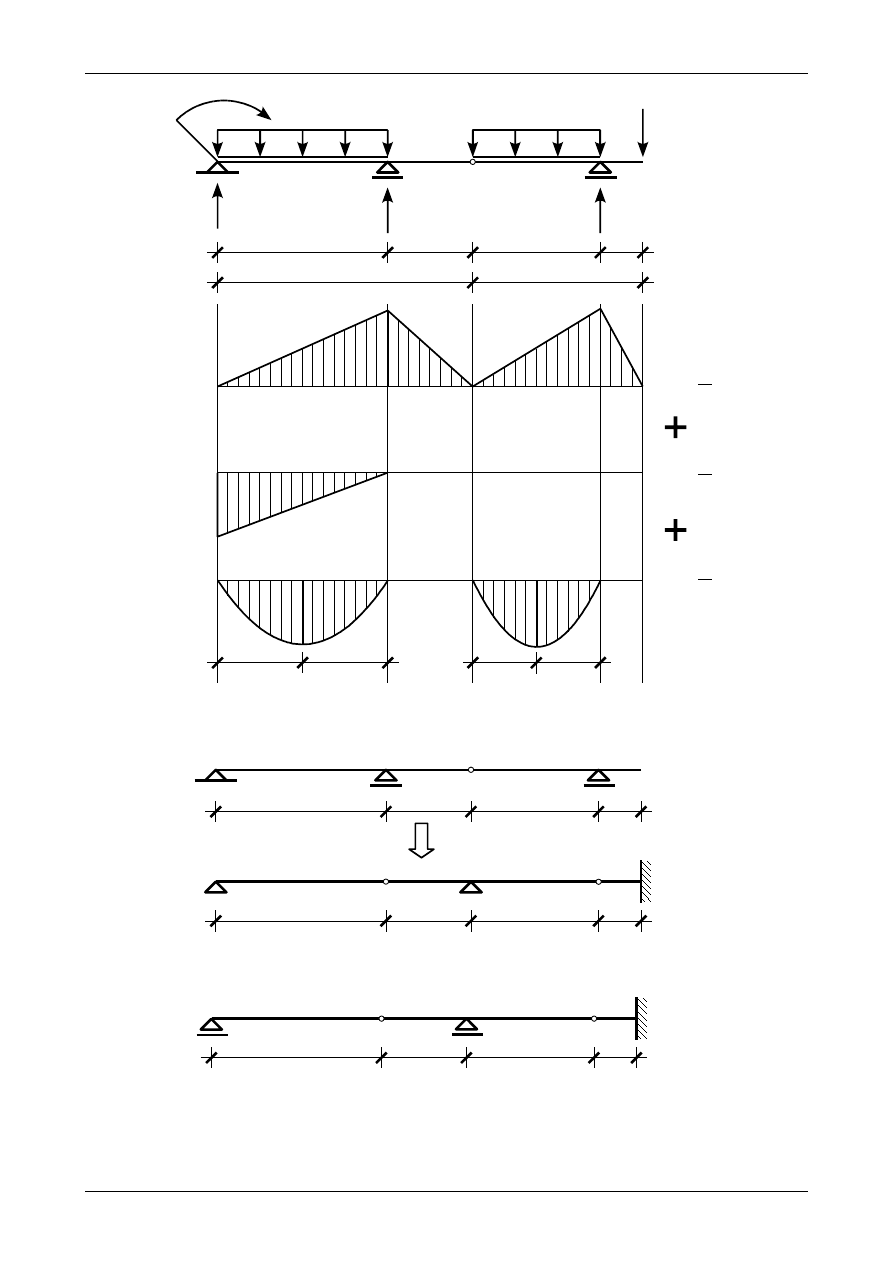
Rys. Z12/5.5. Ostatecznie przerobiony wykres momentów zginających w belce
19,0
1917
=
9,911⋅10
−
3
1
m
.
(Z12/5.17)
Krzywizna w środku paraboli w przedziale CD wynosi
10,13
1175
=
8,621⋅10
−
3
1
m
.
(Z12/5.18)
Krzywizna w punkcie D wynosi
12,0
1175
=
10,21⋅10
−
3
1
m
.
(Z12/5.19)
Rysunek Z12/5.6 przedstawia wykres krzywizn w belce.
Z12/5.4. Belka fikcyjna
Belka fikcyjna musi spełniać warunki brzegowe zadania. Zgodnie z tabelą 12.2 podpora przegubowa
A przechodzi sama w siebie. Podpory przegubowe B i D przechodzą w przeguby rzeczywiste natomiast
przegub rzeczywisty C przechodzi w podporę przegubową. Pierwsze przybliżenie belki fikcyjnej przedsta-
wia rysunek Z12/5.7.
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
6
8,
34
6
9,9
11
0,
0
10
,2
1
0,0
2,0
1,5
1,5
2,0
8,6
21
0,0
0,0
0,0
0,
0
0,0
0,0
8,
346
1917 kNm
2
1175 kNm
2
A
[m]
12,0 kN
4,0
2,0
3,0
1,0
9,0 kN/m
8,0 kN/m
16,0 kNm
B
C
D
E
29,5 kN
34,25 kN
7,25 kN
⋅
10
−
3
[
1
m
]
⋅
10
−
3
[
1
m
]
⋅
10
−
3
[
1
m
]
Rys. Z12/5.6. Wykres krzywizn w belce
A
B
C
D
E
A
B
C
D
E
4,0
2,0
3,0
1,0
4,0
2,0
3,0
1,0
[m]
[m]
Rys. Z12/5.7. Pierwsze przybliżenie belki fikcyjnej
A
B
C
D
E
4,0
2,0
3,0
1,0
[m]
Rys. Z12/5.8. Ostateczna postać belki fikcyjnej
Jak widać belka fikcyjna składa się z trzech tarcz sztywnych, które posiadają dziewięć stopni
swobody. Utwierdzenie E odbiera trzy natomiast dwa przeguby rzeczywiste B i D odbierają cztery stopnie
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
7
swobody. Razem te podpory odbierają siedem stopni swobody. Pozostają nam dwa stopnie swobody, które
przypadają na podpory przegubowe A i C. Czyli podpory te muszą być podporami przegubowo-
przesuwnymi. Rysunek Z12/5.8 przedstawia ostateczną postać belki fikcyjnej.
Z12/5.5. Obciążenie fikcyjne
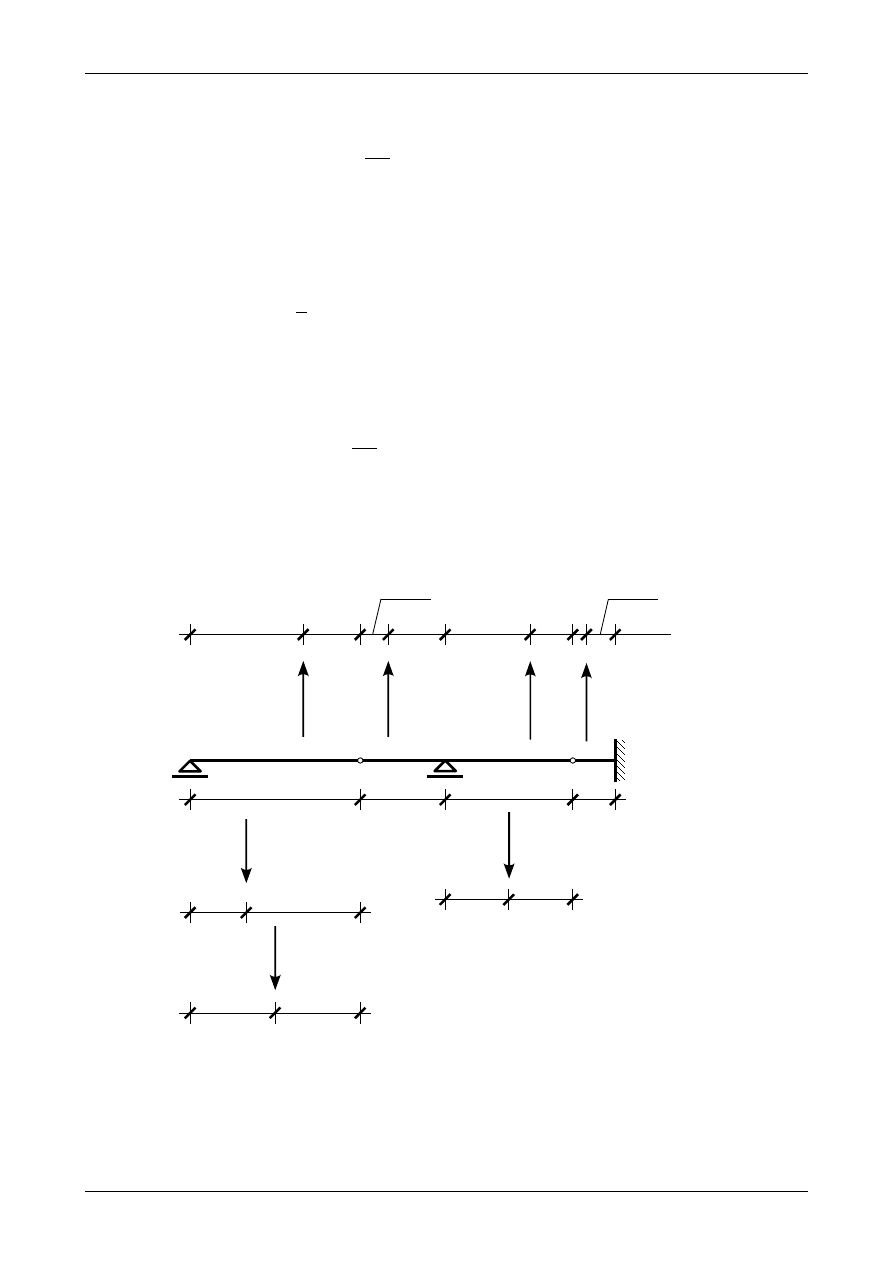
Korzystając z wykresu krzywizn na belce przedstawionych na rysunku Z12/5.6 otrzymamy obciążenie
wtórne belki fikcyjnej. Obciążenie to przedstawia rysunek Z12/5.9.
8,346
9,911
10,21
2,0
1,5
1,5
2,0
8,621
8,346
A
B
C
D
E
4,0
2,0
3,0
1,0
[m]
q
*
⋅
10
−
3
[
1
m
]
Rys.Z12/5.9. Obciążenie wtórne belki fikcyjnej
Obciążenie ciągłe przedstawione na rysunku Z12/5.9 możemy sprowadzić do wtórnych sił wypad-
kowych. Wtórna siła wypadkowa z obciążenia trójkątnego do góry w przedziale AB wynosi
1
2
⋅
9,911⋅10
−
3
⋅
4,0=19,82⋅10
−
3
(Z12/5.20)
i znajduje się ona w odległości
4,0
3
=
1,333 m
(Z12/5.21)
od punktu B. Wtórna siła wypadkowa z obciążenia trójkątnego w dół w przedziale AB wynosi
1
2
⋅
8,346⋅10
−
3
⋅
4,0=16,69⋅10
−
3
(Z12/5.22)
Dr inż. Janusz Dębiński
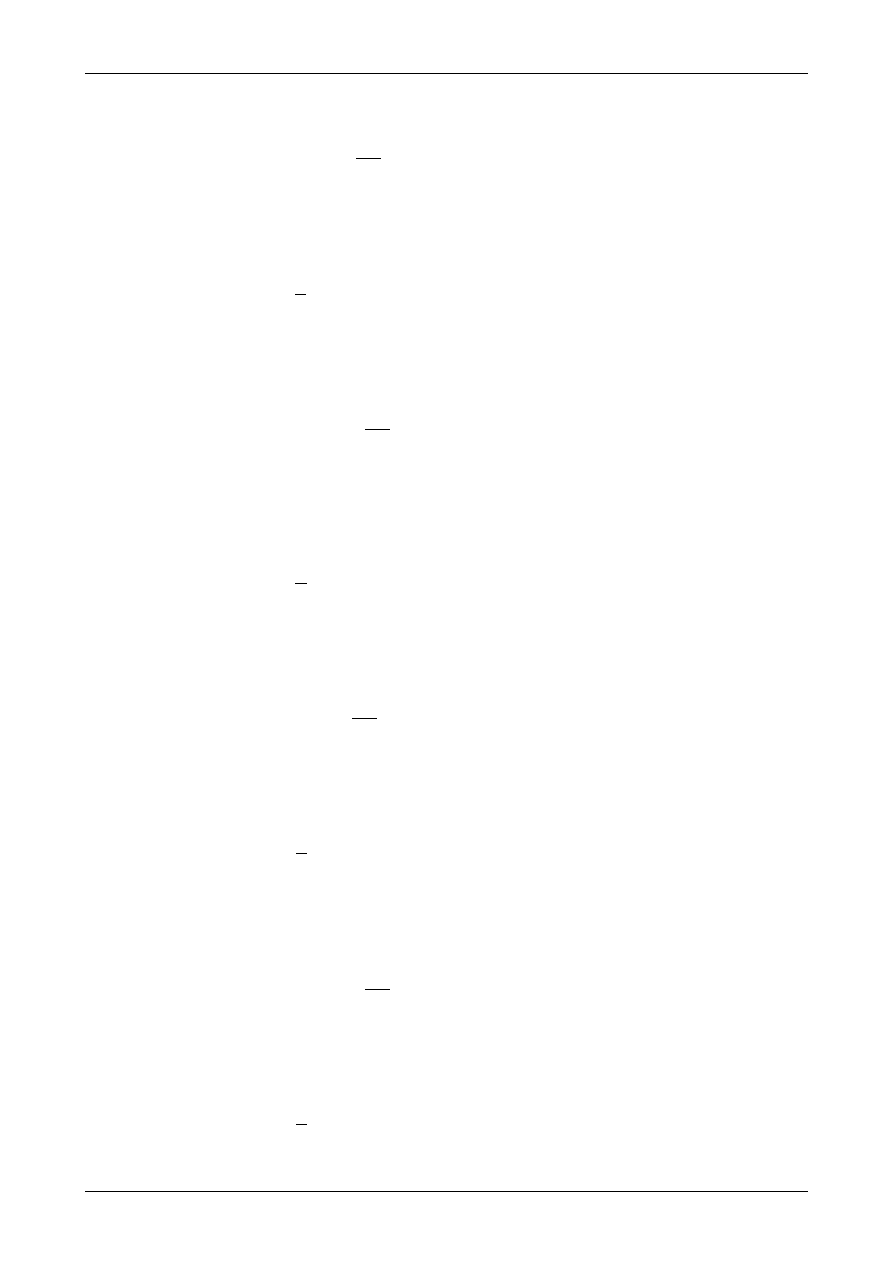
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
8
i znajduje się ona w odległości
4,0
3
=
1,333 m
(Z12/5.23)
od punktu A. Wtórna siła wypadkowa z obciążenia parabolicznego w dół w przedziale AB wynosi
2
3
⋅
8,346⋅10
−
3
⋅
4,0=22,26⋅10
−
3
(Z12/5.24)
i znajduje się ona w odległości
4,0
2
=
2,0 m
(Z12/5.25)
od punktu A czyli w środku przedziału AB. Wtórna siła wypadkowa z obciążenia trójkątnego do góry
w przedziale BC wynosi
1
2
⋅
9,911⋅10
−
3
⋅
2,0=9,911⋅10
−
3
(Z12/5.26)
i znajduje się ona w odległości
2,0
3
=
0,6667 m
(Z12/5.27)
od punktu B. Wtórna siła wypadkowa z obciążenia trójkątnego do góry w przedziale CD wynosi
1
2
⋅
10,21⋅10
−
3
⋅
3,0=15,32⋅10
−
3
(Z12/5.28)
i znajduje się ona w odległości
3,0
3
=
1,0 m
(Z12/5.29)
od punktu D. Wtórna siła wypadkowa z obciążenia parabolicznego w dół w przedziale CD wynosi
2
3
⋅
8,621⋅10
−
3
⋅
3,0=17,24⋅10
−
3
(Z12/5.30)
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
9
i znajduje się ona w odległości
3,0
2
=
1,5 m
(Z12/5.31)
od punktu D czyli w środku przedziału CD. Wtórna siła wypadkowa z obciążenia trójkątnego do góry
w przedziale DE wynosi
1
2
⋅
10,21⋅10
−
3
⋅
1,0=5,105⋅10
−
3
(Z12/5.32)
i znajduje się ona w odległości
1,0
3
=
0,3333 m
(Z12/5.33)
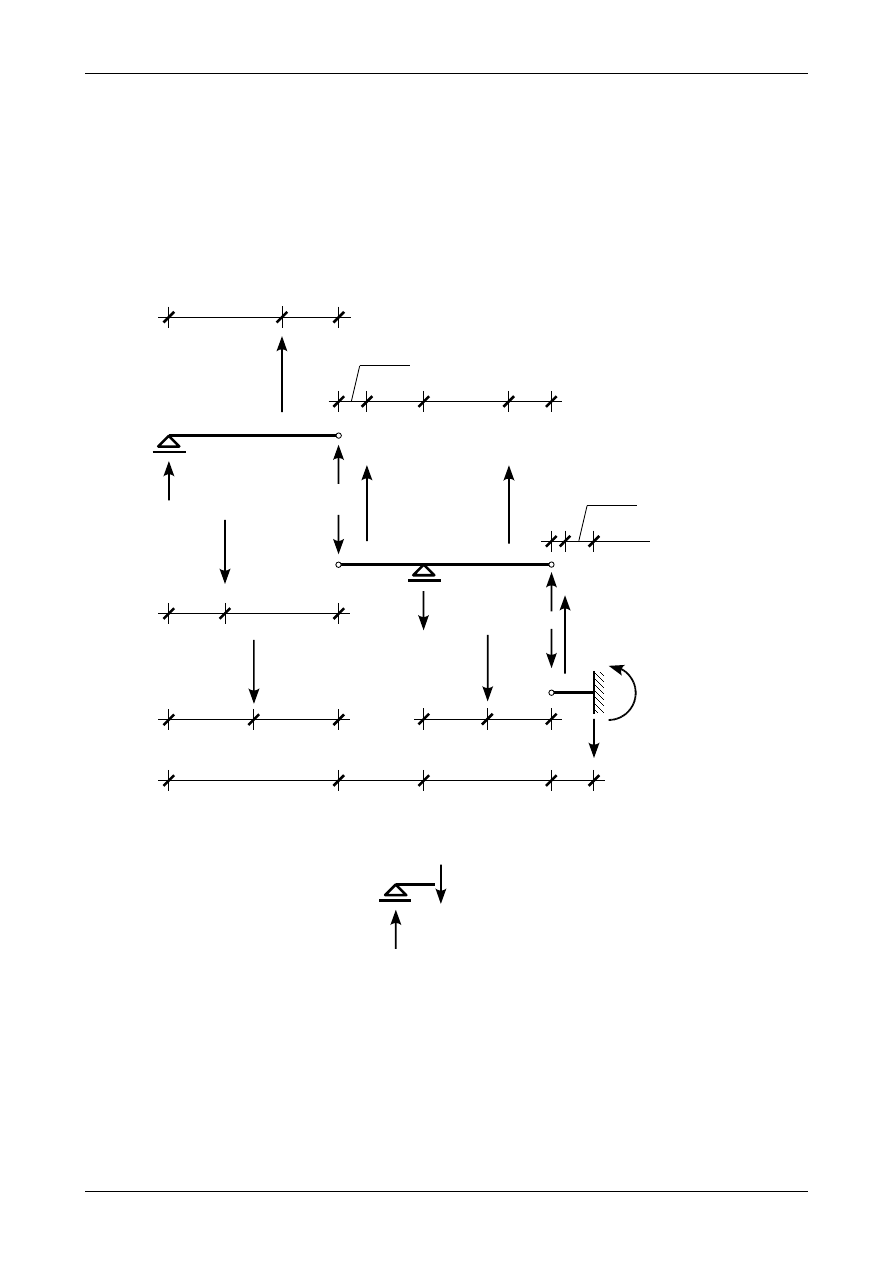
od punktu D. Rysunek Z12/5.10 przedstawia wtórne siły wypadkowe z poszczególnych części obciążenia
ciągłego
16
,6
9
9,
911
5,
10
5
2,0
1,5
1,5
2,0
17
,2
4
22
,2
6
A
B
C
D
E
4,0
2,0
3,0
1,0
[m]
2,667
1,333
2,0
0,6667
1,333
19
,8
2
0,6667
15
,3
2
1,0
0,3333
1,333
2,667
W
*
∙10
-3
[-]
Rys. Z12/5.10. Wtórne siły wypadkowe z części wtórnego obciążenia ciągłego
Z12/5.6. Wyznaczenie reakcji wtórnych
Rysunek Z12/5.11 przedstawia przyjęte zwroty reakcji wtórnych w belce fikcyjnej. Pominiemy
wszystkie reakcje poziome, ponieważ na belce fikcyjnej nie działa żadna siła pozioma.
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
10
16
,6
9
9,9
11
5,1
05
2,0
1,5
1,5
2,0
17
,24
22
,26
A
B
C
D
E
4,0
2,0
3,0
1,0
[m]
0,6667
19
,8
2
15
,32
0,3333
1,333
2,667
1,333
2,0
0,6667
1,0
2,667
1,333
B
D
V
A
*
V
B
*
V
B
*
V
C
*
V
D
*
V
D
*
V
E
*
M
E
*
W
*
∙10
-3
[-]
Rys. Z12/5.11. Przyjęte zwroty reakcji wtórnych
Wtórną reakcję V
A
*
wyznaczymy z równania sumy momentów wszystkich sił wtórnych działających
na belkę AB względem punktu B
M
B
AB *
=
V
A
*
⋅
4,0−16,69⋅10
−
3
⋅
2,667−22,26⋅10
−
3
⋅
2,019,82⋅10
−
3
⋅
1,333=0
V
A
*
=
15,65⋅10
−
3
.
(Z12/5.34)
Wtórna reakcja ma więc zwrot zgodny z założonym. Wtórną reakcję V
B
*
wyznaczymy z równania sumy
momentów wszystkich sił wtórnych działających na belkę AB względem punktu A
M
A
AB *
=−
V
B
*
⋅
4,016,69⋅10
−
3
⋅
1,33322,26⋅10
−
3
⋅
2,0−19,82⋅10
−
3
⋅
2,667=0
V
B
*
=
3,477⋅10
−
3
.
(Z12/5.35)
Wtórna reakcja ma więc zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy równanie
sumy rzutów wszystkich sił wtórnych na belkę AB na oś pionową Y
Y
AB*
=
V
A
*
V
B
*
−
16,69⋅10
−
3
−
22.26⋅10
−
3
19.82⋅10
−
3
=
=
15,65⋅10
−
3
3,477⋅10
−
3
−
16,69⋅10
−
3
−
22.26⋅10
−
3
19.82⋅10
−
3
=
=−
0,003⋅10
−
3
≈
0
.
(Z12/5.36)
Wszystkie siły wtórne działające na belkę AB znajdują się w równowadze.
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
11
Wtórną reakcję V
C
*
wyznaczymy z równania sumy momentów wszystkich sił wtórnych działających
na belkę BD względem punktu D
M
D
BD *
=
V
C
*
⋅
3,0−V
B
*
⋅
5,09,911⋅10
−
3
⋅
4,33315,32⋅10
−
3
⋅
1,0
−
17,24⋅10
−
3
⋅
1,5=0
V
C
*
⋅
3,0−3,477⋅10
−
3
⋅
5,09,911⋅10
−
3
⋅
4,33315,32⋅10
−
3
⋅
1,0
−
17,24⋅10
−
3
⋅
1,5=0
V
C
*
=−
5,006⋅10
−
3
.
(Z12/5.37)
Wtórna reakcja ma więc zwrot przeciwny do założonego. Wtórną reakcję V
D
*
wyznaczymy z równania sumy
momentów wszystkich sił wtórnych działających na belkę BD względem punktu C
M
C
BD *
=−
V
D
*
⋅
3,0−V
B
*
⋅
2,09,911⋅10
−
3
⋅
1,333−15,32⋅10
−
3
⋅
2,0
17,24⋅10
−
3
⋅
1,5=0
−
V
D
*
⋅
3,0−3,477⋅10
−
3
⋅
2,09,911⋅10
−
3
⋅
1,333−15,32⋅10
−
3
⋅
2,0
17,24⋅10
−
3
⋅
1,5=0
V
D
*
=
0,4925⋅10
−
3
.
(Z12/5.38)
Wtórna reakcja ma więc zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy równanie
sumy rzutów wszystkich sił wtórnych na belkę BD na oś pionową Y
Y
BD*
=−
V
B
*
V
C
*
V
D
*
9,911⋅10
−
3
15,32⋅10
−
3
−
17,24⋅10
−
3
=
=−
3,477⋅10
−
3
−
5,006⋅10
−
3
0,4925⋅10
−
3
9,911⋅10
−
3
15,32⋅10
−
3
−
17,24⋅10
−
3
=
0,0005⋅10
−
3
≈
0
.
(Z12/5.39)
Wszystkie siły wtórne działające na belkę BD znajdują się w równowadze.
Wtórną reakcję M
E
*
wyznaczymy z równania sumy momentów wszystkich sił wtórnych działających
na belkę DE względem punktu E
M
E
DE *
=−
M
E
*
−
V
D
*
⋅
1,05,105⋅10
−
3
⋅
0,6667=0
−
M
E
*
−
0,4925⋅10
−
3
⋅
1,05,105⋅10
−
3
⋅
0,6667=0
M
E
*
=
2,911⋅10
−
3
m
.
(Z12/5.40)
Wtórna reakcja ma więc zwrot zgodny z założonym. Wtórną reakcję V
E
*
wyznaczymy z równania sumy
momentów wszystkich sił wtórnych działających na belkę DE względem punktu D
M
D
DE *
=−
V
E
*
⋅
1,0−M
E
*
−
5,105⋅10
−
3
⋅
0,3333=0
−
V
E
*
⋅
1,0−2,911⋅10
−
3
−
5,105⋅10
−
3
⋅
0,3333=0
V
E
*
=−
4,612⋅10
−
3
.
(Z12/5.41)
Wtórna reakcja ma więc zwrot przeciwny do założonego. W celu sprawdzenia obliczeń zastosujemy
równanie sumy rzutów wszystkich sił wtórnych na belkę DE na oś pionową Y
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
12
Y
DE *
=−
V
D
*
V
E
*
5,105⋅10
−
3
=−
0,4925⋅10
−
3
−
4,612⋅10
−
3
5,105⋅10
−
3
=
0,0005⋅10
−
3
≈
0
.
(Z12/5.42)
Wszystkie siły wtórne działające na belkę DE znajdują się w równowadze. Rysunek Z12/5.12 przedstawia
wszystkie belki tworzące belkę fikcyjną wraz z działającymi na nie wtórnymi siłami wypadkowymi z ob-
ciążenia ciągłego oraz wtórnymi reakcjami. Siły te posłużą nam do wyznaczenia odpowiednich wtórnych sił
poprzecznych i momentów zginających w belce fikcyjnej, które to równają kątom obrotu i ugięciom w belce
rzeczywistej.
16
,6
9
9,9
11
5,1
05
2,0
1,5
1,5
2,0
17
,24
22
,26
A
B
C
D
E
4,0
2,0
3,0
1,0
[m]
0,6667
19
,8
2
15
,32
0,3333
1,333
2,667
1,333
2,0
0,6667
1,0
2,667
1,333
B
D
15,65
3,477
3,477
5,006
0,4925
0,4925
4,612
2,911
W
*
∙10
-3
[-]
R
*
∙10
-3
[-]
M
*
∙10
-3
[m]
Rys. Z12/5.12. Prawidłowe zwroty i wartości wtórnych reakcji w belce fikcyjnej
A
15,65
T
A
*
R
*
∙10
-3
[-]
Rys. Z12/5.13. Równowaga w otoczeniu punktu A
Z12/5.7. Wyznaczenie kątów obrotu i ugięć
Rysunek Z12/5.13 przedstawia równowagę sił wtórnych w otoczeniu podpory A w belce fikcyjnej.
Wtórna siła poprzeczna T
A
*
czyli kąt obrotu w punkcie A będzie wynosił
A
=
T
A
*
=
15,65⋅10
−
3
rad
.
(Z12/5.43)
Dr inż. Janusz Dębiński
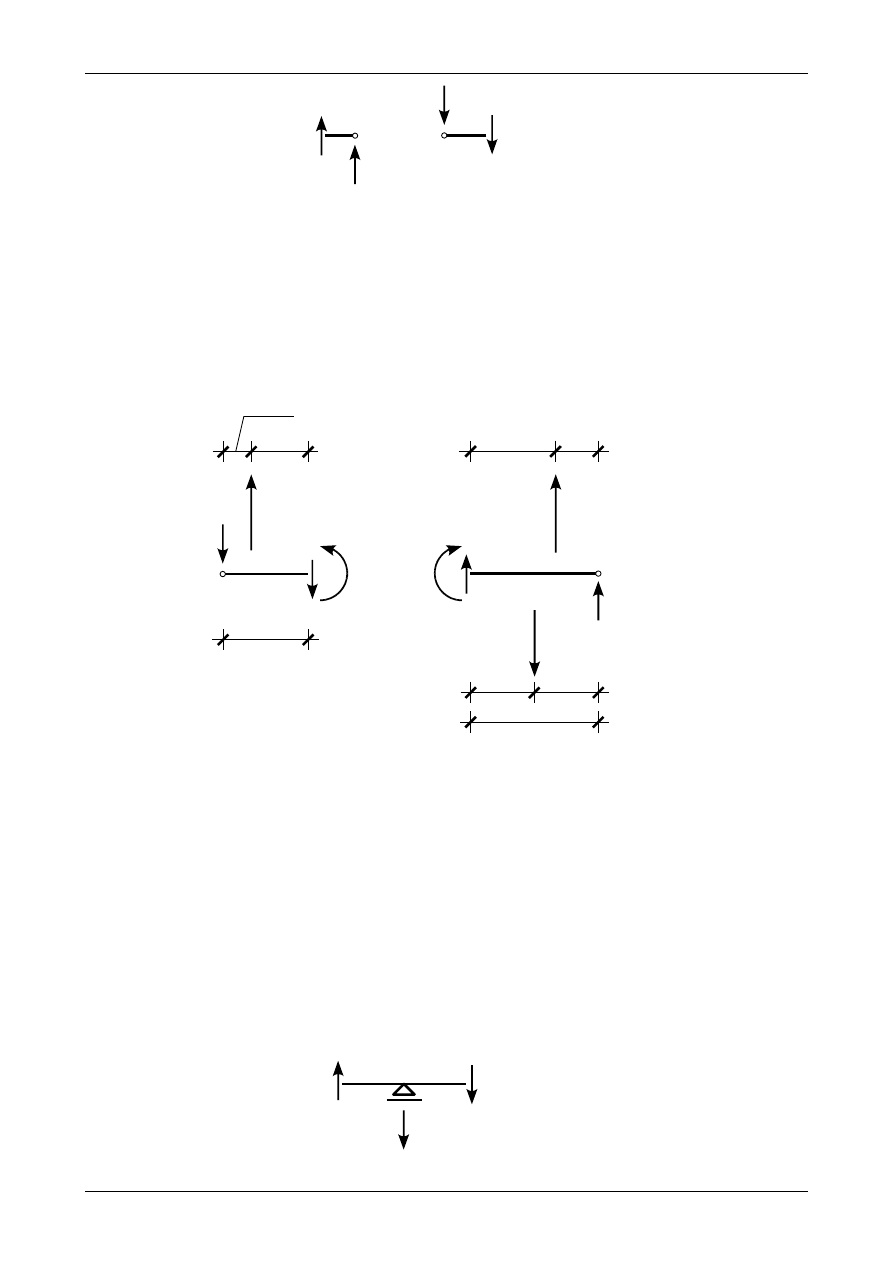
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
13
B
3,477
B
3,477
T
B
(L)*
T
B
(P)*
R
*
∙10
-3
[-]
Rys. Z12/5.14. Równowaga w otoczeniu punktu B
Rysunek Z12/5.14 przedstawia równowagę sił wtórnych w otoczeniu podpory B w belce fikcyjnej.
Wtórna siła poprzeczna T
B
*
czyli kąt obrotu w punkcie B będzie wynosił
B
=
T
B
*
=
T
B
L*
=
T
B
P*
=−
3,477⋅10
−
3
rad
.
(Z12/5.44)
9,
91
1
2,0
[m]
1,333
0,6667
B
3,477
3,0
[m]
15
,3
2
2,0
1,0
D
0,4925
T
C
(L)*
T
C
(P)*
M
C
(L)*
M
C
(P)*
1,5
1,5
17
,2
4
W
*
∙10
-3
[-]
R
*
∙10
-3
[-]
Rys. Z12/5.15. Równowaga w otoczeniu punktu C
Rysunek Z12/5.15 przedstawia równowagę sił wtórnych w otoczeniu podpory C w belce fikcyjnej.
Wtórna siła poprzeczna T
C
(L)*
czyli kąt obrotu w przegubie C z lewej strony będzie wynosił
C
L
=
T
C
L*
=−
3,477⋅10
−
3
9,911⋅10
−
3
=
6,434⋅10
−
3
rad
.
(Z12/5.45)
Wtórna siła poprzeczna T
C
(P)*
czyli kąt obrotu w przegubie C z prawej strony będzie wynosił
C
P
=
T
C
P*
=−
0,4925⋅10
−
3
−
15,32⋅10
−
3
17,24⋅10
−
3
=
1,428⋅10
−
3
rad
.
(Z12/5.46)
C
5,006
6,434
1,428
R
*
∙10
-3
[-]
T
*
∙10
-3
[-]
Rys. Z12/5.16. Równowaga wtórnych sił poprzecznych oraz wtórnej reakcji na podporze C
Dr inż. Janusz Dębiński
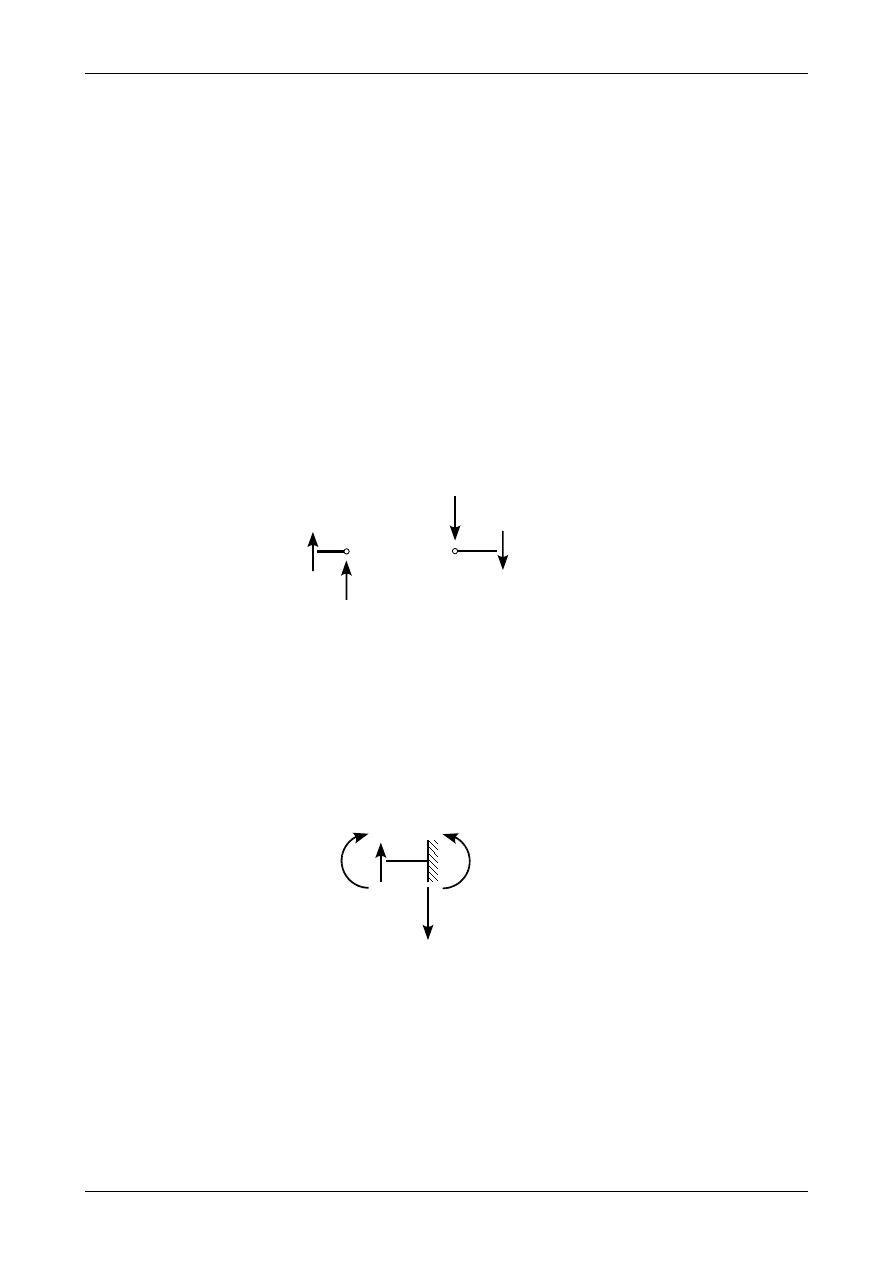
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
14
Rysunek Z12/5.16 przedstawia równowagę wtórnych sił poprzecznych z lewej i prawej strony podpory
C oraz wtórnej reakcji w tej podporze. Zgodnie z rysunkiem Z12/5.15 wtórny moment zginający M
C
(L)*
wynosi
M
C
L*
=−
3,477⋅10
−
3
⋅
2,09,911⋅10
−
3
⋅
1,333=6,257⋅10
−
3
m
.
(Z12/5.47)
Wtórny moment zginający M
C
(P)*
wynosi
M
C
L*
=
0,4925⋅10
−
3
⋅
3,015,32⋅10
−
3
⋅
2,0−17,24⋅10
−
3
⋅
1,5=6,258⋅10
−
3
m
.
(Z12/5.48)
Jak widać oba momenty są w przybliżeniu równe. Jak wiadomo momenty te równają się ugięciu w punkcie
przegubu C. Możemy więc zapisać
w
C
=
6,258⋅10
−
3
m
.
(Z12/5.49)
D
0,4925
D
0,4925
T
D
(L)*
T
D
(P)*
R
*
∙10
-3
[-]
Rys. Z12/5.17. Równowaga w otoczeniu podpory D
Rysunek Z12/5.17 przedstawia równowagę sił wtórnych w otoczeniu podpory D w belce fikcyjnej.
Wtórna siła poprzeczna T
D
*
czyli kąt obrotu w punkcie D będzie wynosił
D
=
T
D
*
=
T
D
L*
=
T
D
P*
=−
0,4925⋅10
−
3
rad
.
(Z12/5.50)
E
4,612
2,911
T
E
*
M
E
*
R
*
∙10
-3
[-]
M
*
∙10
-3
[m]
Rys. Z12/5.18. Równowaga w otoczeniu podpory E
Rysunek Z12/5.18 przedstawia równowagę sił i momentów wtórnych w otoczeniu podpory E w belce
fikcyjnej. Wtórna siła poprzeczna T
E
*
czyli kąt obrotu w punkcie E będzie wynosił
E
=
T
E
*
=
4,612⋅10
−
3
rad
.
(Z12/5.51)
Wtórny moment zginający M
E
*
czyli ugięcie w punkcie E będzie wynosiło
Dr inż. Janusz Dębiński
WM
Z12/5. PRZEMIESZCZENIA W BELKACH – ZADANIE 5
15
w
E
=
M
E
*
=
2,911⋅10
−
3
m
.
(Z12/5.52)
Jak więc widać ugięcia w punkcie C i E są dodatnie czyli w dół.
Dr inż. Janusz Dębiński
Document Outline