WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

1

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

Z12/7.1. Zadanie 7

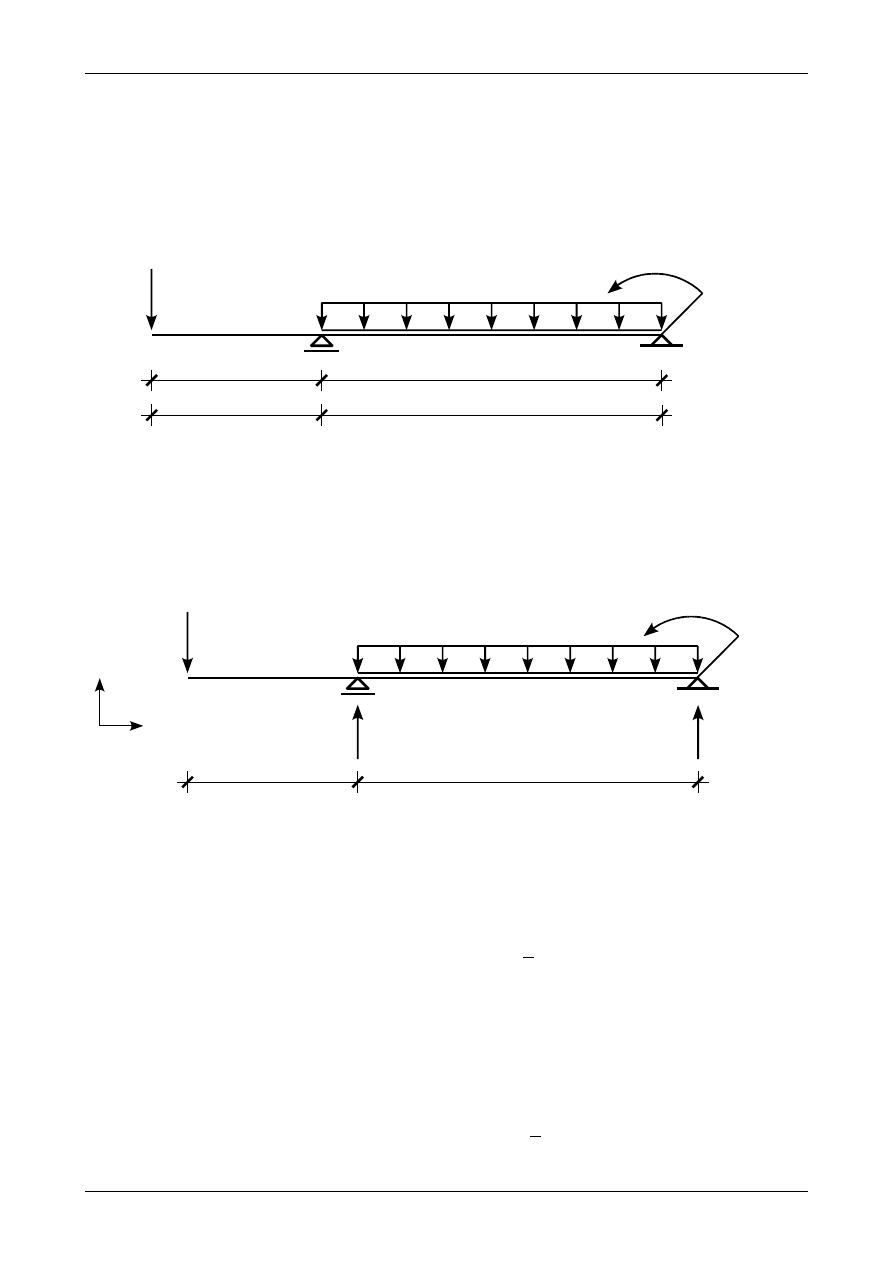
Rysunek Z12/6.1 przedstawia belkę swobodnie podpartą składającą się z dwóch prętów pryzma-

tycznych. Dla belki tej wyznaczyć wartości i zwroty reakcji podporowych a następnie narysować wykresy
siły poprzecznej i momentu zginającego. Na koniec wyznaczyć ugięcie w punkcie A metodą obciążeń
krzywiznami.

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

6200 kNm

2

5100 kNm

2

Rys. Z12/7.1. Belka swobodnie podparta

Z12/7.2. Wyznaczenie wartości i zwrotów reakcji podporowych

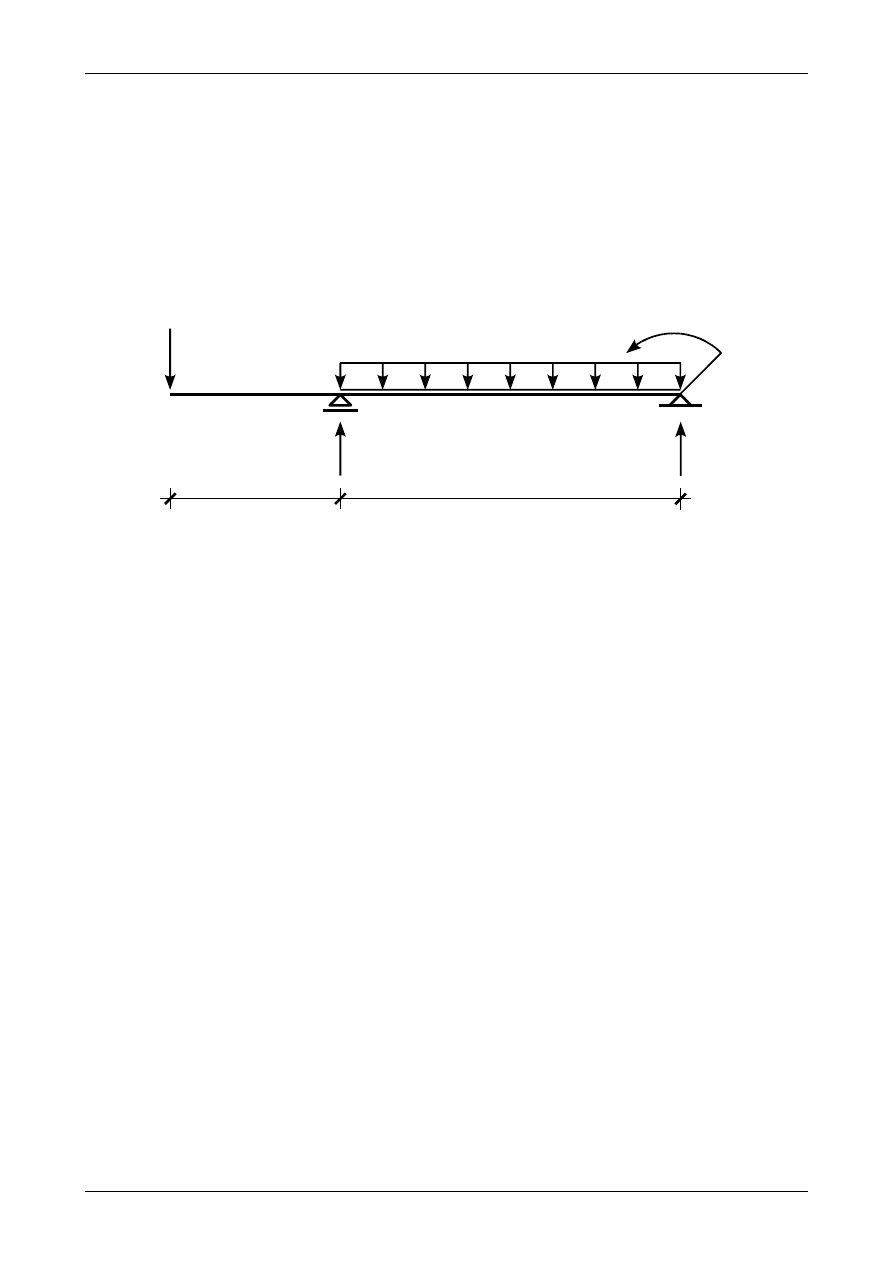
Rysunek Z12/7.2 przedstawia przyjęte zwroty reakcji podporowych. Ze względu na to, że na belkę nie

działają żadne siły poziome reakcja H

C

będzie wynosiła zero.

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

V

B

V

C

X

Y

Rys. Z12/7.2. Przyjęte zwroty reakcji podporowych w belce

Reakcję V

B

wyznaczymy z równania sumy momentów wszystkich sił działających na belkę względem

punktu C



M

C

=

V

B

⋅

4,0−24,0⋅6,0−8,0−16,0⋅4,0⋅

1
2

⋅

4,0=0

V

B

=

70,0 kN

.

(Z12/7.1)

Reakcja ma więc zwrot zgodny z założonym. Reakcję V

C

wyznaczymy z równania sumy momentów

wszystkich sił działających na belkę względem punktu B



M

B

=−

V

C

⋅

4,0−24,0⋅2,0−8,016,0⋅4,0⋅

1
2

⋅

4,0=0

V

B

=

18,0 kN

.

(Z12/7.2)

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

2

Reakcja ma więc zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy równanie sumy
rzutów wszystkich sił działających na belkę na oś pionową Y



Y =0

V

B



V

C

−

24,0−16,0⋅4,0=70,018,0−24,0−64,0=0

.

(Z12/7.3)

Wszystkie siły działające na belkę znajdują się więc w równowadze. Rysunek Z12/7.3 przedstawia
prawidłowe wartości i zwroty reakcji podporowych.

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

Rys. Z12/7.3. Prawidłowe wartości i zwroty reakcji podporowych

Z12/7.3. Wykresy sił przekrojowych

W przedziale AB nie działa żadne obciążenie ciągłe równomiernie rozłożone więc siła poprzeczna

będzie stała natomiast moment zginający będzie funkcją liniową. W przedziale BC działa obciążenie ciągłe
równomiernie rozłożone o wartości 16,0 kN/m w dół więc siła poprzeczna będzie funkcją liniową natomiast
moment zginający będzie funkcją kwadratową, której wykresem jest parabola.

W punkcie A działa siła skupiona o wartości 24,0 kN w dół więc siła poprzeczna w tym punkcie

wynosi

T

A



AB

=−

24,0 kN

.

(Z12/7.4)

W przedziale AB oraz w punkcie B z lewej strony siła poprzeczna wynosi

T

AB

=

T

B



AB

=−

24,0 kN

.

(Z12/7.5)

W punkcie B działa siła skupiona o wartości 70,0 kN do góry więc siła poprzeczna w punkcie B z prawej
strony wynosi

T

B



BC

=−

24,070,0=46,0 kN

.

(Z12/7.6)

Siła poprzeczna w punkcie C wynosi

T

C



BC

=

46,0−16,0⋅4,0=−18,0 kN

.

(Z12/7.7)

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

3

Siła poprzeczna w przedziale BC posiada na obu końcach przedziału wartości przeciwnych znaków. Musi
ona więc posiadać w tym przedziale miejsce zerowe. Zgodnie ze wzorem (5.127) znajduje się ono w od-
ległości

x

0

L

=

46,0
16,0

=

2,875 m

(Z12/7.8)

od punktu B. Natomiast odległość miejsca zerowego siły poprzecznej od punktu C zgodnie ze wzorem
(5.128) wynosi

x

0

P

=

18,0
16,0

=

1,125 m

.

(Z12/7.9)

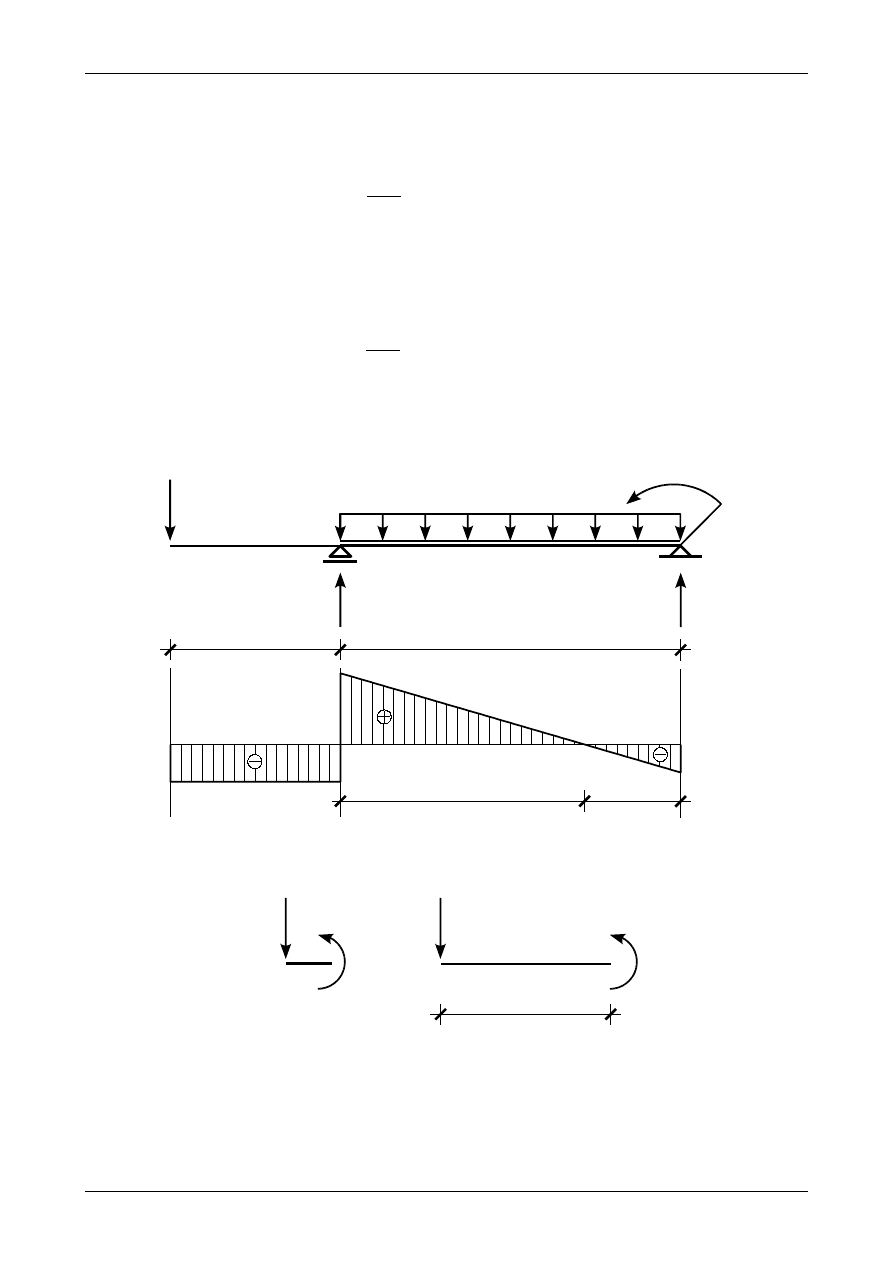
Rysunek Z12/7.4 przedstawia wykres siły poprzecznej w belce.

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

2,875

1,125

T [kN]

24,0

46

,0

18

,0

Rys. Z12/7.4. Wykres siły poprzecznej

A

24,0 kN

M

A

(AB)

A

[m]

2,0

24,0 kN

M

B

(AB)

a)

b)

Rys. Z12/7.5. Równowaga momentów zginających w przedziale AB

Zgodnie z rysunkiem Z12/7.5 a) moment zginający w punkcie A przedziału AB wynosi

M

A



AB

=

0,0 kNm

.

(Z12/7.10)

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

4

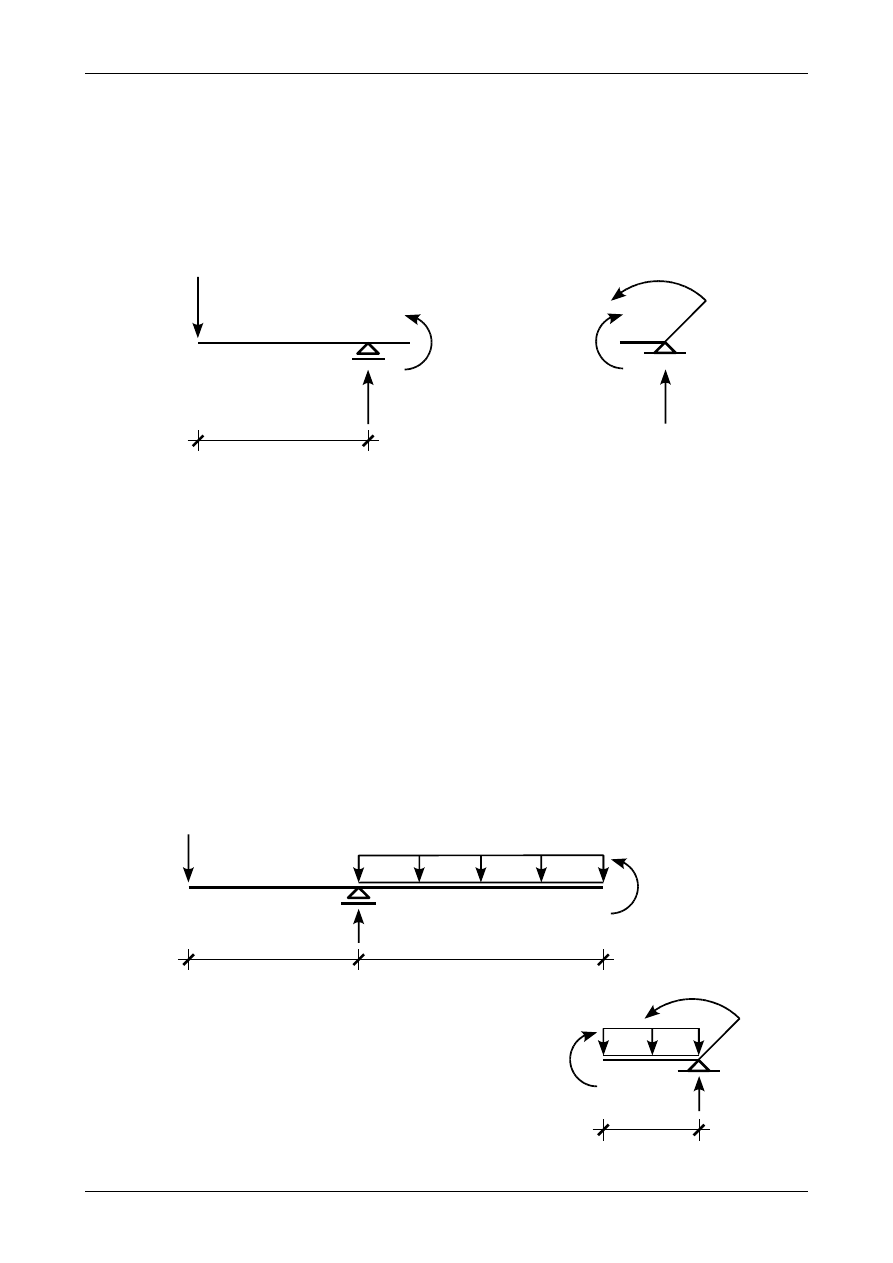
Zgodnie z rysunkiem Z12/7.5 b) moment zginający w punkcie B przedziału AB wynosi

M

B



AB

=−

24,0⋅2,0=−48,0 kNm

.

(Z12/7.11)

Moment ten rozciąga górną część przekroju pręta.

A

[m]

2,0

B

24,0 kN

70,0 kN

M

B

(BC)

8,0 kNm

C

18,0 kN

M

C

(BC)

a)

b)

Rys. Z12/7.6. Równowaga momentów zginających w przedziale BC

Zgodnie z rysunkiem Z12/7.6 a) moment zginający w punkcie B przedziału BC wynosi

M

B



BC

=−

24,0⋅2,0=−48,0 kNm

.

(Z12/7.12)

Moment ten rozciąga górną część przekroju pręta. Zgodnie z rysunkiem Z12/7.6 b) moment zginający
w punkcie C przedziału BC wynosi

M

C



BC

=

8,0 kNm

.

(Z12/7.13)

Moment ten rozciąga dolną część przekroju pręta.

A

[m]

2,875

2,0

16,0 kN/m

B

24,0 kN

70,0 kN

16,0 kN/m

8,0 kNm

C

18,0 kN

1,125

M

EXT

(BC)

M

EXT

(BC)

Rys. Z12/7.7. Równowaga momentów w miejscu ekstremum momentu zginającego

Dr inż. Janusz Dębiński

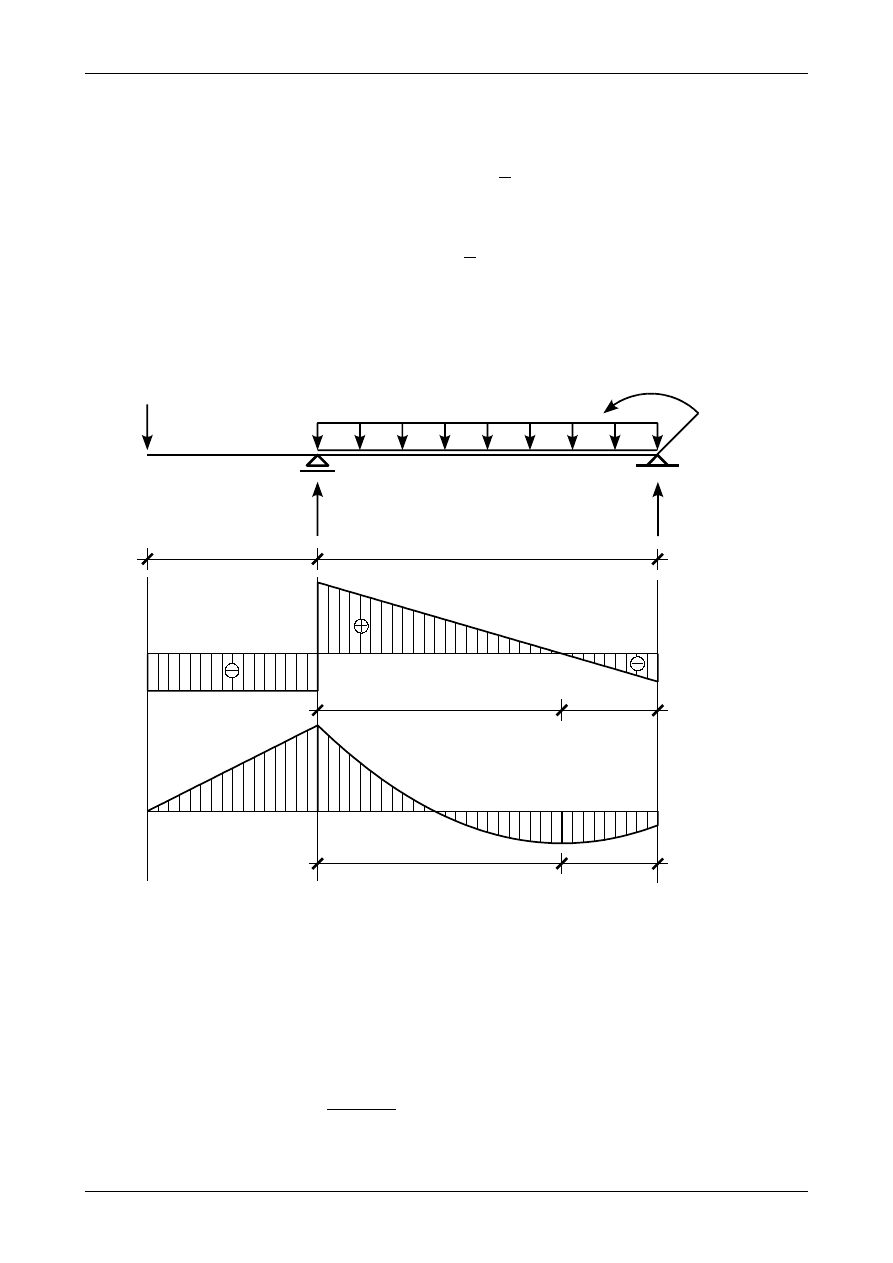
WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

5

W przedziale BC moment zginający będzie posiadał ekstremum, które znajduje się w punkcie miejsca

zerowego siły poprzecznej. Ekstremalny moment zgodnie z rysunkiem Z12/7.7 wynosi

M

EXT



BC

=−

24,0⋅4,87570,0⋅2,875−16,0⋅2,875⋅

1
2

⋅

2,875=18,13 kNm

,

(Z12/7.14)

M

EXT



BC

=

18,0⋅1,1258,0−16,0⋅1,125⋅

1
2

⋅

1,125=18,13 kNm

.

(Z12/7.15)

Moment ten rozciąga dolną część belki. Rysunek Z12/7.8 przedstawia wykresy siły poprzecznej oraz mo-
mentu zginającego w belce.

2,875

1,125

M [kNm]

0,

0

48

,0

18

,1

3

8,0

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

2,875

1,125

T [kN]

24,0

46

,0

18

,0

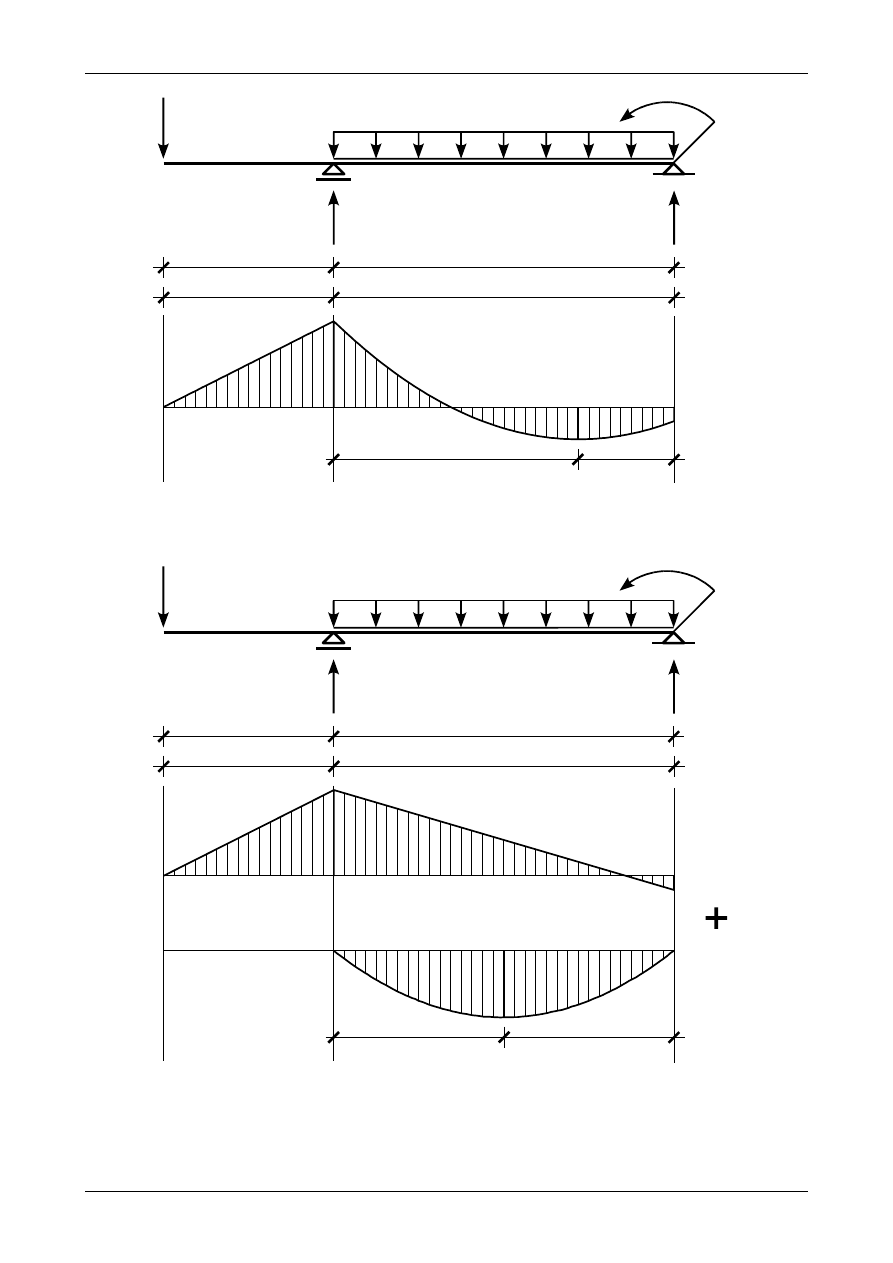
Rys. Z12/7.8. Wykresy sił przekrojowych w belce

Z12/7.4. Przygotowanie wykresu momentu zginającego i obliczenie krzywizn

Rysunek Z12/7.9 przedstawia wykres momentu zginającego w belce. W przedziale BC działa

obciążenie ciągłe równomiernie rozłożone więc możemy połączyć początek i koniec wykresu tym przedziale
oraz dodać parabolę o długości 4,0 m i rzędnej w środku wynoszącej

16,0⋅4,0

2

8

=

32,0 kNm

.

(Z12/7.16)

Rysunek Z12/7.10 przedstawia przerobiony wykres momentów zginających w belce.

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

6

2,875

1,125

M [kNm]

0,

0

48

,0

18

,1

3

8,

0

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

6200 kNm

2

5100 kNm

2

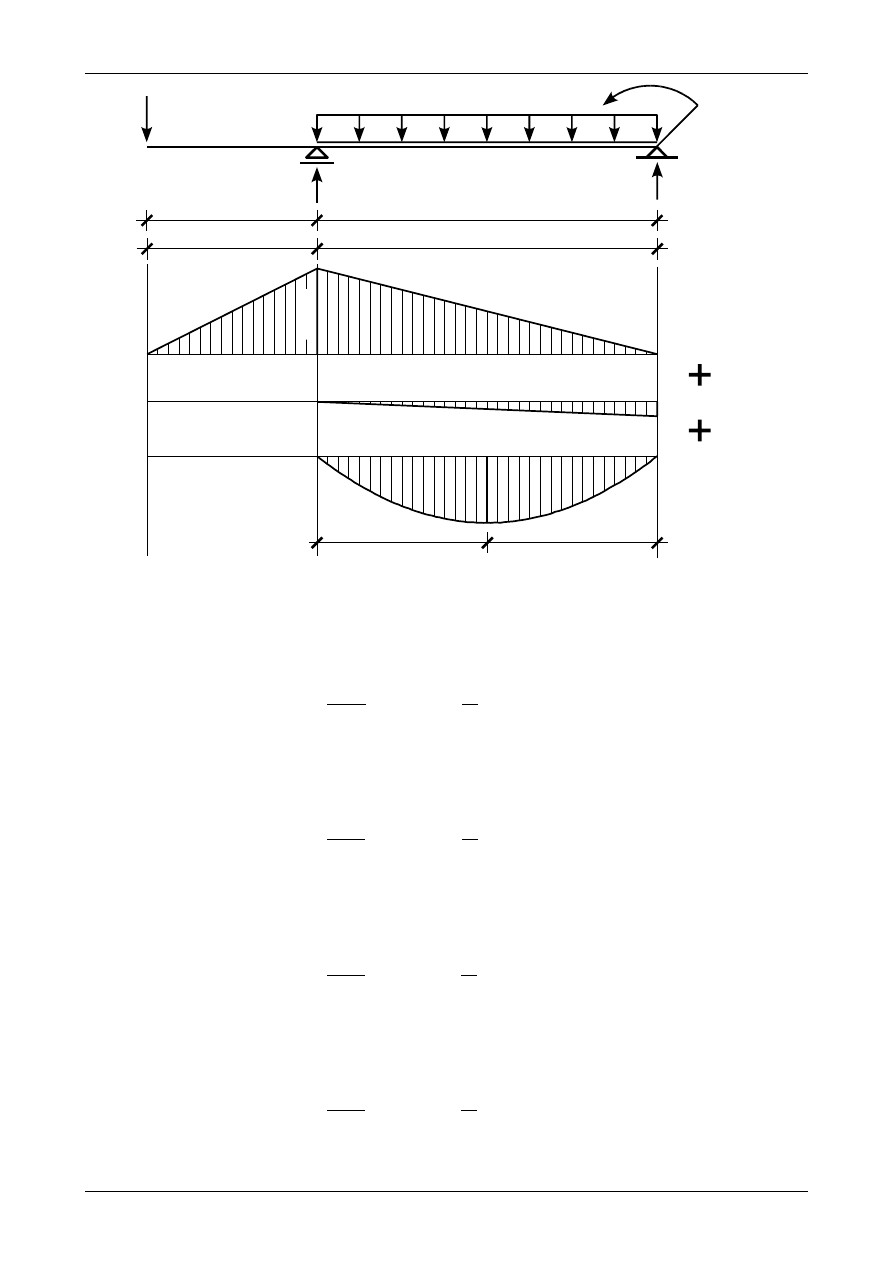
Rys. Z12/7.9. Wykres momentu zginającego w belce

2,0

M [kNm]

0,0

48

,0

32

,0

8,

0

2,0

M [kNm]

0,

0

0,0

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

6200 kNm

2

5100 kNm

2

Rys. Z12/7.10. Przerobiony wykres momentu zginającego

Jak widać na rysunku Z12/7.10 w przedziale BC mamy wykres liniowy przewinięty. Dla wygody

obliczeń przerobimy go do postaci dwóch wykresów liniowych przedstawionych na rysunku Z12/7.11.

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

7

2,0

M [kNm]

0,0

32

,0

0,

0

2,0

8,

0

0,0

M [kNm]

M [kNm]

0,0

0,0

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

6200 kNm

2

5100 kNm

2

48

,0

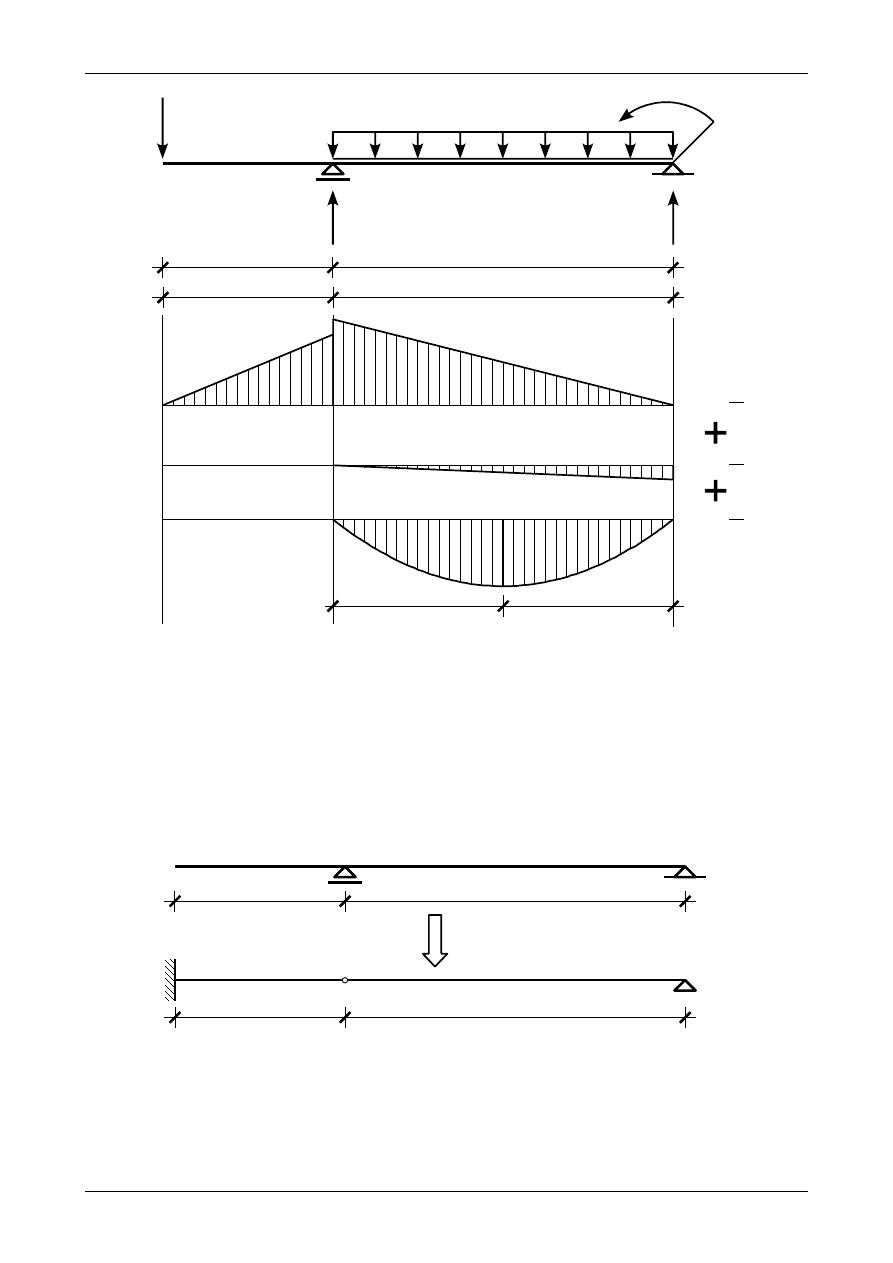
Rys. Z12/7.11. Ostatecznie przerobiony wykres momentu zginającego

Krzywizna w punkcie B w przedziale AB wynosi

48,0

6200

=

7,742⋅10

−

3

1

m

.

(Z12/7.17)

Krzywizna w punkcie B w przedziale BC wynosi

48,0

5100

=

9,412⋅10

−

3

1

m

.

(Z12/7.18)

Krzywizna w punkcie C w przedziale BC wynosi

8,0

5100

=

1,569⋅10

−

3

1

m

.

(Z12/7.19)

Krzywizna w środku paraboli w przedziale BC wynosi

32,0

5100

=

6,275⋅10

−

3

1

m

.

(Z12/7.20)

Rysunek Z12/7.12 przedstawia wykres krzywizn w belce.

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

8

2,0

0,0

7,

742

6,2

75

0,

0

2,0

1,

569

0,0

0,0

0,0

9,4

12

A

[m]

4,0

2,0

16,0 kN/m

8,0 kNm

B

C

24,0 kN

70,0 kN

18,0 kN

6200 kNm

2

5100 kNm

2

⋅

10

−

3

[

1

m

]

⋅

10

−

3

[

1

m

]

⋅

10

−

3

[

1

m

]

Rys. Z12/7.12. Wykres krzywizn w belce

Z12/7.5. Belka fikcyjna

Belka fikcyjna musi spełniać warunki brzegowe zadania. Zgodnie z tabelą 12.2 wolny koniec A prze-

chodzi w utwierdzenie. Podpora przegubowo-przesuwna B przechodzi w przegub rzeczywisty natomiast
podpora przegubowo-nieprzesuwna C przechodzi w podporę przegubową. Pierwsze przybliżenie belki
fikcyjnej przedstawia rysunek Z12/7.13.

A

B

C

[m]

4,0

2,0

A

B

C

[m]

4,0

2,0

Rys. Z12/7.13. Pierwsze przybliżenie belki fikcyjnej

Jak widać belka fikcyjna składa się z dwóch tarcz sztywnych, które posiadają sześć stopni swobody.

Utwierdzenie A odbiera trzy natomiast przegub rzeczywisty B odbiera dwa stopnie swobody. Razem te
podpory odbierają pięć stopni swobody. Pozostaje nam jeden stopień swobody czyli podpora przegubowa
C musi być podporą przegubowo-przesuwną. Rysunek Z12/7.14 przedstawia ostateczną postać belki fikcyj-
nej.

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

9

A

B

C

[m]

4,0

2,0

Rys. Z12/7.14. Ostateczna postać belki fikcyjnej

Z12/7.6. Obciążenie fikcyjne

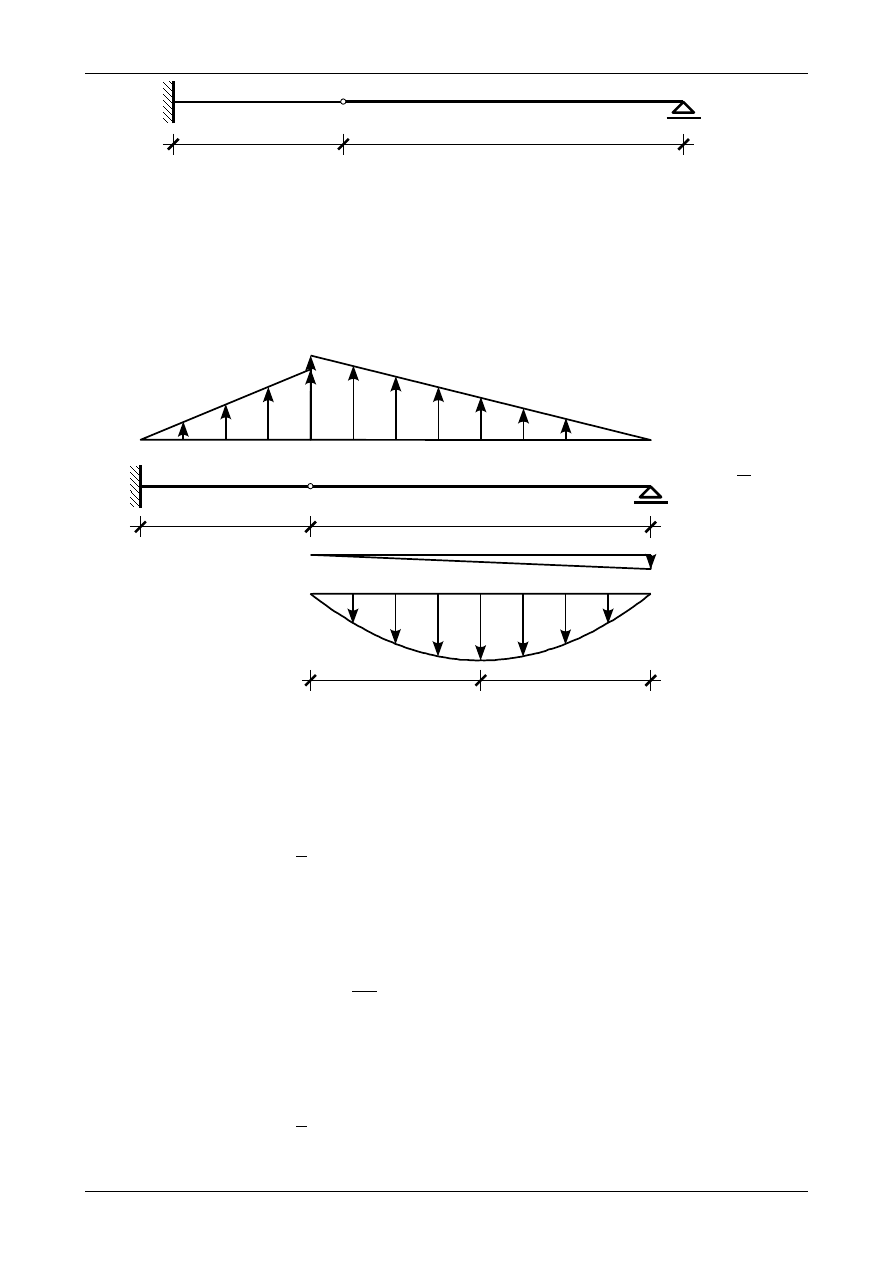
Korzystając z wykresu krzywizn na belce przedstawionych na rysunku Z12/7.12 otrzymamy obcią-

żenie wtórne belki fikcyjnej. Obciążenie to przedstawia rysunek Z12/7.15.

[m]

4,0

2,0

2,0

7,742

6,

27

5

2,0

1,569

9,412

A

B

C

q

*

⋅

10

−

3

[

1

m

]

Rys. Z12/7.15. Obciążenie wtórne belki fikcyjnej

Obciążenie ciągłe przedstawione na rysunku Z12/7.15 możemy sprowadzić do wtórnych sił wypad-

kowych. Wtórna siła wypadkowa z obciążenia trójkątnego do góry w przedziale AB wynosi

1
2

⋅

7,742⋅10

−

3

⋅

2,0=7,742⋅10

−

3

(Z12/7.21)

i znajduje się ona w odległości

2,0

3

=

0,6667 m

(Z12/7.22)

od punktu B. Wtórna siła wypadkowa z obciążenia trójkątnego do góry w przedziale BC wynosi

1
2

⋅

9,412⋅10

−

3

⋅

4,0=18,82⋅10

−

3

(Z12/7.23)

Dr inż. Janusz Dębiński

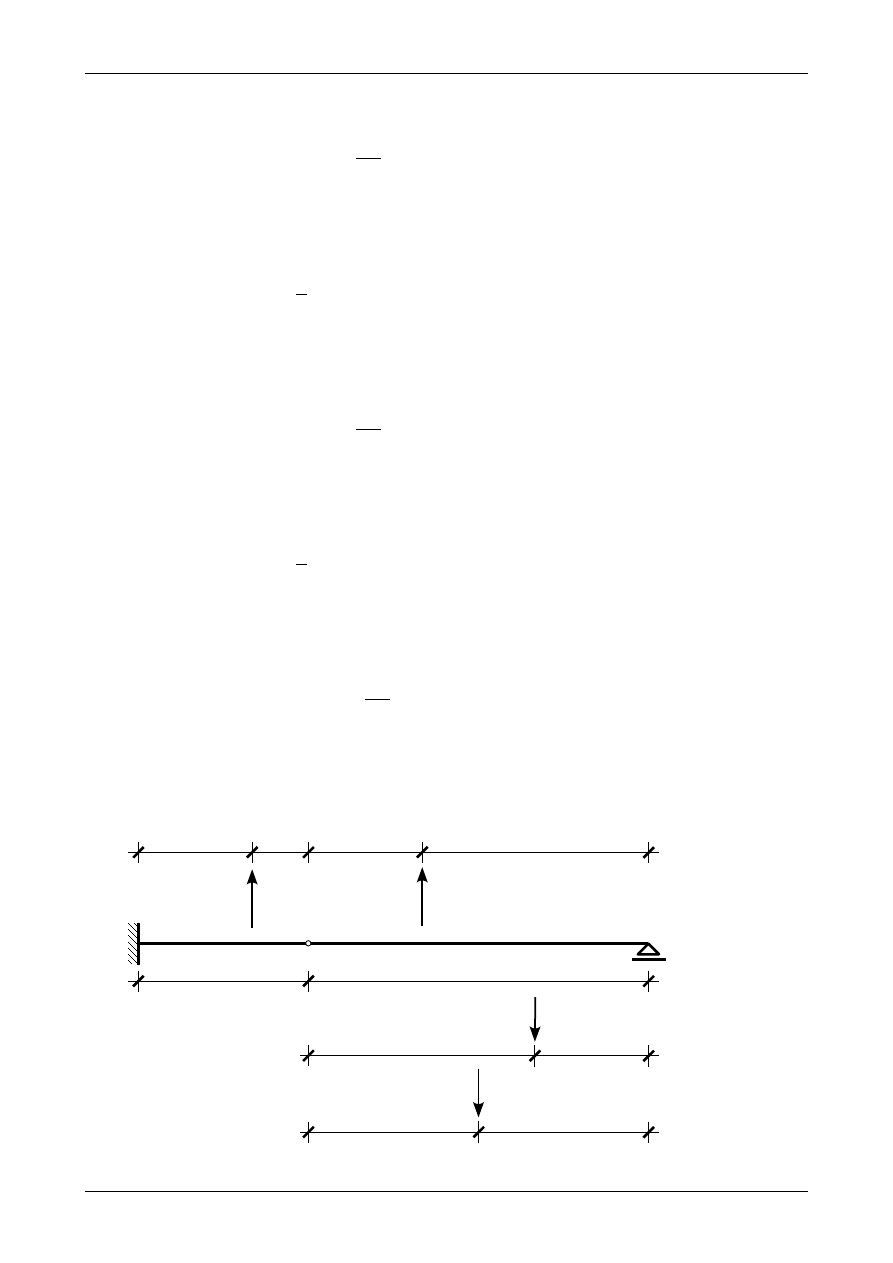
WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

10

i znajduje się ona w odległości

4,0

3

=

1,333 m

(Z12/7.24)

od punktu B. Wtórna siła wypadkowa z obciążenia trójkątnego w dół w przedziale BC wynosi

1
2

⋅

1,569⋅10

−

3

⋅

4,0=3,138⋅10

−

3

(Z12/7.25)

i znajduje się ona w odległości

4,0

3

=

1,333 m

(Z12/7.26)

od punktu C. Wtórna siła wypadkowa z obciążenia parabolicznego w dół w przedziale BC wynosi

2
3

⋅

6,275⋅10

−

3

⋅

4,0=16,73⋅10

−

3

(Z12/7.27)

i znajduje się ona w odległości

4,0

2

=

2,0 m

(Z12/7.28)

od punktu B czyli znajduje się w środku przedziału BC. Rysunek Z12/7.16 przedstawia wtórne siły wypad-
kowe z obciążenia ciągłego na belce fikcyjnej.

[m]

4,0

2,0

2,0

7,

74

2

16

,7

3

2,0

3,1

38

18

,8

2

2,667

1,333

1,333

0,6667

2,667

1,333

A

B

C

W

*

∙10

-3

[-]

Rys. Z12/7.16. Wtórne siły wypadkowe z obciążenia ciągłego

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

11

Z12/7.7. Wtórne reakcje oraz ugięcie w punkcie A

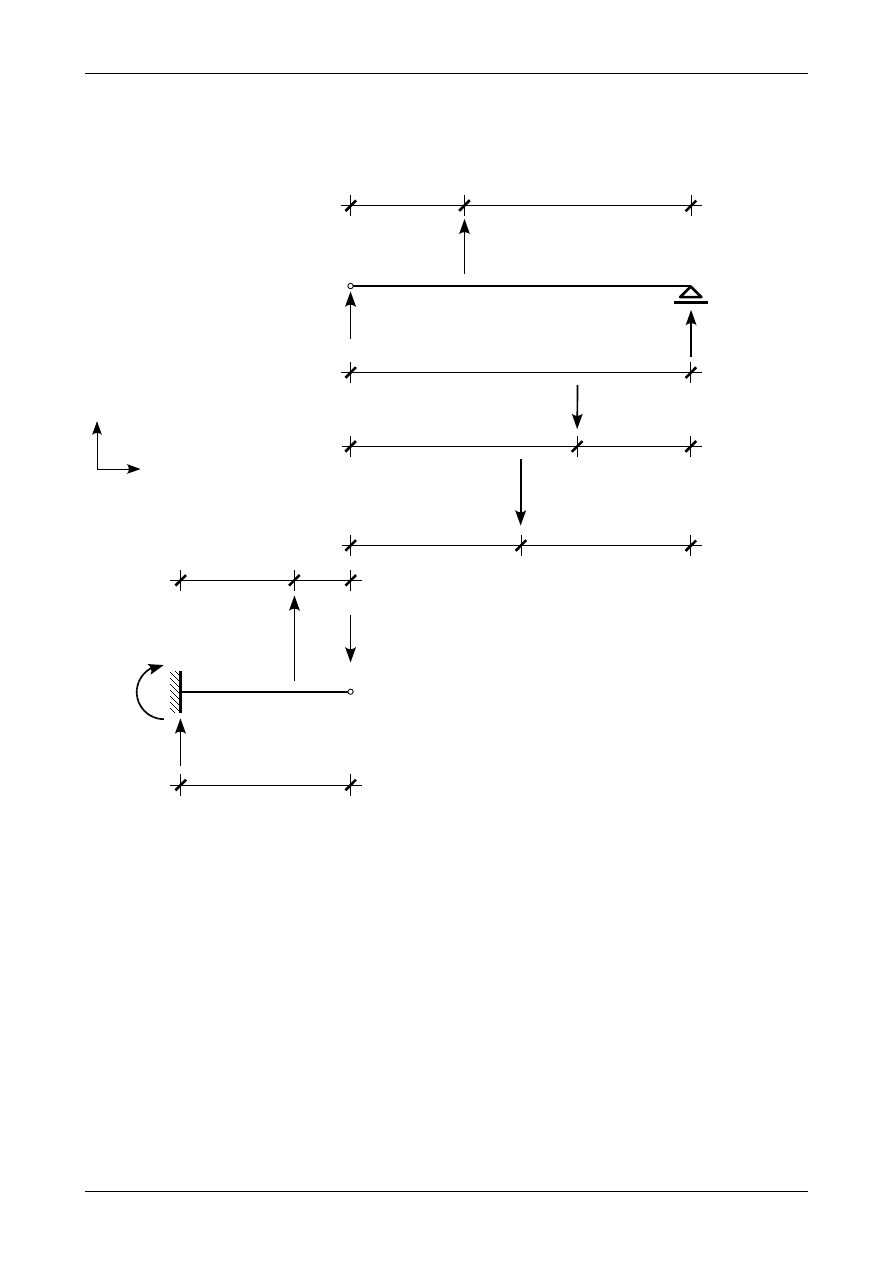
Rysunek Z12/7.17 przedstawia założone zwroty wtórnych reakcji w belce fikcyjnej. Ze względu na

brak obciążeń poziomych poziome reakcje wtórne będą równe zero.

B

C

[m]

4,0

2,0

16

,7

3

2,0

3,

138

18

,8

2

1,333

0,6667

2,667

1,333

A

B

2,0

7,7

42

2,667

1,333

M

A

*

V

A

*

V

B

*

V

B

*

V

C

*

W

*

∙10

-3

[-]

X

Y

Rys. Z12/7.17. Założone zwroty wtórnych reakcji w belce fikcyjnej

Wtórną reakcję V

B

*

wyznaczymy z równania sumy momentów wszystkich sił wtórnych działających

na belkę BC względem punktu C



M

C



BC *

=

V

B

*

⋅

4,018,82⋅10

−

3

⋅

2,667−3,138⋅10

−

3

⋅

1,333−16,73⋅10

−

3

⋅

2,0=0

V

B

*

=−

3,137⋅10

−

3

.

(Z12/7.29)

Reakcja ma zwrot przeciwny do założonego. Wtórną reakcję V

C

*

wyznaczymy z równania sumy momentów

wszystkich sił wtórnych działających na belkę BC względem punktu B



M

B



BC *

=−

V

C

*

⋅

4,0−18,82⋅10

−

3

⋅

1,3333,138⋅10

−

3

⋅

2,66716,73⋅10

−

3

⋅

2,0=0

V

C

*

=

4,185⋅10

−

3

.

(Z12/7.30)

Dr inż. Janusz Dębiński

WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

12

B

C

[m]

4,0

2,0

1,673

2,0

3,138

18,82

1,333

0,6667

2,667

1,333

A

B

2,0

7,742

2,667

1,333

4,185

3,137

3,137

10,88

16,59

W

*

∙10

-3

[-]

R

*

∙10

-3

[-]

M

*

∙10

-3

[m]

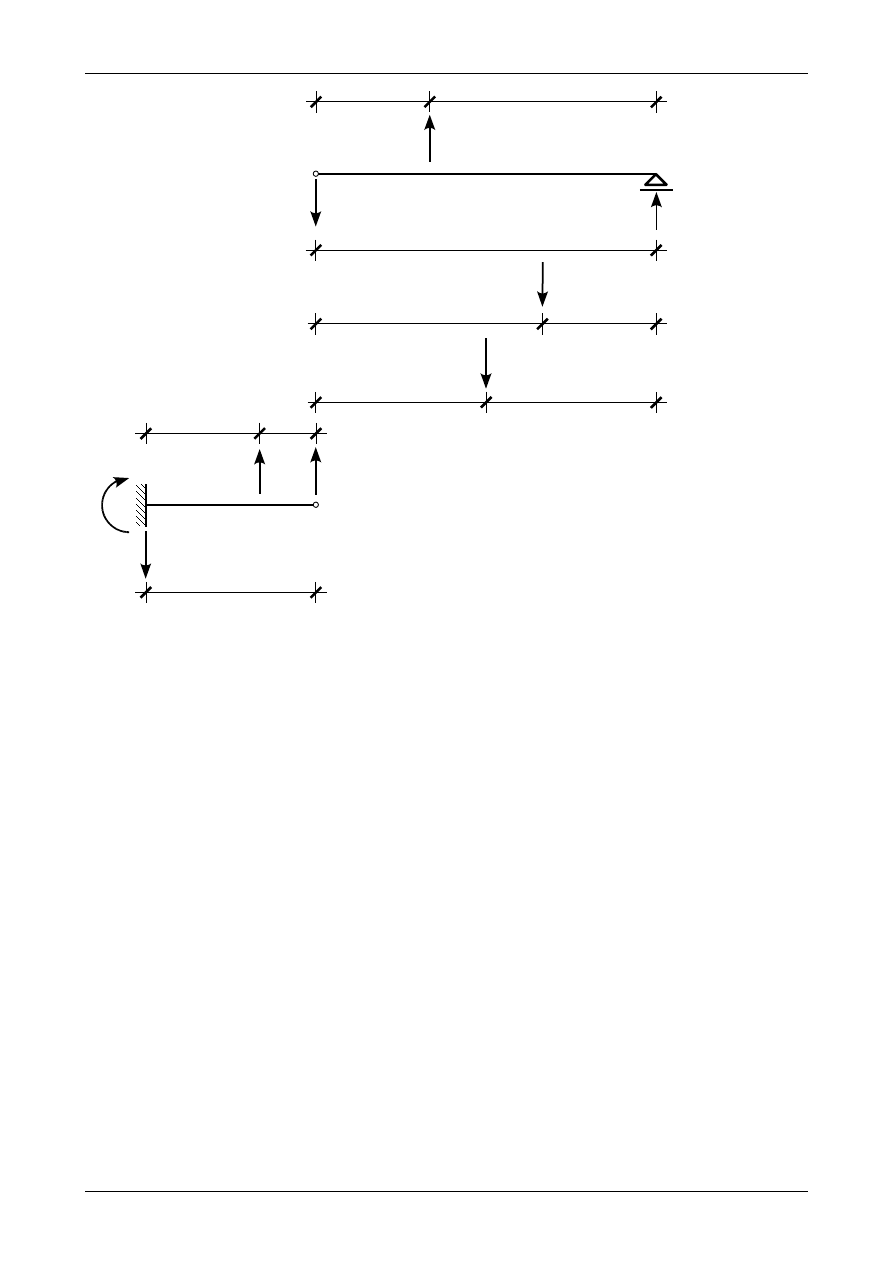
Rys. Z12/7.18. Prawidłowe wartości i zwroty wtórnych reakcji w belce fikcyjnej

Reakcja ma zwrot zgodny z założonym. W celu sprawdzenia obliczeń zastosujemy równanie sumy rzutów
wszystkich sił wtórnych na belkę BC na oś pionową Y



Y



BC *

=

V

B

*



V

C

*



18,82⋅10

−

3

−

3,138⋅10

−

3

−

16,73⋅10

−

3

=

=−

3,137⋅10

−

3



4,185⋅10

−

3



18,82⋅10

−

3

−

3,138⋅10

−

3

−

16,73⋅10

−

3

=

0

.

(Z12/7.31)

Reakcje wtórne działające na belkę BC znajdują się w równowadze. Wtórną reakcję M

A

*

wyznaczymy

z równania sumy momentów wszystkich sił wtórnych działających na belkę AB względem punktu A



M

A



AB *

=

M

A

*



V

B

*

⋅

2,0−7,742⋅10

−

3

⋅

1,333=0

M

A

*

−

3,137⋅10

−

3

⋅

2,0−7,742⋅10

−

3

⋅

1,333=0

M

A

*

=

16,59⋅10

−

3

m

.

(Z12/7.32)

Reakcja ma zwrot zgodny z założonym. Wtórną reakcję V

A

*

wyznaczymy z równania sumy momentów

wszystkich sił wtórnych działających na belkę AB względem punktu B



M

B



AB *

=

V

A

*

⋅

2,0M

A

*



7,742⋅10

−

3

⋅

0,6667=0

V

A

*

⋅

2,016,59⋅10

−

3



7,742⋅10

−

3

⋅

0,6667=0

V

A

*

=−

10,88⋅10

−

3

.

(Z12/7.33)

Dr inż. Janusz Dębiński

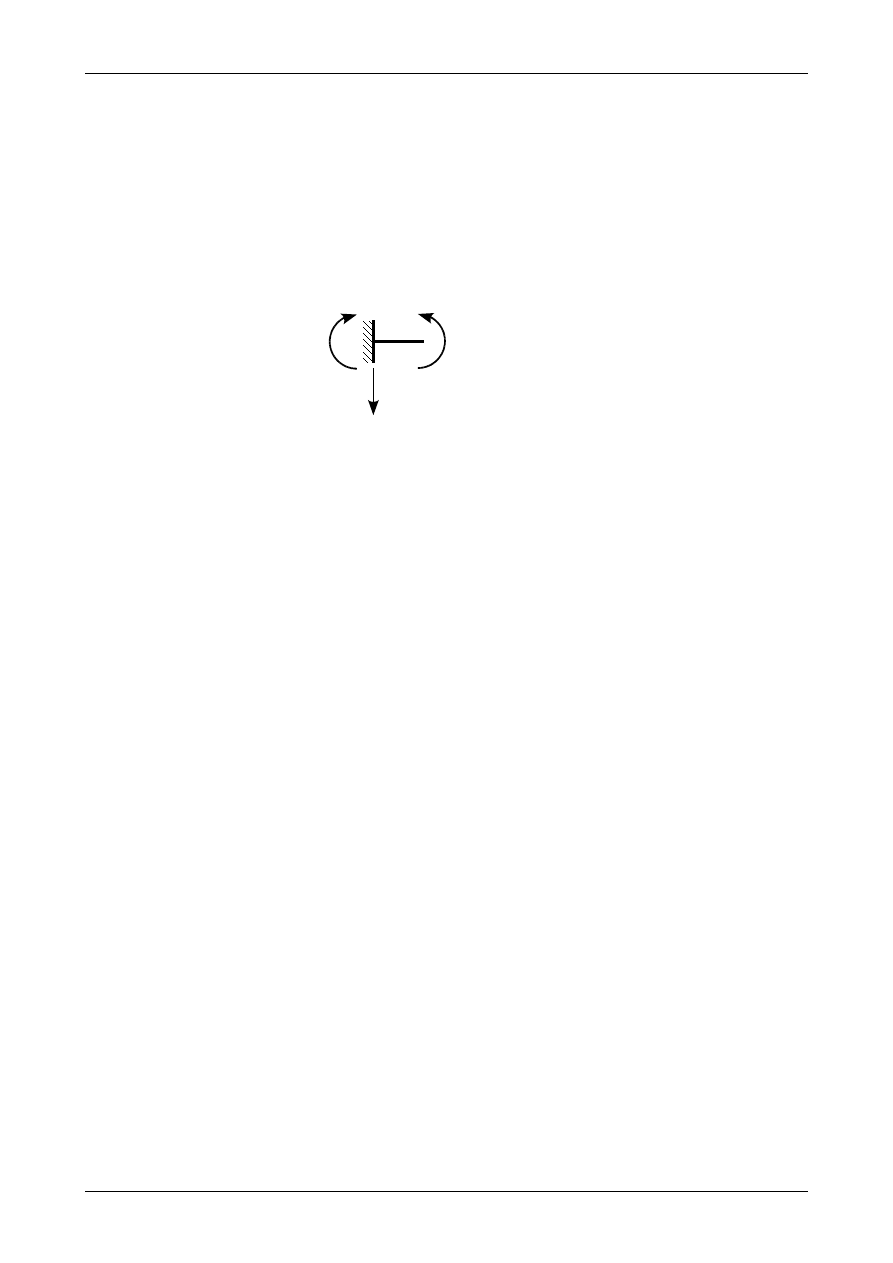
WM

Z12/7. PRZEMIESZCZENIA W BELKACH – ZADANIE 7

13

W celu sprawdzenia obliczeń zastosujemy równanie sumy rzutów wszystkich sił wtórnych na belkę AB na
oś pionową Y



Y



AB *

=

V

A

*

−

V

B

*



7,742⋅10

−

3

=−

10,88⋅10

−

3

−



−

3,137⋅10

−

3





7,742⋅10

−

3

=

0

.

(Z12/7.34)

Rysunek Z12/7.18 przedstawia prawidłowe wartości i zwroty wtórnych reakcji we wszystkich więzach belki
fikcyjnej.

A

10,88

16,59

M

A

*

R

*

∙10

-3

[-]

M

*

∙10

-3

[m]

Rys. Z12/7.19. Równowaga momentów w otoczeniu utwierdzenia A

Rysunek Z12/7.19 przedstawia równowagę w otoczeniu utwierdzenia A. Moment zginający w punkcie

A czyli ugięcie w tym punkcie wynosi

w

A

=

M

A

*

=

16,59⋅10

−

3

m

.

(Z12/7.35)

Ugięcie to jest dodatnie czyli belka przemieści się w punkcie A w dół.

Dr inż. Janusz Dębiński