WM
Z6/1. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 1
1
Z6/1. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 1
Z6/1.1. Zadanie 1
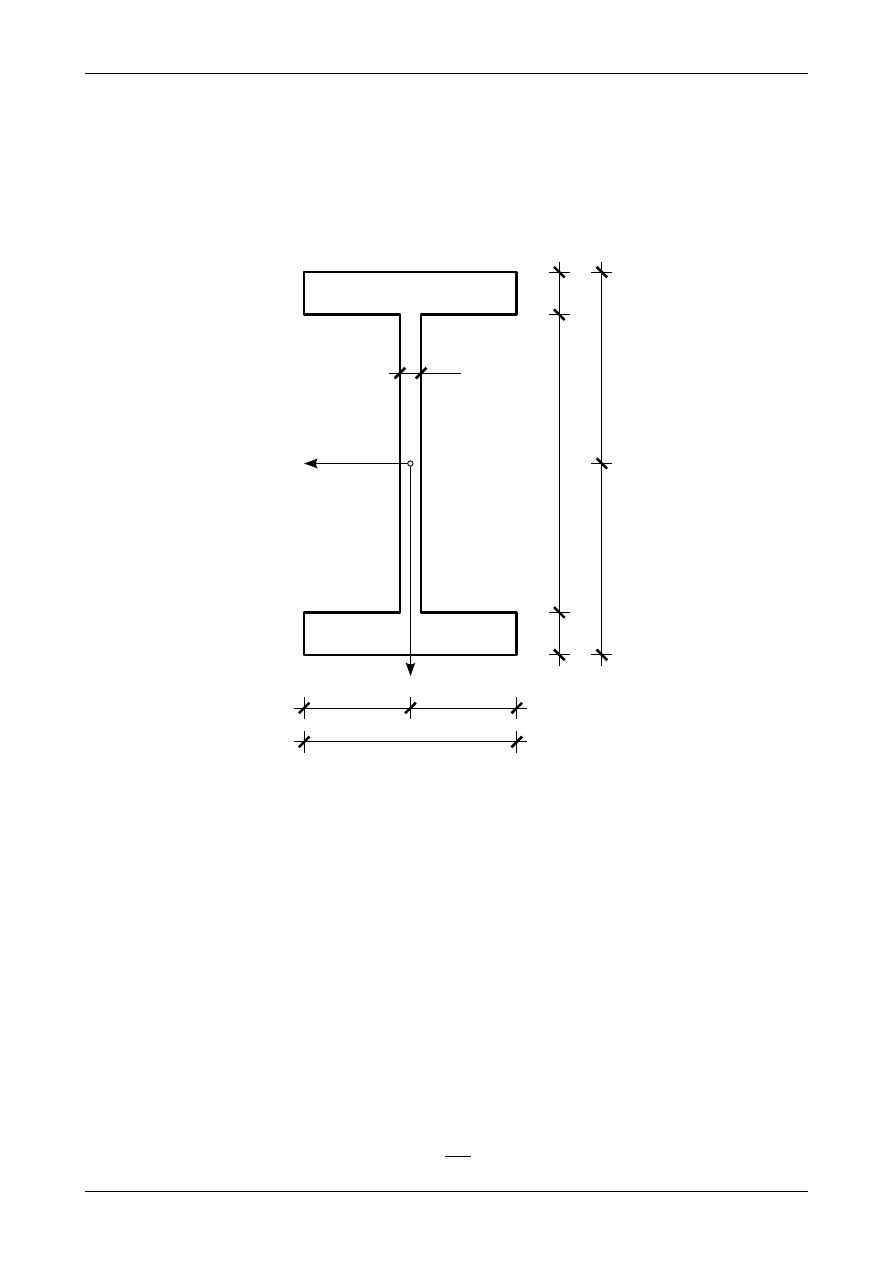
Pręt o przekroju blachownicowym jest to pręt, który jest zbudowany z blach połączonych między sobą
za pomocą spawania. Rysunek Z6/1.1 przedstawia blachownicę o przekroju dwuteowym. Wszystkie
wymiary dwuteownika podane są w centymetrach. Grubości blach użytych na półki są jednakowe. W przek-
roju tym wyznaczymy wartości głównych momentów bezwładności.
4,0
Z
0
=Z
gl
Y
0
=Y
gl
20,0
10,0
10,0
28
,0
4,0
18
,0
18
,0
2,0
[cm]
sc
Rys. Z6/1.1. Blachownica dwuteowa
Z6/1.2. Wyznaczenie środka ciężkości
Ponieważ przekrój dwuteowy posiada dwie osie symetrii środek ciężkości znajduje się w punkcie ich
przecięcia. Rysunek Z6/1.1 przedstawia położenie środka ciężkości.
Z6/1.3. Główne momenty bezwładności
Ponieważ osie środkowe są także osiami symetrii to możemy stwierdzić, że dewiacyjny moment
bezwładności dwuteownika w układzie osi środkowych Y
0
Z
0
wynosi zero. Jeżeli wynosi on zero to układ osi
środkowych Y
0
Z
0
jest także układem osi głównych.
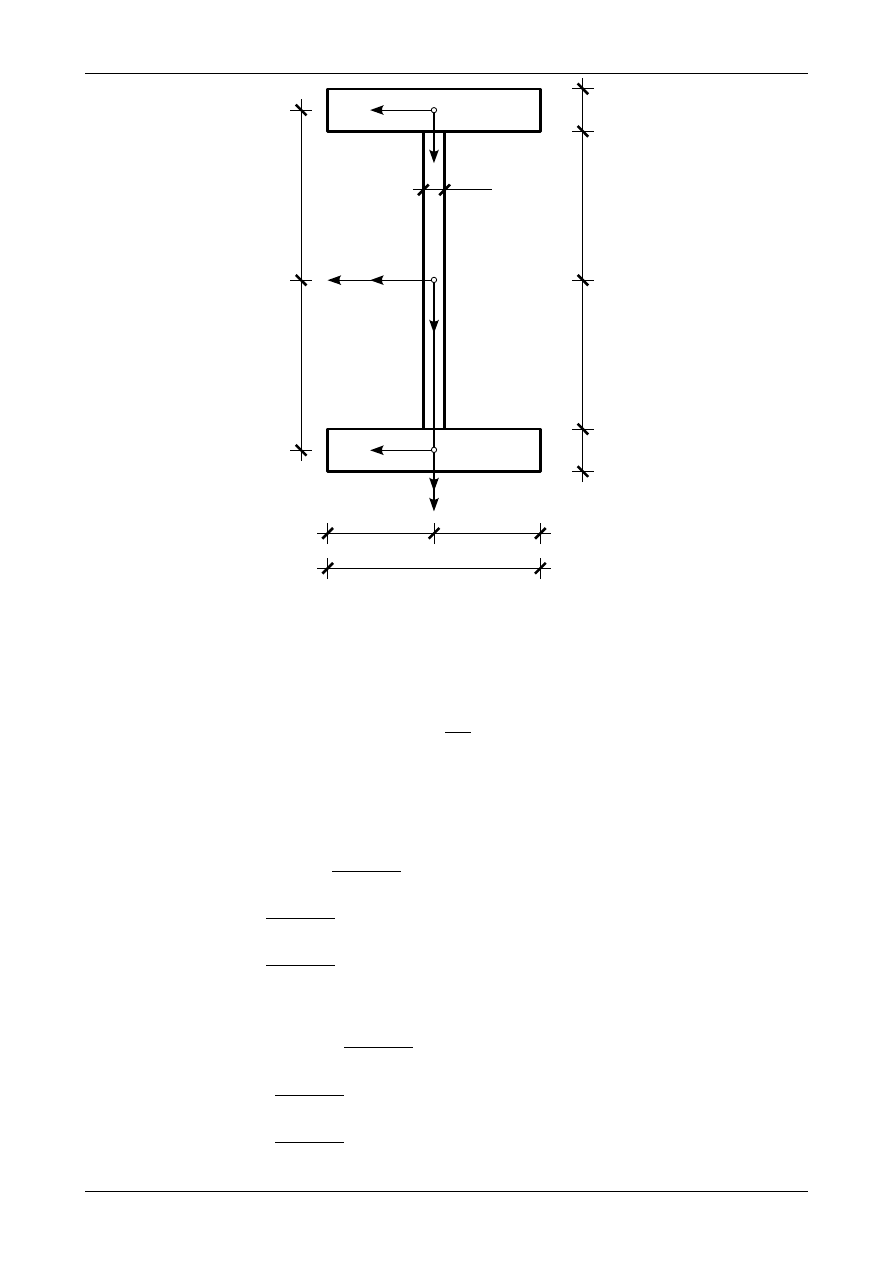
Na rysunku Z6/1.2 przedstawiono najbardziej naturalny podział przekroju dwuteowego na trzy
prostokąty: półkę górną i dolną o wymiarach 20,0 cm na 4,0 cm oraz środnik o wymiarach 28,0 cm na 2,0
cm. Środki ciężkości figur numer 1, 2 i 3 posiadają współrzędne
y
01
=
0,0 cm z
01
=−
14,0
4,0
2
=−
16,0 cm
,
(Z6/1.1)
Dr inż. Janusz Dębiński
WM
Z6/1. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 1
2
10,0
10,0
20,0
4,
0
14
,0
4,
0
14
,0
16
,0
16
,0
Z
0
=Z
gl
Y
0
=Y
gl
Z
01
Y
01
Z
02
Y
02
Z
03
Y
03
sc
3
[cm]
2,0
sc
1
sc=sc
2
Rys. Z6/1.2. Podział dwuteownika na figury składowe
y
02
=
0,0 cm z
02
=
0,0 cm
,
(Z6/1.2)
y
03
=
0,0 cm z
03
=
14,0
4,0
2
=
16,0 cm
.
(Z6/1.3)
Zgodnie ze wzorami (6.31), (6.32) momenty bezwładności względem osi Y
gl
i Z
gl
wynoszą
J
Y0
=
J
Ygl
=
20,0⋅4,0
3
12
−
16,0
2
⋅
20,0⋅4,0
2,0⋅28,0
3
12
0,0
2
⋅
28,0⋅2,0
20,0⋅4,0
3
12
16,0
2
⋅
20,0⋅4,0=44830 cm
4
.
(Z6/1.4)
J
Z0
=
J
Zgl
=
4,0⋅20,0
3
12
0,0
2
⋅
20,0⋅4,0
28,0⋅2,0
3
12
0,0
2
⋅
28,0⋅2,0
4,0⋅20,0
3
12
0,0
2
⋅
20,0⋅4,0=5352 cm
4
.
(Z6/1.5)
Dr inż. Janusz Dębiński
WM
Z6/1. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 1
3
Ponieważ moment bezwładności względem osi Y
0
=Y
gl
jest bardzo często wykorzystywanym momen-
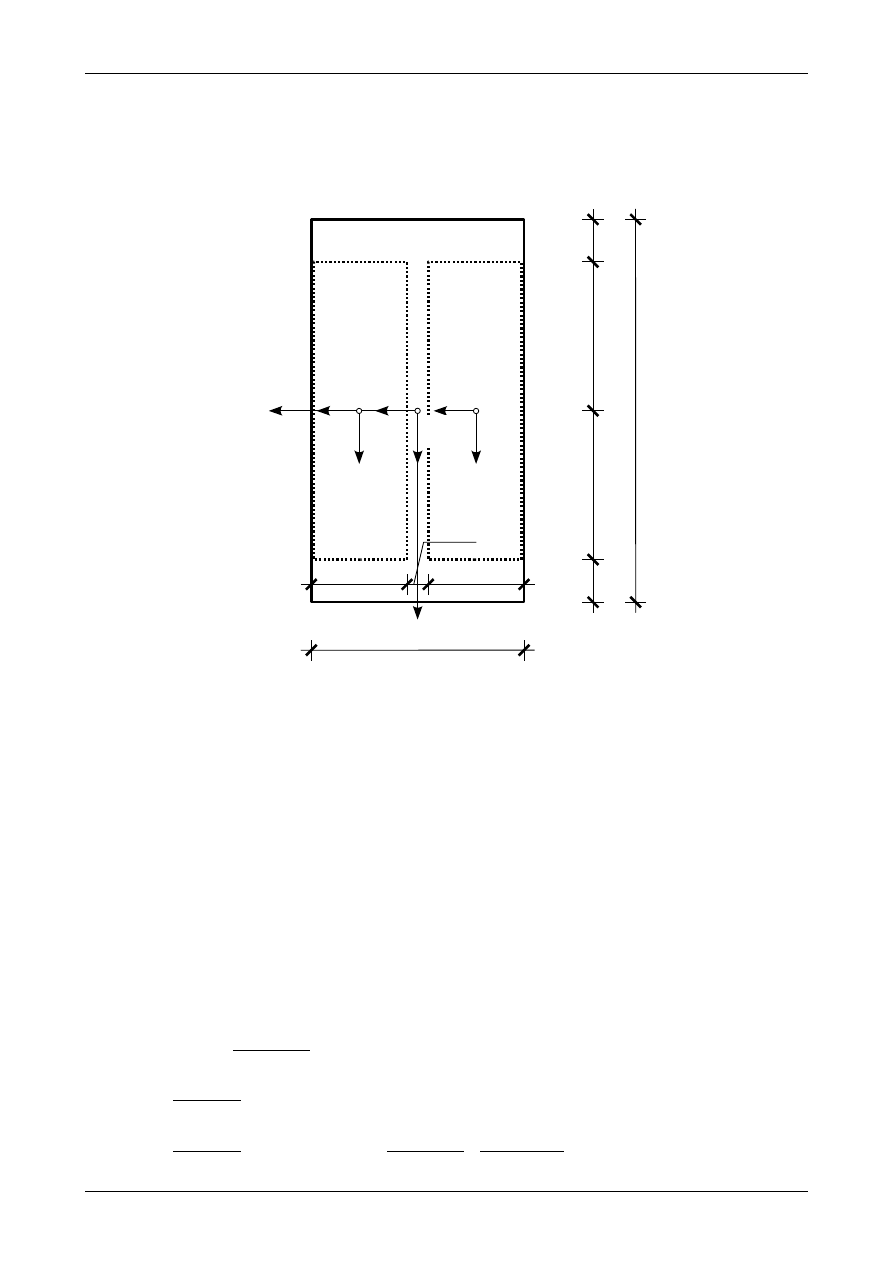
tem bezwładności należałoby poszukać szybszej drogi jego obliczenia. Na rysunku Z6/1.3 przedstawiony
został podział dwuteownika w celu wyznaczenia momentu bezwładności względem osi Y
0
=Y
gl
. Jak widać
składa się on z dużego prostokąta o wymiarach 20,0 cm na 36,0 cm oraz odjętych dwóch prostokątów
o wymiarach 9,0 cm na 28,0 cm.
4,0
14
,0
4,0
14
,0
36
,0
20,0
Z
0
=Z
gl
Y
0
=Y
gl
Z
01
Y
01
Z
02
Y
02
Y
03
Z
03
[cm]
9,0
9,0
2,0
sc
2
sc=sc
1
sc
3
Rys. Z6/1.3. Podział dwuteownika na figury składowe
Środki ciężkości figur numer 1, 2 i 3 posiadają współrzędną z
równą
z
01
=
0,0 cm
,
(Z6/1.6)
z
02
=
0,0 cm
,
(Z6/1.7)
z
03
=
0,0 cm
.
(Z6/1.8)
Zgodnie ze wzorem (6.31) moment bezwładności względem osi Y
0
=Y
gl
wynosi
J
Y0
=
J
Ygl
=
20,0⋅36,0
3
12
0,0
2
⋅
20,0⋅36,0
−
9,0⋅28,0
3
12
0,0
2
⋅
9,0⋅28,0
−
9,0⋅28,0
3
12
0,0
2
⋅
9,0⋅28,0
=
20,0⋅36,0
3
12
−
2⋅9,0⋅28,0
3
12
=
44830 cm
4
.
(Z6/1.9)
Dr inż. Janusz Dębiński
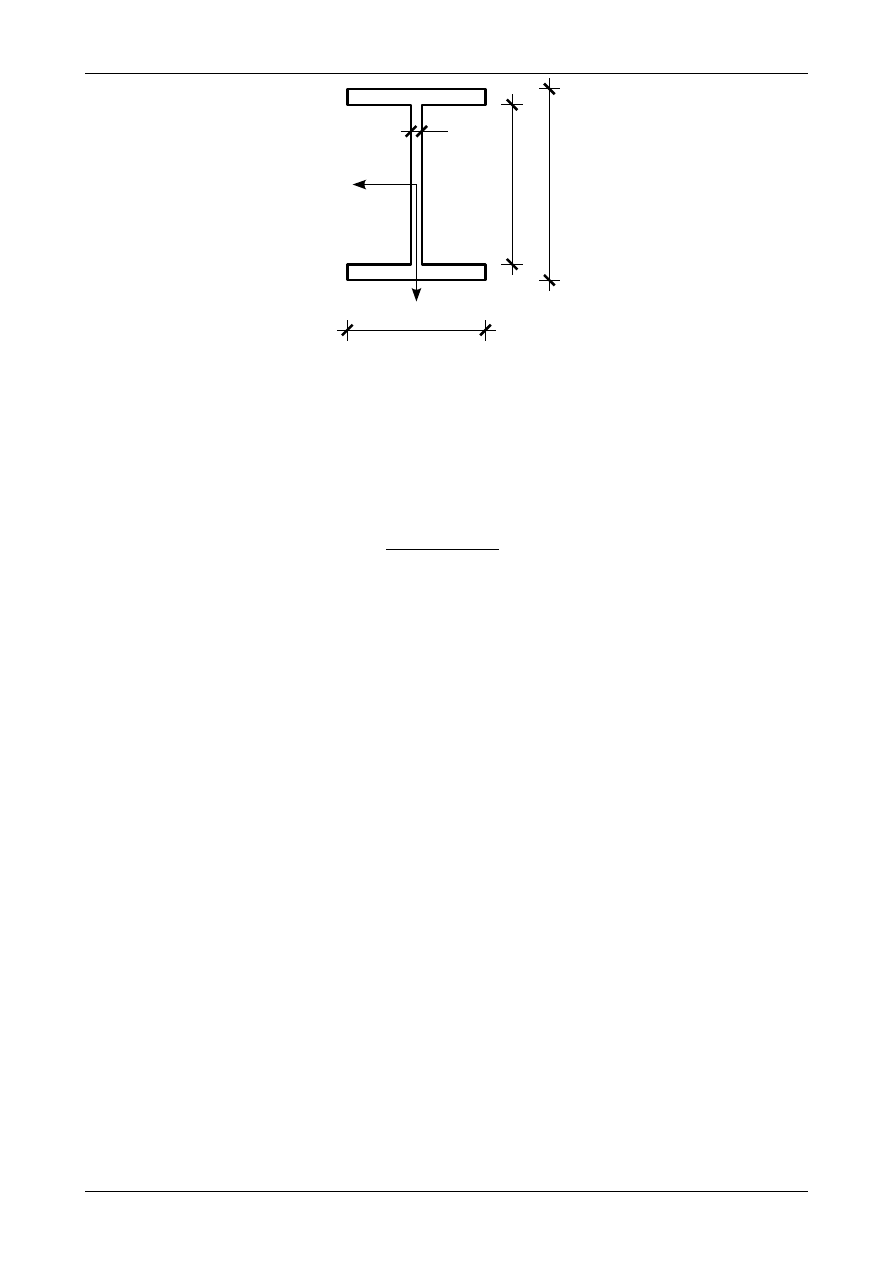
WM
Z6/1. CHARAKTERYSTYKI GEOMETRYCZNE PRZEKROJU – ZADANIE 1
4
Z
0
=Z
gl
Y
0
=Y
gl
s
g
h
h
S
Rys. Z6/1.4. Ogólne wymiary dowolnego dwuteownika
Moment bezwładności względem osi Z
0
=Z
gl
najwygodniej jest liczyć przy podziale dwuteownika
według rysunku Z6/1.2 i wzoru (6.32) natomiast moment bezwładności względem osi Y
0
=Y
gl
najwygodniej
jest liczyć przy podziale dwuteownika według rysunku Z6/1.3 i wzoru (6.31). Rysunek Z6/1.4 przedstawia
dwuteownik. Moment bezwładności dwuteownika względem osi Y
0
=Y
gl
ogólnie wynosi
J
Y0
=
J
Ygl
=
s⋅h
3
−
s− g
⋅
h
s
3
12
.
(Z6/1.10)
Dr inż. Janusz Dębiński