
Janusz Kacerka
Dyskretne Układy
Regulacji
————————————————————————————————————————
Semestr 5 Elektrotechnika
Rozdział 5

Rozdział 5
5.Stabilność układów dyskretnych
Pierwiastki równania charakterystycznego transmitancji układu dyskretnego (4.21)
decydują o przebiegu odpowiedzi dyskretnej tego układu w czasie. Stabilność układu, to
znaczy zdolność układu do powrotu do stanu równowagi, rozważa się bez sygnału
wejściowego, czyli dla układu autonomicznego przy niezerowych warunkach
początkowych.
5.1 Matematyczne warunki stabilności układów dyskretnych
Równanie różnicowe (4.18) układu dla sygnału wejściowego u(n)=0 ma postać
0
)
(
)
1
(
...
)
1
(
)
(
0
1
1
=
+
+
+
+
−
+
+
+
−
n
y
a
n
y
a
k
n
y
a
k
n
y
a
k
k
(5.1)
3
Dyskretne Układy Regulacji
Przekształcenie Z równania, po zastosowaniu wzoru na transformatę funkcji
przesuniętej (4.4)

Rozdział 5
(
)
[
]
( )
( )
∑
−
=
−
−
=
+
1
0
k
i
i
k
k
z
i
f
z
F
z
k
n
f
Z
przy niezerowych warunkach początkowych, ma postać
( )
[
]
( )
0
...
0
0
1
1
=
−
+
+
+
−
−
z
W
a
z
a
z
a
z
F
k
k
k
k
(5.2)
Transformata odpowiedzi na warunki początkowe jest określona wzorem
( )
( )
( )
( )
z
M
z
W
a
z
a
z
a
z
W
z
F
k
k
k
k
0
0
1
1
0
...
=
+
+
+
=
−
−
(5.3)
Pierwiastki równania M(z)=0 mogą być rzeczywiste lub zespolone sprzężone.
Składniki odpowiedzi f(n) mają postać
( )
( )
0
Im
=
=
i
n
i
i
i
z
z
C
n
f
(5.4)
4
Dyskretne Układy Regulacji
lub

Rozdział 5
( )
( )
( )
(
)
θ
±
θ
−
θ
+
θ
−
+
θ
+
=
+
=
+
=
j
n
j
n
j
n
n
j
i
n
j
i
i
re
z
dla
e
e
Cr
re
C
re
C
n
f
1
(5.5)
W zależności od położenia pierwiastków na płaszczyźnie zmiennej zespolonej,
przebiegi składników odpowiedzi mogą zanikać w funkcji czasu aperiodycznie,
oscylacyjnie lub przeciwnie, narastać do nieskończoności.
Przykład 5.1
Dane jest równanie różnicowe (5.6). Należy wyznaczyć przebieg rozwiązania przy
danym warunku początkowym bez wymuszenia.
(
)
( )
( )
k
bu
k
ax
k
x
+
=
+1
(5.6)
Rozwiązanie.
( )
( )
( )
k
bu
a
x
a
k
x
k
i
i
k
k
∑
=
−
−
+
=
0
1
0
(5.7)
5
Dyskretne Układy Regulacji
Zakładając, że nie ma wymuszenia otrzymuje się
Rozdział 5
( )
( )
0
x
a
k
x
k
=
(5.8)
Przekształcenie Z równania (5.6), przy wykorzystaniu wzoru na transformatę Z funkcji
przesuniętej (4.4), jest określone wzorem
( )
( )
( )
( )
z
bU
z
aX
zx
z
zX
+
=
−
0
(5.9)
skąd
( )
( )
( )
z
U
a
z
b
x
a
z
z
z
X
−
+
−
=
0
(5.10)
Biegun transformaty X(z) z
i
=z
1
=a, zatem
( ) ( ) ( )
( )
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
−
−
a
z
z
bU
Z
x
a
a
k
x
k
1
1
0
(5.11)
dla u(k)=0
6
Dyskretne Układy Regulacji
( ) ( ) ( )
[
]
( )
0
,...
,
,
,
1
0
3
2
x
a
a
a
x
a
k
x
k
=
=
(5.12)

Rozdział 5
Z postaci rozwiązania wynika, że przebieg odpowiedzi w funkcji czasu zanika, jeżeli
|a|<1.
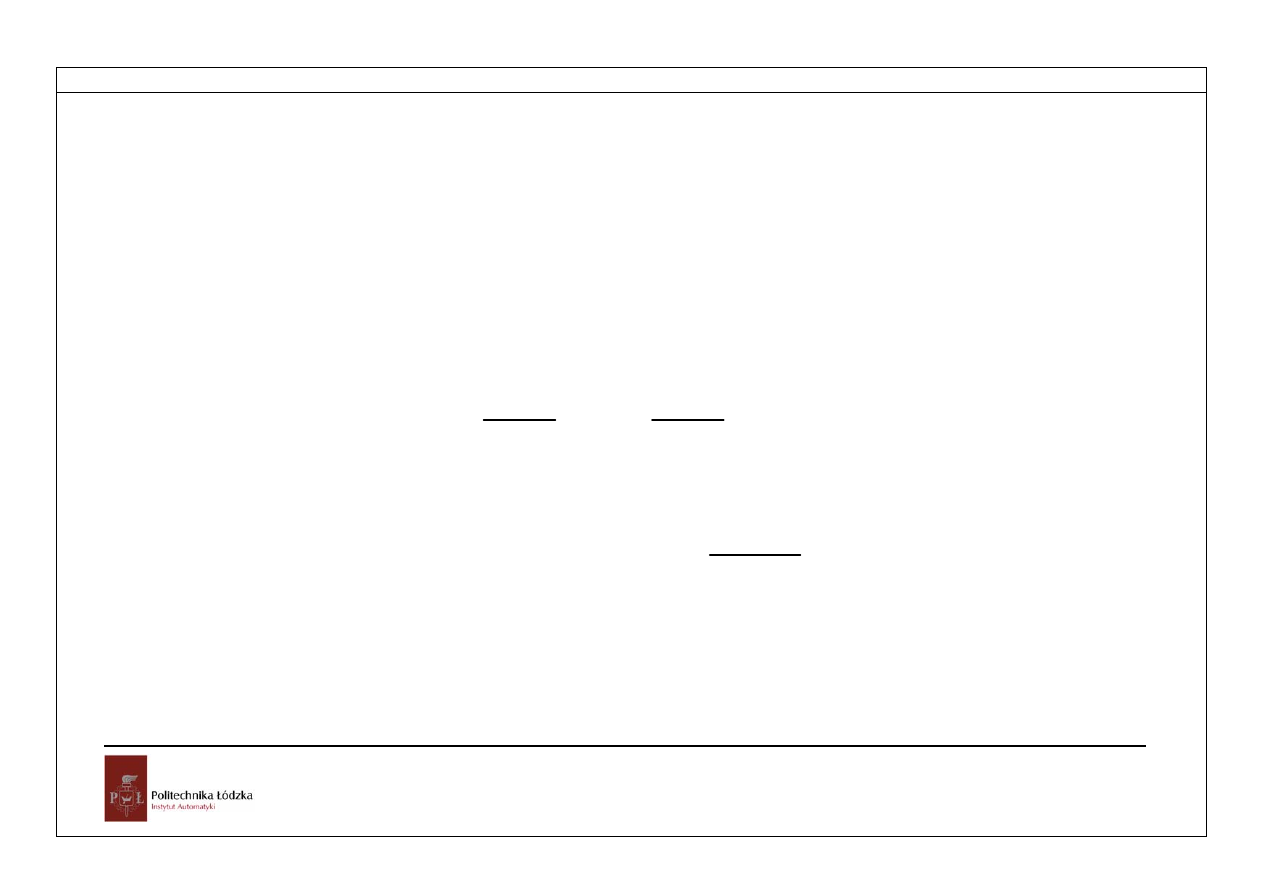
Przykładowy przebieg wyznaczony za pomocą Matlaba dla 1>a>0
figure(1)
%x(0)=1;
a=0.5;
k=[0 1 2 3 5 6 7 8];
y=a.^k;
7
Dyskretne Układy Regulacji
stairs(y),xlabel(
'Próbki czasu k'
),ylabel(
'Wartości y(k)'
),grid

Rozdział 5
1
2
3
4
5
6
7
8
9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Próbki czasu k
Wa
rt
o
ś
ci
y(
k
)
Rys.5.1. Przebieg odpowiedzi układu dla a=0.5
Przykład odpowiedzi dla a<0.
a=-0.5;
y=a.^k;
%y=[1 a a^2 a^3 a^4 a^5 a^6 a^7 a^8];
stairs(y),xlabel(
'Próbki czasu k'
),ylabel(
'Wartości y(k)'
),grid
8
Dyskretne Układy Regulacji

Rozdział 5
1
2
3
4
5
6
7
8
9
-0.5
0
0.5
1
Próbki czasu k
Wa
rt
o
ś
ci
y(
k
)
Rys.5.2. Przebieg odpowiedzi układu dla a=-0.5
Przykład odpowiedzi dla pierwiastków zespolonych sprzężonych
r=0.8;
teta=pi/6;
%teta=pi;
fi=0;
k=0:20;
9
Dyskretne Układy Regulacji
y=r.^k.*cos(k*teta+fi);

Rozdział 5
%stairs(k,y),xlabel(
'Próbki czasu k'
),ylabel(
'Wartości y(k)'
),grid
stem(k,y),xlabel(
'Próbki czasu k'
),ylabel(
'Wartości y(k)'
),grid
Pierwiastki w programie mają postać
;
6
/
;
8
.
0
π
=
=
θ
=
=
θ
±
teta
r
re
z
j
(5.13)
10
Dyskretne Układy Regulacji
Rozdział 5
0
2
4
6
8
10
12
14
16
18
20
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Próbki czasu k
W
ar
to
œ
ci
y(
k)
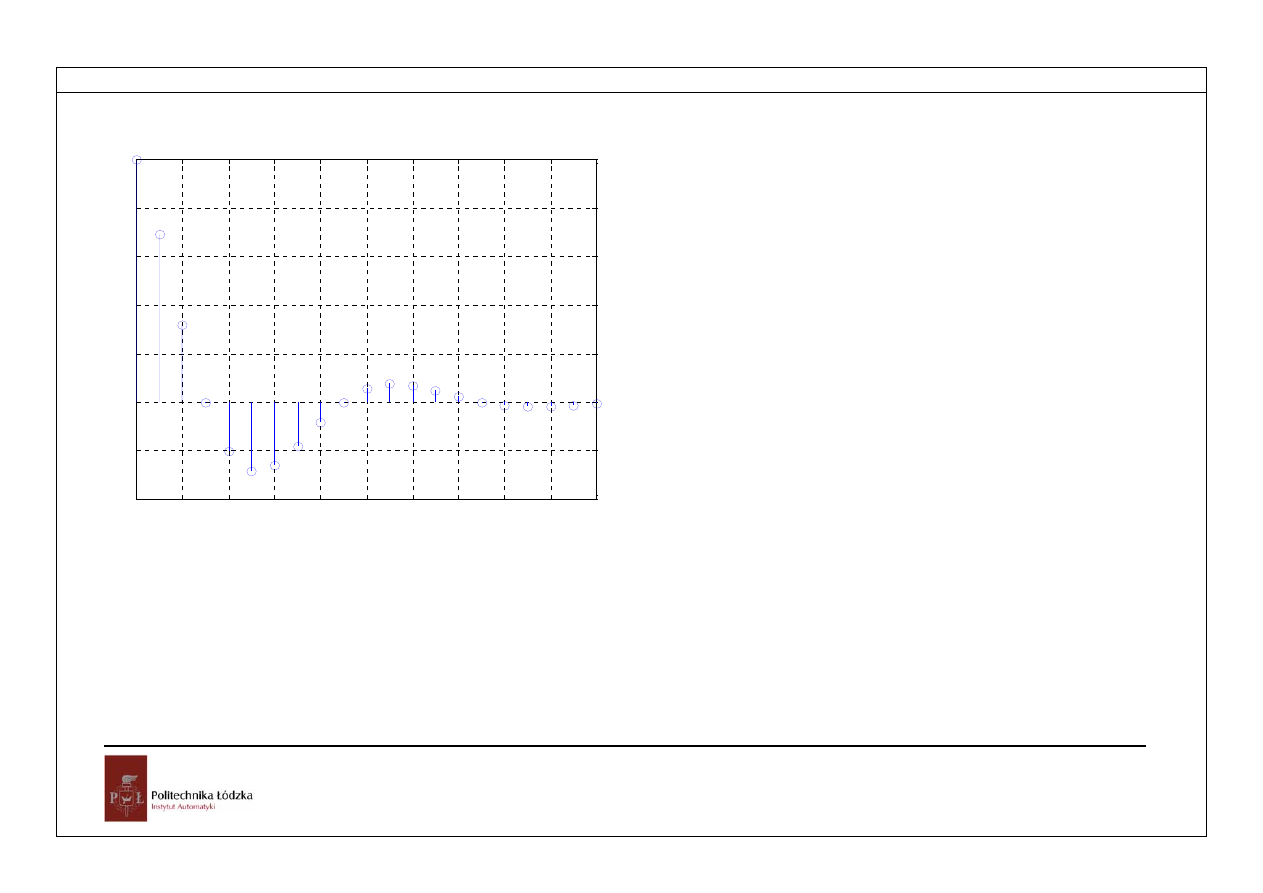
Rys.5.3.Odpowiedź układu dla pierwiastków zespolonych sprzężonych, |z|<1
Dla przypadku |z|>1 przyjęto dane liczbowe
11
Dyskretne Układy Regulacji
r=1.1;

Rozdział 5
teta=pi/6;
fi=0;
k=0:20;
y=r.^k.*cos(k*teta+fi);
stem(k,y),xlabel(
'Próbki czasu k'
),ylabel(
'Wartości y(k)'
),grid
Pierwiastki w programie mają postać
1
;
6
/
;
1
.
1
>
=
=
π
=
=
θ
=
=
θ
±
θ
±
r
re
z
teta
r
re
z
j
j
(5.14)
12
Dyskretne Układy Regulacji
Rozdział 5
0
2
4
6
8
10
12
14
16
18
20
-6
-5
-4
-3
-2
-1
0
1
2
3
4
Próbki czasu k
W
ar
to
œ
ci
y(
k)
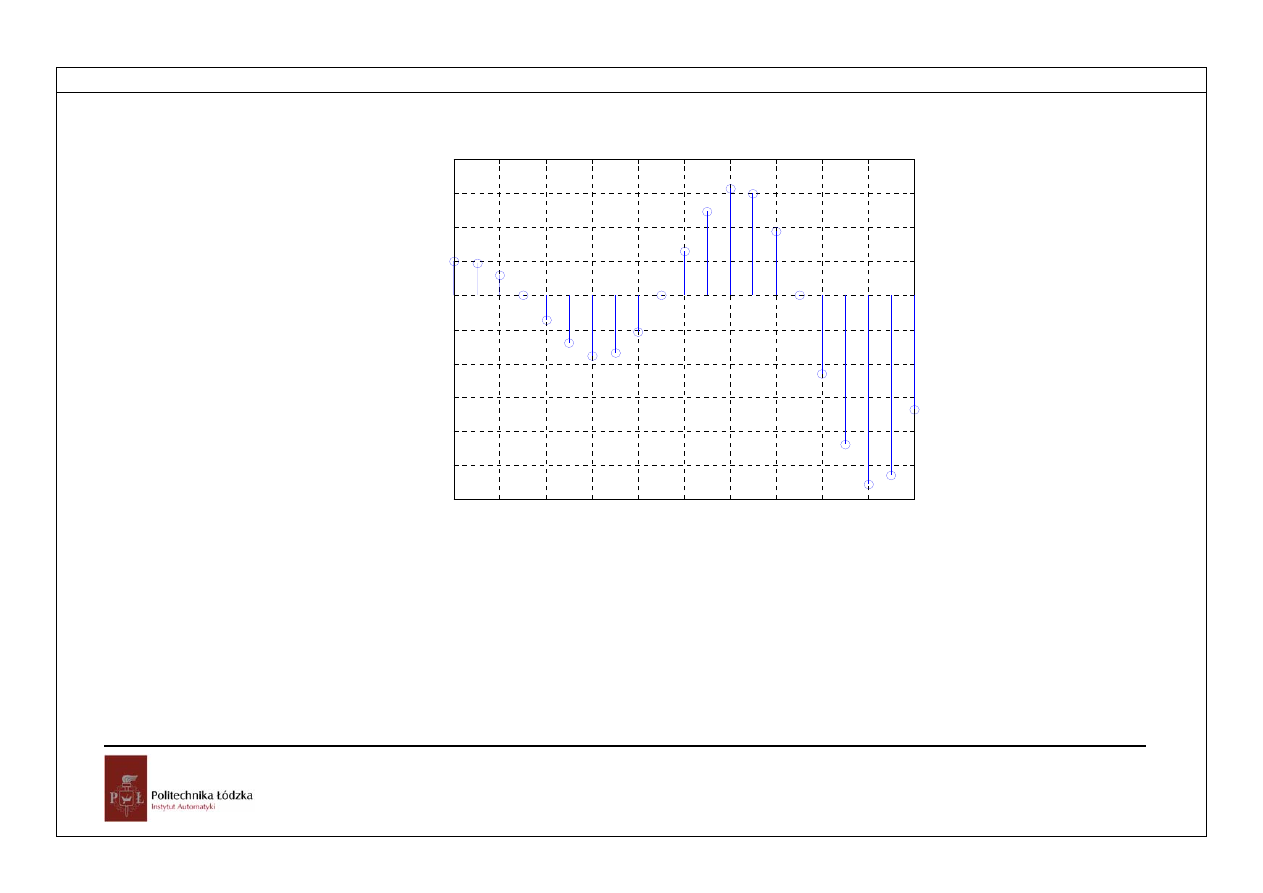
Rys.5.3.Odpowiedź układu dla pierwiastków zespolonych sprzężonych, |z|>1
13
Dyskretne Układy Regulacji
Odpowiedź dla pierwiastka a=1;

Rozdział 5
1
2
3
4
5
6
7
8
9
10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Rys.5.4 Odpowiedź dla pierwiastka z=a=1
14
Dyskretne Układy Regulacji
Odpowiedź dla pierwiastka a=-1;

Rozdział 5
1
2
3
4
5
6
7
8
9
10
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Rys.5.5. Odpowiedź układu dla pierwiastka z=a=-1
15
Dyskretne Układy Regulacji
Przedstawione przebiegi świadczą o tym, że przebiegi zanikają wówczas, gdy spełniony
jest warunek

Rozdział 5
1
<
z
(5.15)
Warunek oznacza, że pierwiastki równania charakterystycznego układu stabilnego
powinny leżeć wewnątrz koła o promieniu jednostkowym na płaszczyźnie zmiennej
zespolonej z.
5.2 Kryterium stabilności Hurwitza
Z matematycznego warunku stabilności (5.15) wynika, że do sprawdzenia stabilności
należy znać położenie pierwiastków równania charakterystycznego. Wymóg ten jest
trudny do spełnienia w przypadku wielomianów wyższych stopni. Równania stopnia 5 i
wyższych w ogólnej postaci nie mogą być rozwiązane za pomocą pierwiastków. Z tego
powodu korzysta się z kryteriów stabilności, które pozwalają ocenić stabilność układu.
16
Dyskretne Układy Regulacji
Kryteria stabilności znane z teorii układów liniowych ciągłych mogą mieć zastosowanie
w przypadku układów dyskretnych po przekształceniu

Rozdział 5
1
1
−
+
=
w
w
z
(5.16)
Przekształcenie to odwzorowuje wnętrze koła o promieniu jednostkowym na
płaszczyźnie zespolonej z na lewą półpłaszczyznę płaszczyzny zmiennej zespolonej w.
Współczynniki wielomianu otrzymanego po przekształceniu biliniowym (5.16)
wykorzystuje się w standardowych kryteriach Hurwitza lub Routha. Przeszkodą w
stosowaniu takiego sposobu jest konieczność dokonania przekształcenia równania
wyjściowego, co może okazać się pracochłonne w przypadku układów wyższych rzędów.
Przykład 5.2
Zbadać stabilność układu, którego równanie charakterystyczne ma postać
0
0
1
2
=
+
+
a
z
a
z
(5.17)
17
Dyskretne Układy Regulacji
Przekształcenie biliniowe (5.16) prowadzi do równania

Rozdział 5
(
)
(
)(
)
(
)
(
)
(
)
0
1
1
2
1
0
2
1
2
0
1
1
1
1
0
1
1
1
1
1
0
0
2
0
1
0
0
2
0
1
2
1
2
2
0
1
2
0
1
2
=
−
+
+
−
+
+
+
→
→
=
+
−
+
−
+
+
+
→
=
−
+
−
+
+
+
→
=
+
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
a
a
w
a
w
a
a
a
wa
w
a
a
w
a
w
w
w
a
w
w
a
w
a
w
w
a
w
w
(5.18)
Z kryterium Hurwitza dla układów ciągłych wynikają warunki stabilności
(
)
(
)
0
1
0
1
2
0
1
1
0
0
0
1
>
−
+
>
−
>
+
+
a
a
a
a
a
(5.19)
18
Dyskretne Układy Regulacji
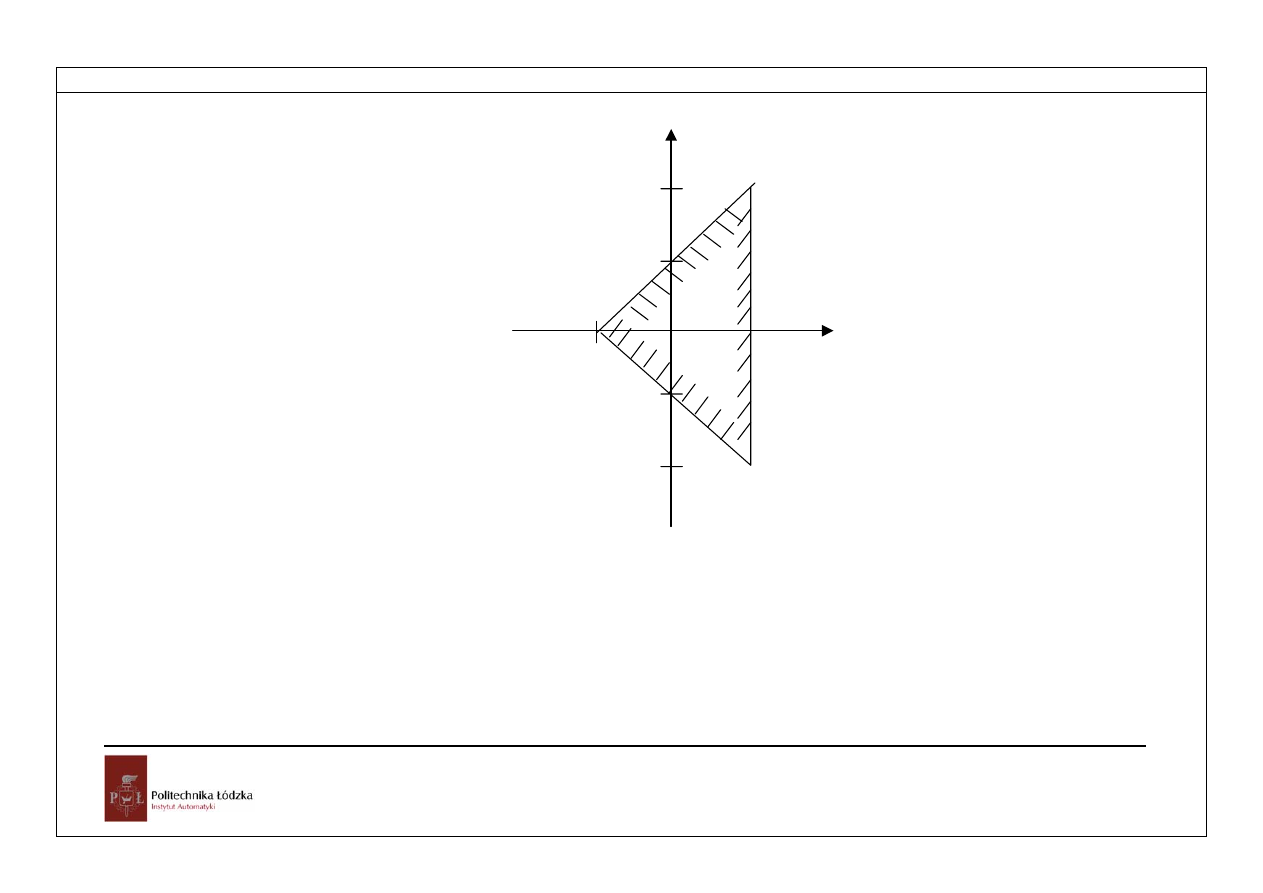
Przy projektowaniu układów regulacji wygodnie jest przedstawić powyższy warunek
na płaszczyźnie we współrzędnych (a
0
,a
1
) [6],[7].
Rozdział 5
1
-1
-1
1
2
-2
a
0
a
1
Rys.5.6. Obszar stabilności układu drugiego rzędu
5.3 Kryterium częstotliwościowe Nyquista
19
Dyskretne Układy Regulacji
Kryterium Nyquista, podobnie jak w układach ciągłych, polega na badaniu przebiegu

Rozdział 5
charakterystyki amplitudowo-fazowej. Równanie okręgu jednostkowego na płaszczyźnie
zmiennej zespolonej Z można przedstawić w postaci
s
T
j
e
z
ω
=
(5.20)
Aby narysować okrąg jednostkowy wystarczy zmieniać argument z w granicach
π
<
ω
<
π
−
π
<
ω
<
s
s
T
T
lub
2
0
(5.21)
Mianownik transmitancji dyskretnej można przedstawić w postaci iloczynu dwumianów
( )
(
)
∏
=
−
=
k
i
i
k
z
z
a
z
M
1
(5.22)
gdzie z
i
– pierwiastki równania charakterystycznego rzędu k.
20
Dyskretne Układy Regulacji
Zmiana argumentu
ωT
s
w podanych granicach (5.21) powoduje zmianę argumentu
M(j
ωT
s
) w granicach określonych przez położenie pierwiastków z
i
względem okręgu

Rozdział 5
jednostkowego. Jeżeli pierwiastki są położone wewnątrz okręgu jednostkowego, to
zmiana argumentu jest określona wzorem
( )
[
]
(
)
∏
∑
=
=
ω
π
≤
ω
≤
π
−
=
π
≤
ω
≤
π
−
π
=
π
=
−
Δ
=
Δ
ω
k
i
k
i
i
T
j
k
T
e
z
T
k
i
z
e
a
z
M
s
s
s
T
j
s
1
1
2
2
arg
arg
(5.23)
Jeżeli są pierwiastki położone zewnątrz okręgu, to przyrost argumentu dwumianu dla
każdego z tych pierwiastków przy podanych zmianach
ωT
s
jest równy zeru i dla m takich
pierwiastków wzór (5.23) przyjmie postać
( )
[
]
(
)
(
)
∏
=
ω
π
≤
ω
≤
π
−
=
π
≤
ω
≤
π
−
−
π
=
−
Δ
=
Δ
ω
k
i
i
T
j
k
T
e
z
T
m
k
z
e
a
z
M
s
s
s
T
j
s
1
2
arg
arg
(5.24)
W określonych przypadkach (porównaj uwagi o transmitancjach układów zamkniętych)
transmitancję dyskretną układu ze sprzężeniem zwrotnym można przedstawić w postaci
21
Dyskretne Układy Regulacji
( )
( )
( )
( )
( )
( )
z
M
z
L
z
G
gdzie
z
G
z
G
z
G
o
o
o
o
o
=
+
=
,
1
(5.25)

Rozdział 5
Wielomian charakterystyczny układu otwartego oznaczono M
o
(z) a licznik
transmitancji układu otwartego L
o
(z). Z postaci transmitancji układu zamkniętego wynika,
że wielomian charakterystyczny układu zamkniętego ma postać M(z)= L
o
(z)+ M
o
(z). W
kryterium Nyquista bada się przyrost argumentu wyrażenia 1+G
o
(z). Dla układu otwartego
stabilnego i układu stabilnego po zamknięciu otrzymuje się:
( )
[
]
( )
( )
( )
( )
( )
( )
0
2
2
arg
arg
arg
1
arg
1
arg
=
π
−
π
=
Δ
−
Δ
=
=
Δ
=
⎥
⎦
⎤
⎢
⎣
⎡
+
Δ
=
+
Δ
ω
π
≤
ω
≤
π
−
ω
π
≤
ω
≤
π
−
ω
ω
π
≤
ω
≤
π
−
ω
ω
π
≤
ω
≤
π
−
ω
π
≤
ω
≤
π
−
k
k
e
M
e
M
e
M
e
M
e
M
e
L
e
G
s
s
s
s
s
s
s
s
s
s
s
s
T
j
o
T
T
j
T
T
j
o
T
j
T
T
j
o
T
j
o
T
T
j
o
T
(5.26)
22
Dyskretne Układy Regulacji
Dla układu otwartego niestabilnego (m pierwiastków poza okręgiem jednostkowym)
otrzymuje się dla układu stabilnego w stanie zamkniętym

Rozdział 5
( )
( )
( )
( )
( )
( )
(
)
π
=
π
−
−
π
=
Δ
−
Δ
=
=
Δ
=
⎥
⎦
⎤
⎢
⎣
⎡
+
Δ
ω
π
≤
ω
≤
π
−
ω
π
≤
ω
≤
π
−
ω
ω
π
≤
ω
≤
π
−
ω
ω
π
≤
ω
≤
π
−
m
m
k
k
e
M
e
M
e
M
e
M
e
M
e
L
s
s
s
s
s
s
s
s
s
s
T
j
o
T
T
j
T
T
j
o
T
j
T
T
j
o
T
j
o
T
2
2
2
arg
arg
arg
1
arg
(5.27)
Interpretacja geometryczna kryterium Nyquista wynika ze spostrzeżenia, że wykres
( )
( )
( )
s
s
s
T
j
o
T
j
o
T
j
o
e
G
e
M
e
L
ω
ω
ω
+
=
+
1
1
(5.28)
można przedstawić na płaszczyźnie zmiennej zespolonej w układzie współrzędnych
( )
( )
[
]
( )
( )
[
]
s
s
T
j
o
s
T
j
o
s
e
G
T
Q
e
G
T
P
ω
ω
=
ω
=
ω
Im
Re
,
(5.29)
23
Dyskretne Układy Regulacji
rysując tylko charakterystykę amplitudowo- fazową układu otwartego G
o
. Przyrost
argumentu, który należy wskazać, korzystając z przebiegu charakterystyki 1+G
o
, (wzór
5.26 i 5.27), wymaga określenia obrotu wektora 1+G
o
wokół punktu (–1, j0). Przyrost
argumentu wynosi 0, gdy punkt charakterystyczny (–1, j0) leży poza charakterystyka G
o
.
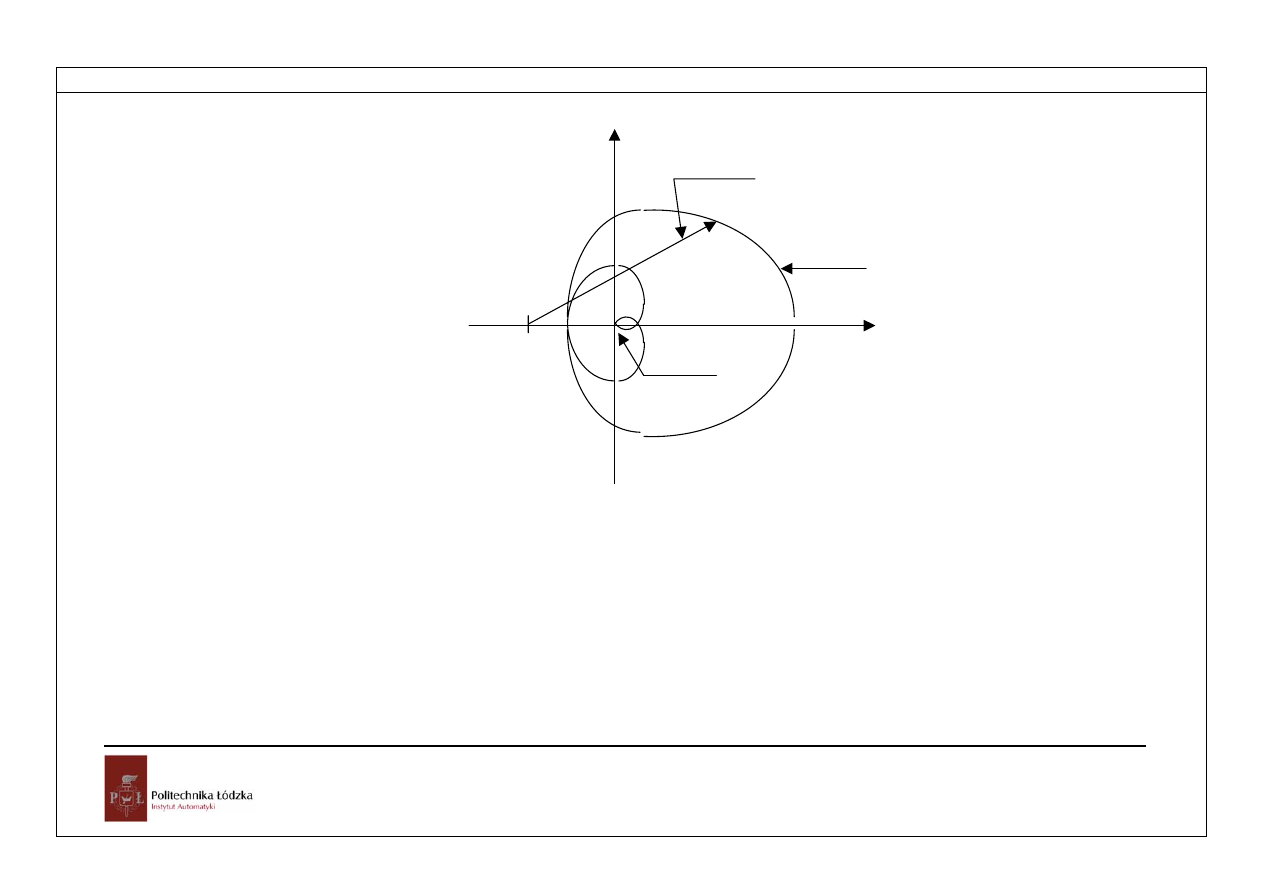
Rozdział 5
1+G
o
(e
j
ωTs
G
o
(e
j
ωTs
)
P(
ωTs)
Q(
ωTs)
1+j0
ωTs=π
Rys.5.7. Charakterystyka amplitudowo-fazowa Nyquista
Twierdzenie Nyquista
Układ regulacji będzie stabilny, gdy charakterystyka amplitudowo fazowa stabilnego
układu otwartego nie obejmuje punktu charakterystycznego (–1, j0).
24
Dyskretne Układy Regulacji
Przykład 5.3

Rozdział 5
Określić stabilność układu regulacji (układu zamkniętego), gdy transmitancja
dyskretna układu otwartego jest określona wzorami
( ) (
)(
)(
)
( ) (
)(
)
1
.
0
2
.
0
)
3
.
0
4
.
0
5
.
0
1
)
−
−
=
=
−
−
=
z
z
z
z
G
b
z
z
z
z
G
a
o
o
,
(5.30)
Charakterystyki amplitudowo-fazowe zostały obliczone i wykreślone w programie
Matlab Control Toolbox
disp(
'Stabilnosc wg kryterium Nyquista'
)
Ts=0.1, disp(
'Okres impulsowania'
)
z=tf(
'z'
,Ts), disp(
'Definicja zmiennej z'
)
disp(
'Transmitancja ukladu otwartego'
)
Goz=1/((z-0.5)*(z-0.4)*(z-0.3)),
disp(
'Transmitancja ukladu zamknietego'
)
25
Dyskretne Układy Regulacji
Gz=feedback(Goz,1)

Rozdział 5
disp(
'parametry transmitancji'
)
[num,den]=tfdata(Gz,
'v'
)
abs(roots(den)), disp(
'moduly pierwiastkow'
)
figure(1)
nyquist(Goz),grid on
xlabel(
'P(wTs)'
),ylabel(
'Q(wTs)'
)
% Transmitancja b)
Goz=z/((z-0.2)*(z-0.1))
Gz=feedback(Goz,1,-1)
[num,den]=tfdata(Gz,
'v'
)
abs(roots(den))
figure(2)
26
Dyskretne Układy Regulacji
nyquist(Goz),xlabel(
'P(wTs)'
),ylabel(
'Q(wTs)'
)

Rozdział 5
P(wTs)
Q(
w
T
s)
Nyquist Diagrams
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
From: U(1)
To
: Y
(1
)
1+Go(wTs)
27
Dyskretne Układy Regulacji
Rys.5.8. Charakterystyki układu a), niestabilnego w stanie zamkniętym

Rozdział 5
P(wTs)
Q(
w
T
s)
Nyquist Diagrams
-1
-0.5
0
0.5
1
1.5
-1.5
-1
-0.5
0
0.5
1
1.5
From: U(1)
To
: Y
(1
)
1+Go(wTs)
Rys.5.9.Charakterystyki układu b), stabilnego w stanie zamkniętym
28
Dyskretne Układy Regulacji
Wyniki obliczeń w linii poleceń

Rozdział 5
Stabilność wg kryterium Nyquista
Ts = 0.1000 Okres impulsowania
Transfer function:z
Sampling time: 0.1
Definicja zmiennej z
Transmitancja układu otwartego
Transfer function:
1
-----------------------------
z^3 - 1.2 z^2 + 0.47 z - 0.06
Sampling time: 0.1
Transmitancja układu zamkniętego
29
Dyskretne Układy Regulacji
Transfer function:

Rozdział 5
1
-----------------------------
z^3 - 1.2 z^2 + 0.47 z + 0.94
Sampling time: 0.1
parametry transmitancji
num = 0 0 0 1
den = 1.0000 -1.2000 0.4700 0.9400
ans = 1.2482 1.2482 0.6033 moduły pierwiastków
b)Transfer function:
z
------------------
z^2 - 0.3 z + 0.02
30
Dyskretne Układy Regulacji
Sampling time: 0.1

Rozdział 5
Transfer function:
z
------------------
z^2 + 0.7 z + 0.02
Sampling time: 0.1
num = 0 1 0
den = 1.0000 0.7000 0.0200
ans = 0.6702 0.0298
W przypadku a) moduły pierwiastków są większe niż 1 a zatem leżą poza okręgiem
jednostkowym i układ jest niestabilny. W przypadku b) pierwiastki leżą wewnątrz okręgu
jednostkowego i układ jest stabilny.
31
Dyskretne Układy Regulacji
Koniec przykładu 5.3

Literatura
Literatura
[1] Ackerman J.: Regulacja impulsowa. WNT, Warszawa 1976
[2] Brzózka J.: Regulatory cyfrowe w automatyce. Mikom, Warszawa2002
[3] Brzózka J.: Regulatory i układy automatyki. Mikom, Warszawa2004
[4] Dębowski A.: Automatyka. Podstawy teorii. WNT, Warszawa 2008
[5] Gessing R.: Teoria sterowania. Część I. Układy liniowe. Skrypt uczelniany ' Politechniki Śląskiej nr 1302,
Gliwice 1987.
[6] Kaczorek T.: Teoria sterowania. T.1. PWN, Warszawa 1977
[7] Kaczorek T.: Teoria układów regulacji automatycznej. WNT, Warszawa 1977
[8] Laboratorium Teorii Sterowania i Podstaw Automatyki, Błachuta M. [red.]: (praca zbiorowa), Wydawnictwo
Politechniki Śląskiej nr 2082
[9] Markowski A., Kostro J., Lewandowski A.: Automatyka w pytaniach i odpowiedziach. WNT, Warszawa 1979
[10] Markowski J.: Elementy urządzenia i układy automatyki. WSiP, Warszawa 2006
[11] Mutambara A.: Design and Analysis of Control Systems. CRC Press, New York, 1999
[12] Niederliński A.: Systemy i sterowanie. Wyd. Politechniki Śląskiej, skrypt Nr 746, Gliwice 1978
[13] Ogata K.: Discrete – time control systems. Prentice Hall Inter., Englewood Cliffs 1987
[14] PN-88 M-42000 Automatyka i pomiary przemysłowe. Terminologia
[15] Rumatowski K.: podstawy automatyki. Część 2. Układy dyskretne i stochastyczne. Wydawnictwo Politechniki
Poznańskiej, Poznań 2005
[16] Schönfeld R.: Digitale Regelung elektrischer Abtriebe. VEB Verlag, Berlin 1987
[17] Schönfeld R.: Grundlagen der automatischen Steuerung. VEB Verlag, Berlin 1984
[18] Sinha N.K.: Controls systems. John Wiley &Sons, New York 1995
32
Dyskretne Układy Regulacji
[19] Takahashi Y., Rabins M., Auslander D.: Sterowanie i systemy dynamiczne. WNT, Warszawa 1976

Literatura
[20] Tewari A.: Modern Control Design with Matlab and Simulink. John Wiley & Sons Ltd, New York 2002
[21] Wajs K.: Linie pierwiastkowe w automatyce. WNT, Warszawa 1973
[22] http://pl.wikipedia.org/wiki/SCADA
[23] http://pl.wikipedia.org/wiki/System_czasu_rzeczywistego
33
Dyskretne Układy Regulacji
Document Outline
Wyszukiwarka
Podobne podstrony:
6 Dyskretne układy regulacji, rozdział 9 Jakość dyskretnych układów regulacji
4 Dyskretne układy regulacji, rozdział 6 Podstawowe struktury układów regulacji
1 Dyskretne układy regulacji, rozdział 1 i 2, Wstęp Dyskretny układ regulacji
5 Dyskretne uklady regulacji, Nieznany (2)
2 Dyskretne uklady regulacji, Nieznany
3 Dyskretne uklady regulacji, Nieznany (2)
4 Dyskretne uklady regulacji, Nieznany (2)
Ćwiczenie 8 Stabilność układów regulacji
Badanie stabilności układów na podstawie kryterium Nyquista Zapas?zy i wzmocnienia
Badanie zapasu stabilności układów dyn
Układy logiczne cz.2, Laboratorium układów elektronicznych
Stabilność układów automatyki
B molekularna wykład regulacja translacji i stabilności mRNA Kopia
9 Układy regulacji położenia złącz manipulatora
ciagle uklady regulacji, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, szkola, AUTOMA
więcej podobnych podstron
