
Bogdan Wolski
M
ateriały dydaktyczne opracowane dla potrzeb projektu
„Opracowanie i wdrożenie programu studiów inżynierskich geodezja
i kartografia w Społecznej Wyższej Szkole Przedsiębiorczości
i Zarządzania w Łodzi”
Społeczna Wyższa Szkoła Przedsiębiorczości i Zarządzania
Łódź 2011

2
Spis treści
1. Algebra macierzy
1.1. Rodzaje macierzy, Operacje na macierzach ……………………………... 3
1.2. Rozkład macierzy na czynniki trójkątne i trapezowe ............................... 3
1.3. Odwrotność macierzy. Wyznaczanie macierzy odwrotnej za pomocą
kofaktorów ………………………………………………………………….…. 5
1.4. Rozwiązywanie układów równań liniowych ……………………………….. 6
2. Elementy teorii błędów. Przedziały ufności …………………… ……….… 10
3. Wyrównanie obserwacji bezpośrednich. Propagacja błędów
3.1. Wyrównanie obserwacji bezpośrednich……………………………….…... 15
3.2. Propagacja błędów ………………………………………………………….. 18
3.3. Optymalizacja programu obserwacji ………………………………………. 19
4. Metoda parametryczna. Wyrównanie sieci niwelacyjnej
4.1. Model zagadnienia wyrównawczego ……………...……………….……… 21
4.2. Metoda najmniejszych kwadratów. Układ równań normalnych ………… 22
4.3. Algorytm obliczeń ……………………………………………………………. 24
4.4. Przykład wyrównania sieci niwelacyjnej ………………….……………….. 25
5. Metoda parametryczna. Wyrównanie sieci liniowo-kątowej
5.1. Model zagadnienia wyrównawczego ………
…
….………………………… 29
5.2. Ocena dokładności ……………………………………………………..…… 32
5.3. Algorytm obliczeń ……………………………………………………………. 33
5.4. Przykład wyrównania sieci liniowo-kątowej ………
…
…….………………. 34
6. Metoda warunkowa
6.1. Model zagadnienia wyrównawczego …………………………………….. 41
6.2. Przykłady równań warunkowych ………………
…
………….…………… 41
6.3. Algorytm metody warunkowej ……………………………………..……… 43
6.4. Przykład wyrównania sieci niwelacyjnej …………………………………. 45
7. Metody mieszane ………………………………………………………………..
7.1. Metoda parametryczna z warunkami dla parametrów …………………. 49
7.2.Metoda uproszczona ……………......………………………
…
….………… 52

3
1. Algebra macierzy
1.1. Rodzaje macierzy. Operacje na macierzach
Macierz
A - tablica liczb o wymiarach n, m
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
.
...
...
...
...
...
...
...
...
A
3
2
1
2
23
22
21
1
13
12
11
nm
n
n
n
m
m
a
a
a
a
a
a
a
a
a
a
a
a
§
Macierz transponowana
n
m
n,m
,
T
A
A
=
§
Macierz diagonalna
D
i,j
= 0 dla i
¹ j
§
Macierz symetryczna
D
i,j
= D
ji
§
Macierz kwadratowa
n = m
Dwie macierze mogą być przez siebie pomnożone, o ile liczba kolumn pierwszej z
nich jest równa liczbie wierszy drugiej macierzy
k
n
k
m
m
n
,
,
,
C
B
A
=
×
§
Iloczyn wielu macierzy
s
n
s
r
r
k
k
m
m
n
,
,
,
,
,
F
D
C
B
A
=
×
×
×
§
Iloczyn macierzy z kontrolą
ú
û
ù
ê
ë
é
-
-
-
-
-
=
ú
û
ù
ê
ë
é
-
-
×
ú
û
ù
ê
ë
é
-
12
4
2
8
6
30
6
11
12
1
3
3
2
0
2
6
2
1
4
3
0
2
4
3
1.2. Rozkład macierzy na czynniki trójkątne i trapezowe
Macierz A np. stopnia trzeciego można rozłożyć na macierze trójkątne H
T
i G
ú
ú
ú
û
ù
ê
ê
ê
ë
é
×
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
1
0
0
1
0
1
0
0
0
23
13
12
33
23
13
22
12
11
,
g
g
g
h
h
h
h
h
h
A
n
n

4
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
24
1
0
1
0
23
14
13
12
22
21
11
24
23
22
21
14
13
12
11
g
g
g
g
g
h
h
h
a
a
a
a
a
a
a
a
m
n,
m
n,
T
m
n,
G
H
A
×
=
Macierze H
T
i G wyznaczane są z definicji mnożenia macierzy przy założeniu
elementów oporowych.
§
Macierz prostokątną poziomą A n < m można rozłożyć na trójkątną H
T
i trapezową G
§
Macierz symetryczną można rozłożyć na iloczyn macierzy, z których jedna
jest transpozą drugiej
R
R
A
T
×
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
×
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
1
0
0
1
0
1
0
0
0
A
23
13
12
33
23
13
22
12
11
33
32
31
23
22
21
13
12
11
r
r
r
r
r
r
r
r
r
a
a
a
a
a
a
a
a
a
Przykład 1.1.
Macierz A o wymiarach n=2 oraz m=2 rozłożyć na macierze
trójkątne H
T
i G
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
1
0
1
0
4
2
2
4
12
22
12
11
g
h
h
h
a
11
=h
11
× 1 ® h
11
=4
a
12
=4
× g
12
® g
12
=4
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
1
0
5
.
0
1
0
4
4
2
2
4
22
12
h
h
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
1
0
5
.
0
1
3
2
0
4
4
2
2
4
A H
T
G
A H
T
G
A H
T
G
A H
T
G

5
1.3. Odwrotność macierzy. Wyznaczanie macierzy odwrotnej za
pomocą kofaktorów
Jeżeli macierz kwadratowa A o wymiarach n
´n jest nieosobliwa tj. det(A)¹0, to
istnieje jedna macierz odwrotna
n
n
n
n
n
n
,
1
1
,
,
I
A
A
A
A
=
×
=
×
-
-
( )
[
]
T
1
A
adj
)
A
det(
1
A
=
-
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
nn
n
n
n
n
k
k
k
k
k
k
k
k
k
....
....
....
....
....
....
....
)
A
adj(
2
1
2
22
21
1
12
11
przy czym kofaktorem k
ij
elementu a
ij
wyznacznika det(A) nazywane jest wyrażenie
( )
ij
j
i
ij
M
k
+
-
= 1
gdzie i – numer wiersz, j – numer kolumny. Wartości minorów M
ij
wyznacznika
det(A) obliczane są jako podwyznaczniki utworzone z pozostałych elementów
wyznacznika det(A) po wykreśleniu i-tego wiersza oraz j-tej kolumny
Przykład 1.2.
Wyznaczyć odwrotność macierzy A za pomocą macierzy kofaktorów.
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
42
10
3
10
8
6
3
6
9
A
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
-
-
-
-
-
=
+
+
+
+
+
+
+
+
+
33
3
3
32
2
3
31
1
3
23
3
2
22
2
2
21
1
2
13
3
1
12
2
1
11
1
1
1
1
1
1
1
1
1
1
1
A
adj
M
M
M
M
M
M
M
M
M
Podwyznaczniki – wartości minorów M
ij
wyznacznika det(A) utworzone po
wykreśleniu i-tego wiersza oraz j-tej kolumny
236
42
10
10
8
det
11
=
ú
û
ù
ê
ë
é
=
M
222
42
3
10
6
det
12
=
ú
û
ù
ê
ë
é
=
M
36
10
3
8
6
det
13
=
ú
û
ù
ê
ë
é
=
M
369
42
3
3
9
det
22
=
ú
û
ù
ê
ë
é
=
M
72
10
3
6
9
det
23
=
ú
û
ù
ê
ë
é
=
M
36
8
6
6
9
det
33
=
ú
û
ù
ê
ë
é
=
M

6
( )
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
=
36
72
36
72
369
222
36
222
236
A
adj
Det(A) = 9
´8´42 + 6´10´3 + 3´6´10 - 3´8´3 - 9´10´10 - 6´6´42
Det(A) = 900
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
=
-
36
72
36
72
369
222
36
222
236
900
1
1
A
1.4. Rozwiązywanie układów równań liniowych
1.4.1. Metoda nieoznaczona; za pomocą odwrotności macierzy
Układ równań
0
2
2
1
1
10
1
2
12
1
11
...
..........
.
..........
..........
..........
..........
..........
.
..........
n
m
nm
n
n
m
m
a
x
a
x
a
x
a
a
x
a
x
a
x
a
=
+
=
+
+
zapisany macierzowo ma postać
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
nm
n
n
m
m
m
n
a
a
a
a
a
a
a
a
a
....
....
....
....
....
....
....
A
2
1
2
22
21
1
12
11
,
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
m
m
x
x
x
...
X
2
1
1
,
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
n
n
l
l
l
...
L
2
1
1
,
L
AX
=
Przykład 1.3. Zapisać macierzowo układ równań
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
=
-
0400
.
0
0800
.
0
0400
.
0
0800
.
0
4100
.
0
2467
.
0
0400
.
0
2467
.
0
2622
.
0
1
A
x
1
+ 3x
2
- x
3
= -1
x
2
- x
3
= 0
x
1
- 2x
3
= 1

7
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
=
2
0
1
1
1
0
1
3
1
A
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
3
2
1
X
x
x
x
ú
ú
ú
û
ù
ê
ê
ê
ë
é-
=
1
0
1
L
W metodzie nieoznaczonej wykorzystuje się inwers macierzy powstały przy
przekształceniu równania
L
AX
=
/A
-1
A
-1
×A×X = A
-1
×L
L
A
X
1
×
=
-
Przykład 1.4.
Rozwiązać układ równań metodą nieoznaczoną
12
4
2
8
3
4
=
+
=
+
y
x
y
x
ú
û
ù
ê
ë
é
=
4
2
3
4
A
ú
û
ù
ê
ë
é
=
12
8
L
Det(A) = 10
( )
[
]
ú
û
ù
ê
ë
é
-
-
=
ú
û
ù
ê
ë
é
-
=
=
-
4
.
0
2
.
0
3
.
0
4
.
0
4
3
2
4
10
1
A
adj
)
A
Det(
1
A
T
T
1
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
-
-
=
12
8
4
.
0
2
.
0
3
.
0
4
.
0
X
ú
û
ù
ê
ë
é-
=
2
.
3
4
.
0
X
1.4.2. Metoda oznaczona; macierze
H
T
, G
L
Ze współczynników przy niewiadomych (macierz A) i wyrazów wolnych (wektor L)
tworzymy macierz blokową B = [A;L], którą rozkładamy na macierz trójkątną H
T
i trapezową G
L
= [G;L
G
].
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
×
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
gn
g
g
nm
n
n
n
nm
n
n
m
m
l
l
g
l
g
g
h
h
h
h
h
h
l
a
a
a
l
a
a
a
l
a
a
a
1
...
0
0
...
...
...
...
...
...
1
0
...
1
...
0
...
...
...
0
...
0
...
0
....
...
...
...
...
...
....
....
2
11
1
11
11
2
1
22
21
11
2
1
2
2
22
21
1
1
12
11
A L H
T
G L
G
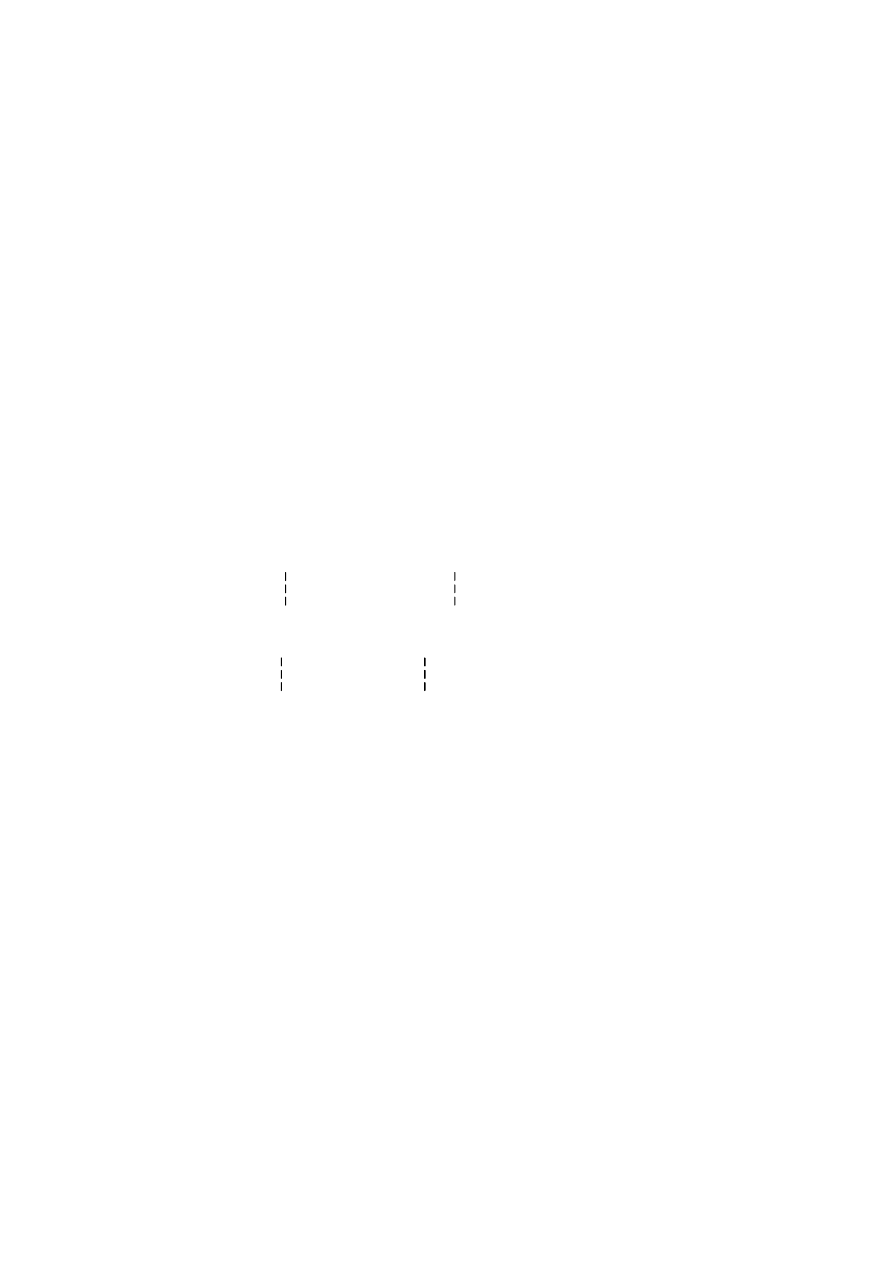
8
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
×
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
gn
g
g
n
n
n
l
l
l
x
x
x
g
g
g
2
1
2
1
2
1
12
...
1
...
0
0
...
...
...
...
...
1
0
...
1
Niewiadome- elementy wektora X - wyznaczamy rozwiązując układ równań
G
×X = L
G
Przykład 1.5. Rozwiązać układ równań liniowych metodą oznaczoną rozkładając
macierz B na macierz trójkątną H
T
i trapezową G
L
= [G;L
G
]
4x + 2y = 8
2x + 4y = 13
Wyznacznik Det(A) = 16 - 6 = 10, macierz nie jest osobliwa, daje się więc rozłożyć
na dwie macierze trójkątne
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
=
2
1
12
22
21
11
1
0
1
0
13
4
2
8
2
4
B
g
g
l
l
g
h
h
h
A L H
T
G L
G
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
=
3
1
0
2
5
.
0
1
3
2
0
4
13
4
2
8
2
4
B
Zgodnie z wzorem
G
×X = L
G
ú
û
ù
ê
ë
é
=
ú
û
ù
ê
ë
é
×
ú
û
ù
ê
ë
é
3
2
1
0
5
.
0
1
2
1
x
x
Poprawność rozwiązania sprawdzamy podstawiając wyznaczone niewiadome do
układu równań
4
× 0.5 + 2 × 3 = 8
2
× 0.5 + 4 × 3 = 13
1.4.3. Metoda oznaczona; macierze
R
T
, R
L
Gdy macierz A jest symetryczna, tworzymy macierz blokową B = [A;L], którą
rozkładamy na macierz trójkątną R
T
i trapezową R
L
= [R;L
R
].
G X L
G
ú
û
ù
ê
ë
é
=
3
5
.
0
X

9
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
×
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
rn
nn
r
n
r
n
nn
n
n
n
nn
n
n
n
n
l
r
l
r
r
l
r
r
r
r
r
r
r
r
r
l
a
a
a
l
a
a
a
l
a
a
a
...
0
0
...
...
...
...
...
...
0
...
...
0
...
...
...
0
...
0
...
0
....
...
...
...
...
...
....
....
2
2
22
1
1
12
11
2
1
22
21
11
2
1
2
2
22
21
1
1
12
11
Niewiadome X wyznaczamy rozwiązując zredukowany układ równań
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
×
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
rn
r
r
n
n
n
l
l
l
x
x
x
r
r
r
...
...
1
...
0
0
...
...
...
...
...
1
0
...
1
2
1
2
1
2
1
12
Przykład 1.6.
Rozwiązać układ równań
9x + 6y + 3z = 18
6x + 8y + 10z = 24
3x +10y +42z = 55
rozkładając macierz B na macierz trójkątną R
T
i trapezową R
L
=[R;L
R
]. Det A≠ 0.
ú
ú
ú
û
ù
ê
ê
ê
ë
é
×
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
5
5
0
0
6
4
2
0
6
1
2
3
5
4
1
0
2
2
0
0
3
55
42
10
3
24
10
8
6
18
3
6
9
B
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
×
ú
ú
ú
û
ù
ê
ê
ê
ë
é
5
6
6
5
0
0
4
2
0
1
2
3
3
2
1
x
x
x
R X L
R
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
1
1
1
X
Kontrola obliczeń
9·1 + 6·1 + 3·1 = 18
6·1 + 8·1 + 10·1 = 24
3·1 +10·1 + 42·1 = 55
A L R
T
R L
R
R X L
R
A L R
T
R L
R

10
2. Elementy teorii błędów. Przedziały ufności
W praktyce pomiarowej występują trzy rodzaje błędów:
§
grube,
§
systematyczne,
§
przypadkowe.
Według kryterium metody pomiaru obserwacje mogą być:
§
bezpośrednie,
§
pośrednie.
Według kryterium dokładności wyniki pomiaru dzielimy na:
§
jednakowo dokładne,
§
różnodokładne.
Cel zagadnień wyrównawczych:
§
wyznaczenie wartości najprawdopodobniejszych,
§
oszacowanie dokładności obserwacji pojedynczych, względnych, wartości
przeciętnych oraz funkcji wyznaczonych analizowanych zmiennych.
Podstawowymi parametrami opisującymi zmienną losową x są: wartość przeciętna
å
=
n
i
śr
x
n
x
1
1
(2.1)
i odchylenie standardowe σ
x
(
)
å
-
=
n
śr
i
x
x
x
n
1
2
1
s
(2.2)
W zadaniach praktycznych odchylenie standardowe σ
x
zastępowane jest jego
estymatorem. Wartość ta wyznaczona jest na podstawie wyników pomiaru i w tej
postaci nazywana jest błędem średnim. W zadaniach geodezyjnych (tylko)
oznaczana przez m. W innych dyscyplinach określana jest mianem błędu
standardowego i oznaczana jest symbolem s.
(
)
å
-
-
=
n
śr
i
x
x
n
m
1
2
1
1
(2.3)
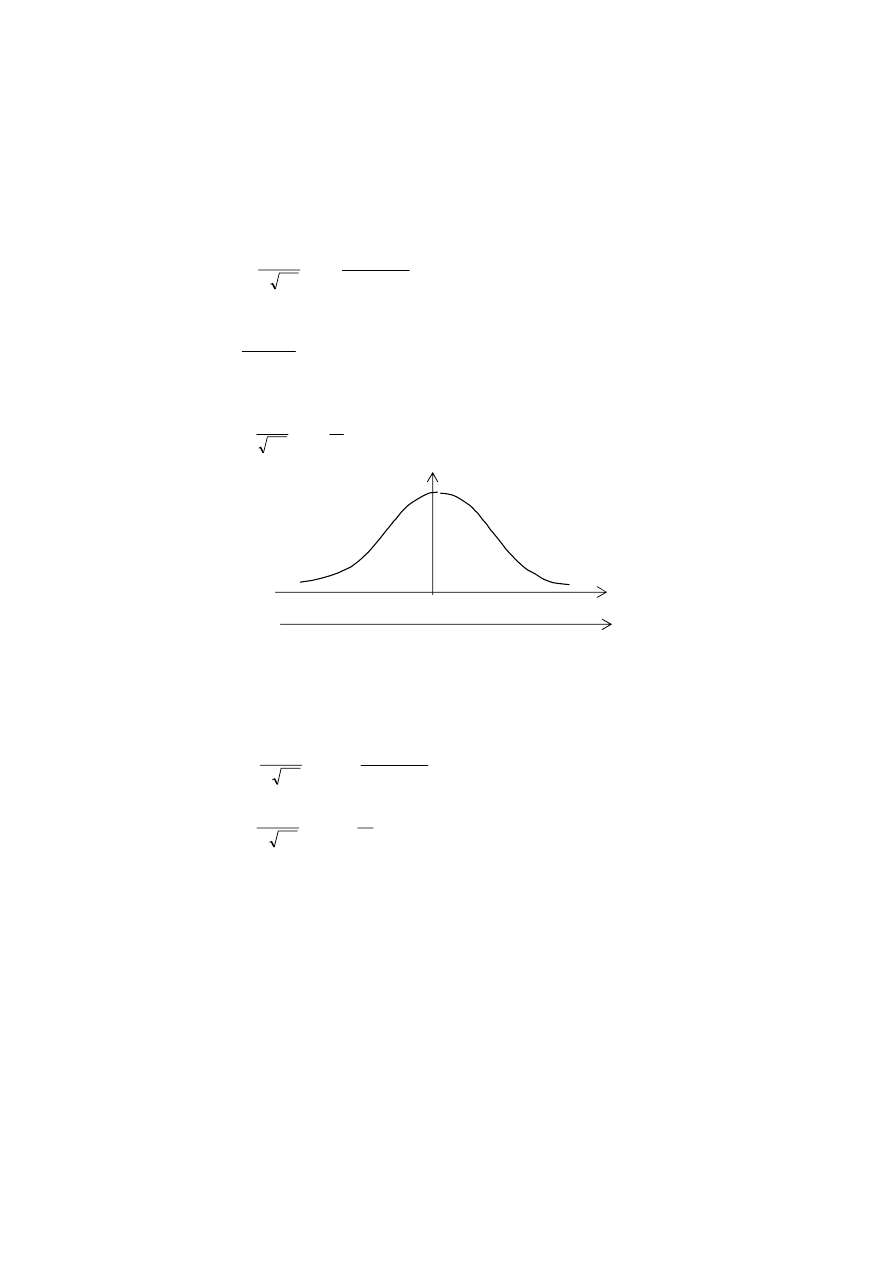
Rozkład normalny. Rozkład empiryczny w miarę wzrostu liczby danych przyjmuje
kształt rozkładu normalnego o funkcji gęstości opisanej wartością przeciętną oraz
odchyleniem standardowym.
11
(
)
ú
ú
û
ù
ê
ê
ë
é
-
-
=
2
2
2
exp
2
1
)
(
s
p
s
śr
i
x
x
x
p
(2.4)
Zmienna standaryzowana. Wprowadzenie tzw. zmiennej standaryzowanej t
s
śr
i
i
x
x
t
-
=
(2.5)
przy założeniu
s = 1 przekształca wzór (2.4) do postaci
ú
ú
û
ù
ê
ê
ë
é
-
=
2
exp
2
1
)
(
2
t
t
p
p
(2.6)
Rys. 2.1. Funkcja gęstości rozkładu normalnego zmiennej standaryzowanej
Dystrybuanta. Przy rozwiązywaniu zadań praktycznych wykorzystywana jest
dystrybuanta
(
)
dx
x
x
x
D
x
śr
i
ò
¥
-
ú
ú
û
ù
ê
ê
ë
é
-
-
=
2
2
2
exp
2
1
)
(
s
p
s
(2.7)
dt
t
t
D
t
ò
¥
-
ú
ú
û
ù
ê
ê
ë
é
-
=
2
exp
2
1
)
(
2
p
s
(2.8)
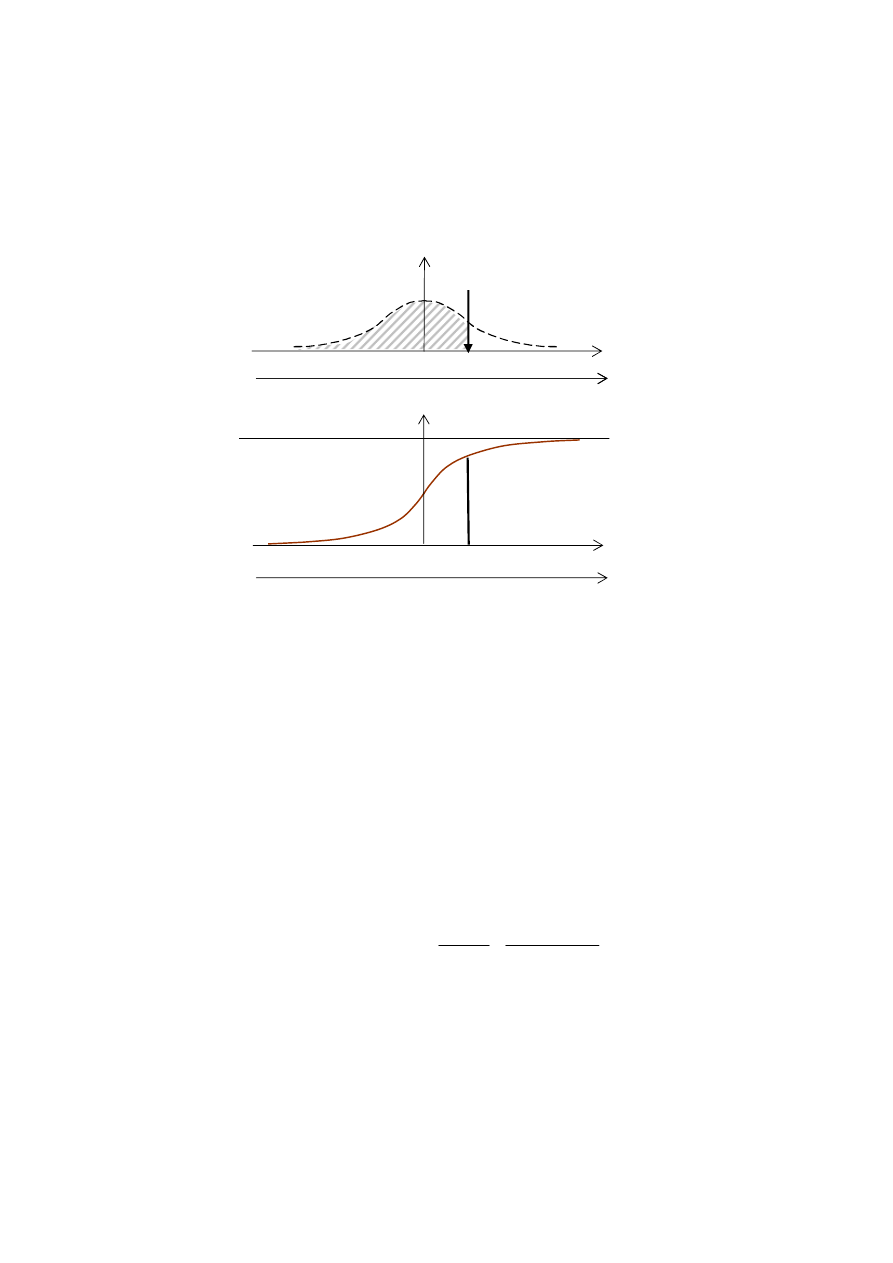
Dystrybuanta określa prawdopodobieństwo wystąpienia wartości zmiennej x w
przedziale
á- ¥, x
2
ñ, jak na rys. 2.2.
ï ï ï ï ï ï ï ï ï ï ï
2
s s 0 s 2s
_
_
_
_
0,4
0,2
ï ï ï ï ï ï ï ï ï ï ï
2 1 0 1 2
t
x
P
12
Rys. 2.2. Dystrybuanta rozkładu normalnego. Rzędna D(t = 0,8) jest miarą powierzchni
zakreślonej na rys. 2.1.
Przedziały ufności. Aby wyznaczyć prawdopodobieństwo P, że zmienna x
znajdzie się w przedziale
áx
1
, x
2
ñ należy wyznaczyć dystrybuanty dla obu wartości
zmiennej x po ich uprzedniej standaryzacji wzorem (2.5). Szukane
prawdopodobieństwo P{x
1
á x á x
2
} jest różnicą wartości prawdopodobieństw.
P{x
1
áx áx
2
} = P(x
2
) - P(x
1
) = D(t
2
) - D(t
1
) (2.9)
Zadania praktyczne rozwiązuje się za pomocą tablic.
Przykład 2.1. Dla zbioru danych stanowiącego wynik pomiaru odległości {145.33,
145.39, 145.30} obliczyć prawdopodobieństwo P{ x
ñ 145.39 }
Dla podanych wartości wyznaczamy:
· wartość przeciętną
d
śr
= 145,34
· błąd standardowy pojedynczej obserwacji m = 0,045
· zmienną standaryzowaną
11
,
1
045
,
0
34
,
145
39
,
145
=
-
=
-
=
m
d
d
t
śr
i
0,5
D(t = 0,8)
1.0
D(t)
ï ï ï ï ï ï ï ï ï ï ï
- 2 - 1 0 1 2
t
ï ï ï ï ï ï ï ï ï ï ï
- 2
s - s 0 s 2s
x
_
_
_
t = 0,8
0.5
P(t)
ï ï ï ï ï ï ï ï ï ï ï
- 2 - 1 0 1 2
t
_
_
ï ï ï ï ï ï ï ï ï ï ï
- 2 - 1 0 1 2
t
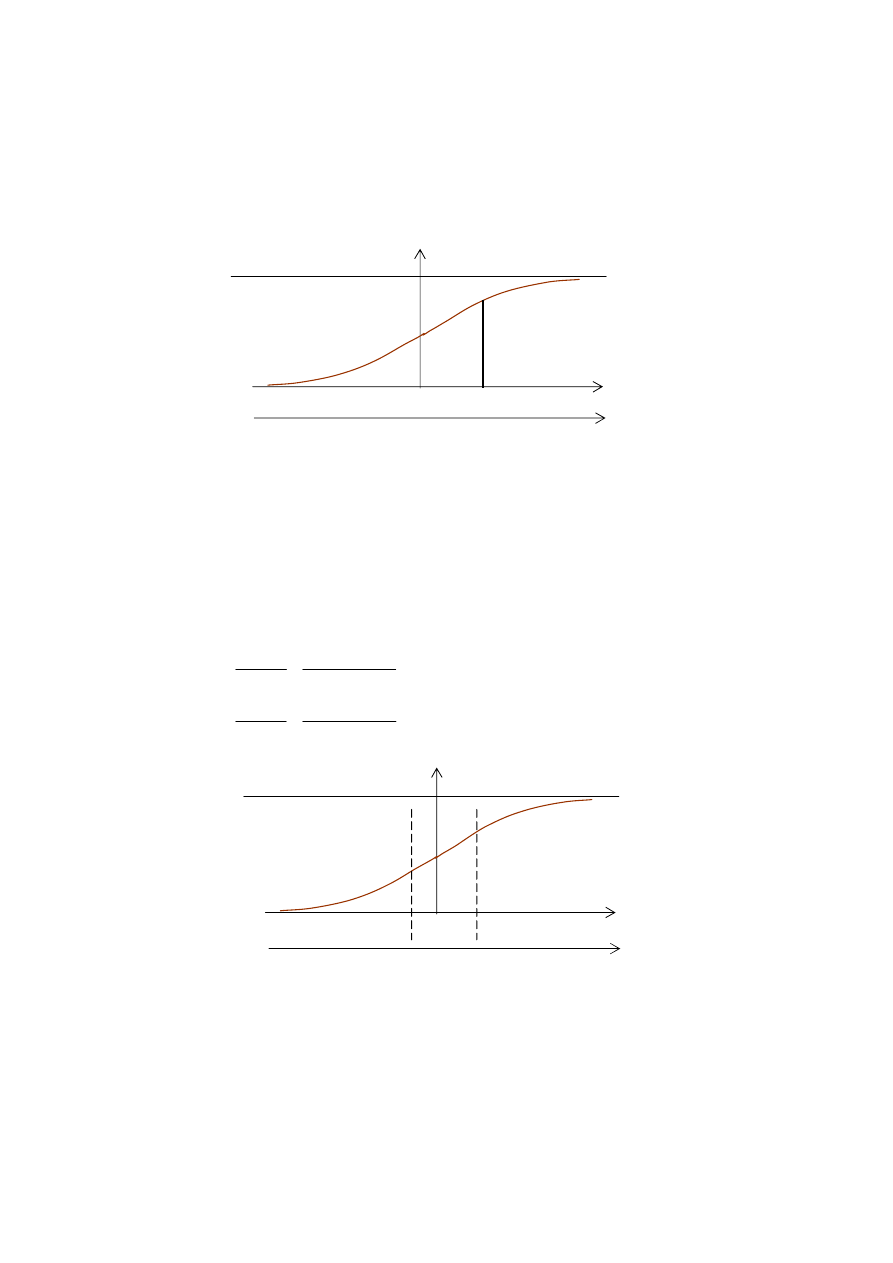
13
Rys. 2.3. Ilustracja do przykładu 2.1
Z tablic dystrybuanty rozkładu normalnego dla zmiennej t = 1.11 odczytujemy
P(t) = 0,279. Szukane prawdopodobieństwo wynosi
P{x
1
áxáx
2
}= 0,5 + 0,366 = 0,866
Przykład 2.2. Obliczyć prawdopodobieństwo P {145.33
á x
śr
á 145.36} dla wyników
obserwacji jak w przykładzie 2.1.
Podobnie jak w przykładzie 2.1 parametry rozkładu wynoszą d
śr
= 145,34,
m = 0,045 , m
śr
= 0,026.
Stąd
385
,
0
026
,
0
34
,
145
33
,
145
-
=
-
=
-
=
m
d
d
t
śr
i
769
,
0
026
,
0
34
,
145
36
,
145
=
-
=
-
=
m
d
d
t
śr
i
Rys. 2.4. Ilustracja do przykładu 2.2
_
_
_
1.0
0,5
ï ï ï ï ï ï ï ï ï ï ï
2 1 0 1 2
t
ï ï ï ï ï ï ï ï ï ï ï
2m
śr
m
śr
0 m
śr
2m
śr
D(t)
x
śr
_
_
_
1.0
0,5
ï ï ï ï ï ï ï ï ï ï ï
2m m 0 m 2m
D(t)
x
ï ï ï ï ï ï ï ï ï ï ï
- 2 - 1 0 1 2
t

14
Z tablic odczytujemy P(t
1
) = 0,149 oraz P(t
2
) = 0,279, stąd
P{145.38
á x
śr
á 145.45} = P(t
1
) + P(t
2
) = 0,428
P{145.38
á x
śr
á 145.45} = 0,428
Przykład 2.3. Dla zmiennej
a obliczyć przedział ufności áa
1
,
a
2
ñ o prawdopodo-
bieństwie P = 0,90, dla danych {112.71
g
, 112,75
g
, 112,76
g
}, przy założeniu, że
|
a
1
| = |
a
2
|.
Wartość przeciętna
a
śr
i błąd standardowy m wyznaczone dla zbioru danych
wynoszą:
a
śr
= 112,74
g
, m = 0,026
g
.
Ponieważ przedmiotem analizy jest tylko zmienna
a nie ma potrzeby wyznaczania
błędu m
śr
. Dla P/2 (przedział jest symetryczny), w tablicy dystrybuanty rozkładu
normalnego znajdujemy t
a
= 1,65. Wartość
a
1
wyznaczana jest ze wzoru na
zmienną standaryzowaną.
m
t
śr
1
1
a
a
a
-
=
70
,
112
74
,
112
65
,
1
026
,
0
1
1
=
+
×
-
=
+
×
-
=
śr
t
m
a
a
a
78
,
112
74
.
112
65
,
1
026
,
0
1
2
=
+
×
=
+
×
-
=
śr
t
m
a
a
a
Szukany przedział wyznaczają granice
á112.70, 112.78
ñ.
15
3. Wyrównanie obserwacji bezpośrednich
Propagacja błędów
3.1. Wyrównanie obserwacji bezpośrednich
Wyrównanie obserwacji zbioru
[
]
T
2
1
1
,
,...
,
L
n
n
l
l
l
=
obejmuje wyznaczenie wartości
przeciętnych oraz błędów standardowych.
Przykład 3.1. Różnicę wysokości Δh
AB
pomierzono 4 razy z jednakową
dokładnością. Wyznaczyć wartość średnią, błąd średni pojedynczej obserwacji i
błąd średni wartości przeciętnej.
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
473
.
1
475
.
1
470
.
1
474
.
1
l
1
,
4
l
śr
= 1.473 v
i
= l
śr
- l
i
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
+
-
+
=
000
.
0
002
.
0
003
.
0
001
.
0
v
1
,
4
Błąd średni pojedynczej obserwacji wynosi
m =
mm
006
.
0
1
4
10
98
6
=
-
×
-
Błąd średni wartości przeciętnej
m
śr
= 0.003 mm
Interpretacja błędów
l
1
= 1.474 ± 0.006
á1.468, 1.480ñ
l
2
= 1.470 ± 0.006
á1.464, 1.476ñ
l
3
= 1.475 ± 0.006
á1.469, 1.481ñ
l
4
= 1.473 ± 0.006
á1.467, 1.469ñ
L
= 1.473 ± 0.003
á1.470, 1.476ñ
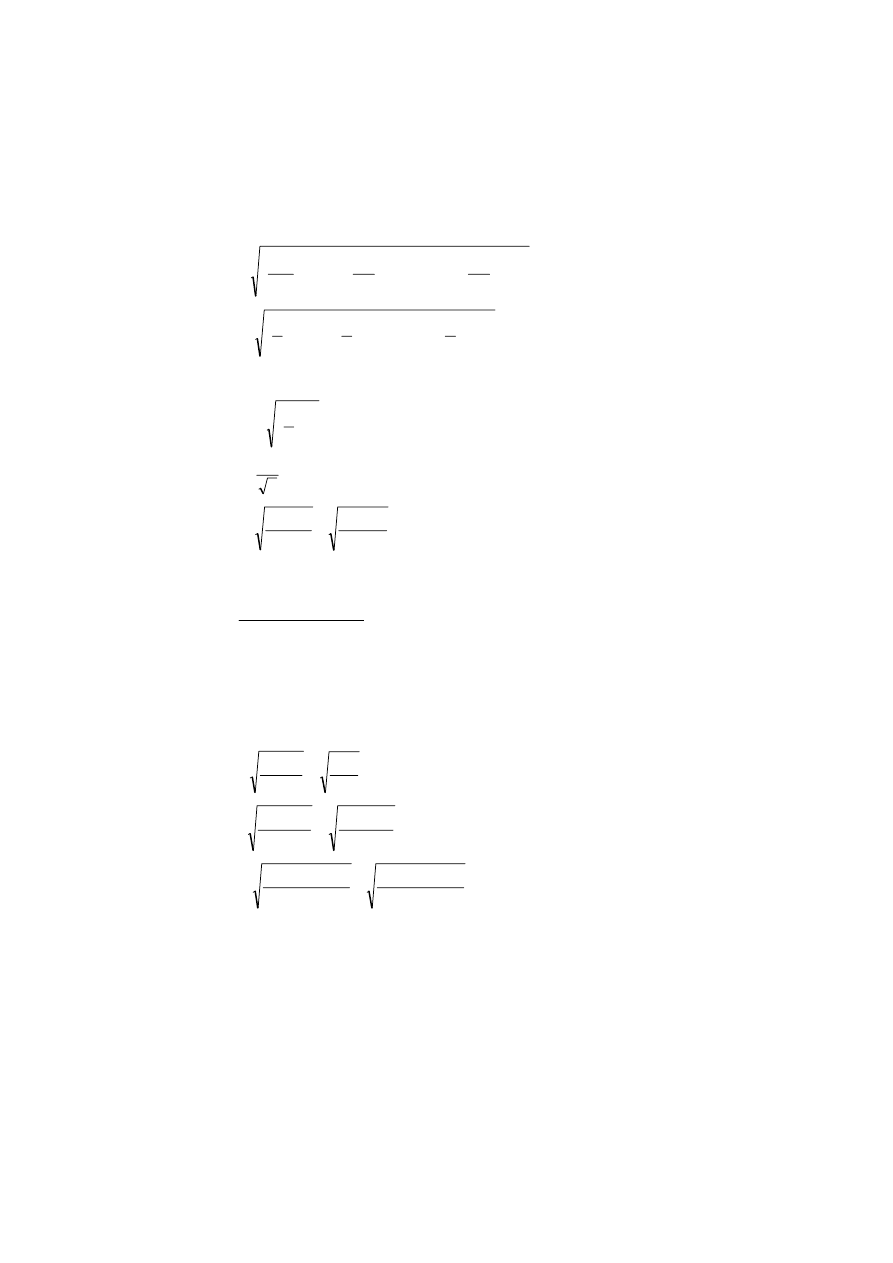
Błąd standardowy średniej arytmetycznej
n
l
l
i
śr
å
=
n
l
n
l
n
l
l
n
i
śr
.....
2
+
+
=
Na podstawie prawa przenoszenia błędów można przyjąć, że
16
2
2
1
2
2
2
1
2
1
2
1
.........
n
l
r
l
r
l
śr
ls
m
l
l
m
l
l
m
l
l
m
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
=
2
2
2
2
2
2
1
2
1
.........
1
1
n
l
l
l
lśś
m
n
m
n
m
n
m
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
=
m
m
m
m
n
l
l
l
=
=
=
.
..........
2
1
n
n
m
m
lsr
2
1
÷
ø
ö
ç
è
æ
=
n
m
m
lśś
=
(
)
)
1
(
v
v
1
T
2
-
=
-
=
å
n
n
n
n
v
m
lśś
Wyrównanie obserwacji bezpośrednich niejednakowo dokładnych
n
n
n
p
p
p
l
p
l
p
l
p
L
...
...
2
1
2
2
1
1
+
+
+
+
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
n
n
l
l
l
....
l
2
1
1
,
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
n
n
p
p
p
..
0
0
..
..
..
..
0
..
0
0
..
0
p
2
1
1
,
1
v
v
1
T
2
0
-
=
-
=
å
n
n
pv
m
(
)
)
1
(
v
p
v
1
T
2
-
×
=
-
=
å
n
p
n
p
pv
m
i
i
i
(
)
(
)
1
)
(
v
v
1
)
(
T
2
-
×
=
-
×
=
å
å
å
n
p
n
p
v
m
i
i
śr
Przykład 3.2. Różnicę wysokości Δh
AB
pomierzono 4 razy. Każdy pomiar
wykonano innym instrumentem z różną dokładnością (m). Wyznaczyć wartość
najprawdopodobniejszą, błąd średni wartości przeciętnej m
śr
i błędy średnie
poszczególnych obserwacji m
ii
.

17
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
473
.
1
475
.
1
470
.
1
474
.
1
l
1
,
4
[ ]
m
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
003
,
0
002
,
0
001
,
0
004
,
0
m
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
=
-
-
-
-
2
2
2
2
003
.
0
0
0
0
0
002
.
0
0
0
0
0
001
.
0
0
0
0
0
004
.
0
p
ú
û
ù
ê
ë
é
-
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
=
2
10
0
0
0
0
25
0
0
0
0
100
0
0
0
0
25
,
6
10
111111
0
0
0
0
250000
0
0
0
0
1000000
0
0
0
0
62500
p
4
m
n
n
n
śr
p
p
p
l
p
l
p
l
p
l
...
...
2
1
2
2
1
1
+
+
+
+
=
=
4713
.
1
141
449
.
207
=
[
]
0017
,
0
0037
,
0
0013
,
0
0027
,
0
v
T
-
-
-
=
[
]
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
-
-
-
×
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
×
-
-
-
=
0017
,
0
0037
,
0
0013
,
0
0027
,
0
11
0
0
0
0
25
0
0
0
0
100
0
0
0
0
25
,
6
10
0017
,
0
0037
,
0
0013
,
0
0027
,
0
pv
v
4
T
v
T
pv = 5,8389
395
,
1
1
4
8389
,
5
0
=
-
=
m
- wartość niemianowana
Błąd średni wartości przeciętnej m
śr
mm
p
m
i
śr
0012
.
0
141
10
395
,
1
395
,
1
4
=
×
=
=
å
Błędy średnie obserwacji m
i
.
3.2. Propagacja błędów pomiaru
W większości zadań geodezyjnych
poszukiwane wartości wyznaczane są
pośrednio ze związku funkcyjnego
0042
.
0
10
10
395
,
1
0028
.
0
25
10
395
,
1
0014
.
0
100
10
395
,
1
0057
.
0
25
,
6
10
395
,
1
4
4
4
3
4
2
4
1
=
×
=
=
×
=
=
×
=
=
×
=
m
m
m
m

18
u = f(x,y,z…), w którym bezpośrednio mierzone są wielkości x, y, z. Jeśli wielkości
mierzone bezpośrednio są losowe i znane są parametry ich rozkładów normalnych
(wartości przeciętne i błędy średnie), to błąd średni m
u
można wyznaczyć za
pomocą prawa przenoszenia się błędów.
(
) (
)
.....
...
,
,
...
,
,
0
0
0
0
0
0
+
D
÷
ø
ö
ç
è
æ
¶
¶
+
D
÷÷
ø
ö
çç
è
æ
¶
¶
+
D
÷
ø
ö
ç
è
æ
¶
¶
+
=
z
z
u
y
y
u
x
x
u
z
y
x
f
z
y
x
u
(3.1)
Δx = x - x
0
, Δy = y - y
0
, Δz = z - z
0.
(
)
.....
...
,
,
0
0
0
+
÷
ø
ö
ç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷
ø
ö
ç
è
æ
¶
¶
=
z
z
u
y
y
u
x
x
u
z
y
x
u
(3.2)
Bląd standardowy m
u
wyznaczany jest ze wzoru
...
m
z
u
m
y
u
m
x
u
m
2
Z
2
2
y
2
2
X
2
u
+
÷
ø
ö
ç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷
ø
ö
ç
è
æ
¶
¶
=
0
0
0
(3.3)
Wzór (3.3) jest poprawny pod warunkiem, że zmienne x,y,z,… są losowe i
nieskorelowane, czyli wzajemnie niezależne. W przypadku, gdy ten ostatni
warunek nie jest spełniony, w prawie przenoszenia się błędów należy uwzględnić
korelację zmiennych opisanych za pomocą macierzy kowariancji.
Przykład 3.3. Współrzędne punktu 1 wyznaczono metodą biegunową ze
stanowiska B w nawiązaniu do punktu osnowy A, jak na rys. 3.2. Obliczyć błędy
standardowe m
X1
, m
Y1
punktu 1 dla danych:
Azumut Az
BA
= 165.88
g
, m
BA
= 0.02
g
β = 72.40
g
, m
β
= 0.01
g
l = 87.10 m, m
l
= 0.02
g
m
XB
= 0.06 m , m
YB
= 0.04 m
Współrzędne punktu 1 wyznaczane są z zależności:
1
1
B
B
X
X
X
D
+
=
1
1
B
B
Y
Y
Y
D
+
=
1
1
cos
B
B
Az
l
X
X
×
+
=
1
1
sin
B
B
Az
l
Y
Y
×
+
=
Na podstawie prawa propagacji błędów losowych błędy standardowe wyznaczane
są z zależności:
2
1
1
2
2
2
1
2
2
2
1
sin
cos
B
B
l
B
XB
X
m
Az
l
m
Az
m
m
×
×
+
×
+
=
2
1
1
2
2
2
1
2
2
2
1
cos
sin
B
B
l
B
YB
Y
m
Az
l
m
Az
m
m
×
×
+
×
+
=
β
B
º
º
1
A
º
l
Rys. 3.2

19
Uwzględniając w powyższych zależnościach, że
b
+
=
BA
B
Az
Az
1
m
m
m
BA
B
+
=
2
2
1
oraz wyrażając błędy standardowe kąta β oraz wyznaczonych azymutów, tj. Az
B1,
Az
BA
, Az
B1
w jednostkach łukowych (w zadaniu podano je w jednostkach
gradowych)
p
2
400
)
(
1
)
(
1
Ł
B
g
g
B
Az
Az
=
wzory na m
X1
, m
Y1
przyjmują postać
(
)
(
)
1
2
2
2
2
2
1
2
2
2
2
1
sin
200
/
cos
B
BA
B
l
XB
X
Az
l
m
m
Az
m
m
m
×
+
+
×
+
=
b
p
(
)
(
)
1
2
2
2
2
2
1
2
2
2
2
1
cos
200
/
sin
B
BA
B
l
YB
Y
Az
l
m
m
Az
m
m
m
×
+
+
×
+
=
b
p
Podstawiając do powyższych wzorów dane liczbowe otrzymujemy
(
) (
) (
)
(
)
(
)
2
2
2
2
2
2
2
1
28
,
238
sin
1
,
87
01
,
0
02
,
0
200
/
28
,
238
cos
04
,
0
06
,
0
×
×
+
+
×
+
=
p
X
m
(
) (
) (
)
(
)
(
)
2
2
2
2
2
2
2
1
28
,
238
cos
10
,
87
01
,
0
02
,
0
200
/
28
,
238
sin
02
,
0
04
,
0
×
×
+
+
×
+
=
p
Y
m
Szukane wartości błędów standardowych współrzędnych punktu 1 wynoszą:
m
X1
= 0.07 [m]
m
Y1
= 0.05 [m].
3.3. Optymalizacja programu obserwacji
P
rawo przenoszenia się błędów jest wykorzystywane przy projektowaniu
pomiaru. Zadanie optymalizacji polega na dopasowaniu błędów składowych tak, by
ich suma wyznaczona z prawa przenoszenia się błędów nie przekroczyła przyjętej
wartości.
Przykład 3.4. Z jaką dokładnością należy wykonać pomiary zbiornika o wymiarach
(przybliżonych) h = 12 m i promieniu R = 8 m, aby jego kubaturę wyznaczyć
z błędem standardowym m
V
= 0,1%.
Ponieważ kubatura zbiornika w przybliżeniu wynosi V = π R
2
h = 2400 m
3
, stąd
oczekiwany błąd standardowy wynosi m
V
@ 2,5 m
3
. Przyjmując, że promień walca
zostanie wyznaczony na podstawie pomiaru obwodu zbiornika, tj. ze wzoru R = L/π,
objętość obliczyć można ze wzoru
h
L
V
2
4
1
p
=
Stosując prawo przenoszenia się błędów

20
2
2
2
2
2
2
4
2
4
1
h
L
V
m
L
m
Lh
m
÷
÷
ø
ö
ç
ç
è
æ
+
÷
ø
ö
ç
è
æ
=
p
p
i podstawiając L = 2πR oraz m
L
= m
h
= m otrzymujemy
( )
( )
2
2
2
2
2
2
m
R
m
Rh
m
V
p
+
=
.
Stąd szukana dokładność pomiaru m wynosi
2
2
2
1
R
h
R
m
m
V
p
+
£
=
+
£
2
2
2
8
12
8
4
5
,
2
p
p
m
0,14 [m]

21
5. Metoda parametryczna.
Wyrównanie sieci liniowo-kątowej
5.1. Model zagadnienia wyrównawczego
W metodzie parametrycznej zwanej również metod pośredniczącą wielkości
mierzone są funkcją wyznaczanych wielkości (parametrów), czyli
(
)
(
)
(
)
m
n
m
m
X
X
X
F
l
X
X
X
F
l
X
X
X
F
l
....
,
.
..........
..........
..........
....
,
....
,
2
1
2
1
2
2
1
1
=
=
=
(5.1)
Celem obliczeń jest wyznaczenie wyrównanych wartości l
i
wyr
, z których każda różni
się od wartości obserwowanej l
i
ob
o wartość poprawki v
i
ob
i
wyr
i
i
l
l
v
-
=
dla i <1,n > (5.2)
Po rozpisaniu zależności (5.2) dla wszystkich n wyników pomiarów powstaje układ
równań poprawek stanowiący podstawę procesu wyrównawczego. Jeśli w
zależnościach (5.1) funkcja F(X
1
,X
2
..X
n
) ma postać nieliniową, to konieczne jest
przekształcenie równań obserwacyjnych za pomocą szeregu Taylora
(
)
m
m
n
dX
y
F
dX
y
F
dX
x
F
X
X
X
F
X
X
X
F
0
2
0
1
0
0
0
2
0
1
2
1
..
.)
..
,
(
...
,
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷
ø
ö
ç
è
æ
¶
¶
+
=
,
(
)
0
0
2
0
1
0
2
1
......
...
,
l
dX
y
F
dX
y
F
dX
x
F
X
X
X
F
m
n
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷÷
ø
ö
çç
è
æ
¶
¶
+
÷
ø
ö
ç
è
æ
¶
¶
=
(5.3)
Po przekształceniu powstaje układ równań poprawek
ob
i
i
m
im
i
i
i
l
l
dX
a
dX
a
dX
a
v
-
+
+
+
=
0
2
2
1
1
...
(5.4)
i
m
im
i
i
i
l
dX
a
dX
a
dX
a
v
+
+
+
=
...
2
2
1
1
(5.5)
0
0
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
=
÷
÷
ø
ö
ç
ç
è
æ
¶
¶
=
j
j
ij
X
l
X
F
a
,
ob
i
i
i
l
l
l
-
=
0
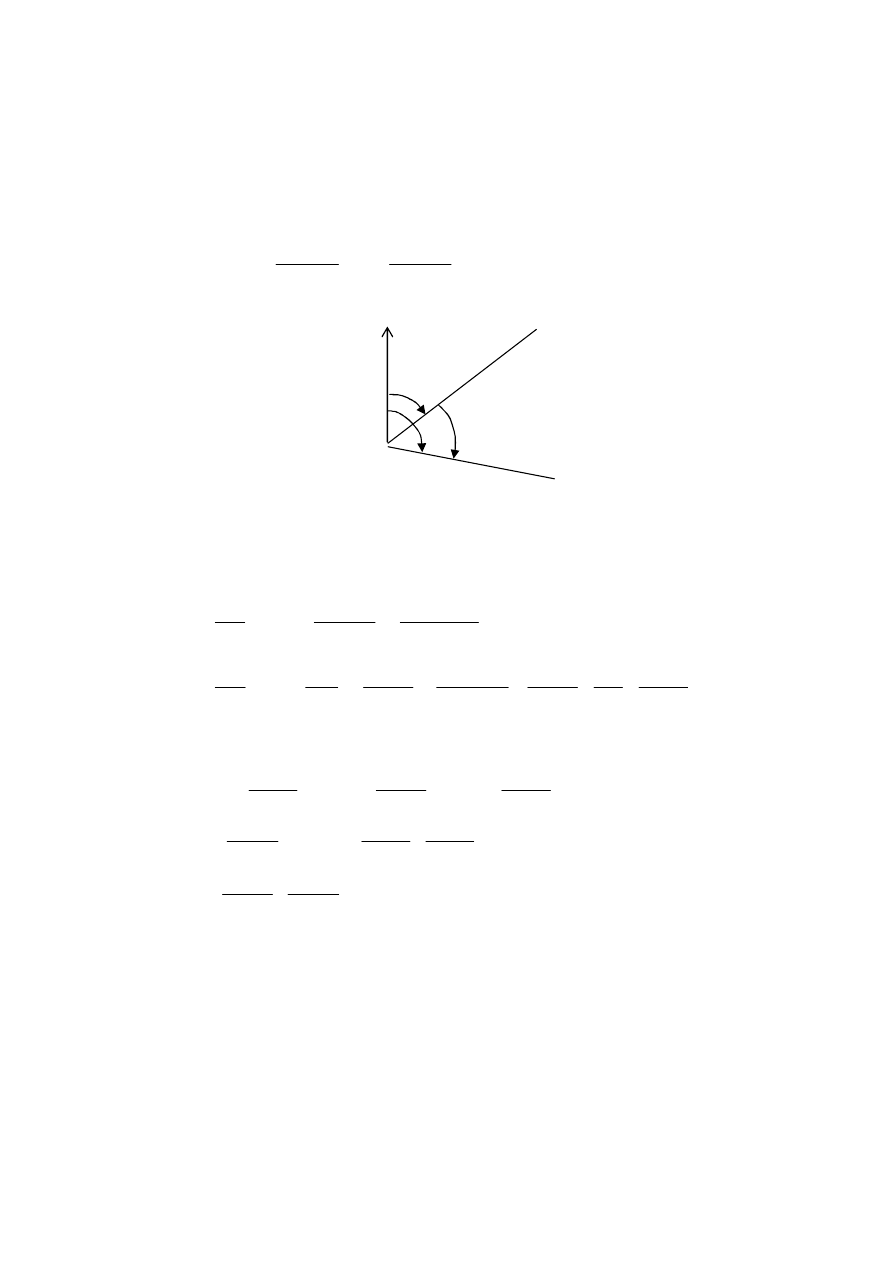
Równanie poprawek kąta poziomego. W przypadku kąta poziomego
b funkcja
(5.1) zdefiniowana jest przez współrzędne trzech punktów
(
)
C
C
P
P
L
L
Y
X
Y
X
Y
X
F
,
,
,
,
,
=
b
22
C
L
C
L
C
P
C
P
X
X
Y
Y
arctg
X
X
Y
Y
arctg
-
-
-
-
-
=
b
(5.6)
Rys.5.1
Zgodnie z wzorem (5.3) należy wyznaczyć pochodne funkcji
b (5.6) względem
wszystkich parametrów występujących we wzorze (9.8), tj. X
L
, Y
L
, X
P
, Y
P
, X
C
, Y
C
.
Przykładowo pierwsza pochodna cząstkowa względem X
L
, ma postać
1)
(
)
(
)
2
2
1
/
1
C
L
C
L
C
L
C
L
L
X
X
Y
Y
X
X
Y
Y
X
-
-
-
ú
ú
û
ù
ê
ê
ë
é
÷÷
ø
ö
çç
è
æ
-
-
+
-
=
¶
¶
b
(
)
(
)
L
L
L
L
L
L
L
L
L
L
L
L
L
L
d
Az
d
Y
X
Y
Y
X
X
X
Y
X
Y
X
sin
1
/
1
2
2
2
2
2
=
D
=
D
D
÷÷
ø
ö
çç
è
æ
D
+
D
D
=
D
D
ú
ú
û
ù
ê
ê
ë
é
÷÷
ø
ö
çç
è
æ
D
D
+
=
¶
¶
b
Po obliczeniu wszystkich pochodnych cząstkowych względem poszczególnych
współrzędnych postać równania obserwacji kąta poziomego β wynosi
i
C
cc
P
P
L
L
C
cc
L
L
P
P
cc
P
P
P
P
cc
P
P
L
cc
L
L
L
cc
L
L
i
l
dY
d
Az
d
Az
dX
d
Az
d
Az
dY
d
Az
dX
d
Az
dY
d
Az
dX
d
Az
v
b
b
r
r
r
r
r
r
+
÷
÷
ø
ö
ç
ç
è
æ
-
+
÷
÷
ø
ö
ç
ç
è
æ
-
+
+
-
-
=
)
(
cos
cos
)
(
sin
sin
)
(
cos
)
(
sin
)
(
cos
)
(
sin
0
0
0
0
0
0
0
0
(5.7)
lub w postaci
L(X
L
,Y
L
)
X
Az
L
Az
P
dP
dL
β
P(X
P
,Y
P
)
C(X
C
,Y
C
)
°
°
°
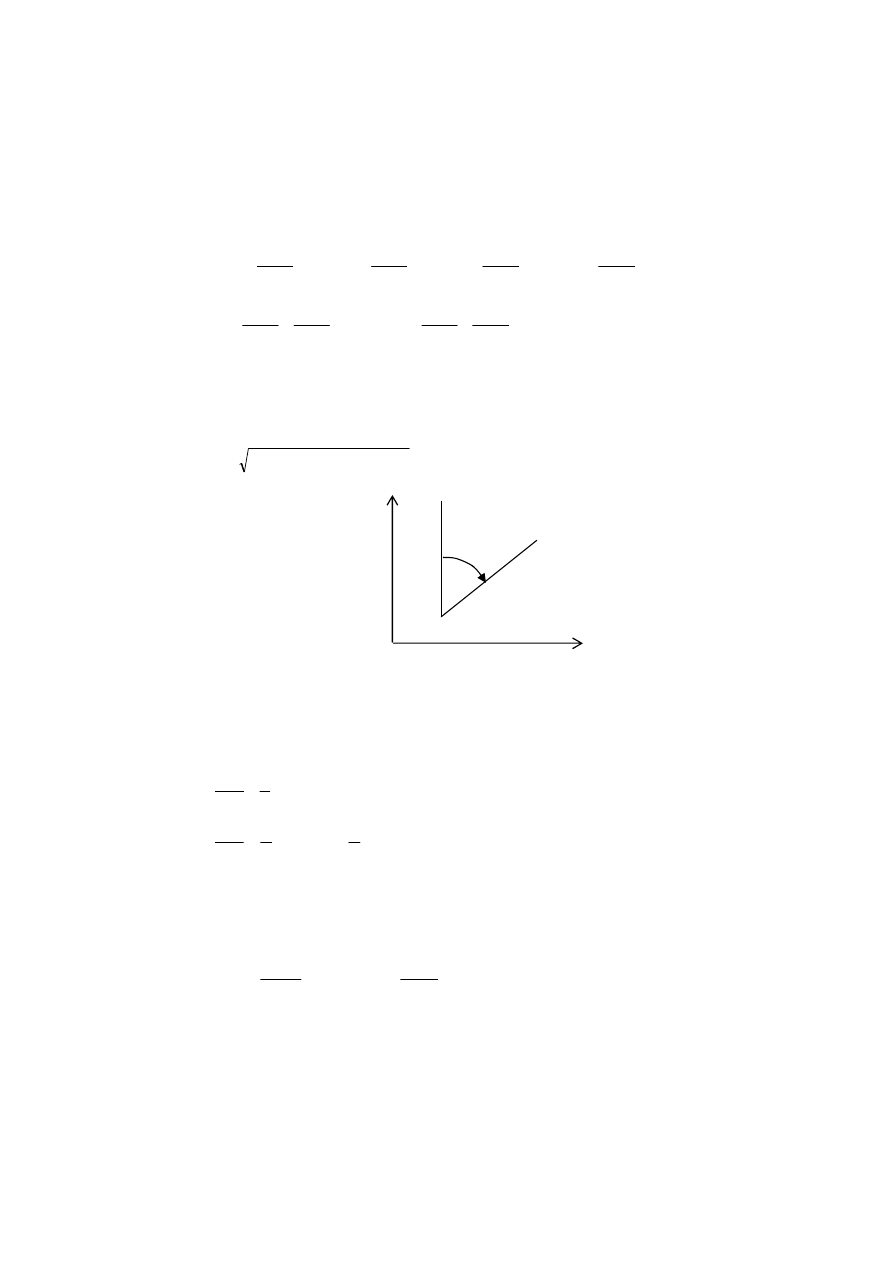
23
( )
( )
( )
( )
( ) ( )
( ) ( )
i
C
cc
P
P
L
L
C
cc
L
L
P
P
P
cc
P
P
P
cc
P
P
L
cc
L
L
L
cc
L
L
i
l
dY
d
X
d
X
dX
d
Y
d
Y
dY
d
X
dX
d
Y
dY
d
X
dX
d
Y
v
+
÷
÷
ø
ö
ç
ç
è
æ
D
-
D
+
÷
÷
ø
ö
ç
ç
è
æ
D
-
D
+
D
+
D
-
D
-
D
=
)
(
)
(
)
(
)
(
)
(
)
(
2
0
0
2
0
0
2
0
0
2
0
0
2
0
0
2
0
0
2
0
0
2
0
0
r
r
r
r
r
r
b
gdzie
(
)
ob
i
i
ob
i
C
C
P
P
L
L
i
l
l
l
Y
X
Y
X
Y
X
F
l
b
b
b
b
-
=
-
=
0
0
0
0
0
0
0
,
,
,
,
,
.
(5.8)
Równanie poprawek dla długości odcinka. W przestrzeni dwuwymiarowej
odcinek PK zdefiniowany jest jednoznacznie przez współrzędne X,Y jego końców,
(
) (
)
2
2
P
K
P
K
X
X
Y
Y
d
-
+
-
=
. (5.9)
Rys. 5.2
.
Dla wyznaczenia równania poprawek należy przekształcić zależność (5.9) do
postaci liniowej za pomocą wzoru Taylora. W tym celu należy wyznaczyć
pochodne wielkości mierzonej względem poszczególnych parametrów
(współrzędnych końców odcinka. W przypadku parametru Y
K
wynosi
(
) (
)
[
]
(
)
P
K
P
K
P
K
K
Y
Y
X
X
Y
Y
Y
d
-
-
+
-
=
¶
¶
-
2
2
1
2
/
1
2
2
(
)
Az
Az
d
d
Y
Y
d
Y
d
P
K
K
sin
sin
1
1
=
×
=
-
=
¶
¶
(5.10)
Uwzględniając azymut analizowanej długości (Az
PK
), równanie poprawek dla
długości d przyjmuje ostatecznie postać
v
dPK
= cos Az
PK
(dX
K
- dX
P
) + sin Az
PK
(dY
K
- dY
P
) + l
d
(5.11)
lub
d
P
K
PK
PK
P
K
PK
PK
dPK
l
dX
dY
d
Y
dX
dX
d
X
v
+
-
D
+
-
D
=
)
(
)
(
(5.12)
gdzie
K
P
X
Az
PK
Y
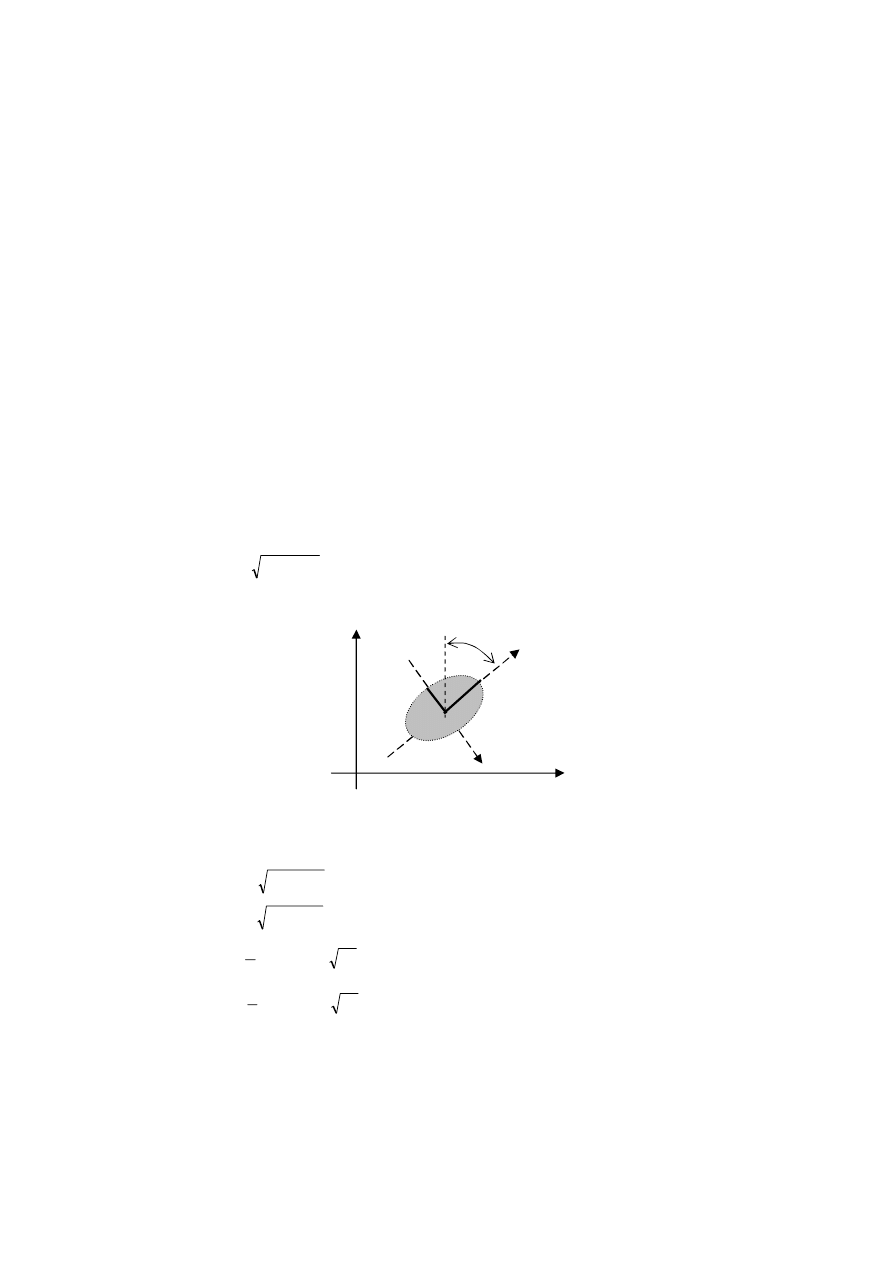
24
(
)
ob
d
d
ob
d
K
K
P
P
d
l
l
l
Y
X
Y
X
F
l
-
=
-
=
0
0
0
0
0
,
,
,
(5.13)
Równanie poprawek dla różnicy wysokości. Ponieważ różnica wysokości
h=F(H
K
,H
P
) zapisana jest w postaci liniowej
v
i
= H
K
– H
P
+ h (5.14)
stąd równanie poprawek można wyprowadzić bez zastosowania wzoru Taylora.
v
i
= dH
K
– dH
P
+ h
i
(5.15)
5.2. Ocena dokładności
Ocena formułowana jest za pomocą:
§
błędu położenia punktu,
§
elipsy ufności,
§
błędów średnich wyrównanych obserwacji.
Błąd położenia punktu określa formuła
2
2
Y
X
P
m
m
m
+
=
(5.16)
Obszar ufności najpełniej określa elipsa ufności (rys.5.3).
Rys. 5.3. Pole elipsy wewnątrz której punkt znajduje się z prawdopodobieństwem
g
Elipsę identyfikują jej półosie a, b oraz kąt skręcenia
j,
g
l
F
m
a
×
=
-1
1
0
2
(5.17)
g
l
F
m
b
×
=
-1
2
0
2
(5.18)
(
)
i
Yi
Xi
P
P
D
-
+
=
2
1
1
l
(5.19)
(
)
i
Yi
Xi
P
P
D
+
+
=
2
1
2
l
(5.20)
X
Y
Y’
X’
a
b
j
Y’

25
(
)
2
2
4
XiYi
Yi
Xi
P
P
P
+
-
=
D
(5.21)
Kąt skręcenia
j wyznaczany jest ze wzoru
Yi
Xi
XiYi
P
P
P
arctg
-
=
2
2
1
j
(5.22)
We wzorach na wartości własne macierzy
l
1
(5.19),
l
2
(5.20) oraz kąt skręcenia
j
(5.22) wielkości P są wyznaczane z zależności
ú
û
ù
ê
ë
é
=
=
Y
XY
XY
X
P
P
P
P
PA
A
P
T
(5.23)
Wartość F konieczna przy obliczaniu elementów elipsy przyjmowana jest z tablic
F - Snedecora dla n - r stopni swobody (n – liczba obserwacji, r – liczba
niewiadomych). Najczęściej stosowane wartości F podano w tab. 5.1.
Tablica 5.1
n - r
g
0,95
0,99
1
2
3
4
199.50
19.00
9.55
6.94
5000
99.01
30.83
17.99
5.3. Algorytm obliczeń
Obliczenia wykonywane są według algorytmu, który oparty jest na metodzie
najmniejszych kwadratów. Algorytm jest realizowany w następujących etapach.
Zestawienie wyników obserwacji
Układ równań obserwacyjnych
Równania poprawek
Układ równań normalnych.
Rozwiązanie układu równań normalnych
Wektor poprawek
Wyrównane wartości wielkości obserwowanych
Kontrole obliczeń
Współczynnik wariancji m
o
2
Macierz kowariancji i błędy średnie wyznaczanych parametrów
Błędy średnie wyrównanych wielkości obserwowanych
Przedział (obszar) ufności, elipsa ufności.
26
Kontrola 1 polega na porównaniu wartości s = s' obliczonych ze wzorów
s = V
T
V lub s = V
T
P
V
s’ = L
T
×
P
×A×X + L
T
×
P
×L
W kontroli 2 wartości wyrównane wyliczane są dwoma sposobami
l
wyr
= l
ob
+ V
l
wyr
= A
×dX + L
0
Proces iteracyjny. Istotną częścią algorytmu jest iteracyjny tryb obliczeń. Model
zagadnienia jest nieliniowy, a w algorytmie aproksymacji wykorzystuje się tylko
pierwszą pochodną. Wyniki pierwszego rozwiązania są traktowane jako wartości
przybliżone i wprowadzone do algorytmu w drugiej iteracji. Obliczenia są
prowadzone w pętli programu komputerowego tak długo, aż wartość korekty
będzie dostatecznie mała, np. równa 0.1 wyniku uzyskanego w poprzedniej iteracji.
Duże znaczenie ma dokładność przybliżonych wartości niewiadomych
stanowiących punkt startowy. Im wartości te są bliższe prawidłowego rozwiązania,
tym mniej iteracji trzeba dla uzyskania poprawnego wyniku. Jeśli jednak punkt
startowy będzie zbyt odległy, proces iteracyjny może nie dać poprawnego
rozwiązania, lub być rozbieżny.
5.4. Przykład wyrównania sieci liniowo-kątowej
Wyrównać elementarną sieć liniowo-kątową przedstawioną na rys. 5.4. Wyniki
pomiarów zestawiono w tabl. 5.2. Obliczyć:
§
współrzędne p.3
§
błędy średnie wyrównanych obserwacji
β
1
, β
2
, β
3
, d
1,3
, d
2,3
.
Wyniki pomiarów Tablica 5.2
Wielkość
pomierzona
Wynik
pomiaru
Błąd
pomiaru
β
1
ob
69.4555
10
cc
β
2
ob
73.2860
20
cc
β
3
ob
57,2635
30
cc
d
1,3
ob
174.960
0.02 m
d
2,3
ob
169.954
0.01 m
Punkt
X
Y
1
100.000
200.000
2
100.000
350.000
2
1
X
β
1
Y
3
β
2
d
13
d
23
Rys. 5.4
β
3
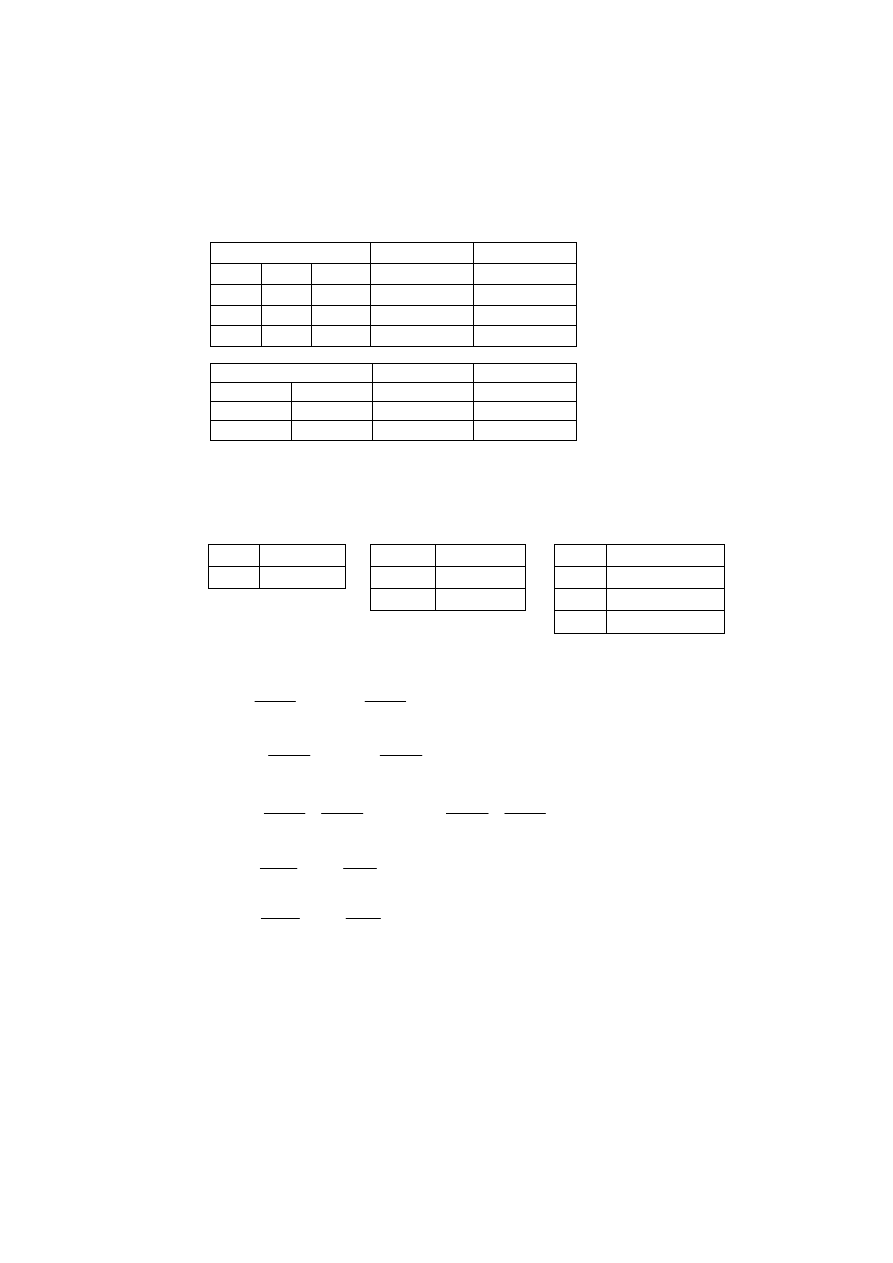
27
Oznaczenie kąta
Wartość kąta Błąd pomiaru
L
P
C
β
i
ob
m
βi
-
3
2
1
69,4555
10
cc
1
3
2
73,2860
20
cc
2
1
3
57,2635
30
cc
Oznaczenie długości
Długość boku Błąd pomiaru
P
K
d
i
ob
m
di
-
1
3
174.960
0.020
2
3
169.954
0.010
Przybliżone wartości niewiadomych - współrzędnych p.3(X
3
0
,Y
3
0
) oraz wielkości
obserwowanych
β
1
0
, β
2
0
,
β
3
0
, d
1,3
0
, d
2,3
0
wyznaczono p
rzyjmując
d
1,3
0
= d
1,3
ob
,
β
1
0
=
β
1
ob
.
Na podstawie tak ustalonych współrzędnych wyznaczono następnie wartości
d
2,3
0
,
β
2
0
oraz azymuty Az
13
0
i Az
23
0
X
3
0
255.2054
β
1
0
69.4555
g
d
1,3
0
174.9600 m
Y
3
0
280.7606
β
2
0
73.28628
g
d
2,3
0
169.9495 m
β
3
0
57,25822
g
Az
13
0
30.54450
g
Az
23
0
373.28628
g
Równania poprawek
V = A
×dX + L; L = L
0
- L
ob
( )
( )
( )
( )
( ) ( )
( ) ( )
23
3
0
23
0
23
3
0
23
0
23
23
13
3
0
13
0
13
3
0
13
0
13
13
3
3
2
0
31
0
31
2
0
32
0
32
3
2
0
32
0
32
2
0
31
0
31
3
2
3
2
0
23
0
23
3
2
0
23
0
23
2
1
3
2
0
13
0
13
3
2
0
13
0
13
1
d
d
d
d
cc
cc
cc
cc
cc
cc
l
dY
d
Y
dX
d
X
v
l
dY
d
Y
dX
d
X
v
l
dY
d
X
d
X
dX
d
Y
d
Y
v
l
dY
d
X
dX
d
Y
v
l
dY
d
X
dX
d
Y
v
+
D
+
D
=
+
D
+
D
=
+
÷
÷
ø
ö
ç
ç
è
æ
D
-
D
+
÷
÷
ø
ö
ç
ç
è
æ
D
-
D
=
+
D
+
D
-
=
+
D
-
D
=
b
b
b
b
b
b
r
r
r
r
r
r
gdzie
ob
ob
ob
l
l
l
l
l
l
l
l
l
3
0
3
3
2
0
2
2
1
0
1
1
b
b
b
b
b
b
b
b
b
-
=
-
=
-
=
ob
d
d
d
ob
d
d
d
l
l
l
l
l
l
13
0
13
13
13
0
13
13
.
-
=
-
=
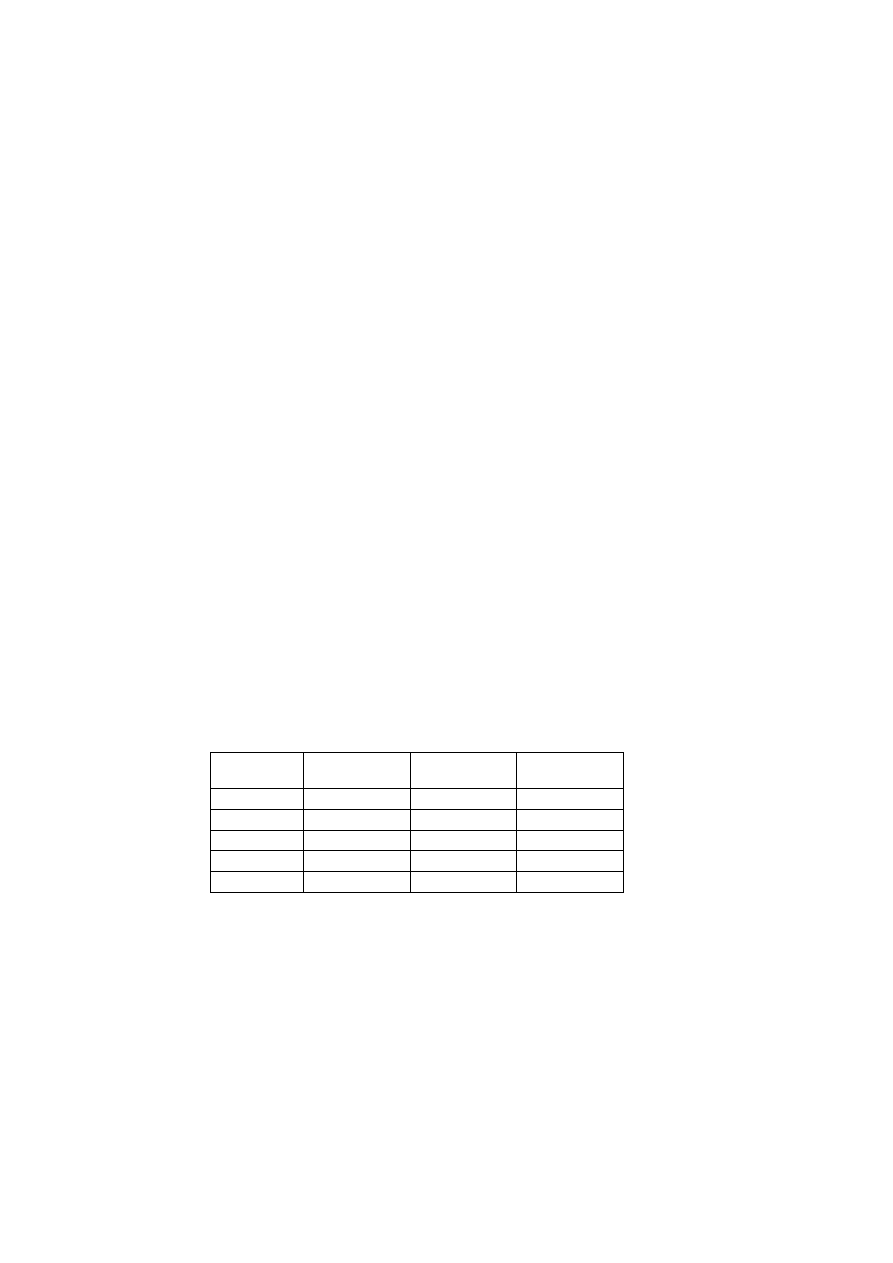
28
Macierze występujące w układzie równań normalnych
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
=
407412
,
0
913245
,
0
461594
,
0
887091
,
0
134
,
193
723
,
3205
955
,
3420
138
,
1526
822
,
3227
585
,
1679
A
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
=
m
m
cc
cc
cc
00452
,
0
0
8
,
52
8
,
2
0
L
Jednostki elementów macierzy A, L, P są metryczne i kątowe.
Układ równań normalnych
A
T
P
×A ×dX + A
T
P
×L = 0
Rozwiązanie układu równań normalnych
dX = – (A
T
P
×A)
-1
A
T
×P×L
ú
û
ù
ê
ë
é
=
135679,623
43170,941
-
43170,941
-
55758,808
PA
A
T
ú
û
ù
ê
ë
é
=
70686
,
53
439226
,
157
PL
A
T
(
)
ú
û
ù
ê
ë
é
-
-
-
-
-
-
=
-
05
E
7795
,
9
07
E
57172
,
7
07
E
57172
,
7
05
E
37967
,
2
PA
A
1
T
m
ú
û
ù
ê
ë
é
-
-
=
00172
,
0
00415
,
0
dX
Wartości parametrów - wyrównanych współrzędnych pkt.3
X
= X
0
+ dX
X
3
= 255,20544 - 0,00415 = 255,20129
Y
3
= 280,76059-0,00172 = 280,75887
Wektor poprawek
V = A
×dX + L
Wyrównane wartości wielkości obserwowanych
β
i
wyr
=
β
i
ob
+ v
i
d
i
wyr
=
d
i
ob
+ v
i
Wielkość
pomierzona
Wynik pomiaru
Poprawka
v
Wartości
wyrównane
β
1
69.4555
g
-1,4
cc
69.4554
g
β
2
73.2860
g
-9,4
cc
73.2851
g
β
3
57,2635
g
-39,2
cc
57,2596
d
1,3
174.960 m
-0,0045 m
174.9555 m
d
2,3
169.954 m
-0,0076 m
169.9464 m
Kontrola 1
V
T
P
×V = L
T
×
P
×A×dX + L
T
×P×L
2,575729 = 2,575729
Kontrola 2. Obliczenie wyrównanych wartości obserwacji na podstawie wyrówna-
nych współrzędnych. W tym celu należy wyznaczyć azymuty Az
12
, Az
13
, Az
23
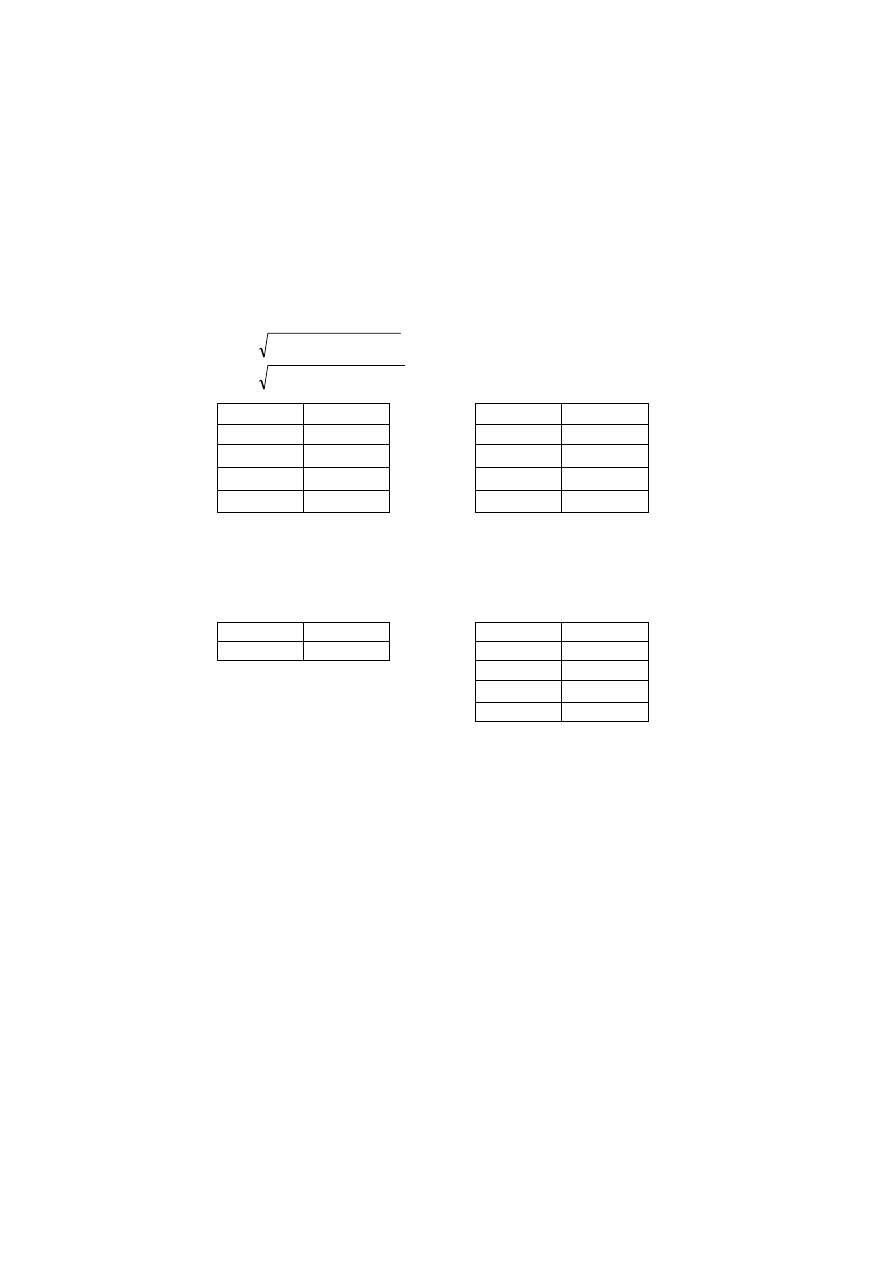
29
32
31
3
21
23
2
13
12
1
Az
Az
Az
Az
Az
Az
wyr
wyr
wyr
-
=
-
=
-
=
b
b
b
(
) (
)
(
) (
)
2
2
3
2
2
3
23
2
1
3
2
1
3
13
Y
Y
X
X
d
Y
Y
X
X
d
wyr
wyr
-
+
-
=
-
+
-
=
X
3
wyr
255,2013
β
1
wyr
69.45535
g
Y
3
wyr
280,7589
β
2
wyr
73.28506
g
Az
12
wyr
100.0000
g
β
3
wyr
57.25958
g
Az
13
wyr
30.54465
g
d
1,3
wyr
174.9555 m
Az
23
wyr
373.28507
g
d
2,3
wyr
169.9464 m
Wartości wyrównane obliczone dwoma sposobami są identyczne.
II iteracja
Jako przybliżone wartości niewiadomych - współrzędnych p.3 (X
3
0
,Y
3
0
) oraz
wielkości obserwowanych
β
1
0
, β
2
0
, β
3
0
, d
1,3
0
, d
2,3
0
p
rzyjmujemy wyniki I iteracji.
X
3
0
255,2013
β
1
0
69.45535
g
Y
3
0
280,7589
β
2
0
73.28506
g
β
3
0
57,25959
g
d
1,3
0
174.9555 m
d
2,3
0
169.9464 m
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
=
407429
,
0
913237
,
0
461597
,
0
887090
,
0
088
,
193
867
,
3205
988
,
3420
231
,
1526
900
,
3227
636
,
1679
A
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
-
=
m
m
cc
cc
cc
00762
,
0
00445
,
0
2
,
39
3
,
9
5
,
1
L
Układ równań normalnych
A
T
P
×A ×dX + A
T
P
×L = 0
Rozwiązanie układu równań normalnych
dX = – (A
T
P
×A)
-1
A
T
×P×L
]
1
[
T
135685,4
43173,2
-
43173,2
-
55762,08
PA
A
ú
û
ù
ê
ë
é
=
[ ]
m
ú
û
ù
ê
ë
é-
=
181563
,
3
47316
,
0
PL
A
T
(
)
[ ]
1
1
T
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
PA
A
ú
û
ù
ê
ë
é
-
-
-
-
=
-
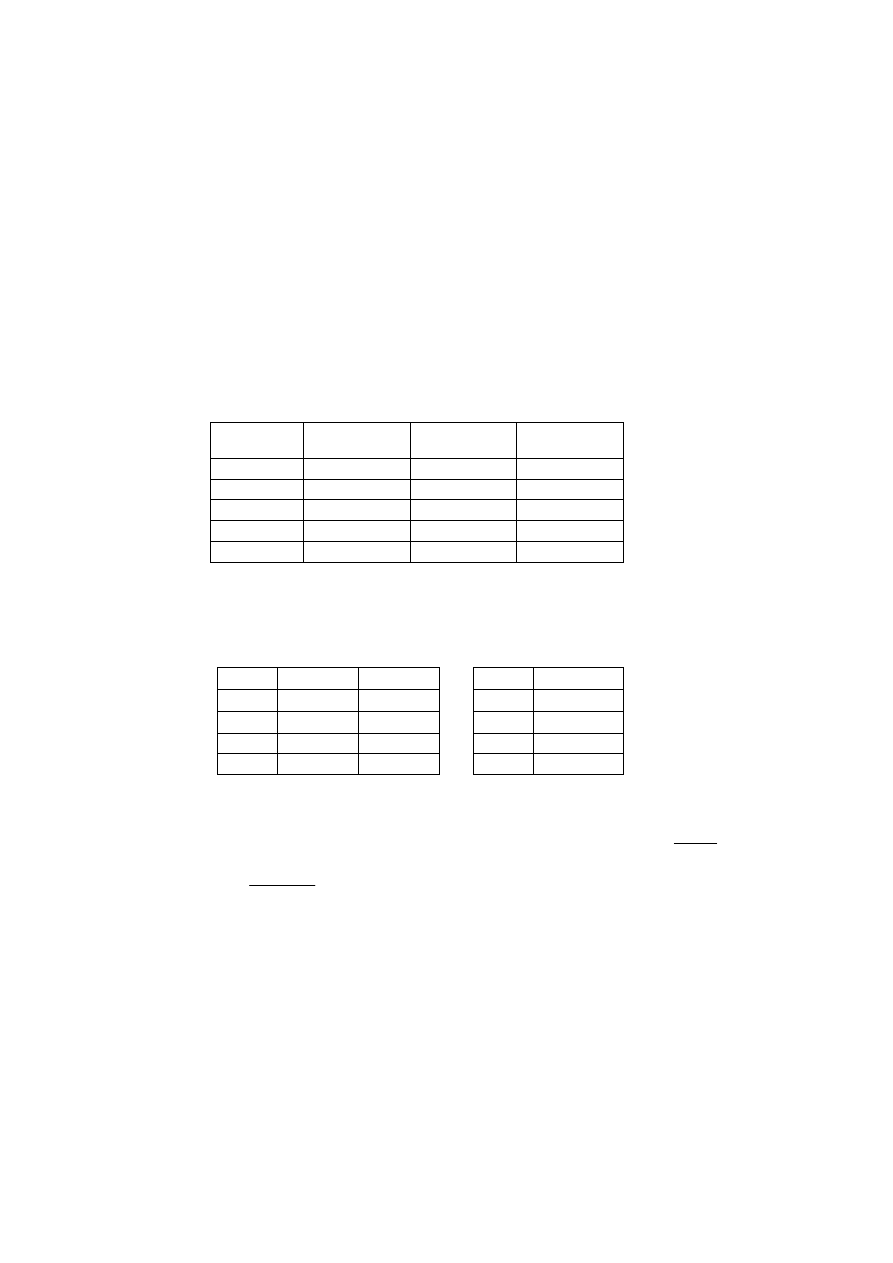
30
[ ]
m
ú
û
ù
ê
ë
é
-
-
=
000028
,
0
000013
,
0
dX
Wartości parametrów - wyrównanych współrzędnych pkt.3.
X
= X
0
+ dX
X
3
= 255,20129 + 0,00170 = 255,20299
Y
3
= 280,75887+ 0,00035 = 280,75922
Uzyskany wynik jest praktycznie identyczny z rezultatem I iteracji z dokładnością
do kilku setnych części milimetra.
Wektor poprawek V = A
×dX + L
Wielkość
pomierzona
Wynik pomiaru
Poprawka
v
Wartości
wyrównane
β
1
69.4555
g
-1.4
cc
69.4554
g
β
2
73.2860
g
-9.4
cc
73.2851
g
β
3
57.2635
g
-39.2
cc
57.2596
g
d
1,3
174.960 m
-0,0045 m
174.9555 m
d
2,3
169.954 m
-0,0076 m
169.9464 m
Kontrola obliczeń 1
V
T
P
×V = L
T
×
A
×dX + L
T
×P×L
2,57562 = 2,57562
Kontrola obliczeń 2. Obliczenie wyrównanych wartości obserwacji na podstawie
wyrównanych współrzędnych
X
Y
b
1
wyr
69.45536
g
1
100.000
200.000
b
2
wyr
73.28506
g
2
100.000
350.000
b
3
wyr
57.25959
3
255.2013 280.7589
d
1-3
wyr
174.9555 m
d
2-3
wyr
169.9464 m
ANALIZA DOKŁADNOŚCI
Współczynnik wariancji m
o
2
u
n
m
-
=
PV
V
T
2
0
16818
,
0
2
5
0,504547
2
0
=
-
=
m
Macierz kowariancji
(
)
1
T
2
0
PA
A
-
= m
C
X
ú
û
ù
ê
ë
é
-
-
-
-
=
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
16818
,
0
X
C
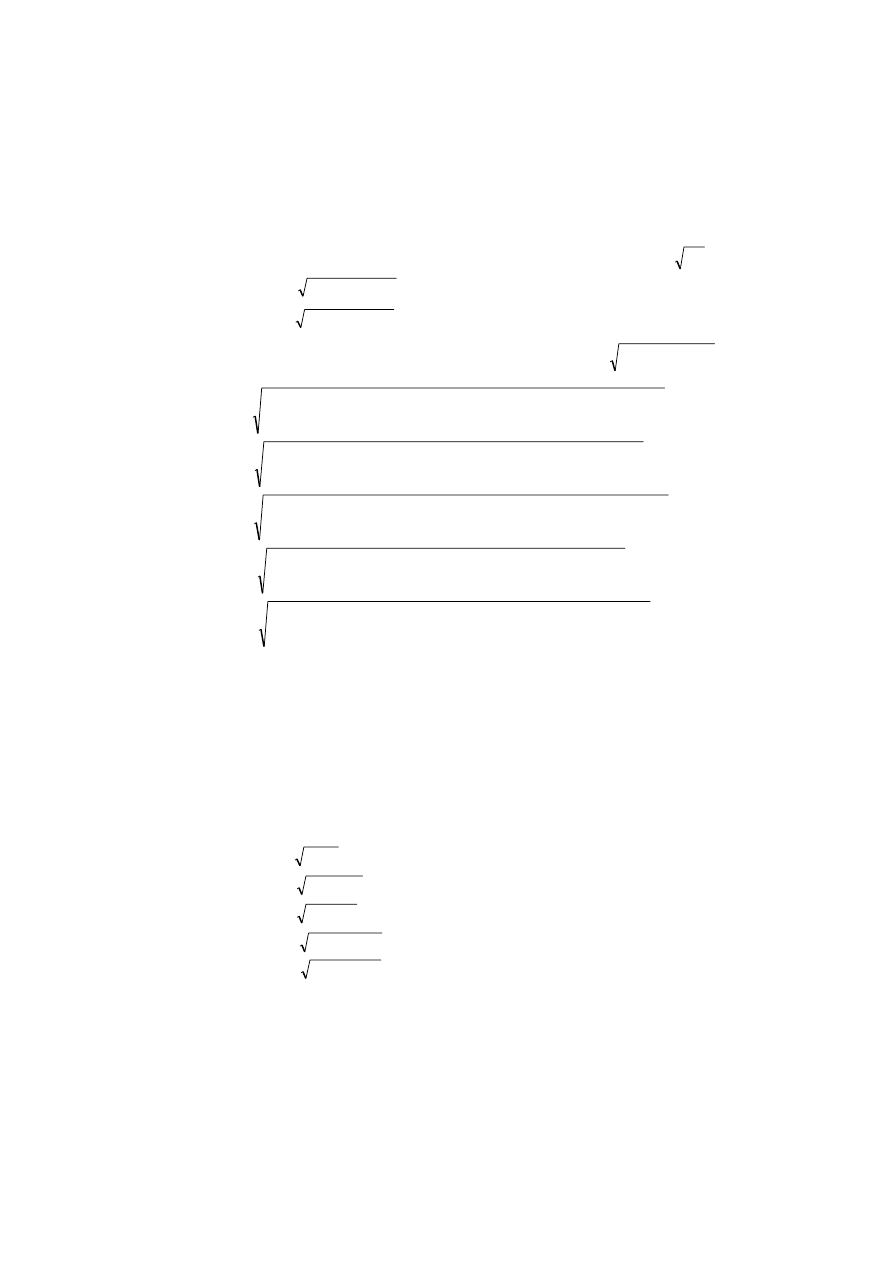
31
Błędy średnie wyznaczanych parametrów
jj
Xj
q
m
m
0
=
m
E
m
X
0020
,
0
05
37954
,
2
4101
,
0
3
=
-
=
m
E
m
Y
0013
,
0
05
77909
,
9
4101
,
0
3
=
-
=
Błędy średnie wyrównanych obserwacji
(
)
T
i
i
i
a
a
m
m
1
T
0
PA
A
-
=
[
]
[
]
[
]
[
]
[
]
m
m
m
m
m
m
m
d
d
cc
cc
cc
0016
,
0
4074
,
0
9132
,
0
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
4074
,
0
9132
,
0
4101
,
0
0021
,
0
4616
,
0
8871
,
0
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
4616
,
0
8871
,
0
4101
,
0
5
,
6
09
,
193
87
,
3205
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
09
,
193
87
,
3205
4101
,
0
5
,
6
99
,
3420
23
,
1526
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
99
,
3420
23
,
1526
4101
,
0
8
,
3
90
,
3227
64
,
1679
06
E
77909
,
9
06
E
57136
,
7
06
E
57136
,
7
05
E
37954
,
2
90
,
3227
64
,
1679
4101
,
0
23
13
3
2
1
=
ú
û
ù
ê
ë
é
-
ú
û
ù
ê
ë
é
-
-
-
-
-
=
=
ú
û
ù
ê
ë
é
ú
û
ù
ê
ë
é
-
-
-
-
=
=
ú
û
ù
ê
ë
é
-
-
ú
û
ù
ê
ë
é
-
-
-
-
-
-
=
=
ú
û
ù
ê
ë
é
ú
û
ù
ê
ë
é
-
-
-
-
=
=
ú
û
ù
ê
ë
é
-
ú
û
ù
ê
ë
é
-
-
-
-
-
=
b
b
b
Wyznaczenie błędów średnich wyrównanych obserwacji za pomocą
ich macierzy kowariancji.
T
X
L
A
AC
C
=
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
-
-
-
-
-
-
-
-
-
-
=
05
583
,
1
05
793
,
1
0603
,
0
0385
,
0
0219
,
0
05
793
,
1
05
701
,
2
0810
,
0
0759
,
0
0051
,
0
0603
,
0
0810
,
0
297
,
254
156
,
208
14
,
46
0385
,
0
0759
,
0
156
,
208
938
,
248
78
,
40
0219
,
0
0051
,
0
14
,
46
78
,
40
92
,
86
16818
,
0
E
E
E
E
C
L
m
0016
,
0
05
583
,
1
4101
,
0
m
0021
,
0
05
701
,
2
4101
,
0
5
,
6
297
,
254
4101
,
0
5
,
6
9383
,
248
4101
,
0
8
,
3
92
,
86
4101
,
0
23
13
2
2
1
=
-
=
=
-
=
=
=
=
=
=
=
E
m
E
m
m
m
m
d
d
cc
cc
cc
b
b
b
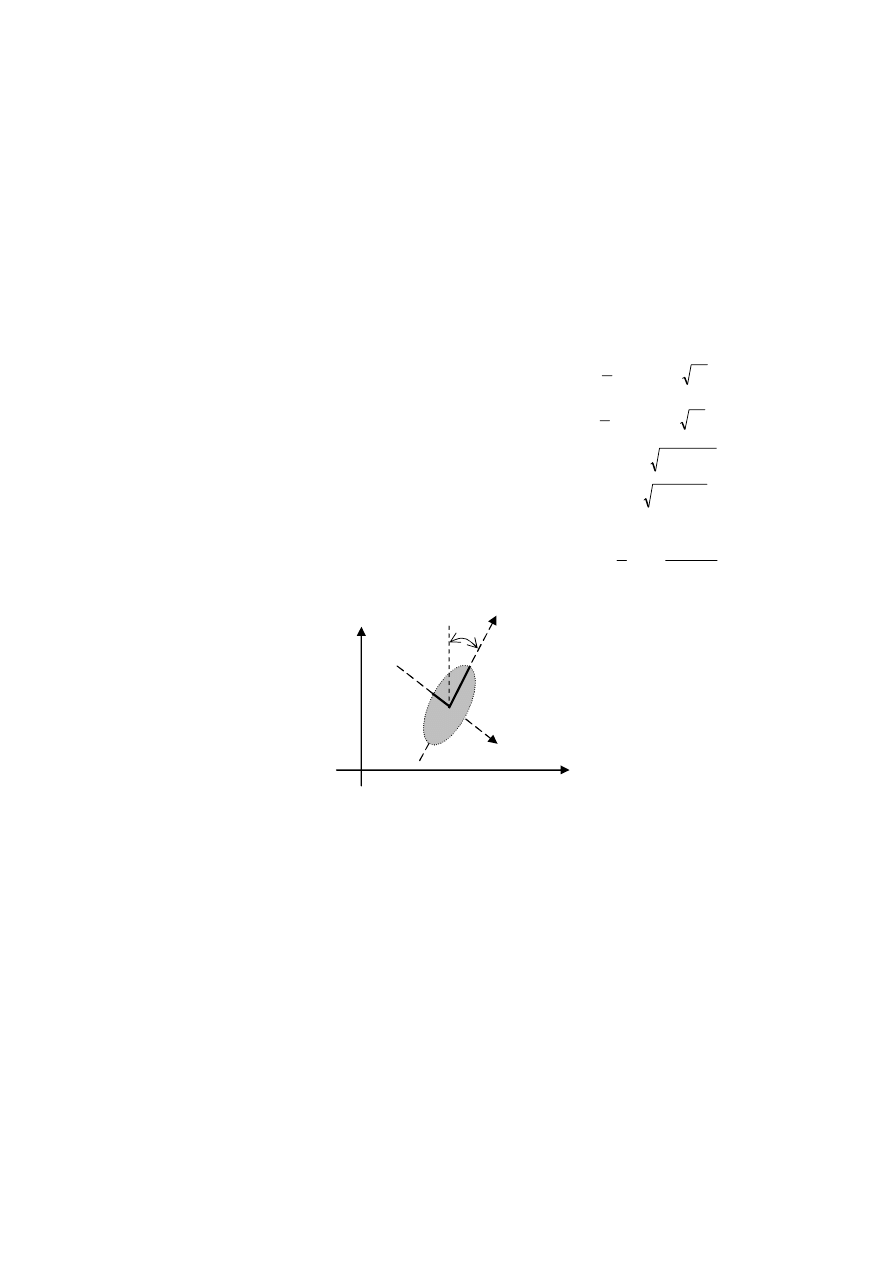
32
Elipsa błędów, półosie a, b
ú
û
ù
ê
ë
é
=
2
135679,623
9
43170,9409
-
9
43170,9409
-
8
55758,8079
P
ú
û
ù
ê
ë
é
=
=
Y
XY
XY
X
P
P
P
P
PA
A
P
T
D = 13843444328
(
)
2
2
4
XiYi
Yi
Xi
P
P
P
+
-
=
D
l
1
= 36894,66
(
)
i
Yi
Xi
P
P
D
-
+
=
2
1
1
l
l
2
= 154552,83
(
)
i
Yi
Xi
P
P
D
+
+
=
2
1
2
l
a = 0,0093
g
l
F
m
a
×
=
-1
1
0
2
b = 0,0046
g
l F
m
b
×
=
-1
2
0
2
Kąt skręcenia
j
j = 26,23
g
Yi
Xi
XiYi
P
P
P
arctg
-
=
2
2
1
j
Rys. 5.5. Elipsa błędów punktu 3 dla prawdopodobieństwa
g
= 95%
X
Y
X’
a
b
j
Y’
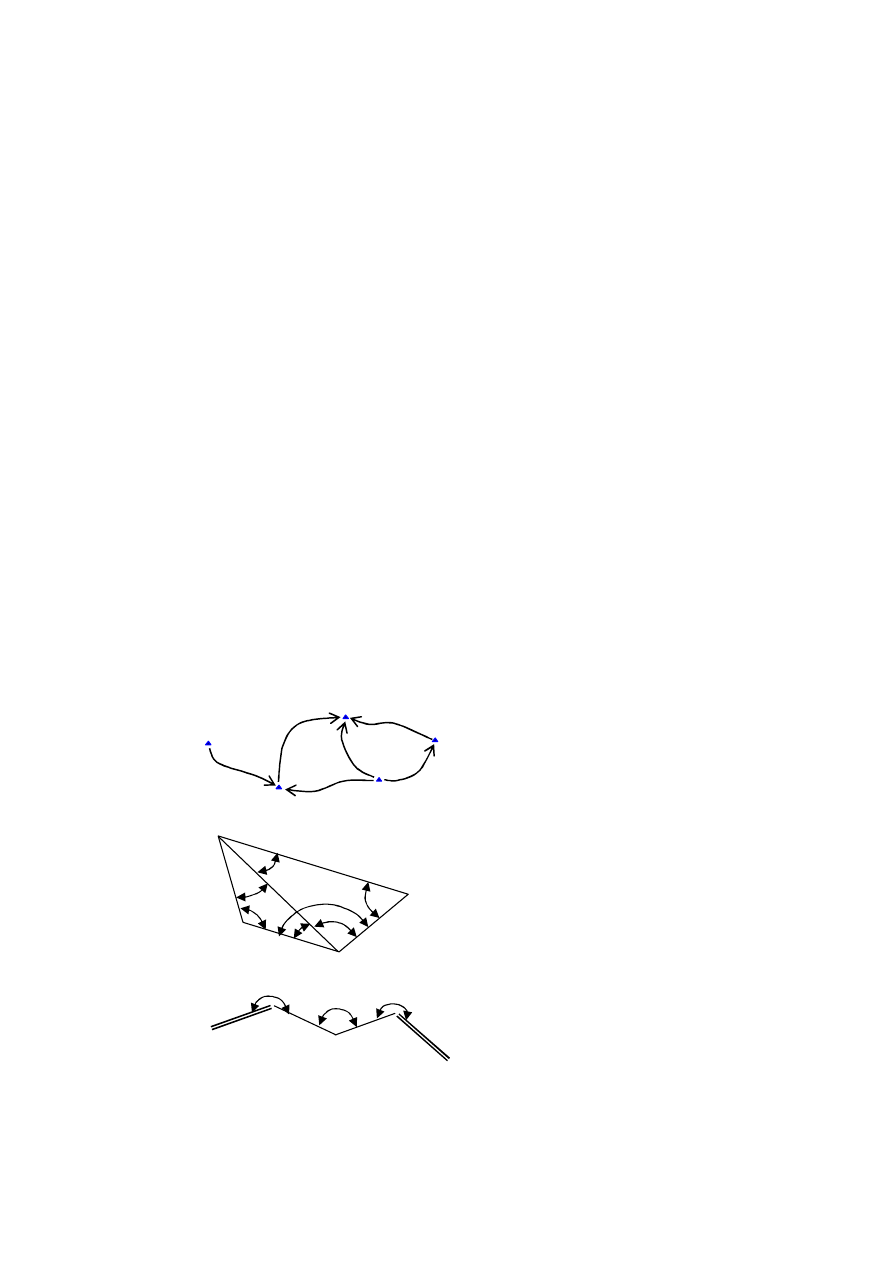
33
6. Metoda warunkowa
6.1. Model zagadnienia wyrównawczego
W metodzie warunkowej przedmiotem analizy są zależności pomiędzy
wielkościami podlegającymi wyrównaniu. W trójkącie np. zachodzi
g
200
3
2
1
=
+
+
a
a
a
.
Model zagadnienia ma postać układu „f” niezależnych równań warunkowych
(
)
(
)
(
)
0
,...
,
.......
..........
..........
0
,...
,
0
,...
,
2
1
2
1
2
2
1
1
=
Y
=
Y
=
Y
n
f
n
n
x
x
x
x
x
x
x
x
x
W powyższym układzie równań, inaczej niż w metodzie parametrycznej, nie
występują parametry – współrzędne punktów. Dzięki temu metoda warunkowa
może być stosowana także w przypadku, gdy nie ma punktów stałych.
6.2. Przykłady równań warunkowych
h
1
+ h
2
- h
3
+ H
R2
- H
R1
= 0
h
2
- h
4
+ h
5
= 0
h
3
- h
4
+ h
6
= 0
α
1
+ α
2
+ α
3
- 200
g
= 0
α
4
+ α
5
+ α
6
- 200
g
= 0
α
7
- α
2
- α
3
= 0
A
°
°
B
°
C
d
1
D
°
α
1
d
2
α
2
α
3
α
6
α
1
α
2
α
3
α
4
α
5
α
7
Rp. 1
Rp. 2
H.1
H.2
H.3
h
1
h
2
h
3
h
4
h
5
h
6
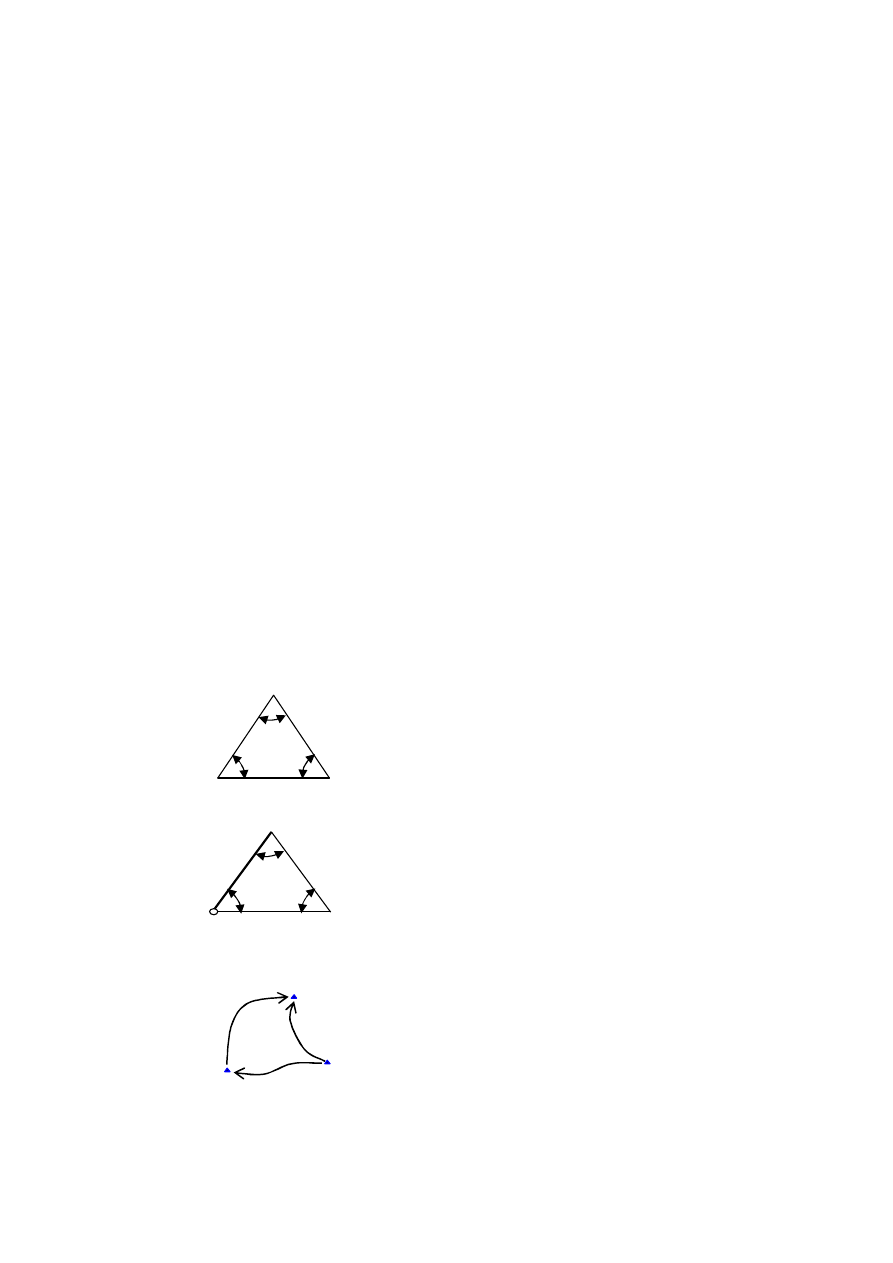
34
α
1
+ α
2
+ α
3
- 3
´200
g
+A
AB
– A
CD
= 0
d
1
cos(A
AB
+ α
1
– 200
g
)
- d
2
cos(A
AB
+ α
1
+ α
2
– 400
g
) – X
B
+ X
C
= 0
d
1
sin(A
AB
+ α
1
– 200
g
)
- d
2
sin(A
AB
+ α
1
+ α
2
– 400
g
) – Y
B
+ Y
C
= 0
Liczba równań warunkowych, defekt sieci
.
Liczbę równań warunkowych
ustala się z wzoru
f = n – r + d
f – liczba równań warunkowych,
n - liczba obserwacji,
r – liczba niewiadomych,
d – defekt.
Defekt d wyznaczany jest jako suma defektu zewnętrznego d
z
i wewnętrznego d
w
d = d
z
+ d
w
Defekt zewnętrzny równa się liczbie stopni swobody całej sieci względem osi
układu współrzędnych. Są to obroty i przesunięcia względem tych osi. Sieć jest
swobodna jeśli defekt d
z
¹ 0.
Defekt wewnętrzny charakteryzuje możliwość wzajemnego przemieszczania się
punktów sieci. Praktycznie jest to liczba brakujących obserwacji niezbędnych.
Defekt eliminuje nawiązanie sieci do punktów o znanych współrzędnych.
Przykłady sieci elementarnych
n = 3
d
z
= 3
d
w
= 1 (trójkąt może się powiększać)
d = d
z
+ d
w
= 4
r = 3
´ 2 = 6
f = n – r + d = 3 – 6 + 4 = 1
n = 4
d
z
= 1 (możliwy jest tylko obrót)
d
w
= 0
d = d
z
+ d
w
= 1
r = 2
´2 = 4
f = n – r + d = 4 – 4 + 1 = 1
n = 3
d
z
= 1
d
w
= 0
a
1
α
2
α
3
α
1
α
2
α
3
l
A
h
2
h
3
h
1

35
d = d
z
+ d
w
= 0
r = 1
´ 3 = 3 (Rzędne H trzech punktów)
f = n – r + d = 3 – 3 + 1 = 1
n = 3
d
z
= 0
d
w
= 0
d = d
z
+ d
w
= 0
r = 1
´ 2 = 2 (Rzędne H dwóch punktów)
f = n – r + d = 3 – 2 + 0 = 1
n = 6
d
z
= 3
d
w
= 0
d = d
z
+ d
w
= 3
r = 4
´ 2 = 8 (X,Y czterech punktów)
f = n – r + d = 6 – 8 + 3 = 1. Jedno równanie
wykorzystujące wzór sinusów.
6.3. Algorytm metody warunkowej
Jeśli w układzie
(
)
(
)
(
)
0
,...
,
.......
..........
..........
0
,...
,
0
,...
,
2
1
2
1
2
2
1
1
=
Y
=
Y
=
Y
n
m
n
n
x
x
x
x
x
x
x
x
x
(6.1)
podstawić w miejsce x
i
wyrażenie
x
i
= x
i
obs
+ v
i
(6.2)
to uzyskujemy:
(
)
(
)
(
)
0
,...
,
.......
..........
..........
0
,...
,
0
,...
,
2
2
1
1
2
2
1
1
2
2
2
1
1
1
=
+
+
+
Y
=
+
+
+
Y
=
+
+
+
Y
n
ob
n
ob
ob
m
n
ob
n
ob
ob
n
ob
n
ob
ob
v
x
v
x
v
x
v
x
v
x
v
x
v
x
v
x
v
x
(6.3)
Co macierzowo zapisujemy w postaci
(
)
0
V
x
Ψ
ob
=
+
Jeśli równania (6.3) nie są liniowe, to każdą z funkcji
y rozwijamy w szereg Taylora
ograniczając się do pierwszych tj. liniowych wyrazów
h
2
h
3
h
1
Rp
α
1
α
2
l
l
l
α
3
36
( )
(
) ( )
( )
v
ob
x
x
Ψ
x
Ψ
v
x
Ψ
x
Ψ
x
x
ob
ob
=
¶
¶
+
=
+
=
. (6.4)
Szukamy następnie
( )
{
}
PV
V
V
ξ
min
T
=
gdzie V - minimalizuje funkcję celu
( )
V
ξ
,
a także spełnia równanie warunkowe
BV + L = 0
(6.5)
Przy rozwiązaniu r układu równań wprowadza się tzw. korelaty. Są to mnożniki
k
= [k
1
, k
2
, ..... k
f
]
T
,
których wektor wyznacza się ze wzoru
k = - (BP
-1
B
T
)
-1
L
(6.6)
Wektor poprawek i obserwacji wyrównanych wyznaczane są ze wzorów
V = P
-1
B
T
k
(6.7)
Wyrównane wartości rzędnych wyznaczane są na podstawie poprawek.
x
wyr
= x
ob
+ V
(6.8)
w przypadku przewyższeń
h
wyr
= h
ob
+ V
Kontrola 1 s = s’
V
T
PV = - k
T
L
Kontrola 2. Kontrola polega na sprawdzeniu warunków (6.1)
Ocena dokładności.
Błąd średni wyrównanych wysokości wyznaczany jest jako
funkcja wyrównanych wysokości
[
]
j
1
1
T
1
T
1
j
j
1
T
j
2
0
F
BP
)
B
(BP
B
P
F
F
P
F
-
-
-
-
-
-
= m
m
Xj
j = 1, 2....r (6.9)
gdzie
r
n
m
-
=
PV
V
T
2
0
ú
û
ù
ê
ë
é
¶
¶
¶
¶
¶
¶
=
n
x
F
x
F
x
F
,......
,
F
2
1
T
j
(6.10)
Błąd średni wyrównanych wysokości obliczany jest na podstawie macierzy
wyrównanych obserwacji wyznaczanej ze wzoru
[
]
1
1
T
1
T
1
1
2
0
,
BP
)
B
(BP
B
P
P
-
-
-
-
-
-
= m
C
wyr
x
(6.11)

37
[
]
i
i
wyr
x
wyr
xi
C
m
,
,
,
=
(6.12)
Wartości [C
x,wyr
]
i,i
odczytywane są z macierzy (6.11).
6.4. Przykład wyrównania sieci niwelacyjnej
Wyrównać sieć niwelacyjną metodą warunkową
Wyniki pomiaru
h
1
ob
= - 0.663 m m
1
= 0,01 H
R1
= 111.770 m
h
2
ob
= 2.308 m m
2
= 0,02 H
R2
= 115.430 m
h
3
ob
= - 2.008 m m
3
= 0,02
h
4
ob
= - 0.624 m m
4
= 0,01
h
5
ob
= - 2.920 m m
5
= 0,02
h
6
ob
= 1.370 m m
6
= 0,01
Obliczyć:
§
wyrównane rzędne reperów H
1
wyr
,
H
2
wyr
,
H
3
wyr
,
§
wyrównane wartości przewyższeń h
1
wyr
, h
2
wyr
, h
3
wyr
, h
4
wyr
h
5
wyr
, h
6
wyr
,
§
błędy średnie wyrównanych wysokości m
H1
, m
H2
, m
H3
,
§
błędy średnie wyrównanych przewyższeń m
hi
.
Liczba równań warunkowych
n = 6, r = 3, d = d
z
+ d
w
= 0
f = n – r + d = 6 – 3 + 0 = 3
Równania warunkowe
h
2
- h
4
+ h
5
= 0
h
1 +
h
2
– h
3
+ H
R1
– H
R2
= 0
- h
3
+ h
4
- h
6
= 0
Rp. 1
Rp. 2
H.1
H.2
H.3
h
1
h
2
h
3
h
4
h
5
h
6

38
Po podstawieniu h
i
= h
i
ob
+ v
i
h
2
ob
+ v
2
– h
4
ob
- v
4
+ h
5
ob
+ v
5
= 0
h
1
ob
+ v
1
+ h
2
ob
+ v
2
– h
3
ob
– v
3
+ H
R1
– H
R2
= 0
-h
3
ob
– v
3
+ h
4
ob
+ v
4
– h
6
ob
– v
6
= 0
Układ równań warunkowych
v
2
– v
4
+ v
5
+ 0.012 = 0
v
1
+ v
2
– v
3
– 0.007
= 0
– v
3
+ v
4
- v
6
+ 0.014
= 0
Zestawienie macierzy
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
=
1
0
1
1
0
0
0
0
0
1
1
1
0
1
1
0
1
0
B
[ ]
m
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
=
014
,
0
007
,
0
012
,
0
L
ú
û
ù
ê
ë
é
-
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
=
2
/
1
0
0
0
0
0
0
/
1
0
0
0
0
0
0
/
1
0
0
0
0
0
0
/
1
0
0
0
0
0
0
/
1
0
0
0
0
0
0
/
1
p
2
6
2
5
2
4
2
3
2
2
2
1
m
m
m
m
m
m
m
ú
û
ù
ê
ë
é
-
-
-
-
-
-
-
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
=
2
10000
0
0
0
0
0
0
2500
0
0
0
0
0
0
10000
0
0
0
0
0
0
2500
0
0
0
0
0
0
2500
0
0
0
0
0
0
10000
p
1
1
1
1
1
1
1
m
Wektor korelat k = - (BP
-1
B
T
)
-1
L
(
)
úû
ù
êë
é
-
ú
û
ù
ê
ë
é
-
-
-
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
=
×
2
73
,
3170
22
,
1951
51
,
1219
22
,
1951
36
,
2585
85
,
1365
51
,
1219
85
,
1365
66
,
1853
2
0006
,
0
0004
,
0
0001
,
0
0004
,
0
0009
,
0
0004
,
0
0001
,
0
0004
,
0
0009
,
0
B
P
B
1
1
T
1
m
m

39
ú
û
ù
ê
ë
é
-
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
=
1
683
,
72
61,805
48,878
-
k
m
Wektor poprawek V = P
-1
B
T
k
i wektor obserwacji (przewyższeń) wyrównanych h
wyr
= h
ob
+ V
[ ]
m
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
-
-
=
0073
,
0
0196
,
0
0024
,
0
0044
,
0
0052
,
0
0062
,
0
V
[ ]
m
wyr
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
=
+
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
=
3773
,
1
2,9396
-
0,6264
-
2,0036
-
2,3132
0,6568
-
V
370
,
1
2,920
-
0,624
-
2,008
-
2,308
0,663
-
h
Wyrównane wysokości reperów H
wyr
= F
j
(h
wyr
)
H
1
wyr
= H
Rp1
+ h
1
wyr
= 111.1132
H
2
wyr
= H
Rp2
+ h
3
wyr
= 113.4264
H
3
wyr
= H
Rp2
– h
6
wyr
= 114.0527
Kontrola 1. s = s’
s = V
T
PV = 2.036732
s’ = - k
T
L = 2.036732
Kontrola 2. Sprawdzenie warunków
h
2
- h
4
+ h
5
= 0,0000
h
1 +
h
2
– h
3
+ H
R1
– H
R2
= 0,0000
- h
3
+ h
4
- h
6
= 0,0000
Ocena dokładności
67891
,
0
3
036732
,
2
PV
V
T
2
0
=
=
-
=
r
n
m
Błąd wyrównanych wysokości
[
]
j
1
1
T
1
T
1
j
j
1
T
j
2
0
2
F
BP
)
B
(BP
B
P
F
F
P
F
-
-
-
-
-
-
= m
m
Xj
Dla wyznaczenia wysokości H
1
, H
2
, H
3
przyjęto następujące zależności:
H
1
= H
Rp1
+ h
1
H
2
= H
Rp2
+ h
3
H
3
= H
Rp2
– h
6
Wzory te wykorzystano przy wyznaczaniu błędów średnich wyrównanych wartości
rzędnych H
1
, H
2
, H
3
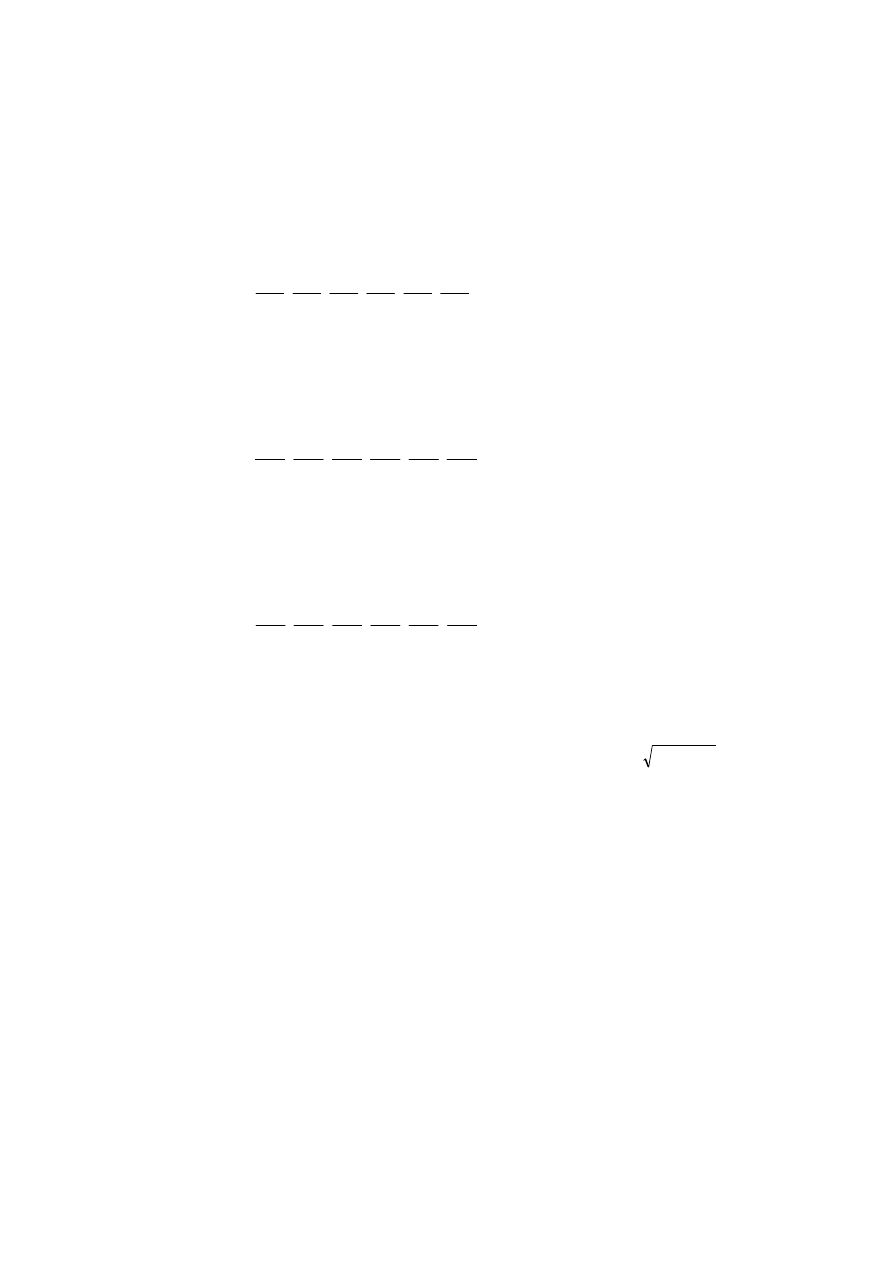
40
Błąd średni wyrównanej wysokości H
1
ú
û
ù
ê
ë
é
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
=
6
1
5
1
4
1
3
1
2
1
1
1
T
1
,
,
,
,
,
F
h
H
h
H
h
H
h
H
h
H
h
H
[
]
0
0
0
0
0
1
F
T
1
=
[
]
=
-
1
1
T
1
F
P
F
0,0001
=
-
-
-
-
1
1
1
T
1
T
1
1
F
BP
)
B
(BP
B
P
F
2,5854E-05
[
]
1
1
1
T
1
T
1
1
1
1
T
1
2
1
F
BP
)
B
(BP
B
P
F
F
P
F
67891
,
0
-
-
-
-
-
-
=
H
m
= 5,03387-05
m
H1
= 0,0071 [m]
Błąd średni wyrównanej wysokości H
2
ú
û
ù
ê
ë
é
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
=
6
2
5
2
4
2
3
2
2
2
1
2
T
2
,
,
,
,
,
F
h
H
h
H
h
H
h
H
h
H
h
H
[
]
0
0
0
1
0
0
F
T
2
=
[
]
=
-
2
1
T
2
F
P
F
0,0004
=
-
-
-
-
1
1
1
T
1
T
1
1
F
BP
)
B
(BP
B
P
F
- 1,1994E-08
[
]
2
1
1
T
1
T
1
2
2
1
T
2
2
2
F
BP
)
B
(BP
B
P
F
F
P
F
67891
,
0
-
-
-
-
-
-
=
H
m
= 0,00027157
m
H2
= 0,0165 [m]
Błąd średni wyrównanej wysokości H
3
ú
û
ù
ê
ë
é
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
¶
=
6
3
5
3
4
3
3
3
2
3
1
3
T
3
,
,
,
,
,
F
h
H
h
H
h
H
h
H
h
H
h
H
[
]
1
0
0
0
0
0
F
T
3
-
=
[
]
=
-
3
1
T
3
F
P
F
=
-
-
-
-
1
1
1
T
1
T
1
1
F
BP
)
B
(BP
B
P
F
[
]
3
1
1
T
1
T
1
3
3
1
T
3
2
3
F
BP
)
B
(BP
B
P
F
F
P
F
67891
,
0
-
-
-
-
-
-
=
H
m
= 4,63646E-05
m
H3
= 0,0068 [m]
Błędy średnie wyrównanych obserwacji h
i
wyr
i
i
wyr
h
wyr
h
C
m
,
,
,
)
(
=
[
]
1
1
T
1
T
1
1
2
0
,
BP
)
B
(BP
B
P
P
-
-
-
-
-
-
= m
C
wyr
h
)
05
41463
,
7
(
2
0
2
1
-
×
=
E
m
m
h
m
h1
= 0,0071 [m]
0001268
,
0
2
0
2
2
×
= m
m
h
m
h2
= 0,0093 [m]
0001034
,
0
2
0
2
3
×
= m
m
h
m
h3
= 0,0084 [m]
)
05
41463
,
7
(
2
0
2
4
-
×
=
E
m
m
h
m
h4
= 0,0071 [m]
0001034
,
0
2
0
2
5
×
= m
m
h
m
h5
= 0,0084 [m]
)
05
82927
,
6
(
2
0
2
6
-
×
=
E
m
m
h
m
h6
= 0,0068 [m]

41
7. Metody mieszane
7.1. Metoda parametryczna z warunkami dla parametrów
W niektórych zadaniach pomiarowych równocześnie występują elementy
modelu parametrycznego i warunkowego. Warunki mogą np. dotyczyć
współrzędnych punktów sieci, gdy zadane jest ich wzajemne położenie. W takim
przypadku poza układem równań obserwacyjnych l
i
= F(x):
(
)
(
)
(
)
r
n
n
r
r
X
X
X
F
l
X
X
X
F
l
X
X
X
F
l
,
,
,
........
..........
..........
..........
,
,
,
,
,
,
2
1
2
1
2
2
2
1
1
1
K
K
K
=
=
=
należy utworzyć układ równań warunkowych
Y(X) = 0 wiążących parametry X
1
,
X
2
,X
3
(
)
(
)
(
)
0
,
,
,
........
..........
..........
..........
0
,
,
,
0
,
,
,
2
1
2
1
2
2
1
1
=
Y
=
Y
=
Y
r
n
r
r
X
X
X
X
X
X
X
X
X
K
K
K
Układ równań
( )
X
F
x
=
można przekształcić do liniowej postaci równań poprawek
L
AdX
V
+
=
a równania warunkowe
( )
0
X
Ψ
= można zastąpić układem równań
0
Δ
BdX
=
+
Zadanie wyrównawcze polega na rozwiązaniu problemu optymalizacyjnego przy
warunku
min
PV
V
T
=
sformułowanego układem:
0
Δ
BdX
V
L
AdX
=
+
=
+
Algorytm rozwiązania zadania wyrównawczego obejmuje wyznaczenie korelat k,
poprawek dx oraz poprawek v:
(
)
(
)
úû
ù
êë
é -
úû
ù
êë
é
-
=
-
-
-
PL
A
PA
A
B
Δ
B
PA
A
B
k
T
1
T
1
T
1
T
(
) (
)
k
B
PL
A
PA
A
dx
1
T
T
T
-
-
=
-
L
AdX
V
+
=
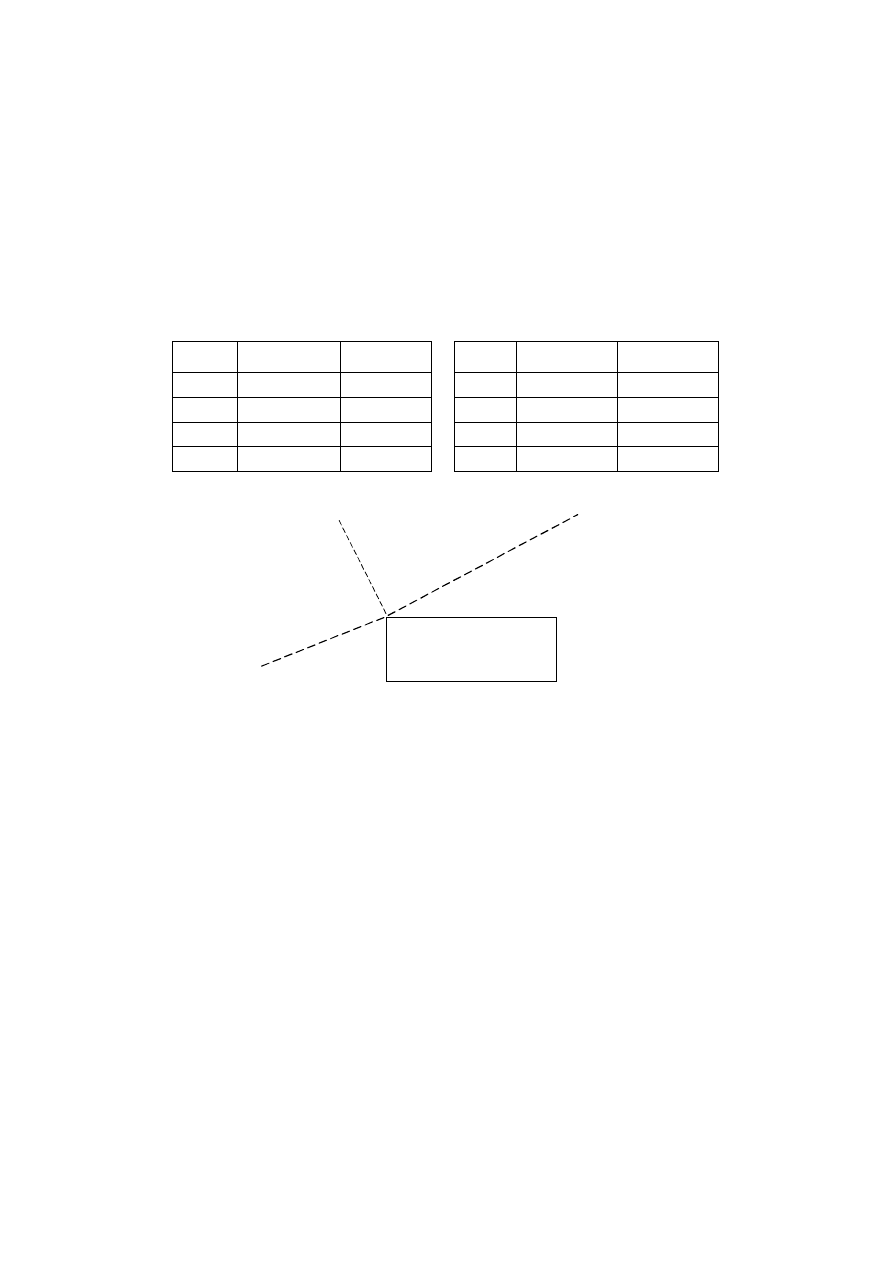
42
Przykład 7.1. Obliczyć współrzędne pkt.
5 wyznaczającego narożnik
projektowanego obiektu jak na rys. 7.1, przy warunku d
54
= 182,312m. Znane są
współrzędne punktów 1, 2, 3, 4 w układzie (X,Y) oraz odległości d
51
= 151,581 m,
d
52
= 244,275 m, d
53
= 255,235 m.
Tablica 5.1
Punkt
X [m]
Y[m]
Wynik
pomiaru
Błąd pomiaru
1
1 400,200
2
389,750
d
51
151,581
0,012
2
1 450,080
2
550,150
d
52
244,275
0,012
3
1 359,880
2
640,360
d
53
255,235
0,005
4
1 219,960
2
589,840
Rys. 7.1
Współrzędne przybliżone punktu 5:
860
,
2409
180
,
1250
0
5
0
5
=
=
y
x
Równania poprawek, budowane na podstawie ogólnego równania (5.11) – str.31.
ob
PK
PK
K
PK
K
PK
P
PK
P
PK
d
d
d
dy
A
dx
A
dy
A
dx
A
PK
v
-
+
+
+
-
-
=
0
cos
cos
sin
cos
)
(
ob
d
d
dy
Az
dx
Az
v
51
0
51
5
51
5
51
51
sin
cos
-
+
-
-
=
obs
d
d
dy
Az
dx
Az
v
52
0
52
5
52
5
52
52
sin
cos
-
+
-
-
=
obs
d
d
dy
Az
dx
Az
v
53
0
53
5
53
5
53
53
sin
cos
-
+
-
-
=
Zestawienie macierzy
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
-
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
-
-
-
=
9030
,
0
4297
,
0
5745
,
0
8185
,
0
1336
,
0
9910
,
0
sin
cos
sin
cos
sin
cos
A
53
53
52
52
51
51
Az
Az
Az
Az
Az
Az
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
-
-
=
38
59
219
L
53
0
53
52
0
52
51
0
51
ob
ob
ob
d
d
d
d
d
d
5
4
3
2
d
52
1
°
°
°
°
°
d
51
d
53
d
54

43
ú
ú
ú
û
ù
ê
ê
ê
ë
é
×
×
=
ú
ú
ú
û
ù
ê
ê
ê
ë
é
=
-
-
-
-
-
04
,
0
0
0
0
10
9
,
6
0
0
0
10
9
,
6
0
0
0
0
0
0
P
3
3
1
53
1
52
2
51
m
m
m
Równanie warunkowe
(
) (
)
0
54
2
0
5
4
2
0
5
4
=
-
-
+
-
b
y
y
x
x
(postać nieliniowa)
0
sin
cos
54
0
54
5
54
5
54
=
-
+
-
-
b
b
dy
Az
dx
Az
(postać zlinearyzowana) gdzie
m
b
499
,
182
0
54
=
Zestawienie macierzy
[
] [
]
9862
,
0
1656
,
0
sin
cos
B
54
54
-
=
-
-
=
Az
Az
187
Δ
54
0
54
=
-
=
b
b
Obliczenie poprawek
ú
û
ù
ê
ë
é
=
03503
,
0
01787
,
0
01787
,
0
01886
,
0
PA
A
T
(
)
ú
û
ù
ê
ë
é
-
-
=
-
27
,
55
37
,
52
37
,
52
65
,
102
PA
A
1
T
(
)
68
,
73
B
PA
A
B
T
1
T
=
-
(
)
0136
,
0
B
PA
A
B
1
T
1
T
=
úû
ù
êë
é
-
-
(
)
99
,
20
PL
A
PA
A
B
Δ
T
1
T
=
-
-
oraz
(
)
(
)
285
,
0
PL
A
PA
A
B
Δ
B
PA
A
B
k
T
1
T
1
T
1
T
-
=
úû
ù
êë
é -
úû
ù
êë
é
-
=
-
-
-
(
) (
)
ú
û
ù
ê
ë
é-
=
-
-
=
-
5
,
154
0
,
212
k
B
PL
A
PA
A
dx
T
T
1
T
]
[
3
,
10
5
,
25
5
,
11
L
Adx
V
mm
ú
ú
ú
û
ù
ê
ê
ê
ë
é
-
=
+
=
Wyrównane współrzędne punktu Z
014
,
2410
154
,
0
860
,
2409
968
,
1249
212
,
0
180
,
1250
5
0
5
5
5
0
5
5
=
-
=
+
=
=
-
=
+
=
dy
y
y
dx
x
x
wyr
wyr
Kontrola obliczeń
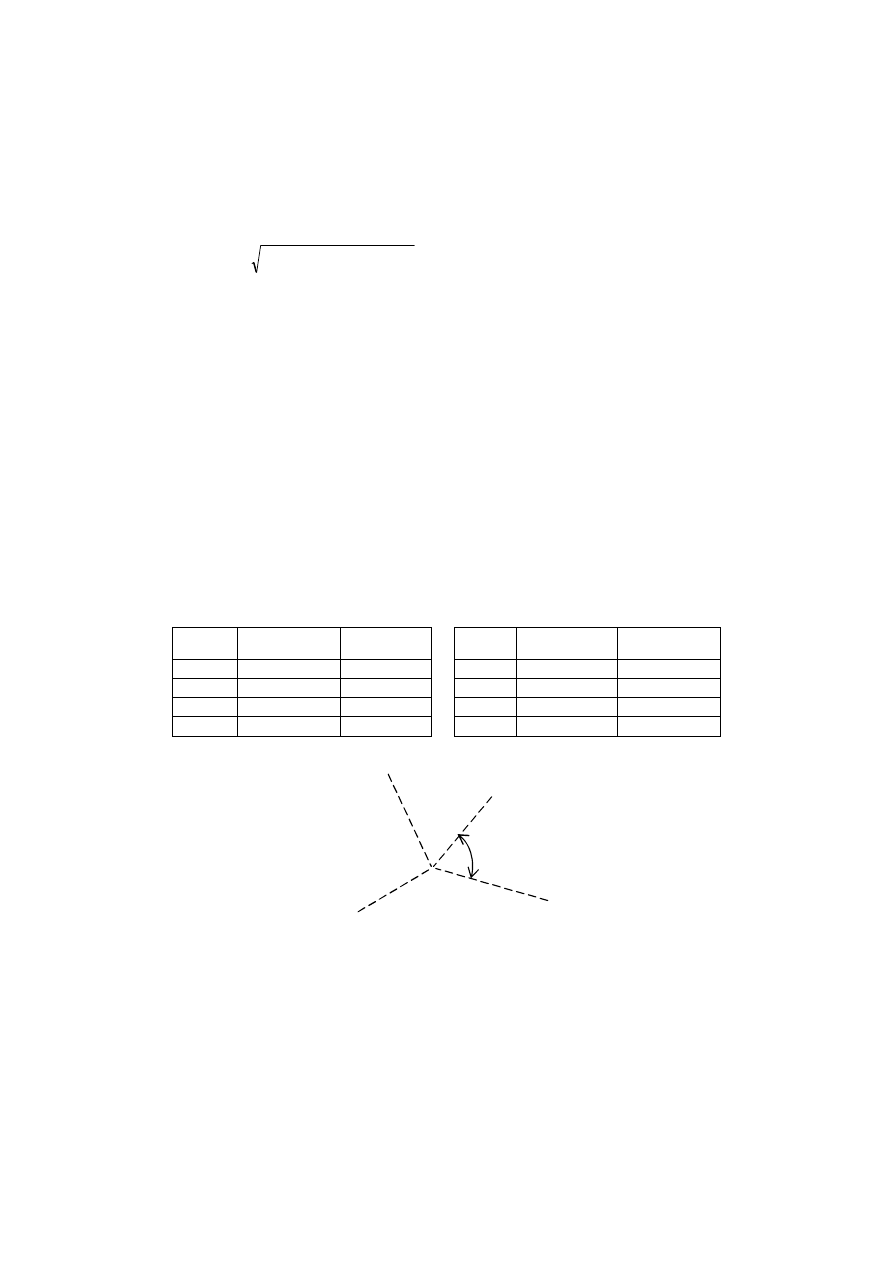
44
(
) (
)
312
,
182
2
5
4
2
5
4
54
=
-
+
-
=
wyr
wyr
y
y
x
x
d
7.2. Metoda wag
Jeżeli zadanie opisuje układ równań poprawek
V = A·dx + L
oraz warunek
B dV +
D
= 0
to równanie warunkowe można traktować jako dodatkowe równanie parametryczne
o nieskończenie dużej wadze.
Takie podejście spełnia założenia metod mieszanych, jakkolwiek w sposób
uproszczony. Z praktycznego punktu widzenia metoda uproszczona jest w pełni
wystarczająca i poprawna.
Przykład 7.1. Wyznaczyć współrzędne punktu 5 dla zadania jak na rys. 7.2.
Współrzędne punktów 1, 2, 3 (przyjęte jako bezbłędne) oraz wyniki pomiaru
odległości zamieszczono w tablicy 7.2. W zadaniu należy spełnić warunek
β = 103.8622
g
.
Tablica 7.2
Punkt
X [m]
Y[m]
Wynik
pomiaru
Błąd pomiaru
1
310,055
604,728
d
51
171,580
0,008
2
635.417
701,009
d
52
210.671
0,015
3
566,200
780, 080
d
53
148,235
0,005
4
381,725
834,716
d
54
113,609
0,010
Rys. 7.2
Układ równań poprawek rozpisany według ogólnego wzoru (5.11) tworzą cztery
równania dla długości oraz jedno równanie dla kąta β.
1
4
2
3
5
°
°
°
°
°
β

45
ob
ob
v
ob
ob
d
d
dy
Az
dx
Az
v
d
d
dy
Az
dx
Az
v
d
d
dy
Az
dx
Az
v
d
d
dy
Az
dx
Az
v
54
0
54
5
54
5
54
54
53
0
53
5
53
5
53
53
52
0
52
5
52
5
52
52
51
0
51
5
51
5
51
51
sin
cos
sin
cos
sin
cos
sin
cos
-
+
-
-
=
-
+
-
-
=
-
+
-
-
=
-
+
-
-
=
ob
cc
cc
dY
d
Az
d
Az
dX
d
Az
d
Az
v
b
b
r
r
b
-
+
÷
÷
ø
ö
ç
ç
è
æ
-
+
÷
÷
ø
ö
ç
ç
è
æ
-
=
0
5
0
53
53
0
52
52
5
0
52
52
0
53
53
)
(
cos
cos
)
(
sin
sin
Zestawienie macierzy
ú
ú
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
-
-
-
-
-
-
=
0
53
53
0
52
52
0
52
52
0
53
53
0
54
0
54
0
53
0
53
0
52
0
52
0
51
0
51
cos
cos
sin
sin
sin
cos
sin
cos
sin
cos
sin
cos
A
d
Az
d
Az
d
Az
d
Az
Az
Az
Az
Az
Az
Az
Az
Az
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
-
-
-
-
-
=
103.8622
113,609
148,235
210.671
171,580
L
0
0
54
0
53
0
52
0
51
b
d
d
d
d
ú
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ê
ë
é
=
12
2
-
2
-
2
-
-2
10
0
0
0
0
0
0,010
0
0
0
0
0
0,005
0
0
0
0
0
0,015
0
0
0
0
0
0,008
P
W macierzy wag przyjęto, że błąd pomiaru kąta m
b
= 0,000001
g
. Stąd waga p
b
[ ]
2
12
6
2
1
10
10
1
1
-
-
=
=
=
g
m
p
b
b
Algorytm rozwiązania zadania jest identyczny jak w metodzie parametrycznej;
(przykład 5.4).
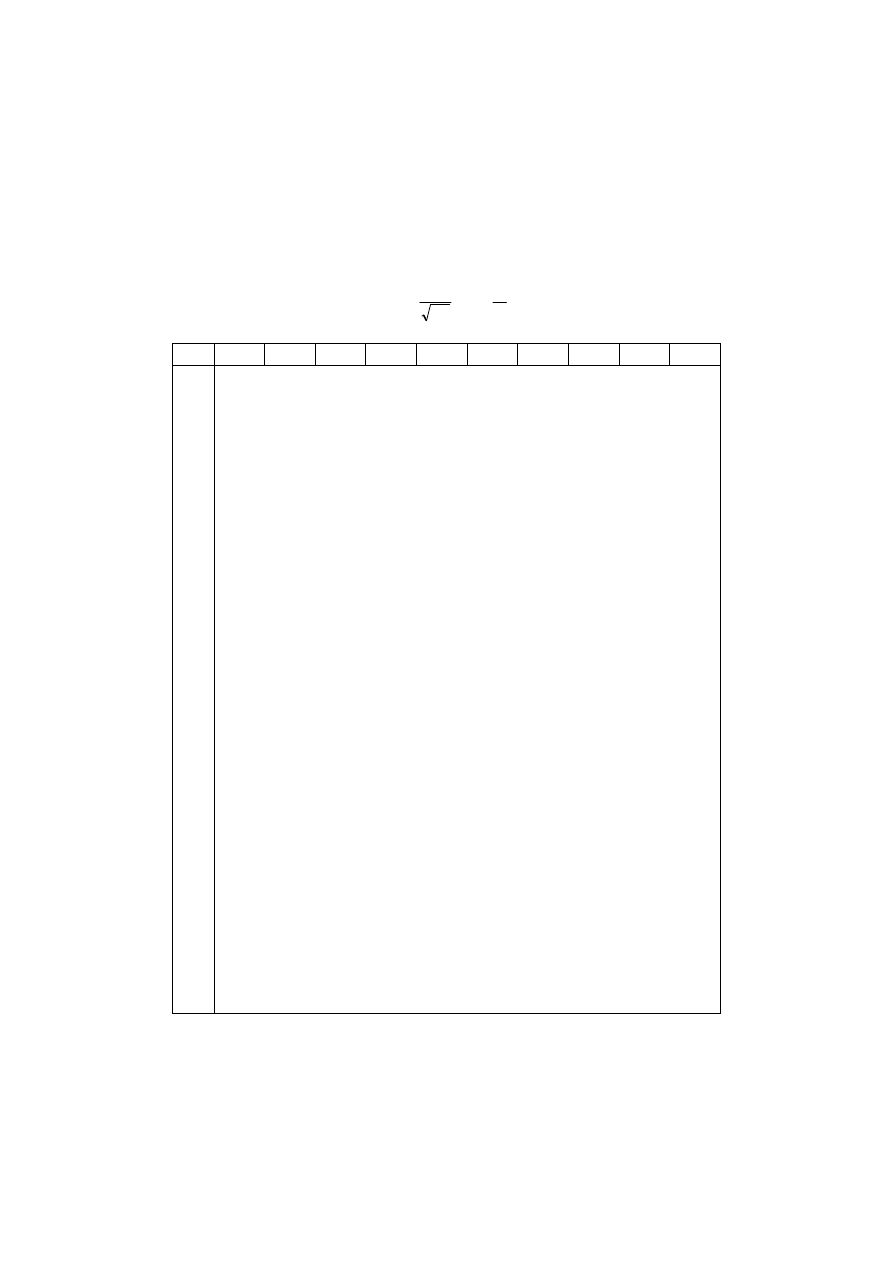
46
Wartości liczbowe funkcji gęstości rozkładu normalnego
ú
ú
û
ù
ê
ê
ë
é
-
=
2
exp
2
1
)
(
2
t
t
p
p
t
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
3989
3989
3989 3988 3986
3984 3982 3980
3977 3973
0,1
3970
3965
3961 3956 3951
3945 3939 3932
3925 3918
0,2
3910
3902
3894 3885 3876
3867 3857 3847
3836 3825
0,3
3814
3802
3790 3778 3765
3752 3739 3726
3712 3697
0,4
3683
3668
3653 3637 3621
3605 3589 3572
3555 3538
0,5
3521
3503
3485 3467 3448
3429 3410 3391
3372 3352
0,6
3392
3312
3292 3271 3251
3230 3209 3187
3166 3144
0,7
3123
3101
3079 3056 3034
3011 2989 2966
2943 2920
0,8
2897
2874
2850 2827 2803
2780 2756 2732
2709 2685
0,9
2661
2637
2613 2589 2565
2541 2516 2492
2468 2444
1,0
2420
2396
2371 2347 2323
2299 2275 2251
2227 2203
1,1
2179
2155
2131 2107 2083
2059 2036 2012
1989 1965
1,2
1942
1919
1895 1672 1849
1826 1804 1781
1758 1736
1,3
1714
1601
1669 1647 1626
1604 1582 1561
1539 1518
1,4
1497
1476
1456 1435 1415
1394 1374 1354
1334 1315
1,5
1295
1276
1257 1238 1219
1200 1182 1163
1145 1127
1,6
1109
1092
1074 1057 1040
1023 1006 0989
0973 0957
1,7
0940
0925
0909 0893 0878
0863 0848 0833
0818 0804
1,8
0790
0775
0761 0748 0734
0721 0707 0694
0681 0669
1,9
0656
0644
0632 0620 0608
0596 0584 0573
0562 0551
2,0
0540
0529
0519 0508 0498
0488 0478 0468
0459 0449
2,1
0440
0431
0422 0413 0404
0396 0387 0379
0371 0363
2,2
0355
0347
0339 0332 0325
0317 0310 0303
0297 0290
2,3
0283
0277
0270 0264 0258
0252 0246 0241
0235 0229
2,4
0224
0219
0213 0208 0203
0198 0194 0189
0184 0180
2,5
0175
0171
0167 0163 0158
0154 0151 0147
0143 0139
2,6
0136
0132
0129 0126 0122
0119 0116 0113
0110 0107
2,7
0104
0101
0099 0096 0093
0091 0088 0086
0084 0081
2,8
0079
0077
0075 0073 0071
0069 0067 0065
0063 0061
2,9
0060
0058
0056 0055 0053
0051 0050 0048
0047 0046
3,0
0044
0043
0042 0040 0039
0038 0037 0036
0035 0034
3,5
0009
0008
0008 0008 0008
0007 0007 0007
0007 0006
4,0
0001
0001
0001 0001 0001
0001 0001 0001
0001 0001

47
Dystrybuanta rozkładu normalnego
dt
t
t
F
t
ò
ú
ú
û
ù
ê
ê
ë
é
-
=
0
2
2
exp
2
1
p
D(t) = 0,5 + F|t| dla t
ñ 0
D(t) = 0,5 – F|t| dla t
á 0
t
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0000
0040
0080 0120 0159
0199 0239 0270
0319 0359
0,1
0398
0438
0478 0517 0557
0596 0636 0675
0714 0753
0,2
0793
0832
0871 0910 0948
0987 1026 1064
1103 1141
0,3
1179
1217
1255 1293 1331
1368 1406 1443
1480 1517
0,4
1554
1591
1628 1664 1700
1736 1772 1808
1844 1879
0,5
1915
1950
1985 2019 2054
2088 2123 2157
2190 2224
0,6
2257
2291
2324 2357 2389
2422 2454 2486
2518 2549
0,7
2580
2612
2642 2673 2704
2734 2764 2794
2823 2852
0,8
2881
2910
2939 2967 2995
3023 3051 3078
3106 3133
0,9
3159
3186
3212 3238 3264
3289 3315 3340
3365 3389
1,0
3413
3438
3461 3485 3508
3531 3554 3577
3599 3621
1,1
3643
3665
3686 3718 3729
3749 3770 3790
3810 3830
1,2
3849
3869
3888 3907 3925
3944 3962 3980
3997 4015
1,3
4032
4049
4066 4083 4099
4115 4131 4147
4162 4177
1,4
4192
4207
4222 4236 4251
4265 4279 4292
4306 4319
1,5
4332
4345
4357 4370 4382
4394 4406 4418
4430 4441
1,6
4452
4463
4474 4485 4495
4505 4515 4525
4535 4545
1,7
4554
4564
4573 4582 4591
4590 4608 4616
4625 4633
1,8
4641
4649
4656 4664 4671
4678 4686 4693
4699 4706
1,9
4713
4719
4726 4732 4738
4744 4750 4758
4762 4767
2,0
4773
4778
4783 4788 4793
4798 4803 4808
4812 4817
2,1
4821
4826
4830 4834 4838
4842 4846 4850
4854 4857
2,2
4861
4865
4868 4871 4875
4878 4881 4884
4887 4890
2,3
4893
4896
4898 4901 4904
4906 4909 4911
4913 4916
2,4
4918
4920
4922 4925 4927
4929
4931
4932
4934
4936
2,5
4938
4940
4941 4943 4945
4946
4948
4949
4951
4952
2,6
4953
4955
4956 4957 4959
4960
4961
4962
4953
4964
2,7
4965
4966
4967 4968 4969
4970
4971
4972
4973
4974
2,8
4974
4975
4976 4977 4977
4978
4979
4980
4900
4981
2,9
4981
4982
4963 4984 4934
4984
4985
4985
4986
4986
3,0
4986
4987
4987 4988 4988
4988
4989
4989
4989
4990
3,5
49977 4991 4991 4991 4992
4992 4992 4992
4993 4993

48
Wyszukiwarka
Podobne podstrony:
czesc III, WSKiZ, Materialoznawstwo w, Materialoznawstwo prof. dr hab. inz Boleslaw Jurkowski [ częś
czesc II, WSKiZ, Materialoznawstwo w, Materialoznawstwo prof. dr hab. inz Boleslaw Jurkowski [ część
czesc I, WSKiZ, Materialoznawstwo w, Materialoznawstwo prof. dr hab. inz Boleslaw Jurkowski [ część
Projektowanie baz danych [ prof dr hab inz Zbyszko Krolikowski], Transformacja EER material dydaktyc
Zarządzanie Projektem prof dr hab inż J ?sl
prof dr hab inż Handkiewicz Andrzej, Elektronika Cyfrowa, Automat synchroniczny 2
prof dr hab inż Handkiewicz Andrzej, Elektronika Cyfrowa, Rejestr cykliczny 2
Egzamin - pytania IFP, Studia Finanse i Rachunkowość FiR UMCS, Instrumenty finansowania przedsiębior
3687 Podanie,o,zwolnienie,z,czesci,oplat,za,punkty,ECTS,do,dr,hab ,inz ,Pawel,Drozdziel,prof ,PL
dr hab inż prof P P Andrzej Rybarczyk, Elektrotechnika, Zadania
strona startowa na prof zw dr hab inż Józefa Wojnarowskiego, dr h c
I Frejman, Metodologia badań pedagogicznych - wykład - prof. dr hab. S. Frejman
PEDcw w4s6, aaa VI semestr, PEDcw prof. dr hab. J.Pięta
egzamin prof dr hab Urlich
BUD WODNE Wyklad 1 dr hab inz Nieznany
TEORIA STOSUNKÓW MIĘDZYNARODOWYCH, Uczelnia - notatki, prof. dr hab. Sebastian Wojciechowski
II Frejman, Metodologia badań pedagogicznych - wykład - prof. dr hab. S. Frejman
prof dr hab M Smejda,Harmoniza Nieznany
więcej podobnych podstron