W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

2

2

Z

Z

A

A

S

S

A

A

D

D

A

A

Z

Z

A

A

C

C

H

H

O

O

W

W

A

A

N

N

I

I

A

A

M

M

A

A

S

S

Y

Y

I

I

Z

Z

W

W

I

I

Ą

Ą

Z

Z

A

A

N

N

E

E

Z

Z

N

N

I

I

Ą

Ą

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

A

A

.

.

D

D

R

R

U

U

G

G

A

A

Z

Z

A

A

S

S

A

A

D

D

A

A

D

D

Y

Y

N

N

A

A

M

M

I

I

K

K

I

I

.

.

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

R

R

O

O

D

D

Z

Z

A

A

J

J

E

E

W

W

I

I

E

E

L

L

K

K

O

O

Ś

Ś

C

C

I

I

W

W

Y

Y

S

S

T

T

E

E

P

P

U

U

J

J

Ą

Ą

C

C

Y

Y

C

C

H

H

W

W

F

F

I

I

Z

Z

Y

Y

C

C

E

E

intensywne

ekstensywne

ciśnienie, masa właściwa,

temperatura, prędkość,

natężenie pola

elektrycznego, entalpia

właściwa,

itp.…

są określone w każdym

miejscu ciała

masa, ładunek

elektryczny, pęd, siła,

moc, energia, moment

magnetyczny, entalpia

itp.…

są zdefiniowane dla ciała

1

2

3

1

2

3

F(

...)

F(

)

F(

)

F(

) ...

     

      

Istotna cecha wielkości ekstensywnych:

ich wartość obliczona dla

sumy ciał jest równa sumie ich wartości obliczonych dla
poszczególnych ciał.
Ciało: w

k

k

i

,



    

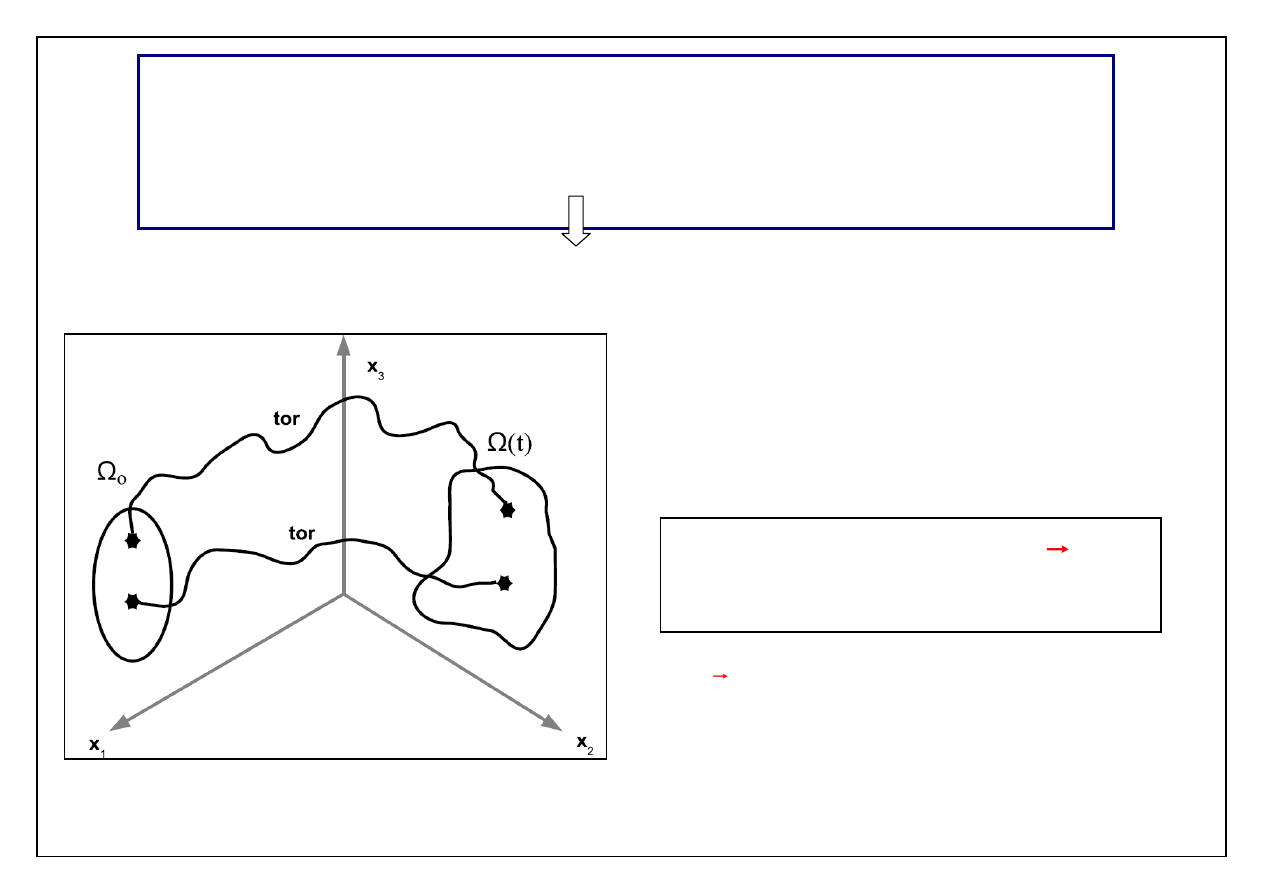
Wielkość ekstensywną F
ok

reślamy jako całkę obliczaną

po obszarze wypełnionym przez
ciało

(t )

F F(t)

f (t, r)d











f (t, r)

-

to „gęstość” wielkości

F

albo

inaczej

– wielkość właściwa

F

Pochodna wielkości ekstensywnej:

(t )

dF

df

f (

v) d

dt

dt









 













Masę jako wielkość ekstensywną zapisujemy tak:

(t )

m

(t, r)d













-

gęstość masy albo masa właściwa

(t)



-

obraz obszaru

o



,

zawiera niezmienny zbiór punktów materialnych

wypełniających obszar

o



w chwili początkowej

Z

Z

A

A

S

S

A

A

D

D

A

A

Z

Z

A

A

C

C

H

H

O

O

W

W

A

A

N

N

I

I

A

A

M

M

A

A

S

S

Y

Y

(t )

dm

d

(

v) d

0

dt

dt

 









 

 











Można pokazać, że skoro powyższe równanie zachodzi dla każdego Ω to ma to
miejsce wtedy i tylko wtedy, gdy fu

nkcja podcałkowa znika.

Zatem:

d

(

v)

(v

)

(

v) 0

dt

t







 



  

    



Masa tego samego zbioru punktów materialnych jest stała

.

Całkowa postać prawa

zachowania masy

( v)

0

t







  





Różniczkowa postać prawa

zachowania masy



Jeśli

przepływ jest stacjonarny

, co oznacza, że żaden parametr

jawnie nie zależy od czasu prawo zachowania masy redukuje się do
postaci:

( v) (v

)

(

v) 0



 



    



Jeżeli

const





, czyli substancja ma niezmienną masę właściwą, to

dostajemy

v

0

  

Powyższe równanie jest tożsame z równaniem

3

1

2

1

2

3

v

v

v

diw v

0

x

x

x





















Równanie różniczkowe wyrażające zasadę zachowania masy
nazywamy

RÓWNANIEM CIĄGŁOŚCI.

Jeśli

const





to

o

d

d

  

, co oznacza, że substancja o stałej masie

właściwej zachowuje objętość.

WARUNEK ZNIKANIA DIWERGENCJI

PRĘDKOŚCI

v

0

  

NIEZALEŻNIE OD WŁASNOŚCI GĘSTOŚCI MASY

PROWADZI DO ZACHOWANIA OBJĘTOŚCI

OŚRODKA CIĄGŁEGO

D

D

R

R

U

U

G

G

A

A

Z

Z

A

A

S

S

A

A

D

D

A

A

D

D

Y

Y

N

N

A

A

M

M

I

I

K

K

I

I

P

ęd jest wielkością ekstensywną, zatem

(t )

P

v d











d





-

o

kreśla elementarną masę

dm

zawartą w małym obszarze

dΩ

v dm

v d







-

określa elementarny pęd

dP

Pochodna pędu układu materialnego względem

czasu jest równa sumie sił zewnętrznych

dzia

łających na układ

.

S

S

I

I

Ł

Ł

Y

Y

D

D

Z

Z

I

I

Ł

Ł

A

A

J

J

Ą

Ą

C

C

E

E

N

N

A

A

O

O

Ś

Ś

R

R

O

O

D

D

E

E

K

K

C

C

I

I

Ą

Ą

G

G

Ł

Ł

Y

Y

SIŁA POWIERZCHNIOWA

-

siła

działająca na brzeg obszaru Ω(t)

A

A

F

f dA





f

-

powierzchniowa gęstość siły

dA

-

płatek powierzchni

A

czyli brzegu

obszaru

Ω(t)

SIŁA OBJĘTOŚCIOWA

-

siła związana

z masą i pewnym polem siłowym,
działa na wnętrze obszaru Ω(t)

F

F d













F

-

natężenie pola siłowego

d





-

elementarna masa

Ω(t)

f dA

F d





dA

dΩ