WSTĘP DO TOPOLOGII

Politechnika Krakowska
im. Tadeusza Kościuszki
Notatki do wykładu
autorstwa dra Marcina Skrzyńskiego
opracowali
Gabriela Aleksiewicz-Drab
Dariusz Kasiarz

Przedmowa
Skrypt oparty jest na semestralnych wykładach ze Wstępu do topologii prowadzonych przez dra
Marcina Skrzyńskiego w Instytucie Matematyki Politechniki Krakowskiej i przeznaczony dla stu-
dentów pierwszego roku Matematyki w finansach i ekonomii. Celem przedmiotu jest zaznajomienie
studentów z najważniejszymi pojęciami i twierdzeniami oraz typowymi przykładami i zadaniami
elementarnej topologii i teorii przestrzeni metrycznych (z naciskiem na przestrzenie euklidesowe).
Przedmiot ma wyposażyć adeptów w wiedzę i umiejętności topologiczne niezbędne do studiowania
analizy matematycznej i funkcjonalnej, geometrii i równań różniczkowych.
Kraków, czerwiec 2011
Gabriela Aleksiewicz-Drab
d
Dariusz Kasiarz
Tam, dokąd nie umiemy wejść sami,
dostajemy się matematyką.
Sporządzamy z niej wózki do poruszania się
w nieludzkich obszarach świata.

Spis treści
ii
1
25
42
55
68
74
77

Rozdział 1
Przestrzenie metryczne
Definicja 1. 1 Metryką
w zbiorze X 6= Ø nazywa się każdą funkcję
d : X × X 3 (x, y) 7→ d(x, y) ∈ [0, ∞) ⊂ R, spełniającą następujące warunki:
(M
1
) ∀
x,y∈X
d(x, y) = 0 ⇔ x = y,
(M
2
) ∀
x,y∈X
d(x, y) = d(y, x),
(M
3
) ∀
x,y,z∈X
d(x, z) ¬ d(x, y) + d(y, z).
Definicja 1. 2 Przestrzenią metryczną
nazywa się parę (X, d), w której X jest zbiorem niepustym,
d natomiast jest metryką w zbiorze X.
Twierdzenie 1. 1. (Druga nierówność trójkąta)
Przypuśćmy, że d jest metryką w zbiorze X.
Wówczas
∀
x,y,z∈X
: |d(x, z) − d(y, z)| ¬ d(x, y).
Dowód.
Na mocy (M
3
) mamy, iż:
d(x, z) ¬ d(x, y) + d(y, z), d(y, z) ¬ d(y, x) + d(x, z).
A zatem korzystając z warunku (M
2
):
−d(x, y) ¬ d(x, z) − d(y, z) ¬ d(x, y).
Oznacza to, że
|d(x, z) − d(y, z)| ¬ d(x, y),
co kończy nasz dowód.

2
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Przykład.
1. Funkcja d : R × R 3 (x, y) 7→ |x − y| ∈ [0, ∞) jest metryką w zbiorze liczb rzeczywistych,
zwaną
metryką naturalną
.
2. Niech n ∈ N \ {0}. Każda z funkcji d
1
, d
2
, d
∞
: R
n
× R
n
→ [0, ∞) zdefiniowanych za pomocą
wzorów:
d
1
(x, y) =
n
P
i=1
|x
i
− y
i
|
Manhattan
,
d
2
(x, y) =
s
n
P
i=1
(x
i
− y
i
)
2
Euklidesowa
,
d
∞
(x, y) =
n
max
i=1
|x
i
− y
i
|
Czebyszewa
,
gdzie x = (x
1
, . . . , x
n
) oraz y = (y
1
, . . . , y
n
), jest metryką w przestrzeni R
n
.
Zauważmy, że jeśli n = 1, to każda z metryk d
1
, d
2
, d
∞
jest po prostu metryką naturalną
w zbiorze R.
3. Niech X będzie zbiorem niepustym. Rozważmy zbiór B(X, R) wszystkich funkcji f : X → R
ograniczonych. Wówczas funkcja d
∞
= B(X, R) × B(X, R) → [0, ∞) zdefiniowana poprawnie
za pomocą wzoru d
∞
(f, g) := sup{|f (x) − g(x)| : x ∈ X} jest metryką w zbiorze B(X, R),
zwaną
metryką Czebyszewa
(inaczej metryką supremową).
4. Niech X będzie zbiorem niepustym i niech n ∈ N \ {0}. Rozważmy iloczyn kartezjański
X
n
= X × . . . × X
|
{z
}
n razy
. Funkcja d
H
: X
n
× X
n
→ [0, ∞) zdefiniowana za pomocą wzoru
d
H
(a, b) = #{i ∈ {1, . . . , n} : a
i
6= b
i
}, gdzie a = (a
1
, . . . , a
n
) oraz b = (b
1
, . . . , b
n
), jest
metryką w zbiorze X
n
, zwaną
metryką Hamminga
.
5. Rozważając w poprzednim przykładzie przypadek n = 1, otrzymujemy metrykę d w zbiorze
X, zdefiniowaną za pomocą wzoru
d(x, y) =
1, gdy x 6= y,
0, gdy x = y,
zwaną
metryką dyskretną
.

3
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
UWAGA 1
Niech (X, d) będzie przestrzenią metryczną i niech Y ⊆ X będzie zbiorem niepustym. Wówczas
funkcja d |
Y ×Y
: Y × Y 3 (x, y) 7→ d(x, y) ∈ [0, ∞) jest metryką w zbiorze Y zwaną
metryką induko-
waną
z przestrzeni (X, d). Przestrzenie metryczne (Y, d |
Y ×Y
) nazywa się czasami podprzestrzenią
przestrzeni (X, d).
Definicja 1. 3
Niech (X, d) będzie przestrzenią metryczną. Wybierzmy punkt x
0
∈ X.
(1)
Kulą otwartą
w przestrzeni (X, d) o środku x
0
i promieniu ε ∈ R
+
nazywa się zbiór
B (x
0
, ε)
def
= {x ∈ X : d (x
0
, x) < ε}.
(2)
Kulą domkniętą
w przestrzeni (X, d) o środku w x
0
i promieniu ρ ∈ R
+
nazywa się zbiór
B (x
0
, ρ)
def
= {x ∈ X : d(x
0
, x) ¬ ρ}.
(3)
Sferą
w przestrzeni (X, d) o środku w x
0
i promieniu δ ∈ R
+
nazywa się zbiór
S (x
0
, δ)
def
= {x ∈ X : d(x
0
, x) = δ}.
UWAGA 2
a) ρ = 0 ⇒ B (x
0
, ρ) = S (x
0
, ρ) = {x
0
}
b) ∀
ε∈R
+
B (x
0
, ε) = B (x
0
, ε) ∪ S (x
0
, ε)
c) x
0
∈ B (x
0
, ε)
Przykład.
Przykłady kul w metryce:
1 naturalnej na prostej R:
B (x
0
, ε)
def
= {x ∈ X : |x
0
− x| < ε} = {x ∈ R : x
0
− ε < x < x
0
+ ε}
x
0
x
0
− ε
x
0
+ ε
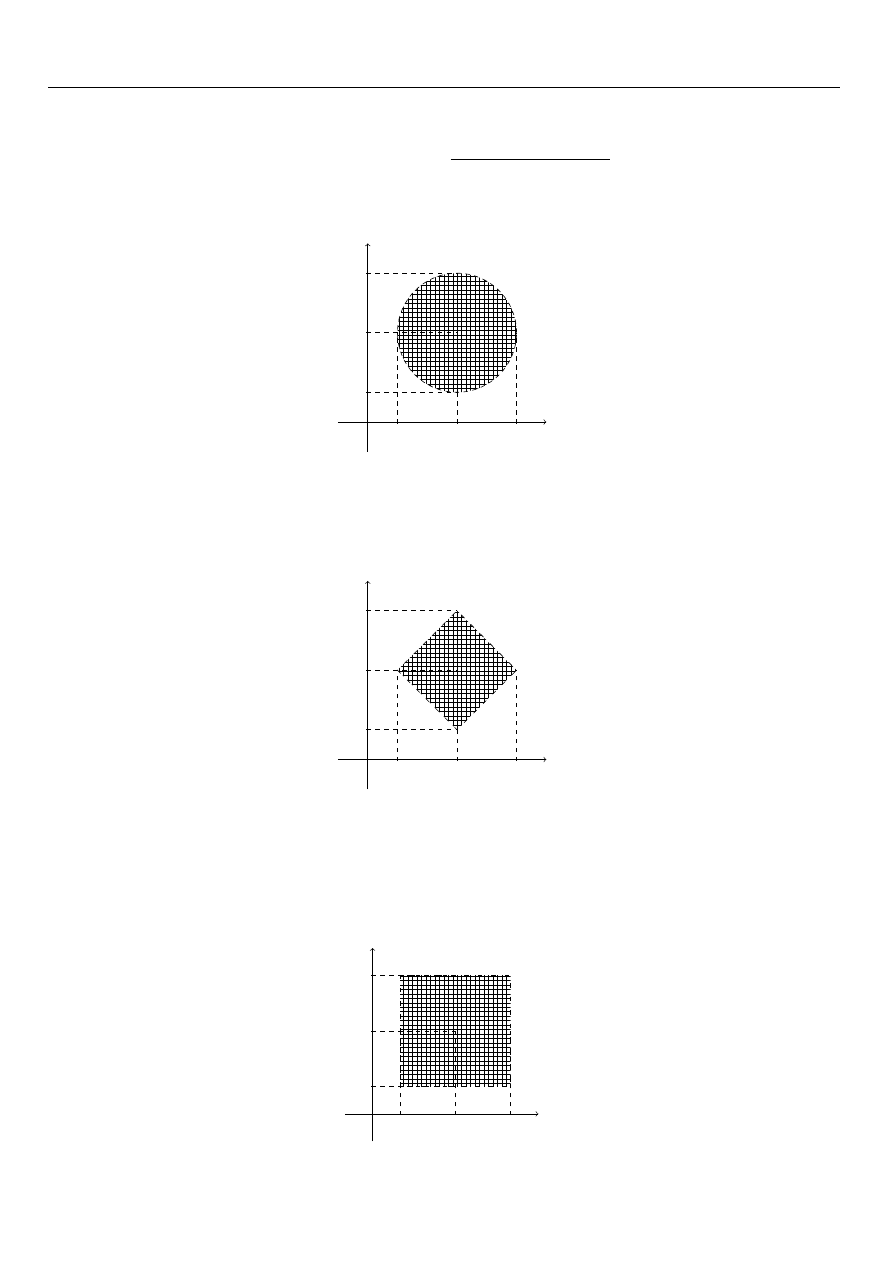
4
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
2 euklidesowej na płaszczyźnie R
2
:
B ((x
0
, y
0
), ε)
def
= {(x, y) ∈ R
2
:
q
(x
0
− x)
2
+ (y
0
− y)
2
< ε} =
= {(x, y) ∈ R
2
: (x
0
− x)
2
+ (y
0
− y)
2
< ε
2
}
x
y
y
0
+ ε
y
0
y
0
− ε
x
0
− ε
x
0
x
0
+ ε
3 manhattan ponownie na R
2
.
B ((x
0
, y
0
), ε)
def
= {(x, y) ∈ R
2
: |x
0
− x| + |y
0
− y| < ε}
x
y
y
0
+ ε
y
0
y
0
− ε
x
0
− ε
x
0
x
0
+ ε
4 maksimum na płaszczyźnie R
2
.
B ((x
y
, y
0
), ε)
def
= {(x, y) ∈ R
2
: max{|x
0
− x|, |y
0
− y|} < ε} =
= {(x, y) ∈ R
2
: |x
0
− ε < x < x
0
+ ε, y
0
− ε < y < y
0
+ ε}
x
y
y
0
+ ε
y
0
y
0
− ε
x
0
− ε
x
0
x
0
+ ε

5
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
5 Niech d będzie metryką dyskretną w zbiorze X oraz x
0
∈ X. Ponadto niech ε, ρ ∈ R
+
. Wówczas
B (x
0
, ε) =
{x
0
}, gdy ε ¬ 1,
X,
gdy ε > 1,
S (x
0
, ρ) =
{x
0
},
gdy ρ = 0,
Ø,
gdy 0 < ρ < 1 albo ρ > 1,
X \ {x
0
},
gdy ρ = 1.
Definicja 1. 4
Podzbiór Y przestrzeni metrycznej (X, d) jest
ograniczony
, jeśli
∃
x
0
∈X
∃
ε∈[0,∞)
: Y ⊆ B (x
0
, ε) .
UWAGA 3
a) Każda kula i każda sfera jest zbiorem ograniczonym.
b) Zbiór pusty jest zbiorem ograniczonym.
c) Przecięcie dowolnej, niepustej rodziny podzbiorów ograniczonych przestrzeni metrycznej jest
podzbiorem ograniczonym tej przestrzeni.
d) Suma dowolnej, skończonej rodziny podzbiorów ograniczonych danej przestrzeni metrycznej jest
podzbiorem ograniczonym tej przestrzeni.
Definicja 1. 5 Średnicą
podzbioru Y przestrzeni metrycznej (X, d) nazywa się
diam (Y ) := sup{d(x, y) : x, y ∈ Y }.
Przykład.
Niech ε ∈ R
+
oraz x
0
∈ X. Jeśli x, y ∈ B(x
0
, ε), to d(x, y) ¬ d(x, x
0
) + d(y, y
0
) < 2ε. W takim
razie diam (B) (x
0
, ε) := sup{d(x, y) ¬ 2ε : x, y ∈ B(x
0
, ε)}. Przypuśćmy teraz, że d jest metryką
dyskretną. W takim razie
diam (B)(x
0
, ε) =
diam {x
0
} = 0, gdy ε ¬ 1,
diam (X) ¬ 1,
gdy ε > 1.

6
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 2.
Niech (X, d) będzie przestrzenią metryczną i niech Y, Z ⊆ X. Wówczas
(i) diam (Y ) ∈ [0, ∞) ∪ {±∞},
(ii) diam (Y ) = −∞ ⇔ Y = Ø,
(iii) diam (Y ) = 0 ⇔ #Y = 1,
(iv) Y ⊆ Z ⇒ diam (Y ) ¬ diam (Z),
(v) diam (Y ) < ∞ wtedy i tylko wtedy, gdy Y jest zbiorem ograniczonym.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Definicja 1. 6 Odległością między podzbiorami
Y oraz Z przestrzeni metrycznej (X, d) nazywa się
dist (Y, Z)
def
= inf{d(y, z) : y ∈ Y, z ∈ Z}.
UWAGA 4
a) ∀
x,y∈X
dist ({x}, {y}) = d(x, y)
b) dist (Y, Z) ∈ [0, ∞)
c) dist (Y, Z) = ∞ ⇔ (Y = Ø ∨ Z = Ø)
d) Y ∩ Z 6= Ø ⇒ dist (Y, Z) = 0 (ale nie na odwrót, patrz następny przykład nr 1)
e) Dla punktu x ∈ X piszemy dist (x, Y ) zamiast dist ({x}, Y ) i mówimy o
odległości punktu x od
zbioru Y
(dist (x, Y ) = inf{d(x, y) : y ∈ Y }) .
7
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Przykład.
1. Rozważmy zbiór R z metryką naturalną. Przypomnijmy, że e := lim
n→∞
1 +
1
n
n
∈ R \ Q
i odnotujmy, że
1 +
1
n
n
∈ Q dla każdego n naturalnego poza zerem. W takim razie
0 ¬ dist (R \ Q, Q) ¬ inf{|e −
1 +
1
n
n
| : n ∈ N} = 0, stąd dist (R \ Q, Q) = 0.
2. Rozważmy metrykę euklidesową na płaszczyźnie R
2
. Policzmy odleglość punktu (x
0
, y
0
) od
prostej l ⊂ R
2
o równaniu y = ax + b.
dist ((x
0
, y
0
), l)
def
= inf{
q
(x − x
0
)
2
+ (y − y
0
)
2
: (x, y) ∈ l}
!
=
!
=
q
inf{(x − x
0
)
2
+ (y − y
0
)
2
: (x, y) ∈ l} =
q
inf{(x − x
0
)
2
+ (ax + b − y
0
)
2
: x ∈ l} =
=
q
inf{(1 + a
2
)x
2
+ (2ab − 2ay
0
− 2x
0
)x + x
2
0
+ b
2
+ y
2
0
− 2by
0
: x ∈ l}
Podstawmy x
w
=
ay
0
+x
0
−ab
1+a
2
.
q
(1 + a
2
)x
2
w
+ (2ab − 2ay
0
− 2x
0
)x
w
+ x
2
0
+ b
2
+ y
2
0
− 2by
0
=
=
s
a
2
x
2
0
− 2by
0
− 2ax
0
y
0
+ 2abx
0
+ y
2
0
+ b
2
1 + a
2
=
=
s
(y
0
− b − ax
0
)
2
1 + a
2
=
|y
0
− b − ax
0
|
√
1 + a
2
Definicja 1. 7
Ciąg (a
n
) = (a
n
)
∞
n=1
punktów przestrzeni metrycznej (X, d) jest:
(1)
ograniczony
, jeżeli zbiór jego wyrazów, czyli {a
n
: n ∈ N \ {0}} jest ograniczony,
(2)
ciągiem Cauchy’ego
, jeśli ∀
ε∈R
+
∃
N ∈N\{0}
∀
m,n∈N\{0}
: m, n N ⇒ d(a
m
, a
n
) < ε,
(3)
zbieżny
do punktu g ∈ X (zapis: lim
n→∞
a
n
= g albo a
n
d
−−−→
n→∞
g), jeśli
∀
ε∈R
+
∃
N ∈N\{0}
∀
n∈N\{0}
: n N ⇒ d(a
n
, g) < ε.
UWAGA 5
a
n
d
−−−→
n→∞
g ⇔ ∀
ε∈R
+
∃
N ∈N\{0}
∀
n∈N\{0}
: n N ⇒ a
n
∈ B(g, ε)
8
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 3.
Dla ciągu (a
n
) punktów przestrzeni metryczej (X, d) i punktu g ∈ X następu-
jące warunki są równoważne:
(i) a
n
d
−−−→
n→∞
g,
(ii) lim
n→∞
d(a
n
, g) = 0 (zwykła granica ciągu liczbowego).
Dowód.
a
n
d
−−−→
n→∞
g
m
∀
ε∈R
+
∃
N ∈N\{0}
∀
n∈N\{0}
: n N ⇒ d(a
n
, g) < ε
m
∀
ε∈R
+
∃
N ∈N\{0}
∀
n∈N\{0}
: n N ⇒ |d(a
n
, g) − 0| < ε
m
lim
n→∞
d(a
n
, g) = 0
Twierdzenie 1. 4. (o jednoznaczności granicy)
Każdy ciąg punktów danej przestrzeni metrycz-
nej ma w tej przestrzeni
co najwyżej jedną
granicę.
Dowód.
Niech (a
n
) będzie ciągiem punktów przestrzeni metrycznej (X, d). Przypuśćmy, że a
n
d
−−−→
n→∞
g
1
oraz
a
n
d
−−−→
n→∞
g
2
dla pewnych g
1
, g
2
∈ X. Wówczas przy (dowolnie) ustalonym ε ∈ R
+
∃
N
1
,N
2
∈N\{0}
∀
n∈N\{0}
n N
1
⇒ d(a
n
, g
1
) <
ε
2
,
n N
2
⇒ d(a
n
, g
2
) <
ε
2
.
Połóżmy N = max{N
1
, N
2
}. Wtedy 0 ¬ d(g
1
, g
2
) ¬ d(a
n
, g
1
) + d(a
n
, g
2
) ¬
ε
2
+
ε
2
= ε dla każdego
n ∈ N \ {0}. Z uwagi na dowolność liczby ε, z powyższych nierówności wynika, że d(g
1
, g
2
) = 0,
skąd g
1
= g
2
.
Twierdzenie 1. 5.
Niech (a
n
) będzie takim ciągiem punktów przestrzeni metrycznej (X, d),
że
∃
n
0
∈N\{0}
∀
n∈N\{0}
: n n
0
⇒ a
n
= a
n
0
.
Wówczas lim
n→∞
a
n
= a
n
0
.

9
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Dowód.
Ustalmy ε > 0 (dowolne). Jeśli wskaźnik n jest niemniejszy od n
0
,
to
d (a
n
, a
n
0
) = d (a
n
0
, a
n
0
) = 0 < ε.
Twierdzenie 1. 6.
Jeśli ciąg punktów danej przestrzeni metrycznej jest zbieżny do pewnego punktu
tej przestrzeni, to każdy jego podciąg jest zbieżny do tegoż punktu.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 1. 7.
Każdy zbieżny ciąg punktów przestrzeni metrycznej jest ciągiem Cauchy’ego.
Dowód.
Niech (a
n
) będzie ciągiem punktów przestrzeni metrycznej (X, d). Załóżmy, że a
n
d
−−−→
n→∞
g dla
pewnego g ∈ X. Wybierzmy (dowolne) ε ∈ R
+
. Zatem ∃
N ∈N\{0}
∀
n∈N\{0}
: n N ⇒ d(a
n
, g) <
ε
2
.
Jeśli teraz wskaźniki m, n N , to d(a
m
, a
n
) ¬ d(a
m
, g) + d(a
n
, g) <
ε
2
+
ε
2
= ε. Wykazaliśmy zatem,
że (a
n
) jest ciągiem Cauchy’ego.
Twierdzenie 1. 8.
Każdy ciąg Cauchy’ego jest ograniczony.
Dowód.
Niech (a
n
) będzie ciągiem Cauchy’ego punktów przestrzeni metrycznej (X, d).
Wobec tego ∃
N ∈N\{0}
∀
m,n∈N\{0}
: m, n N ⇒ d(a
m
, a
n
) < 1.
Połóżmy ρ = max{1, d(a
1
, a
N
), . . . , d(a
N −1
, a
N
)}. Dla dowolnego wskaźnika n mamy wtedy
d(a
n
, a
N
) ¬ ρ. Skoro tak, to a
n
∈ B (a
N
, ρ) dla każdego n ∈ N\{0}, skąd już wynika ogranianiczenie
ciągu (a
n
).
Przykład.
1. Rozważmy R z metryką naturalną. Ciąg ((−1)
n
) jest wtedy ograniczony (bo zawiera się w kuli
domkniętej o środku w x
0
= 0 i promieniu ε = 1 dla każdego n). Nie jest on jednak ciągiem
Cauchy’ego, bowiem ∀
m,n∈N\{0}
: m − n = 1 ⇒ |(−1)
m
− (−1)
n
| = 2.
2. Ponieważ lim
n→∞
1 +
1
n
n
= e, to ciąg
1 +
1
n
n
jest ciągiem Cauchy’ego w R z metryką
naturalną. Wszystkie wyrazy tego ciągu są liczbami wymiernymi. Skoro tak, to nasz ciąg jest
ciągiem Cauchy’ego w Q z (indukowaną) metryką naturalną. Niestety ciąg ten nie jest zbieżny
w Q z (indukowaną) metryką naturalną, bo e /
∈ Q.

10
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 9.
Dla ciagu
a
(k)
∞
k=1
punktów przestrzeni R
n
, w którym a
(k)
=
a
(k)
1
, . . . , a
(k)
n
i punktu g = (g
1
, . . . , g
n
) ∈ R
n
następujące warunki są równoważne:
(i) a
(k)
d
1
−−−→
k→∞
g,
(ii) a
(k)
d
2
−−−→
k→∞
g,
(iii) a
(k)
d
∞
−−−→
k→∞
g,
(iv) ∀
i∈{1,...,n}
lim
k→∞
a
(k)
i
= g (granica ciągu liczbowego).
Dowód.
(ii) =⇒ (iv)
Przypuśćmy, że a
(k)
d
2
−−−→
k→∞
g, czyli że lim
k→∞
d
2
a
(k)
, g
= 0.
Przypomnijmy, że d
2
a
(k)
, g
=
s
n
P
i=1
a
(k)
i
− g
i
2
. Zauważmy, że:
∀
j∈{1...,n}
∀
n∈N\{0}
: 0 ¬ |a
(k)
j
− g
j
| =
r
a
(k)
j
− g
j
2
¬
v
u
u
t
n
X
i=1
a
(k)
i
− g
i
2
= d
2
a
(k)
, g
,
czyli 0 ¬ |a
(k)
j
− g
j
| ¬ d
2
a
(k)
, g
. Z twierdzenia o trzech ciągach otrzymujemy, że
∀
j∈{1,...,n}
:
lim
k→∞
a
(k)
j
= g
j
.
(iv) =⇒ (ii)
Przypuśćmy, że ∀
i∈{1,...,n}
lim
k→∞
a
(k)
i
= g
i
, czyli że ∀
i∈{1,...,n}
lim
k→∞
| a
(k)
i
− g
i
|= 0. Zauważmy następnie,
iż dla dowolnego k ∈ N \ {0} zachodzi:
0 ¬ d
2
a
(k)
, g
=
v
u
u
t
n
X
i=1
a
(k)
i
− g
i
2
¬
s
n ·
n
max
i=1
a
(k)
i
− g
i
2
=
=
√
n ·
n
max
i=1
| a
(k)
i
− g
i
|¬
√
n ·
n
X
i=1
| a
(k)
i
− g
i
| .
Stosując do powyższych nierówności twierdzenie o trzech ciągach otrzymujemy, co następuje:
lim
k→∞
a
(k)
, g
= 0, co znaczy, że a
(k)
d
2
−−−→
k→∞
g.
(i) ⇐⇒ (iv)
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(iii) ⇐⇒ (iv)
Dowód pozostawiamy czytelnikowi jako ćwiczenie.

11
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Przykład.
1.
n
q
n
3
+ sin(n),
n+5
n
2
+n−1
· cos(1 −
4
√
n),
n+1
n+2
n
d
2
−−−→
n→∞
1, 0,
1
e
2. Ciąg
n
q
n
3
+ sin(n),
n+5
n
2
+n−1
· cos(1 −
4
√
n),
3n+1
n+2
n
nie jest zbieżny w R
3
z metryką euklide-
sową, ponieważ lim
n→∞
3n+1
n+2
n
= ∞.
Definicja 1. 8
Przestrzeń metryczna jest
zupełna
, jeśli każdy ciąg Cauchy’ego punktów tej prze-
strzeni jest zbieżny do pewnego punktu tejże przestrzeni.
Przykład.
1. Q z (indukowaną) metryką naturalną nie jest zupełną przestrzenią metryczną z uwagi na ciąg
1 +
1
n
n
, którego granicą przy n → ∞ jest liczba e /
∈ Q.
2. Niech n będzie dowolną liczbą naturalną różną od zera. Zbiór R
n
\ (0, . . . , 0) z (indukowaną)
metryką euklidesową nie jest zupełną przestrzenią metryczną z uwagi na to,
iż R
n
\ (0, . . . , 0) 3
1
n
, 0, . . . , 0
d
2
−−−→
n→∞
(0, . . . , 0) /
∈ R
n
\ (0, . . . , 0).
Twierdzenie 1. 10.
Niech n ∈ N \ {0} i niech d ∈ {d
1
, d
2
, d
∞
}. Wówczas przestrzeń metryczna
(R
n
, d) jest zupełna ( w szczególności R z metryką naturalną jest zupełną przestrzenią metryczną).
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 1. 11.
Niech X będzie niepustym zbiorem. Przestrzeń metryczna (B (X, R) , d
∞
) jest
zupełna.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Definicja 1. 9
Niech (X, d) będzie przestrzenią metryczną. Zbiór U ⊆ X jest
otwarty
,
jeśli ∀
x∈U
∃
ε∈R
+
B(x, ε) ⊆ U .
X
U
b
x

12
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
UWAGA 6
Inaczej mówiąc, U jest otwarty, jeśli ∀
x∈U
∃
ε∈R
+
∀
y∈X
d(x, y) < ε ⇒ y ∈ U.
Definicja 1. 10
Rodzinę wszystkich podzbiorów otwartych przestrzeni metrycznej (X, d) nazywa
się
topologią
tej przestrzeni.
(Topologię przestrzeni (X, d) będziemy oznaczać jako Top (X, d)).
Twierdzenie 1. 12.
Niech (X, d) będzie przestrzenią metryczną. Niech ponadto x ∈ X,
ε ∈ R
+
oraz q ∈ [0, ∞). Wówczas B (x, ε) oraz X \
B (x, q) są zbiorami otwartymi.
Dowód. (Kula otwarta)
Zajmijmy się kulą otwartą. Weźmy pod uwagę dowolny punkt y ∈ B (x, ε). Wówczas d(y, x) < ε.
Skoro tak, to r := ε − d(x, y) ∈ R
+
. Jeśli teraz z ∈ B (y, r), to:
d(z, x) ¬ d(z, y) + d(y, x) < r + d(y, x) = ε − d(x, y) + d(x, y) = ε.
Pokazaliśmy w ten sposób, że B(y, r) ⊆ B(x, ε). Ze względu na dowolność y ∈ B(x, ε) dowód jest
zakończony.
Dowód. (Dopełnienie kuli domkniętej)
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 1. 13.
Niech (X, d) będzie przestrzenią metryczną. Wówczas:
(i) Ø, X ∈ Top (X, d),
(ii) U, V ∈ Top ((X, d)) ⇒ U ∩ V ∈ Top (X, d),
(iii) Jeżeli {U
i
}
i∈I
jest dowolną rodziną podzbiorów otwartych (X, d), to
S
i∈I
U
i
także jest podzbiorem
otwartym tej przestrzeni.
Dowód.
(i) Oczywiste.
(ii) Przypuścmy, że U, V ∈ Top (X, d). Rozważmy (dowolny) punkt x ∈ U ∩ V . Ponieważ x ∈ U
oraz U ∈ Top (X, d), to istnieje taki ε
1
dodatni, że B(x, ε
1
) ⊆ U . Podobnie, skoro x ∈ V oraz
V ∈ Top (X, d), to istnieje taki ε
2
dodatni, iż B(x, ε
2
) ⊆ V . Połóżmy teraz ε = min{ε
1
, ε
2
}.
Wówczas ε > 0, co więcej, B(x, ε) = B(x, ε
1
) ∩ B(x, ε
2
) ⊆ U ∩ V .

13
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
(iii) Przypuśćmy, że {U
i
}
i∈I
jest rodziną podzbiorów otwartych przestrzeni (X, d). Weźmy teraz
pod uwagę (dowolny) punkt x ∈
S
i∈I
U
i
. Z definicji sumy mnogościowej, istnieje taki index
i
0
∈ I, że x ∈ U
i
0
. Ponieważ U
i
0
∈ Top (X, d), to istnieje ε ∈ R
+
, że B(x, ε) ⊆ U
i
0
. Zatem
podsumowując, B(x, ε) ⊆ U
i
0
⊆
S
i∈I
U
i
.
Wniosek.
(s ∈ N \ {0}, U
1
, . . . , U
s
∈ Top (X, d)) ⇒ U
1
∩ . . . ∩ U
s
∈ Top (X, d)
Przykład.
Rozważmy prostą R wyposażoną w metrykę naturalną oraz ciąg przedziałów
−
1
n
,
1
n
∞
n=1
. Każdy
z tych przedziałów jest podzbiorem otwartym rozważanej przestrzeni jako kula otwarta o środku
w punkcie 0 oraz promieniu
1
n
. Tymczasem
∞
T
n=1
−
1
n
,
1
n
= {0} i nie jest podzbiorem otwartym tej
przestrzeni.
Twierdzenie 1. 14.
Niech x oraz y będą dowolnymi, różnymi od siebie punktami przestrzeni me-
trycznej (X, d). Wówczas
∃
U,V ∈Top (X,d)
:
x ∈ U,
y ∈ V,
U ∩ V = Ø.
Dowód.
Przyjmijmy, że ε = d(x, y). Ponieważ x 6= y, to ε > 0. Zdefiniujmy U = B
x,
ε
2
oraz
V = B
y,
ε
2
. W takim razie U, V ∈ Top (X, d), x ∈ U oraz y ∈ V . Gdyby wówczas istniał punkt
z ∈ U ∩ V , to ε = d(x, y) ¬ d(x, z) + d(z, y) <
ε
2
+
ε
2
= ε, co jest oczywiście sprzeczne. Skoro tak,
to U ∩ V = Ø.
y
x
ε
2
ε
2
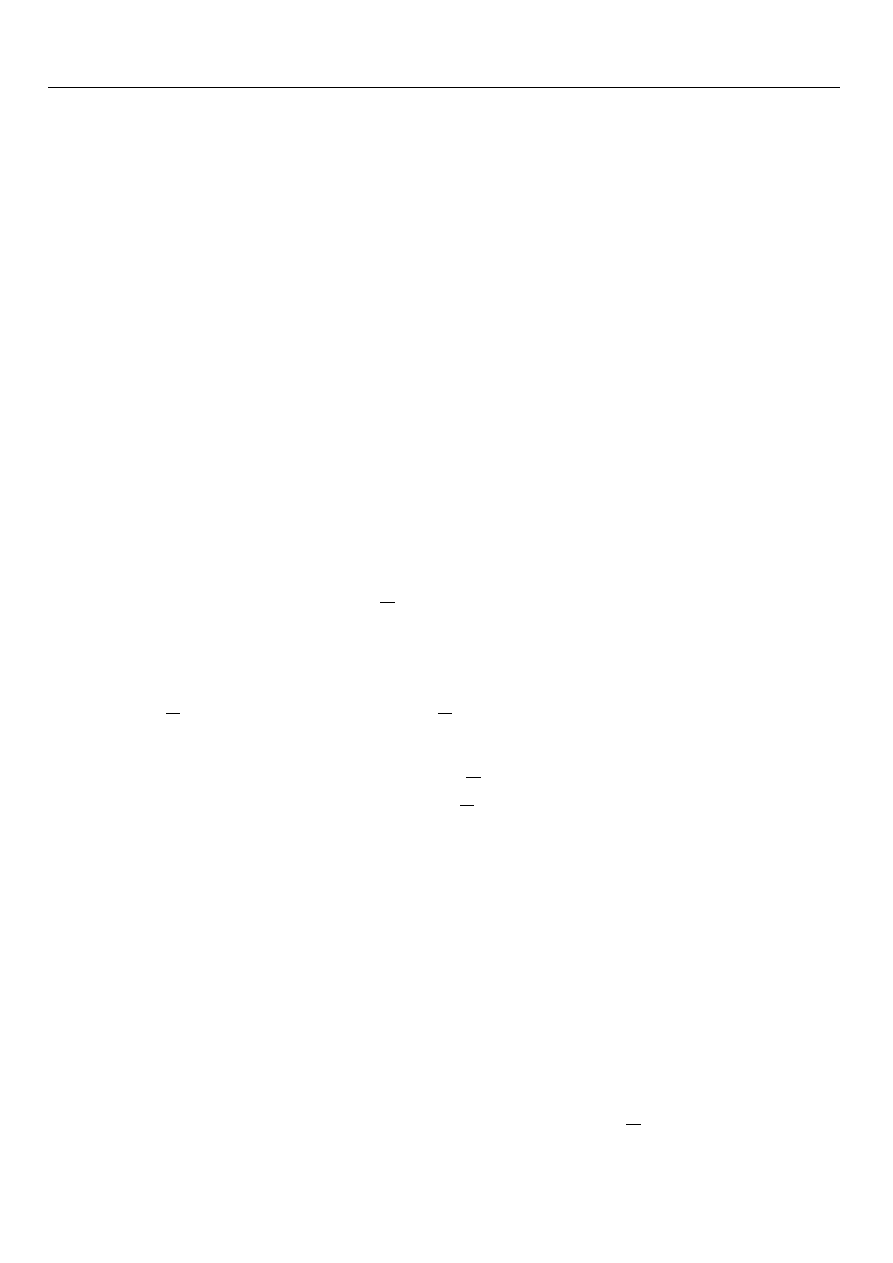
14
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
UWAGA 7
Powyższe twierdzenie można sformułować następująco: Każda przestrzeń metrycza jest
przestrze-
nią Hausdorffa
(czyli T
2
-przestrzenią).
Definicja 1. 11 Otoczeniem
(otwartym) punktu x przestrzeni metrycznej (X, d) nazywa się każdy
taki zbiór otwarty U ∈ Top (X, d), że x ∈ U .
UWAGA 8
Każda kula otwarta o środku w danym punkcie przestrzeni metrycznej jest otoczeniem tego
punktu. Także cała rozważana przestrzeń jest otoczeniem tego punktu.
Definicja 1. 12
Podzbiór C przestrzeni metrycznej (X, d) jest
domknięty
, jeśli X \C ∈ Top (X, d).
Definicja 1. 13
Rodzinę wszystkich podzbiorów domkniętych przestrzeni metrycznej (X, d) na-
zywa się
kotopologią
tej przestrzeni i oznacza jako Cotop(X, d).
Twierdzenie 1. 15.
Niech (X, d) będzie przestrzenią metryczą. Ponadto niech x ∈ X oraz
ρ ∈ [0, ∞) ⊂ R. Wówczas kula domknięta B(x, ρ) oraz sfera S(x, ρ) są podzbiorami domkniętymi
przestrzeni (X, d).
Dowód.
Wiemy, że X \
B(x, ρ) ∈ Top (X, d). Skoro tak, to B(x, ρ) jest podzbiorem domkniętym.
Następnie
X \ S(x, ρ) =
X \ {x} = X \ B(x, ρ),
gdy ρ = 0,
B(x, ρ) ∪
X \ B(x, ρ)
, gdy ρ > 0.
Ponieważ każda kula otwarta i dopełnienie kuli domkniętej to zbiory otwarte oraz suma dwóch
zbiorów otwartych jest zbiorem otwartym, to z powyższej równości wynika, że
X \ S(x, ρ) ∈ Top (X, d),
co znaczy, że S(x, ρ) jest zbiorem domkniętym.
Wniosek.
Każdy jednopunktowy podzbiór dowolnej przestrzeni metrycznej jest domknięty.
Dowód.
Niech (X, d) będzie przestrzenią metryczną i niech x ∈ X. Wówczas {x} =
B(x, 0).

15
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 16.
Niech (X, d) będzie przestrzenią metryczną. Wówczas:
(i) Ø, X ∈ Cotop(X, d),
(ii) C, D ∈ Cotop(X, d) ⇒ C ∪ D ∈ Cotop(X, d),
(iii) jeśli {C
i
}
i∈I
jest dowolną rodziną podzbiorów domkniętych przestrzeni metrycznej (X, d),
to
T
i∈I
C
i
też jest podzbiorem domkniętym tej przestrzeni.
Dowód.
(i) Wiadomo, że Ø, X ∈ Top (X, d). Ø = X \ X oraz X = X \ Ø.
(ii) Powiedzmy, że C, D ∈ Cotop(X, d). Wówczas X \ (C ∪ D) = (X \ C) ∩ (X \ D). Ponadto X \
C, X \ D ∈ Top (X, d). Ponieważ przecięcie dwóch zbiorów otwartych jest zbiorem otwartym,
to z powyższego wynika, że X \ (C ∪ D) ∈ Top (X, d), co oznacza,
że C ∪ D ∈ Cotop(X, d).
(iii) Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Wniosek.
(s ∈ N \ {0}, C
1
, . . . , C
s
∈ Cotop(X, d)) ⇒ C
1
∪ . . . ∪ C
s
∈ Cotop(X, d)
UWAGA 9
Jeśli (X, d) jest przestrzenią metryczną to zbiory Ø oraz X są w tej przestrzeni otwarto-domknięte.
Przykład.
1. Q nie jest podzbiorem otwartym prostej R wyposażonej w metrykę naturalną, bowiem Q
jest zbiorem przeliczalnym, a każdy niepusty przedział otwarty prostej jest nieprzeliczalny.
Również R \ Q nie jest podzbiorem otwartym prostej R (bowiem jeśli weźmiemy r, s ∈ R \ Q,
gdzie r < s, to istnieje taka liczba q ∈ Q, że r < q < s). Skoro tak, to Q nie jest zbiorem
domkniętym. Dokładnie tak samo R \ Q nie jest ani podzbiorem otwartym, ani domkniętym
prostej R z metryką naturalną.
2. Jeśli q ∈ Q, to {q} jest podzbiorem domkniętym prostej R wyposażonej w metrykę naturalną.
Tymczasem Q =
S
q∈Q
{q} nie jest podzbiorem domkniętym tej prostej.
16
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 17.
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Następujące wa-
runki są wówczas równoważne dla punktu x ∈ X:
(i) Każde otoczenie punktu x ma niepuste przecięcie ze zbiorem A,
(ii) ∀
ε∈R
+
A ∩ B(x, ε) 6= Ø,
(iii) Istnieje ciąg (a
n
)
∞
n=1
elementów zbioru A taki, że a
n
d
2
−−−→
n→∞
x.
Dowód.
(i) =⇒ (ii)
Każda kula otwarta jest otoczeniem swojego środka.
(ii) =⇒ (iii)
Załóżmy, że warunek (ii) jest spełniony. Wówczas ∀
n∈N\{0}
A ∩ B
x,
1
n
6= Ø.
Mając dane n ∈ N \ {0} wybieramy (dokładnie jeden) punkt a
n
∈ A ∩ B
x,
1
n
. W ten sposób
otrzymaliśmy ciąg (a
n
)
∞
n=1
elementów zbioru A. Ponieważ ∀
n∈N\{0}
: 0 ¬ d(a
n
, x) <
1
n
, to z twier-
dzenia o trzech ciągach lim
n→∞
d(a
n
, x) = 0, co jest równoważne z a
n
d
2
−−−→
n→∞
x.
(iii) =⇒ (i)
Przypuścmy, że warunek (iii) jest spełniony. Niech U będzie (dowolnym) otoczeniem puktu x. Po-
nieważ x ∈ U oraz U ∈ Top (X, d), to ∃
ε∈R
+
: B(x, ε) ⊆ U . Na mocy definicji granicy ciągu i faktu,
że a
n
d
2
−−−→
n→∞
x otrzymujemy, iż ∃
N ∈N\{0}
: a
N
∈ B(x, ε). Skoro tak, to a
N
∈ A ∩ B(x, ε) ⊆ A ∩ U .
W takim razie A ∩ U 6= Ø.
Definicja 1. 14
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Punkt x z tej przestrze-
ni jest
punktem granicznym
zbioru A, jeśli spełnia którykolwiek z warunków powyższego twierdze-
nia.
Definicja 1. 15
Zbiór wszystkich punktów granicznych danego podzbioru przestrzeni metrycznej
nazywa się
domknięciem
tego podzbioru i oznacza się jako
A albo cl(A).
Przykład.
Rozważmy podzbiór A = (−1, 2) ∪ (2, 3] prostej R wyposażonej w metrykę naturalną. Jeżeli x ∈ R
jest punktem granicznym tego podzbioru, to istnieje ciąg (a
n
)
∞
n=1
elementów tego pozdbioru taki,
że lim
n→∞
a
n
= x. Ponieważ ∀
n∈N\{0}
− 1 < a
n
¬ 3, to −1 ¬ x ¬ 3 (twierdzenie o osłabieniu
nierówności przy przejściu do granicy). W ten sposób udowodniliśmy, że A ⊆ [−1, 3].
Jeżeli teraz a ∈ A, to lim
n→∞
a ∈ A. Następnie A 3 −1 +
1
n
−−−→
n→∞
−1 ∈ A. W końcu
A 3 2 −
1
n
−−−→
n→∞
2 ∈ A. W ten sposób udowodniliśmy, że [−1, 3] ⊆ A. Podsumowując,
[−1, 3] = A.
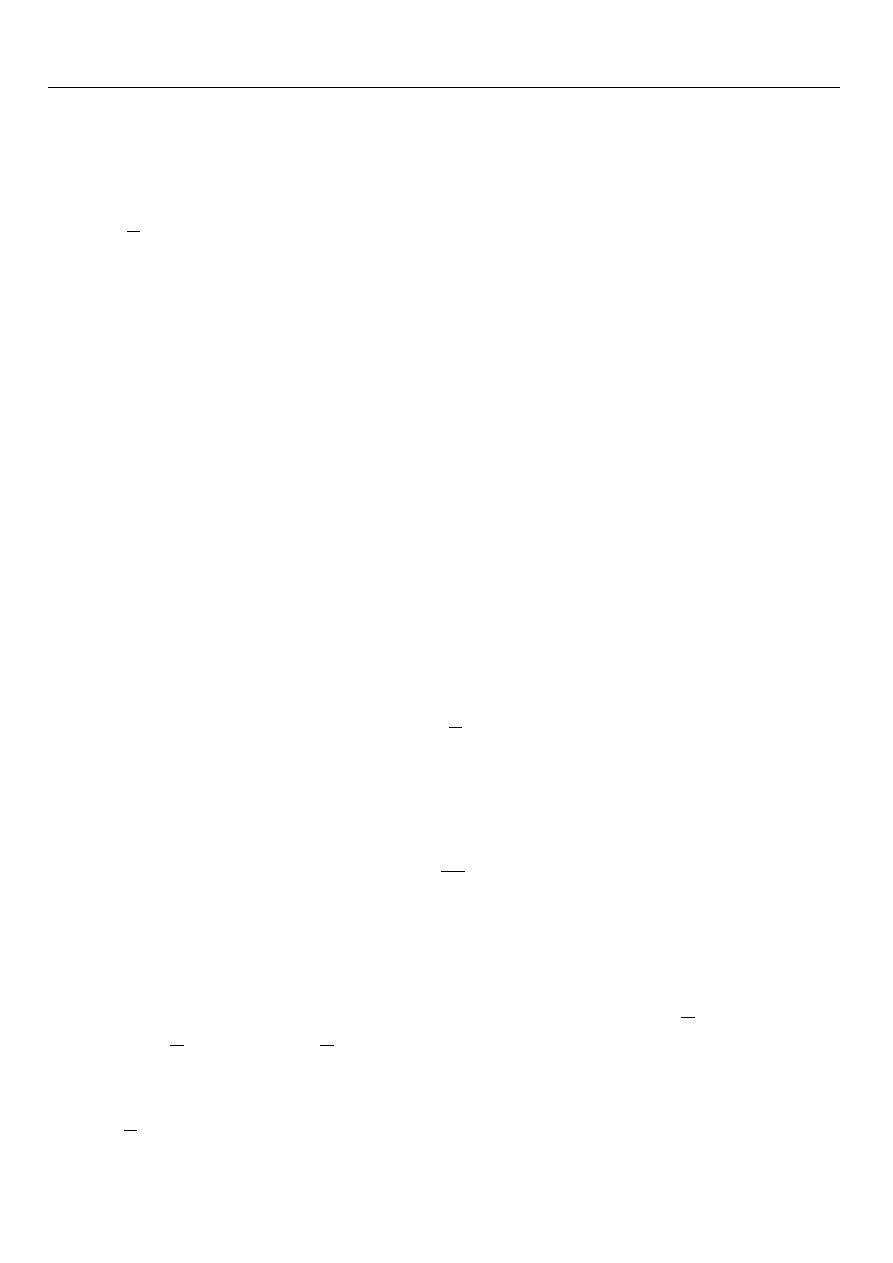
17
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 18.
Dla podzbioru A przestrzeni metrycznej (X, d) następujące warunki są rów-
noważne:
(i) A ∈ Cotop(X, d),
(ii) A =
A,
(iii) Każdy punkt graniczny zbioru A należy do zbioru A.
UWAGA 10
Każdy podzbiór dowolnej przestrzeni metrycznej jest zawarty w swoim domknięciu
Dowód.
(ii) ⇐⇒ (iii)
Oczywiste, patrz powyższa uwaga.
¬(i) ⇐⇒ ¬(ii)
¬(i) ⇔ A 6∈ Cotop(X, d) ⇔ X \ A 6∈ Top (X, d) ⇔ ∃
x∈X\A
: ∀
ε∈R
+
A ∩ B(x, ε) 6= Ø ⇔
⇔ ∃
x
0
∈X
¬
∃
ε∈R
+
: A ∩ B(x
0
, ε) = Ø
⇔ ∃
x
0
∈R
+
¬
∃
x
0
∈R
+
: B(xε) ⊆ X \ A
⇔ ¬(ii)
¬(i) ⇐⇒ ¬(iii)
¬(i) ⇔ A 6∈ Cotop(X, d) ⇔ X \ A 6∈ Top (X, d) ⇔ ∃
x∈X\A
: ∀
ε∈R
+
A ∩ B(x, ε) 6= Ø ⇔
⇔ ∃
x
0
∈X\A
: x ∈ A ⇔ ¬(iii)
Przykład.
1. Rozważmy podzbiór E = {(x, y, z) ∈ R
3
: 0 < x
2
+ y
2
+ (z − 1)
2
¬ 1, z < 2} przestrzeni
metrycznej (R
3
, d
2
). Ponieważ E 3
0, 0, 2 −
1
n+1
d
2
−−−→
n→∞
(0, 0, 2), to tzw. ”biegun północny”
jest punktem granicznym zbioru E. Ponieważ nie należy on jednocześnie do samego zbioru
E, to ten zbiór nie jest domknięty, nie jest on wszakże też otwarty.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
2. Rozważmy Q jako podzbiór prostej R z metryką naturalną. Wiadomo, że dla każdego x ∈ R
istnieje ciąg (q
n
)
∞
n=1
liczb wymiernych taki, że lim
n→∞
q
n
= x. Skoro tak, to R ⊆ Q. Ponadto jest
pewne, iż Q ⊆ R, zatem R = Q.
Twierdzenie 1. 19.
Niech A będzie podzbiorem przestrzeni metrycznej (X, d).
Wówczas A =
T
{C ∈ Cotop(X, d) : C ⊇ A}.
18
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Dowód.
” ⊆ ” Niech x ∈
A i niech C ∈ Cotop(X, d) będzie takim zbiorem, że C ⊇ A. Wystarczy pokazać,
że x ∈ C. Ponieważ x jest punktem granicznym zbioru A, to istnieje ciąg (a
n
)
∞
n=1
elementów
tego zbioru, że a
n
d
−−−→
n→∞
x. Jednakże ciąg (a
n
)
∞
n=1
jest także ciągiem elementów C, zatem
x jest punktem granicznym tegoż zbioru. Ponieważ jest on domknięty, to z faktu, iż x jest
punktem granicznym C, wynika, że x ∈ C.
” ⊇ ” Przypuśćmy, że x ∈ X \ A. Wówczas ∃
ε∈R
+
: A ∩ B(x, ε) 6= Ø. Zauważmy, iż x /
∈ X \ B(x, ε).
Następnie X \ B(x, ε) ∈ Cotop(X, d). W końcu A ⊆ X \ B(x, ε). Podsumowując,
∃
C
0
∈Cotop(X,d)
:
A ⊆ C
0
,
x /
∈ C
0
.
Skoro tak, to x /
∈
T
{C ∈ Cotop(X, d) : C ⊇ A}. Pokazaliśmy w ten sposób,
że X \
A ⊆ X \
T
{C ∈ Cotop(X, d) : C ⊇ A}. Przechodząc teraz do dopełnień otrzymujemy
T
{C ∈ Cotop(X, d) : C ⊇ A} ⊆ A.
Wniosek.
1 Domkniecie dowolnego zbioru danej przestrzeni metrycznej jest podzbiorem domkniętym tej
przestrzeni.
2 Niech A będzie podzbiorem przestrzeni metrycznej (X, d) i niech C ∈ Cotop(X, d). Jeśli wtedy
A ⊆ C, to także A ⊆ C.
Przykład.
Wróćmy do zbioru E zdefiniowanego w poprzednim zestawie przykładów. Ponieważ
E ⊆ {(x, y, z) ∈ R
3
: x
2
+ y
2
+ (z − 1)
2
¬ 1} = B ((0, 0, 1), 1) oraz B ((0, 0, 1), 1) ∈ Cotop (R
3
, d
2
),
to (z wniosku 2 ) mamy E ⊆ B ((0, 0, 1), 1). Ponieważ E = B ((0, 0, 1), 1) \ {(0, 0, 1), (0, 0, 2)},
E ⊆ E, (0, 0, 2) ∈ E (udowodniliśmy ten fakt wcześniej) oraz
E 3
0, 0, 1 +
1
n+1
d
2
−−−→
n→∞
(0, 0, 1), to B ((0, 0, 1), 1) ⊆ E. Podsumowując, E = B ((0, 0, 1), 1).
Twierdzenie 1. 20.
Niech A i B będą podzbiorami przestrzeni metrycznej (X, d). Wówczas:
(i) A ⊆ B ⇒ A ⊆ B,
(ii) (A) = A,
(iii) A ∪ B = A ∪ B.

19
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Dowód.
(i) Jeśli A ⊆ B, to każdy punkt graniczny zbioru A jest także punktem granicznym zbioru B.
(ii) Wiemy, że
A ∈ Cotop(X, d) (wniosek 1 ). Ponadto podzbiór przestrzeni metrycznej jest
domknięty wtedy i tylko wtedy, gdy jest swoim domknięciem.
(iii) Ponieważ A ⊆
A oraz B ⊆ B, to A ∪ B ⊆ A ∪ B. Ponieważ A, B ∈ Cotop(X, d) oraz suma
dwóch zbiorów domkniętych jest zbiorem domkniętym, to A ∪ B ∈ Cotop(X, d). Na mocy
wniosku 2 , z podkreślonych faktów wynika, że A ∪ B ⊆ A ∪ B.
Z drugiej strony, A ⊆ A ∪ B ⊆ A ∪ B(wniosek 2 ). Z tego już wynika, iż A ∪ B ⊆ A ∪ B.
Wniosek.
Jeśli A
1
, . . . , A
s
, gdzie s ∈ N \ {0}, są podzbiorami przestrzeni metrycznej (X, d),
to A
1
∪ . . . ∪ A
s
= A
1
∪ . . . ∪ A
s
.
Definicja 1. 16
Podzbiór D przestrzeni metrycznej (X, d) jest
gęsty
(w tej przestrzeni), jeśli jego
domknięcie jest całą przestrzenią (D = X).
Twierdzenie 1. 21.
Dla podzbioru D przestrzeni metrycznej (X, d) następujące warunki są rów-
noważne:
(i) D jest gęsty,
(ii) ∀
x∈X
∀
ε∈R
+
D ∩ B(x, ε) 6= Ø,
(iii) ∀
U ∈Top (X,d)
U 6= Ø ⇒ U ∩ D 6= Ø.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Przykład.
1. Jeśli (X, d) jest przestrzenią metryczną, to zbiór X jest gęsty w tej przestrzeni (bowiem
X ∈ Cotop(X, d)).
2. Niech n ∈ N \ {0} i niech (x
1
, . . . , x
n
) ∈ R
n
.
Wiadomo, że istnieją takie ciągi
q
(1)
k
∞
k=1
, . . . ,
q
(n)
k
∞
k=1
liczb wymiernych, że x
i
= lim
k→∞
g
(i)
k
dla i = 1, . . . , n. Skoro tak, to Q 3
q
(1)
k
, . . . , q
(n)
k
d
2
−−−→
k→∞
(x
1
, . . . , x
n
). Wykazaliśmy w ten
sposób, że każdy punkt przestrzeni R
n
wyposażonej w metrykę euklidesową jest punktem
granicznym zbioru Q
n
. Wobec tego Q
n
= R
n
, co znaczy, że zbiór Q jest gęsty w przestrzeni
metrycznej (R
n
, d
2
).

20
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
3. Zbiór Z nie jest podzbiorem gęstym prostej R wyposażonej w metrykę naturalną d. Zauważmy
bowiem, że R \ Z =
S
m∈Z
(m, m + 1) ∈ Top (R, d), skąd Z ∈ Cotop(R, d), więc Z = Z 6= R.
Definicja 1. 17
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Punkt x ∈ X jest
punktem wewnętrznym
zbioru A, jeśli ∃
ε∈R
+
B(x, ε) ⊆ A.
x
ε
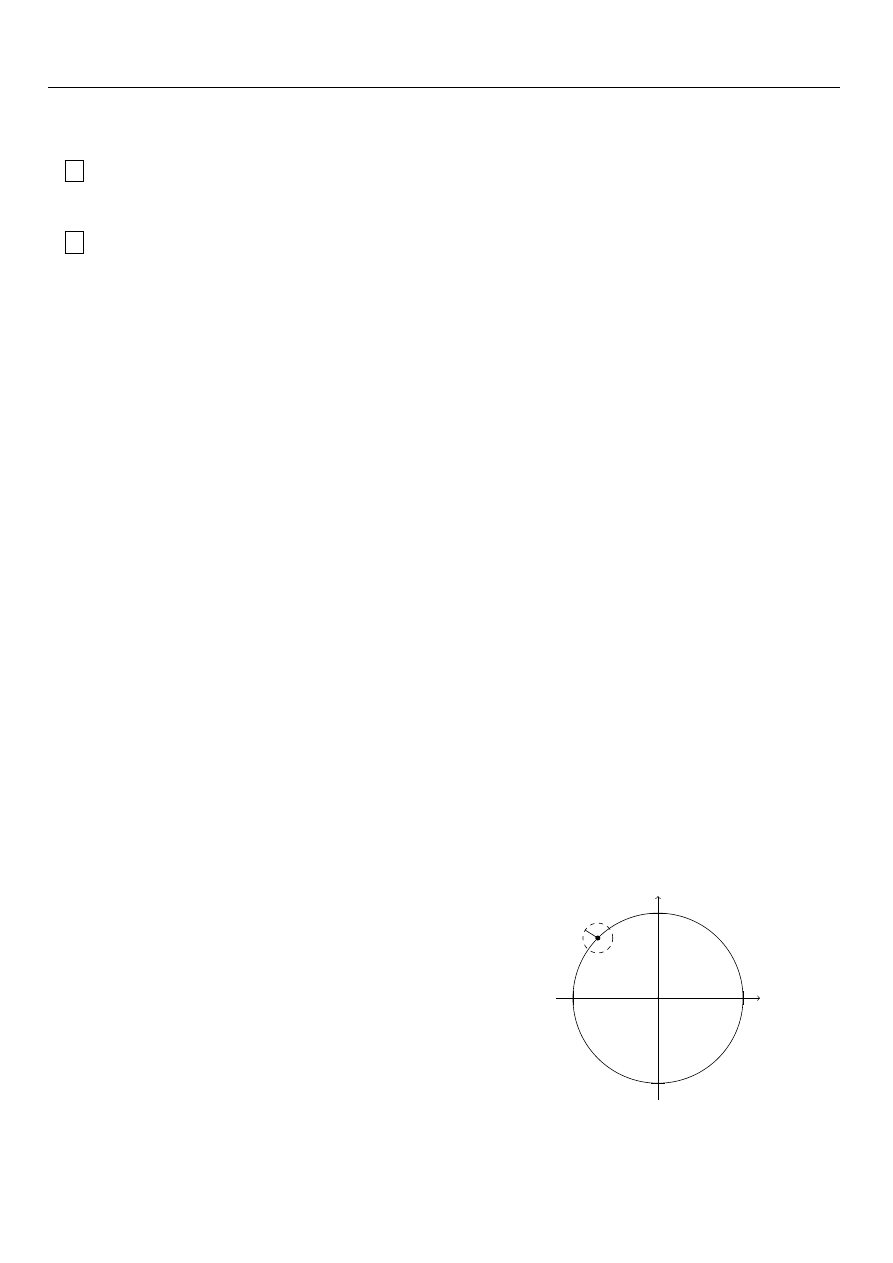
Definicja 1. 18 Wnętrzem
podzbioru A przestrzeni metrycznej (X, d) nazywa się zbiór int (A)
wszystkich punktów wewnętrznych tego podzbioru.
UWAGA 11
int (A) ⊆ A
Twierdzenie 1. 22.
Niech A będzie podzbiorem przestrzeni metrycznej (X, d).
Wówczas int (A) =
S
{U ∈ Top (X, d) :A⊇U}.
Dowód.
” ⊆ ” Niech x ∈ int(A). Wówczas ∃
ε∈R
+
: B(x, ε) ⊆ A. Ponieważ B(x, ε) ∈ Top (X, d),
to B(x, ε) ⊆
S
{U ∈ Top (X, d) : A ⊇ U }, skąd już x ∈
S
{U ∈ Top (X, d) : A ⊇ U }.
” ⊇ ” Przypuścmy, że U ∈ Top (X, d) jest takim zbiorem, że A ⊇ U . Niech x ∈ U . Wystarczy
pokazać, że x ∈ int (A). Skoro x ∈ U oraz U ∈ Top (X, d), to ∃
ε∈R
+
B(x, ε) ⊆ U . W takim
razie B(x, ε) ⊆ A, skąd już x ∈ int (A).
21
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Wniosek.
1 Wnętrze dowolnego podzbioru danej przestrzeni metrycznej jest podzbiorem otwartym tej
przestrzeni.
2 Podzbiór A przestrzeni metrycznej (X, d) jest otwarty wtedy i tylko wtedy, gdy A = int (A).
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 1. 23.
Niech A i B będą podzbiorami przestrzeni metrycznej (X, d). Wówczas:
(i) A ⊆ B ⇒ int (A) ⊆ int (B),
(ii) int (int (A)) = int (A),
(iii) int (A ∩ B) = int (A) ∩ int (B).
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Wniosek.
Jeśli A
1
, . . . , A
s
, gdzie s ∈ N \ {0}, są podzbiorami przestrzeni metrycznej (X, d),
to int (A
1
∩ . . . ∩ A
s
) = int (A) ∩ . . . ∩ int (A
s
).
Przykład.
1. Rozważmy okrąg S
1
= {(x, y) ∈ R
2
: x
2
+ y
2
= 1} jako podzbiór przestrzeni metrycznej
(R
2
, d
2
). Wiemy, że jest on zbiorem domkniętym.
Jest wiadome, że ∀
P ∈S
1
∀
ε∈R
+
: B(x, ε) 6⊆ S
1
. W takim
razie int (S
1
) = Ø.
x
y
−1
−1
1
1
P
ε
0
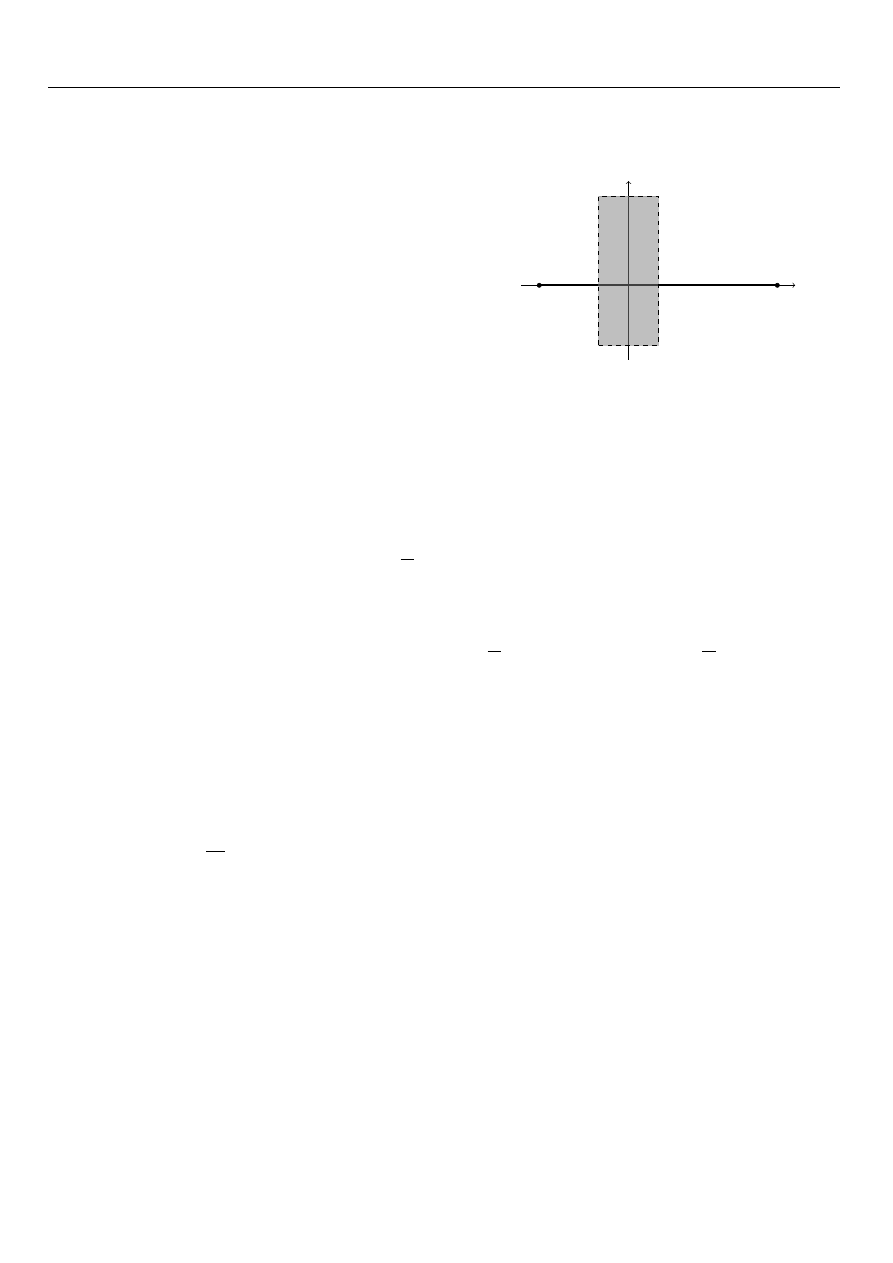
22
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
2. Rozważmy podzbiór Z = ((−1, 1) × (−2, 3)) ∪ ([−3, 5] × {0}) przestrzeni metrycznej (R
2
, d
2
).
Ponieważ prostokąt (−1, 1) × (−2, 3) ∈ Top (X, d) oraz
(−1, 1) × (−2, 3) ⊂ Z, to
(−1, 1) × (−2, 3) ⊆ int (Z). Jest widoczne, iż
∀
P ∈([−3,−1]∪[1,5])×{0}
∀
ε∈R
+
B(P, ε) 6⊆ Z.
Ponieważ int (Z) ⊆ Z, to z powyższych zawierań wy-
nika, że int (Z) = (−1, 1) × (−2, 3).
x
y
(−3, 0)
(5, 0)
3. Łatwo sprawdzić, że na prostej R z metryką naturalną d mamy int (Q) = int (R \ Q) = Ø.
Tymczasem int (Q ∪ (R \ Q)) = int (R) = R.
Definicja 1. 19
Podzbiór A przestrzeni metrycznej (X, d) jest:
(1)
brzegowy
, jeśli int (A) = Ø,
(2)
nigdzie gęsty
(w tej przestrzeni), jeśli int (
A) = Ø.
UWAGA 12
Każdy zbiór nigdzie gęsty jest brzegowy (bowiem A ⊆ A, więc także int (A) ⊆ int (A)).
Przykład.
1. Na prostej R z metryką naturalną zbiory Q oraz R \ Q są brzegowe, ale nie są nigdzie gęste
(bowiem ich domknięcie to cała przestrzeń).
2. Okrąg S
1
jest podzbiorem nigdzie gęstym przestrzeni metrycznej (R
2
, d
2
)
(ponieważ int (S
1
) = int (S
1
) = Ø).
Definicja 1. 20 Brzegiem
podzbioru A przestrzeni metrycznej (X, d) nazywamy zbiór
∂A := cl (A) \ int (A). (Zamiast ∂A pisze się również bd (A)).
Twierdzenie 1. 24.
Jeżeli A jest podzbiorem przestrzeni metrycznej (X, d), to ∂A ∈ Cotop(X, d).
Dowód.
Zauważmy, że ∂A := cl (A) \ int (A) = cl (A) ∩ (X \ int (A)). Przypomnijmy również,
że int (A) ∈ Top (X, d) oraz cl (A) ∈ Cotop(X, d). W takim razie X \ int (A) ∈ Cotop(X, d).
Podsumowując ∂A jest zbiorem domkniętym jako przecięcie dwóch zbiorów domkniętych.
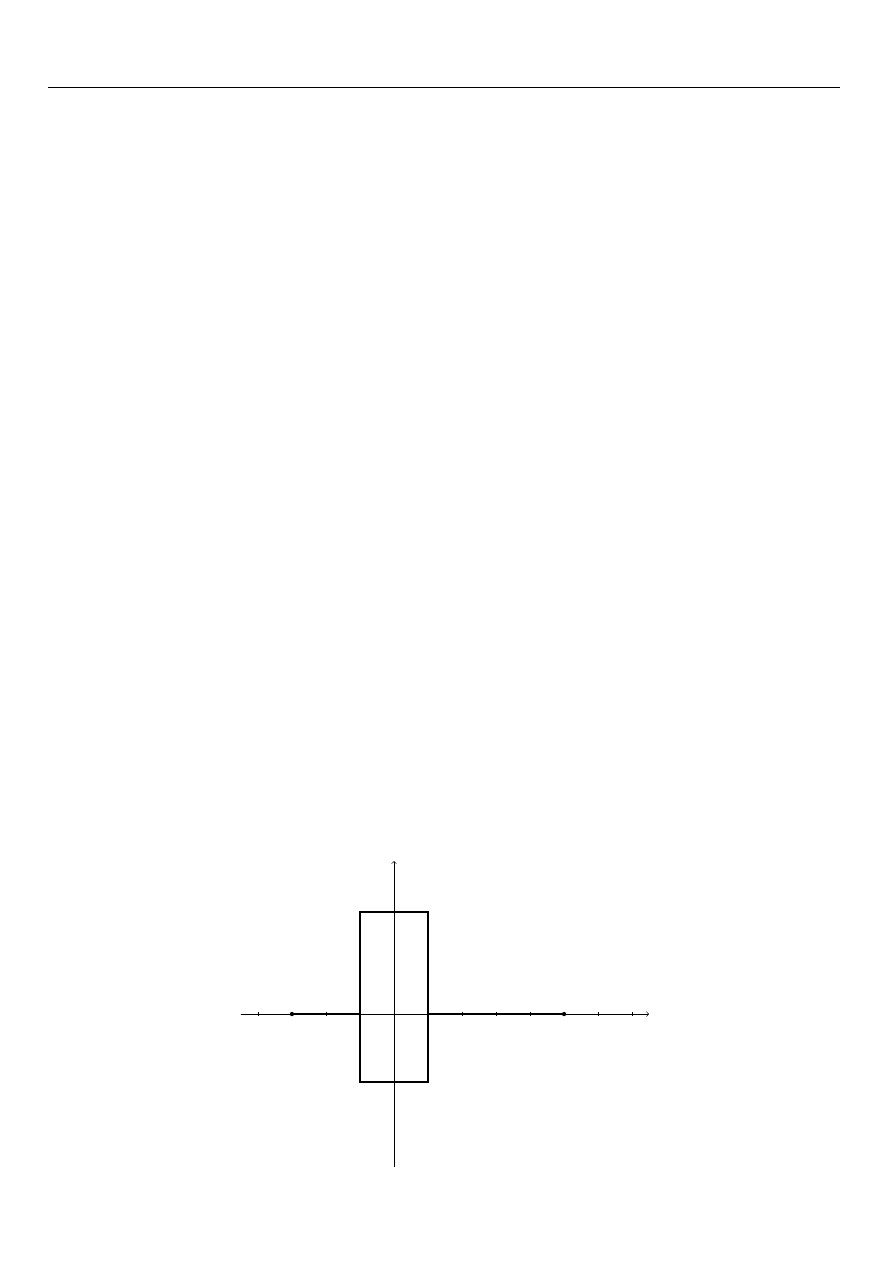
23
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
Twierdzenie 1. 25.
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Dla punktu x ∈ X
następujące warunki są równoważne:
(i) x ∈ ∂A (czyli x jest punktem brzegowym zbioru A),
(ii) ∀
ε∈R
+
B(x, ε) \ A 6= Ø,
A ∩ B(x, ε) 6= Ø,
(iii) ∀
U ∈Top (X,d)
x ∈ U ⇒
U ∩ A 6= Ø,
U \ A 6= Ø.
UWAGA 13
cl (A) = int (A) ∪ ∂A = A ∪ ∂A
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Przykład.
1. Wróćmy do zbioru Z (podzbiór przestrzeni metrycznej (R
2
, d
2
)) z wcześniejszego wykładu.
Stwierdziliśmy, że int (Z) = (−1, 1) × (−2, 3).
Następnie
cl (Z) = cl (((−1, 1) × (−2, 3)) ∪ ([−3, 5] × {0})) =
= cl ((−1, 1) × (−2, 3)) ∪ cl ([−3, 5] × {0}) =
= ([−1, 1] × [−2, 3]) ∪ ([−3, 5] × {0}).
Ostatecznie brzeg zbioru: Z
∂Z := cl (Z)\int (Z) = ([−1, 1]×{−2, 3})∪({−1, 1}×[−2, 3])∪([1, 5]×{0})∪([−3, −1]×{0}).
x
y
−4
−4
−3
−3
−2
−2
−1
−1
1
1
2
2
3
3
4
4
5
5
6
6
7
7

24
ROZDZIAŁ 1. PRZESTRZENIE METRYCZNE
2. Wróćmy do podzbioru E przestrzeni metrycznej (R
3
, d
2
). Pokazaliśmy, że cl (E) = B((0, 0, 1), 1).
Łatwo wykazać, że int (E) = B((0, 0, 1), 1) \ {(0, 0, 1)}. Pokazanie tego faktu polecamy czy-
telnikowi jako ćwiczenie.
W takim razie ∂E := cl (E) \ int (E) = S((0, 0, 1), 1) ∪ {(0, 0, 1)}.
Definicja 1. 21
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Punkt x ∈ X jest
punktem zewnętrznym
tego podzbioru, jeśli ∃
ε∈R
+
A ∩ B(x, ε) = Ø.
A
x
ε
Definicja 1. 22 Zewnętrzem podzbioru
A przestrzeni metrycznej (X, d) nazywa się zbiór wszyst-
kich punktów zewnętrznych tego podzbioru. Zewnętrze zbioru A oznacza się przez ext (A).
Twierdzenie 1. 26.
Niech A będzie podzbiorem przestrzeni metrycznej (X, d). Wówczas:
(i) ext (A) = X \ cl (A),
(ii) ext (A) ∈ Top (X, d),
(iii) X = int (A) ∪ ∂A ∪ ext (A), przy czym zbiory po prawej stronie równania są parami
rozłączne.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.

Rozdział 2
Ciągłość
Twierdzenie 2. 1.
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi. Dla punktu a ∈ X
i odwzorowania f : X → Y następujące warunki są równoważne:
(i) ∀
ε∈R
+
∃
δ∈R
+
∀
x∈X
d(x, a) < δ ⇒ ρ(f (x), f (a)) < ε,
(ii) ∀
ε∈R
+
∃
δ∈R
+
f (B(a, δ)) ⊆ B(f (a), ε),
(iii) f (x
n
)
ρ
−−−→
n→∞
f (a), dla każdego takiego ciągu (x
n
)
∞
n=1
punktów przestrzeni metrycznej (X, d),
że x
n
d
−−−→
n→∞
a.
Dowód.
(i) ⇐⇒ (ii)
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(i) =⇒ (iii)
Załóżmy, że warunek (i) jest spełniony. Niech (x
n
)
∞
n=1
będzie takim ciągiem punktów przestrzeni
metrycznej (X, d), że x
n
d
−−−→
n→∞
a. Zakończymy dowód implikacji, jeśli pokażemy, że
f (x
n
)
ρ
−−−→
n→∞
f (a).
Niech zatem ε ∈ R
+
(dowolne). Niech ponadto δ ∈ R
+
będzie liczbą dobraną do powyższego ε
na mocy warunku (i). Ponieważ x
n
d
−−−→
n→∞
a, to
∃
N ∈N\{0}
∀
n∈N\{0}
n > N ⇒ d(x
n
, a) < δ.
Jeśli teraz n
> N , to ρ(f (x
n
), f (a)) < ε.
¬ (i) =⇒ ¬ (iii)
Załóżmy, że
∃
ε∈R
+
∀
δ∈R
+
∃
x∈X
d(x, a) < δ,
ρ(f (x), f (a)) > ε.

26
ROZDZIAŁ 2. CIĄGŁOŚĆ
Dla n ∈ N \ {0} (dowolnego) wybierzmy (jeden) punkt x
n
∈ X taki, że d(x
n
, a) <
1
n
oraz
ρ(f (x
n
), f (a))
> ε.
Zdefiniowaliśmy ciąg (x
n
)
∞
n=1
punktów przestrzeni metrycznej (X, d). Ponieważ 0
6 (x
n
, a) <
1
n
,
dla każdego n, to lim
n→∞
d(x
n
, a) = 0, co oznacza, że x
n
d
−−−→
n→∞
a.
Jednocześnie ρ(f (x
n
), f (a))
> ε > 0, dla każdego n, z czego natychmiast wynika, że ciąg (f (x
n
))
∞
n=1
nie zmierza do f (a) w przestrzeni (Y, ρ).
Uzyskaliśmy zatem zaprzeczenie warunku (iii).
Definicja 2. 1
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi.
Odwzorowanie f : X → Y jest
ciągłe w a ∈ X
jeśli spełnia któryś z warunków poprzedniego
twierdzenia.
UWAGA 14
a) Definicja ciągłości w punkcie za pomocą warunku (i) nazywa się definicją Cauchy’ego lub
epsilonowo-deltową.
b) Definicja ciągłości w punkcie za pomocą warunku (iii) nazywa się definicją Heinego lub ciągową.
c) Jeśli X ⊆ R ∧ X 6= Ø, d-metryka naturalna w tym podzbiorze (indukowana z R), Y = R,
ρ jest metryką naturalną w R, to nasza definicja ciągłości w punkcie sprowadza się do definicji
znanej ze Wstępu do Analizy Matematycznej.
Twierdzenie 2. 2.
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi. Dla f : X → Y nastę-
pujące warunki są równoważne:
(i) f jest ciągła w każdym punkcie swojej dziedziny,
(ii) ∀
U ⊆Y
U ∈ Top (Y, ρ) ⇒ f
−1
(U ) ∈ Top (X, d),
(iii) ∀
C⊆Y
C ∈ Cotop(Y, ρ) ⇒ f
−1
(C) ∈ Cotop(X, d),
(iv) ∀
S⊆X
f (S) ⊆ f (S).
Dowód.
(i)=⇒(ii)
Przypuśćmy, że warunek (i) jest spełniony i wybierzmy (dowolnie) zbiór otwarty U ∈ Top (Y, ρ).
Mamy pokazać, że f
−1
(U ) ∈ Top (X, d). Niech zatem x ∈ f
−1
(U ). Zakłończymy dowód implikacji,
jeśli znajdziemy taką liczbę r ∈ R
+
, że B(x, r) ⊆ f
−1
(U ). Skoro x ∈ f
−1
(U ), to f (x) ∈ U . Ponieważ
27
ROZDZIAŁ 2. CIĄGŁOŚĆ
U ∈ Top (X, d), to ∃
ε∈R
+
B(f (x), ε) ⊆ U . Z założenia, odwzorowanie f jest ciągłe w punkcie x.
Skorzystaliśmy z warunku (ii) w twierdzeniu definiującym ciągłość w punkcie.
Widzimy, że ∃
δ∈R
+
f (B(x, δ)) ⊆ B(f (x), ε). Skoro tak, to (wprost z definici przeciwobrazu)
B(x, ρ) ⊆ f
−1
(B(f (x), ε)). Ponieważ B(f (x), ε) ⊆ U , to f
−1
(B(f (x), ε)) ⊆ f
−1
(U ). Dowód impli-
kacji kończymy zatem kładąc r = δ.
(ii)=⇒(i)
Załóżmy, że warunek (ii) jest spełniony. Wybierzmy a ∈ X (dowolne). Zakończymy dowód impli-
kacji, jeśli pokażemy, że odwzorowanie f jest ciągłe w punkcie a. Ustalmy zatem ε ∈ R
+
. Ponieważ
B(f (a), ε) ∈ Top (Y, ρ), to f
−1
(B(f (a), ε)) ∈ Top (X, d). Zauważmy,
że f (x) ∈ B(f (a), ε). W takim razie a ∈ f
−1
(B(f (a), ε)). Wskutek otwartości zbioru f
−1
(B(f (a), ε)),
istnieje r ∈ R
+
takie, że B(a, r) ⊆ f
−1
(B(f (a), ε)). Wobec tego, f (B(a, r)) ⊆ B(f (a), ε).
W ten sposób udowodniliśmy, że
∀
ε∈R
+
∃
r∈R
+
f (B(a, r)) ⊆ B(f (a), ε),
co znaczy, że odwzorowanie f jest ciągłe w punkcie a.
(ii)=⇒(iii)
Załóżmy, że warunek (ii) jest spełniony. Wybierzmy C ∈ Cotop((Y, ρ)).
Musimy pokazać, że f
−1
(C) ∈ Cotop(X, d). Zauważmy, że Y \ C ∈ Top (Y, ρ).
Następnie
X \ f
−1
(C) = {x ∈ X : f (x) 6= C} = {x ∈ X : f (x) ∈ Y \ C} = f
−1
(Y \ C) ∈ Top (X, d).
Skoro tak, to f
−1
(C) ∈ Cotop(X, d).
(iii)=⇒(ii)
Analogicznie do powyższego. Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(i)=⇒(iv)
Załóżmy, że warunek (i) jest spełniony. Wybierzmy zbiór S ⊆ X (dowolny). Niech a ∈ X będzie
punktem granicznym tego zbioru. Wówczas istnieje taki ciąg (x
n
)
∞
n=1
elementów zbioru S,
że x
n
d
−−−→
n→∞
a. Ponieważ (z warunku (i)) odwzorowanie f jest ciągłe w punkcie a, to (z definicji He-
inego) f (x
n
)
ρ
−−−→
n→∞
f (x). Ponieważ (f (x
n
))
∞
n=1
jest ciągiem elementów zbioru f (S), to z powyższych
rozważań wynika, że f (a) jest punktem granicznym zbioru f (S). Udowodniliśmy w ten sposób,
że ∀
a∈X
a ∈ S ⇒ f (a) ∈ f (S), co znaczy, że f (S) ⊆ f (S).
(iv)=⇒(iii)
Załóżmy, że warunek (iv) jest spełniony. Wybierzmy (dowolnie) C ∈ Cotop(Y, ρ). Musimy pokazać,
że f
−1
(C) ∈ Cotop(X, d), czyli że f
−1
(C) = f
−1
(C). Inkluzja f
−1
(C) ⊆ f
−1
(C) jest oczywista.
Pozostaje pokazać, że f
−1
(C) ⊆ f
−1
(C).
Mamy, co następuje: f (f
−1
(C)) ⊆ f (f
−1
(C)) ⊆ C = C. Skoro tak, to f
−1
(C) ⊆ f
−1
(C).

28
ROZDZIAŁ 2. CIĄGŁOŚĆ
Definicja 2. 2
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi.
Odwzorowanie f : X → Y jest
ciągłe
jeśli spełnia któryś z warunków poprzedniego twierdzenia.
Przykład.
Rozważmy przestrzeń metryczną (R
2
, d
2
) i przestrzeń metryczną (R, d), gdzie d jest metryką natu-
ralną. Udowodnimy, że funkcja f : R
2
3 (x, y) 7→ xy ∈ R jest ciągła, czyli dla każdego
(a, b) ∈ R
2
jest ciągła w tym punkcie. Skorzystamy z definicji Heinego. Przypuśćmy, że ((x
n
, y
n
))
∞
n=1
jest takim ciągiem punktów przestrzeni metrycznej (R
2
, d
2
), że (x
n
, y
n
)
d
2
−−−→
n→∞
(a, b).
Wówczas a = lim
n→∞
x
n
oraz b = lim
n→∞
y
n
, wobec tego
lim
n→∞
f (x
n
, y
n
) = lim
n→∞
(x
n
· y
n
) = lim
n→∞
x
n
· lim
n→∞
y
n
= ab = f (a, b).
Udowodniliśmy, że odwzorowanie f jest ciągłe w punkcie (a, b).
1. Ponieważ {1} jest podzbiorem domkniętym przestrzeni metrycznej (R, d), gdzie d jest metryką
naturalną, to z ciągłości funkcji f wynika, że
Cotop(R
2
, d
2
) 3 f
−1
({1}) = f
−1
(1)
def
= {(x, y) ∈ R
2
: f(x, y) = 1} = {(x, y) ∈ R
2
: xy = 1}.
x
y
f (x, y)
Podobnie, ponieważ (−∞, 1) jest podzbiorem otwartym przestrzeni metrycznej (R, d), to
Top (R
2
, d
2
) 3 f
−1
((−∞, 1))
def
= {(x, y) ∈ R
2
: f (x, y) < 1} = {(x, y) ∈ R
2
: xy < 1}.
x
y

29
ROZDZIAŁ 2. CIĄGŁOŚĆ
2. Rozważmy przestrzeń metryczne (B(X, R), d
∞
) oraz (R, d), gdzie d jest metryką naturalną.
Ustalmy x
0
∈ X. Funkcja Φ : B(X, R) 3 f 7→ f(x
0
) ∈ R jest wtedy ciągła. Faktycznie,
jeżeli g ∈ B(X, R) oraz (f
n
)
∞
n=1
jest ciągiem elementów zbioru B(X, R) takim, że f
n
d
∞
−−−→
n→∞
g,
to w szczególności lim
n→∞
f
n
(x
0
) = g(x
0
), czyli lim
n→∞
Φ(f
n
) = Φ(g). (Definicja Heinego ciągłości
w punkcie.) Ponieważ (−∞, 1] oraz [1, ∞) ∈ Cotop(R, d), to z powyższej ciągłości wynika,
że
{f ∈ B(X, R) : |f(x
0
)|
> 1} = {f ∈ B(X, R) : f (x
0
)
> 1} ∪ {f ∈ B(X, R) : f (x
0
)
6 −1} =
= {f ∈ B(X, R) : Φ(f ) > 1} ∪ {f ∈ B(X, R) : Φ(f ) ∈ (−∞, −1)} =
= Φ
−1
([1, ∞) ∪ Φ
−1
((−∞, −1)) ∈ Cotop(B(X, R), d
∞
).
(Skorzystaliśmy tu z faktu, że suma skończenie wielu zbiorów domkniętych jest zbiorem do-
mkniętym.)
3. ! Rozważmy R z metryką naturalną.
Funkcję Dirichleta
definiuje się za pomocą wzoru:
D(x) =
1, gdy x ∈ Q,
0, gdy x /
∈ Q.
Ustalmy x ∈ R (dowolne). Przypuśćmy, że x jest liczbą wymierną. Wówczas (x +
√
2
n
)
∞
n=1
jest
ciągiem liczb niewymiernych; przy czym lim
n→∞
x +
√
2
n
= x.
Ponieważ lim
n→∞
D(x +
√
2
n
) = 0 6= 1 = D(x), to funkcja D nie jest ciągła w punkcie x. (Definicja
Heinego.) Przypuśćmy teraz, że x jest liczbą niewymierną. Istnieje wówczas taki ciąg (q
n
)
∞
n=1
liczb wymiernych, że lim
n→∞
g
n
= x. Ponieważ lim
n→∞
D(g
n
) = 1 6= 0 = D(x), to funkcja D nie
jest ciągła w punkcie x.
Udowodniliśmy w ten sposób, że funkcja Dirichleta nie jest ciągła w żadnym punkcie!
Twierdzenie 2. 3.
! Każda funkcja wielomianowa f : R
n
→ R (tylko dodawanie, odejmowanie
i mnożenie stałych współczynników oraz zmiennych x
1
, . . . , x
n
, jak n = 2,
to np. f (x, y) = 4x
8
− 10xy
3
+ 13y
5
− 794) jest ciągła przy metryce euklidesowej w R
n
i metryce
naturalnej w R.
Szkic dowodu.
Korzystamy z definicji Heinego ciągłości w punkcie, twierdzenia charakteryzującego zbieżność cią-
gów w przestrzeni metrycznej (R
n
, d
2
) oraz twierdzeń o granicy sumy i iloczynu dwóch ciągów
liczbowych.
Definicja 2. 3
Niech A, B, C będą zbiorami. Przypuśćmy, że C 6= Ø. Niech następnie
ϕ : A → C oraz ψ : B → C. Załóżmy, że ∀
x∈A∩B
ϕ(X) = ψ(X).
Sklejeniem odwzorowań
ϕ oraz ψ

30
ROZDZIAŁ 2. CIĄGŁOŚĆ
nazywa się wówczas odwzorowanie ϕ ∪ ψ : A ∪ B → C. Zdefiniowane za pomocą wzoru:
(ϕ ∪ ψ)(x)
ϕ(x), gdy x ∈ A,
ψ(x), gdy x ∈ B.
Twierdzenie 2. 4.
Niech (X, d) oraz (Y, ρ) będą przestrzeniami metrycznymi.
Niech ponadto y
0
∈ Y oraz A ⊆ X będzie zbiorem niepustym. Wówczas:
(i) id
X
jest odwzorowaniem ciągłym,
(ii) odwzorowanie stałe c : X 3 x 7→ y
0
∈ Y jest ciągłe,
(iii) jeżeli f : X → Y jest odwzorowaniem ciągłym, to zawężenie f |
A
: A 3 x 7→ f (x) ∈ Y jest
odwzorowaniem ciągłym przy metryce indukowanej d|
A×A
w zbiorze A.
Dowód.
(i) Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(ii) Niech V ∈ Top (Y, ρ). Musimy pokazać, że c
−1
(V ) ∈ Top (X, d).
Zauważmy, że
c
−1
(V ) =
Ø, gdy y
0
/
∈ V,
X, gdy y
0
∈ V.
Tak czy inaczej, c
−1
(V ) ∈ Top (X, d)
(iii) Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 2. 5.
! Każda
funkcja wymierna
f : R
n
◦
−→ R (tylko dodawanie, odejmowanie, mno-
żenie i dzielenie stałych współczynników oraz zmiennych x
1
, . . . , x
n
, jak n = 2,
to np. f : R
2
\ S
1
3 (x, y) 7→
x
7
+xy
3
−3x+y
x
2
+y
2
−1
∈ R) jest ciągła przy indukowanej z R
n
metryce euklide-
sowej w swojej dziedzinie i metryce naturalnej w R.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 2. 6.
Niech (X, d), (Y, ρ) oraz (Z, δ) będą przestrzeniami metrycznymi. Przypuśćmy,
że odwzorowania f : X → Y oraz g : Y → Z są ciągłe. Wówczas złożenie g ◦ f : X → Z jest
również funkcją ciągłą.

31
ROZDZIAŁ 2. CIĄGŁOŚĆ
Dowód.
Niech zatem V ∈ Top (Z, δ). Musimy pokazać, że (g ◦ f )
−1
(V ) ∈ Top (X, d).
Zauważmy, że
(g ◦ f )
−1
(V )
def
= {x ∈ X : (g ◦ f )(x) ∈ V } =
= {x ∈ X : g(f (x)) ∈ V } = {x ∈ X : f (x) ∈ g
−1
(V )} =
= {x ∈ X : x ∈ f
−1
(g
−1
(V ))} = f
−1
(g
−1
(V )).
Ponieważ V ∈ Top (Z, δ), g natomiast jest odwzorowaniem ciągłym, to g
−1
(V ) ∈ Top (Y, ρ).
Ponieważ g
−1
(V ) ∈ Top (Y, ρ) oraz f jest odwzorowaniem ciągłym, to
(g ◦ f )
−1
(V ) = f
−1
(g
−1
(V )) ∈ Top (X, d).
Lemat 1. Niech A będzie niepustym podzbiorem otwartym przestrzeni metrycznej (X, d). Wów-
czas Top (A, d|
A×A
) ⊆ Top (X, d).
Dowód.
Przypuśćmy, że V ∈ Top (A, d|
A×A
). Niech x ∈ V (dowolny punkt). Ponieważ V ∈ Top (A, d|
A×A
),
to
∃
r
1
∈R
+
: B
A
(x, r
1
)
def
= {y ∈ A : d(y, x) < r
1
} ⊆ V.
Ponieważ A ∈ Top (X, d) oraz V ⊆ A, to
∃
r
2
∈R
+
: B
A
(x, r
2
)
def
= {y ∈ X : d(y, x) < r
2
} ⊆ A.
Połóżmy r = min{r
1
, r
2
}. Wówczas r ∈ R
+
. Weźmy pod uwagę dowolny taki punkt y ∈ X,
że d(y, x) < r. Ponieważ d(y, x) < r
2
, to y ∈ A. Ponieważ d(y, x) < r
1
oraz y ∈ A, to y ∈ V .
Pokazaliśmy w ten sposób, że B(x, r)
def
= {y ∈ X : d(y, x) < r} ⊆ V . Z uwagi na dowolność punktu
x wynika, że V ∈ Top (X, d).
Twierdzenie 2. 7. (*)
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi. Niech ponadto
A, B ⊆ X będą niepustymi zbiorami otwartymi spełniającymi warunek A ∪ B = X. Przypuść-
my, że odwzorowania ϕ : A → Y oraz ψ : B → Y są ciągłe przy metrykach indukowanych d|
A×A
oraz d|
B×B
. Załóżmy w końcu, że ∀
x∈A∩B
ϕ(x) = ψ(x). Wówczas sklejenie ϕ ∪ ψ : X → Y jest
odwzorowaniem ciągłym.
Dowód.
Niech V ∈ Top (Y, ρ). Musimy pokazać, że (ϕ ∪ ψ)
−1
(V ) ∈ Top (X, d).
Zauważmy, że
(ϕ ∪ ψ)
−1
(x)
def
= {x ∈ X : (ϕ ∪ ψ)(x) ∈ V } =

32
ROZDZIAŁ 2. CIĄGŁOŚĆ
= {x ∈ A : ϕ(x) ∈ V } ∪ {x ∈ X : ψ(x) ∈ V } = ϕ
−1
(V ) ∪ ψ
−1
(V ).
Ponieważ ϕ oraz ψ są odwzorowaniami ciągłymi, to ϕ
−1
(V ) ∈ Top (A, d|
A×A
) oraz
ψ
−1
(V ) ∈ Top (B, d|
B×B
). Z lematu i faktu, że A, B ∈ Top (X, d), wynika,
że ϕ
−1
(V ), ψ
−1
(V ) ∈ Top (X, d). Ponieważ suma dowolnej rodziny zbiorów otwartych jest zbiorem
otwartym to dostajemy finalnie (ϕ ∪ ψ)
−1
(V ) ∈ Top (X, d).
UWAGA 15
Twierdzenie * pozostaje prawdziwe, jeśli słowo otwartymi zastąpimy słowem domkniętymi.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Przykład.
1. Rozważmy przedziały (−∞, 0], [0, ∞) prostej R. Każdy z nich jest podzbiorem domkniętym
przestrzeni metrycznej (R, d), gdzie d jest metryką naturalną.
Co więcej (−∞, 0] ∪ [0, ∞) = R. Każda z funkcji ϕ : (−∞, 0] 3 x 7→ x ∈ R oraz
ψ : [0, ∞) 3 x 7→ x
2
∈ R jest ciągła przy metryce indukowanej z (R, d) w swojej dziedzinie
(zawężenie funkcji ciągłych określonych w R). W końcu ϕ(0) = 0 = ψ(0).
Skoro tak, to ϕ ∪ ψ : R → R jest funkcją ciągłą przy metryce naturalnej w R.
x
y
y = (ϕ ∪ ψ) (x)
2. Rozważmy podzbiory {(0, 0)} i R
2
\{(0, 0)} płaszczyzny R
2
wyposażonej w metrykę euklideso-
wą. Tylko pierwszy z nich jest domknięty. Tylko drugi z nich jest otwarty. Funkcja f : R
2
→ R
zdefiniowana za pomocą wzoru:
f (x, y)
0, gdy x = y = 0,
xy
x
2
+y
2
, gdy (x, y) 6= (0, 0).
jest sklejeniem dwóch funkcji ciągłych (przy indukowanej metryce euklidesowej) stale równej
0 w zbiorze {(0, 0)} i wymiernej w zbiorze R
2
\ {(0, 0)}. Niestety funkcja f nie jest ciągła

33
ROZDZIAŁ 2. CIĄGŁOŚĆ
w punkcie (0, 0) (przy metryce naturalnej w R).
Faktycznie, (
1
n
,
1
n
)
d
2
−−−→
n→∞
(0, 0) oraz f (
1
n
,
1
n
) =
1
n2
1
n2
1
n2
=
1
2
6= 0 = f (0, 0),
dla każdego n ∈ N \ {0}. (Definicja Heinego.)
3. ! Rozważmy przedział [0, 2π) wyposażony w indukowaną metrykę naturalną oraz okrąg
S
1
⊂ R wyposażony w indukowaną metrykę euklidesową.
Odwzorowanie γ : [0, 2π) 3 t 7→ (cos t, sin t) ∈ S
1
jest wówczas ciągłą bijekcją.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
x
y
−2
−2
−1
−1
1
1
2
2
y(t)
t
cos
2π −
1
n
, sin
2π −
1
n
Zajmijmy się odwzorowaniem odwrotnym
γ
−1
: S
1
→ [0, 2π). Łatwo zauważyć, że γ
−1
(x, y) = Arg(x + iy) dla dowolnego (x, y) ∈ S
1
.
Odwzorowanie to nie jest ciągłe w punkcie (1, 0). Faktycznie,
S
1
3 (cos(2π −
1
n
), sin(2π − f 1n))
d
2
−−−→
n→∞
(cos(2π), sin(2π)) = (1, 0),
podczas, gdy
lim
n→∞
(γ
−1
(cos(2π −
1
n
), sin(2π −
1
n
))) =
= lim
n→∞
2π −
1
n
= 2π 6= 0 = γ
−1
(1, 0).
Definicja 2. 4
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi.
Odwzorowanie h : X → Y jest
homeomorfizmem
jeśli jest
ciągłe
,
bijektywne
i
odwzorowanie od-
wrotne
h
−1
: Y → X jest
ciągłe
.
UWAGA 16
a) Odwzorowanie identycznościowe id
X
: X 3 x 7→ x ∈ X jest homeomorfizmem.
b) Odwzorowanie odwrotne do homeomorfizmu jest homeomorfizmem (
autohomeomorfizmem
).

34
ROZDZIAŁ 2. CIĄGŁOŚĆ
c) Złożenie homeomorfizmu też jest homeomorfizmem.
d) f : X → Y jest homeomorfizmem oraz zbiór A ⊆ X jest otwarty (domknięty), to zbiór h(A) też
jest otwarty (domknięty).
Definicja 2. 5
Mówimy, że przestrzenie metryczne (X, d) i (Y, ρ) są
homeomorficzne
jeżeli istnieje
homeomorfizm h : X → Y (ozn. (X, d)
H
∼
= (Y, ρ)).
UWAGA 17
a) (X, d)
H
∼
= (X, d),
b) (X, d)
H
∼
= (Y, ρ) =⇒ (Y, ρ)
H
∼
= (X, d),
c) (X, d)
H
∼
= (Y, ρ) i (Y, ρ)
H
∼
= (Z, δ) =⇒ (X, d)
H
∼
= (Z, δ).
Przykład.
Przestrzeń (−1, 1) z metryką naturalną jest homeomorficzna z R z metryką naturalną.
(−1, 1) 3 x 7→ tg (
πx
2
) ∈ R
Definicja 2. 6
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi.
Odwzorowanie h : X → Y nazywamy
izometrią
, jeżeli ∀
x
1
,x
2
∈X
ρ(h(x
1
), h(x
2
)) = d(x
1
, x
2
).
UWAGA 18
a) Odwzorowanie identycznościowe jest izometrią.
b) Złożenie izometrii jest izometrią.
Twierdzenie 2. 8.
Niech (X, d) oraz (Y, ρ) będą przestrzeniami metrycznymi.
Niech ponadto h : X → Y będzie
izometrią
. Wówczas h jest
różnowartościowe
oraz
ciągłe
.
Dowód.
Załóżmy, że h(x
1
) = h(x
2
), z aksjomatu określoności ρ(h(x
1
), h(x
2
)) = 0. Ponieważ h jest izometrią,
to d(x
1
, x
2
) = 0. Teraz ponownie korzystając z aksjomatu określoności x
1
= x
2
.
Ciągłość.
Niech a ∈ X. Wówczas ∀
ε>0
∃
δ>0
∀
x∈X
d(a, x) < δ ⇒ ρ(h(a), h(x)) < ε.
Ponieważ d(a, x) = ρ(h(a), h(x)). Biorąc dowolne ε > 0 oraz dobierając δ = ε nasza implikacja jest
spełniona.

35
ROZDZIAŁ 2. CIĄGŁOŚĆ
UWAGA 19
Surjektywna izometria jest bijekcją, przy czym jej odwzorowanie odwrotne też jest izometrią.
Przykład.
1. Weźmy przestrzeń R z metryką naturalną oraz B(R, R) z metryką Czebyszewa.
R 3 t → funkcja stała, równa t ∈ B(R, R)
jest izometrią, ale nie jest surjekcją.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
2. Translacja o wektor w przestrzeni R
n
z metryką euklidesową jest izometrią. Niech v ∈ R
n
.
Wówczas T
v
(x) = x + v.
d
2
(T
v
(x), T
v
(y)) =
q
(x
1
+ v − y
1
− v
1
)
2
+ · · · + (x
n
+ v
n
− y
n
− v
n
)
2
= d
2
(x, y)
3. Podobieństwo R
n
z metryką euklidesową w skali λ 6= 1 jest autohomeomorfizmem, ale nie jest
izometrią.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Definicja 2. 7
Przestrzenie metryczne (X, d) i (Y, ρ) są
izometryczne
jeśli istnieje odwzorowanie
h : X → Y , które jest
izometrią
oraz
surjekcją
((X, d)
I
∼
= (Y, ρ)).
UWAGA 20
a) (X, d)
I
∼
= (X, d),
b) (X, d)
I
∼
= (Y, ρ) =⇒ (Y, ρ)
I
∼
= (X, d),
c) (X, d)
I
∼
= (Y, ρ) i (Y, ρ)
I
∼
= (Z, δ) =⇒ (X, d)
I
∼
= (Z, δ).
Twierdzenie 2. 9.
Niech (X, d)
I
∼
= (Y, ρ). Jeżeli przestrzeń metryczna (X, d) jest
ograniczona
(zupełna)
, to przestrzeń (Y, ρ) też jest ograniczona (zupełna).
Dowód.
Ograniczoność.
Niech (X, d) będzie ograniczona, h : X → Y będzie izometrią oraz surjekcja.
∞ > diam(X) = sup{d(x, y) : x, y ∈ X} = sup{ρ(h(x), h(y)) : x, y ∈ X} =

36
ROZDZIAŁ 2. CIĄGŁOŚĆ
= sup{ρ(a, b) : a, b ∈ Y } = diam(Y )
Wynika z tego, że przestrzeń metryczna (Y, ρ) jest ograniczona.
Zupełność.
Niech (X, d) będzie zupełna, f : Y → X będzie izometrią oraz surjekcją. Niech ponadto (y
n
)
∞
n=1
bę-
dzie ciągiem Cauchy’ego w (Y, ρ). Dowód zakończymy pokazując, że (y
n
) ma granicę w Y . Połóżmy
x
n
= f (y
n
).
∀
ε>0
∃
n
0
∈N\{0}
∀
m,n∈N\{0}
m, n > n
0
⇒ ρ(y
n
, y
m
) < ε
⇓
∀
ε>0
∃
n
0
∈N\{0}
∀
m,n∈N\{0}
m, n > n
0
⇒ d(f (y
n
), f (y
m
)) < ε
⇓
∀
ε>0
∃
n
0
∈N\{0}
∀
m,n∈N\{0}
m, n > n
0
⇒ d(x
n
, x
m
) < ε
Zatem otrzymujemy, że (x
n
) jest ciągiem Cauchy’ego w przestrzeni metrycznej (X, d).
x
n
d
−−−→
n→∞
g ⇔ d(x
n
, g) → 0 ⇔ ρ(f
−1
(x
n
), f
−1
(g)) → 0 ⇔ ρ(y
n
, f
−1
(y)) → 0 ⇔ y
n
ρ
−−−→
n→∞
f
−1
(y) ∈ Y.
Twierdzenie 2. 10.
Dowolne dwie przestrzenie izometryczne są homeomorficzne. (Nie na od-
wrót!)
Dowód.
Wniosek z poprzednich twiedzeń oraz uwag.
Przykład.
1. Przestrzenie (−1, 1) z indukowaną metryką naturalną oraz R z metryką naturalną nie są
izometryczne. Bowiem jedna przestrzeń jest ograniczona, a druga nie. Inaczej, jedna z nich
jest zupełna, a druga nie.
2. Przestrzenie (−1, 1) z indukowaną metryką naturalną oraz [−1, 1] z indukowaną metryką
naturalną nie są izometryczne.
Uzasadnienie: (1 −
1
n
)
∞
n=1
nie ma podciągu zbieżnego w (−1, 1).
Załóżmy, że h : (−1, 1) → [−1, 1] jest homeomorfizmem. Skoro tak, to (h(1 −
1
n
))
∞
n=1
nie
ma podciągu zbieżnego w [−1, 1]. Tymczasem z twierdzenia Bolzano-Weirestrassa wiemy,
że każdy ciąg o elementach w [−1, 1] zawiera podciąg zbieżny w tym przedziale.

37
ROZDZIAŁ 2. CIĄGŁOŚĆ
Twierdzenie 2. 11.
Niech (X
1
, d
1
), . . . , (X
s
, d
s
) będą przestrzeniami metrycznymi
i niech X = X
1
× · · · × X
s
. Wówczas funkcja d : X × X → [0, ∞) zdefiniowana za pomocą wzoru
d(x, y) =
v
u
u
t
n
X
i=1
(d
i
(x
i
y
i
))
2
jest metryką w X.
Dowód.
Warunek identyczności oraz symetryczności pozostawiamy czytelnikowi jako ćwiczenie.
M3) Nierówność trójkąta: ∀
x,y,z∈X
d(x, y) 6 d(x, z) + d(z, y).
Skorzystamy z nierówności Schwarza:
~
(
n
X
i=1
a
i
b
i
)
2
6 (
n
X
i=1
a
2
i
) · (
n
X
i=1
b
2
i
)
Rozpiszmy:
(d(x, y))
2
=
s
X
i=1
(d
i
(x
i
, y
i
)) ¬
s
X
i=1
(d
i
(x
i
, z
i
) + d
i
(z
i
, y
i
))
2
=
s
X
i=1
(d
i
(x
i
, z
i
))
2
+
s
X
i=1
(d
i
(z
i
, y
i
))
2
+
+2
s
X
i=1
(d
i
(x
i
, z
i
) · d
i
(z
i
, y
i
))
2 ~
¬
s
X
i=1
(d
i
(x
i
, z
i
))
2
+
s
X
i=1
(d
i
(z
i
, y
i
))
2
+
+2
v
u
u
t
s
X
i=1
(d
i
(x
i
, z
i
))
2
·
v
u
u
t
s
X
i=1
(d
i
(z
i
, y
i
))
2
=
v
u
u
t
s
X
i=1
(d
i
(x
i
, z
i
))
2
+
v
u
u
t
s
X
i=1
(d
i
(x
i
, z
i
))
2
2
= (d(x, z) + d(z, y))
2
Definicja 2. 8
Niech (X
1
, d
1
) . . . (X
s
, d
s
) będą przestrzeniami metrycznymi.
Niech ponadto X = X
1
× · · · × X
s
. Przestrzeń (X, d) nazywamy
iloczynem metrycznym
, gdzie d
jest funkcją zdefiniowaną w poprzednim twierdzeniu. Piszemy (X, d) = (X
1
, d
1
) × . . . × (X
s
, d
s
).
Przykład.
1. Przestrzeń R
n
z metryką euklidesową jest iloczynem metrycznym przestrzeni R z metryką
naturalną.
2. Przestrzeń R
n×m
z metryką euklidesową jest iloczynem metrycznym przestrzeni R
n
i R
m
z metrykami euklidesowymi.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 2. 12.
Niech (X, d) będzie iloczynem metrycznym przestrzeni (X
1
, d
1
) . . . (X
s
, d
s
).
Wówczas dla ciągu (x
(n)
)
∞
n=1
= ((x
(n)
1
, x
(n)
2
, . . . , x
(n)
n
))
∞
n=1
w przestrzeni metrycznej (X, d) oraz dla
punktu g = (g
1
, . . . , g
s
) ∈ X następujące warunki są równoważne:

38
ROZDZIAŁ 2. CIĄGŁOŚĆ
(i) x
(n)
d
−−−→
n→∞
g,
(ii) ∀
i=1,...,s
X
1
3 x
i
d
i
−−−→
n→∞
g
i
∈ X.
Dowód.
x
(n)
d
−−−→
n→∞
g ⇐⇒ d(x
(n)
, g) −−−→
n→∞
0 ⇐⇒
v
u
u
t
s
X
i=1
d
x
(n)
i
, y
(n)
i
2
−−−→
n→∞
0 ⇐⇒
⇐⇒ ∀
i=1,...,s
d
i
(x
(n)
i
, g
i
) −−−→
n→∞
0 ⇐⇒ ∀
i=1,...,s
x
(n)
i
d
i
−−−→
n→∞
g
i
Twierdzenie 2. 13.
Niech (X, d) będzie iloczynem metrycznym przestrzeni metrycznych
(X
1
, d
1
), . . . , (X
s
, d
s
). Niech ponadto Z
i
⊆ X dla i = 1, . . . , s. Jeżeli zbiór Z
i
jest zbiorem domknię-
tym (otwartym) w przestrzeni (X, d) dla każdego i = 1, . . . , s, to Z = Z
1
× . . . × Z
s
jest domknięty
(otwarty) w przestrzeni (X, d).
Dowód.
Domkniętość.
Niech Z
i
∈ Cotop(X
1
, d
i
). Niech (g
1
, . . . , g
s
) będzie punktem granicznym zbioru Z. Musimy pokazać,
że (g
1
, . . . , g
s
) ∈ Z. Skoro (g
1
, . . . , g
s
) jest punktem granicznym, to istnieje ciąg ((x
(n)
1
, . . . , x
(n)
s
))
∞
n=1
w Z, że Z 3 (x
(n)
1
, . . . , x
(n)
s
)
d
i
−→ (g
1
, . . . , g
s
). Na mocy poprzedniego twierdzenia
∀
i=1,...,s
x
(n)
i
d
−−−→
n→∞
g
i
, ale Z ∈ Cotop(X
i
, d
i
). Zatem g
i
∈ Z, czyli (g
1
, . . . , g
s
) ∈ Z
1
× . . . × Z
s
= Z
dla każdego i = 1, . . . , s
Otwartość.
Załóżmy, że Z ∈ Top (X, d).
Z ∈ Top (X, d) ⇐⇒ X \ Z ∈ Cotop(X, d)
X \ Z = (X
1
× . . . × X
s
) \ (Z
1
× . . . × Z
s
) =
s
[
i=1
X
i
× . . . × X
i−1
× (X
i
\ Z
i
) × X
i+1
× . . . × X
s
X \ Z - jest podzbiorem domkniętym iloczynu kartezjańskiego zbiorów domkniętych. Suma skoń-
czonej ilości zbiorów domkniętych jest zbiorem domkniętym. Zatem X \ Z ∈ Cotop(X
i
, d
i
)
Twierdzenie 2. 14.
Niech (X, d) będzie iloczynem metrycznym przestrzeni metrycznych
(X
1
, d
1
), . . . , (X
s
, . . . , d
s
). Przestrzeń (X
i
, d
i
) jest zupełna dla każdego i = 1, . . . , s wtedy i tylko
wtedy, gdy (X, d) jest zupełna.

39
ROZDZIAŁ 2. CIĄGŁOŚĆ
Definicja 2. 9
Niech (X
1
, d
1
), . . . (X
s
, d
s
), gdzie s ∈ N \ {0}, będą przestrzeniami metrycznymi
i niech (X, d) = (X
1
, d
1
) × . . . × (X
s
, d
s
). Wybieramy i = 1, . . . , s.
Projekcją
(czyli rzutowaniem)
na i-tą składową nazywa się odwzorowanie π
i
: X 3 (x
1
, . . . , x
s
) 7→ x
i
∈ X.
Twierdzenie 2. 15.
Niech (X, d) oraz i będą jak w powyszej definicji. Wówczas
(i) rzutowanie π
i
jest surjekcją,
(ii) rzutowanie π
i
jest odwzorowaniem ciągłym,
(iii) U ∈ Top (X, d) =⇒ π
i
(U ) ∈ Top (X
i
, d
i
).
Dowód.
(i) Oczywiste.
(ii) Niech V ∈ Top (X
i
, d
i
). Zakończymy dowód własności, jeśli pokażemy, że π
−1
i
(V ) ∈ Top (X, d).
π
−1
i
(V )
def
= {((x
1
, . . . , x
s
) ∈ X : x
i
∈ V } = X
1
× . . . × X
i−1
× V × X
i+1
× . . . × X
s
Ponieważ X
i
∈ Top (X
i
, d
i
) oraz iloczyn kartezjański zbiorów otwartych jest zbiorem otwartym,
to z powyższej równości wynika, że π
−1
i
(V ) ∈ Top (X, d).
(iii) Powiedzmy, że U ∈ Top (X, d). Wystarczy (dowolny) punkt a ∈ π
i
(U ). Zakończymy dowód
jeżeli pokażemy, że ∃
ε∈R
+
B(a, ε) ⊆ π
i
(U ).
Ponieważ a ∈ π
i
(U ), to y = (x
1
, . . . , x
i−1
, a, x
i+1
, . . . , x
s
) ∈ U dla pewnych
x
1
∈ X
1
, . . . , x
i−1
∈ X
i−1
, x
i+1
∈ X
i+1
, . . . , x
s
∈ X
s
. Skoro U ∈ Top (X, d), to ∃
ε∈R
+
B(y, ε) ⊆ π
i
(U ).
Jeżeli teraz d(a, b) < ε dla pewnego t ∈ X
i
, to
d(y, (x
1
, . . . , x
i−1
, b, x
i+1
, . . . , x
s
)) =
=
q
d
1
(x
1
, x
1
)
2
+ . . . + d
i−1
(x
i−1
, x
i−1
)
2
+ d
i
(a, b)
2
+ d
i+1
(x
i+1
, x
i+1
)
2
+ . . . + d
s
(x
s
, x
s
)
2
=
=
q
d
i
(a, b)
2
= d
i
(a, b) < ε.
Tak więc
(x
1
, . . . , x
i−1
, b, x
i+1
, . . . , x
s
) ∈ U,
skąd już
b = π
i
(x
1
, . . . , x
i−1
, b, x
i+1
, . . . , x
s
) ∈ π
i
(U ).
Definicja 2. 10
Niech (X, d) oraz (Y, ρ) będą przestrzeniami metrycznymi.
Odwzorowanie f : X → Y jest
otwarte
, jeśli f (U ) ∈ Top (Y, ρ) dla każdego U ∈ Top (X, d).
40
ROZDZIAŁ 2. CIĄGŁOŚĆ
Przykład.
1. Rozważmy funkcję f : R → R zdefiniowaną przez
f (x) =
x + 1, gdy x < −1,
0, gdy |x| ¬ 1,
x − 1, gdy x 1,
jest ciągła (przy metryce naturalnej).
Funkcja ta nie jest otwarta w sensie powyższej defnini-
cji, bo f ((−2,
1
2
)) = (−1, 0] nie jest podzbiorem otwar-
tym prostej R wyposażonej w metrykę naturalną.
x
y
f (x)
−1
−2
1
2
1
Rozważmy projekcję π
i
: R
2
3 (x, y) 7→ x ∈ R. Wiemy,
że H = {(x, y) ∈ R
2
: xy = 1} jest podzbiorem do-
mkniętym przestrzeni R
2
wyposażonej w metrykę eu-
klidesową. Niestety π
i
(H) = R
∗
nie jest podzbiorem
domkniętym prostej R wyposażonej w metrykę natu-
ralną.
x
y
Definicja 2. 11
Niech A, B
1
, . . . , B
s
, gdzie s ∈ N \ {0} będą zbiorami. Przypuśćmy, że B
1
, . . . , B
s
są niepuste.
Zestawieniem odwzorowań
f
1
: A → B
1
, . . . , f
s
: A → B
s
nazywa się odwzorowanie
(f
1
, . . . , f
s
) : A 3 a 7→ (f
1
(a), . . . , f
s
(a)) ∈ B
1
× . . . × B
s
.
Twierdzenie 2. 16.
Niech (X, d), (y
1
, ρ
1
), . . . , (Y
s
, ρ
s
), gdzie s ∈ N \ {0}, będą przestrzeniami
metrycznymi i niech (Y, ρ) = (Y
1
, ρ
1
) × . . . × (Y
s
, ρ
s
). Niech ponadto f
1
: X → Y
1
, . . . , f
s
: X → Y
s

41
ROZDZIAŁ 2. CIĄGŁOŚĆ
będą odwzorowaniami ciągłymi. Wówczas zestawienie (f
1
, . . . , f
s
) : X → Y jesto odwzoroawniem
ciągłym.
Dowód.
(Definicja Heinego). Wybierzmy (dowolny) punkt a ∈ X. Niech (x
n
)
∞
n=1
będzie ciągiem punktów
przestrzeni (X, d) takim, że x
n
d
−−−→
n→∞
a.
Musimy tylko pokazać, że (f
1
, . . . , f
s
)(x
n
)
ρ
−−−→
n→∞
(f
1
, . . . , f
s
)(a).
Liczymy korzystając z ciągłości odwzorowań f
1
, . . . , f
s
w punkcie a.
(f
1
, . . . , f
s
)(x
n
) = (f
1
(x
n
), . . . , f
s
(x
n
))
ρ
−−−→
n→∞
(f
1
(a), . . . , f
s
(a)) = (f
1
, . . . , f
s
)(a)
Przykład.
Odwzorowanie Φ : R
3
3 (x, y, z) 7→ (x + y
3
− 2y, x − 1, 2
2
x
y − 5xy + y
3
− 1) jest ciągłe przy metryce
euklidesowej d
2
w przestrzeni R
3
, bowiem jest ono zestawieniem trzech funkcji wielomianowych,
więc ciągłych przy metryce d
2
i metryce naturalnej d na prostej R,
oraz (R
3
, d
2
) = (R, d) × (R, d) × (R, d).

Rozdział 3
Zwartość
Definicja 3. 1
Podzbiór Z przestrzeni metrycznej (X, d) jest
zwarty
jeśli każdy ciąg (z
n
)
∞
n=1
ele-
mentów tego podzbioru ma (przynajmniej jeden) podciąg zbieżny do elementu tegoż podzbioru.
Przykład.
1. Każdy podzbiór skończony dowolnej przestrzeni metrycznej jest zwarty.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
2. Przestrzeń metryczna (R, d), gdzie d jest metryką naturalną nie jest zwarta, bowiem ciąg
(n)
∞
n=1
nie ma żadnego podciągu zbieżnego do granicy skończonej.
3. Przedział [0, 1) nie jest podzbiorem zwartym prostej R z metryką naturalną, bowiem każdy
podciąg ciągu (1 −
1
n
)
∞
n=1
jest zbieżny do jedynki.
Twierdzenie 3. 1.
Niech Z będzie podzbiorem zwartym przestrzeni metrycznej (X, d). Wówczas
Z jest domknięty i ograniczony.
Dowód.
Domkniętość
Niech x ∈ X będzie punktem granicznym zbioru Z. Musimy pokazać, że x ∈ Z.
Ponieważ x jest punktem granicznym zbioru Z, to istnieje taki ciąg (z
n
)
∞
n=1
elementów tego zbioru,
że z
n
d
−−−→
n→∞
x. Ze zwartości wynika zatem, że istnieje podciąg (x
n
k
)
∞
k=1
ciągu (z
n
) i istnieje punkt
z ∈ Z taki, że z
n
k
d
−−−→
k→∞
z. Zauważmy, że jednocześnie z
n
k
d
−−−→
k→∞
x (jako podciąg ciągu zbieżnego).
Ponieważ każdy ciąg ma dokładnie jedną granicę, to x = z, czyli x ∈ Z
Ograniczoność
Przypuśćmy, że zbiór Z nie jest ograniczony i wybieramy punkt β ∈ Z. Z nieograniczoności wynika

43
ROZDZIAŁ 3. ZWARTOŚĆ
teraz, że ∀
n∈N\{0}
∃
z
n
∈Z
: d(β, z
n
) > n. Zdefiniowaliśmy przy okazji ciąg (z
n
)
∞
n=1
elementów zbioru
Z. Łatwo sprawdzić, że każdy podciąg tego ciągu jest nieograniczony, więc dowód zostawiamy
czytelnikowi. W konsekwencji nie jest on zbieżny w przestrzeni (X, d). Znaleźliśmy zatem ciąg
elementów zbioru Z nie mającego żadnego podciągu zbieżnego do elementu zbioru Z, co prowadzi
do sprzeczności.
Przykład.
Niech Y będzie nieskończonym podzbiorem przestrzeni metrycznej (X, d), gdzie d jest metryką
dyskretną. Wówczas Y jest domknięty i ograniczony w (X, d).
Dowód tego faktu pozostawiamy czytelnikowi jako ćwiczenie.
Jeśli jednak (y
n
)
∞
n=1
jest ciągiem różnowartościowym elementów zbioru Y , to (y
n
)
∞
n=1
nie ma
w ogóle żadnego podciągu zbieżnego w (X, d). Wobec tego zbiór Y nie jest zwarty.
Twierdzenie 3. 2. (O obrazie ciągłym zbioru zwartego)
Niech (X, d) oraz (Y, ρ) będą prze-
strzeniami metrycznymi. Ponadto niech f : X → Y będzie odwzorowaniem ciągłym. Jeśli wówczas
Z jest podzbiorem zwartym przestrzeni metrycznej (X, d), to f (Z) jest podzbiorem zwartym prze-
strzeni (Y, ρ).
Dowód.
Niech (y
n
)
∞
n=1
będzie (dowolnym) ciągiem elementów zbioru f (Z). Musimy pokazać, że ten ciąg
zawiera przynajmniej jeden podciąg zbieżny do elementu tegoż zbioru.
Dla dowolnego n ∈ N \ {0} wybierzmy (dokładnie jeden) punkt z
n
∈ Z taki, że y
n
= f (z
n
).
Dostaliśmy ciąg (z
n
)
∞
n=1
elementów zbioru Z. Ponieważ Z jest zwarty, to istnieje taki podciąg
(z
n
k
)
∞
k=1
ciągu (z
n
)
∞
n=1
i ∃
z∈Z
: z
n
k
d
−−−→
k→∞
z. Wobec tego za sprawą ciągłości odwzorowania f
w punkcie z mamy:
y
n
k
= f (z
n
k
)
ρ
−−−→
k→∞
f (z) ∈ f (Z).
Skoro tak, to (y
n
k
)
∞
k=1
jest podciągiem ciągu (y
n
)
∞
n=1
zbieżnym do pewnego elementu zbioru f (Z).
Przykład.
Rozważmy funkcję c : R 3 x 7→ e ∈ R. Jest ona ciągła przy metryce naturalnej. Następnie {e}
jest podzbiorem zwartym prostej R z metryką naturalną. Niestety przeciwobraz c
−1
(e) = R nie jest
zwarty.
Twierdzenie 3. 3.
Każda zwarta przestrzeń metryczna jest zupełna. (Nie na odwrót!)

44
ROZDZIAŁ 3. ZWARTOŚĆ
UWAGA 21
Prosta R z metryką naturalną jest przestrzenią metryczną zupełną, ale nie jest przestrzenią
metryczną zwartą.
Dowód.
Niech (X, d) będzie zwartą przestrzenią metryczną. Niech ponadto (x
n
)
∞
n=1
będzie ciągiem Cau-
chy’ego elementów tej przestrzeni (dowolnym). Ze zwartości wynika, że istnieje taki podciąg (x
n
k
)
∞
k=1
i istnieje taki punkt x ∈ X, że x
n
k
d
−−−→
n→∞
x. Pokażemy, że x
n
d
−−−→
n→∞
x.
Niech zatem ε ∈ R
+
. Z powyższych uwag wynika, że
∃
N ∈N\{0}
∀
m,n∈N\{0}
: m, n N =⇒ d(x
m
, x
n
) <
ε
2
∃
K∈N\{0}
∀
k∈N\{0}
: k K =⇒ d(x, x
k
) <
ε
2
.
Z definicji podciągu wynika, że
∃
l∈N\{0}
:
l k,
n
l
N.
Skoro tak, to jeśli n N , to
d(x, x
n
) ¬ d(x, x
n
l
) + d(x
n
l
, x
n
) <
ε
2
+
ε
2
= ε.
Twierdzenie 3. 4.
Przypuśćmy, że przestrzenie metryczne (X, d) i (Y, ρ) są homeomorficzne i że jed-
na z nich jest zwarta. Wówczas druga także jest zwarta.
Dowód.
Powiedzmy, że (X, d) jest zwarta. Niech ponadto f : X → Y będzie homeomorfizmem. Wówczas, na
mocy twierdzenia o obrazie ciągłym zbioru zwartego, Y = f (x) jest podzbiorem zwartym przestrzeni
(Y, ρ).
UWAGA 22
a) Powyższe twierdzenie można wypowiedzieć w następujący sposób: Zwartość jest własnością
topologiczną (czyli niezmienniczą względem homeomorfizmów).
b) Zupełność nie jest własnością topologiczną (Bowiem wyposażone w metrykę naturalną zbiory
R i (−1, 1) ⊂ R są homeomorficzne, ale tylko jeden z nich jest przestrzenią metryczną zupeł-
ną.) Zupełność jest natomiast własnością metryczną (tzn. jeśli dwie przestrzenie metryczne są
izometryczne i jedna z nich jest zupełna, to druga także jest zupełna.)

45
ROZDZIAŁ 3. ZWARTOŚĆ
Lemat 2. Niech Z będzie podzbiorem zwartym przestrzeni metrycznej (X, d).
Niech ponadto C ∈ Cotop(X, d) będzie zbiorem zwartym w Z.
Wówczas C jest podzbiorem zwartym przestrzeni (X, d).
Dowód.
Niech (c
n
)
∞
n=1
będzie (dowolnym) ciągiem elementów zbioru C. Wtedy (c
n
)
∞
n=1
jest też ciągiem
elementów zbioru Z. Ponieważ Z jest zwarta, to istnieje taki podciąg (c
n
k
)
∞
k=1
i istnieje taki punkt
z ∈ Z, że c
n
k
d
−−−→
k→∞
z
(k → ∞). Ponieważ C jest zbiorem domkniętym, to z powyższej zbieżności
wynika, że z ∈ C. Pokazaliśmy w ten sposób, że dowolny ciąg elementów zbioru C ma podciąg
zbieżny do elementu tegoż zbioru.
Twierdzenie 3. 5.
Niech {Z
t
}
t∈T
, gdzie T 6= ∅, będzie (dowolną, niepustą) rodziną podzbiorów
zwartych przestrzeni metrycznej (X, d). Wówczas
T
t∈T
Z
t
jest także podzbiorem zwartym tej prze-
strzeni.
Dowód.
Ponieważ Z
t
jest dla każdego t ∈ T , podzbiorem zwartym przestrzeni (X, d), to Z
t
∈ Cotop(X, d).
W konsekwencji zatem
T
t∈T
Z
t
∈ Cotop(X, d). Wybierzmy t
0
∈ T . Wtedy
T
t∈T
Z
t
⊆ Z
t
0
. W takim
razie rozważane przecięcie jest zbiorem domkniętym zawartym w zbiorze zwartym, więc - na mocy
Lematu 2 - jest zbiorem zwartym.
Twierdzenie 3. 6.
! Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi. Przypuśćmy, że prze-
strzeń (X, d) jest zwarta. Niech ponadto f : X → Y będzie ciągłą bijekcją. Wówczas f jest home-
omorfizmem.
Dowód.
Musimy tylko pokazać, że f
−1
: Y → X jest odwzorowaniem ciągłym.
Niech zatem C ∈ Cotop(X, d). Zakończymy dowód jeśli pokażemy, że (f
−1
)
−1
(C) ∈ Cotop((Y, ρ)).
Zauważmy najpierw, że (f
−1
)
−1
(C) = f (C). Ponieważ przestrzeń (X, d) jest zwarta
i C ∈ Cotop(X, d), to C jest podzbiorem zwartym przestrzeni metrycznej (X, d) (na mocy Lematu
2). Skoro tak, to f (C) jest podzbiorem zwartym przestrzeni metrycznej (Y, ρ) (twierdzenie o obrazie
ciągłym zbioru zwartego). W takim razie f
−1
(C) = f (C) ∈ Cotop(Y, ρ).
Twierdzenie 3. 7. (Bolzano-Weierstrassa)
Każdy ograniczony ciąg liczb rzeczywistych ma (przy-
najmniej jeden) podciąg zbieżny do skończonej granicy.
Dowód.
Wstęp do Analizy Matematycznej

46
ROZDZIAŁ 3. ZWARTOŚĆ
Definicja 3. 2
Niech m ∈ N \ {0}.
Kostką m-wymiarową
nazywa się każdy zbiór postaci
I
1
× · · · × I
m
, gdzie I
1
· · · I
m
⊂ R są przedziałami domkniętymi i ograniczonymi.
Twierdzenie 3. 8.
Dla dowolnego m ∈ N \ {0} każda kostka m-wymiarowa jest podzbiorem zwar-
tym przestrzeni metrycznej (R
m
, d
2
).
Dowód.
Indukcja względem wymiaru.
Niech najpierw I będzie domkniętym i ograniczonym przedziałem prostej R. Musimy wykazać,
że I jest podzbiorem zwartym tejże prostej wyposażonej w metrykę naturalną. Niech zatem (a
n
)
∞
n=1
będzie (dowolnym) ciągiem elementów przedziału I. Wówczas (a
n
)
∞
n=1
jest ograniczonym ciągiem
liczb rzeczywistych. Na mocy twierdzenia Bolzano-Weierstrassa istnieje taki podciąg (a
n
k
)
∞
k=1
i ist-
nieje taka liczba a ∈ R, że lim
n→∞
a
n
k
= a (zwykła granica ciągu liczbowego). Ponieważ I jest
podzbiorem domkniętym prostej R wyposażonej w metrykę naturalną, to z powyższej zbieżności
wynika, że a ∈ I. W ten sposób pokazaliśmy, że dowolny ciąg elementów przedziału I ma pod-
ciąg zbieżny do pewnego elementu tegoż przedziału. Ustalmy następnie m ∈ N \ {0} i załóżmy,
że dla każdego q ∈ {1, · · · , m} dowolna kostka q-wymiarowa jest podzbiorem zwartym przestrzeni
metrycznej (R
2
, d
2
). Niech C = I
1
× · · · × I
m
× I
m+1
będzie kostką (m + 1)-wymiarową. Zakończymy
dowód, jeśli pokażemy, że C jest podzbiorem zwartym przestrzeni metrycznej (R
m+1
, d
2
).
Niech zatem ((x
(n)
, y
n
))
∞
n=1
, gdzie x
(n)
= (x
(n)
1
, · · · , (x
(n)
n
) ∈ I
1
× · · · × I
m
oraz y
n
∈ I
m+1
⊂ R będzie
(dowolnym) ciągiem elementów kostki C. Na mocy założenia indukcyjnego kostka m-wymiarowa
I
1
× · · · × I
m
jest podzbiorem zwartym przestrzeni metrycznej (R
m
, d
2
). W takim razie istnieje taki
podciąg (x
(n
k
)
)
∞
k=1
ciągu
x
(n)
i istnieje taki punkt g = (g
1
, . . . , g
m
) należący do kostki I
m
,
że x
(n
k
)
d
2
−−−→
k→∞
g. Rozważmy podciąg
x
(n
k
)
, y
n
k
∞
k=1
ciągu ((x
(n)
, y
n
)). Wtedy (y
n
k
)
∞
k=1
jest ciągiem
domkniętym i ograniczonym przedziału I
m+1
. Wobec tego istnieje taki podciąg
y
n
kl
∞
l=1
i istnieje
taka liczba h ∈ I
m+1
,
że lim
l→∞
y
n
kl
= h. Rozważmy podciąg
x
(n
kl
)
, y
n
kl
∞
l=1
ciągu
x
(n)
, y
n
. Ponieważ x
n
kl
d
2
−−−→
l→∞
g
(podciąg ciągu zbieżnego) i lim
l→∞
y
n
kl
= h, to
x
(n
kl
)
, y
n
kl
d
2
−−−→
l→∞
(g, h) ∈ I
1
× . . . × I
m
× I
m+1
= C
W ten sposób udowodniliśmy, że dowolny ciąg elementów kostki C zawiera podciąg zbiżny do
pewnego elementu tejże kostki.
Twierdzenie 3. 9.
Dla podzbioru Z przestrzeni metrycznej (R
m
, d
2
), m ∈ N \ {0} następujące
warunki są równoważne:
(i) Z jest zwarty,
47
ROZDZIAŁ 3. ZWARTOŚĆ
(ii) Z jest domknięty i ograniczony.
Dowód.
(i) ⇒ (ii)
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(ii) ⇒ (i)
Przypuśćmy, że (ii) jest spełniony. Ponieważ Z jest ograniczony w przestrzeni (R
m
, d
2
), to istnieje
kostka m-wymiarowa C, taka że Z ⊆ C.
Kostka ta na mocy (ii) jest podzbiorem zwartym przestrzeni (R
m
, d
2
). Skoro tak, to Z jest zbiorem
domkniętym, zwartym w zbiorze zwartym, więc Z jest zwarty.
Przykład.
1. Sfera m-wymiarowa S
m def
= {(x
1
, . . . , x
m+1
) ∈ R
m+1
: x
2
1
+ . . . + x
2
m+a
= 1} jest podzbiorem
zwartym przestrzeni (R
m
, d
2
).
2. Kula
B
def
= {(x
1
, . . . , x
m
) ∈ R
m
: x
2
1
+ . . . + x
2
m
¬ 1} jest podzbiorem zwartym (R
m
, d
2
).
3. Każda prosta jest podzbiorem domkniętym przestrzeni (R
m
, d
2
). Żadna taka prosta nie jest
jednak zwarta, nie jest bowiem ograniczona.
4.
s
Trójkąt {(x, y) ∈ R
2
: 1−|x| y > 0} jest podzbiorem
ograniczonym przestrzeni metrycznej (R
2
, d
2
), ale nie
jest w tej przestrzeni zwarty, bo nie jest domknięty.
x
y
−1
1
1
1
Twierdzenie 3. 10. (Weierstrassa o osiąganiu kresów)
Niech Z 6= Ø będzie podzbiorem zwar-
tym przestrzeni metrycznej (X, d) i niech f : Z 7→ R będzie funkcją ciągłą (przy metryce induko-
wanej z (X, d) i naturalnej w R). Wówczas
∃
α,β∈Z
f (α) = sup
z∈Z
{f (z)},
f (β) = inf
z∈Z
{f (z)}.
Dowód.
Ponieważ Z jest zbiorem zwartym, to f (Z) jest podzbiorem zwartym prostej R wyposażonej w me-
trykę naturalną (twierdzenie o obrazie ciągłym zbioru zwartego). Skoro tak, to f (Z) jest podzbiorem
ograniczonym tejże prostej, tzn. ma skończone kresy zarówno górny jak i dolny. Połóżmy
u = sup{f (Z)} oraz w = inf{f (Z)}. Istnieją wtedy takie ciągi (x
n
)
∞
n=1
, (y
n
)
∞
n=1
elementów zbioru

48
ROZDZIAŁ 3. ZWARTOŚĆ
Z, że u − lim
n→∞
x
n
,
w = lim
n→∞
y
n
. Wskutek zwartości zbioru Z, istnieją takie podciągi (x
n
k
)
∞
k=1
,
(y
n
k
)
∞
k=1
i takie punkty α, β ∈ Z, że x
n
k
d
−−−→
k→∞
α i y
n
k
d
−−−→
k→∞
β.
W takim razie, za sprawą ciągłości funkcji f w punktach α, β mamy, co następuje:
lim
k→∞
f (x
n
k
) = f (α) = lim
n→∞
f (x
n
) = u = sup{f (Z)},
lim
k→∞
f (y
n
k
) = f (β) = lim
n→∞
f (y
n
) = w = inf{f (Z)}.
Twierdzenie 3. 11. (Klasyczna wersja twierdzenia Weierstrassa o osiąganiu kresów)
Niech I będzie domkniętym i ograniczonym przedziałem prostej R. Niech ponadto f : I → R będzie
funkcją ciągłą (w zwykłym sensie). Wówczas
∃
α,β∈I
:
f (α) = sup{f (I)},
f (β) = inf{f (I)}.
Dowód.
Wystarczy zauważyć, że I jest podzbiorem zwartym prostej R wyposażonej w metrykę naturalną
i zastosować poprzednie twierdzenie.
Twierdzenie 3. 12.
Niech (Z
n
) będzie zstępującym ciągiem niepustych podzbiorów zwartych prze-
strzeni metrycznej (X, d). Wówczas
∞
T
n=1
Z
n
6= Ø
UWAGA 23
To, że ciąg (Z
n
) jest zstępujący znaczy, że Z
1
⊇ Z
2
⊇ Z
3
⊇ . . .
Dowód.
Dla dowolnego n ∈ N\{0} wybieramy (dokładnie jeden) punkt x
n
∈ Z
n
. Ponieważ (Z
n
) jest ciągiem
zstępującym, to x
n
∈ Z
n
dla każdego n ∈ N \ {0}.
Ze zwartości zbioru Z wynika, że istnieje taki podciąg (x
n
k
)
∞
k=1
ciągu (x
n
)
∞
n=1
i istnieje taki punkt
g ∈ Z
1
, że x
n
k
d
−−−→
k→∞
g.
Wybierzmy (dowolnie) l ∈ N \ {0}. Zauważmy, że x
n
∈ Z
l
dla każdego n l (bowiem ciąg (Z
n
)
∞
n=1
jest zstępujący). Wobec tego prawie wszystkie wyrazy podciągu (x
n
k
)
∞
k=1
są elementami zbioru Z
l
(bowiem ciąg (n
k
)
∞
k=1
jest silnie rosnący). Skoro x
n
k
d
−−−→
k→∞
g oraz Z
l
∈ Cotop(X, d) (każdy zbiór
zwarty jest domknięty), to g ∈ Z
l
. W ten sposób wykazaliśmy, że g ∈
∞
T
n=1
Z
l
.
49
ROZDZIAŁ 3. ZWARTOŚĆ
Przykład.
Ciąg przedziałów ([n, ∞))
∞
n=1
domkniętych prostej R jest zstępujący oraz przecięcie
∞
T
n=1
[n, ∞) = Ø. Zauważmy, że żaden z tych przedziałów nie jest podzbiorem zwartym prostej R
wyposażonej w metrykę naturalną (przedziały te są domkniętymi i nieprzeliczalnymi podzbiorami
prostej R z metryką naturalną).
Lemat 3. Przypuśćmy, że Z jest niepustym podzbiorem zwartym przestrzeni metrycznej (X, d).
Wówczas ∀
ε∈R
+
∃
s∈N\{0}
∃
x
1
,...,x
s
∈Z
: Z ⊆
s
S
i=1
B(x
i
, ε).
Dowód.
Udowodnijmy tezę przy pomocy kontrapozycji. Przypuśćmy, że
∀
ε∈R
+
∃
s∈N\{0}
∃
x
1
,...,x
s
∈Z
: Z \
s
[
i=1
B(x
i
, ε) 6= Ø.
Mamy pokazać, że Z nie jest wtedy podzbiorem zwartym przestrzeni metrycznej (X, d). Wybierzmy
x
1
∈ Z. Wówczas Z \ B(x
1
, ε) 6= Ø. Wybierzmy (dokładnie jeden) punkt x
2
∈ Z \ B(x
2
, ε) i zauważ-
my, że d(x
1
, x
2
) ε. Załóżmy teraz, że dla pewnego n ∈ N\{0} mamy takie punkty x
1
, . . . , x
n
∈ Z,
że ∀
k,l∈{1,...,n}
: k 6= l ⇒ d(x
k
, x
l
) ε. Wówczas Z \
n
S
i=1
B(x
i
, ε) 6= Ø. Wybierzmy zatem (dokładnie
jeden) punkt x
n+1
∈ Z \
n
S
i=1
B(x
i
, ε). Zauważmy, że d(x
n+1
, x
i
) ε dla i = 1, . . . , n. Zdefiniowaliśmy
indukcyjnie ciąg {x
n
}
∞
n=1
elementów zbioru Z mających tę własność, że
∀
n
1
,n
2
∈N\{0}
: n
1
6= n
2
⇒ d(x
n
1
, x
n
2
) ε.
W takim razie żaden podciąg ciągu (x
n
)
∞
n=1
nie jest ciągiem Cauchy’ego w przestrzeni metrycznej
(X, d). Dowód tego faktu pozostawiamy czytelnikowi jako ćwiczenie.
Wobec tego ciąg (x
n
)
∞
n=1
nie posiada żadnego podciągu zbieżnego w przestrzeni metrycznej (X, d),
skąd już Z nie jest podzbiorem zwartym tej przestrzeni.
Definicja 3. 3 Pokryciem otwartym
podzbioru Y przestrzeni metrycznej (X, d) nazywa się każdą
taką rodzinę (U
t
)
t∈T
podzbiorów otwartych tej przestrzeni, że Y ⊆
S
t∈T
U
t
.
X
Y
t
3
U
U
U
U
t
t
t
1
2
4

50
ROZDZIAŁ 3. ZWARTOŚĆ
Definicja 3. 4 Podpokryciem skończonym
pokrycia otwartego (U
t
)
t∈T
podzbioru Y przestrzeni me-
trycznej (X, d) nazywa się każdą taką podrodzinę (U
t
)
t∈S
, gdzie S ⊆ T takie, że S jest podzbiorem
skończonym oraz Y ⊆
S
t∈S
U
t
.
Przykład.
1. Rodzina przedziałów ((−∞, 1) , (−8, 17), (3, ∞)) jest skończonym pokryciem otwartym pro-
stej R wyposażonej w metrykę naturalną.
2. Ciąg (−n, n)
∞
n=1
przedziałów otwartych jest pokryciem otwartym prostej R z metryką natu-
ralną (bowiem
∞
S
n=1
(−n, n) = R). To pokrycie nie zawiera żadnego podpokrycia skończonego,
bowiem jeśli istnieje S ⊆ N \ {0} będące zbiorem niepustym i skończonym,
to
S
s∈S
(−n, n) = (max s, max s) 6= R.
3. Rodzina kół otwartych (B ((0, 0), ε))
ε∈R
+
jest nieprzeliczalnym pokryciem otwartym płaszczy-
zny R
2
wyposażonej w metrykę euklidesową, jednak nie zawiera żadnego pokrycia skończo-
nego.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 3. 13. (Borela-Lebesgue’a)
Dla podzbioru Z przestrzeni metrycznej (X, d) nastę-
pujące warunki są równoważne:
(i) Z jest zwarty.
(ii) Każde pokrycie otwarte zbioru Z w przestrzeni (X, d) zawiera (przynajmniej jedno) podpokry-
cie skończone.
Dowód.
(i)=⇒ (ii)
Załóżmy, że Z, gdzie Z 6= Ø, jest podzbiorem zwartym przestrzeni metrycznej (X, d). Na mocy
Lematu 3.
O
∀
n∈N\{0}
∃
s
n
∈N\{0}
∃
x
(n)
1
,...,x
(n)
n
∈Z
: Z ⊆
s
n
[
i=1
B
x
(n)
i
,
1
n
Niech x ∈ Z będzie dowolnie ustalone. Ponadto niech (U
t
) będzie (dowolnym) pokryciem otwar-
tym zbioru Z z przestrzeni metrycznej (X, d). Ponieważ (U
t
)
t∈T
jest pokryciem otwartym zbioru

51
ROZDZIAŁ 3. ZWARTOŚĆ
Z, to ∃
t
x
∈T
∃
ε∈R
+
: B (x, ε) ⊆ U
t
x
. Niech m ∈ N \ {0} będzie taką liczbą, że
1
m
<
ε
x
2
. Z własności
N
wynika, iż ∃
j∈{1,...,s
n
x ∈ B
x
(m)
j
,
1
m
. Jeśli teraz y ∈ B
x
(n)
j
,
1
m
, to :
d(y, x) ¬ d
y, x
(m)
j
+ d
x
(m)
j
, x
<
1
m
+
1
m
< 2 ·
ε
x
2
= ε
x
.
Wobec tego B
x
(m)
,
1
m
⊆ B (x, ε
x
) ⊆ U
t
x
.
Udowodniliśmy w ten sposób, że :
(∗∗) ∀
x∈Z
∃
t
x
∈T
∃
m∈N\{0}
∃
j∈{1,...,s
n
}
: x ∈ B
x
(m)
j
,
1
m
⊆ U
t
x
.
Niech E będzie zbiorem wszystkich takich par (n, j), że n ∈ N \ {0}, j ∈ {1, . . . , s
n
}
oraz ∃
t∈T
: B
x
(n)
j
,
1
n
⊆ U
t
. Zbiór ten jest oczywiście co najwyżej przeliczalny. Z własności (∗∗)
wynika, że E 6= Ø. Ustawmy wszystkie elementy zbioru E w ciąg (ξ
k
)
∞
k=1
. Dla dowolnego k ∈ N\{0}
wybieramy (dokładnie jeden) wskaźnik x ∈ t
k
∈ T taki, że B
x
(n)
j
,
1
n
⊆ U
t
k
, gdzie (n, j) ∈ ξ
k
.
W ten sposób zdefiniowaliśmy ciąg (U
t
k
)
∞
k=1
elementów pokrycia (U
t
)
t∈T
.
Niech znowu x ∈ Z (dowolny punkt). Z własności (∗∗) wynika, że x ∈ U
t
k
dla pewnego k ∈ N\{0}.
Skoro tak, to Z ⊆
∞
S
k=1
U
t
k
. Pokazaliśmy, że (U
t
k
)
∞
k=1
jest co najwyżej przeliczalnym pokryciem otwar-
tym zbioru Z.
Przypuśćmy, że pokrycie (U
t
k
)
∞
k=1
nie zawiera żadnego pokrycia skończonego. Wówczas dla dowol-
nego s ∈ N \ {0} mamy Z
s
= Z \
s
S
k=1
= Z ∩
X \
s
S
k=1
U
t
k
6= Ø.
Jest widoczne, że ciąg (Z
s
)
∞
s=1
podzbiorów przestrzeni metrycznej (X, d) jest zstępujący. Następnie
każdy zbiór Z
s
jest zwarty jako zbiór domknięty zawarty w zbiorze zwartym. Tymczasem
∞
\
s=1
Z
s
=
∞
\
s=1
Z ∩
X \
s
[
k=1
U
t
k
!!
= Z ∩
∞
\
s=1
X \
∞
[
t=1
U
t
!
= Z ∩
X \
∞
[
s=1
s
[
k=1
U
t
k
!
=
= Z ∩
X \
∞
[
k=1
U
t
k
!
= Z \
∞
[
k=1
U
t
k
= Ø.
Doszliśmy do sprzeczności z twierdzeniem Cantora. W takim razie pokrycie (U
t
k
)
∞
k=1
zawiera co naj-
mniej jedno podpokrycie skończone, stąd już pokrycie (U
t
)
t∈T
zawiera (przynajmniej jedno) pokry-
cie skończone.
¬(i) =⇒ ¬(ii)
Przypuśćmy, że Z nie jest zbiorem zwartym. Wówczas istnieje ciąg (x
n
)
∞
n=1
elementów tego zbioru,
który nie posiada żadnego podciągu zbieżnego do elementów tego podzbioru. Zauważmy, że jeśli
{U
1
, . . . , U
s
}, gdzie s ∈ N \ {0}, jest skończonym pokryciem otwartym zbioru Z,
to w którymś ze zbiorów U
1
, . . . , U
s
leży nieskończenie wiele wyrazów ciągu (x
n
)
∞
n=1
. Gdyby istniał
taki punkt x ∈ Z taki, że w każdej kuli B
x,
1
n
x
znajduje się tylko skończenie wiele wyrazów ciągu
(x
n
)
∞
n=1
, to istniałby taki podciąg (x
n
k
)
∞
k=1
, że x
n
k
d
−−−→
k→∞
x, sprzeczność (dowód pozostawiamy czy-
telnikowi). Skoro tak, to dla każdego x ∈ Z istnieje taka liczba n
x
∈ N\{0}, że w kuli B
x,
1
n
x
znaj-
duje się tylko skończenie wiele wyrazów ciągu (x
n
)
∞
n=1
. Zauważmy, że rodzina
B
x,
1
n
x
x∈Z
jest

52
ROZDZIAŁ 3. ZWARTOŚĆ
pokryciem otwartym zbioru Z w przestrzeni metrycznej (X, d). Gdyby to pokrycie miało jakieś pod-
pokrycie skończone, to powstałaby sprzeczność z podkreślonego faktu. Skoro tak, to
B
x,
1
n
x
x∈Z
jest pokryciem otwartym zbioru Z niezawierającym żadnego pokrycia skończonego.
Wniosek.
Niech Z
1
, . . . , Z
w
, gdzie w ∈ N \ {0}, będą podzbiorami zwartymi przestrzeni metrycznej (X, d).
Wówczas Z
1
∪ . . . ∪ Z
w
też jest podzbiorem zwartym tej przestrzeni.
Dowód.
Niech (U
t
)
t∈T
będzie pokryciem otwartym zbioru Z
1
∪ . . . ∪ Z
w
w przestrzeni metrycznej (X, d).
Zakończymy dowód, jeśli pokażemy, że to pokrycie zawiera podpokrycie skończone (twierdzenie
Borela-Lebesgue’a). Ponieważ Z
i
, gdzie i ∈ {1, . . . , w} jest zbiorem zwartym oraz (U
t
)
t∈T
jest
pokryciem otwartym zbioru Z, istnieje taki skończony zbiór S
i⊆T
, że Z
i
⊆
S
t∈S
U
t
. Połóżmy
S
1
∪ . . . ∪ S
w
. Wówczas S jest skończonym podzbiorem zbioru wskaźników T oraz:
Z
1
∪ . . . ∪ Z
w
⊆
[
t∈S
1
U
t
∪ . . . ∪
[
t∈S
w
U
t
=
[
t∈S
U
t
.
Wobec tego (U
t
)
t∈S
jest podpokryciem skończonym pokrycia otwartego (U
t
)
t∈T
zbioru
Z
1
∪ . . . ∪ Z
w
.
Twierdzenie 3. 14.
Niech s ∈ N \ {0} i niech (X
1
, d
1
), . . . , (X
s
, d
2
) będą przestrzeniami metrycz-
nymi. Połóżmy (X, d) = (X
1
× . . . × X
s
). Niech ponadto Z
i
będzie dla i = 1, . . . , s podzbiorem
zwartym przestrzeni (X
i
, d
i
). Wówczas Z
1
× . . . × Z
s
jest podzbiorem zwartym iloczynu (X, d).
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Lemat 4. (Lebesgue’a) Niech {U
t
}
t∈T
będzie pokryciem otwartym zwartej przestrzeni metrycznej
(X, d). Wówczas
∃
λ∈R
+
∀
A⊆X
(diam (A) < λ =⇒ ∃
t
A
∈T : A⊆U
tA
).
Dowód.
Niech x ∈ X (dowolny punkt). Wtedy x ∈ U
t
Ax
dla pewnego t
x
∈ T . Korzystając z otwartości
zbioru U
t
x
wybierzmy (dokładnie jedną) liczbę λ
x
∈ R
+
taką, że B(x, 2λ
x
) ⊆ U
t
x
.
Rodzina {B(x, λ
x
)}
x∈X
jest pokryciem otwartym przestrzeni metrycznej (X, d). Wskutek zwartości
∃
s∈N\{0}
∃
x
1
,...,x
s
∈X
s
S
i=1
B(x
i
, λ
i
). Połóżmy λ = min{λ
x
1
, . . . , λ
x
s
}. Wówczas λ ∈ R
+
. Przypuśćmy,
że A ⊆ X jest (dowolnym) zbiorem spełniającym warunek diam (A) < λ. Niech ponadto a ∈ A.

53
ROZDZIAŁ 3. ZWARTOŚĆ
Z definicji średnicy wynika, że A ⊆ B(a, diam (A)) ⊆ B(a, λ). Ponadto ∃
j∈{1,...,s} a∈B(x
j
,λ
xj
)
. Jeśli
teraz y ∈ B(a, λ), to
d(y, x
j
) ¬ d(y, a) + d(a, x
j
) < λ + λ
x
j
¬ 2λ
x
j
.
W ten sposób udowodniliśmy, że B(a, λ) ⊆ B(x
j
, 2λ
x
j
).
Ponieważ A ⊆ B(a, λ) oraz B(x
j
, 2λ
x
j
) ⊆ U
t
xj
, to A ⊆ U
t
xj
. Kończymy dowód kładąc t
A
= t
x
j
.
UWAGA 24
Liczbę λ z powyższego lematu nazywa się
liczbą Lebesgue’a
pokrycia {U
t
}
t
∈ T.
Definicja 3. 5
Niech (X, d) oraz (Y, ρ) będą przestrzeniami metrycznymi i niech f : X → Y .
Odwzorowanie f jest
jednostajnie ciągłe
, jeśli
∀
ε∈R
+
∃
δ=δ(ε)∈R
+
∀
x,y∈X
d(x, y) < δ =⇒ ρ(f (x), f (y)) < ε.
UWAGA 25
1. Każde odwzorowanie jednostajnie ciągłe jest ciągłe. Bowiem - w sytuacji z definicji - odwzo-
rowanie f jest ciągłe wtedy i tylko wtedy, gdy
∀
x∈X
∀
ε∈R
+
∃
δ=δ(ε)∈R
+
∀
y∈X
d(x, y) < δ =⇒ ρ(f (x), f (y)) < ε.
(Nie na odwrót!)
2. Każda izometria jest odwzorowaniem jednostajnie ciągłym (δ = ε).
3. Złożenie dwóch odwzorowań jednostajnie ciągłych jest jednostajnie ciągłe.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Przykład.
Funkcja ϕ : R
+
3 t 7→
1
t
∈ R jest ciągła (przy metryce naturalnej). Rozważmy ε = 1 i dowolną
liczbę δ ∈ R
+
. Jest jasne, że |
1
n
−
1
n+1
| =
1
n(n+1)
< δ dla pewnego n ∈ N \ {0}. Połóżmy x =
1
n
oraz
y =
1
n+1
. Wówczas |ϕ(x) − ϕ(y)| = |n − (n + 1)| = 1 ε. W ten sposób udowodniliśmy, że funkcja
ϕ nie jest jednostajnie ciągła.
Twierdzenie 3. 15. (Heinego)
Niech (X, d) i (Y, ρ) będą przestrzeniami metrycznymi. Niech po-
nadto f : X → Y będzie odwzorowaniem ciągłym. Przypuśćmy, że przestrzeń (X, d) jest zwarta.
Wówczas odwzorowanie f jest jednostajnie ciągłe.

54
ROZDZIAŁ 3. ZWARTOŚĆ
Dowód.
Wybierzmy (dowolnie) ε ∈ R
+
. Niech x ∈ X (dowolny punkt). Korzystając z ciągłości wybierzmy
(dokładnie jedną) liczbę δ
x
∈ R
+
taką, że ρ(f (x), f (y)) <
ε
2
dla każdego y ∈ B(x, δ
x
) (Kula w prze-
strzeni (X, d)). Rodzina {B(x, δ
x
)}
x∈X
jest pokryciem otwartym przestrzeni metrycznej (X, d).
Niech δ będzie (pewną) liczbą Lebesgue’a pokrycia {B(x, δ
x
)}
x∈X
. Jeżeli teraz punkty x, y ∈ X
spełniają warunek d(x, y) < δ, to diam {X, y} = d(x, y) < δ, stąd x, y ∈ B(x
0
, δ
x
0
) dla pewnego
x
0
∈ X. W takim razie
ρ(f (x), f (y)) ¬ ρ(f (x), f (x
0
)) + ρ(f (x
0
), f (y)) <
ε
2
+
ε
2
= ε.
Definicja 3. 6
Przestrzeń metryczna jest
lokalnie zwarta
, jeśli
∀
x∈X
∃
U ∈Top (X,d)
:
x ∈ U,
cl (U ) jest podzbiorem zwatrym przestrzeni metrycznej(X, d).
Przykład.
1. Każda zwarta przestrzeń metryczna jest lokalnie zwarta (U = X).
2. Przestrzeń (R
n
, d
2
) jest dla każdego n ∈ N \ {0} niezwarta, ale lokalnie zwarta. (Bowiem
w tej przestrzeni cl (B(x, ε)) = B(x, ε) jest dla każdego punktu x i każdego ε ∈ R
+
zbiorem
zwartym.)
3. Żadna nieskończenie wymiarowa przestrzeń Hilberta nie jest lokalnie zwarta.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.

Rozdział 4
Spójność
Definicja 4. 1
Podzbiór C przestrzeni metrycznej (X, d) jest
spójny
jeśli
∀
U,V ∈Top (X,d)
(C ⊆ U ∪ V, C ∩ U ∩ V = Ø) =⇒ (C ∩ U = Ø ∨ C ∩ V = Ø).
UWAGA 26
1. W następniku implikacji można równie dobrze wpisać C ⊆ U ∨ C ⊆ V.
2. Przestrzeń (X, d) jest spójna wtedy i tylko wtedy, gdy
∀
U,V ∈Top (X,d)
(X = U ∪ V, U ∩ V = Ø) =⇒ (X = U ∨ X = V ).
Definicja 4. 2
Podzbiór D przestrzeni metrycznej (X, d) jest niespójny, jeśli nie jest spójny, czyli
jeśli
∃
U,V ∈Top (X,d)
:
D ⊆ U ∪ V,
D ∩ U ∩ V = Ø,
D ∩ U 6= Ø,
D ∩ V 6= Ø.
Przykład.
1. Każdy co najwyżej jednoelementowy podzbiór dowolnej przestrzeni metrycznej jest spójny.
2. Jeśli S jest przynajmniej 2-elementowym podzbiorem skończonym przestrzeni metrycznej
(X, d), to S jest niespójny. (Bowiem wybierzmy x
0
= S.
Połóżmy U = X \ {x
0
} oraz Y = (X \ S) ∪ {x
0
}. Wówczas U, V ∈ Top (X, d), S ⊆ U ∪ V ,
S ∩ U ∩ V = Ø, S ∩ U = S \ {x
0
} 6= Ø oraz S ∩ V = {x
0
}.)

56
ROZDZIAŁ 4. SPÓJNOŚĆ
3. Podzbiór R
∗
prostej R wyposażonej w metrykę naturalną jest niespójny. (Rozważmy bowiem
U = (−∞, 0) oraz V = (0, ∞).)
4. Q jest podzbiorem niespójnym prostej R wyposażonej w metrykę naturalną. (Weźmy pod
uwagę U = (−∞,
√
2) oraz V = (
√
2, ∞).)
5. Zbior {(x, y) ∈ R
2
: x
2
+ y
2
6= 1} = {(x, y) ∈ R
2
: x
2
+ y
2
< 1} ∪ {(x, y) ∈ R
2
: x
2
+ y
2
> 1}
jest, jako podzbiór przestrzeni metrycznej (R
2
, d
2
), niespójny.
Twierdzenie 4. 1. (o obrazie ciągłym zbioru spójnego)
Niech (X, d) i (Y, ρ) będą przestrze-
niami metrycznymi. Niech f : X → Y będzie odwzorowaniem ciągłym. Przypuśćmy, że zbiór C ⊆ X
jest spójny. Wówczas f (C) jest podzbiorem spójnym przestrzeni metrycznej (Y, ρ).
Dowód.
Załóżmy, że f (C) ⊆ U ∪ V dla pewnych U, V ∈ Top (Y, ρ), przy czym U ∩ V ∩ f (C) = Ø. Musimy
pokazać, że f (C) ⊆ U lub f (C) ⊆ V. Zauważmy, że
C ⊆ f
−1
(f (C)) ⊆ f
−1
(U ∪ V ) = f
−1
(U ) ∪ f
−1
(V ).
Następnie
C ∩ f
−1
(U ) ∩ f
−1
(V ) ⊆ f
−1
(f (C)) ∩ f
−1
(U ) ∩ f
−1
(V ) = f
−1
(f (C) ∩ U ∩ V ) = f
−1
(Ø) = Ø,
skąd C ∩ f
−1
(U ) ∩ f
−1
(V ) = Ø. W końcu, dzięki ciągłości odwzorowania f ,
mamy f
−1
(U ), f
−1
(V ) ∈ Top (X, d). Wobec tego, ze spójności zbioru C wynika, że C ⊆ f
−1
(U ) lub
C ⊆ f
−1
(V ). Skoro tak, to f (C) ⊆ f (f
−1
(U )) ⊆ U lub f (C) ⊆ f (f
−1
(V )) ⊆ V.
Wniosek.
Jeżeli dwie przestrzenie metryczne są homeomorficzne i jedna z nich jest spójna, to druga też jest
spójna. (Inaczej mówiąc spójność jest własnością topologiczną.)
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 4. 2. (o połączeniu zbiorem spójnym)
Niech C będzie podzbiorem przestrzeni
metrycznej (X, d). Wówczas następujące warunki są równoważne:
(i) C jest spójny,
(ii) ∀
x,y∈C
∃
D⊆C
x, y ∈ D,
D − podzbiór spójny przestrzeni metrycznej(X, d).

57
ROZDZIAŁ 4. SPÓJNOŚĆ
Dowód.
(i)=⇒(ii)
Oczywiste. (D = C)
¬(i)=⇒ ¬(ii)
Przypuśćmy, że zbiór C jest niespójny. Wówczas
∃
U,V ∈Top (X,d)
:
C ⊆ U ∪ V,
C ∩ U ∩ V = Ø,
C ∩ U 6= Ø,
C ∩ V 6= Ø.
Wybierzmy punkt x ∈ C ∩ U oraz punkt y ∈ C ∩ V . Niech D ⊆ C będzie (dowolnym) takim
zbiorem, że x, y ∈ D. Wówczas D ⊆ U ∪ V , D ∩ U ∩ V = Ø, x ∈ D ∩ U oraz y ∈ D ∩ V. W takim
razie zbiór D jest niespójny. Otrzymaliśmy zaprzeczenie warunku (ii).
Definicja 4. 3
Podzbiór Z przestrzeni metrycznej (X, d) nazywa się
CONTINUUM
, jeżeli jest
niepusty, zwarty i spójny.
Twierdzenie 4. 3.
Niech (C
t
) będzie rodziną podzbiorów spójnych przestrzeni metrycznej (X, d).
Przypuśćmy, że
T
t∈T
C
t
6= Ø. Wówczas
T
t∈T
C
t
również jest podzbiorem spójnym przestrzeni (X, d).
Dowód.
Niech A oraz B będą podzbiorami spójnymi przestrzeni metrycznej (X, d). Załóżmy, że A ∩ B 6= Ø.
Niech następnie U, V ∈ Top (X, d) będą (dowolnymi) takimi zbiorami, że U ∪ V ⊇ A ∪ B oraz
(A ∪ B) ∩ U ∩ B = Ø. Jest widoczne, że A ⊆ U ∪ V . Ponadto A ∩ U ∩ V ⊆ (A ∪ B) ∩ U ∩ V = Ø.
Wskutek spójności zatem A ⊆ U lub A ⊆ V . Dokładnie tak samo pokazujemy, że B ⊆ U lub
B ⊆ V . Przypuśćmy, że A ⊆ U oraz B ⊆ V . Wtedy Ø = A ∩ B ⊆ U ∩ V ∩ (A ∪ B) = Ø, co oznacza
oczywiście sprzeczność. W ten sam sposób uzyskujemy sprzeczność zakładając,
że A ⊆ V , natomiast B ⊆ U .
W ten sposób udowodniliśmy, że (A ⊆ U ∧ B ⊆ U ) lub (A ⊆ V ∧ B ⊆ V ), czyli że (A ∪ B) ⊆ U
albo (A ∪ B) ⊆ V . Skoro tak, to A ∪ B jest podzbiorem spójnym przestrzeni (X, d).
Niech następnie x, y ∈
S
t∈T
C
t
(dowolne punkty). Wówczas x ∈ C
t
x
i y ∈ C
t
y
, t
x
, t
y
∈ T . Przy-
puśćmy, że zbiory C
t
x
oraz C
t
y
są spójne. Zauważmy, że Ø 6=
T
t∈T
C
t
⊆ C
t
x
∩ C
t
y
. Wobec tego, za
prawą poprzedniej części dowodu C
t
x
∪ C
t
y
jest podzbiorem spójnym przestrzeni (X, d). Jest jasne,
że x, y ∈ C
t
x
∪ C
t
y
⊆
S
t∈T
C
t
. W ten sposób udowodniliśmy, że
∀
x,y∈
S
t∈T
C
t
∃
D⊆
S
t∈T
C
t
:
x, y ∈ D
D- podzbiór spójny (X, d).
Wobec tego spójność sumy
S
t∈T
C
t
wynika z twierdzenia o połączeniu zbiorem spójnym.
58
ROZDZIAŁ 4. SPÓJNOŚĆ
UWAGA 27
Przecięcie rodziny podzbiorów spójnych danej przestrzeni metrycznej na ogół nie jest podzbiorem
spójnym tej przestrzeni. Dopełnienie podzbioru spójnego tej przestrzeni również.
Twierdzenie 4. 4.
Niech s ∈ N \ {0} i niech (X
1
, d
1
) , . . . , (X
s
, d
s
) będą przestrzeniami metrycz-
nymi. Niech ponadto C
i
będzie dla i = 1, . . . , s podzbiorem spójnym przestrzeni mietrycznej (X
i
, d
i
).
Wówczas C
i
× . . . × C
s
jest podzbiorem spójnym iloczynu metrycznego (X
1
, d
1
) × . . . × (X
s
, d
s
).
Dowód. (indukcja względem s)
Dla s = 1 jest oczywiste.
Ustalmy k ∈ N \ {0}. Załóżmy, że jeśli (Y
1
, d
1
) , . . . , (Y
k
, d
k
) są przestrzeniami metrycznymi oraz
C
i
jest dla i = 1, . . . , k podzbiorem spójnym przestrzeni (X
i
, d
i
), to C
1
× . . . × C
k
jest podzbiorem
spójnym przestrzeni (Y
1
, d
1
) × . . . × (Y
s
, d
s
).
Niech teraz (Z
1
, δ
1
) , . . . , (Z
k+1
, δ
k+1
) będą przestrzeniami metrycznymi i niech
D
1
⊆ Z
1
. . . D
k+1
⊆ Z
k+1
będą zbiorami spójnymi.
Zakończymy dowód, jeśli pokażemy, że D
1
× . . . × D
k+1
jest podzbiorem spójnym iloczynu metrycz-
nego (Z
1
, δ
1
) × . . . × (Z
k+1
, δ
k+1
).
Połóżmy (Z, δ) = (Z
1
, δ
1
) , . . . , (Z
k
, δ
k
). Zauważmy, że
(Z, δ) × (Z
k+1
, δ
k+1
) = (Z
1
, δ
1
) × . . . × (Z
k+1
, δ
k+1
)
Dowód powyższej własności pozostawiamy czytelnikowi jako ćwiczenie.
Następnie, na mocy założenia indukcyjnego
D = D
1
×. . .×D
k
jest podzbiorem spójnym przestrzeni
metrycznej (Z, δ). Niech x, y ∈ D, a, b ∈ D
k+1
. Odwzo-
rowanie f : Z
k+1
3 t → (x, t) ∈ Z ×Z
k+1
jest izometrią
między przestrzeniami metrycznymi (Z
k+1
, δ
k+1
) oraz
(Z, δ) × (Z
k+1
, δ
k+1
), czego dowód również pozostawia-
my czytelnikowi jako ćwiczenie.
Z
Z
k+1
D × {b}
b
a
x
y
D
D
k+1
Skoro tak, to {x} × D
k+1
= {(x, t)
t∈D
k+1
} = f (D
k+1
) jest podzbiorem spójnym przestrzeni
(Z, δ) × (Z
k+1
, δ
k+1
) (z twierdzenia o obrazie ciągłym zbioru spójnego).
Podobnie wykazujemy, że D × {b} jest podzbiorem spójnym (Z, δ) × (Z
k+1
, δ
k+1
).

59
ROZDZIAŁ 4. SPÓJNOŚĆ
Jest jasne, że (x, a) oraz (y, b) należą do ({x} × D
k+1
) ∪ (D × {b}) ⊆ D × D
k+1
. W końcu
(D × {b}) ∧ ({x} × D
k+1
) = {(x, b)}. Ponieważ zbiory {x} × D
k+1
oraz D × {b} są spójne oraz ich
przecięcie jest niepuste, to suma tych zbiorów jest podzbiorem spójnym przestrzeni
(Z, δ) × (Z
k+1
, δ
k1
). W ten sposób udowodniliśmy, że
∀
α,β∈D
1
×...×D
k+1
∃
E⊆D
1
×...×D
k+1
:
α, β ∈ E,
E jest podzbiorem spójnym przestrzeni
(Z
1
, δ
1
) × . . . × (Z
k+1
, δ
k+1
)
Skoro tak, to z twierdzenia o połączeniu zbiorem spójnym wynika, że D − 1 × . . . × D
k+1
jest
podzbiorem spójnym przestrzeni (Z
1
, δ
1
) × . . . × (Z
k+1
, δ
k+1
).
Lemat 5. Dla podzbioru C przestrzeni metrycznej (X, d) następujące warunki są równoważne:
1. C jest spójny,
2. ∀
E,F ∈Cotop(X,d)
(C ⊆ E ∪ F, C ∩ E ∩ F = Ø) ⇒ (C ⊆ E ∨ C ⊆ F )
Dowód.
(i) ⇒ (ii)
Przypuśćmy, że C jest spójny i że zbiory E, F ∈ Cotop(X, d) spełniają warunki C ⊆ E ∪ F oraz
C ∩ E ∩ F = Ø. Połóżmy U = X \ E oraz V = X \ F . Wówczas U, V ∈ Top (X, d).
Zauważmy, że
Ø = C ∩ E ∩ F = C ∩ ((X \ U ) ∩ (X \ V )) = C ∩ (X \ (U ∪ V )) ,
skąd C ⊆ U ∪ V .
Ponadto, skoro C ⊆ E ∪ F , to
Ø = C ∩ (X \ (U ∪ V )) = C ∩ (X \ E) ∩ (X \ F ) = C ∩ U ∩ V,
ze spójności wynika, że C ⊆ U lub C ⊆ V , co znaczy, że C ∩ E = Ø lub C ∩ V = Ø, skąd
C ⊆ E ∨ C ⊆ F .
(ii) ⇒ (i)
Dowód jest analogiczny do przeprowadzonego w drugą stronę, dlatego pozostawiamy go czytelnikowi
jako ćwiczenie.
Twierdzenie 4. 5.
Niech C będzie podzbiorem spójnym przestrzeni metrycznej (X, d). Wówczas
C również jest podzbiorem spójnym tej przestrzeni.
Dowód.
Przypuśćmy, że E, F ∈ Cotop(X, d) są podzbiorami spójnymi, C ⊆ E ∪ F oraz C ∩ E ∩ F = Ø.
Musimy pokazać, że C ⊆ E lub C ⊆ F . Ponieważ C ⊆ C, to C ⊆ E ∪ F oraz C ∩ E ∩ F = Ø. Ze
spójności C mamy, że C ⊆ E lub C ⊆ F . Wobec tego C ⊆ E = E lub C ⊆ F = F .

60
ROZDZIAŁ 4. SPÓJNOŚĆ
UWAGA 28
Wnętrze, brzeg, zewętrze podzbioru spójnego danej przestrzeni metrycznej nie są na ogół spójne.
Twierdzenie 4. 6.
Dla podzbiorów C prostej R wyposażonej w indukowaną metrykę naturalną
następujące warunki są równoważne:
(i) C jest spójny,
(ii) C jest (jakimś) przedziałem.
Dowód.
(i) ⇒ (ii)
Przypuśćmy, że C jest spójny. Niech a = inf{C} oraz b = sup{C}.
Oznacza to, że a, b ∈ R ∪ {−∞, +∞}. Załóżmy, że a, b ∈ R i a < b.
Wtedy C ⊆ [a, b]. Gdyby jakaś liczba x ∈ (a, b) ⊂ R nie była elementem zbioru C,
to C ⊆ (−∞, x) ∪ (x, ∞), przy czym (−∞, x) ∩ C 6= Ø oraz (x, ∞) ∩ C 6= Ø, co przeczyłoby
spójności zbioru C (bowiem (−∞, x), (x, ∞) ∈ Top (R, d) oraz C ∩ (−∞, x) ∩ (x, ∞) = Ø). W ten
sposób udowodniliśmy, że (a, b) ⊆ C ⊆ [a, b], z czego wynika, że C jest przedziałem.
Załóżmy następnie, że a ∈ R oraz b = +∞. Wówczas C ⊆ [a, ∞) oraz istnieje ciąg (b
n
)
∞
n=1
elementów zbioru C, taki, że lim
n→∞
b
n
= ∞. Podobnie jak w poprzedniej części dowodu, wykazujemy,
że (a, b
n
) ⊆ C, dla każdego n ∈ N \ {0}. Skoro tak, to (a, ∞) =
∞
S
n=1
(a, b
n
) ⊆ C ⊆ [a, ∞), z czego
wynika, że C jest przedziałem.
Przypadki (−∞, b) oraz (−∞, ∞) pozostawiamy czytelnikowi jako ćwiczenie.
(ii) ⇒ (i) Załóżmy, że C = [0, 1]. Przypuśćmy, że E, F ∈ Cotop(R, d) spełniają warunki:
[0, 1] ⊆ E ∪ F oraz [0, 1] ∩ E ∩ F = Ø. Dodatkowo załóżmy, że 1 ∈ F . Przypuśćmy, że E ∩ [0, 1] 6= Ø.
Połóżmy a = sup{E ∩ [0, 1]}. Wówczas a ∈ R. Ponieważ E ∩ [0, 1] ∈ Cotop(R, d), to a ∈ E ∩ [0, 1].
Ponieważ (E ∩ [0, 1]) ∩ (F ∩ [0, 1]) = Ø oraz 1 ∈ F , to a < 1. Z faktu, że [0, 1] ⊆ E ∪ F i z definicji
kresu górnego wynika, że Ø 6= (a, 1) ⊆ F ∩ [0, 1]. Ponieważ F ∩ [0, 1] ∈ Cotop(R, d), to z powyższej
indukcji wynika, iż [a, 1] = (a, 1) ⊆ F ∩ [0, 1]. W konsekwencji a ∈ [0, 1] ∩ F ∩ E, co prowadzi
do sprzeczności. Udowodniliśmy w ten sposób, że jeśli 1 ∈ F , to [0, 1] ⊆ F . Dokładnie tak samo,
z faktu, że 1 ∈ E wynika, iż [0, 1] ⊆ E. Wobec tego
∀
E,F ∈Cotop(R,d)
([0, 1] ⊆ E ∩ F ) ∧ ([0, 1] ∩ E ∩ F = Ø) ⇒ [0, 1] ⊆ E ∨ [0, 1] ⊆ F,
czyli [0, 1] jest podzbiorem spójnym przestrzeni metrycznej (R, d). Przypuśćmy teraz, że C jest
dowolnym przedziałem ograniczonym i domkniętym. Wówczas C jest obrazem przedziału [0, 1]
przez funkcję ciągłą i liniową f : R → R. Spójność C wynika zatem z poprzedniej części dowodu
i z twierdzenia o obrazie ciągłym zbioru spójnego.
Niech w końcu C będzie dowolnym przedziałem i niech x, y ∈ C będą takie, że x < y. Wówczas

61
ROZDZIAŁ 4. SPÓJNOŚĆ
[x, y] ⊆ C, x, y ∈ [x, y] oraz [x, y] jest podzbiorem spójnym przestrzeni (R, d). Spójność C wynika
zatem z twierdzenia o połączeniu zbiorem spójnym.
Twierdzenie 4. 7.
Niech C będzie podzbiorem spójnym przestrzeni metrycznej (X, d).
Niech f : C → R będzie ciągła (przy metryce indukowanej z d w zbiorze C, oraz metryce naturalnej
w R). Wówczas ∀
x,y∈C
∀
α∈R
(f (x) < α < f (y) =⇒ ∃
z∈C
f (z) = α).
Dowód.
Niech x, y ∈ C, oraz niech α ∈ R spełnia nierówność f (x) < α < f (y). f (C) ⊂ R jest zbiorem
spójnym, jako obraz funkcji ciągłej na zbiorze spójnym, a więc f (C) jest przedziałem. Ponieważ
f (x), f (y) ∈ f (C) ⊂ R, to [f (x), f (y)] ⊆ f (C). Ponieważ α ∈ [f (x), f (y)], to istnieje takie x ∈ C,
że f (z) = α.
Wniosek.
Niech f : R ⊃ [a, b] → R będzie funkcją ciągłą. Niech f (a) 6= f (b) oraz niech d ∈ R spełnia
nierówność f (a) < d < f (b) lub f (a) > d > f (b). Wówczas istnieje c ∈ [a, b], że f (c) = d.
Twierdzenie 4. 8.
Dla dowolnego m ∈ N \ {0} każda m-wymiarowa kostka jest podzbiorem spój-
nym przestrzeni metrycznej (R
n
, d
2
).
Dowód.
Niech C = I
1
× · · · × I
m
, gdzie I
1
× · · · × I
m
⊂ R są przedziałami domkniętymi i ograniczony-
mi. Oczywiście przedziały I
i
są zbiorami spójnymi w R z metryką naturalną. Zatem korzystając
z twierdzenia o iloczynie kartezjańskim zbiorów spójnych otrzymujemy,
że C = I
1
× · · · × I
m
⊆ (R, d) × · · · × (R, d) = (R
m
, d
2
), (gdzie d-metryka naturalna) jest zbiorem
spójnym.
Twierdzenie 4. 9.
Okrąg S
1
jest podzbiorem spójnym przestrzeni metrycznej (R
2
, d
2
).
Dowód.
Oczywiście przedział [0, 2π) jest zbiorem spójnym w R z metryką naturalną oraz
γ : [0, 2π) 3 t 7→ (cos t, sin t) ∈ S
1
jest ciągłą bijekcją, a więc S
1
jest podzbiorem spójnym
przestrzeni metrycznej (R
2
, d
2
).
Definicja 4. 4
Niech X będzie przestrzenią wektorową nad R. Zbiór A ⊆ X jest
wypukły
wtedy,
gdy: ∀
x,y∈A
∀
t∈[0,1]
tx + (1 − t)y ∈ A.

62
ROZDZIAŁ 4. SPÓJNOŚĆ
UWAGA 29
[x, y] := {tx + (1 − t)y : t ∈ R, 0 6 t 6 1} - odcinek łączący x oraz y w X.
Twierdzenie 4. 10.
Niech (X, k · k) będzie rzeczywistą przestrzenią unormowaną. Wówczas każdy
podzbiór wypukły A ⊆ X jest zbiorem spójnym. (Metryka indukowana z normą.)
Dowód.
Niech A ⊆ X będzie zbiorem wypukłym, czyli ∀
x,y∈A
∀
t∈[0,1]
tx + (1 − t)y ∈ A. Zauważmy, że dla
każdych x, y ∈ A odwzorowanie ϕ : [0, 1] 3 t 7→ xt + (1 − t)y ∈ X jest ciągłe, a więc odcinek
[x, y] = ϕ([0, 1]) ⊆ A, jest zbiorem spójnym. Skoro tak, to korzystając z twierdzenia o połączeniu
zbiorem spójnym otrzymujemy, że A jest podzbiorem spójnym naszej przestrzeni (X, k · k).
Przykład.
1. Każda kula dowolnej przestrzeni unormowanej jest spójna.
2. Każdy prostopadłościan, sfera oraz torus są podzbiorami spójnymi przestrzeni metrycznej
(R
3
, d
2
).
3. Każda przestrzeń (R
n
, d
2
) jest spójna.
Definicja 4. 5
Niech Y będzie podzbiorem przestrzeni metrycznej (X, d).
Składową
S zbioru Y ,
wyznaczoną przez punkt p ∈ Y nazywamy: S =
S
{C ⊆ Y : C − spójny, p ∈ C}.
Twierdzenie 4. 11.
Każda składowa S podzbioru Y przestrzeni metrycznej (X, d) jest spójna.
Co więcej S jest maksymalnym zbiorem spójnym, tzn. jeżeli D ⊆ Y jest zbiorem spójnym, to zachodzi
wynikanie S ⊆ D ⇒ D = S.
Dowód.
Niech S będzie składową zbioru Y wyznaczoną przez p ∈ Y , S =
S
{C ⊆ Y : C −spójny, ∈ C. Skoro
tak, to na mocy twierdzenia o sumie zbiorów spójnych otrzymujemy, że S jest zbiorem spójnym.
Jeśli D ⊆ Y byłoby takim zbiorem spójnym, że składowa S ⊆ D, to punkt p ∈ D. Skoro tak, to
D ⊆ S, a w rezultacie D = S.
Twierdzenie 4. 12.
Niech Y będzie podzbiorem przestrzeni metrycznej (X, d). Wówczas:
(i) Y jest sumą swoich składowych,
(ii) składowe zbioru Y są parami rozłączne.

63
ROZDZIAŁ 4. SPÓJNOŚĆ
Dowód.
(i) Dowód pozostawiamy czytelnikowi jako ćwiczenie.
(ii) Gdyby składowe S
1
, S
2
zbioru Y były takie, że S
1
∩ S
2
6= ∅, to istniałby p ∈ S
1
∩ S
2
. Wówczas
zbiór S = S
1
∪ S
2
⊆ Y byłby zbiorem spójnym, przy czym S
1
⊆ S
1
∪ S
2
oraz S
2
⊆ S
1
∪ S
2
.
Wobec maksymalności składowych S
1
oraz S
2
otrzymujemy, że S
1
= S
2
= S.
Przykład.
1. Zbiór jest spójny wtedy i tylko wtedy, gdy jest swoją jedyną składową.
2. Jeśli przestrzeni metrycznej (X, d) jest dyskretna, to {{x}} : x ∈ X} jest rodziną wszystkich
składowych tej przestrzeni.
3. Składowymi zbioru Q będącego podzbiorem R z metryką naturalną śa zbiory jednopunktowe.
Rzeczywiście, gdyby pewna składowa S ⊂ Q zawierała dwie liczby wymierne x, y takie,
że x < y, to istniałoby t ∈ R \ Q takie, że x < t < y. Skoro tak, to zbiory S ∩ (∞, t), S ∩ (t, ∞)
byłyby niepuste, rozłączne, otwarte w podprzestrzeni S dawałyby w sumie S. Z tego wynika,
że S byłby zbiorem niespójnym.
4. Składowymi zbioru X = [0, 1] ∪ (1, 3) będącego podzbiorem prostej R z metryką naturalną
są zbiory [0, 1] oraz (2, 3).
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Lemat 6. Podzbiór Z przestrzeni metrycznej (X, d) jest niespójny wtedy i tylko wtedy, gdy istnieje
podzbiór otwarto-domknięty W przestrzeni metrycznej (Z, d|
Z×Z
) taki, że W 6= ∅ oraz W 6= Z.
Dowód.
”⇒”
∃
U,V ∈Top ((X,d))
Z ⊆ U ∪ V,
U ∩ V ∩ Z = ∅,
U ∩ Z 6= ∅, V ∩ Z 6= ∅.
Łatwo pokazać, że (Z ∩ U ), (Z ∩ V ) ∈ Top (Z, d|
Z×Z
).
Zauważmy, że (U ∩ Z) ∩ (U ∩ Z) = ∅, (U ∩ Z) ∪ (V ∩ Z) = Z.
Skoro tak, to U ∩ Z = Z \ (V ∩ Z) ∈ Cotop(Z, d|
Z×Z
).

64
ROZDZIAŁ 4. SPÓJNOŚĆ
”⇐”
Niech W będzie nietrywialnym zbiorem otwarto-domkniętym w (Z, d|
Z×Z
).
Zauważmy, że ∅ 6= Z 6= W oraz ∅ 6= Z \W 6= Z. Co więcej W ∪(Z \W ) = Z oraz W ∩(Z \W ) = ∅.
Zauważmy też, że Z \W ∈ Top (Z, d|
Z×Z
). Pokazaliśmy więc, że istnieją takie zbiory W, Z \W , które
są otwarte w Z, rozłąćzne, niepuste oraz dające w sumie Z. Zatem Z jest podzbiorem niespójnym
przestrzeni metrycznej (X, d).
Twierdzenie 4. 13.
Niech G ∈ Top (R
n
, d
2
). Zbiór G jest spójny wtedy i tylko wtedy, gdy każde
dwa punkty x, y ∈ G można połączyć łamaną całkowicie zawartą w zbiorze G.
Dowód.
”⇐”
Niech x, y ∈ G oraz niech Lxy oznacza łamaną łączącą punkty x oraz y.
Lxy = [a
0
, a
1
] ∪ [a
1
, a
2
] ∪ · · · ∪ [a
n−1
, a
n
], gdzie a
i
∈ G, a
0
= x, a
n
= y. Jasne jest, że odcinki
[a
i−1
, a
i
] są spójne dla i = 0, . . . , n. Zauważmy, że [a
0
, a
1
] ∪ [a
1
∪ a
2
] jest spójny, ponieważ jest
sumą zbiorów spójnych o niepustym przecięciu. Przez trywialną indukcję otrzymujemy, że łamana
Lxy = [a
0
, a
1
] ∪ [a
1
, a
2
] ∪ · · · ∪ [a
n−1
, a
n
] jest zbiorem spójnym. Skoro tak, to na mocy twierdzenia
o połączeniu zbiorem spójnym otrzymujemy, że G jest zbiorem spójnym.
”⇒”
Ustalmy p
0
∈ G. Zdefiniujmy H := {q ∈ G : istnieje łamana L ⊂ G łącząca punkty p
0
oraz q}.
Dowód zakończymy jeśli pokażemy, że H = G. Niech q
1
∈ G będzie punktem granicznym zbioru H.
Ponieważ G jest zbiorem otwartym, to ∃
ε>0
B(q
1
, ε) ⊆ G. Ponieważ q
1
jest punktem granicznym,
to H ∩ B(q
1
, ε) 6= ∅. Wobec tego istnieje y ∈ H ∩ B(q
1
, ε). Ponieważ y ∈ H, to y możemy połączyć
z p
0
łamaną zawartą w G. Zauważmy, że [y, q
1
] ⊆ B(g
1
, ε). Skoro tak, to q
1
∈ H. Wobec tego
H jest zbiorem domkniętym w G z indukowaną metryką euklidesową. Pokażemy teraz, że H jest
podzbiorem otwartym w G z indukowaną metryką euklidesową. Niech q
2
∈ H będzie dowolnym
punktem. Wówczas istnieje ε
1
∈ R
+
: B(q
2
, ε
1
) ⊆ G. Niech u ∈ B(q
2
, ε
1
). Oczywiste jest, że p
0
możemy połączyć z q
2
pewną łamaną L zawartą w G. Zauważmy, że [u, q
2
] ⊆ B(q
2
, ε
1
) ⊆ G. Skoro
tak, to L ∪ [u, q
2
] otrzymujemy łamaną zawartą w G łączącą p
0
z u. Wobec tego B(q
2
, ε
1
) ⊆ H. Z
dowolności punktu q
2
wynika, że H jest zbiorem otwartym w G z indukowaną metryką euklidesową.
Pokazaliśmy, że H jest zbiorem otwarto-domkniętym w G. Ponieważ H 6= ∅ (p
0
∈ H) oraz G-
spójny, to na mocy poprzedniego lematu H = G.
UWAGA 30
Niepusty, otwarty i spójny podzbiór danej przestrzeni metrycznej nazywa się
obszarem
(w tej
przestrzeni).

65
ROZDZIAŁ 4. SPÓJNOŚĆ
Przykład.
Niech (a, b) ∈ R
2
i niech r, R ∈ R
+
. Załóżmy, że r < R.
Pierścień {(x, y) ∈ R
2
: r
2
< (x − a)
2
+ (y − b)
2
< R
2
} jest wówczas (niewypukłym) obszarem
przestrzeni metrycznej (R
2
, d
2
).
x
y
a
b
r
R
Twierdzenie 4. 14.
Niech (X, d) oraz (Y, ρ) będą przestrzeniami metrycznymi. Oznaczmy przez
S rodzinę wszystkich składowych (spójnych) przestrzeni metrycznej (X, d), przez T natomiast -
rodzinę wszystkich składowych (spójnych) przestrzeni metrycznej (Y, ρ). Niech ponadto h : X → Y
będzie homeomorfizmem tych przestrzeni. Wówczas:
(i) ∀
S⊆X
S ∈ S ⇒ h(S) ∈ T,
(ii) odwzorowanie S 3 S 7→ h(S) ∈ T jest bijekcją.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Przykład.
Zbiory (−1, 7) ∪ (8, 19) ∪ (23, 79) oraz (−2, 4) ∪ (5, 19), oba wyposażone w indukowaną z R mertykę
naturalną, nie są homeomorficzne, bowiem pierwszy z nich ma dokładnie trzy składowe, drugi
natomiast dokładnie dwie.
Definicja 4. 6 Drogą
w przestrzeni metrycznej (X, d) nazywa się każde odwzorowanie ciągłe
ϕ : I → X, gdzie I = [0, 1] ⊂ R. (W przedziale I indukowana metryka naturalna.)

66
ROZDZIAŁ 4. SPÓJNOŚĆ
UWAGA 31
a) Jeśli ϕ : I → X jest drogą w przestrzeni metrycznej (X, d), to obraz ϕ(I) jest zwartym i spójnym
podzbiorem tej przestrzeni (continuum).
b) Jeśli ϕ(0) = ϕ(1) = x
0
dla pewnej drogi ϕ : I → X w przestrzeni metrycznej (X, d), to tą trogę
nazywa się
pętlą
zaczepioną w punkcie x
0
.
Przykład.
1. Odwzorowanie ϕ : I 3 t 7→ (cos(2πt), sin(2πt), t) ∈ R
3
jest drogą w przestrzeni metrycznej
(R
3
, d
2
) o początku w punkcie (1, 0, 0) i końcu w punkcie (1, 0, 1). (Odcinek helisy.)
2. Odwzorowanie π : I → R
2
zdefiniowane za pomocą wzoru:
π(t)
(3t, 3t), gdy 0
6 t 6
1
3
(3 − 6t, 1), gdy
1
3
6 t 6
2
3
(3t − 3, −3t + 3), gdy
2
3
6 t 6 1
jest pętlą na płaszczyźnie (R
2
, d
2
), zaczepioną w punkcie (0, 0).
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
x
y
−1
1
Definicja 4. 7
Przestrzeń metryczna (X, d) jest
drogowo spójna
, jeśli dla dowolnych dwóch punk-
tów x, y ∈ X istnieje droga ϕ : I → X taka, że ϕ(0) = X oraz ϕ(1) = Y .
Twierdzenie 4. 15.
(i) Każdy niepusty podzbiór wypukły dowolnej przestrzeni unormowanej
(X, k · k) nad ciałem R, wyposażony w metrykę naturalną indukowaną przez normę k · k,
jest drogą spójną przestrzeni metrycznej .
(ii) Każda przestrzeń metryczna drogowo spójna jest spójna.
Dowód.
(i) Jeżeli x, y ∈ W , to odcinek I 3 t 7→ (1 − t)x + ty ∈ X jest drogą łączącą punkty x oraz y
i leżącą w zbiorze W .

67
ROZDZIAŁ 4. SPÓJNOŚĆ
(ii) Wynika natychmiast z twierdzenia o połączeniu zbiorem spójnym. (Ponieważ jeśli ϕ : I → X
jest drogą w przestrzeni metrycznej (X, d), to ϕ(I) jest podzbiorem spójnym tej przestrze-
ni.)
UWAGA 32
Istnieją przestrzenie spójne, które nie są drogowo spójne!

Rozdział 5
Równoważność metryk
Definicja 5. 1
Metryki d
1
oraz d
2
w zbiorze X 6= ∅ są
równoważne
(będziemy pisać d
1
∼ d
2
), jeśli
Top (X, d
1
) = Top (X, d
2
).
UWAGA 33
Równoważność metryk jest relacją równoważności w zbiorze {d : X×X → [0, ∞) ⊂ R|d jest metryką}.
Przykład.
Niech d będzie metryką naturalną w R, ρ natomiast metryką dyskretną w R. Metryki d oraz ρ nie
są wówczas równoważne, bowiem {0} ∈ Top (R, ρ) \ Top (R, d).
Twierdzenie 5. 1.
Niech d
1
oraz d
2
będą metrykami w zbiorze X 6= ∅. Przez B
i
(x, r) oznaczmy
kulę otwartą o środku w pukncie x i promieniu r w przestrzeni petrycznej (x, d
j
), j = 1, 2. Wówczas
następujące warunki są równoważne:
(i) d
1
∼ d
2
,
(ii)
∀
x∈X
∀
ε∈R
+
∃
r
1
,r
2
∈R
+
B
1
(x, r
1
) ⊆ B
2
(x, ε),
B
2
(x, r
2
) ⊆ B
1
(x, ε).
69
ROZDZIAŁ 5. RÓWNOWAŻNOŚĆ METRYK
Dowód.
(i)⇒ (ii)
Przypuśćmy, że d
1
∼ d
2
. Wybierzmy x ∈ X oraz ε ∈ R
+
(jedno i drugie doowlne). Ponieważ
x ∈ B
2
(x, ε) oraz B
2
(x, ε) ∈ Top (X, d
2
) = Top (X, d
1
), to ∃
r
1
∈R
+
B
1
(x, r
1
) ⊆ B
2
(x, ε). Dokładnie
tak samo pokazujemy, że ∃
r
2
∈R
+
B
1
(x, r
2
) ⊆ B
2
(x, ε).
(ii)⇒ (i)
Załóżmy, że warunek (ii) jest spełniony. Wybierzmy dowolnie zbiór U ∈ Top (X, d
1
). Jeśli x ∈ U ,
to ∃
ε∈R
+
B
1
(x, ε) ⊆ U . Na mocy założenia (ii) mamy ∃
r
1
∈R
+
B
2
(x, r
2
) ⊆ B
1
(x, ε). Skoro tak, to
B
2
(x, r
2
) ⊆ U. Wykazaliśmy w ten sposób, że ∀
x∈U
∃
r
2
∈R
+
B
2
(x, r
2
) ⊆ U , co znaczy,
że U ∈ Top (X, d
2
). Dokładnie tak samo dowodzimy, że każdy podzbiór otwarty przestrzeni me-
trycznej (X, d
2
) jest podzbiorem otwartym przestrzeni metrycznej (X, d
1
).
Podsumowując Top (X, d
1
) = Top (X, d
2
).
Przykład.
1. Narysujemy, że metryki d
2
oraz d
1
na płaszczyźnie R
2
są równoważne.

70
ROZDZIAŁ 5. RÓWNOWAŻNOŚĆ METRYK
x
y
r
1
r
2
a
b
x
y
r
1
r
2
a
b
2. Niech d
1
oraz d
2
będą metrykami w co najmniej dwuelementowym zbiorze skończonym X.
Wówczas d
1
∼ d
2
. Wybierzmy bowiem (dowolnie) punkt x ∈ X oraz liczbę ε ∈ R
+
. Połóżmy
r
1
= min{d
1
(x, y) : y ∈ X \ {x}}. Wówczas r
1
∈ R
+
.
Co więcej B
1
(x, r
1
) = {x} ⊆ B
2
(x, ε).
Analogicznie pokazujemy, że ∃
r
2
∈R
+
B
2
(x, r
2
) ⊆ B
1
(x, ε). (Oznaczenie jak w ostatnim twier-
dzeniu.)
Twierdzenie 5. 2.
Niech d
1
oraz d
2
będą równoważnymi metrykami w zbiorze X 6= ∅. Niech
ponadto (Y, ρ) będzie przestrzenią metryczną, f : X → Y , niech (x
n
)
∞
n=1
będzie ciągiem elementów
zbioru X i niech y ∈ X. Wówczas:
(i) odwzorowanie f jest ciągłe względem metryki d
1
wtedy i tylko wtedy, gdy jest ciągłe względem
metryki d
2
.
(ii) x
n
d
1
−−−→
n→∞
g ⇐⇒ x
n
d
2
−−−→
n→∞
g.
Dowód.
(i) Przypuśćmy, że f jest ciągłe względem metryki d
1
. Niech V będzie (dowolnym) podzbiorem
otwartym przestrzeni metrycznej (Y, ρ). Wówczas f
−1
(V ) ∈ Top (X, d
1
) = Top (X, d
2
). Pokazaliśmy
w ten sposób, że odwzorowanie f jest ciągłe względem metryki d
2
. Odwrotna implikacja dokładnie
tak samo.
(ii) Przypuśćmy, że x
n
d
1∞
−−−→
n→∞
g. Niech U ∈ Top (X, d
2
) będzie dowolnym otoczeniem punktu g.
Ponieważ Top (X, d
2
) = Top (X, d
1
), to U jest otoczeniem punktu g w przestrzeni metrycznej
(X, d
1
). Skoro tak, to ∃
N ∈N\{0}
∀
n∈N\{0}
n > N ⇒ x
n
∈ U . Wobec tego x
d
1∞
−−−→
n→∞
g. Odwrotan
implikacja - dokładnie tak samo.

71
ROZDZIAŁ 5. RÓWNOWAŻNOŚĆ METRYK
Twierdzenie 5. 3.
Niech d
1
oraz d
2
będą równoważnymi metrykami w zbiorze X 6= ∅. Oznaczmy
przez K
i
rodzinę wszystkich podzbiorów zwartych przestrzeni metrycznej (X, d
i
), przez C
j
natomiast -
rodzinę wszystkich podzbiorów spójnych przestrzeni metrycznej (X, d
j
), (j = 1, 2). Wówczas K
1
= K
2
oraz C
1
= C
2
.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Definicja 5. 2
Metryki d
1
oraz d
2
w zbiorze X 6= ∅ są
lipschitzowsko
(czyli
jednostajnie
)
równo-
ważne
jeśli ∃
m,M ∈R
+
∀
x,y∈X
md
2
(x, y)
6 d
1
(x, y)
6 Md
2
(x, y).
UWAGA 34
Lipschitzowska równoważność jest relacją równoważnośći
w zbiorze {d : X × X → [0, ∞) ⊂ R | d jest metryką}.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 5. 4.
Metryki d
1
, d
2
oraz d
∞
w przestrzeni metrycznej R
n
są lipschitzowsko równo-
ważne.
Dowód.
Niech x, y ∈ R
n
. Powiedzmy, że x = (x
1
, . . . , x
n
) oraz y = (y
1
, . . . , y
n
). Wówczas
d
1
(x, y) =
n
X
i=1
|x
i
− y
i
| 6 n ·
n
max
i=1
|x
i
− y
i
| = n · d
∞
(x, y)
6 n ·
n
X
i=1
|x
i
− y
i
| = n · d
1
(x, y).
d
∞
(x, y) =
n
max
i=1
|x
i
− y
i
| 6
v
u
u
t
n
X
i=1
(x
i
− y
i
)
2
= d
2
(x, y)
6
6
r
n ·
n
max
i=1
(x
i
− y
i
)
2
=
√
n ·
n
max
i=1
|x
i
− y
i
| =
√
n · d
∞
(x, y).
Udowodniliśmy w ten sposób, że
∀
x,y∈R
n
1
n
d
1
(x, y)
6 d
∞
(x, y)
6 d
1
(x, y),
d
∞
(x, y)
6 d
2
(x, y)
6
√
nd
∞
(x, y).
Mamy zatem lipschitzowską równoważność metryk d
1
i d
∞
i lipschitzowską równoważność metryk
d
∞
oraz d
2
. Lipschitzowska równoważność metryk d
1
i d
2
wynika z przechodniości relacji.
Wniosek.
Metryki d
1
, d
2
oraz d
∞
w przestrzeni R
n
są parami równoważne.

72
ROZDZIAŁ 5. RÓWNOWAŻNOŚĆ METRYK
Twierdzenie 5. 5.
Przypuśćmy, że d
1
oraz d
2
są lipschitzowsko równoważnymi metrykami w zbio-
rze X 6= ∅. Wówczas:
(i) Przestrzeń metryczna (X, d
1
) jest ograniczona wtedy i tylko wtedy, gdy przestrzeń metryczna
(X, d
2
) jest ograniczona.
(ii) Przestrzeń metryczna (X, d
1
) jest zupełna wtedy i tylko wtedy, gdy przestrzeń metryczna
(X, d
2
) jest zupełna.
Dowód.
(i) Załóżmy, że przestrzeń metryczna (X, d
1
) jest ograniczona. Wiemy, że
∃
m,M ∈R
+
∀
x,y∈X
md
2
(x, y) ¬ d
1
(x, y) ¬ M d
2
(x, y).
Powiedzmy, że D
i
to średnica przestrzeni (X, d
i
), gdzie i=1,2. Dla dowolnych x, y ∈ X mamy
wówczas:
d
2
(x, y) ¬
1
m
d
1
(x, y) ¬
1
m
D
1
.
Wobec tego D
2
def
= sup
x,y∈X
(d
2
(x, y)) ¬
1
m
D
1
< ∞
z uwagi na ograniczoność przestrzeni metrycznej (X, d
1
). W takim razie przestrzeń metryczna
(X, d
2
) jest ograniczona. Dokładnie tak samo pokazujemy, że ograniczoności (X, d
2
) wynika
ograniczoność (X, d
1
).
(ii) Dowód pozostawiamy czytelnikowi jako ćwiczenie.
Twierdzenie 5. 6.
Niech d będzie metryką w zbiorze X 6= Ø. Wówczas funkcja
δ : X × X 3 (x, y) → δ(x, y)
def
=
d(x,y)
1+d(x,y)
∈ [0, ∞) ⊂ R
jest również metryką w zbiorze X, równoważną metryce d i taką, że przestrzeń metryczna (x, δ)
jest ograniczona.
Dowód.
Pozostawiamy czytelnikowi sprawdzenie, że δ spełnia warunki metryki.
Zauważmy, że ∀
x,y∈X
: δ(x, y) < 1. Wobec tego przesteń metryczna (X, δ) jest ograniczona.
Wybierzmy (dowolnie) x
0
∈ X oraz ε ∈ R
+
. Połóżmy r
1
= ε oraz r
2
=
ε
1+ε
. Odnotujmy, że r
2
< 1.
Jeśli teraz d(x
0
, y) < 1 dla pewnego y ∈ X, to δ(x, y) =
d(x
0
,y)
1+d(x
0
,y)
¬ d(x
0
, y) < ε. W ten sposób
udowodniliśmy, że B
d
(x
0
, y) ⊆ B
δ
(x
0
, y).
Jeśli w końcu δ(x
0
, y) < r
2
dla pewnego y ∈ X, to

73
ROZDZIAŁ 5. RÓWNOWAŻNOŚĆ METRYK
d(x
0
, y) =
δ(x
0
,y)
1−δ(x
0
,y)
<
r
2
1−r
2
=
ε
1+ε
1−
ε
1+ε
=
ε
1+ε
1
1+ε
= ε
W ten sposób udowodniliśmy, że B
δ
(x
0
, r
2
) ⊆ B
d
(x
0
, ε). Równoważność metryk d oraz δ wynika
z charakteryzacji wykonanej wcześniej.
Przykład.
Niech d będzie metryką naturalną w R, δ będzie metryką w tymże zbiorze zdefiniowaną przez
δ(x, y) =
d(x,y)
1+d(x,y)
=
|x−y|
1−|x−y|
. Na mocy poprzedniego twierdzenia d δ. Jest widoczne, że przestrzeń
metryczna (R, δ) jest ograniczona. Tymczasem przestrzeń (R, d) nie jest ograniczona. W takim razie
metryki d oraz δ nie są lipschitzowsko równoważne.
UWAGA 35
Jeśli metrykę euklidesową d
2
przestrzeni R
2
zastąpi się metryką d
1
albo d
∞
, to nie zmieni się
nic w kwestii zbieżności ciągów, ograniczoności, zwartości, spójności podzbiorów, zupełności oraz
ścisłości odwzorowań określonych w tej przestrzeni.

Rozdział 6
Topologia ogólna
Definicja 6. 1
Niech τ będzie pewną (dowolną) rodziną podzbiorów zbioru X. Rodzinę tę nazywa
się
TOPOLOGIĄ
(w X), jeśli spełnia warunki:
(T 1) Ø ∈ τ oraz X ∈ τ ,
(T 2) U, V ∈ τ ⇒ U ∩ V ∈ τ ,
(T 3) jeśli (U
ι
)
ι∈I
jest (dowolną) podrodziną rodziny τ , to
S
ι∈I
U
ι
∈ τ
UWAGA 36
Jeśli s ∈ N \ {0}, U
1
, . . . , U
s
∈ τ , to U
1
∩ . . . ∩ U
s
∈ τ .
Definicja 6. 2 Przestrzenią topologiczną
nazywa się parę (X, τ ), w której X jest (dowolnym)
zbiorem, τ natomiast topologią w sensie powyższej definicji w zbiorze X.
Definicja 6. 3
Niech (X, τ ) będzie przestrzenią topologiczną.
Podzbiorem otwartym
tej przestrzeni
nazywa się każdy element topologii τ .
Definicja 6. 4
Zbiór C ⊆ X jest domknięty w przestrzeni (X, τ ), jeśli X \ C ∈ τ .
Definicja 6. 5
Rodzinę wszystkich podzbiorów domkniętych przestrzeni topologicznej (X, τ ) na-
zywa się
KOTOPOLOGIĄ
tej przestrzeni.
Twierdzenie 6. 1.
Niech σ będzie kotopologią przestrzeni topologicznej (X, τ ). Wówczas:
(i) Ø ∈ σ oraz X ∈ σ,

75
ROZDZIAŁ 6. TOPOLOGIA OGÓLNA
(ii) (s ∈ N \ {0}, C
1
, . . . , C
s
∈ σ) ⇒ C
1
∪ . . . ∪ C
s
∈ σ,
(iii) Jak (C
ι
)
ι∈I
jest dowolną podrodziną kotopologii σ, to
T
ι∈I
C
ι
∈ σ.
Dowód.
Dowód pozostawiamy czytelnikowi jako ćwiczenie.
UWAGA 37
Jeśli (X, τ ) jest przestrzenią topologiczną, to Ø oraz X są podzbiorami otwarto-domkniętymi.
Rodzinę wszystkich podzbiorów otwarto-domknietych oznaczamy jako Clop
Definicja 6. 6 Otoczeniem (otwartym)
punktu x
0
przestrzeni topologicznej (X, τ ) nazywa się każ-
dy taki zbiór U ∈ τ , że x
0
∈ τ .
Przykład.
1. Niech X będzie dowolnym zbiorem. Rodzina τ
B
:= {Ø, X} jest wówczas topologią w zbiorze
X zwaną
topologią banalną
albo
antydyskretną
. Kotopologią (X, τ
B
) jest {Ø, X}.
2. Niech X będzie (dowolnym) zbiorem. Rodziną 2
X
wszystkich podzbiorów tego zbioru jest
wówczas topologią w tym zbiorze, zwaną
topologią dyskretną
. Kotopologią przestrzeni
X, 2
X
jest {X \ U : U ∈ 2
X
} = 2
X
(inaczej mówiąc, w przestrzeni topologicznej
X, 2
X
wszystkie
podzbiory są otwarto-domknięte).
3. Niech X będzie (dowolnym) zbiorem niepustym i niech x
0
∈ X. Rodzina
τ
0
def
= {U ⊆ X : x
0
∈ U } ∪ {Ø} jest wówczas topologią w zbiorze X, zwaną
topologią
wyróżnionego punktu
x
0
. Kotopologią tej przestrzeni jest
{X \ U : U ∈ τ } = {C ⊆ X : x
0
/
∈ C} ∪ {X}
4. Niech X będzie dowolnym zbiorem. Rodzina
τ
c
def
= {U ∈ X : X \ U jest zbiorem skończonym} ∪ {Ø}
jest wówczas topologią w zbiorze X, zwaną
topologią dopełnień skończonych
. Faktycznie,
Ø ∈ τ
c
. Ponieważ X \ X = Ø, to X ∈ τ
c
. Jeśli U, V ∈ τ
c
\ {Ø}, to zbiory X \ U oraz X \ V
są skończone. Wobec tego (X \ U ) ∪ (X \ V ) = X \ (U ∩ V ) jest zbiorem skończonym, skąd
U ∩ V ∈ τ
c
. Jeśli w końcu (U
ι
)
ι∈I
jest podrodziną rodziny τ
c
taką, że ∃
ι
0
∈I
: M
c
0
6= Ø,
to X \ U
ι
0
⊇
T
ι∈I
(X \ U
ι
) = X \
S
ι∈I
U
ι
oraz X \ U
ι
0
jest zbiorem skończonym, skąd już
S
ι∈I
U
ι
∈ τ
c
.

76
ROZDZIAŁ 6. TOPOLOGIA OGÓLNA
Kotopologią przestrzeni (X, τ
c
) jest
{X \ U : U ∈ τ
c
} = {C ⊆: C jest zbiorem skończonym } ∪ {X}.
Zauważmy, że jeśli X jest zbiorem skończonym, to topologia τ
c
jest identyczna z topologia
dyskretną w zbiorze X.
5. Jeśli d jest metryką w zbiorze X 6= Ø, to Top (X, d) jest topologią w tym zbiorze, zwaną
topologią zadaną przez metrykę
d albo
topologią naturalną
przestrzeni metrycznej (X, d).
Definicja 6. 7
Przestrzeń topologiczna (X, τ ) jest
metryzowalna
, jeśli X 6= Ø oraz istnieje taka
metryka d w zbiorze X, że τ := Top (X, d).
Przykład.
Rozważmy topologię dyskretną 2
X
w zbiorze X 6= Ø. Niech d będzie metryką dyskretną w tym
zbiorze. Ponieważ Top (X, d) = 2
X
, w takim razie przestrzeń topologiczna
X, 2
X
jest metryzo-
walna.
Definicja 6. 8
Przestrzeń topologiczna (X, τ ) jest
przestrzenią Hausdorffa
, jeśli
∀
x,y∈X
x 6= y ⇒ ∃
U,V ∈τ
x ∈ U,
y ∈ V,
U ∩ V = Ø
Twierdzenie 6. 2.
Każda metryzowalna przestrzeń topologiczna jest przestrzenią Hausdorffa.
UWAGA 38
Istnieją nie metryzowalne przestrzenie Hausdorffa
Dowód.
Niech (X, τ ) będzie taką przestrzenią topologiczną, że X 6= Ø oraz τ = Top (X, d) dla pewnej
metryki d w zbiorze X. Niech następnie x, y ∈ X będą różnymi od siebie punktami. Połóżmy
ε =
1
2
d(x, y). Wówczas ε ∈ R
+
. Następnie połóżmy U = B(x, ε) oraz V = B(y, ε). Wtedy x ∈ U ,
y ∈ V , U ∩ V = Ø oraz U, V ∈ τ .

Wykaz oznaczeń
N
liczby naturalne
N \ {0}
liczby naturalne bez zera
Q
liczby wymierne
R
liczby rzeczywiste
R
+
liczby rzeczywiste dodatnie
Z
liczby całkowite
(X, d)
przestrzeń metryczna
B(a, r)
kula otwarta o środku a i promieniu r
B(a, r)
kula domknięta o środku a i promieniu r
S(a, r)
sfera o środku a i promieniu r
d
1
metryka Manhatan
d
2
metryka Euklidesowa
d
H
metryka Hamminga
d
∞
metryka Czebyszewa
R
n
przestrzeń n-wymiarowa
int (A)
wnętrze zbioru A
∂A
brzeg zbioru A
cl (A),
A
domknięcie zbioru A
Top (X, d)
topologia przestrzeni mertycznej (X, d)
Cotop(X, d)
kotopologia przestrzeni mertycznej (X, d)
S
1
okrąg jednostkowy w R
2
f |
A
zawężenie f do A
diam (Y )
średnica zbioru Y
dist (X, Y )
odległość między zbiorami X i Y
ext (A)
zewnętrze zbioru A
(X, d)
H
∼
= (Y, ρ)
homeomorfizm przestrzeni (X, d) oraz (Y, ρ)
(X, d)
I
∼
= (Y, ρ)
izomorfizm przestrzeni (X, d) oraz (Y, ρ)
Document Outline
- Przedmowa
- Przestrzenie metryczne
- Ciagłosc
- Zwartosc
- Spójnosc
- Równowaznosc metryk
- Topologia ogólna
- Wykaz oznaczen
Wyszukiwarka
Podobne podstrony:
1) Wykład ze wstępu do socjologii, Prezentacje
Wyklady ze wstepu do matematyki Wprowadzenie do teorii mnogosci Guzicki Wojciech zakrzewski Piotr
W Guzicki Wyklady ze wstępu do matematyki
Szkoły i kierunki psychologii klinicznej WYKŁAD SPECJALIZACYJNY-Krystyna Drat-Ruszczak, KLINICZNA py
ZAGADNIENIA DO KOLOKWIUM ZE WSTĘPU DO PRAWOZNAWSTWA, Wstęp do prawoznawstwa, Wstęp do prawoznawstwa
Repetytorium ze wstepu do prawa
Przesyłam zagadnienia egzaminacyjne ze Wstępu do nauki o języku
Zakres materialu obowiazujacego do egzaminu ze Wstepu do Matematyki, Matematyka stosowana, Logika
Tematy na egzamin ustny ze wstępu do nauki o komunikowaniu
Pytania ze Wstepu do Panstwa i Prawa
lista studentow ze wstepu do pr Nieznany
Repetytorium ze wstepu do prawa-1, Sem. 1, Wstęp do prawoznawstwa
Testy ze wstępu do prawoznawstwa3
Odpowiedzi do pytań z egzaminu ustnego ze Wstępu do Logiki i Teorii Mnogości
repetytorium ze wstępu do prawa
więcej podobnych podstron