
WYKŁADY Z ALGEBRY LINIOWEJ
I


UNIWERSYTET w BIAŁYMSTOKU
Instytut Matematyki
Ryszard R. Andruszkiewicz
WYKŁADY Z ALGEBRY LINIOWEJ
I
Białystok 2005

Copyright c
Uniwersytet w Białymstoku, Białystok 2005
ISBN 83-7431-57-X
Korekta
Magdalena Sobolewska
Redakcja techniczna i skład komputerowy
Ryszard R. Andruszkiewicz
Wydawnictwo Uniwersytetu w Białymstoku
15-097 Białystok, ul. M. Skłodowskiej-Curie 14,
tel. (085) 745 70 58, 745 70 59
Druk i oprawa:
Mazowieckie Zakłady Graficzne s.c.
tel. (086) 275 41 31
Spis treści
6
8
Działanie w zbiorze . . . . . . . . . . . . . . . . . . . .
8
Określenie ciała; przykłady ciał . . . . . . . . . . . . .
8
. . . . . . . . . . . . . . . .
12
16
Konstrukcja ciała liczb zespolonych . . . . . . . . . . .
16
egania liczb zespolonych . . . . . . . . .
21
Własności modułu liczb zespolonych
. . . . . . . . . .
21
Pierwiastek kwadratowy z liczb
zespolonych . . . . . . . . . . . . . . . . . . . . . . . .
23
25
Postać trygonometryczna liczby
zespolonej . . . . . . . . . . . . . . . . . . . . . . . . .
25
Własności argumentu liczby
zespolonej . . . . . . . . . . . . . . . . . . . . . . . . .
26
Interpretacja geometryczna mnożenia liczb zespolonych
28
Pierwiastkowanie liczb zespolonych . . . . . . . . . . .
28
Pierwiastki pierwotne z jedności . . . . . . . . . . . . .
29
31
azane z układami równań linio-
wych . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
5

6
Spis treści
Operacje elementarne nad układem równań liniowych .
34
Metoda eliminacji Gaussa . . . . . . . . . . . . . . . .
35
39
. . . . . . . . . . . . . . . . . . . . . . . .
39
Określenie macierzy . . . . . . . . . . . . . . . . . . . .
42
Określenie wyznacznika . . . . . . . . . . . . . . . . . .
43
46
Własności wyznaczników . . . . . . . . . . . . . . . . .
46
Operacje elementarne na macierzy . . . . . . . . . . . .
50
Obliczanie wyznacznika za pomoc
operacji elementarnych . . . . . . . . . . . . . . . . . .
51
Rozwinięcie Laplace’a i wzory Cramera
53
ecie Laplace’a . . . . . . . . . . . . . . . . . . .
53
Wzory Cramera . . . . . . . . . . . . . . . . . . . . . .
57
61
Podstawowe operacje na macierzach . . . . . . . . . . .
61
Algebra macierzy kwadratowych . . . . . . . . . . . . .
65
Odwracanie macierzy . . . . . . . . . . . . . . . . . . .
68
Odwracanie macierzy przy pomocy
operacji elementarnych . . . . . . . . . . . . . . . . . .
70
71
Określenie przestrzeni liniowej . . . . . . . . . . . . . .
71
Przykłady przestrzeni liniowych . . . . . . . . . . . . .
72
Własności działań na wektorach . . . . . . . . . . . . .
74
10 Podprzestrzenie przestrzeni liniowych
77
10.1 Określenie podprzestrzeni
. . . . . . . . . . . . . . . .
77
10.2 Podprzestrzenie generowane i ich
. . . . . . . . . . . . . . . . . . . . . . . . .
78
10.3 Kombinacja liniowa wektorów . . . . . . . . . . . . . .
81
10.4 Operacje elementarne na układach wektorów . . . . . .
83

Spis treści
7
11 Baza i wymiar przestrzeni liniowej
85
11.1 Liniowa niezależność wektorów . . . . . . . . . . . . . .
85
11.2 Baza przestrzeni liniowej . . . . . . . . . . . . . . . . .
88
11.3 Wymiar przestrzeni liniowej . . . . . . . . . . . . . . .
91
12 Izomorfizmy. Sumy proste. Hiperpłaszczyzny
96
12.1 Izomorfizmy przestrzeni liniowych . . . . . . . . . . . .
96
12.2 Suma prosta podprzestrzeni . . . . . . . . . . . . . . .
98
12.3 Hiperpłaszczyzny liniowe . . . . . . . . . . . . . . . . .
99
12.4 Podprzestrzenie przestrzeni
ednych . . . . . . . . . . . . . . . . . . . . . . . 100
102
edu macierzy . . . . . . . . . . . . . . . . 102
edu macierzy . . . . . . . . . . . . 105
13.3 Twierdzenie Kroneckera-Capellie’go . . . . . . . . . . . 107
110
14.1 Konstrukcja przestrzeni ilorazowej . . . . . . . . . . . . 110
14.2 Baza i wymiar przestrzeni ilorazowej
. . . . . . . . . . 113
15 Przekształcenia liniowe i ich zastosowania
115
15.1 Przekształcenia liniowe i ich
. . . . . . . . . . . . . . . . . . . . . . . . . 115
15.2 Twierdzenie o izomorfizmie . . . . . . . . . . . . . . . . 119
15.3 Przykłady i zastosowania
przekształceń liniowych . . . . . . . . . . . . . . . . . . 121
126

Wstęp
Niniejsza książka jest podręcznikiem do przedmiotu Algebra liniowa
I wykładanego w Instytucie Matematyki Uniwersytetu w Białymstoku
w oparciu o następujący program:
Aksjomaty ciała. Pojęcie ciała liczbowego. Konstrukcja ciała
liczb zespolonych, ciało liczb zespolonych. Geometryczna inter-
pretacja liczb zespolonych, trygonometryczna postać liczb zespo-
lonych, twierdzenie de Moivre’a, pierwiastkowanie liczb zespolo-
nych. Pojęcie układu równań liniowych, układ równań jednorod-
nych, rozwi
,
azanie układu, metoda Gaussa rozwi
,
azywania ukła-
dów równań liniowych. Wyznacznik i jego własności, twierdze-
nie Laplace’a. Twierdzenie Cramera. Rz
,
ad macierzy i operacje
na macierzach nie zmieniaj
,
ace rzędu. Twierdzenie Kroneckera-
Capelli’ego. Mnożenie macierzy. Twierdzenie Cauchy’ego i jego
zastosowania. Pojęcie przestrzeni liniowej. Podprzestrzenie prze-
strzeni liniowej. Kombinacja liniowa wektorów. Liniowa niezależ-
ność wektorów, baza i wymiar przestrzeni liniowej, współrzędne.
Lemat Steinitza. Wymiar przestrzeni i podprzestrzeni. Suma i
przecięcie podprzestrzeni, ich wymiary. Przestrzeń ilorazowa i
jej wymiar. Przekształcenia liniowe przestrzeni liniowych. J
,
adro
i obraz przekształcenia liniowego. Monomorfizm, endomorfizm,
epimorfizm, izomorfizm. Zasadnicze twierdzenie o izomorfizmach
przestrzeni liniowych.
Wieloletnie doświadczenia autora związane z wykładaniem algebry
liniowej pokazały, że przedmiot ten sprawia spore trudności studen-
tom. Okazało się, że powyższy program nie jest łatwo zrealizować
8

Wstęp
9
w trakcie piętnastu wykładów w sposób przystępny dla słuchaczy bez
dysponowania dobrymi materiałami dydaktycznymi. Okazało się też,
że odsyłanie studentów do literatury nie jest (z wielu powodów) sku-
tecznym rozwiązaniem problemu. Właśnie dlatego powstał ten skrypt.
W oparciu o materiał tu umieszczony można sprawnie prowadzić wy-
kłady ubogacając je dodatkowymi przykładami, uwagami dydaktycz-
nymi, informacjami historycznymi, ciekawostkami, zadaniami, proble-
mami, itp.
W podręczniku liczbami naturalnymi będziemy nazywali dodatnie
liczby całkowite, zaś sam zbiór wszystkich liczb naturalnych będziemy
oznaczali przez N. Zatem N = {1, 2, . . .}. Ponadto N
0
= {0, 1, 2, . . .}.
Koniec dowodu oznaczamy symbolem
.
Autor dziękuje mgr Magdalenie Sobolewskiej za pomoc w składzie
komputerowym tego podręcznika.
Autor

Rozdział 1
Pojęcie ciała
1.1
Działanie w zbiorze
Definicja 1.1.
Działaniem w niepustym zbiorze A nazywamy
każde odwzorowanie zbioru A × A w zbiór A. Jeżeli ◦ jest działaniem
w zbiorze A i a, b ∈ A, to ◦((a, b)) oznaczamy przez a ◦ b i nazywamy
wynikiem działania ◦ na parze (a, b).
Działania będziemy oznaczali symbolami: ◦, ·, +, ⊕, itd.
Przykład 1.1. Niech m > 1 b
,
edzie liczb
,
a naturaln
,
a oraz niech
Z
m
= {0, 1, . . . , m − 1}. W zbiorze Z
m
określamy dodawanie modulo
m oznaczane przez ⊕
m
i mnożenie modulo m oznaczane przez
m
w
ten sposób, że dla dowolnych a, b ∈ Z
m
:
a ⊕
m
b = reszta z dzielenia a + b przez m,
(1.1)
a
m
b = reszta z dzielenia a · b przez m.
(1.2)
Np. 2
4
2 = 0, 2 ⊕
5
4 = 1, itd.
1.2
Określenie ciała; przykłady ciał
Niech K b
,
edzie zbiorem posiadaj
,
acym co najmniej dwa elementy. Niech
+ i · b
,
ed
,
a działaniami w zbiorze K zwanymi odpowiednio dodawaniem
10

Pojęcie ciała
11
i mnożeniem oraz niech b
,
ed
,
a wyróżnione w zbiorze K dwa elementy
nazywane zerem i jedynk
,
a i oznaczane symbolami 0 i 1 odpowiednio.
Powiemy, że K z tymi działaniami i wyróżnionymi elementami 0, 1 jest
ciałem, jeżeli spełnione s
,
a nast
,
epuj
,
ace warunki (aksjomaty ciała):
A1. ∀
a,b∈K
a + b = b + a.
A2. ∀
a,b,c∈K
(a + b) + c = a + (b + c) .
A3. ∀
a∈K
a + 0 = a.
A4. ∀
a∈K
∃
x∈K
a + x = 0.
A5. ∀
a,b∈K
a · b = b · a.
A6. ∀
a,b,c∈K
(a · b) · c = a · (b · c).
A7. ∀
a∈K
a · 1 = a.
A8. ∀
a,b,c∈K
a · (b + c) = a · b + a · c.
A9. ∀
a∈K\{0}
∃
y∈K
a · y = 1.
Podstawowym przykładem ciała jest ciało liczb wymiernych (ze
zwykłym dodawaniem i mnożeniem liczb). Oznaczamy je przez Q.
Zbiór liczb rzeczywistych ze zwykłymi działaniami dodawania i mno-
żenia tworzy ciało. Oznaczamy je przez R i nazywamy ciałem liczb
rzeczywistych.
Definicja 1.2. Każdy podzbiór K ciała R zawieraj
,
acy liczby 0, 1,
który jest ciałem ze wzgl
,
edu na zwykłe dodawanie i zwykłe mnożenie
liczb rzeczywistych (obci
,
ete do K) nazywamy ciałem liczbowym.
Stwierdzenie 1.1. Podzbiór K ⊆ R jest ciałem liczbowym wtedy
i tylko wtedy, gdy 0, 1 ∈ K oraz dla dowolnych a, b ∈ K: a − b ∈ K
i dla dowolnych a ∈ K, b ∈ K \ {0}:
a
b
∈ K.
Dowód ⇒. Z założenia 0, 1 ∈ K. Weźmy dowolne b ∈ K. Wtedy
istnieje x ∈ K takie, że b + x = 0, sk
,
ad −b ∈ K dla każdego b ∈ K.
Niech a, b ∈ K. Wtedy −b ∈ K, wi
,
ec a − b = a + (−b) ∈ K. Weźmy
dowolne b ∈ K \ {0}. Wtedy istnieje y ∈ K takie, że b · y = 1,
sk
,
ad
1
b
∈ K dla każdego b ∈ K \ {0}. Zatem dla dowolnych a ∈ K,
b ∈ K \ {0} mamy, że
a
b
= a ·
1
b
∈ K, bo a,
1
b
∈ K.
⇐. Z założenia mamy, że 0, 1 ∈ K. Weźmy dowolne a, b ∈ K.
Wtedy −b = 0 − b ∈ K, wi
,
ec aksjomat A4 jest spełniony w K oraz
a + b = a − (−b) ∈ K, czyli dodawanie jest wykonalne w K. Ponieważ
12
Wykłady z algebry liniowej I
aksjomaty A1-A3 s
,
a spełnione w R, wi
,
ec tym bardziej s
,
a one spełnione
w K. Niech b ∈ K \ {0}. Wtedy
1
b
∈ K, bo 1 ∈ K. Wynika st
,
ad, że
aksjomat A9 jest spełniony w K. Weźmy dowolne a ∈ K, b ∈ K \ {0}.
Wtedy a · b = a ·
1
1
b
∈ K, gdyż
1
b
∈ K. Ponadto dla a ∈ K jest
a · 0 = 0 ∈ K, wi
,
ec mnożenie jest wykonalne w K. St
,
ad aksjomaty
A5-A8 też s
,
a spełnione w K i ostatecznie K jest ciałem.
Przykład 1.2. Niech d > 1 b
,
edzie liczb
,
a naturaln
,
a, która nie
jest podzielna przez kwadrat liczby pierwszej (np. 2,3,5,6,7,10, itd.).
Wówczas zbiór Q(
√
d) = {x + y
√
d : x, y ∈ Q} jest ciałem liczbowym,
bo 0 = 0 + 0 ·
√
d, 1 = 1 + 0 ·
√
d oraz dla x
1
, x
2
, y
1
, y
2
∈ Q:
(x
1
+ y
1
√
d) − (x
2
+ y
2
√
d) = (x
1
− x
2
) + (y
1
− y
2
)
√
d ∈ Q(
√
d),
bo x
1
− x
2
, y
1
− y
2
∈ Q. Zauważmy też, że dla dowolnych x, y ∈ Q:
x + y
√
d = 0 ⇔ x = y = 0.
(1.3)
Rzeczywiście, jeśli x + y
√
d = 0, to dla y 6= 0,
√
d = −
x
y
∈ Q, wi
,
ec
istniej
,
a wzgl
,
ednie pierwsze liczby naturalne a, b takie, że
√
d =
a
b
, sk
,
ad
b
2
d = a
2
. Ale d > 1, wi
,
ec a > 1 i istnieje liczba pierwsza p taka, że p|a.
Zatem p
2
|b
2
d oraz p nie dzieli b, gdyż liczby a i b s
,
a wzgl
,
ednie pierwsze,
czyli st
,
ad p
2
|d i mamy sprzeczność z określeniem liczby d. Zatem y = 0
i w konsekwencji x = 0. Jeśli zaś x = y = 0, to oczywiście x+y
√
d = 0.
Niech teraz x
1
, x
2
, y
1
, y
2
∈ Q b
,
ed
,
a takie, że x
2
+ y
2
√
d 6= 0. Wtedy
z (1.3) mamy, że x
2
− y
2
√
d 6= 0, wi
,
ec
x
1
+y
1
√
d
x
2
+y
2
√
d
(x
1
+y
1
√
d)(x
2
−y
2
√
d)
(x
2
+y
2
√
d)(x
2
−y
2
√
d)
=
(x
1
x
2
−y
1
y
2
d)+(y
1
x
2
−x
1
y
2
)
√
d
x
2
2
−dy
2
2
=
x
1
x
2
−y
1
y
2
d
x
2
2
−dy
2
2
+
y
1
x
2
−x
1
y
2
x
2
2
−dy
2
2
√
d ∈ Q(
√
d). Zatem
na mocy stwierdzenia 1.1, Q(
√
d) jest ciałem liczbowym.
Przykład 1.3. Zbiór {x + y
3
√
2 : x, y ∈ Q} nie jest ciałem liczbo-
wym, gdyż można pokazać, że
3
√
4 =
3
√
2 ·
3
√
2 nie należy do tego zbioru.
Przykład 1.4. Niech p b
,
edzie dowoln
,
a liczb
,
a pierwsz
,
a. Wów-
czas zbiór Z
p
z działaniami ⊕
p
i
p
określonymi w przykładzie 1.1
i z wyróżnionymi elementami 0, 1 tworzy ciało, które ma dokładnie p-
elementów. W dowodzie tego faktu wykorzystuje si
,
e tzw. twierdzenie

Pojęcie ciała
13
o dzieleniu z reszt
,
a, z którego wynika, że dla dowolnej liczby całko-
witej a istnieje dokładnie jedna para (q, r) liczb całkowitych taka, że
a = q · p + r i r ∈ Z
p
. Weźmy dowolne a, b ∈ Z
p
. Z przemienności do-
dawania i z przemienności mnożenia liczb całkowitych od razu wynika,
że a ⊕
p
b = b ⊕
p
a i a
p
b = b
p
a. Ponadto
a ⊕
p
0 = [reszta z dzielenia a + 0 = a przez p] = a,
a
p
1 = [reszta z dzielenia a · 1 = a przez p] = a.
Jeżeli a 6= 0, to a > 0, wi
,
ec p − a ∈ Z
p
oraz
a ⊕
p
(p − a) = [ reszta z dzielenia a + (p − a) = p przez p] = 0
i 0 ⊕
p
0 = 0, wi
,
ec aksjomat A4 jest spełniony. Weźmy dowolne a, b, c ∈
Z
p
. Wtedy istnieje q
1
∈ Z takie, że a + b = q
1
p + a ⊕
p
b. Ponadto
istnieje q
2
∈ Z takie, że (a ⊕
p
b) + c = q
2
p + [(a ⊕
p
b) ⊕
p
c], wi
,
ec
a + b + c = (q
1
+ q
2
)p + [(a ⊕
p
b) ⊕
p
c], czyli
(a ⊕
p
b) ⊕
p
c = reszta z dzielenia a + b + c przez p.
Podobnie pokazujemy, że a ⊕
p
(b ⊕
p
c) = reszta z dzielenia a + b + c
przez p, wi
,
ec (a ⊕
p
b) ⊕
p
c = a ⊕
p
(b ⊕
p
c). Zupełnie analogicznie
dowodzimy, że (a
p
b)
p
c = a
p
(b
p
c) oraz a
p
(b ⊕
p
c) = a
p
b ⊕
p
a
p
c. Weźmy teraz dowolne a ∈ Z
p
\ {0}. Zauważmy, że elementy
a
p
0, a
p
1, . . . , a
p
(p−1) s
,
a parami różne, gdyż inaczej istniej
,
a liczby
całkowite x, y ∈ {0, 1, . . . , p − 1} takie, że x > y oraz a
p
x = a
p
y,
sk
,
ad p|ax − ay, czyli p|a(x − y). Ale p nie dzieli a, wi
,
ec p|x − y. Lecz
x−y jest liczb
,
a naturaln
,
a mniejsz
,
a od p, wi
,
ec mamy sprzeczność. St
,
ad
wynika, że {a
p
0, a
p
1, . . . , a
p
(−1)} = {0, 1, . . . , p − 1}, wi
,
ec dla
pewnego t ∈ Z
p
jest a
p
t = 1. Zatem aksjomat A9 też jest spełniony
i ostatecznie Z
p
jest ciałem.
Przykład 1.5. Nie istnieje ciało, które ma 6 elementów, ale ist-
niej
,
a ciała 4-ro i 8-mio elementowe.

14
Wykłady z algebry liniowej I
1.3
Własności działań w ciele
Niech (K, +, ·, 0, 1) b
,
edzie dowolnym ciałem. Wówczas zachodz
,
a
nast
,
epuj
,
ace własności:
Własność 1.1. Prawa skracania równości:
(a) jeśli a + c = b + c, to a = b,
(b) jeśli a · c = b · c i c 6= 0, to a = b.
Dowód.
(a).
Z A4 istnieje t ∈ K takie, że c + t = 0, wi
,
ec
(a + b) + t = (b + c) + t, sk
,
ad z A2: a + (c + t) = b + (c + t), czyli
a + 0 = b + 0 i z A3: a = b.
(b). Z A9 istnieje y ∈ K takie, że c · y = 1, wi
,
ec (a · c) · y = (b · c) · y,
sk
,
ad z A6, a · (c · y) = b · (c · y), czyli a · 1 = b · 1, a wi
,
ec z A7, a = b.
Własność 1.2. Element x z A4 jest wyznaczony jednoznacznie
przez element a.
Dowód. Niech y ∈ K b
,
edzie takie, że a + y = 0. Wtedy a + y =
a + x, sk
,
ad z A1 i własności 1.1(a) mamy, że y = x.
Uwaga 1.1. Ten jedyny element x z A4 nazywamy elementem
przeciwnym do a i oznaczamy przez (−a). Ponieważ z A1: (−a) + a =
0, wi
,
ec a jest elementem przeciwnym do (−a) i mamy wzór:
−(−a) = a.
Własność 1.3. a · 0 = 0.
Dowód. Z A3: 0 = 0 + 0, wi
,
ec a · 0 = a · (0 + 0) = a · 0 + a · 0, na
mocy A8. St
,
ad z A3 i A1: 0 + a · 0 = a · 0 + a · 0 i z własności 1.1(a),
a · 0 = 0.
Własność 1.4. 0 6= 1.
Dowód. Ponieważ zbiór K ma co najmniej dwa elementy, wi
,
ec
istnieje a ∈ K takie, że a 6= 0 i wtedy z A7: a = a · 1 oraz z własności
1.3: a · 0 = 0 6= a, wi
,
ec 0 6= 1.
Własność 1.5. Element y z A9 jest wyznaczony jednoznacznie
przez element a.

Pojęcie ciała
15
Dowód. Niech z ∈ K b
,
edzie taki, że a · z = 1. Wtedy na mocy
A5, z · a = y · a i a 6= 0, wi
,
ec na mocy własności 1.1(b), z = y.
Uwaga 1.2. Ten jedyny element y z A9 nazywamy elementem
odwrotnym do elementu a 6= 0 i oznaczamy przez a
−1
lub
1
a
. Jeśli
a
−1
= 0, to 1 = a · a
−1
= a · 0 = 0, na mocy własności 1.3 i 0 = 1
wbrew własności 1.4. Zatem a
−1
6= 0 oraz z A5, a
−1
· a = 1, czyli a jest
elementem odwrotnym do elementu a
−1
i dla dowolnego a 6= 0 mamy
wzór:
(a
−1
)
−1
= a.
Własność 1.6. (−a) · b = a · (−b) = −(a · b) oraz (−a) · (−b) = a · b.
Dowód. Na mocy A8 i własności 1.3 mamy, że a · (−b) + a · b =
a · (b + (−b)) = a · 0 = 0, wi
,
ec a · (−b) jest elementem przeciwnym do
a · b, czyli a · (−b) = −(a · b). St
,
ad i z A5 mamy, że (−a) · b = b · (−a) =
−(b · a) = −(a · b) oraz (−a) · (−b) = −[(−a) · b] = −[−(a · b)] = a · b.
Odejmowanie w ciele K określamy nast
,
epuj
,
aco:
a − b
def
= a + (−b).
(1.4)
Własność 1.7. a · (b − c) = a · b − a · c.
Dowód. Z (1.4), A8 i z własności 1.6 mamy, że a · (b − c) =
a · (b + (−c)) = a · b + a · (−c) = a · b + [−(a · c)] = a · b − a · c.
Dzielenie przez niezerowe elementy b w ciele określamy nast
,
epuj
,
aco:
a
b
def
= a · b
−1
.
(1.5)
Własność 1.8. Jeżeli a 6= 0 i b 6= 0, to a · b 6= 0.
Dowód. Weźmy dowolne a, b ∈ K \ {0}. Jeżeli a · b = 0, to na
mocy A5 i własności 1.3, a · b = 0 · b, sk
,
ad a = 0 na mocy własności
1.1(b) i mamy sprzeczność. Zatem a · b 6= 0.
Uwaga 1.3. Niech a, b ∈ K \ {0}. Wtedy z własności 1.8 jest
a · b 6= 0 oraz (a · b) · (
1
a
·
1
b
) = (a ·
1
a
) · (b ·
1
b
) = 1 · 1 = 1, wi
,
ec mamy
wzór:
16
Wykłady z algebry liniowej I
1
a·b
=
1
a
·
1
b
.
W ciele K możemy określić iloczyn elementu a ∈ K przez dowoln
,
a
liczb
,
e całkowit
,
a n w nast
,
epuj
,
acy sposób:
n·a
def
=
a + a + . . . + a
|
{z
}
n
, gdy n jest liczb
,
a naturaln
,
a
0
, gdy n = 0
(−a) + (−a) + . . . + (−a)
|
{z
}
|n|
, gdy n < 0
.
(1.6)
Można wykazać (jest to żmudne), że dla dowolnych liczb całkowi-
tych m, n i dla dowolnych a, b ∈ K zachodz
,
a własności:
Własność 1.9. na + ma = (n + m)a oraz na − ma = (n − m)a.
Własność 1.10. n(ma) = (nm)a.
Własność 1.11. (na) · (mb) = (nm)(a · b).
Własność 1.12. na + nb = n(a + b).
W ciele K możemy też określić całkowit
,
a nieujemn
,
a pot
,
eg
,
e dowol-
nego elementu a ∈ K przyjmuj
,
ac, że
a
0
= 1
(1.7)
a
n
= a · a · . . . · a
|
{z
}
n
dla naturalnych n.
(1.8)
Przez prost
,
a indukcj
,
e można wykazać, że wówczas dla dowolnych
m, n ∈ N
0
oraz dla dowolnych a, b ∈ K zachodz
,
a wzory:
Własność 1.13. a
n
· a
m
= a
n+m
.
Własność 1.14. (a
n
)
m
= a
nm
.
Własność 1.15. (a · b)
n
= a
n
· b
n
.
Własność 1.16. (a + b)
n
=
n
X
k=0
n
k
a
n−k
· b
k
.

Pojęcie ciała
17
Dla niezerowych elementów a ciała K możemy rozszerzyć definicj
,
e
(1.7)-(1.8) na wszystkie liczby całkowite n w ten sposób, że dla n < 0:
a
n
=
1
a
−n
.
(1.9)
Można wykazać, że wówczas własności 1.13-1.15 s
,
a prawdziwe dla do-
wolnych liczb całkowitych m, n i dla dowolnych a, b ∈ K \ {0}.

Rozdział 2
Ciało liczb zespolonych I
2.1
Konstrukcja ciała liczb zespolonych
W zbiorze R × R wprowadzamy działania + i · przy pomocy wzorów:
(a
1
, b
1
) + (a
2
, b
2
) = (a
1
+ a
2
, b
1
+ b
2
),
(2.1)
(a
1
, b
1
) · (a
2
, b
2
) = (a
1
· a
2
− b
1
· b
2
, a
1
· b
2
+ a
2
· b
1
),
(2.2)
dla dowolnych a
1
, a
2
, b
1
, b
2
∈ R.
Twierdzenie 2.1. Struktura algebraiczna (C, +, ·, (0, 0), (1, 0)) two-
rzy ciało.
Dowód. Sprawdzamy kolejno prawdziwość wszystkich aksjomatów
ciała. Niech a, b, a
1
, a
2
, a
3
, b
1
, b
2
, b
3
b
,
ed
,
a dowolnymi liczbami rzeczywi-
stymi.
A1. Na mocy wzoru (2.1) i przemienności dodawania liczb rzeczy-
wistych
(a
2
, b
2
)+(a
1
, b
1
) = (a
2
+a
1
, b
2
+b
1
) = (a
1
+a
2
, b
1
+b
2
) = (a
1
, b
1
)+(a
2
, b
2
).
A2. Na mocy wzoru (2.1) i ł
,
aczności dodawania liczb rzeczywistych
[(a
1
, b
1
) + (a
2
, b
2
)] + (a
3
, b
3
) = (a
1
+ a
2
, b
1
+ b
2
) + (a
3
, b
3
) =
([a
1
+ a
2
] + a
3
, [b
1
+ b
2
] + b
3
) = (a
1
+ [a
2
+ a
3
], b
1
+ [b
2
+ b
3
]) = (a
1
, b
1
) +
(a
2
+ a
3
, b
2
+ b
3
) = (a
1
, b
1
) + [(a
2
, b
2
) + (a
3
, b
3
)].
A3. Na mocy wzoru (2.1) i tego, że 0 jest elementem neutralnym
dodawania liczb rzeczywistych (a, b) + (0, 0) = (a + 0, b + 0) = (a, b).
18
Ciało liczb zespolonych I
19
A4. Na mocy wzoru (2.1) (a, b) + (−a, −b) = (a + (−a), b + (−b)) =
(0, 0).
A5. Na mocy wzoru (2.2) i przemienności mnożenia liczb rzeczy-
wistych (a
2
, b
2
) · (a
1
, b
1
) = (a
2
· a
1
− b
2
· b
1
, a
2
· b
1
+ a
1
· b
2
) =
(a
1
· a
2
− b
1
· b
2
, a
1
· b
2
+ a
2
· b
1
) = (a
1
, b
1
) · (a
2
, b
2
).
A6. Na mocy wzoru (2.2), ł
,
aczności i przemienności mnożenia
liczb rzeczywistych, a także rozdzielności mnożenia liczb rzeczywistych
wzgl
,
edem dodawania (odejmowania) liczb rzeczywistych
[(a
1
, b
1
) · (a
2
, b
2
)] · (a
3
, b
3
) = (a
1
a
2
− b
1
b
2
, a
1
b
2
+ a
2
b
1
) · (a
3
, b
3
) =
([a
1
a
2
− b
1
b
2
] · a
3
− [a
1
b
2
+ a
2
b
1
] · b
3
, [a
1
a
2
− b
1
b
2
] · b
3
+ a
3
· [a
1
b
2
+ a
2
b
1
]) =
(a
1
a
2
a
3
− b
1
b
2
a
3
− a
1
b
2
b
3
− a
2
b
1
b
3
, a
1
a
2
b
3
− b
1
b
2
b
3
+ a
3
a
1
b
2
+ a
3
a
2
b
1
) oraz
(a
1
, b
1
) · [(a
2
, b
2
) · (a
3
, b
3
)] = (a
1
, b
1
) · (a
2
a
3
− b
2
b
3
, a
2
b
3
+ a
3
b
2
) =
(a
1
· [a
2
a
3
− b
2
b
3
] − b
1
· [a
2
b
3
+ a
3
b
2
], a
1
· [a
2
b
3
+ a
3
b
2
] + [a
2
a
3
− b
2
b
3
] · b
1
) =
(a
1
a
2
a
3
− a
1
b
2
b
3
− b
1
a
2
b
3
− b
1
a
3
b
2
, a
1
a
2
b
3
+ a
1
a
3
b
2
+ a
2
a
3
b
1
− b
2
b
3
b
1
).
Zatem (a
1
, b
1
) · [(a
2
, b
2
) · (a
3
, b
3
)] = [(a
1
, b
1
) · (a
2
, b
2
)] · (a
3
, b
3
).
A7. Na mocy wzoru (2.2) i różnych praw działań na liczbach rze-
czywistych (jakich?) (a
1
, b
1
) · (a, 0) = (a
1
· a − b
1
· 0, a
1
· 0 + a · b
1
) =
(a · a
1
, a · b
1
), wi
,
ec w szczególności dla a = 1: (a
1
, b
1
) · (1, 0) = (a
1
, b
1
),
gdyż 1 jest elementem neutralnym mnożenia liczb rzeczywistych.
A8. Na mocy wzorów (2.1) i (2.2) oraz różnych praw działań aryt-
metycznych na liczbach rzeczywistych (jakich?)
(a
1
, b
1
) · [(a
2
, b
2
) + (a
3
, b
3
)] = (a
1
, b
1
) · (a
2
+ a
3
, b
2
+ b
3
) =
(a
1
· [a
2
+ a
3
] − b
1
· [b
2
+ b
3
], a
1
· [b
2
+ b
3
] + [a
2
+ a
3
] · b
1
) =
(a
1
a
2
+ a
1
a
3
− b
1
b
2
− b
1
b
3
, a
1
b
2
+ a
1
b
3
+ a
2
b
1
+ a
3
b
1
) =
(a
1
a
2
− b
1
b
2
, a
1
b
2
+ a
2
b
1
) + (a
1
a
3
− b
1
b
3
, a
1
b
3
+ a
3
b
1
) = (a
1
, b
1
) · (a
2
, b
2
) +
(a
1
, b
1
) · (a
3
, b
3
).
A9. Niech (a, b) 6= (0, 0). Wtedy a 6= 0 lub b 6= 0, sk
,
ad a
2
+ b
2
> 0.
Zatem liczby
a
a
2
+b
2
i
−b
a
2
+b
2
s
,
a dobrze określone oraz ze wzoru (2.2)
(a, b)·(
a
a
2
+b
2
,
−b
a
2
+b
2
) = (a·
a
a
2
+b
2
−b·
(−b)
a
2
+b
2
, a
(−b)
a
2
+b
2
+
a
a
2
+b
2
·b) = (
a
2
+b
2
a
2
+b
2
, 0) =
(1, 0).
Otrzymane w ten sposób ciało oznaczamy przez C i nazywamy
ciałem liczb zespolonych. Elementy ciała C nazywamy liczbami
zespolonymi i oznaczamy literami: z, w, z
1
, z
2
itd. Geometrycznie
liczby zespolone można wi
,
ec traktować jako punkty na płaszczyźnie.

20
Wykłady z algebry liniowej I
Ze wzoru (2.1) wynika, że liczby zespolone dodajemy analogicznie jak
wektory na płaszczyźnie zaczepione w pocz
,
atku układu współrz
,
ednych.
Z tego powodu liczb
,
e zespolon
,
a (a, b) możemy utożsamić z wektorem
o pocz
,
atku w punkcie (0, 0) i końcu w punkcie (a, b). Interpretacja geo-
metryczna mnożenia liczb zespolonych jest bardziej złożona (podamy
j
,
a później).
Z określeń (2.1) i (2.2) i z dowodu twierdzenia 2.1 wynika od razu,
że dla dowolnych liczb rzeczywistych a, b
(a, 0) = (b, 0) ⇔ a = b,
(a, 0) + (b, 0) = (a + b, 0),
(a, 0) · (b, 0) = (a · b, 0),
−(a, 0) = (−a, 0),
(a, 0)
−1
= (
1
a
, 0) dla a 6= 0.
Z tego powodu dla liczb rzeczywistych a można dokonać utożsa-
mienia:
(a, 0) ≡ a.
(2.3)
Przy takim utożsamieniu R ⊆ C.
Liczb
,
e zespolon
,
a
i = (0, 1)
(2.4)
nazywamy jednostk
,
a urojon
,
a. Zachodzi dla niej bardzo ważny wzór:
i
2
= −1.
(2.5)
Rzeczywiście, na mocy wzoru (2.2):
i
2
= (0, 1) · (0, 1) = (0 · 0 − 1 · 1, 0 · 1 + 0 · 1) = (−1, 0) ≡ −1.
Z dowodu twierdzenia 2.1 dla dowolnych liczb rzeczywistych a, b
mamy, że (a, b) = (a, 0) + (0, b) = (a, 0) + (b, 0) · (0, 1) ≡ a + bi. Zatem
dla a, b ∈ R można dokonać utożsamienia:
(a, b) ≡ a + bi.
(2.6)
Otrzymujemy w ten sposób postać algebraiczn
,
a a + bi liczby zespolonej
(a, b).
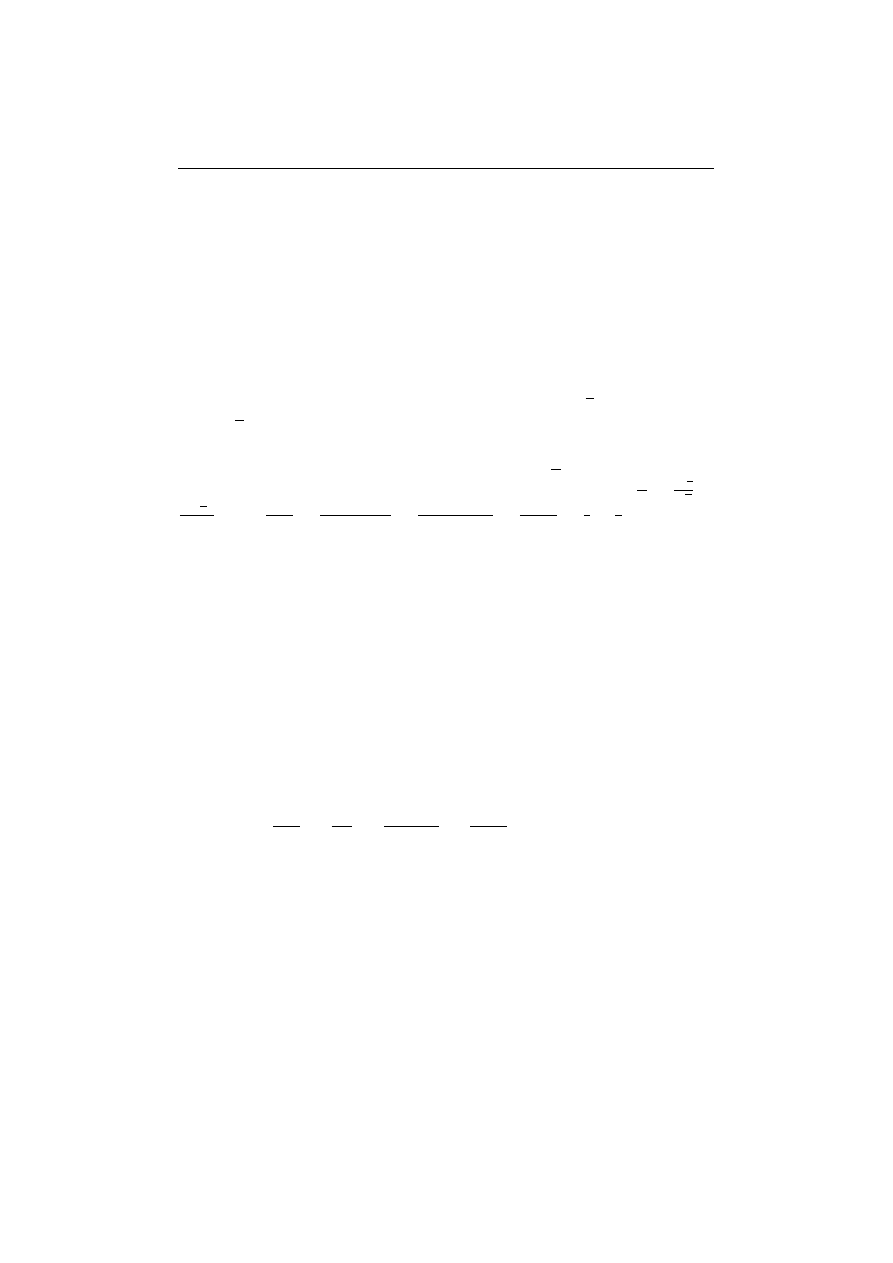
Ciało liczb zespolonych I
21
Dodawanie, odejmowanie i mnożenie liczb zespolonych zapisanych
w postaci algebraicznej wykonuje si
,
e zatem tak samo jak dodawanie,
odejmowanie i mnożenie wielomianów zmiennej i, przy czym należy
pami
,
etać o tym, że w miejsce i
2
należy zawsze podstawić (−1). Np.
(1+2i)·(3−i) = 3−i+6i−2i
2
= 3+5i+2 = 5+5i, (1+2i)+(3−i) = 4+i,
(1 + 2i) − (3 − i) = −2 + 3i.
Natomiast przy dzieleniu liczb zepolonych wygodnie jest wykorzy-
stywać tzw. liczby sprz
,
eżone. Jeżeli a i b s
,
a liczbami rzeczywistymi, to
liczb
,
a sprz
,
eżon
,
a do liczby z = a + bi nazywamy liczb
,
e z = a − bi. Wów-
czas z · z = (a + bi) · (a − bi) = a
2
− b
2
i
2
= a
2
− b
2
· (−1) = a
2
+ b
2
∈ R.
Zatem aby podzielić liczb
,
e zespolon
,
a w przez liczb
,
e zespolon
,
a
z 6= 0 należy licznik i mianownik ułamka
w
z
pomnożyć przez
liczb
,
e sprz
,
eżon
,
a z mianownikiem tego ułamka, czyli
w
z
=
w·z
z·z
=
w·z
a
2
+b
2
. Np.
2+3i
1+i
=
(2+3i)·(1−i)
(1+i)·(1−i)
=
2−2i+3i−3i
2
1
2
+1
2
=
2+i+3
2
=
5
2
+
1
2
i.
Przykład 2.1. Wyznaczymy wszystkie liczby zespolone z speł-
niaj
,
ace równanie:
(1 + 2i) · (z − i) + (4i − 3) · (1 − i · z) + 1 + 7i = 0.
Mamy, że (1 + 2i) · (−i) = −i − 2 · (−1) = 2 − i oraz (4i − 3) · (−i) =
−4 · (−1) + 3i = 4 + 3i. Zatem nasze równanie przybiera postać:
(1 + 2i) · z + 2 − i + 4i − 3 + (4 + 3i) · z + 1 + 7i = 0,
czyli
(5 + 5i) · z = −10i.
Zatem z =
−10i
5+5i
=
−2i
1+i
=
−2i·(1−i)
1
2
+1
2
=
−2i−2
2
= −1 − i. St
,
ad jedynym
rozwi
,
azaniem naszego równania w liczbach zespolonych jest z = −1−i.
Jeżeli a, b s
,
a liczbami rzeczywistymi oraz z = a + bi, to cz
,
eści
,
a rze-
czywist
,
a liczby zespolonej z nazywamy liczb
,
e re(z) = a, zaś cz
,
eści
,
a
urojon
,
a liczby z nazywamy liczb
,
e (rzeczywist
,
a!)
im(z) = b.
Np.
re(i) = 0 oraz im(i) = 1. Łatwo zauważyć, że re(z+w) = re(z)+re(w)

22
Wykłady z algebry liniowej I
dla dowolnych liczb zespolonych z, w. Ponadto z tych oznaczeń wy-
nika natychmiast, że dwie liczby zespolone zapisane w postaci
algebraicznej s
,
a równe wtedy i tylko wtedy, gdy ich cz
,
eści
rzeczywiste s
,
a równe i ich cz
,
eści urojone s
,
a równe.
Przykład 2.2. Wyznaczymy wszystkie liczby rzeczywiste x, y
takie, że
x · (1 − i) · (2 + i) + 2y · (2 − i)
2
= −6 + 8i.
W tym celu obliczamy najpierw (1−i)·(2+i) = 2+i−2i−(−1) = 3−i
oraz (2 − i)
2
= 4 − 4i + (−1) = 3 − 4i. Zatem nasze równanie przybiera
postać:
x · (3 − i) + y · (6 − 8i) = −6 + 8i,
czyli
(3x + 6y) + (−x − 8y) · i = −6 + 8i.
Zatem z porównania cz
,
eści rzeczywistych i urojonych uzyskujemy, że
liczby x, y musz
,
a spełniać układ równań:
3x+ 6y = −6
−x− 8y = 8
.
Z drugiego równania wyliczamy x = −8y − 8 i podstawiamy do rów-
nania pierwszego. W ten sposób uzyskamy, że y = −1 oraz x = 0.
Modułem liczby zespolonej z = a + bi, gdzie a, b ∈ R nazywamy
liczb
,
e rzeczywist
,
a nieujemn
,
a
|z| =
√
a
2
+ b
2
.
(2.7)
Z tych określeń mamy od razu, że
re(z) ≤ |z| oraz im(z) ≤ |z|,
(2.8)
z · z = |z|
2
.
(2.9)
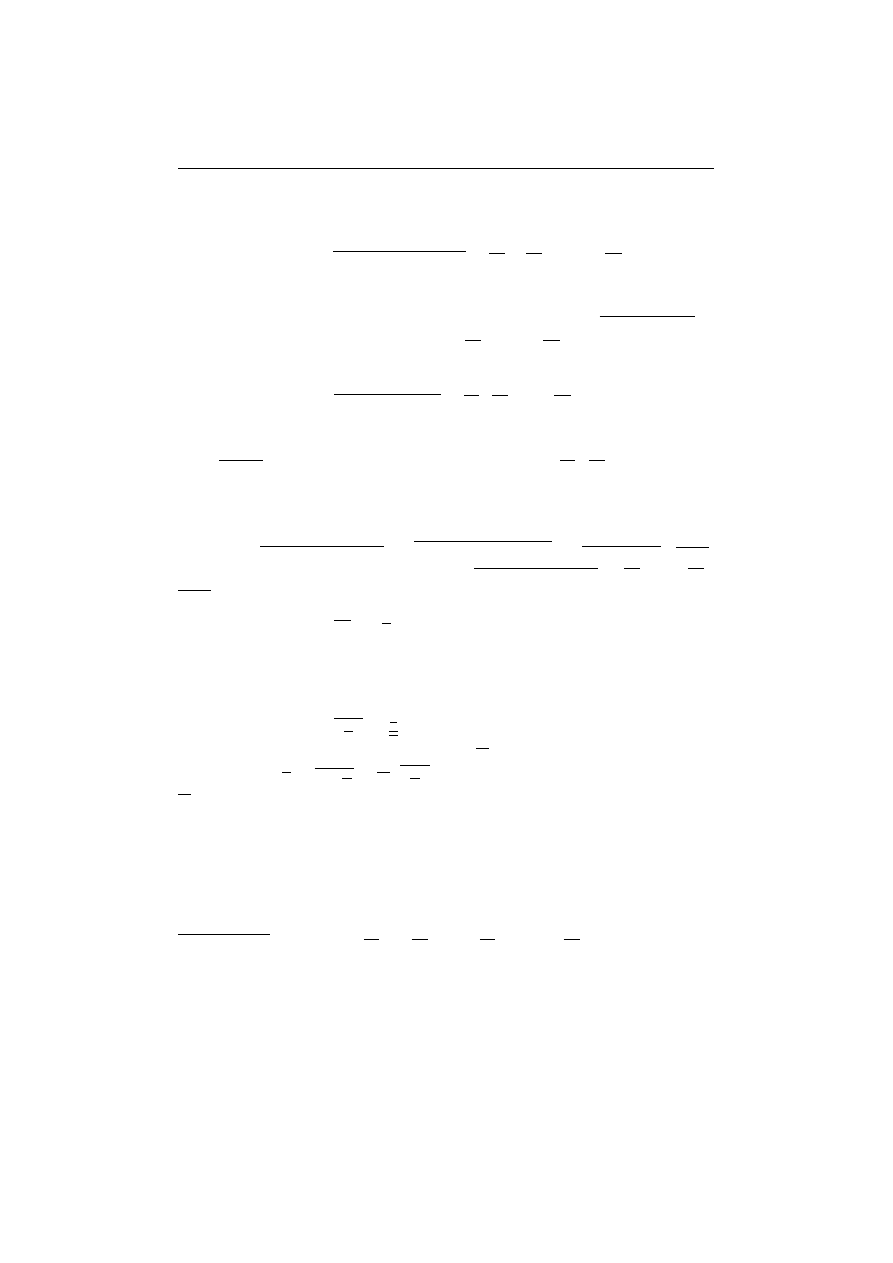
Ciało liczb zespolonych I
23
2.2
Własności sprz
,
egania liczb zespolonych
Własność 2.1. z
1
+ z
2
+ . . . + z
n
= z
1
+ z
2
+ . . . + z
n
.
Dowód. Istniej
,
a liczby rzeczywiste a
1
, . . . , a
n
, b
1
, . . . , b
n
takie, że
z
k
= a
k
+ b
k
i dla k = 1, . . . , n. Zatem z
1
+ . . . + z
n
= (a
1
+ b
1
i) +
. . . + (a
n
+ b
n
i) = (a
1
+ . . . + a
n
) + (b
1
+ . . . + b
n
)i, sk
,
ad z
1
+ . . . + z
n
=
(a
1
+ . . . + a
n
) − (b
1
+ . . . + b
n
)i oraz z
1
+ . . . + z
n
= (a
1
− b
1
i) + . . . +
(a
n
− b
n
i) = (a
1
+ . . . + a
n
) − (b
1
+ . . . + b
n
)i, sk
,
ad mamy tez
,
e.
Własność 2.2. z
1
· z
2
· . . . · z
n
= z
1
· z
2
· . . . · z
n
.
Dowód. Dla n = 2 istniej
,
a liczby rzeczywiste a
1
, a
2
, b
1
, b
2
takie, że
z
1
= a
1
+b
1
i oraz z
2
= a
2
+b
2
i. St
,
ad z
1
·z
2
= (a
1
a
2
−b
1
b
2
)+(a
1
b
2
+a
2
b
1
)i,
czyli z
1
· z
2
= (a
1
a
2
− b
1
b
2
) − (a
1
b
2
+ a
2
b
1
)i oraz z
1
· z
2
= (a
1
− b
1
i) ·
(a
2
− b
2
i) = (a
1
a
2
− b
1
b
2
) − (a
1
b
2
+ a
2
b
1
)i, czyli teza zachodzi dla n = 2.
Załóżmy teraz, że teza zachodzi dla pewnego naturalnego n. Wówczas
dla liczb zespolonych z
1
, . . . , z
n
, z
n+1
na mocy pierwszej cz
,
eści dowodu
mamy, że z
1
· . . . · z
n
· z
n+1
= (z
1
· . . . · z
n
) · z
n+1
= z
1
· . . . · z
n
· z
n+1
,
wi
,
ec na mocy założenia indukcyjnego z
1
· . . . · z
n
· z
n+1
= z
1
· . . . · z
n
·
z
n+1
. St
,
ad na mocy zasady indukcji mamy tez
,
e.
Własność 2.3. z
n
= (z)
n
.
Dowód. Wystarczy w poprzednim wzorze podstawić
z = z
1
= . . . = z
n
.
Własność 2.4.
z
w
=
z
w
, w 6= 0.
Dowód. Ponieważ w 6= 0, wi
,
ec też w 6= 0 (dlaczego?). Z własności
2.2 mamy, że z = w ·
z
w
= w ·
z
w
, sk
,
ad po podzieleniu obu stron przez
w uzyskamy tez
,
e.
2.3
Własności modułu liczb zespolonych
Własność 2.5. |z
1
· z
2
· . . . · z
n
| = |z
1
| · |z
2
| · . . . · |z
n
|.
Dowód. Na mocy (2.9) i własności 2.2: |z
1
· . . . · z
n
|
2
= (z
1
· . . . · z
n
) ·
(z
1
· . . . · z
n
) = z
1
·. . .·z
n
·z
1
·. . .·z
n
= (z
1
·z
1
)·. . .·(z
n
·z
n
) = |z
1
|
2
·. . .·|z
n
|
2
,
sk
,
ad po spierwiastkowaniu obu stron uzyskamy tez
,
e.
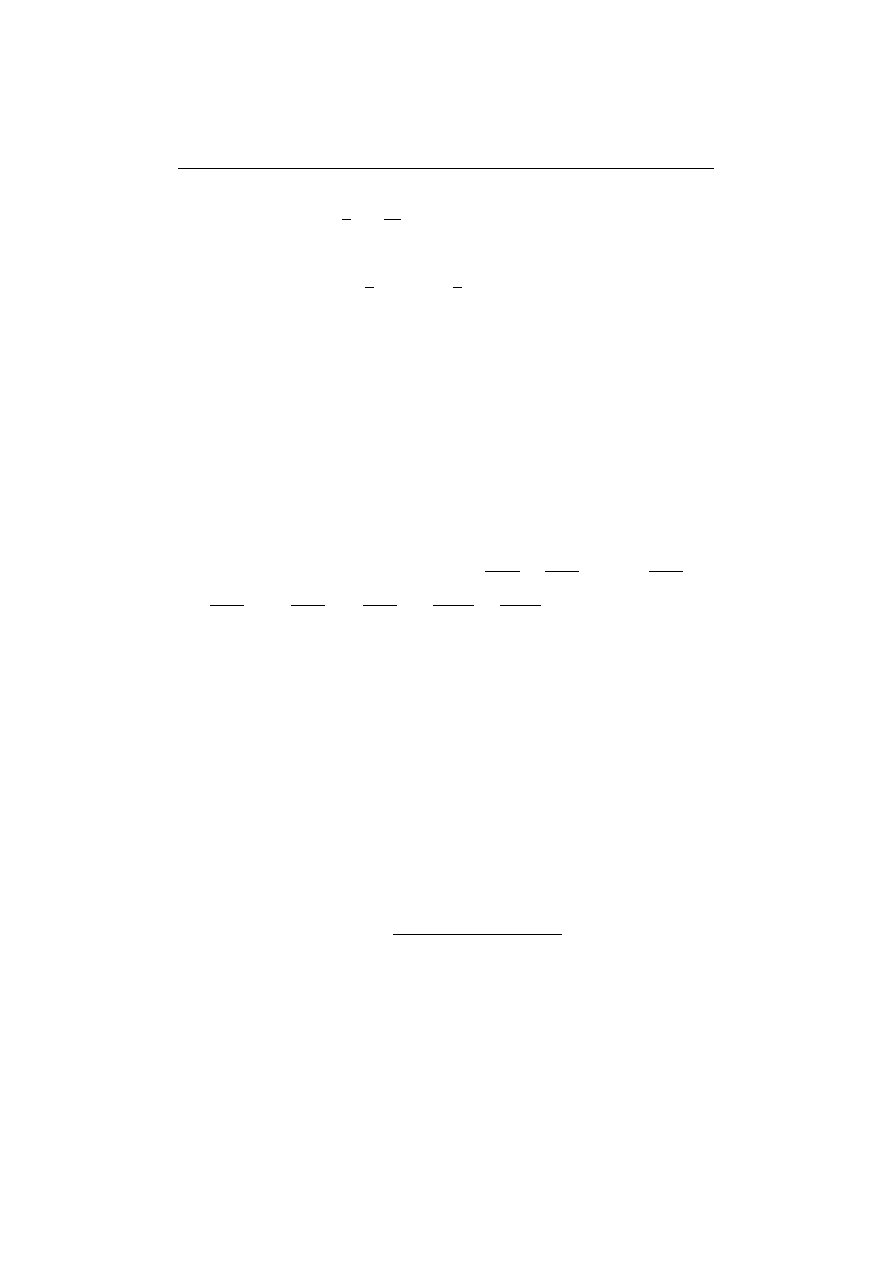
24
Wykłady z algebry liniowej I
Własność 2.6.
z
w
=
|z|
|w|
, w 6= 0.
Dowód. Ponieważ w 6= 0, wi
,
ec też |w| 6= 0 (dlaczego?). Na mocy
własności 2.5 |z| =
w ·
z
w
= |w| ·
z
w
, wi
,
ec po podzieleniu obu stron
przez |w| uzyskamy tez
,
e.
Własność 2.7. |z
n
| = |z|
n
.
Dowód. Wystarczy podstawić z = z
1
= . . . = z
n
w własności
2.5.
Własność 2.8. |z
1
+ z
2
+ . . . + z
n
| ≤ |z
1
| + |z
2
| + . . . + |z
n
|.
Dowód. Stosujemy indukcj
,
e wzgl
,
edem n. Niech n = 2. Jeśli
z
1
+ z
2
= 0, to nasz wzór zachodzi. Załóżmy dalej, że z
1
+ z
2
6= 0.
Wtedy |z
1
+ z
2
| > 0. Ponadto 1 = re
z
1
z
1
+z
2
+
z
2
z
1
+z
2
= re
z
1
z
1
+z
2
+
re
z
2
z
1
+z
2
≤
z
1
z
1
+z
2
+
z
2
z
1
+z
2
=
|z
1
|
|z
1
+z
2
|
+
|z
2
|
|z
1
+z
2
|
, sk
,
ad po pomnożeniu
obu stron przez |z
1
+ z
2
| uzyskamy tez
,
e dla n = 2.
Załóżmy teraz, że nasza nierówność zachodzi dla pewnej liczby na-
turalnej n i niech z
1
, . . . , z
n+1
b
,
ed
,
a dowolnymi liczbami zespolonymi.
Wówczas z pierwszej cz
,
eści dowodu i z założenia indukcyjnego mamy,
że |z
1
+ . . . + z
n+1
| = |(z
1
+ . . . + z
n
) + z
n+1
| ≤ |z
1
+ . . . + z
n
| + |z
n+1
| ≤
|z
1
|+. . .+|z
n
|+|z
n+1
|, czyli nasza nierówność zachodzi dla liczby n+1.
St
,
ad na mocy zasady indukcji mamy tez
,
e.
Własność 2.9. |z − w| = odległość punktu z od punktu w.
Dowód. Istniej
,
a liczby rzeczywiste a
1
, a
2
, b
1
, b
2
takie, że z = a
1
+
b
1
i ≡ (a
1
, b
1
) oraz w = a
2
+ b
2
i ≡ (a
2
, b
2
). Ponadto z − w = (a
1
− a
2
) +
(b
1
− b
2
)i, wi
,
ec |z − w| =
p(a
1
− a
2
)
2
+ (b
1
− b
2
)
2
. Zatem z geometrii
analitycznej mamy tez
,
e.
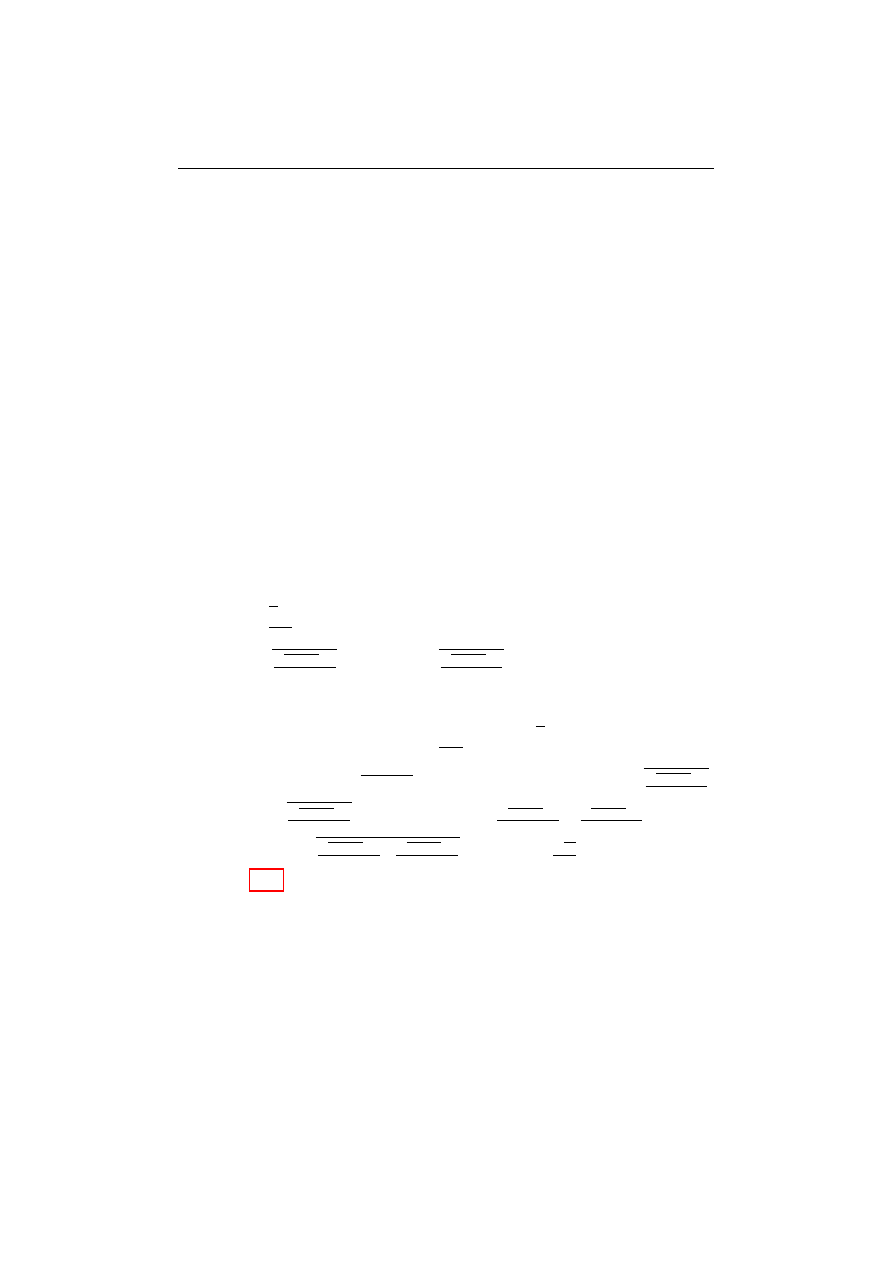
Ciało liczb zespolonych I
25
2.4
Pierwiastek kwadratowy z liczb
zespolonych
Funkcj
,
e znak liczby rzeczywistej x określamy nast
,
epuj
,
aco:
sgn(x) =
1 je´sli x > 0
0 je´sli x = 0
−1 je´sli x < 0
.
(2.10)
Łatwo zauważyć, że |x| = sgn(x)·x dla każdego x ∈ R oraz (sgn(x))
2
= 1
dla x 6= 0.
Niech ω = x + yi, gdzie x, y ∈ R. Wtedy ω
2
= (x + yi)
2
=
x
2
+ 2xyi + y
2
· (−1) = (x
2
− y
2
) + 2xyi. Zatem dla a, b ∈ R:
ω
2
= a + bi ⇔
x
2
− y
2
= a
2xy = b
.
(2.11)
Twierdzenie 2.2. Niech a, b ∈ R oraz
ω =
√
a
je´sli b = 0 i a ≥ 0
√
−a · i
je´sli b = 0 i a < 0
q
√
a
2
+b
2
+a
2
+ sgn(b) ·
q
√
a
2
+b
2
−a
2
· i je´sli b 6= 0
.
(2.12)
Wtedy ω
2
= a + bi. Ponadto {z ∈ C : z
2
= a + bi} = {ω, −ω}.
Dowód. Dla a ≥ 0 i b = 0 mamy, że (
√
a)
2
= a = a + bi. Dla
a < 0 i b = 0 jest −a > 0 oraz (
√
−a · i)
2
= (−a) · (−1) = a = a + bi.
Dla b 6= 0 mamy, że
√
a
2
+ b
2
± a > 0. Oznaczmy x =
q
√
a
2
+b
2
+a
2
,
y = sgn(b) ·
q
√
a
2
+b
2
−a
2
. Wtedy x
2
− y
2
=
√
a
2
+b
2
+a
2
−
√
a
2
+b
2
−a
2
= a oraz
2xy = 2sgn(b) ·
q
√
a
2
+b
2
+a
2
·
√
a
2
+b
2
−a
2
= 2sgn(b) ·
√
b
2
2
= sgn(b) · |b| = b.
Zatem z (2.11) mamy, że (x + yi)
2
= a + bi. Kończy to dowód pierwszej
cz
,
eści twierdzenia.
Zauważmy, że (−ω)
2
= ω
2
= a + bi. Jeśli zaś z ∈ C jest takie, że
z
2
= a + bi, to z
2
= ω
2
, sk
,
ad 0 = z
2
− ω
2
= (z − ω) · (z + ω), wi
,
ec
z = ω lub z = −ω. Zatem twierdzenie jest udowodnione.

26
Wykłady z algebry liniowej I
Liczb
,
e zespolon
,
a ω nazywamy pierwiastkiem kwadratowym z liczby
zespolonej z, jeżeli ω
2
= z. Twierdzenie 2.2 mówi zatem, że z każdej
liczby zespolonej można wyci
,
agn
,
ać pierwiastek kwadratowy i podaje
wzory na te pierwiastki. Czasami pierwiastek kwadratowy z liczby
zespolonej z oznaczamy przez
√
z, ale należy być bardzo ostrożnym
przy stosowaniu tego oznaczenia.
Z twierdzenia 2.2 wynika też, że dowolne równanie kwadratowe
az
2
+ bz + c = 0,
(2.13)
o współczynnikach zespolonych a, b, c, a 6= 0 posiada pierwiastek ze-
spolony. Mianowicie oznaczmy ∆ = b
2
− 4ac. Wtedy istnieje liczba
zespolona ω taka, że ω
2
= ∆. Ponadto az
2
+ bz + c = a · [z
2
+
b
a
z +
c
a
] =
a · [(z +
b
2a
)
2
−
b
2
4a
2
+
4ac
4a
2
] = a · [(z +
b
2a
)
2
−
b
2
−4ac
4a
2
] = a · [(z +
b
2a
)
2
−
ω
2
4a
2
] =
a · (z +
b
2a
+
ω
2a
) · (z +
b
2a
−
ω
2a
), sk
,
ad wynika, że wszystkimi pierwiastkami
zespolonymi równania (2.13) s
,
a:
z
1
=
−b−ω
2a
oraz z
2
=
−b+ω
2a
.
Rozdział 3
Ciało liczb zespolonych II
3.1
Postać trygonometryczna liczby
zespolonej
Niech z b
,
edzie niezerow
,
a liczb
,
a zespolon
,
a. Wówczas istniej
,
a liczby
rzeczywiste a, b, takie, że
z = a + bi
(3.1)
oraz a 6= 0 lub b 6= 0.
Liczb
,
e z możemy traktować jako punkt
(a, b) płaszczyzny, którego odległość od punktu (0, 0) jest równa |z| =
√
a
2
+ b
2
.
Oznaczmy przez φ miar
,
e k
,
ata skierowanego jaki tworzy
wektor ~
Oz z osi
,
a OX w orientacji płaszczyzny przeciwnej do ruchów
wskazówek zegara. Wtedy mamy, że φ ∈ [0, 2π) oraz
cos φ =
a
√
a
2
+b
2
sin φ =
b
√
a
2
+b
2
.
(3.2)
Otrzymujemy st
,
ad wzór
z = |z|(cos φ + i sin φ),
(3.3)
który nazywamy postaci
,
a trygonometryczn
,
a liczby zespolonej z. Liczb
,
e
φ nazywamy argumentem głównym liczby z i oznaczamy przez Arg(z).
27

28
Wykłady z algebry liniowej I
Natomiast każd
,
a liczb
,
e rzeczywist
,
a α = φ + 2kπ dla całkowitych k
nazywamy argumentem liczby z i oznaczamy przez arg(z). Oczywiście
dla takich α mamy, że z = |z|(cos α + i sin α). Możemy wi
,
ec napisać
wzór
z = |z|[cos arg(z) + i sin arg(z)].
(3.4)
Na odwrót, niech r b
,
edzie dodatni
,
a liczb
,
a rzeczywist
,
a i niech β b
,
edzie
liczb
,
a rzeczywist
,
a tak
,
a, że z = r(cos β + i sin β). Wówczas |z| = |r| ·
| cos β + i sin β| = r ·
p
sin
2
β + cos
2
β = r, sk
,
ad cos β = cos φ oraz
sin β = sin φ, wi
,
ec z trygonometrii mamy, że istnieje liczba całkowita
k taka, że β = φ + 2kπ.
Dla niezerowych liczb zespolonych z, w równość arg(z) = arg(w)
b
,
edziemy dalej rozumieli w ten sposób, że liczby arg(z) i arg(w) różni
,
a
si
,
e jedynie o całkowit
,
a wielokrotność liczby 2π.
3.2
Własności argumentu liczby
zespolonej
Własność 3.1. Dla dowolnych niezerowych liczb zespolonych
z
1
, z
2
, . . . , z
n
zachodzi wzór:
arg(z
1
· z
2
· . . . · z
n
) = arg(z
1
) + arg(z
2
) + . . . + arg(z
n
).
(3.5)
Dowód. Stosujemy indukcj
,
e wzgl
,
edem n. Dla n = 2 oznaczmy
arg(z
1
) = α, arg(z
2
) = β. Wtedy z
1
= |z
1
|(cos α + i sin α) oraz z
2
=
|z
2
|(cos β +i sin β). Zatem z
1
·z
2
= |z
1
|·|z
2
|((cos α·cos β −sin α·sin β)+
i(cos α·sin β +cos β ·sin α)) = |z
1
|·|z
2
|[cos(α+β)+i sin(α+β)], na mocy
znanych wzorów trygonometrycznych. St
,
ad rzeczywiście arg(z
1
· z
2
) =
arg(z
1
) + arg(z
2
) i wzór (3.5) zachodzi dla n = 2.
Niech teraz wzór (3.5) zachodzi dla pewnej liczby naturalnej n ≥ 2.
Weźmy dowolne niezerowe liczby zespolone z
1
, . . . , z
n
, z
n+1
. Wówczas
z pierwszej cz
,
eści dowodu i z założenia indukcyjnego otrzymamy, że
arg(z
1
· . . . · z
n
· z
n+1
) = arg((z
1
· . . . · z
n
) · z
n+1
) = arg(z
1
· . . . · z
n
) +
arg(z
n+1
) = arg(z
1
)+. . .+arg(z
n
)+arg(z
n+1
), czyli wzór (3.5) zachodzi
dla n + 1.

Ciało liczb zespolonych II
29
Zatem na mocy zasady indukcji wzór (3.5) zachodzi dla dowolnego
naturalnego n ≥ 2.
Własność 3.2. Podstawiaj
,
ac z
1
= z
2
= . . . = z
n
= cos α + i sin α
we wzorze (3.5) i wykorzystuj
,
ac (3.4) uzyskujemy natychmiast tzw.
wzór de Moivre’a:
(cos α + i sin α)
n
= cos nα + i sin nα dla n = 1, 2, 3, . . . .
(3.6)
Własność 3.3. Dla dowolnych niezerowych liczb zespolonych z,
w zachodzi wzór:
arg
z
w
= arg(z) − arg(w).
(3.7)
Dowód. Ponieważ z = w ·
z
w
, wi
,
ec ze wzoru (3.5) (dla n = 2)
uzyskujemy, że arg(z) = arg(w) + arg
z
w
, sk
,
ad mamy tez
,
e.
Własność 3.4. Dla dowolnej niezerowej liczby zespolonej z mamy,
że
arg(z) = arg
1
z
= − arg(z).
(3.8)
Dowód.
Zauważmy, że 0 jest argumentem dowolnej dodatniej
liczby rzeczywistej. Ponadto z · z = |z|
2
, wi
,
ec ze wzoru (3.5):
0 = arg(z · z) = arg(z) + arg(z), sk
,
ad arg(z) = − arg(z). Ponadto ze
wzoru (3.7): arg
1
z
= arg(1) − arg(z) = 0 − arg(z) = − arg(z). Zatem
wzór (3.8) jest udowodniony.
Własność 3.5. Dla dowolnej niezerowej liczby zespolonej z zacho-
dzi wzór:
arg(−z) = π + arg(z).
(3.9)
Dowód. Zauważmy, że π jest argumentem liczby (-1), wi
,
ec ze
wzoru (3.5) arg(−z) = arg(−1) + arg(z) = π + arg(z).
Zadanie 3.1. Pokazać, że dla dowolnej niezerowej liczby zespolonej
z:
(a) arg(−
z) = π − arg(z), (b) arg(iz) =
π
2
+ arg(z).

30
Wykłady z algebry liniowej I
3.3
Interpretacja geometryczna mnożenia
liczb zespolonych
Ze wzoru (3.5) otrzymujemy natychmiast, że aby pomnożyć niezerowe
liczby zespolone należy pomnożyć ich moduły i dodać ich argumenty.
Niech z
0
b
,
edzie ustalon
,
a niezerow
,
a liczb
,
a zespolon
,
a.
Wówczas ze
wzoru (3.5) dla n = 2 wynika, że przekształcenie z 7→ z
0
· z dla zespo-
lonych z jest złożeniem obrotu o k
,
at o mierze Arg(z
0
) i jednokładności
o środku O i skali |z
0
|.
3.4
Pierwiastkowanie liczb zespolonych
Niech n b
,
edzie dowoln
,
a liczb
,
a naturaln
,
a. Pierwiastkiem n-tego stop-
nia z liczby zespolonej z nazywamy każd
,
a tak
,
a liczb
,
e zespolon
,
a ω,
że ω
n
= z. Łatwo zauważyć, że jedynym pierwiastkiem n-tego stopnia
z liczby 0 jest 0. Dla niezerowych liczb zespolonych zachodzi natomiast
nast
,
epuj
,
ace
Twierdzenie 3.1. Jeśli z jest niezerow
,
a liczb
,
a zespolon
,
a oraz z =
|z|(cos φ + i sin φ), to istnieje dokładnie n różnych pierwiastków n-tego
stopnia z liczby z i wszystkie te pierwiastki daj
,
a si
,
e uj
,
ać wzorem
ω
k
=
n
p|z|
cos
φ + 2kπ
n
+ i sin
φ + 2kπ
n
, k = 0, 1, . . . , n − 1.
(3.10)
Dowód. Ze wzoru de Moivre’a dla k = 0, 1, . . . , n − 1 mamy, że
ω
n
k
= |z|[cos(φ + 2kπ) + i sin(φ + 2kπ)] = |z|(cos φ + i sin φ) = z, wi
,
ec
liczby (3.10) s
,
a pierwiastkami n-tego stopnia z liczby z. Niech teraz
k, l ∈ {0, 1, . . . , n − 1} b
,
ed
,
a takie, że ω
k
= ω
l
. Wówczas istnieje liczba
całkowita t taka, że
φ+2kπ
n
−
φ+2lπ
n
= 2tπ, sk
,
ad k − l = t · n. Ale
−n < k − l < n, wi
,
ec t = 0 i k = l. Zatem liczby (3.10) s
,
a parami
różne.
Niech teraz ω b
,
edzie pierwiastkiem n-tego stopnia z liczby z. Po-
nieważ z 6= 0, wi
,
ec też ω 6= 0. Zatem istnieje liczba rzeczywista α

Ciało liczb zespolonych II
31
taka, że ω = |ω|(cos α + i sin α). St
,
ad ze wzoru de Moivre’a mamy, że
z = ω
n
= |ω|
n
(cos nα + i sin nα). Zatem |ω|
n
= |z| oraz nα = φ + 2sπ
dla pewnego całkowitego s. Dziel
,
ac s przez n z reszt
,
a uzyskamy, że
istnieje liczba całkowita q i istnieje k ∈ {0, 1, . . . , n − 1} takie, że
s = qn + k. Zatem α =
φ+2kπ
n
+ 2qπ, sk
,
ad wynika, że ω = ω
k
.
Kończy to dowód naszego twierdzenia.
3.5
Pierwiastki pierwotne z jedności
Niech n b
,
edzie ustalon
,
a liczb
,
a naturaln
,
a. Ponieważ 1 = cos 0 + i sin 0,
wi
,
ec ze wzoru (3.10) otrzymujemy n różnych pierwiastków n-tego stop-
nia z 1:
k
= cos
2kπ
n
+ i sin
2kπ
n
,
dla k = 0, 1, . . . , n − 1.
(3.11)
Zatem zbiór C
n
= {z ∈ C : z
n
= 1} posiada dokładnie n elementów
oraz
C
n
= {cos
2kπ
n
+ i sin
2kπ
n
:
k = 0, 1, . . . , n − 1}.
(3.12)
Liczb
,
e zespolon
,
a ω nazywamy pierwiastkiem pierwotnym n-tego stop-
nia z jedności, jeżeli ω
n
= 1 oraz nie istnieje liczba naturalna m < n
taka, że ω
m
= 1.
Twierdzenie 3.2. Dla liczby zespolonej ω nast
,
epuj
,
ace warunki s
,
a
równoważne:
(i) ω jest pierwiastkiem pierwotnym n-tego stopnia z jedności;
(ii) ω =
k
dla pewnego k wzgl
,
ednie pierwszego z liczb
,
a n;
(iii) C
n
= {1, ω, ω
2
, . . . , ω
n−1
}.
Dowód. (i)⇒(ii). Załóżmy, że ω jest pierwiastkiem pierwotnym
n-tego stopnia z jedności. Zatem ω
n
= 1 oraz ω
s
6= 1 dla wszystkich
liczb naturalnych s < n. Ponadto istnieje k ∈ {0, 1, . . . , n − 1} takie,
że ω =
k
. Załóżmy, że liczby k i n nie s
,
a wzgl
,
ednie pierwsze. Wówczas
istnieje liczba naturalna d > 1 oraz istniej
,
a liczby całkowite l i m > 0
takie, że k = dl oraz n = dm. St
,
ad m jest liczb
,
a naturaln
,
a mniejsz
,
a od

32
Wykłady z algebry liniowej I
n oraz ze wzoru de Moivre’a ω
m
= cos
2kmπ
n
+ i sin
2kmπ
n
= cos
2ldmπ
dm
+
i sin
2ldmπ
dm
= cos(2lπ) + i sin(2lπ) = 1 i mamy sprzeczność.
(ii)⇒(iii). Załóżmy, że ω =
k
dla pewnego k ∈ {0, 1, . . . , n − 1}
wzgl
,
ednie pierwszego z liczb
,
a n. Wtedy ω
n
= 1, sk
,
ad dla całkowitych t:
(ω
t
)
n
= (ω
n
)
t
= 1
t
= 1. Zatem {1, ω, ω
2
, . . . , ω
n−1
} ⊆ C
n
. Wystarczy
zatem wykazać, że liczby 1, ω, ω
2
, . . . , ω
n−1
s
,
a parami różne. Załóżmy,
że tak nie jest. Wówczas istniej
,
a p, q ∈ {0, 1, . . . , n − 1} takie, że p > q
oraz ω
p
= ω
q
. St
,
ad 1 = ω
p−q
=
p−q
k
= cos
2k(p−q)π
n
+ i sin
2k(p−q)π
n
na
mocy wzoru de Moivre’a. Zatem istnieje liczba całkowita s taka, że
2k(p−q)π
n
= 2sπ, sk
,
ad n|k(p − q). Ale liczby n i k s
,
a wzgl
,
ednie pierwsze,
wi
,
ec z zasadniczego twierdzenia arytmetyki n|p − q. Ponadto p − q jest
liczb
,
a naturaln
,
a mniejsz
,
a od n, wi
,
ec mamy sprzeczność.
(iii)⇒(i). Załóżmy, że C
n
= {1, ω, ω
2
, . . . , ω
n−1
}. Ponieważ zbiór
C
n
ma dokładnie n elementów, wi
,
ec liczby 1, ω, ω
2
, . . . , ω
n−1
s
,
a parami
różne, sk
,
ad ω
m
6= 1 dla liczb naturalnych m < n oraz ω
n
= 1. Zatem
ω jest pierwiastkiem pierwotnym n-tego stopnia z jedności.
Z powyższego twierdzenia wynika od razu nast
,
epuj
,
acy
Wniosek 3.1. Dla k ∈ {0, 1, . . . , n−1} liczba
k
jest pierwiastkiem
pierwotnym n-tego stopnia z jedności wtedy i tylko wtedy, gdy liczby k
i n s
,
a wzgl
,
ednie pierwsze.
Twierdzenie 3.3 (Zasadnicze Twierdzenie Algebry). Dla do-
wolnej liczby naturalnej n i dla dowolnych liczb zespolonych a
0
, a
1
, . . . ,
a
n
takich, że a
n
6= 0 równanie algebraiczne
a
n
z
n
+ a
n−1
z
n−1
+ . . . + a
1
z + a
0
= 0
posiada pierwiastek zespolony.
Dowód tego twierdzenia jest długi (zostanie podany dopiero na dru-
gim roku).

Rozdział 4
Układy równań liniowych
4.1
Podstawowe pojęcia zwi
,
azane z ukła-
dami równań liniowych
Układem m równań liniowych o niewiadomych x
1
, x
2
, . . ., x
n
nad cia-
łem K nazywamy układ równań postaci:
a
11
x
1
+
a
12
x
2
+ . . . +
a
1n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+ . . . +
a
2n
x
n
=
b
2
. . . . .
.
. . . . .
.
. . .
.
. . . . . .
.
. .
a
m1
x
1
+ a
m2
x
2
+ . . . + a
mn
x
n
= b
m
,
(4.1)
gdzie współczynniki a
ij
(dla i = 1, . . . , m; j = 1, . . . , n) oraz elementy
b
i
(dla i = 1, . . . , m) należ
,
a do ciała K. Układ ten nazywamy jedno-
rodnym, gdy b
1
= b
2
= . . . = b
m
= 0.
Definicja 4.1. Powiemy, że równanie
a
1
x
1
+ a
2
x
2
+ . . . + a
n
x
n
= b
(4.2)
jest kombinacj
,
a liniow
,
a równań układu (4.1), jeżeli istniej
,
a c
1
, c
2
, . . . ,
c
m
∈ K (zwane współczynnikami tej kombinacji) takie, że po pomno-
żeniu stronami i-tego równania przez c
i
dla i = 1, . . . , m i dodaniu
33
34
Wykłady z algebry liniowej I
stronami otrzymanych równań uzyskamy równanie (4.2), tzn.
b =
m
X
i=1
c
i
b
i
oraz a
j
=
m
X
i=1
c
i
a
ij
dla j = 1, 2, . . . , n.
(4.3)
Uwaga 4.1. Zauważmy, że jeśli równanie (4.2) jest kombinacj
,
a
liniow
,
a pewnych równań układu (4.1), to jest ono także kombinacj
,
a
liniow
,
a wszystkich równań tego układu (brakuj
,
ace współczynniki s
,
a
równe 0).
Definicja 4.2. Rozwi
,
azaniem układu (4.1) nazywamy każdy taki
ci
,
ag (p
1
, p
2
, . . . , p
n
) elementów ciała K, że po zast
,
apieniu w równaniach
tego układu niewiadomych x
1
, x
2
, . . . , x
n
elementami p
1
, p
2
, . . . , p
n
otrzymamy równości prawdziwe w ciele K (tj. gdy a
i1
p
1
+ a
i2
p
2
+ . . . +
a
in
p
n
= b
i
dla i = 1, 2, . . . , m).
Twierdzenie 4.1. Każde rozwi
,
azanie układu (4.1) jest rozwi
,
azaniem
każdego równania b
,
ed
,
acego kombinacj
,
a liniow
,
a równań układu (4.1).
Dowód. Załóżmy, że równanie (4.2) jest kombinacj
,
a liniow
,
a o współ-
czynnikach c
1
, c
2
, . . . , c
m
równań układu (4.1) i niech (p
1
, p
2
, . . . , p
n
)
b
,
edzie rozwi
,
azaniem układu (4.1). Wtedy
a
11
p
1
+
a
12
p
2
+ . . . +
a
1n
p
n
=
b
1
a
21
p
1
+
a
22
p
2
+ . . . +
a
2n
p
n
=
b
2
. . . . .
.
. . . . .
.
. . .
.
. . . . .
.
. .
a
m1
p
1
+ a
m2
p
2
+ . . . + a
mn
p
n
= b
m
,
wi
,
ec po pomnożeniu obu stron i-tej równości przez c
i
dla i = 1, . . . , m
i dodaniu stronami otrzymanych równości uzyskamy na mocy wzorów
(4.3), że
a
1
p
1
+ a
2
p
2
+ . . . + a
n
p
n
= b,
czyli (p
1
, p
2
, . . . , p
n
) jest rozwi
,
azaniem równania (4.2).
Definicja 4.3.
Dwa układy równań liniowych (U
1
) i (U
2
) z n
niewiadomymi x
1
, . . . , x
n
nad ciałem K nazywamy równoważnymi, gdy
każde równanie układu (U
1
) jest kombinacj
,
a liniow
,
a równań układu
(U
2
) i odwrotnie. Piszemy wtedy (U
1
) ≡ (U
2
).
Układy równań liniowych
35
Z twierdzenia 4.1 wynika od razu nast
,
epuj
,
ace
Twierdzenie 4.2. Równoważne układy równań liniowych posia-
daj
,
a identyczne zbiory rozwi
,
azań.
Definicja 4.4. Układ równań liniowych z n niewiadomymi x
1
, x
2
,
. . . , x
n
nazywamy sprzecznym, gdy równanie 0·x
1
+0·x
2
+. . .+0·x
n
= 1
jest kombinacj
,
a liniow
,
a równań tego układu.
Ponieważ równanie 0 · x
1
+ 0 · x
2
+ . . . + 0 · x
n
= 1 nie posiada
rozwi
,
azania, wi
,
ec z powyższej definicji oraz z twierdzenia 4.1 wynika
od razu nast
,
epuj
,
ace
Twierdzenie 4.3. Sprzeczny układ równań liniowych nie posiada
rozwi
,
azania.
Lemat 4.1. Załóżmy, że i-te równanie dla i = 1, . . . , k układu
równań
a
0
11
x
1
+ a
0
12
x
2
+ . . . + a
0
1n
x
n
= b
0
1
a
0
21
x
1
+ a
0
22
x
2
+ . . . + a
0
2n
x
n
= b
0
2
. . . . .
.
. . . . .
.
. . .
.
. . . . .
.
.
a
0
k1
x
1
+ a
0
k2
x
2
+ . . . + a
0
kn
x
n
= b
0
k
,
(4.4)
jest kombinacj
,
a liniow
,
a równań układu (4.1) o współczynnikach c
i1
, c
i2
,
. . . , c
im
. Jeżeli równanie (4.2) jest kombinacj
,
a liniow
,
a równań układu
(4.4) o współczynnikach c
1
, c
2
, . . . , c
k
. Wówczas równanie (4.2) jest
kombinacj
,
a liniow
,
a równań układu (4.1) o współczynnikach
k
X
i=1
c
i
c
i1
,
k
X
i=1
c
i
c
i2
, . . . ,
k
X
i=1
c
i
c
im
.
Dowód.
Na mocy (4.3) mamy, że dla i = 1, 2, . . . , k: a
0
ij
=
m
X
t=1
c
it
a
tj
dla j = 1, 2, . . . , n oraz b
0
i
=
m
X
t=1
c
it
b
t
. Ponadto a
j
=
k
X
i=1
c
i
a
0
ij
dla j = 1, 2, . . . , n oraz b =
k
X
i=1
c
i
b
0
i
. Zatem dla j = 1, 2, . . . , n:

36
Wykłady z algebry liniowej I
a
j
=
k
X
i=1
c
i
·
m
X
t=1
c
it
a
tj
!
=
k
X
i=1
m
X
t=1
c
i
c
it
a
tj
=
m
X
t=1
k
X
i=1
c
i
c
it
a
tj
=
m
X
t=1
k
X
i=1
c
i
c
it
!
a
tj
oraz b =
k
X
i=1
c
i
·
m
X
t=1
c
it
b
t
!
=
k
X
i=1
m
X
t=1
c
i
c
it
b
t
=
m
X
t=1
k
X
i=1
c
i
c
it
b
t
=
m
X
t=1
k
X
i=1
c
i
c
it
!
b
t
, sk
,
ad na mocy (4.3) mamy tez
,
e.
Z lematu wynika od razu, że jeśli równanie 0·x
1
+0·x
2
+. . .+0·x
n
=
a, gdzie a 6= 0 jest kombinacj
,
a liniow
,
a równań układu (4.1), to układ
ten jest sprzeczny. Ponadto z lematu wynikaj
,
a od razu nast
,
epuj
,
ace
twierdzenia:
Twierdzenie 4.4.
Załóżmy, że układy równań liniowych (U
1
)
i (U
2
) z n niewiadomymi x
1
, x
2
, . . . , x
n
s
,
a równoważne. Wówczas układ
(U
1
) jest sprzeczny wtedy i tylko wtedy, gdy układ (U
2
) jest sprzeczny.
Twierdzenie 4.5. Niech (U
1
), (U
2
), (U
3
) b
,
ed
,
a układami równań
liniowych z n niewiadomymi x
1
, x
2
, . . . , x
n
nad ciałem K. Wówczas:
(i) (U
1
) ≡ (U
1
);
(ii) jeżeli (U
1
) ≡ (U
2
), to (U
2
) ≡ (U
1
);
(iii) jeżeli (U
1
) ≡ (U
2
) i (U
2
) ≡ (U
3
), to (U
1
) ≡ (U
3
).
Problem rozwi
,
azania układu równań liniowych polega na znale-
zieniu wszystkich rozwi
,
azań tego układu.
Bardzo użyteczne przy
rozwi
,
azywaniu tego problemu s
,
a tzw. operacje elementarne.
4.2
Operacje elementarne nad układem
równań liniowych
(i). Zamiana miejscami równania i-tego z równaniem j-tym (i 6= j)
oznaczana przez r
i
↔ r
j
. Operacja odwrotna: r
i
↔ r
j
.
(ii). Pomnożenie i-tego równania przez niezerowy skalar a oznaczana
przez a · r
i
. Operacja odwrotna:
1
a
· r
i
.
(iii). Dodanie do i-tego równania równania j-tego (i 6= j) pomnożo-
nego przez dowolny skalar a oznaczana przez r
i
+a·r
j
. Przy tej operacji

Układy równań liniowych
37
zmieniamy tylko równanie i-te! Operacja odwrotna: r
i
+ (−a) · r
j
.
(iv). Wykreślenie powtarzaj
,
acych si
,
e kopii pewnego równania.
(v). Wykreślenie równań postaci 0 · x
1
+ 0 · x
2
+ . . . + 0 · x
n
= 0 (gdy
liczba równań jest wi
,
eksza od 1).
(vi).
Zamiana kolejności niewiadomych x
i
oraz x
j
(i 6= j) w każ-
dym równaniu oznaczana przez x
i
↔ x
j
. W wyniku zastosowania tej
operacji równanie
a
1
x
1
+ . . . + a
i
x
i
+ . . . + a
j
x
j
+ . . . + a
n
x
n
= b
przechodzi na równanie
a
1
x
1
+ . . . + a
j
x
j
+ . . . + a
i
x
i
+ . . . + a
n
x
n
= b.
Z definicji układów równoważnych mamy zatem, że jeśli układ (U
2
)
powstaje z układu (U
1
) przez wykonanie operacji elementarnej, to
układy (U
1
) i (U
2
) s
,
a równoważne. Zatem z twierdzeń 4.2, 4.4 i 4.5
przez prost
,
a indukcj
,
e otrzymujemy st
,
ad od razu nast
,
epuj
,
ace
Twierdzenie 4.6. Załóżmy, że układ (U
0
) równań liniowych po-
wstaje z układu (U ) przez kolejne wykonanie skończonej liczby opera-
cji elementarnych. Wówczas układy te s
,
a równoważne, maj
,
a te same
zbiory rozwi
,
azań i układ (U ) jest sprzeczny wtedy i tylko wtedy, gdy
układ (U
0
) jest sprzeczny.
Na twierdzeniu 4.6 opiera si
,
e metoda rozwi
,
azywania układów rów-
nań liniowych zwana metod
,
a eliminacji Gaussa.
4.3
Metoda eliminacji Gaussa
Metoda eliminacji Gaussa polega na znalezieniu dla danego układu
(4.1), (w którym a
ij
6= 0 dla pewnych i, j) przy pomocy operacji
elementarnych równoważnego mu układu (4.5), który po ewentualnej
38
Wykłady z algebry liniowej I
permutacji niewiadomych x
1
, . . . , x
n
ma postać:
x
1
+ c
1 k+1
x
k+1
+ . . . + c
1n
x
n
= d
1
x
2
+ c
2 k+1
x
k+1
+ . . . + c
2n
x
n
= d
2
x
3
+ c
3 k+1
x
k+1
+ . . . + c
3n
x
n
= d
3
. ..
..
.
..
.
..
.
x
k
+ c
k k+1
x
k+1
+ . . . + c
kn
x
n
= d
k
0 = d
k+1
.
(4.5)
Jeżeli d
k+1
6= 0, to układ (4.5) jest sprzeczny (i z twierdzenia 4.3 nie
ma rozwi
,
azania), a wi
,
ec na mocy twierdzenia 4.6, układ (4.1) też jest
sprzeczny i nie ma rozwi
,
azania.
Jeżeli d
k+1
= 0 i k = n, to układ (4.1) posiada dokładnie jedno
rozwi
,
azanie:
x
1
= d
1
, x
2
= d
2
, . . . , x
n
= d
n
.
(4.6)
Jeżeli d
k+1
= 0 oraz k < n, to x
k+1
, x
k+2
, . . . , x
n
s
,
a dowolnymi
skalarami (nazywamy je parametrami), zaś pozostałe niewiadome wy-
liczamy z równań układu (4.5), tzn.
x
i
= d
i
− c
i k+1
x
k+1
− . . . − c
in
x
n
dla i = 1, 2, . . . , k.
(4.7)
Aby sprowadzić układ (4.1) do postaci (4.5) należy najpierw przy
pomocy operacji elementarnych przekształcić go do układu postaci:
x
1
+
a
0
12
x
2
+
. . . +
a
0
1n
x
n
= b
0
1
a
0
21
x
1
+
a
0
22
x
2
+
. . . +
a
0
2n
x
n
= b
0
2
..
.
..
.
. ..
..
.
a
0
m1
x
1
+ a
0
m2
x
2
+ . . . + a
0
mn
x
n
= b
0
m
.
(4.8)
Robimy to np. w ten sposób, że najpierw znajdujemy element a
ij
6= 0,
a nast
,
epnie przez operacje: x
1
↔ x
j
, r
1
↔ r
i
,
1
a
ij
· r
1
doprowadzamy
Nast
,
epnie przy pomocy równania pierwszego eliminujemy zmienn
,
a
x
1
z pozostałych równań układu (4.8) przez wykonanie operacji:

Układy równań liniowych
39
r
2
− a
0
21
· r
1
, r
3
− a
0
31
· r
1
, . . ., r
m
− a
0
m1
· r
1
. Otrzymamy wówczas układ
postaci:
x
1
+
a”
12
x
2
+
. . . +
a”
1n
x
n
= b”
1
a”
22
x
2
+
. . . +
a”
2n
x
n
= b”
2
..
.
. ..
..
.
a”
m2
x
2
+ . . . + a”
mn
x
n
= b”
m
.
(4.9)
Nast
,
epnie stosujemy nasz algorytm do układu:
a”
12
x
2
+
. . . +
a”
1n
x
n
= b”
1
a”
22
x
2
+
. . . +
a”
2n
x
n
= b”
2
..
.
. ..
..
.
a”
m2
x
2
+ . . . + a”
mn
x
n
= b”
m
(4.10)
nie ruszaj
,
ac pierwszego równania układu (4.9). Po skończonej liczbie
kroków uzyskamy układ postaci:
x
1
+ e
12
x
2
+ e
13
x
3
+ . . . + e
1k
x
k
+ e
1 k+1
x
k+1
+ . . . + e
1n
x
n
= f
1
x
2
+ e
23
x
3
+ . . . + e
2k
x
k
+ e
2 k+1
x
k+1
+ . . . + e
2n
x
n
= f
2
x
3
+ . . . + e
3k
x
k
+ e
3 k+1
x
k+1
+ . . . + e
3n
x
n
= f
3
. ..
..
.
x
k
+ e
k k+1
x
k+1
+ . . . + e
kn
x
n
= f
k
0 = f
k+1
.
Jeżeli f
k+1
6= 0, to otrzymany układ jest sprzeczny, a wi
,
ec też układ
(4.1) jest sprzeczny. Jeżeli zaś f
k+1
= 0, to przy pomocy operacji:
r
1
− e
1k
· r
k
, r
2
− e
2k
· r
k
,...,r
k−1
− e
k−1 k
· r
k
eliminujemy zmienn
,
a
x
k
z pocz
,
atkowych k − 1 równań. Później eliminujemy zmienn
,
a x
k−1
z wcześniejszych równań przy pomocy k − 1-szego równania, itd.
W końcu, po skończonej liczbie kroków, uzyskamy w ten sposób układ
(4.5).
Zauważmy jeszcze, że przy stosowaniu metody eliminacji Gaussa
liczba równań układu nie zwi
,
eksza si
,
e. Oznacza to, że jeśli w ukła-
dzie (4.1) liczba równań jest mniejsza od liczby niewiadomych,
to układ ten nie może mieć dokładnie jednego rozwi
,
azania!

40
Wykłady z algebry liniowej I
Ponadto, jeśli układ (4.1) nie ma rozwi
,
azania, to na mocy twier-
dzenia 4.6, układ (4.5) też nie posiada rozwi
,
azania, a wi
,
ec d
k+1
6= 0.
St
,
ad układ (4.5) jest sprzeczny i na mocy twierdzenia 4.6 układ (4.1)
też jest sprzeczny. Uwzgl
,
edniaj
,
ac twierdzenie 4.3 udowodniliśmy w ten
sposób nast
,
epuj
,
ace
Twierdzenie 4.7. Układ równań liniowych jest sprzeczny wtedy
i tylko wtedy, gdy nie posiada rozwi
,
azania.

Rozdział 5
Wyznaczniki I
5.1
Permutacje
Niech n b
,
edzie ustalon
,
a liczb
,
a naturaln
,
a. Niech X
n
= {1, 2, . . . , n}.
Każd
,
a bijekcj
,
e f : X
n
−→ X
n
nazywamy permutacj
,
a zbioru X
n
. Po-
nieważ zbiór X
n
jest skończony, wi
,
ec funkcja f : X
n
−→ X
n
jest
permutacj
,
a wtedy i tylko wtedy, gdy f jest różnowartościowa (lub rów-
noważnie, wtedy i tylko wtedy, gdy f jest ”na”).
Zbiór wszystkich permutacji zbioru X
n
oznaczamy przez S
n
. Jak
wiadomo ze szkoły średniej S
n
posiada dokładnie n! = 1 · 2 · . . . · n
elementów. Ze wst
,
epu do matematyki wynika, że złożenie permuta-
cji zbioru X
n
jest permutacj
,
a tego zbioru, składanie permutacji jest
ł
,
aczne, posiada element neutralny e, którym jest przekształcenie toż-
samościowe zbioru X
n
w siebie i ponadto każda permutacja f ∈ S
n
po-
siada przekształcenie odwrotne f
−1
, które też jest permutacj
,
a zbioru
X
n
(oczywiście f ◦ f
−1
= f
−1
◦ f = e).
Permutacj
,
e f ∈ S
n
wygodnie jest zapisywać w postaci dwuwierszo-
wej tablicy
f =
1
2
. . .
i
. . .
n
f (1) f (2) . . . f (i) . . . f (n)
,
(5.1)
w której w pierwszym wierszu umieszczone s
,
a wszystkie elementy zbioru
X
n
(najcz
,
eściej w porz
,
adku rosn
,
acym), zaś w drugim wierszu umiesz-
41
42
Wykłady z algebry liniowej I
czone s
,
a kolejne obrazy tych elementów przy odwzorowaniu f . Zatem
na przykład
e =
1 2 . . . i . . . n
1 2 . . . i . . . n
.
(5.2)
Inwersj
,
a permutacji f ∈ S
n
nazywamy taki podzbiór dwuelemen-
towy {i, j} zbioru X
n
, że i < j oraz f (i) > f (j). Zbiór wszystkich
inwersji permutacji f ∈ S
n
oznaczamy przez I
f
. Np. I
e
= ∅, wi
,
ec
|I
e
| = 0, czyli permutacja tożsamościowa nie posiada inwersji.
Przykład 5.1. Niech i, j ∈ X
n
, i < j. Oznaczmy przez (i, j)
permutacj
,
e zbioru X
n
, która zamienia miejscami elementy i, j oraz
nie zmienia pozostałych elementów zbioru X
n
(takie permutacje nazy-
wamy transpozycjami). Zatem
(i, j) =
1 2 . . . i − 1 i i + 1 . . . j − 1 j j + 1 . . . n
1 2 . . . i − 1 j
i + 1 . . . j − 1
i
j + 1 . . . n
.
(5.3)
St
,
ad I
(i,j)
= {{i, i + 1}, {i, i + 2}, {i, i + 3}, . . . , {i, j − 1}, {i, j}
|
{z
}
j−i
,
{i + 1, j}, {i + 2, j}, {i + 3, j}, . . . , {j − 1, j}
|
{z
}
(j−1)−i
}.
Zatem |I
(i,j)
| = (j − i) + (j − 1) − i = 2(j − i) − 1. Uzyskaliśmy wi
,
ec,
że każda transpozycja posiada nieparzyst
,
a liczb
,
e wszystkich
inwersji.
Znakiem permutacji f ∈ S
n
nazywamy liczb
,
e sgn(f ) określon
,
a wzo-
rem:
sgn(f ) = (−1)
|I
f
|
.
(5.4)
Powiemy, że permutacja f ∈ S
n
jest parzysta, jeśli sgn(f ) = 1 oraz że
f jest nieparzysta, jeśli sgn(f ) = −1. Zatem z przykładu 5.1 mamy, że
dowolna transpozycja jest permutacj
,
a nieparzyst
,
a. Ponieważ
sgn(e) = (−1)
0
= 1, wi
,
ec permutacja tożsamościowa jest parzysta.
Zbiór wszystkich permutacji parzystych f ∈ S
n
b
,
edziemy oznaczali
przez A
n
.
Wyznaczniki I
43
Twierdzenie 5.1. Dla dowolnych permutacji f, g ∈ S
n
zachodzi
wzór:
sgn(f ◦ g) = sgn(f ) · sgn(g).
(5.5)
W szczególności sgn(f
−1
) = sgn(f ).
Dowód. Oznaczmy przez P
n
rodzin
,
e wszystkich podzbiorów dwu-
elementowych zbioru X
n
. Niech h ∈ S
n
. Weźmy dowolne A ∈ P
n
.
Wtedy A = {i, j} dla pewnych i, j ∈ X
n
, i 6= j. Oznaczmy sgn
h
(A) =
sgn
h(i)−h(j)
i−j
. Określenie to jest poprawne, bo
h(j)−h(i)
j−i
=
−(h(i)−h(j))
−(i−j)
=
h(i)−h(j)
i−j
. Ponadto A ∈ I
h
⇔ sgn
h
(A) = −1. Wynika st
,
ad wzór:
sgn(h) =
Y
A∈P
n
sgn
h
(A).
(5.6)
Łatwo zauważyć, że dowolna permutacja g ∈ S
n
wyznacza bijekcj
,
e
G : P
n
−→ P
n
przy pomocy wzoru G(A) = {g(i), g(j)} dla A = {i, j}.
Wynika st
,
ad, że dla dowolnych f, g ∈ S
n
zachodzi wzór:
sgn(f ) =
Y
A∈P
n
sgn
f
(G(A)).
(5.7)
Ponadto dla A ∈ P
n
mamy, że
sgn
f
(G(A)) · sgn
g
(A) = sgn
f ◦g
(A).
(5.8)
Rzeczywiście, A = {i, j} dla pewnych i, j ∈ X
n
, i 6= j oraz
sgn
f
(G(A)) = sgn
f
({g(i), g(j)}) = sgn
f (g(i))−f (g(j))
g(i)−g(j)
oraz sgn
g
(A) =
sgn
g(i)−g(j)
i−j
. Ale sgn(x) · sgn(y) = sgn(x · y) dla dowolnych liczb
rzeczywistych x, y, wi
,
ec
sgn
f
(G(A)) · sgn
g
(A) = sgn
f (g(i)) − f (g(j))
g(i) − g(j)
·
g(i) − g(j)
i − j
=
sgn
(f ◦ g)(i) − (f ◦ g)(j)
i − j
= sgn
f ◦g
(A).

44
Wykłady z algebry liniowej I
Zatem na mocy (5.6), (5.8) i (5.7) mamy, że sgn(f ◦ g) =
Y
A∈P
n
sgn
f ◦g
(A) =
Y
A∈P
n
[sgn
f
(G(A)) · sgn
g
(A)] =
Y
A∈P
n
sgn
f
(G(A))·
Y
A∈P
n
sgn
g
(A) =
Y
A∈P
n
sgn
f
(A) ·
Y
A∈P
n
sgn
g
(A) = sgn(f ) · sgn(g).
W szczególności mamy st
,
ad, że 1 = sgn(e) = sgn(f ◦ f
−1
) =
sgn(f ) · sgn(f
−1
), czyli sgn(f
−1
) = sgn(f ). Kończy to dowód naszego
twierdzenia.
5.2
Określenie macierzy
Niech K b
,
edzie dowolnym ciałem oraz niech n i m b
,
ed
,
a dowolnymi
liczbami naturalnymi. Prostok
,
atn
,
a tablic
,
e
a
11
a
12
. . .
a
1n
a
21
a
22
. . .
a
2n
..
.
..
.
. ..
..
.
a
m1
a
m2
. . . a
mn
(5.9)
utworzon
,
a z elementów a
ij
(i = 1, 2, . . . , m; j = 1, 2, . . . , n) ciała K
nazywamy m × n-macierz
,
a nad ciałem K. Elementy a
ij
nazywamy
wyrazami macierzy. Rz
,
edy pionowe nazywamy kolumnami, a poziome
- wierszami tej macierzy. Zatem element a
ij
stoi w i-tym wierszu i j-tej
kolumnie rozpatrywanej macierzy.
n × n-macierze, nazywamy macierzami kwadratowymi stopnia n.
Dwie macierze nazywamy równymi, jeżeli jako tablice s
,
a identyczne.
Oznaczenia macierzy: A, B, C, itd.
Dla macierzy (5.9) piszemy też:
A = [a
ij
]
i=1,...,m
j=1,...,n
.
(5.10)
Macierz
,
a transponowan
,
a A
T
m×n-macierzy A postaci (5.9) nazywamy
tak
,
a n × m-macierz, która jako sw
,
a i-t
,
a kolumn
,
e, dla i = 1, 2, . . . , m,

Wyznaczniki I
45
ma i-ty wiersz macierzy A. Zatem
A
T
=
a
11
a
21
. . . a
m1
a
12
a
22
. . . a
m2
..
.
..
.
. ..
..
.
a
1n
a
2n
. . . a
mn
.
(5.11)
5.3
Określenie wyznacznika
Wyznacznikiem macierzy kwadratowej A = [a
ij
]
i=1,...,n
j=1,...,n
stopnia n nad
ciałem K nazywamy nast
,
epuj
,
acy element ciała K:
det(A) =
X
f ∈S
n
sgn(f ) · a
1f (1)
· a
2f (2)
· . . . · a
nf (n)
.
(5.12)
Wyznacznik macierzy A = [a
ij
]
i=1,...,n
j=1,...,n
b
,
edziemy też oznaczali symbo-
lem:
a
11
a
12
. . . a
1n
a
21
a
22
. . . a
2n
..
.
..
.
. ..
..
.
a
n1
a
n2
. . . a
nn
.
(5.13)
Stopień macierzy kwadratowej A nazywa si
,
e również stopniem wy-
znacznika tej macierzy, zaś wiersze (kolumny) macierzy A nazywamy
wierszami (kolumnami) wyznacznika tej macierzy.
Przykład 5.2. Udowodnimy, że dla dowolnych elementów a, b, c, d
ciała K zachodzi wzór:
a b
c d
= a · d − b · c.
(5.14)
Zauważmy, że S
2
= {e, g}, gdzie g = (1, 2) jest transpozycj
,
a. Zatem
sgn(e) = 1 i sgn(g) = −1. Ponadto a
11
= a, a
12
= b, a
21
= c, a
22
= d,
wi
,
ec na mocy definicji wyznacznika
a b
c d
=
X
f ∈S
2
sgn(f ) · a
1f (1)
· a
2f (2)
= sgn(e) · a
11
· a
22
+ sgn(g) · a
12
· a
21
= a · d − b · c.

46
Wykłady z algebry liniowej I
Przykład 5.3. Udowodnimy, że nad dowolnym ciałem K zachodzi
wzór:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
−
−a
13
a
22
a
31
− a
12
a
21
a
33
− a
11
a
23
a
32
.
Mamy tutaj n = 3 oraz S
3
składa si
,
e z nast
,
epuj
,
acych elemen-
tów: e, f
1
=
1 2 3
1 3 2
, f
2
=
1 2 3
2 1 3
, f
3
=
1 2 3
2 3 1
,
f
4
=
1 2 3
3 2 1
, f
5
=
1 2 3
3 1 2
. Ponadto sgn(e) = 1, f
1
, f
2
, f
4
s
,
a transpozycjami, wi
,
ec sgn(f
1
) = sgn(f
2
) = sgn(f
4
) = −1 oraz
|I
f
3
| = 2 i |I
f
5
| = 2, czyli sgn(f
3
) = sgn(f
5
) = 1. Zatem z definicji wy-
znacznika mamy, że
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
=
X
f ∈S
3
sgn(f )a
1f (1)
a
2f (2)
a
3f (3)
=
sgn(e)a
11
a
22
a
33
+sgn(f
1
)a
11
a
23
a
32
+sgn(f
2
)a
12
a
21
a
33
+sgn(f
3
)a
12
a
23
a
31
+
sgn(f
4
)a
13
a
22
a
31
+sgn(f
5
)a
13
a
21
a
32
= a
11
a
22
a
33
−a
11
a
23
a
32
−a
12
a
21
a
33
+
a
12
a
23
a
31
− a
13
a
22
a
31
+ a
13
a
21
a
32
, sk
,
ad z własności dodawania w ciele
wynika nasz wzór. Jednak podany wyżej wzór na wyznacznik stopnia
3 jest zbyt skomplikowany do zapami
,
etania. W zwi
,
azku z tym do obli-
czania wyznaczników stopnia 3 stosuje si
,
e tzw. reguł
,
e Sarrusa. Polega
ona na dopisaniu z prawej strony wyznacznika dwóch jego pierwszych
kolumn i nast
,
epnie wymnożeniu prawoskośnie wyrazów ze znakiem +
oraz lewoskośnie ze znakiem - i dodaniu otrzymanych wyników. Istot-
nie:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
a
11
a
12
a
21
a
22
a
31
a
32
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
−
a
13
a
22
a
31
− a
11
a
23
a
32
− a
12
a
21
a
33
.
Można sprawdzić, że do tego samego rezultatu prowadzi też dopi-
sywanie u dołu wyznacznika dwóch jego pierwszych wierszy.
Przykład 5.4. Udowodnimy, że zachodzi wzór:

Wyznaczniki I
47
a
11
a
12
a
13
. . . a
1n
0
a
22
a
23
. . . a
2n
0
0
a
33
. . . a
3n
..
.
..
.
..
.
. ..
..
.
0
0
0
. . . a
nn
= a
11
a
22
a
33
. . . a
nn
.
Niech f ∈ S
n
oraz f 6= e. Wtedy istnieje najwi
,
eksza liczba naturalna k
taka, że f (k) 6= k. Zatem f (k + 1) = k + 1, f (k + 2) = k + 2, . . . , f (n) =
n, sk
,
ad wynika, że f (k) < k, czyli a
kf (k)
= 0.
Zatem z definicji
wyznacznika mamy, że det(A) =
X
f ∈S
n
sgn(f )a
1f (1)
a
2f (2)
. . . a
nf (n)
=
sgn(e)a
11
a
22
. . . a
nn
= a
11
a
22
. . . a
nn
.

Rozdział 6
Wyznaczniki II
6.1
Własności wyznaczników
Wszystkie macierze wyst
,
epuj
,
ace w podanych niżej własnościach s
,
a ma-
cierzami kwadratowymi nad ustalonym ciałem K, którego elementy
b
,
edziemy nazywali skalarami.
Uwaga 6.1. Niech I oraz J b
,
ed
,
a niepustymi skończonymi zbio-
rami, niech φ : I −→ J b
,
edzie bijekcj
,
a i niech a
j
∈ K dla j ∈ J.
Wtedy
X
i∈I
a
φ(i)
=
X
j∈J
a
j
, gdyż sumujemy te same elementy, lecz być
może w innym porz
,
adku.
Własność 6.1. Wyznacznik macierzy kwadratowej A jest równy
wyznacznikowi jej macierzy transponowanej A
T
:
det(A) = det(A
T
).
Dowód. Niech A = [a
ij
]
i,j=1,...,n
i A
T
= [b
ij
]
i,j=1,...,n
. Wtedy b
ij
=
a
ji
dla i, j = 1, . . . , n. Zatem z definicji wyznacznika:
det(A
T
) =
X
f ∈S
n
sgn(f )b
1f (1)
b
2f (2)
. . . b
nf (n)
=
X
f ∈S
n
sgn(f )a
f (1)1
a
f (2)2
. . . a
f (n)n
.
48

Wyznaczniki II
49
Zauważmy, że dla f ∈ S
n
zachodzi równość
{(f (i), i) : i = 1, 2, . . . , n} = {(j, f
−1
(j)) : j = 1, 2, . . . , n}.
Ale sgn(f ) = sgn(f
−1
) na mocy twierdzenia 5.1 oraz z przemienności
i ł
,
aczności mnożenia w ciele mamy, że
det(A
T
) =
X
f ∈S
n
sgn(f
−1
)a
1f
−1
(1)
a
2f
−1
(2)
. . . a
nf
−1
(n)
.
Ponadto przekształcenie f 7→ f
−1
dla f ∈ S
n
jest bijekcj
,
a zbioru S
n
na zbiór S
n
, wi
,
ec z uwagi 6.1:
det(A
T
) =
X
f ∈S
n
sgn(f )a
1f (1)
a
2f (2)
. . . a
nf (n)
= det(A)
Uwaga 6.2. Z własności 6.1 wynika, że każda własność wy-
znacznika sformułowana w j
,
ezyku wierszy (kolumn) jest praw-
dziwa w przetłumaczeniu na j
,
ezyk kolumn (wierszy). Z tego
powodu wsz
,
edzie dalej b
,
edziemy dowodzili tylko jednej wersji takich
własności.
Własność 6.2. Jeżeli macierz kwadratowa B powstaje z macierzy
kwadratowej A przez pomnożenie wszystkich elementów pewnego jej
wiersza (kolumny) przez ustalony skalar a, to
det(B) = a · det(A).
Dowód.
Niech A = [a
ij
]
i,j=1,...,n
, a ∈ K i złóżmy, że macierz
B = [b
ij
]
i,j=1,...,n
powstaje z A przez pomnożenie k-tego wiersza przez
a. Wtedy b
kj
= aa
kj
dla j = 1, 2, . . . , n oraz b
ij
= a
ij
dla i 6= k oraz
j = 1, 2, . . . , n. Zatem z definicji wyznacznika
det(B) =
X
f ∈S
n
sgn(f )b
1f (1)
. . . b
kf (k)
. . . b
nf (n)
=
=
X
f ∈S
n
sgn(f )a
1f (1)
. . . (aa
kf (k)
) . . . a
nf (n)
=
= a ·
X
f ∈S
n
sgn(f )a
1f (1)
. . . a
kf (k)
. . . a
nf (n)
= a · det(A).

50
Wykłady z algebry liniowej I
Uwaga 6.3. Podstawiaj
,
ac a = 0 w własności 6.2 uzyskamy, że je-
żeli pewien wiersz (kolumna) macierzy kwadratowej A składa si
,
e z sa-
mych zer, to det(A) = 0.
Własność 6.3. Niech g ∈ S
n
i niech macierz B powstaje z macie-
rzy kwadratowej A stopnia n w ten sposób, że i-ty wiersz (kolumn
,
e)
macierzy A przestawiamy na miejsce o numerze g(i) dla i = 1, 2, . . . , n.
Wówczas
det(B) = sgn(g) · det(A).
Dowód. Niech A = [a
ij
]
i,j=1,...,n
oraz B = [b
ij
]
i,j=1,...,n
. Wtedy
z założenia wynika, że b
ij
= a
f (i)j
dla i, j = 1, 2, . . . , n. Z określe-
nia wyznacznika mamy, że det(B) =
X
f ∈S
n
sgn(f )b
1f (1)
b
2f (2)
. . . b
nf (n)
=
X
f ∈S
n
sgn(f )a
g(1)f (1)
a
g(2)f (2)
. . . a
g(n)f (n)
. Ale {(g(i), f (i)) : i = 1, 2, . . . , n}
= {(j, (g
−1
◦ f )(j)) : j = 1, 2, . . . , n}, wi
,
ec z przemienności i ł
,
aczności
mnożenia w ciele mamy, że
a
g(1)f (1)
a
g(2)f (2)
. . . a
g(n)f (n)
= a
1(g
−1
◦f )(1)
a
2(g
−1
◦f )(2)
. . . a
n(g
−1
◦f )(n)
dla f ∈ S
n
. Ponadto z twierdzenia 5.1 wynika, że sgn(f ) = sgn(g) ·
sgn(g
−1
◦ f ) dla f ∈ S
n
, wi
,
ec
det(B) = sgn(g) ·
X
f ∈S
n
sgn(g
−1
◦ f )a
1(g
−1
◦f )(1)
a
2(g
−1
◦f )(2)
. . . a
n(g
−1
◦f )(n)
.
Ale przekształcenie f 7→ g
−1
◦ f dla f ∈ S
n
jest bijekcj
,
a zbioru S
n
na
S
n
, wi
,
ec z uwagi 6.1
det(B) = sgn(g) ·
X
f ∈S
n
sgn(f )a
1f (1)
a
2f (2)
. . . a
nf (n)
= sgn(g) · det(A).
Uwaga 6.4. Jak wiemy sgn(g) = −1 dla dowolnej transpozycji
g. Zatem z własności 6.3 wynika, że jeżeli macierz B powstaje z ma-
cierzy kwadratowej A stopnia n ≥ 2 przez zamian
,
e miejscami dwóch

Wyznaczniki II
51
jej wierszy (kolumn), to det(B) = − det(A) (czyli wyznacznik zmienia
znak!).
Własność 6.4. Niech elementy l-tego wiersza (kolumny) wyznacz-
nika b
,
ed
,
a sumami k-składników:
a
lj
= x
1j
+ x
2j
+ . . . + x
kj
dla j = 1, 2, . . . , n.
Wówczas wyznacznik jest sum
,
a k wyznaczników, które maj
,
a prócz
l-tego wiersza (kolumny) te same wiersze (kolumny) co pierwotny wy-
znacznik.
Natomiast l-ty wiersz (kolumna) i-tego wyznacznika dla
i = 1, 2, . . . , k ma postać:
x
i1
x
i2
. . . x
in
.
Dowód. Oznaczmy pierwotny wyznacznik przez W , zaś pozostałe
wyznaczniki przez W
1
, W
2
, . . . , W
k
odpowiednio. Wówczas z definicji
wyznacznika mamy, że
W =
X
f ∈S
n
sgn(f )a
1f (1)
. . . (x
1f (l)
+ x
2f (l)
+ . . . + x
kf (l)
) . . . a
nf (n)
=
X
f ∈S
n
sgn(f )a
1f (1)
. . . x
1f (l)
. . . a
nf (n)
+
X
f ∈S
n
sgn(f )a
1f (1)
. . . x
2f (l)
. . . a
nf (n)
+ . . . +
X
f ∈S
n
sgn(f )a
1f (1)
. . . x
kf (l)
. . . a
nf (n)
= W
1
+ W
2
+ . . . + W
k
.
Własność 6.5. Jeśli w macierzy kwadratowej dwa wiersze lub
dwie kolumny s
,
a identyczne, to jej wyznacznik jest równy 0.
Dowód. Załóżmy, że i-ty wiersz macierzy A = [a
ij
]
i,j=1,...,n
jest
identyczny z k-tym (i < k) wierszem tej macierzy. Wtedy
a
ij
= a
kj
dla j = 1, 2, . . . , n.
(6.1)
Ale (i, k) ◦ (i, k) = e i sgn((i, k)) = −1, wi
,
ec na mocy twierdzenia 5.1
przekształcenie f 7→ f ◦ (i, k) dla f ∈ A
n
jest bijekcj
,
a zbioru A
n
na
zbiór S
n
\ A
n
. Zatem z uwagi 6.1 mamy, że
X
g∈S
n
\A
n
sgn(g)a
1g(1)
a
2g(2)
. . . a
ng(n)
=
−
X
f ∈A
n
a
1(f ◦(i,k))(1)
a
2(f ◦(i,k))(2)
. . . a
n(f ◦(i,k))(n)
,

52
Wykłady z algebry liniowej I
gdyż sgn(g) = −1 dla g ∈ S
n
\ A
n
.
Ale dla f ∈ A
n
mamy, że
f ((i, k)(i)) = f (k), f ((i, k)(k)) = f (i) oraz dla t 6= i, k jest f ((i, k)(t)) =
f (t), wi
,
ec na mocy (6.1)
a
1(f ◦(i,k))(1)
. . . a
i(f ◦(i,k))(i)
. . . a
k(f ◦(i,k))(k)
. . . a
n(f ◦(i,k))(n)
=
a
1f (1)
. . . a
if (k)
. . . a
kf (i)
. . . a
nf (n)
= a
1f (1)
. . . a
if (i)
. . . a
kf (k)
. . . a
nf (n)
.
St
,
ad det(A) =
X
g∈S
n
sgn(g)a
1g(1)
a
2g(2)
. . . a
ng(n)
=
=
X
g∈A
n
sgn(g)a
1g(1)
a
2g(2)
. . . a
ng(n)
+
X
g∈S
n
\A
n
sgn(g)a
1g(1)
a
2g(2)
. . . a
ng(n)
=
=
X
f ∈A
n
a
1f (1)
a
2f (2)
. . . a
nf (n)
−
X
f ∈A
n
a
1f (1)
a
2f (2)
. . . a
nf (n)
= 0.
Własność 6.6. Wyznacznik nie zmienia wartości, gdy do elemen-
tów jednego wiersza (kolumny) dodać odpowiednie elementy innego
wiersza (kolumny) pomnożone przez ustalony skalar.
Dowód. Niech macierz B powstaje z macierzy kwadratowej A
przez dodanie do l-tego wiersza wiersza k-tego (l 6= k) pomnożonego
przez skalar a. Oznaczmy przez C macierz, która powstaje z macierzy
A przez zast
,
apienie jej l-tego wiersza wierszem k-tym. Wtedy na mocy
własności 6.5 mamy, że det(C) = 0. Ponadto z własności 6.4 i 6.2
mamy, że det(B) = det(A) + a · det(C) = det(A) + a · 0 = det(A).
6.2
Operacje elementarne na macierzy
Bardzo ważne znaczenie w algebrze liniowej odgrywaj
,
a tzw. operacje
elementarne na wierszach lub kolumnach macierzy. Niech A = [a
ij
]
b
,
edzie m × n-macierz
,
a nad ciałem K.
1. Operacje elementarne na wierszach macierzy A:
(i) Pomnożenie i-tego wiersza macierzy A przez niezerowy skalar a.
Przy tej operacji nie zmieniamy wierszy o numerach różnych od i, zaś
każdy wyraz i-tego wiersza mnożymy przez a. Operacj
,
e t
,
e oznaczamy
symbolem a · w
i
.
(ii) Zamiana miejscami i-tego wiersza macierzy A z wierszem j-tym
(i 6= j) macierzy A. Przy tej operacji nie zmieniamy wierszy o nume-

Wyznaczniki II
53
rach różnych od i oraz j. Operacj
,
e t
,
e oznaczamy symbolem w
i
↔ w
j
.
(iii) Dodanie do j-tego wiersza macierzy A i-tego (i 6= j) wiersza
tej macierzy pomnożonego przez dowolny skalar a. Przy tej operacji nie
zmieniamy wierszy o numerach różnych od j. Operacj
,
e t
,
e oznaczamy
przez w
j
+ a · w
i
.
2. Operacje elementarne na kolumnach macierzy A:
(i) Pomnożenie i-tej kolumny macierzy A przez niezerowy skalar a.
Przy tej operacji nie zmieniamy kolumn o numerach różnych od i, zaś
każdy wyraz i-tej kolumny mnożymy przez a. Operacj
,
e t
,
e oznaczamy
symbolem a · k
i
.
(ii) Zamiana miejscami i-tej kolumny macierzy A z kolumn
,
a j-t
,
a
(i 6= j) macierzy A. Przy tej operacji nie zmieniamy kolumn o nume-
rach różnych od i oraz j. Operacj
,
e t
,
e oznaczamy symbolem k
i
↔ k
j
.
(iii) Dodanie do j-tej kolumny macierzy A i-tej (i 6= j) kolumny tej
macierzy pomnożonego przez dowolny skalar a. Przy tej operacji nie
zmieniamy kolumn o numerach różnych od j. Operacj
,
e t
,
e oznaczamy
symbolem k
j
+ a · k
i
.
6.3
Obliczanie wyznacznika za pomoc
,
a
operacji elementarnych
Stosuj
,
ac algorytm podobny do eliminacji Gaussa możemy każd
,
a ma-
cierz kwadratow
,
a A stopnia n nad ciałem K sprowadzić do tzw. postaci
trójk
,
atnej górnej:
B =
b
11
b
12
b
13
. . . a
1n
0
b
22
b
23
. . . b
2n
0
0
b
33
. . . b
3n
..
.
..
.
..
.
. ..
..
.
0
0
0
. . . b
nn
.
Wówczas z przykładu 5.4 mamy, że det(B) = b
11
b
22
. . . b
nn
. Ponadto
z własności wyznacznika podanych w rozdziale 5 wynika, że
det(A) 6= 0 ⇔ det(B) 6= 0.

54
Wykłady z algebry liniowej I
Przykład 6.1.
1 −1
1
−2
1
3 −1
3
−1 −1
4
3
−3
0 −8 −13
w
2
−w
1
=
1 −1
1
−2
0
4 −2
5
−1 −1
4
3
−3
0 −8 −13
w
3
+w
1
=
1 −1
1
−2
0
4 −2
5
0 −2
5
1
−3
0 −8 −13
w
4
+3·w
1
=
1 −1
1
−2
0
4 −2
5
0 −2
5
1
0 −3 −5 −19
w
2
+w
4
=
1 −1
1
−2
0
1 −7 −14
0 −2
5
1
0 −3 −5 −19
w
3
+2·w
2
=
1 −1
1
−2
0
1 −7 −14
0
0 −9 −27
0 −3 −5 −19
w
4
+3·w
2
=
1 −1
1
−2
0
1
−7 −14
0
0
−9 −27
0
0 −26 −61
= (−9) ·
1 −1
1
−2
0
1
−7 −14
0
0
1
3
0
0 −26 −61
w
4
+26·w
3
=
(−9) ·
1 −1
1
−2
0
1 −7 −14
0
0
1
3
0
0
0
17
= (−9) · 1 · 1 · 1 · 17 = −153.

Rozdział 7
Rozwinięcie Laplace’a
i wzory Cramera
7.1
Rozwini
,
ecie Laplace’a
Rozważmy macierz kwadratow
,
a A stopnia n ≥ 2 nad ciałem K:
A =
a
11
. . . a
1j
. . . a
1n
..
.
. ..
..
.
. ..
..
.
a
i1
. . .
a
ij
. . .
a
in
..
.
. ..
..
.
. ..
..
.
a
n1
. . . a
nj
. . . a
nn
.
(7.1)
Dla i, j = 1, 2, . . . , n oznaczmy przez A
ij
macierz kwadratow
,
a stopnia
n − 1, która powstaje z macierzy A przez wykreślenie i-tego wiersza
oraz j-tej kolumny. Zatem
A
ij
=
a
11
. . .
a
1j−1
a
1j+1
. . .
a
1n
..
.
. ..
..
.
..
.
. ..
..
.
a
i−11
. . . a
i−1j−1
a
i−1j+1
. . . a
i−1n
a
i+11
. . . a
i+1j−1
a
i+1j+1
. . . a
i+1n
..
.
. ..
..
.
..
.
. ..
..
.
a
n1
. . .
a
nj−1
a
nj+1
. . .
a
nn
.
(7.2)
55

56
Wykłady z algebry liniowej I
Zauważmy, że jeśli w macierzy
A[i, j] =
a
11
. . .
a
1j−1
0
a
1j+1
. . .
a
1n
a
21
. . .
a
2j−1
0
a
2j+1
. . .
a
2n
..
.
. ..
..
.
..
.
..
.
. ..
..
.
a
i−11
. . . a
i−1j−1
0
a
i−1j+1
. . . a
i−1n
a
i1
. . .
a
ij−1
a
ij
a
ij+1
. . .
a
in
a
i+11
. . . a
i+1j−1
0
a
i+1j+1
. . . a
i+1n
..
.
. ..
..
.
..
.
..
.
. ..
..
.
a
n1
. . .
a
nj−1
0
a
nj+1
. . .
a
nn
(7.3)
zamienimy miejscami j-t
,
a kolumn
,
e z kolumn
,
a j + 1-sz
,
a, nast
,
epnie
j + 1-sz
,
a a j + 2-g
,
a itd., w końcu zamienimy n − 1-sz
,
a kolumn
,
e z n-t
,
a
kolumn
,
a (wykonamy wi
,
ec n − j zamian), to otrzymamy macierz:
A
0
[i, j] =
a
11
. . .
a
1j−1
a
1j+1
. . .
a
1n
0
a
21
. . .
a
2j−1
a
2j+1
. . .
a
2n
0
..
.
. ..
..
.
..
.
. ..
..
.
..
.
a
i−11
. . . a
i−1j−1
a
i−1j+1
. . . a
i−1n
0
a
i1
. . .
a
ij−1
a
ij+1
. . .
a
in
a
ij
a
i+11
. . . a
i+1j−1
a
i+1j+1
. . . a
i+1n
0
..
.
. ..
..
.
..
.
. ..
..
.
..
.
a
n1
. . .
a
nj−1
a
nj+1
. . .
a
nn
0
.
(7.4)
Ponadto z uwagi 6.4 mamy, że
det(A
0
[i, j]) = (−1)
n−j
· det(A[i, j]).
(7.5)
Nast
,
epnie w macierzy (7.4) zamieńmy miejscami i-ty wiersz z i + 1-
szym, i + 1-szy wiersz z i + 2-gim itd. , w końcu zamieńmy miejscami
n − 1-szy wiersz z n-tym (wykonamy wi
,
ec n − i zamian). Otrzymamy
Rozwinięcie Laplace’a i wzory Cramera
57
wtedy macierz
A
00
[i, j] =
a
11
. . .
a
1j−1
a
1j+1
. . .
a
1n
0
a
21
. . .
a
2j−1
a
2j+1
. . .
a
2n
0
..
.
. ..
..
.
..
.
. ..
..
.
..
.
a
i−11
. . . a
i−1j−1
a
i−1j+1
. . . a
i−1n
0
a
i+11
. . . a
i+1j−1
a
i+1j+1
. . . a
i+1n
0
..
.
. ..
..
.
..
.
. ..
..
.
..
.
a
n1
. . .
a
nj−1
a
nj+1
. . .
a
nn
0
a
i1
. . .
a
ij−1
a
ij+1
. . .
a
in
a
ij
.
(7.6)
Z uwagi 6.4 oraz z (7.5) mamy, że det(A
00
[i, j]) = (−1)
n−i
·det(A
0
[i, j]) =
(−1)
n−i
· (−1)
n−j
· det(A[i, j]) = (−1)
−i−j
· det(A[i, j]), wi
,
ec
det(A[i, j]) = (−1)
i+j
· det(A
00
[i, j]).
(7.7)
Ponadto z (7.2) i (7.6) mamy, że
(A
00
[i, j])
nn
= A
ij
.
(7.8)
Lemat 7.1. Niech b
ij
dla i, j = 1, 2, . . . , n b
,
ed
,
a elementami ciała
K takimi, że b
in
= 0 dla i = 1, 2, . . . , n − 1. Niech
B =
b
11
b
12
. . .
b
1n−1
0
b
21
b
22
. . .
b
2n−1
0
..
.
..
.
. ..
..
.
..
.
b
n1
b
n2
. . . b
nn−1
b
nn
. Wtedy det(B) = b
nn
· det(B
nn
).
Dowód. Z definicji wyznacznika mamy, że
det(B) =
X
f ∈S
n
sgn(f )b
1f (1)
b
2f (2)
. . . b
nf (n)
.
Niech T
n
= {f ∈ S
n
: f (n) = n}. Jeśli f ∈ S
n
\ T
n
, to f (n) 6= n,
wi
,
ec istnieje i < n takie, że f (i) = n, sk
,
ad a
if (i)
= 0. Zatem det(B) =
X
f ∈T
n
sgn(f )b
1f (1)
. . . b
n−1f (n−1)
b
nn
= b
nn
·
X
f ∈T
n
sgn(f )b
1f (1)
. . . b
n−1f (n−1)
.
Ale przekształcenie g 7→ ¯
g dla g ∈ S
n−1
dane wzorem

58
Wykłady z algebry liniowej I
1
2
. . .
n − 1
g(1) g(2) . . . g(n − 1)
7→
1
2
. . .
n − 1
n
g(1) g(2) . . . g(n − 1) n
jest bijekcj
,
a zbioru S
n−1
na zbiór T
n
, przy czym I
g
= I
¯
g
, wi
,
ec sgn(g) =
sgn(¯
g) dla g ∈ S
n−1
. Zatem z uwagi 6.1 mamy, że
det(B) = b
nn
·
X
g∈S
n−1
sgn(g)b
1g(1)
b
2g(2)
. . . b
n−1g(n−1)
= b
nn
· det(B
nn
).
Z (7.8),(7.7) oraz z lematu 7.1 mamy, że
det(A[i, j]) = (−1)
i+j
· a
ij
· det(A
ij
).
(7.9)
Ponadto a
kj
= 0 + . . . + 0
|
{z
}
k−1
+a
kj
+ 0 + . . . + 0
|
{z
}
n−k
dla k = 1, 2, . . . , n, wi
,
ec
z własności 6.4 wyznacznika w wersji dla kolumn mamy, że
det(A) = det(A[1, j]) + det(A[2, j]) + . . . + det(A[n, j]).
(7.10)
Zatem z (7.10) oraz z (7.9) uzyskujemy nast
,
epuj
,
ace
Twierdzenie 7.1 (Laplace’a dla kolumn). Dla dowolnej ma-
cierzy kwadratowej A = [a
ij
]
i,j=1,...,n
stopnia n ≥ 2 nad ciałem K i dla
każdego j = 1, 2, . . . , n zachodzi wzór:
det(A) =
(−1)
1+j
a
1j
det(A
1j
) + (−1)
2+j
a
2j
det(A
2j
) + . . . + (−1)
n+j
a
nj
det(A
nj
).
Z własności 6.1 wyznacznika otrzymujemy st
,
ad też nast
,
epuj
,
ace
Twierdzenie 7.2 (Laplace’a dla wierszy). Dla dowolnej ma-
cierzy kwadratowej A = [a
ij
]
i,j=1,...,n
stopnia n ≥ 2 nad ciałem K i dla
każdego i = 1, 2, . . . , n zachodzi wzór:
det(A) =
(−1)
i+1
a
i1
det(A
i1
) + (−1)
i+2
a
i2
det(A
i2
) + . . . + (−1)
i+n
a
in
det(A
in
).
Wniosek 7.1. Niech A = [a
ij
]
i,j=1,...,n
b
,
edzie macierz
,
a kwadra-
tow
,
a stopnia n ≥ 2 nad ciałem K. Wówczas dla dowolnych i, j ∈
{1, 2, . . . , n}, i 6= j:

Rozwinięcie Laplace’a i wzory Cramera
59
(i) a
i1
(−1)
j+1
det(A
j1
)+a
i2
(−1)
j+2
det(A
j2
)+. . .+a
in
(−1)
j+n
det(A
jn
)
= 0 oraz
(ii) a
1i
(−1)
1+j
det(A
1j
)+a
2i
(−1)
2+j
det(A
2j
)+. . .+a
ni
(−1)
n+j
det(A
nj
)
= 0.
Dowód.
Zast
,
apmy w macierzy A wiersz j-ty wierszem i-tym.
Wówczas otrzymana macierz A
0
ma dwa wiersze równe, wi
,
ec z wła-
sności 6.5 wyznacznika mamy, że det(A
0
) = 0. Ale A
0
ij
= A
ij
dla
j = 1, 2, . . . , n, wi
,
ec stosuj
,
ac rozwini
,
ecie Laplace’a wzgl
,
edem j-tego
wiersza macierzy A
0
uzyskamy, że 0 = det(A
0
) = a
i1
(−1)
j+1
det(A
j1
) +
a
i2
(−1)
j+2
det(A
j2
) + . . . + a
in
(−1)
j+n
det(A
jn
), co kończy dowód (i).
Dowód (ii) jest analogiczny.
Uwaga 7.1. Niech A = [a
ij
]
i,j=1,...,n
b
,
edzie macierz
,
a kwadratow
,
a
stopnia n ≥ 2 nad ciałem K. Wówczas skalar
(−1)
i+j
det(A
ij
)
(7.11)
nazywamy dopełnieniem algebraicznym elementu a
ij
w macierzy A.
Wniosek 7.1 możemy zatem wypowiedzieć nast
,
epuj
,
aco: Suma ele-
mentów jakiejś kolumny (wiersza) pomnożonych przez odpo-
wiednie dopełnienia algebraiczne elementów innej kolumny
(wiersza) jest równa 0.
7.2
Wzory Cramera
Niech dany b
,
edzie układ n równań liniowych z n niewiadomymi x
1
, x
2
,
..., x
n
nad ciałem K:
a
11
x
1
+ a
12
x
2
+ . . . + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ . . . + a
2n
x
n
= b
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a
n1
x
1
+ a
n2
x
2
+ . . . + a
nn
x
n
= b
n
.
(7.12)
Oznaczmy przez A
i
(dla i = 1, 2, . . . , n) macierz powstaj
,
ac
,
a z macie-
rzy A tego układu przez zast
,
apienie i-tej kolumny macierzy A kolumn
,
a

60
Wykłady z algebry liniowej I
wyrazów wolnych
b
1
b
2
..
.
b
n
. Zatem
A
1
=
b
1
a
12
. . . a
1n
b
2
a
22
. . . a
2n
..
.
..
.
. ..
..
.
b
n
a
n2
. . . a
nn
, . . . , A
n
=
a
11
a
12
. . . b
1
a
21
a
22
. . . b
2
..
.
..
.
. .. ...
a
n1
a
n2
. . . b
n
.
W = det(A) nazywamy wyznacznikiem głównym układu (7.12). Po-
nadto oznaczmy W
i
= det(A
i
) dla i = 1, . . . , n. Wówczas zachodzi
nast
,
epuj
,
ace
Twierdzenie 7.3 (Cramera). Jeżeli wyznacznik główny układu
(7.12) jest różny od zera, to układ ten posiada dokładnie jedno rozwi
,
azanie
dane wzorami Cramera:
x
1
=
W
1
W
, x
2
=
W
2
W
, . . . , x
n
=
W
n
W
.
(7.13)
Jeżeli zaś W = 0, ale W
i
6= 0 dla pewnego i = 1, . . . , n, to układ (7.12)
nie posiada rozwi
,
azania.
Dowód. Załóżmy, że (p
1
, p
2
, . . . , p
n
) ∈ K
n
jest rozwi
,
azaniem układu
(7.12). Weźmy dowole i = 1, 2, . . . , n i pomnóżmy j-te równanie przez
(−1)
j+i
det(A
ji
) dla j = 1, 2, . . . , n, a nast
,
epnie dodajmy stronami.
Wówczas z wniosku 7.1(ii) i z twierdzenia Laplace’a dla kolumn uzy-
skamy, że det(A) · p
i
= b
1
(−1)
1+i
det(A
1i
) + b
2
(−1)
2+i
det(A
2i
) + . . . +
b
n
(−1)
n+i
det(A
ni
). Ale stosuj
,
ac rozwini
,
ecie Laplace’a wzgl
,
edem i-tej
kolumny uzyskamy, że
W
i
= b
1
(−1)
1+i
det(A
1i
) + . . . + b
n
(−1)
n+i
det(A
ni
),
(7.14)
wi
,
ec
W · p
i
= W
i
dla i = 1, 2, . . . , n.
(7.15)
Jeżeli zatem W = 0 oraz W
i
6= 0 dla pewnego i, to na mocy (7.15)
mamy sprzeczność, czyli w tym przypadku układ (7.12) nie posiada
rozwi
,
azania. Jeżeli zaś W 6= 0, to p
i
=
W
i
W
dla i = 1, 2, . . . , n.

Rozwinięcie Laplace’a i wzory Cramera
61
Pozostaje zatem wykazać, że dla W 6= 0 ci
,
ag (x
1
, x
2
, . . . , x
n
) dany
wzorami (7.13) jest rozwi
,
azaniem układu (7.12). Dla i = 1, 2, . . . , n na
mocy (7.14) mamy, że a
i1
x
1
+ a
i2
x
2
+ . . . + a
in
x
n
=
n
X
j=1
a
ij
W
j
W
=
1
W
·
n
X
j=1
a
ij
W
j
=
1
W
·
n
X
j=1
a
ij
·
n
X
k=1
b
k
(−1)
k+j
det(A
kj
)
!
=
1
W
·
n
X
j=1
n
X
k=1
a
ij
b
k
(−1)
k+j
det(A
kj
) =
1
W
·
n
X
k=1
n
X
j=1
a
ij
b
k
(−1)
k+j
det(A
kj
) =
1
W
·
n
X
k=1
b
k
·
n
X
j=1
a
ij
(−1)
k+j
det(A
kj
)
!
. Ale na mocy wniosku 7.1(i) dla
k 6= i b
,
edzie
n
X
j=1
a
ij
(−1)
k+j
det(A
kj
) = 0 oraz
n
X
j=1
a
ij
(−1)
i+j
det(A
ij
) =
det(A) = W na mocy twierdzenia Laplace’a, wi
,
ec a
i1
x
1
+ a
i2
x
2
+ . . . +
a
in
x
n
=
1
W
b
i
W = b
i
dla i = 1, 2, . . . , n. Zatem ci
,
ag (x
1
, x
2
, . . . , x
n
)
dany wzorami (7.13) jest rozwi
,
azaniem układu (7.12).
Uwaga 7.2. Zauważmy, że twierdzenie Cramera nic nie mówi o
przypadku, gdy W = W
1
= W
2
= . . . = W
n
= 0. W takim przypadku
układ (7.12) może nie mieć rozwi
,
azania albo może mieć wi
,
ecej niż jedno
rozwi
,
azanie. Należy wówczas zastosować inn
,
a metod
,
e, np. eliminacj
,
e
Gaussa.
Uwaga 7.3. Układ równań (7.12), w którym det(A) 6= 0 nazywa
si
,
e układem Cramera.
Z uwagi 6.3 oraz z twierdzenia Cramera mamy natychmiast nast
,
epuj
,
acy
Wniosek 7.2. Jednorodny układ Cramera posiada dokładnie jedno
rozwi
,
azanie: x
1
= x
2
= . . . = x
n
= 0.
Przykład 7.1. Stosuj
,
ac wzory Cramera rozwi
,
ażemy nad ciałem
R układ równań:
62
Wykłady z algebry liniowej I
x
1
+ 2x
2
−
x
3
−
x
4
= −2
2x
1
− 3x
2
−
x
3
+ 2x
4
=
1
4x
1
− 5x
2
+ 2x
3
+ 3x
4
=
5
x
1
−
x
2
−
x
3
−
x
4
= −2
.
Obliczamy najpierw wyznacznik główny naszego układu. Stosu-
jemy kolejno: operacje k
4
+ k
1
, k
3
+ k
1
, k
2
+ k
1
, rozwini
,
ecie Laplace’a
wzgl
,
edem czwartego wiersza, rozwini
,
ecie Laplace’a wzgl
,
edem pierw-
szego wiersza:
W=
1
2 −1 −1
2 −3 −1
2
4 −5
2
3
1 −1 −1 −1
=
1
3 0 0
2 −1 1 4
4 −1 6 7
1
0 0 0
= (−1)
4+1
·1·
3 0 0
−1 1 4
−1 6 7
=
(−1) · 3 · (−1)
1+1
·
1 4
6 7
= (−3) · (7 − 24) = (−3) · (−17) = 51. St
,
ad
W = 51 6= 0, wi
,
ec z twierdzenia Cramera układ nasz posiada dokładnie
jedno rozwi
,
azanie. Obliczamy teraz wyznacznik W
1
stosuj
,
ac kolejno:
operacje k
1
+ k
2
, k
3
− k
4
, k
2
+ 2 · k
4
, rozwini
,
ecie Laplace’a wzgl
,
edem
pierwszego wiersza, operacj
,
e k
2
+ k
3
, rozwini
,
ecie Laplace’a wzgl
,
edem
drugiego wiersza:
W
1
=
−2
2 −1 −1
1 −3 −1
2
5 −5
2
3
−2 −1 −1 −1
=
0
2
0 −1
−2 −3 −3
2
0 −5 −1
3
−3 −1
0 −1
=
0
0
0 −1
−2
1 −3
2
0
1 −1
3
−3 −3
0 −1
= (−1)
1+4
· (−1) ·
−2
1 −3
0
1 −1
−3 −3
0
=
−2 −2 −3
0
0 −1
−3 −3
0
= 0, bo w ostatnim wyznaczniku mamy dwie iden-
tyczne kolumny. Post
,
epuj
,
ac podobnie obliczamy: W
2
= 0 i W
3
= 51.
Zatem ze wzorów Cramera: x
1
=
W
1
W
= 0, x
2
=
W
2
W
= 0 oraz x
3
=
W
3
W
= 1. Wyznacznika W
4
nie musimy już obliczać, bo z pierwszego
równania x
4
= x
1
+ 2x
2
− x
3
+ 2 = 0 + 0 − 1 + 2 = 1.

Rozdział 8
Algebra macierzy
8.1
Podstawowe operacje na macierzach
Oznaczmy przez M
m×n
(K) zbiór wszystkich m × n macierzy nad cia-
łem K. Jeżeli A ∈ M
m×n
(K), to przez [A]
ij
b
,
edziemy oznaczali wyraz
stoj
,
acy w i-tym wierszu i j-tej kolumnie macierzy A. Przypomnijmy
też, że elementy ciała K nazywamy skalarami.
1. Mnożenie macierzy przez skalar. Iloczynem macierzy A ∈
M
m×n
(K) przez skalar a ∈ K nazywamy macierz a · A ∈ M
m×n
(K)
tak
,
a, że
[a · A]
ij
= a · [A]
ij
dla wszystkich i = 1, . . . , m; j = 1, . . . , n. (8.1)
Zatem aby pomnożyć macierz A przez skalar a należy wszystkie
jej wyrazy pomnożyć przez ten skalar.
Zauważmy, że z tego
określenia wynikaj
,
a od razu wzory:
(a · b) · A = a · (b · A) dla dowolnych a, b ∈ K, A ∈ M
m×n
(K). (8.2)
1 · A = A dla każdego A ∈ M
m×n
(K).
(8.3)
2.
Dodawanie macierzy.
Sum
,
a macierzy A, B ∈ M
m×n
(K)
nazywamy macierz A + B ∈ M
m×n
(K) tak
,
a, że
[A + B]
ij
= [A]
ij
+ [B]
ij
dla wszystkich i = 1, . . . , m; j = 1, . . . , n.
(8.4)
63

64
Wykłady z algebry liniowej I
Z tego określenia dla dowolnych A, B, C ∈ M
m×n
(K), a, b ∈ K wyni-
kaj
,
a od razu wzory:
A + B = B + A.
(8.5)
A + (B + C) = (A + B) + C.
(8.6)
(a + b) · A = a · A + b · B.
(8.7)
a · (A + B) = a · A + a · B.
(8.8)
Oznaczmy przez 0
m×n
tak
,
a m×n-macierz, której wszystkie współrz
,
edne
s
,
a równe 0, czyli [0
m×n
]
ij
= 0 dla wszystkich i = 1, . . . , m; j = 1, . . . , n.
Macierz t
,
e nazywamy macierz
,
a zerow
,
a.
Z określenia dodawania macierzy wynika, że dla dowolej macierzy
A ∈ M
m×n
(K):
A + 0
m×n
= 0
m×n
+ A = A.
(8.9)
Macierz
,
a przeciwn
,
a do macierzy A ∈ M
m×n
(K) nazywamy macierz
−A ∈ M
m×n
(K) tak
,
a, że
[−A]
ij
= −[A]
ij
dla wszystkich i = 1, . . . , m; j = 1, . . . , n.
(8.10)
Z tego określenia oraz z definicji dodawania macierzy wynika od razu,
że dla dowolnej macierzy A ∈ M
m×n
(K):
A + (−A) = (−A) + A = 0
m×n
,
(8.11)
(−1) · A = −A.
(8.12)
3. Odejmowanie macierzy. Różnic
,
a macierzy A, B ∈ M
m×n
(K)
nazywamy macierz A − B ∈ M
m×n
(K) tak
,
a, że
[A − B]
ij
= [A]
ij
− [B]
ij
dla i = 1, . . . , m; j = 1, . . . , n.
(8.13)
Zatem dla dowolnych macierzy A, B ∈ M
m×n
(K):
A − B = A + (−B).
(8.14)
4. Mnożenie macierzy. Iloczyn A·B macierzy A i B o współczynni-
kach z ciała K określamy jedynie wówczas, gdy liczba kolumn macie-
rzy A jest równa liczbie wierszy macierzy B. Niech A ∈ M
m×n
(K)

Algebra macierzy
65
i B ∈ M
n×k
(K).
Iloczynem macierzy A i B
nazywamy macierz
A · B ∈ M
m×k
(K) tak
,
a, że
[A · B]
ij
=
n
X
t=1
[A]
it
· [B]
tj
dla i = 1, . . . , m; j = 1, . . . , k.
(8.15)
Zatem aby pomnożyć macierz A ∈ M
m×n
(K) przez macierz B ∈
M
n×k
(K) należy pierwszy wiersz macierzy A pomnożyć (skalarnie)
przez pierwsz
,
a kolumn
,
e macierzy B, nast
,
epnie należy pomnożyć pierw-
szy wiersz macierzy A przez drug
,
a kolumn
,
e macierzy B, itd. W ten
sposób uzyskamy kolejne wyrazy pierwszego wiersza macierzy A · B.
Aby otrzymać drugi wiersz macierzy A · B należy pomnożyć drugi
wiersz macierzy A przez kolejne kolumny macierzy B. W końcu należy
pomnożyć ostatni wiersz macierzy A kolejno przez wszystkie kolumny
macierzy B.
Przykład 8.1. Niech A =
1 0 2
3 1 0
i B =
2 1 1
3 1 0
0 1 4
. Wów-
czas B · A nie ma sensu (gdyż ilość kolumn macierzy B nie jest równa
ilości wierszy macierzy A) oraz A · B =
2 3 9
9 4 3
, bo
1 · 2 + 0 · 3 + 2 · 0 = 2 3 · 2 + 1 · 3 + 0 · 0 = 9
1 · 1 + 0 · 1 + 2 · 1 = 3 3 · 1 + 1 · 1 + 0 · 1 = 4
1 · 1 + 0 · 0 + 2 · 4 = 9 3 · 1 + 1 · 0 + 0 · 4 = 3
.
Wynika st
,
ad, że mnożenie macierzy nie jest na ogół przemienne.
Twierdzenie 8.1. Dla dowolnych macierzy A ∈ M
m×n
(K), B ∈
M
n×k
(K) zachodzi wzór:
(A · B)
T
= B
T
· A
T
.
Dowód. Z określenia macierzy transponowanej wynika, że A
T
∈
M
n×m
(K), B
T
∈ M
k×n
(K) oraz [A
T
]
ij
= [A]
ji
dla i = 1, . . . , n, j =
1, . . . , m i [B
T
]
ij
= [B]
ji
dla i = 1, . . . , k, j = 1, . . . , n. Zatem
B
T
· A
T
∈ M
k×m
(K), (A · B)
T
∈ M
k×m
(K). Ponadto dla wszystkich
możliwych i,j:

66
Wykłady z algebry liniowej I
[(A · B)
T
]
ij
= [A · B]
ji
=
m
X
t=1
[A]
jt
· [B]
ti
=
m
X
t=1
[A
T
]
tj
· [B
T
]
it
=
=
m
X
t=1
[B
T
]
it
· [A
T
]
tj
= [B
T
· A
T
]
ij
.
Twierdzenie 8.2. Mnożenie macierzy jest ł
,
aczne tzn. dla dowol-
nych macierzy A ∈ M
m×n
(K), B ∈ M
n×r
(K), C ∈ M
r×s
(K):
(A · B) · C = A · (B · C).
Dowód. Mamy, że A·B ∈ M
m×r
(K), B·C ∈ M
n×s
(K), (A·B)·C ∈
M
m×s
(K), A·(B ·C) ∈ M
m×s
(K). Zatem macierze A·(B ·C) i (A·B)·C
maj
,
a te same wymiary. Ponadto dla wszystkich możliwych i, j:
[(A · B) · C]
ij
=
r
X
t=1
[A · B]
it
· [C]
tj
r
X
t=1
n
X
l=1
[A]
il
· [B]
lt
!
· [C]
tj
=
=
r
X
t=1
n
X
l=1
([A]
il
· [B]
lt
) · [C]
tj
=
r
X
t=1
n
X
l=1
[A]
il
· ([B]
lt
· [C]
tj
) =
n
X
l=1
r
X
t=1
[A]
il
· ([B]
lt
· [C]
tj
) =
n
X
l=1
[A]
il
·
r
X
t=1
[B]
lt
· [C]
tj
!
=
n
X
l=1
[A]
il
· [B · C]
lj
= [A · (B · C)]
ij
.
Twierdzenie 8.3. Dla każdego a ∈ K i dla dowolnych macierzy
A ∈ M
m×n
(K), B ∈ M
n×k
(K):
a · (A · B) = (a · A) · B = A · (a · B).
Dowód. Dla i = 1, . . . , m, j = 1, . . . , k: [(a · A) · B]
ij
=
=
n
X
t=1
[a · A]
it
· [B]
tj
=
n
X
t=1
(a · [A]
it
) · [B]
tj
= a ·
n
X
t=1
[A]
it
· [B]
tj
=
= a · [A · B]
ij
= [a · (A · B)]
ij
oraz [A · (a · B)]
ij
=
n
X
t=1
[A]
it
· [a · B]
tj
=
n
X
t=1
[A]
it
· (a · [B]
tj
) = a ·
n
X
t=1
[A]
it
· [B]
tj
= a · [A · B]
ij
= [a · (A · B)]
ij
.

Algebra macierzy
67
Twierdzenie 8.4. Mnożenie macierzy jest rozdzielne wzgl
,
edem
dodawania macierzy tzn.
(i) A·(B +C) = A·B +A·C dla dowolnych A ∈ M
m×n
(K), B, C ∈
M
n×k
(K) oraz
(ii) (B +C)·A = B ·A+C ·A dla dowolnych B, C ∈ M
m×n
(K), A ∈
M
n×k
(K).
Dowód. (i). Wystarczy wykazać, że dla wszystkich możliwych i, j:
[A·(B+C)]
ij
= [A·B+A·C]
ij
. Ale [A·(B+C)]
ij
=
n
X
t=1
[A]
it
[B + C]
tj
=
n
X
t=1
[A]
it
· ([B]
tj
+ [C]
tj
) =
n
X
t=1
([A]
it
· [B]
tj
+ [A]
it
· [C]
tj
) =
n
X
t=1
[A]
it
· [B]
tj
+
n
X
t=1
[A]
it
· [C]
tj
= [A · B]
ij
+ [A · C]
ij
= [A · B + A · C]
ij
.
(ii) można udowodnić podobnie jak (i).
8.2
Algebra macierzy kwadratowych
B
,
edziemy dalej pisali M
n
(K) zamiast M
n×n
(K) oraz 0
n
zamiast 0
n×n
.
Dla dowolnych A, B ∈ M
n
(K) mamy, że A + B, A · B ∈ M
n
(K). Po-
nadto mnożenie macierzy kwadratowych jest ł
,
aczne i rozdzielne wzgl
,
e-
dem dodawania macierzy.
Przykład 8.2. Niech n ≥ 2 oraz niech A, B ∈ M
n
(K) b
,
ed
,
a takimi
macierzami, że [A]
11
= 1 i [A]
ij
= 0 dla pozostałych i, j oraz [B]
12
= 1
i [B]
ij
= 0 dla pozostałych i, j. Wtedy B · A = 0
n
oraz A · B = B.
Zatem A · B 6= B · A, czyli mnożenie macierzy kwadratowych stopnia
wi
,
ekszego od 1 nie jest przemienne!.
Macierz
,
a jednostkow
,
a stopnia n nazywamy macierz I
n
∈ M
n
(K),
która ma na głównej przek
,
atnej same jedynki, zaś na pozostałych miej-
scach same zera tzn. [I
n
]
ii
= 1 dla i = 1, 2, . . . , n oraz [I
n
]
ij
= 0 dla
wszystkich i 6= j.
Twierdzenie 8.5. Macierz jednostkowa stopnia n jest elementem
neutralnym mnożenia macierzy w zbiorze M
n
(K) tzn.

68
Wykłady z algebry liniowej I
I
n
· A = A · I
n
= A
dla dowolnej macierzy A ∈ M
n
(K).
Dowód. Dla wszystkich i, j = 1, 2, . . . , n mamy, że [I
n
· A]
ij
=
n
X
t=1
[I
n
]
it
· [A]
tj
= [I
n
]
ii
· [A]
ij
= 1 · [A]
ij
= [A]
ij
oraz [A · I
n
]
ij
=
n
X
t=1
[A]
it
· [I
n
]
tj
= [A]
ij
·[I
n
]
jj
= [A]
ij
·1 = [A]
ij
. Zatem I
n
·A = A·I
n
= A
dla każdego A ∈ M
n
(K).
Macierz
,
a skalarn
,
a stopnia n nazywamy macierz postaci:
a · I
n
dla dowolnego a ∈ K.
Zatem macierz skalarna ma na głównej przek
,
atnej wspólny skalar a, zaś
na pozostałych miejscach same zera. Z poznanych własności mnożenia
macierzy mamy, że dla dowolnej macierzy A ∈ M
n
(K) i dla dowolnego
a ∈ K jest (a·I
n
)·A = a·(I
n
·A) = a·A oraz A·(a·I
n
) = a·(A·I
n
) = a·A.
Twierdzenie 8.6 (Cauchy’ego). Dla dowolnych macierzy kwa-
dratowych A i B tego samego stopnia nad ciałem K zachodzi wzór:
det(A · B) = det(A) · det(B).
Dowód. Niech A, B ∈ M
n
(K). Wówczas [A · B] =
n
X
s=1
[A]
is
· [B]
sj
dla i, j = 1, 2, . . . , n. Zatem każdy wyraz i-tego wiersza macierzy A · B
jest sum
,
a n składników postaci [A]
is
· [B]
sj
. Oznaczmy przez H
j
j-t
,
a
kolumn
,
e macierzy A·B oraz przez A
j
j-t
,
a kolumn
,
e macierzy A. Wtedy
b
,
edziemy mieli, że

Algebra macierzy
69
H
j
=
n
X
s=1
[A]
1s
[B]
sj
n
X
s=1
[A]
2s
[B]
sj
..
.
n
X
s=1
[A]
ns
[B]
sj
=
n
X
s=1
[B]
sj
· A
s
.
Zatem A·B =
"
n
X
s
1
=1
[B]
s
1
1
· A
s
1
,
n
X
s
2
=1
[B]
s
2
2
· A
s
2
, . . . ,
n
X
s
n
=1
[B]
s
n
n
· A
s
n
#
,
sk
,
ad z własności 6.4 stosowanej n-krotnie b
,
edziemy mieli, że
det(A · B) =
n
X
s
1
=1
n
X
s
2
=1
. . .
n
X
s
n
=1
[B]
s
1
1
[B]
s
2
2
. . . [B]
s
n
n
det([A
s
1
, A
s
2
, . . . , A
s
n
]).
Ale jeżeli dwie kolumny macierzy s
,
a identyczne, to jej wyznacznik jest
równy 0, wi
,
ec tylko te składniki naszej sumy mog
,
a być niezerowe,
dla których s
j
i s
k
s
,
a różne dla j 6= k, czyli tylko te, dla których
s
1
, s
2
, . . . , s
n
jest permutacj
,
a liczb 1, 2, . . . , n. Ale dla f ∈ S
n
na mocy
własności 6.3:
det([A
f (1)
, A
f (2)
, . . . , A
f (n)
]) = sgn(f ) · det([A
1
, A
2
, . . . , A
n
]) = sgn(f ) ·
det(A), wi
,
ec det(A · B) = det(A) ·
X
f ∈S
n
sgn(f )[B]
f (1)1
[B]
f (2)2
. . . [B]
f (n)n
= det(A) · det(B
T
) = det(A) · det(B).
Definicja 8.1. Macierz
,
a dopełnień macierzy A ∈ M
n
(K) nazy-
wamy macierz postaci
D(A) =
(−1)
i+j
det(A
ij
)
i,j=1,2,...,n
.
(8.16)

70
Wykłady z algebry liniowej I
Twierdzenie 8.7. Dla dowolnej macierzy A ∈ M
n
(K) zachodzi
wzór:
A · D(A) = D(A) · A = det(A) · I
n
.
Dowód. Dla dowolnych i, j ∈ {1, 2, . . . , n}:
[A · D(A)]
ij
=
n
X
t=1
[A]
it
[D(A)]
tj
=
n
X
t=1
[A]
it
(−1)
t+j
det(A
tj
).
Zatem z twierdzenia Laplace’a oraz z wniosku 7.1: [A·D(A)]
ii
= det(A)
dla i = 1, 2, . . . , n oraz dla i 6= j: [A · D(A)]
ij
= 0. St
,
ad A · D(A) =
det(A) · I
n
.
Podobnie dla i, j ∈ {1, 2, . . . , n}:
[A · D(A)]
ij
=
n
X
t=1
[D(A)]
it
[A]
tj
=
n
X
t=1
(−1)
i+t
det(A
it
)[A]
tj
,
wi
,
ec z twierdzenia Laplace’a i z wniosku 7.1, [D(A) · A]
ii
= det(A)
dla i = 1, 2, . . . , n oraz dla i 6= j mamy, że [D(A) · A]
ij
= 0. Zatem
D(A) · A = det(A) · I
n
.
8.3
Odwracanie macierzy
Definicja 8.2. Powiemy, że macierz A ∈ M
n
(K) jest odwracalna,
jeżeli istnieje taka macierz B ∈ M
n
(K), że
A · B = B · A = I
n
.
(8.17)
Uwaga 8.1. Macierz B we wzorze (8.17) jest wyznaczona jed-
noznacznie (przez macierz A). Rzeczywiście, niech dodatkowo C ∈
M
n
(K) b
,
edzie takie, że A · C = C · A = I
n
. Wtedy C = C · I
n
=
C · (A · B) = (C · A) · B = I
n
· B = B, czyli C = B. W zwi
,
azku z tym
macierz B nazywamy macierz
,
a odwrotn
,
a do macierzy A i oznaczamy
przez A
−1
.

Algebra macierzy
71
Twierdzenie 8.8. Macierz A ∈ M
n
(K) jest odwracalna wtedy
i tylko wtedy, gdy det(A) 6= 0. Jeżeli det(A) 6= 0, to zachodzi wzór:
A
−1
=
1
det(A)
· D(A)
T
.
(8.18)
Dowód.
Załóżmy, że macierz A jest odwracalna.
Wtedy ist-
nieje macierz B ∈ M
n
(K) taka, że A · B = I
n
. Zatem z twierdze-
nia Cauchy’ego det(A) · det(B) = det(I
n
).
Ale det(I
n
) = 1, wi
,
ec
det(A) · det(B) = 1, sk
,
ad det(A) 6= 0.
Na odwrót, załóżmy, że det(A) 6= 0. Wówczas z twierdzenia 8.7:
A ·
1
det(A)
· D(A)
T
=
1
det(A)
· A · D(A)
T
=
1
det(A)
· (det(A) · I
n
) = I
n
i podobnie
1
det(A)
· D(A)
T
·A = I
n
. Zatem macierz A jest odwracalna
i zachodzi wzór (8.18).
Uwaga 8.2. Macierze A ∈ M
n
(K) o wyznaczniku różnym od zera
nazywamy macierzami nieosobliwymi.
Twierdzenie 8.9. Dla dowolnych macierzy A, B ∈ M
n
(K) nast
,
e-
puj
,
ace warunki s
,
a równoważne:
(i) B = A
−1
,
(ii) A · B = I
n
,
(iii) B · A = I
n
.
Dowód. Implikacja (i) ⇒ (ii) jest oczywista.
(ii) ⇒ (iii). Niech A · B = I
n
. Wtedy z twierdzenia Cauchy’ego
det(A) · det(B) = det(I
n
) = 1, sk
,
ad det(A) 6= 0 i na mocy twierdzenia
8.8 istnieje A
−1
. St
,
ad A
−1
· (A · B) = A
−1
· I
n
, czyli (A
−1
· A) · B = A
−1
,
a wi
,
ec I
n
· B = A
−1
, czyli B = A
−1
. Zatem z określenia macierzy
odwrotnej B · A = I
n
.
(iii) ⇒ (i). Załóżmy, że B · A = I
n
. Wtedy z twierdzenia Cau-
chy’ego: det(B) · det(A) = det(I
n
) = 1, czyli det(A) 6= 0. Zatem
z twierdzenia 8.8 istnieje A
−1
oraz (B · A) · A
−1
= I
n
· A
−1
, wi
,
ec
B · (A · A
−1
) = A
−1
, sk
,
ad B · I
n
= A
−1
, a zatem B = A
−1
.

72
Wykłady z algebry liniowej I
Twierdzenie 8.10. Iloczyn macierzy odwracalnych jest macierz
,
a
odwracaln
,
a. Dokładniej, jeżeli macierze A
1
, A
2
, . . . , A
m
∈ M
n
(K) s
,
a
odwracalne, to zachodzi wzór:
(A
1
· A
2
· . . . · A
m
)
−1
= A
−1
m
· A
−1
m−1
· . . . · A
−1
2
· A
−1
1
.
(8.19)
Dowód. Zauważmy, że (A
1
· A
2
· A
m
) · (A
−1
m
· A
−1
m−1
· . . . · A
−1
1
) =
(A
1
· . . . · A
m−1
) · (A
−1
m−1
· . . . · A
−1
1
) = . . . = A
1
· A
−1
1
= I
n
. Zatem na
mocy twierdzenia 8.9 mamy tez
,
e.
8.4
Odwracanie macierzy przy pomocy
operacji elementarnych
Z definicji mnożenia macierzy wynika, że dla dowolnej macierzy
A ∈ M
n
(K) operacji elementarnej na wierszach macierzy A odpowiada
pomnożenie macierzy A z lewej strony przez macierz, która powstaje
z macierzy jednostkowej I
n
przez wykonanie na niej tej samej operacji.
Stosuj
,
ac operacje elementarne na wierszach nieosobliwej macierzy
A możemy j
,
a przekształcić przy pomocy algorytmu Gaussa do macie-
rzy jednostkowej I
n
. Wynika st
,
ad, że istniej
,
a macierze B
1
, B
2
, . . . , B
s
takie, że
B
s
· . . . · B
2
· B
1
· A = I
n
.
(8.20)
Zatem A
−1
= B
s
· . . . · B
2
· B
1
, czyli A
−1
= B
s
· . . . · B
2
· B
1
· I
n
. St
,
ad
macierz A
−1
powstaje z macierzy I
n
przez wykonanie na niej
tych samych operacji elementarnych, co na macierzy A.
W praktyce przy obliczaniu macierzy odwrotnej do macierzy nie-
osobliwej A przy pomocy operacji elementarnych na wierszach
post
,
epujemy w sposób nast
,
epuj
,
acy. Z prawej strony macierzy A do-
pisujemy macierz jednostkow
,
a I
n
tego samego stopnia. Na wierszach
otrzymanej w ten sposób macierzy blokowej [A|I
n
] wykonujemy ope-
racje elementarne aż do uzyskania macierzy blokowej postaci [I
n
|B].
Macierz B jest wtedy macierz
,
a odwrotn
,
a do macierzy A, tj. B = A
−1
.

Rozdział 9
Przestrzenie liniowe
9.1
Określenie przestrzeni liniowej
Niech K b
,
edzie dowolnym ciałem, V -niepustym zbiorem, w którym
określone jest działanie dodawania + i operacja ◦ : K × V −→ V
mnożenia przez elementy z ciała K (przy czym dla a ∈ K oraz α ∈ V
b
,
edziemy pisali a ◦ α zamiast ◦((a, α))) oraz wyróżniony jest element
Θ ∈ V .
Elementy zbioru V b
,
edziemy nazywali wektorami, wektor Θ wekto-
rem zerowym, a elementy ciała K skalarami. Używać b
,
edziemy grec-
kich liter do oznaczania wektorów, a łacińskich do oznaczania skalarów.
Zbiór V (z działaniem +, operacj
,
a ◦ mnożenia przez skalary z ciała
K oraz wyróżnionym elementem Θ) nazywamy przestrzeni
,
a liniow
,
a
nad ciałem K, jeśli spełnione s
,
a nast
,
epuj
,
ace warunki (aksjomaty prze-
strzeni liniowych):
A1. ∀
α,β∈V
α + β = β + α, tj. działanie + jest przemienne;
A2. ∀
α,β,γ∈V
α + (β + γ) = (α + β) + γ, tj. działanie + jest ł
,
aczne;
A3. ∀
α∈V
α + Θ = α, tj. wektor Θ jest elementem neutralnym
działania +;
A4. ∀
α∈V
∃
δ∈V
α + δ = Θ;
A5. ∀
α,β∈V
∀
a∈K
a ◦ (α + β) = a ◦ α + a ◦ β;
A6. ∀
α∈V
∀
a,b∈K
(a + b) ◦ α = a ◦ α + b ◦ α;
73

74
Wykłady z algebry liniowej I
A7. ∀
α∈V
∀
a,b∈K
(a · b) ◦ α = a ◦ (b ◦ α);
A8. ∀
α∈V
1 ◦ α = α.
9.2
Przykłady przestrzeni liniowych
Przykład 9.1. Zbiór jednoelementowy V = {α} z działaniem +
takim, że α + α = α oraz wyróżnionym elementem Θ = α jest prze-
strzeni
,
a liniow
,
a nad dowolnym ciałem K, jeżeli mnożenie ◦ określimy
wzorem: a ◦ α = α dla każdego a ∈ K. Przestrzenie takiej postaci
nazywamy zerowymi.
Przykład 9.2. Niech n b
,
edzie ustalon
,
a liczb
,
a naturaln
,
a, a K do-
wolnym ciałem. Niech K
n
b
,
edzie zbiorem wszystkich ci
,
agów postaci
[a
1
, a
2
, . . . , a
n
], gdzie a
1
, . . . , a
n
∈ K. Sum
,
e dwu ci
,
agów
α = [a
1
, a
2
, . . . , a
n
], β = [b
1
, b
2
, . . . , b
n
] określamy jako
[a
1
+ b
1
, a
2
+ b
2
, . . . , a
n
+ b
n
]; iloczyn a ◦ α dla a ∈ K określamy jako
[aa
1
, aa
2
, . . . , aa
n
]. Niech ponadto Θ = [0, 0, . . . , 0
|
{z
}
n
]. Łatwo sprawdzić,
że aksjomaty A1-A8 s
,
a w tym przypadku spełnione, a wi
,
ec zbiór K
n
z tak określonym dodawaniem i mnożeniem przez skalary oraz z wy-
różnionym wektorem Θ jest przestrzeni
,
a liniow
,
a nad ciałem K. Prze-
strzeń t
,
e oznacza si
,
e przez K
n
i nazywa n-wymiarow
,
a przestrzeni
,
a li-
niow
,
a współrz
,
ednych nad ciałem K. Dla wektora [a
1
, a
2
, . . . , a
n
] ∈ K
n
element a
i
dla i = 1, 2, . . . , n nazywamy i-t
,
a współrz
,
edn
,
a lub i-t
,
a skła-
dow
,
a tego wektora.
Przykład 9.3. Dla dowolnego ciała K oznaczmy przez K
∞
zbiór
wszystkich ci
,
agów nieskończonych [a
1
, a
2
, . . .] o wyrazach z tego ciała.
Dodawanie takich ci
,
agów i mnożenie przez skalary określamy nast
,
epuj
,
a-
co:
[a
1
, a
2
, . . .] + [b
1
, b
2
, . . .] = [a
1
+ b
1
, a
2
+ b
2
, . . .],
a ◦ [a
1
, a
2
, . . .] = [aa
1
, aa
2
, . . .].
Natomiast wektor zerowy określamy jako Θ = [0, 0, . . .]. Łatwo spraw-
dzić, że wówczas aksjomaty A1-A8 też s
,
a spełnione. Otrzyman
,
a w ten
sposób przestrzeń liniow
,
a oznaczamy przez K
∞
.

Przestrzenie liniowe
75
Przykład 9.4. Niech L b
,
edzie dowolnym ciałem. Wówczas pod-
zbiór K ⊆ L zawieraj
,
acy 0 i 1, który jest ciałem ze wzgl
,
edu na wszyst-
kie działania określone w ciele L nazywamy podciałem ciała L. W tej
sytuacji L z działaniem dodawania + ciała, operacj
,
a mnożenia przez
elementy z ciała K i wyróżnionym elementem Θ = 0 jest przestrzeni
,
a
liniow
,
a nad ciałem K. Oznaczamy j
,
a przez L
K
. W szczególności ciało
K jest przestrzeni
,
a liniow
,
a nad K oraz R jest w naturalny sposób
przestrzeni
,
a liniow
,
a nad ciałem liczb wymiernych Q oraz C jest prze-
strzeni
,
a liniow
,
a nad ciałem liczb rzeczywistych.
Przykład 9.5. Zbiór R[x] wszystkich wielomianów zmiennej x
o współczynnikach rzeczywistych ze zwykłym dodawaniem wielomia-
nów i z naturalnym mnożeniem wielomianów przez liczby rzeczywiste
oraz z wyróżnionym elementem Θ = 0 jest przestrzeni
,
a liniow
,
a nad
ciałem R. Oznaczamy j
,
a przez R[x].
Przykład 9.6. Niech m i n b
,
ed
,
a ustalonymi liczbami natural-
nymi i niech K b
,
edzie ciałem. Wówczas zbiór M
m×n
(K) wszystkich
m × n-macierzy o wyrazach z ciała K z naturalnym dodawaniem ma-
cierzy i mnożeniem przez skalary oraz z wyróżnionym elementem Θ =
0
m×n
tworzy przestrzeń liniow
,
a nad ciałem K. Oznaczamy j
,
a przez
M
m×n
(K).
Przykład 9.7. Zbiór wszystkich równań liniowych z n niewiado-
mymi x
1
, x
2
, . . . , x
n
o współczynnikach z ciała K, z naturalnym doda-
waniem równań stronami i naturaln
,
a operacj
,
a mnożenia równań przez
skalary oraz z wektorem Θ rozumianym jako równanie 0 · x
1
+ 0 · x
2
+
. . . + 0 · x
n
= 0 jest przestrzeni
,
a liniow
,
a.
Przykład 9.8.
Niech X b
,
edzie dowolnym niepustym zbiorem
i niech K b
,
edzie ciałem. Oznaczmy przez K
X
zbiór wszystkich funkcji
f : X → K. Dodawanie funkcji z tego zbioru określamy wzorem:
(f + g)(x) = f (x) + g(x) dla x ∈ X.
Natomiast mnożenie przez skalary określamy wzorem:
(a ◦ f )(x) = a · f (x) dla x ∈ X.

76
Wykłady z algebry liniowej I
Łatwo sprawdzić, że w ten sposób otrzymujemy przestrzeń liniow
,
a nad
ciałem K, któr
,
a oznaczamy przez K
X
.
9.3
Własności działań na wektorach
Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad ciałem K. Wówczas
Własność 9.1. Prawo skracania równości:
∀
α,β,γ∈V
[α + β = α + γ ⇒ β = γ].
Dowód. Załóżmy, że α + β = α + γ. Z A4 i z A1 istnieje δ ∈ V
takie, że δ + α = Θ. Zatem z A2 mamy, że (δ + α) + β = (δ + α) + γ,
czyli Θ + β = Θ + γ, a wi
,
ec z A3 i A1 β = γ.
Własność 9.2. Dla każdego wektora α ∈ V istnieje dokładnie
jeden wektor δ ∈ V taki, że α + δ = Θ.
Dowód. Istnienie takiego wektora δ wynika z A4. Jeśli zaś δ
1
∈ V
jest takie, że α + δ
1
= Θ, to α + δ
1
= α + δ, wi
,
ec z własności 9.1 mamy,
że δ
1
= δ.
Uwaga 9.1. Wektor δ ∈ V taki, że α + δ = Θ nazywamy wekto-
rem przeciwnym do wektora α i oznaczamy przez −α. Ponieważ z A1
(−α) + α = Θ, wi
,
ec α jest wektorem przeciwnym do wektora (−α),
czyli mamy wzór:
− (−α) = α dla każdego α ∈ V.
(9.1)
Uwaga 9.2. Można udowodnić, że suma n wektorów z przestrzeni
V nie zależy od sposobu rozstawienia nawiasów. Ponadto z przemien-
ności dodawania wektorów wynika, że suma n wektorów nie zależy też
od kolejności składników.
Własność 9.3. Dla dowolnych wektorów α
1
, α
2
, . . . , α
n
∈ V za-
chodzi wzór:
− (α
1
+ α
2
+ . . . + α
n
) = (−α
1
) + (−α
2
) + . . . + (−α
n
).
(9.2)

Przestrzenie liniowe
77
Dowód. Mamy, że (α
1
+ . . . + α
n
) + [(−α
1
) + . . . + (−α
n
)] =
(α
1
+ (−α
1
)) + . . . + (α
n
+ (−α
n
)) = Θ + . . . + Θ = Θ. Zatem wektor
(−α
1
)+. . .+(−α
n
) jest wektorem przeciwnym do wektora α
1
+. . .+α
n
,
sk
,
ad mamy nasz wzór.
Własność 9.4. Dla dowolnych wektorów α, β ∈ V istnieje dokład-
nie jeden wektor γ ∈ V taki, że α + γ = β. Mianowicie γ = β + (−α).
B
,
edziemy go nazywali różnic
,
a wektorów α i β i oznaczali przez β − α.
Dowód. Mamy, że α + [β + (−α)] = [α + (−α)] + β = Θ + β = β.
Jeżeli ponadto γ
1
∈ V jest takie, że α + γ
1
= β, to α + γ
1
= α + γ,
wi
,
ec z własności 9.1 mamy, że γ
1
= γ.
Uwaga 9.3. Oczywiście dla dowolnego wektora α ∈ V : α −α = Θ,
bo α − α = α + (−α) = Θ.
Własność 9.5. 0 ◦ α = Θ dla dowolnego wektora α ∈ V .
Dowód. Ponieważ 0 = 0+0, wi
,
ec na mocy A6: 0◦α = (0+0)◦α =
0 ◦ α + 0 ◦ α. Zatem z A3 0 ◦ α + Θ = 0 ◦ α + 0 ◦ α i z własności 9.1
Θ = 0 ◦ α.
Własność 9.6. −α = (−1) ◦ α dla dowolnego wektora α ∈ V .
Dowód. Ponieważ α = 1◦α na mocy A8, wi
,
ec z A6 α+(−1)◦α =
1 ◦ α + (−1) ◦ α = (1 + (−1)) ◦ α = 0 ◦ α = Θ na mocy własności 9.5.
Własność 9.7. a ◦ Θ = Θ dla każdego a ∈ K.
Dowód. Z A3 mamy, że Θ = Θ + Θ, wi
,
ec na mocy A5: a ◦ Θ =
a ◦ (Θ + Θ) = a ◦ Θ + a ◦ Θ, czyli na mocy A3, a ◦ Θ + Θ = a ◦ Θ + a ◦ Θ,
wi
,
ec z własności 9.1, Θ = a ◦ Θ.
Własność 9.8. a ◦ α 6= Θ dla dowolnych 0 6= a ∈ K, Θ 6= α ∈ V .
Dowód. Załóżmy, że 0 6= a ∈ K, Θ 6= α ∈ V i a ◦ α = Θ. Wtedy
z własności 9.7 mamy, że Θ = a
−1
◦ (a ◦ α) = (a
−1
· a) ◦ α = 1 ◦ α = α
na mocy A7 i A8, sk
,
ad α = Θ i mamy sprzeczność.
Uwaga 9.4. Z własności 9.5, 9.7 i 9.8 wynika od razu, że dla
dowolnych a ∈ K, α ∈ V :
a ◦ α = Θ ⇔ [a = 0 lub α = Θ].

78
Wykłady z algebry liniowej I
Własność 9.9. (−a) ◦ α = a ◦ (−α) = −(a ◦ α) dla dowolnych
a ∈ K, α ∈ V .
Dowód. Na mocy A6 i własności 9.5 mamy, że (−a) ◦ α + a ◦ α =
((−a) + a) ◦ α = 0 ◦ α = Θ, sk
,
ad (−a) ◦ α = −(a ◦ α). Ponadto z A5
i własności 9.7 a ◦ (−α) + a ◦ α = a ◦ (α + (−α)) = a ◦ Θ = Θ, wi
,
ec
a ◦ (−α) = −(a ◦ α).
Własność 9.10. Dla dowolnego a ∈ K i dla dowolnych wektorów
α
1
, α
2
, . . . , α
n
∈ V :
a ◦ (α
1
+ α
2
+ . . . + α
n
) = a ◦ α
1
+ a ◦ α
2
+ . . . + a ◦ α
n
.
Dowód. Indukcja wzgl
,
edem n. Dla n = 2 teza wynika z A5.
Załóżmy teraz, że teza zachodzi dla pewnej liczby naturalnej n ≥ 2
i niech α
1
, . . . , α
n
, α
n+1
∈ V . Wtedy z założenia indukcyjnego
a ◦ (α
1
+ . . . + α
n
) = a ◦ α
1
+ . . . + a ◦ α
n
.
Zatem na mocy A5 a ◦ (α
1
+ . . . + α
n
+ α
n+1
) = a ◦ ((α
1
+ . . . + α
n
) +
α
n+1
) = a ◦ (α
1
+ . . . + α
n
) + a ◦ α
n+1
= a ◦ α
1
+ . . . + a ◦ α
n
+ a ◦ α
n+1
,
czyli teza zachodzi dla liczby n + 1.
Z własności 9.10 i z A7 wynika od razu
Własność 9.11. Dla dowolnych a, a
1
, . . . , a
n
∈ K, α
1
, . . . , α
n
∈ V :
a ◦ (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = (a · a
1
) ◦ α
1
+ . . . + (a · a
n
) ◦ α
n
.
Uwaga 9.5. Z udowodnionych własności działań na wektorach
można łatwo wyprowadzić nast
,
epuj
,
ace prawa rachunkowe dotycz
,
ace
odejmowania wektorów:
α − (β + γ) = (α − β) − γ, α − (β − γ) = (α − β) + γ,
−(α + β) = (−α) − β, −(α − β) = (−α) + β,
a ◦ (α − β) = a ◦ α − a ◦ β, (a − b) ◦ α = a ◦ α − b ◦ β,
(−a) ◦ (−α) = a ◦ α.

Rozdział 10
Podprzestrzenie przestrzeni
liniowych
10.1
Określenie podprzestrzeni
Definicja 10.1. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad ciałem
K.
Niepusty podzbiór V
1
przestrzeni V nazywamy podprzestrzeni
,
a
przestrzeni V , jeśli ma on nast
,
epuj
,
ace własności:
(I) suma dowolnych dwu wektorów należ
,
acych do V
1
należy do V
1
,
(II) jeśli α ∈ V
1
i a ∈ K, to a ◦ α ∈ V
1
.
Uwaga 10.1. Wektor zerowy Θ należy do każdej podprze-
strzeni V
1
przestrzeni V .
Rzeczywiście, ponieważ V
1
6= ∅, wi
,
ec
istnieje α ∈ V
1
i wówczas z (II) mamy, że 0 ◦ α ∈ V
1
, sk
,
ad z własności
9.5 jest Θ ∈ V
1
.
Uwaga 10.2. Podprzestrzeń V
1
przestrzeni liniowej V nad ciałem
K jest przestrzeni
,
a liniow
,
a nad ciałem K wzgl
,
edem dodawania wek-
torów zredukowanego do V
1
i mnożenia przez skalary zredukowanego
do V
1
. Sprawdzenie prawdziwości aksjomatów A1-A8 nie przedstawia
trudności. Np. z (II) oraz z własności 9.6 wynika, że −α ∈ V
1
dla
każdego α ∈ V
1
.
Każda przestrzeń liniowa V zawiera co najmniej dwie podprzestrze-
nie: zbiór V oraz podprzestrzeń złożon
,
a tylko z wektora Θ. Pierwsz
,
a
79

80
Wykłady z algebry liniowej I
z tych podprzestrzeni nazywamy niewłaściw
,
a, a drug
,
a zerow
,
a.
Twierdzenie 10.1. Cz
,
eść wspólna dowolnej niepustej rodziny pod-
przestrzeni danej przestrzeni liniowej V nad ciałem K jest podprze-
strzeni
,
a przestrzeni V .
Dowód. Niech W b
,
edzie dowoln
,
a niepust
,
a rodzin
,
a podprzestrzeni
przestrzeni liniowej V nad ciałem K i niech W
0
=
\
W ∈W
W . Z uwagi
10.1 mamy, że Θ ∈ W dla każdego W ∈ W. Zatem Θ ∈ W
0
. Niech
α, β ∈ W
0
. Wtedy α, β ∈ W dla każdego W ∈ W, sk
,
ad α + β ∈ W
dla każdego W ∈ W, wi
,
ec α + β ∈ W
0
. Jeśli a ∈ K oraz α ∈ W
0
, to
α ∈ W dla każdego W ∈ W, sk
,
ad a ◦ α ∈ W dla każdego W ∈ W,
wi
,
ec a ◦ α ∈ W
0
. Zatem W
0
jest podprzestrzeni
,
a przestrzeni V .
10.2
Podprzestrzenie generowane i ich
własności
Twierdzenie 10.2. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad cia-
łem K i niech A b
,
edzie dowolnym podzbiorem przestrzeni V . Istnieje
najmniejsza (w sensie inkluzji) podprzestrzeń przestrzeni V zawieraj
,
aca
A.
Dowód. Oznaczmy przez W rodzin
,
e wszystkich podprzestrzeni W
przestrzeni V takich, że A ⊆ W . Rodzina W jest niepusta, bo np. V ∈
W. Z twierdzenia 10.1 mamy, że W
0
=
\
W ∈W
W jest podprzestrzeni
,
a
przestrzeni V , a ponieważ A ⊆ W dla każdego W ∈ W, wi
,
ec A ⊆ W
0
.
Niech teraz V
1
b
,
edzie podprzestrzeni
,
a przestrzeni V tak
,
a, że A ⊆ V
1
.
Wtedy V
1
∈ W, sk
,
ad W
0
⊆ V
1
. Zatem W
0
jest najmniejsz
,
a w sensie
inkluzji podprzestrzeni
,
a przestrzeni V zawieraj
,
ac
,
a zbiór A.
Uwaga 10.3. Najmniejsz
,
a podprzestrzeń przestrzeni liniowej V
zawieraj
,
ac
,
a zbiór A ⊆ V nazywamy podprzestrzeni
,
a rozpi
,
et
,
a na pod-
zbiorze A lub generowan
,
a przez podzbiór A i oznaczamy przez lin(A).
Z tego określenia wynika od razu, że lin(∅) = {Θ}.
Jeśli zbiór A jest skończony i A = {α
1
, α
2
, . . . , α
n
}, to zamiast

Podprzestrzenie przestrzeni liniowych
81
lin({α
1
, α
2
, . . . , α
n
}) b
,
edziemy pisali lin(α
1
, α
2
, . . . , α
n
).
Zauważmy, że dla każdego α ∈ V jest lin(α) = {a ◦ α : a ∈ K}.
Rzeczywiście, α = 1 ◦ α ∈ {a ◦ α : a ∈ K} oraz dla dowolnych a, b ∈ K
mamy, że a ◦ α + b ◦ α = (a + b) ◦ α i a ◦ (b ◦ α) = (ab) ◦ α, wi
,
ec
{a ◦ α : a ∈ K} jest podprzestrzeni
,
a przestrzeni V zawieraj
,
ac
,
a α.
Jeżeli zaś W jest podprzestrzeni
,
a przestrzeni V tak
,
a, że α ∈ W , to dla
dowolnego a ∈ K jest a ◦ α ∈ W , sk
,
ad {a ◦ α : a ∈ K} ⊆ W . Zatem
lin(α) = {a ◦ α : a ∈ K}.
Ponadto z definicji podprzestrzeni generowanej wynika od razu, że
jeżeli A i B s
,
a podzbiorami przestrzeni liniowej V takimi, że A ⊆ B,
to lin(A) ⊆ lin(B).
Twierdzenie 10.3. Niech V
1
, V
2
, . . . , V
n
b
,
ed
,
a podprzestrzeniami
przestrzeni liniowej V nad ciałem K. Wówczas zbiór
V
1
+ V
2
+ . . . + V
n
= {α
1
+ α
2
+ . . . + α
n
: α
i
∈ V
i
dla i = 1, 2, . . . , n}
jest podprzestrzeni
,
a przestrzeni V . Ponadto
V
1
+ V
2
+ . . . + V
n
= lin(V
1
∪ V
2
∪ . . . ∪ V
n
).
Dowód. Niech α
i
∈ V
i
dla i = 1, 2, . . . , n. Wtedy α
i
= Θ + . . . + Θ
|
{z
}
i−1
+ α
i
+ Θ + . . . + Θ
|
{z
}
n−i
, sk
,
ad α
i
∈ V
1
+ . . . + V
n
dla i = 1, 2, . . . , n. Zatem
V
1
∪ . . . ∪ V
n
⊆ V
1
+ . . . + V
n
. Niech α, β ∈ V
1
+ . . . + V
n
. Wtedy
istniej
,
a α
i
, β
i
∈ V
i
dla i = 1, 2, . . . , n takie, że α = α
1
+ . . . + α
n
i β = β
1
+ . . . + β
n
, sk
,
ad α + β = (α
1
+ β
1
) + . . . + (α
n
+ β
n
) ∈
V
1
+ . . . + V
n
, bo α
i
+ β
i
∈ V
i
dla i = 1, 2, . . . , n.
Ponadto dla
a ∈ K mamy, że a ◦ α
i
∈ V
i
dla i = 1, 2, . . . , n, sk
,
ad z własności
9.10 a ◦ α = a ◦ α
1
+ . . . + a ◦ α
n
∈ V
1
+ . . . + V
n
. Zatem V
1
+ . . . + V
n
jest podprzestrzeni
,
a przestrzeni V zawieraj
,
ac
,
a zbiór V
1
∪ . . . ∪ V
n
.
Niech teraz W b
,
edzie dowoln
,
a podprzestrzeni
,
a przestrzeni V tak
,
a,
że V
1
∪ . . . ∪ V
n
⊆ W . Weźmy dowolne α ∈ V
1
+ . . . + V
n
. Wtedy
istniej
,
a α
i
∈ V
i
dla i = 1, 2, . . . , n takie, że α = α
1
+ . . . + α
n
. Ale
α
1
, . . . , α
n
∈ W , wi
,
ec α ∈ W . Zatem V
1
+ . . . + V
n
⊆ W . St
,
ad
V
1
+ . . . + V
n
⊆ lin(V
1
∪ . . . ∪ V
n
). Ale lin(V
1
∪ . . . ∪ V
n
) jest najmniejsz
,
a

82
Wykłady z algebry liniowej I
podprzestrzeni
,
a przestrzeni V zawieraj
,
ac
,
a zbiór V
1
∪. . .∪V
n
, wi
,
ec st
,
ad
V
1
+ . . . + V
n
= lin(V
1
∪ . . . ∪ V
n
).
Twierdzenie 10.4. Dla dowolnych wektorów α
1
, . . . , α
n
przestrzeni
liniowej V nad ciałem K zachodzi wzór:
lin(α
1
, . . . , α
n
) = {a
1
◦ α
1
+ . . . + a
n
◦ α
n
: a
1
, . . . , a
n
∈ K}.
Dowód. Ponieważ α
i
∈ lin(α
i
) dla i = 1, 2, . . . , n, wi
,
ec
{α
1
, . . . , α
n
} ⊆ lin(α
1
) ∪ . . . ∪ lin(α
n
), sk
,
ad lin(α
1
, . . . , α
n
) ⊆
lin(lin(α
1
)∪. . .∪lin(α
n
)). Ponadto {α
i
} ⊆ {α
1
, . . . , α
n
}, wi
,
ec lin(α
i
) ⊆
lin(α
1
, . . . , α
n
) dla i = 1, 2, . . . , n. Zatem lin(lin(α
1
) ∪ . . . ∪ lin(α
n
)) ⊆
lin(α
1
, . . . , α
n
).
St
,
ad lin(α
1
, . . . , α
n
) = lin(lin(α
1
), . . . , lin(α
n
)) =
lin(α
1
) + . . . + lin(α
n
) = {a
1
◦ α
1
+ . . . + a
n
◦ α
n
: a
1
, . . . , a
n
∈ K} na
mocy twierdzenia 10.3 i uwagi 10.3.
Twierdzenie 10.5. Dla dowolnych podzbiorów X i Y przestrzeni
liniowej V nad ciałem K zachodzi wzór:
lin(X ∪ Y ) = lin(X) + lin(Y ).
Dowód. Mamy, że X ⊆ lin(X) ⊆ lin(X ∪ Y ) i Y ⊆ lin(Y ) ⊆
lin(X ∪ Y ), wi
,
ec X ∪ Y ⊆ lin(X ∪ Y ). Ale lin(X ∪ Y ) jest najmniejsz
,
a
podprzestrzeni
,
a zawieraj
,
ac
,
a zbiór X ∪ Y , wi
,
ec st
,
ad lin(X ∪ Y ) ⊆
lin(X) + lin(Y ). Dalej, jeżeli W jest podprzestrzeni
,
a przestrzeni V
zawieraj
,
ac
,
a X ∪ Y , to X ⊆ W , sk
,
ad lin(X) ⊆ W oraz analogicznie
lin(Y ) ⊆ W . Zatem lin(X)∪lin(Y ) ⊆ W i z twierdzenia 10.3 mamy, że
lin(X) + lin(Y ) ⊆ W . Ale W jest dowoln
,
a podprzestrzeni
,
a przestrzeni
V zawieraj
,
ac
,
a zbiór X ∪ Y , wi
,
ec st
,
ad lin(X) + lin(Y ) ⊆ lin(X ∪ Y ).
St
,
ad ostatecznie lin(X ∪ Y ) = lin(X) + lin(Y ).
Z twierdzenia 10.5 mamy natychmiast nast
,
epuj
,
acy
Wniosek 10.1.
Dla dowolnych wektorów α
1
, . . . , α
n
, β
1
, . . . , β
m
przestrzeni liniowej V zachodzi wzór:
lin(α
1
, . . . , α
n
, β
1
, . . . , β
m
) = lin(α
1
, . . . , α
n
) + lin(β
1
, . . . , β
m
).

Podprzestrzenie przestrzeni liniowych
83
Twierdzenie 10.6. Dla dowolnego podzbioru X przestrzeni linio-
wej V nad ciałem K i dla każdego wektora α ∈ V :
α ∈ lin(X) ⇔ lin(X ∪ {α}) = lin(X).
Dowód. Załóżmy, że lin(X ∪ {α}) = lin(X). Ponieważ X ∪ {α} ⊆
lin(X ∪ {α}), wi
,
ec st
,
ad X ∪ {α} ⊆ lin(X), sk
,
ad α ∈ lin(X). Na
odwrót, niech teraz α ∈ lin(X). Weźmy dowoln
,
a podprzestrzeń W
przestrzeni V tak
,
a, że X ⊆ W . Wtedy lin(X) ⊆ W i α ∈ lin(X), wi
,
ec
X ∪ {α} ⊆ W , sk
,
ad lin(X ∪ {α}) ⊆ W . Ale W jest dowoln
,
a podprze-
strzeni
,
a przestrzeni V zawieraj
,
ac
,
a X, wi
,
ec st
,
ad lin(X ∪{α}) ⊆ lin(X).
Ponadto X ⊆ X ∪ {α}, wi
,
ec lin(X) ⊆ lin(X ∪ {α}) i ostatecznie
lin(X ∪ {α}) = lin(X).
10.3
Kombinacja liniowa wektorów
Definicja 10.2. Niech α
1
, α
2
, . . . , α
n
b
,
ed
,
a wektorami przestrzeni
liniowej V nad ciałem K. Powiemy, że wektor α ∈ V jest kombinacj
,
a
liniow
,
a wektorów α
1
, α
2
, . . . , α
n
, jeżeli istniej
,
a skalary a
1
, a
2
, . . . , a
n
∈
K (zwane współczynnikami tej kombinacji) takie, że
α = a
1
◦ α
1
+ a
2
◦ α
2
+ . . . + a
n
◦ α
n
.
(10.1)
Uwaga 10.4. Twierdzenie 10.4 możemy wypowiedzieć nast
,
epuj
,
aco:
lin(α
1
, . . . , α
n
) składa si
,
e ze wszystkich kombinacji liniowych wektorów
α
1
, . . . , α
n
.
Twierdzenie 10.7. Niech X b
,
edzie dowolnym niepustym podzbio-
rem przestrzeni liniowej V nad ciałem K. Wówczas lin(X) jest zbio-
rem wszystkich kombinacji liniowych wszystkich skończonych podzbio-
rów zbioru X.
Dowód. Oznaczmy przez V
1
zbiór wszystkich kombinacji liniowych
wszystkich skończonych podzbiorów zbioru X. Dla α ∈ X mamy, że
α = 1 ◦ α ∈ V
1
, wi
,
ec X ⊆ V
1
. Ponieważ X 6= ∅, wi
,
ec V
1
6= ∅. Niech
a ∈ K oraz α, β ∈ V
1
. Wtedy istniej
,
a α
1
, . . . , α
n
, β
1
, . . . , β
m
∈ X takie,
że α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
oraz β = b
1
◦ β
1
+ . . . + b
m
◦ β
m
. Zatem

84
Wykłady z algebry liniowej I
a ◦ α = (aa
1
) ◦ α
1
+ . . . + (aa
n
)α
n
∈ V
1
oraz α ∈ lin(α
1
, . . . , α
n
) i β ∈
lin(β
1
, . . . , β
m
), wi
,
ec z wniosku 10.1 α+β ∈ lin(α
1
, . . . , α
n
, β
1
, . . . , β
m
),
czyli na mocy uwagi 10.4 α+β ∈ V
1
. St
,
ad V
1
jest podprzestrzeni
,
a prze-
strzeni V zawieraj
,
ac
,
a X. Niech W b
,
edzie dowoln
,
a podprzestrzeni
,
a
przestrzeni V zawieraj
,
ac
,
a X. Wtedy dla dowolnych α
1
, . . . , α
n
∈ X
mamy, że α
1
, . . . , α
n
∈ W , sk
,
ad dla dowolnych a
1
, . . . , a
n
∈ K jest
a
1
◦ α
1
+ . . . + a
n
◦ α
n
∈ W . Zatem V
1
⊆ W , czyli V
1
jest naj-
mniejsz
,
a podprzestrzeni
,
a przestrzeni X zawieraj
,
ac
,
a zbiór X. Zatem
V
1
= lin(X).
Twierdzenie 10.8.
Niech α, α
1
, . . . , α
n
, β
1
, . . . , β
m
b
,
ed
,
a wekto-
rami przestrzeni liniowej V nad ciałem K. Jeżeli wektor α jest kom-
binacj
,
a liniow
,
a wektorów β
1
, . . . , β
m
oraz dla i = 1, 2, . . . , m wektor β
i
jest kombinacj
,
a liniow
,
a wektorów α
1
, . . . , α
n
, to wektor α jest kombi-
nacj
,
a liniow
,
a wektorów α
1
, . . . , α
n
.
Dowód. Z uwagi 10.4 mamy, że β
1
, . . . , β
m
∈ lin(α
1
, . . . , α
n
). Za-
tem lin(β
1
, . . . , β
m
) ⊆ lin(α
1
, . . . , α
n
). Ale z uwagi 10.4
α ∈ lin(β
1
, . . . , β
m
), wi
,
ec st
,
ad α ∈ lin(α
1
, . . . , α
n
), czyli z uwagi 10.4
wektor α jest kombinacj
,
a liniow
,
a wektorów α
1
, . . . , α
n
.
Przykład 10.1. Niech K b
,
edzie ciałem i niech n ∈ N. W prze-
strzeni K
n
określamy wektory
ε
1
= [1, 0, 0, . . . , 0], ε
2
= [0, 1, 0, . . . , 0], ε
3
= [0, 0, 1, . . . , 0], . . . ,
ε
n
= [0, 0, 0, . . . , 1]
Dla dowolnych skalarów a
1
, . . . , a
n
∈ K
a
1
◦ ε
1
= [a
1
, 0, 0, . . . , 0]
a
2
◦ ε
2
= [0, a
2
, 0, . . . , 0]
a
3
◦ ε
3
= [0, 0, a
3
, . . . , 0]
. . . . . . . . . . . . . . . . . . . . . . .
a
n
◦ ε
n
= [0, 0, 0, . . . , a
n
]
,
wi
,
ec po dodaniu stronami tych równości uzyskamy wzór:
[a
1
, a
2
, . . . , a
n
] = a
1
◦ ε
1
+ a
2
◦ ε
2
+ . . . + a
n
◦ ε
n
.
(10.2)

Podprzestrzenie przestrzeni liniowych
85
Z tego wzoru wynika zatem, że każdy wektor przestrzeni K
n
jest kombi-
nacj
,
a liniow
,
a wektorów ε
1
, . . . , ε
n
, czyli K
n
= lin(ε
1
, . . . , ε
n
). Mówimy
też, że wektory ε
1
, . . . , ε
n
generuj
,
a przestrzeń K
n
.
10.4
Operacje elementarne na układach
wektorów
Niech α
1
, . . . , α
n
b
,
ed
,
a dowolnymi wektorami przestrzeni liniowej V nad
ciałem K. Wyróżniamy nast
,
epuj
,
ace operacje elementarne nad ukła-
dem wektorów (α
1
, . . . , α
n
):
O1. Zamiana miejscami wektorów α
i
z α
j
(dla i 6= j) oznaczana
przez w
i
↔ w
j
. Oczywiście operacja ta jest do siebie odwrotna.
O2. Pomnożenie i-tego wektora przez niezerowy skalar a ∈ K,
oznaczenie: a · w
i
. Ponieważ dla a 6= 0 jest a
−1
◦ (a ◦ α
i
) = (a
−1
a) ◦ α
i
=
1 ◦ α
i
= α
i
, wi
,
ec operacj
,
a odwrotn
,
a do a · w
i
jest operacja a
−1
· w
i
.
O3. Dodanie do wektora α
i
wektora α
j
(dla i 6= j) pomnożonego
przez dowolny skalar a ∈ K, oznaczenie: w
i
+ a · w
j
. Ponieważ (α
i
+
a ◦ α
j
) + (−a) ◦ α
j
= α
i
+ a ◦ α
j
+ (−(a ◦ α
j
)) = α
i
, wi
,
ec operacj
,
a
odwrotn
,
a do operacji w
i
+ a · w
j
jest operacja w
i
+ (−a) · w
j
.
Twierdzenie 10.9. Jeżeli układ wektorów (β
1
, . . . , β
n
) przestrzeni
liniowej V nad ciałem K powstaje z układu wektorów (α
1
, . . . , α
n
) przez
kolejne wykonanie skończonej liczby operacji elementarnych, to
lin(β
1
, . . . , β
n
) = lin(α
1
, . . . , α
n
).
Dowód. Indukcja pozwala nam ograniczyć si
,
e do jednej opera-
cji. Ponadto operacje elementarne s
,
a odwracalne, wi
,
ec wystarczy wy-
kazać, że lin(β
1
, . . . , β
n
) ⊆ lin(α
1
, . . . , α
n
), czyli, że {β
1
, . . . , β
n
} ⊆
lin(α
1
, . . . , α
n
). Dla operacji O1 jest to oczywiste. Dla operacji O2
mamy, że β
j
= α
j
dla j 6= i oraz β
i
= a ◦ α
i
∈ lin(α
1
, . . . , α
n
). Dla
operacji O3 β
k
= α
k
dla k 6= i oraz β
i
= α
i
+ a ◦ α
j
∈ lin(α
1
, . . . , α
n
).

86
Wykłady z algebry liniowej I
Przykład 10.2. Sprawdzimy, czy wektor [1, 2, 3] należy do pod-
przestrzeni W = lin([1, 3, 2], [1, 2, 1], [2, 5, 3]) przestrzeni liniowej R
3
.
Po wykonaniu operacji w
2
− w
1
, w
3
− 2w
1
uzyskamy na mocy twier-
dzenia 10.9, że W = lin([1, 3, 2], [0, −1, −1], [0, −1, −1]) =
lin([1, 3, 2], [0, −1, −1]) = {x ◦ [1, 3, 2] + y ◦ [0, −1, −1] : x, y ∈ R} =
{[x, 3x−y, 2x−y] : x, y ∈ R}. Zatem [1, 2, 3] ∈ W wtedy i tylko wtedy,
gdy istniej
,
a x, y ∈ R takie, że [1, 2, 3] = [x, 3x − y, 2x − y], czyli gdy
x = 1 oraz 3x − y = 2x − y = −1, a wi
,
ec gdy x = 1 i x = 0. Uzyskana
sprzeczność pokazuje, że [1, 2, 3] 6∈ W .

Rozdział 11
Baza i wymiar przestrzeni
liniowej
11.1
Liniowa niezależność wektorów
Niech α
1
, . . . , α
n
b
,
ed
,
a dowolnymi wektorami przestrzeni liniowej V nad
ciałem K. Powiemy, że układ wektorów (α
1
, . . . , α
n
) jest liniowo za-
leżny, jeżeli istniej
,
a skalary a
1
, . . . , a
n
∈ K nie wszystkie równe 0 i ta-
kie, że a
1
◦ α
1
+ . . . + a
n
◦ α
n
= Θ.
Przykład 11.1. Wektory Θ, α
1
, . . . , α
n
∈ V s
,
a liniowo zależne, bo
np. 1 ◦ Θ + 0 ◦ α
1
+ . . . + 0 ◦ α
n
= Θ oraz 1 6= 0.
Uwaga 11.1. Jeżeli układ wektorów (α
1
, . . . , α
n
) jest liniowo za-
leżny, to dla dowolnej permutacji f ∈ S
n
układ (α
f (1)
, . . . , α
f (n)
) też
jest liniowo zależny.
Przykład 11.2. Wektory α, α, α
1
, . . . , α
n
s
,
a liniowo zależne, bo
1 ◦ α + (−1) ◦ α + 0 ◦ α
1
+ . . . + 0 ◦ α
n
= Θ i 1 6= 0.
Definicja 11.1. Powiemy, że układ wektorów (α
1
, . . . , α
n
) prze-
strzeni liniowej V nad ciałem K jest liniowo niezależny, jeżeli nie jest
on liniowo zależny, tzn.
∀
a
1
,...,a
n
∈K
[a
1
◦ α
1
+ . . . + a
n
◦ α
n
= Θ ⇒ a
1
= . . . = a
n
= 0].
87

88
Wykłady z algebry liniowej I
Przykład 11.3. Ze wzoru (10.2) wynika od razu, że układ wekto-
rów (ε
1
, . . . , ε
n
) przestrzeni K
n
jest liniowo niezależny.
Uwaga 11.2. Z uwagi 11.1 wynika, że jeśli układ wektorów
(α
1
, . . . , α
n
) przestrzeni liniowej V jest liniowo niezależny (w skrócie
lnz), to dla dowolnej permutacji f ∈ S
n
układ (α
f (1)
, . . . , α
f (n)
) też
jest liniowo niezależny. Ponadto z przykładu 11.2 wynika, że wtedy
α
i
6= α
j
dla i 6= j. Możemy zatem powiedzieć, że zbiór wektorów
{α
1
, . . . , α
n
} jest liniowo niezależny. Dalej, z przykładu 11.1 wynika, że
Θ 6∈ {α
1
, . . . , α
n
}. Jeżeli X = {β
1
, . . . , β
k
} jest niepustym podzbiorem
zbioru {α
1
, . . . , α
n
}, to zbiór X też jest liniowo niezależny, gdyż w
przeciwnym wypadku istniałyby skalary b
1
, . . . , b
k
nie wszystkie równe
0 i takie, że b
1
◦ β
1
+ . . . + b
k
◦ β
k
= Θ i wówczas uzupełniaj
,
ac ci
,
ag
(b
1
, . . . , b
k
) zerami uzyskamy ci
,
ag (a
1
, . . . , a
n
) taki, że a
1
◦ α
1
+ . . . +
a
n
◦ α
n
= Θ, wbrew liniowej niezależności zbioru {α
1
, . . . , α
n
}.
Z uwagi 11.2 wynika zatem, że definicj
,
e liniowej niezależności można
rozszerzyć na dowolne podzbiory przestrzeni liniowej.
Definicja 11.2. Powiemy, że podzbiór X przestrzeni liniowej V
nad ciałem K jest liniowo niezależny (w skrócie lnz), jeżeli każdy skoń-
czony podzbiór zbioru X jest liniowo niezależny. Zbiór pusty wektorów
uważamy za liniowo niezależny.
Z uwagi 11.2 oraz z tej definicji mamy od razu nast
,
epuj
,
ace
Twierdzenie 11.1. Dowolny podzbiór liniowo niezależnego zbioru
wektorów przestrzeni liniowej jest zbiorem liniowo niezależnym.
Przykład 11.4. W przestrzeni V = R[x] nad ciałem R zbiór
{1, x, x
2
, . . .} jest liniowo niezależny.
Zadanie 11.1. Pokazać, że w przestrzeni R
Q
zbiór
{log p : p jest liczb
,
a pierwsz
,
a} jest liniowo niezależny.
Przykład 11.5. Jeżeli α jest niezerowym wektorem przestrzeni
liniowej V nad ciałem K, to zbiór {α} jest liniowo niezależny. Rzeczy-
wiście, niech a ∈ K b
,
edzie takie, że a ◦ α = Θ. Wtedy z uwagi 9.4
mamy, że a = 0, czyli zbiór {α} jest lnz.

Baza i wymiar przestrzeni liniowej
89
Twierdzenie 11.2. Jeżeli układ wektorów (β
1
, . . . , β
n
) przestrzeni
liniowej V nad ciałem K powstaje z układu (α
1
, . . . , α
n
) przez kolejne
wykonanie skończonej liczby operacji elementarnych, to układ
(β
1
, . . . , β
n
) jest liniowo niezależny wtedy i tylko wtedy, gdy układ
(α
1
, . . . , α
n
) jest liniowo niezależny.
Dowód. Indukcja pozwala nam ograniczyć si
,
e do jednej operacji
elementarnej. Ponadto operacje elementarne s
,
a odwracalne, wi
,
ec wy-
starczy wykazać, że jeżeli układ (α
1
, . . . , α
n
) jest lnz, to układ
(β
1
, . . . , β
n
) jest lnz. Dla operacji O1 jest to oczywiste. Dla operacji
O2 mamy, że β
j
= α
j
dla j 6= i oraz β
i
= a ◦ α
i
dla pewnego a 6= 0.
Weźmy dowolne a
1
, . . . , a
n
∈ K takie, że a
1
◦ β
1
+ . . . + a
n
◦ β
n
= Θ.
Wtedy a
1
◦ α
1
+ . . . + (a
i
a) ◦ α
i
+ . . . + a
n
◦ α
n
= Θ. St
,
ad z liniowej
niezależności układu (α
1
, . . . , α
n
) mamy, że a
1
= a
2
= . . . = a
i
a =
. . . = a
n
= 0. Ale a 6= 0, wi
,
ec st
,
ad a
1
= . . . = a
i
= . . . = a
n
= 0, czyli
układ (β
1
, . . . , β
n
) jest lnz.
Dla operacji O3 bez zmniejszania ogólności możemy zakładać, że
b
1
= α
1
+ a ◦ α
2
oraz β
j
= α
j
dla j = 2, . . . , n. Weźmy dowolne
a
1
, . . . , a
n
∈ K takie, że a
1
◦ β
1
+ . . . + a
n
◦ β
n
= Θ. Wtedy
a
1
◦ (α
1
+ a ◦ α
2
) + a
2
◦ α
2
+ . . . + a
n
◦ α
n
= Θ, czyli a
1
◦ α
1
+ (a
1
a +
a
2
) ◦ α
2
+ . . . + a
n
◦ α
n
= Θ, sk
,
ad z lnz układu (α
1
, . . . , α
n
) mamy, że
a
1
= a
1
a + a
2
= a
3
= . . . = a
n
= 0, czyli a
1
= a
2
= . . . = a
n
= 0, a
wi
,
ec układ (β
1
, . . . , β
n
) jest lnz.
Twierdzenie 11.3. Niech X b
,
edzie zbiorem liniowo niezależnym
wektorów przestrzeni liniowej V nad ciałem K. Wówczas dla każdego
wektora α ∈ V :
α ∈ lin(X) ⇔ [α ∈ X lub zbiór X ∪ {α} jest liniowo zależny].
Dowód.
⇐. Załóżmy, że α 6∈ lin(X). Wtedy α 6∈ X, gdyż
X ⊆ lin(X). Zatem zbiór X ∪ {α} jest liniowo zależny. Ale zbiór X
jest liniowo niezależny, wi
,
ec istniej
,
a parami różne wektory α
1
, . . . , α
n
∈
X takie, że zbiór {α, α
1
, . . . , α
n
} jest liniowo zależny. Zatem istniej
,
a
skalary a, a
1
, . . . , a
n
∈ K nie wszystkie równe 0 i takie, że a ◦ α + a
1
◦
α
1
+. . .+a
n
◦α
n
= Θ. St
,
ad z liniowej niezależności wektorów α
1
, . . . , α
n
wynika, że a 6= 0. Zatem α = (−
a
1
a
) ◦ α
1
+ . . . + (−
a
n
a
) ◦ α
n
∈ lin(X),
czyli α ∈ lin(X) na mocy twierdzenia 10.7 i mamy sprzeczność.

90
Wykłady z algebry liniowej I
⇒. Na mocy twierdzenia 10.7 istniej
,
a α
1
, . . . , α
n
∈ X oraz a
1
, . . . ,
a
n
∈ K takie, że α = a
1
◦α
1
+. . .+a
n
◦α
n
. Zatem 1◦α+(−a
1
) ◦ α
1
+ . . .+
(−a
n
) ◦ α
n
= Θ, sk
,
ad wynika, że α ∈ X albo α 6∈ X i zbiór X ∪ {α}
jest liniowo zależny.
11.2
Baza przestrzeni liniowej
Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad ciałem K. Powiemy, że pod-
zbiór X ⊆ V jest maksymalnym zbiorem liniowo niezależnym, jeśli
X jest zbiorem liniowo niezależnym oraz dla każdego zbioru liniowo
niezależnego Y ⊆ V takiego, że X ⊆ Y jest X = Y .
Definicja 11.3. Każdy maksymalny liniowo niezależny podzbiór
X wektorów przestrzeni liniowej V nad ciałem K nazywamy baz
,
a tej
przestrzeni.
Twierdzenie 11.4. Każdy liniowo niezależny zbiór wektorów X
0
przestrzeni liniowej V nad ciałem K można rozszerzyć do bazy X ⊇ X
0
tej przestrzeni.
Dowód. Niech A b
,
edzie rodzin
,
a wszystkich podzbiorów liniowo
niezależnych przestrzeni V zawieraj
,
acych zbiór X
0
. Wtedy A 6= ∅, bo
X
0
∈ A. Ponadto zbiór A jest cz
,
eściowo uporz
,
adkowany przez inkluzj
,
e
zbiorów. Jeżeli B jest łańcuchem w A, tzn. dla dowolnych Y, Z ∈ B
jest Y ⊆ Z lub Z ⊆ Y , to Y
0
=
S
Y ∈B
Y też jest zbiorem liniowo nie-
zależnym, gdyż dla dowolnych α
1
, . . . , α
n
∈ Y
0
istniej
,
a Y
1
, . . . , Y
n
∈ B
takie, że α
i
∈ Y
i
dla i = 1, . . . , n. Wtedy istnieje k ≤ n takie, że
Y
i
⊆ Y
k
dla każdego i = 1, . . . , n, sk
,
ad α
1
, . . . , α
n
∈ Y
k
. Ale zbiór Y
k
jest liniowo niezależny, wi
,
ec zbiór {α
1
, . . . , α
n
} też jest liniowo nieza-
leżny. Zatem w A każdy łańcuch ma ograniczenie górne, wi
,
ec z lematu
Kuratowskiego-Zorna istnieje w A element maksymalny X, który jest
szukan
,
a baz
,
a przestrzeni V zawieraj
,
ac
,
a X
0
.
Ponieważ zbiór pusty jest liniowo niezależny, wi
,
ec z twierdzenia
11.4 mamy natychmiast nast
,
epuj
,
ace
Twierdzenie 11.5. Każda przestrzeń liniowa posiada baz
,
e.

Baza i wymiar przestrzeni liniowej
91
Twierdzenie 11.6. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad cia-
łem K. Zbiór X ⊆ V jest baz
,
a przestrzeni V wtedy i tylko wtedy, gdy
X jest zbiorem liniowo niezależnym oraz V = lin(X) (tzn. X generuje
V ).
Dowód.
Załóżmy, że X jest baz
,
a przestrzeni V .
Wówczas X
jest zbiorem liniowo niezależnym. Weźmy dowolne α ∈ V i załóżmy,
że α 6∈ lin(X). Wtedy z twierdzenia 11.3 wynika, że α 6∈ X oraz
zbiór X ∪ {α} jest liniowo niezależny. Zatem X nie jest maksymalnym
zbiorem liniowo niezależnym i mamy sprzeczność.
Na odwrót, załóżmy, że zbiór X jest liniowo niezależny oraz V =
lin(X). Weźmy dowolny liniowo niezależny zbiór Y ⊆ V taki, że X ⊆
Y . Gdyby X 6= Y , to dla pewnego α ∈ Y byłoby, że α 6∈ X i zbiór X ∪
{α} ⊆ Y jest liniowo niezależny. Zatem z twierdzenia 11.3 mielibyśmy,
że α 6∈ lin(X) = V , co prowadzi do sprzeczności. Zatem X = Y i zbiór
X jest baz
,
a przestrzeni V .
Przykład 11.6. Ponieważ zbiór {1, x, x
2
, . . .} generuje przestrzeń
R[x] i jest liniowo niezależny, wi
,
ec na mocy twierdzenia 11.6 jest on
baz
,
a tej przestrzeni.
Przykład 11.7. Niech K b
,
edzie dowolnym ciałem i niech n ∈ N.
Wówczas z twierdzenia 11.6 oraz z przykładów 10.1 i 11.3 wynika od
razu, że zbiór {ε
1
, . . . , ε
n
} jest baz
,
a przestrzeni K
n
. Nazywamy j
,
a baz
,
a
kanoniczn
,
a.
Z twierdzeń 10.9, 11.2 i 11.6 wynika od razu nast
,
epuj
,
ace
Twierdzenie 11.7. Niech α
1
, . . . , α
n
b
,
ed
,
a parami różnymi wekto-
rami i niech beta
1
, . . . , β
n
b
,
ed
,
a parami różnymi wektorami przestrzeni
liniowej V . Załóżmy, że układ wektorów (β
1
, . . . , β
n
) powstaje z układu
(α
1
, . . . , α
n
) przez kolejne zastosowanie skończonej liczby operacji ele-
mentarnych. Wówczas zbiór {β
1
, . . . , β
n
} jest baz
,
a przestrzeni V wtedy
i tylko wtedy, gdy zbiór {α
1
, . . . , α
n
} jest baz
,
a tej przestrzeni.
Twierdzenie 11.8. Niech α
1
, . . . , α
n
b
,
ed
,
a wektorami przestrzeni
liniowej V nad ciałem K.
Wówczas każdy maksymalny (wzgl
,
edem
liczby elementów) podzbiór liniowo niezależny A ⊆ {α
1
, . . . , α
n
} jest
baz
,
a podprzestrzeni lin(α
1
, . . . , α
n
).

92
Wykłady z algebry liniowej I
Dowód. Niech A ⊆ {α
1
, . . . , α
n
} b
,
edzie maksymalnym (wzgl
,
edem
liczby elementów) podzbiorem liniowo niezależnym. Wówczas oczy-
wiście lin(A) ⊆ lin(α
1
, . . . , α
n
) = W .
Niech i = 1, . . . , n.
Jeśli
α
i
∈ A, to α
i
∈ lin(A); jeśli zaś α
i
6∈ A, to z maksymalności A
wynika, że zbiór A ∪ {α
i
} jest liniowo zależny. Zatem z twierdzenia
11.3 α
i
∈ lin(A). St
,
ad {α
1
, . . . , α
n
} ⊆ lin(A), czyli W ⊆ lin(A)
i ostatecznie lin(A) = W . Zatem z twierdzenia 11.6 zbiór A jest baz
,
a
podprzestrzeni W .
Twierdzenie 11.9. Niech α
1
, . . . , α
n
b
,
ed
,
a parami różnymi wekto-
rami przestrzeni liniowej V nad ciałem K. Wówczas zbiór {α
1
, . . . , α
n
}
jest baz
,
a przestrzeni V wtedy i tylko wtedy, gdy każdy wektor α ∈ V
można jednoznacznie zapisać w postaci
α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
dla pewnych a
1
, . . . , a
n
∈ K.
Dowód. Załóżmy, że zbiór {α
1
, . . . , α
n
} jest baz
,
a przestrzeni V .
Wówczas z twierdzenia 11.6 mamy, że V = lin(α
1
, . . . , α
n
) oraz zbiór
{α
1
, . . . , α
n
} jest liniowo niezależny. Zatem dla dowolnego α ∈ V ist-
niej
,
a a
1
, . . . , a
n
∈ K takie, że α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
.
Jeśli
b
1
, . . . , b
n
∈ K s
,
a takie, że α = b
1
◦ α
1
+ . . . + b
n
◦ α
n
, to a
1
◦ α
1
+ . . . +
a
n
◦α
n
= b
1
◦α
1
+. . .+b
n
◦α
n
, czyli (a
1
−b
1
)◦α
1
+. . .+(a
n
−b
n
)◦α
n
= Θ,
wi
,
ec z liniowej niezależności zbioru {α
1
, . . . , α
n
} mamy, że a
i
− b
i
= 0,
czyli a
i
= b
i
dla i = 1, . . . , n.
Na odwrót, jeżeli a
1
, . . . , a
n
∈ K s
,
a takie, że a
1
◦ α
1
+ . . . + a
n
◦ α
n
= Θ, to a
1
◦α
1
+. . .+a
n
◦α
n
= 0◦α
1
+. . .+0◦α
n
, sk
,
ad z jednoznaczności
zapisu wektora a
i
= 0 dla i = 1, . . . , n, czyli zbiór {α
1
, . . . , α
n
} jest
liniowo niezależny.
Ponadto z założenia V = lin(α
1
, . . . , α
n
), wi
,
ec
z twierdzenia 11.6 zbiór {α
1
, . . . , α
n
} jest baz
,
a przestrzeni V .
Definicja 11.4. Niech {α
1
, . . . , α
n
} b
,
edzie baz
,
a przestrzeni linio-
wej V nad ciałem K. Wówczas ci
,
ag (α
1
, . . . , α
n
) nazywamy baz
,
a
uporz
,
adkowan
,
a przestrzeni V . Niech α ∈ V . Wtedy na mocy twier-
dzenia 11.9 istnieje dokładnie jeden ci
,
ag (a
1
, . . . , a
n
) ∈ K
n
taki, że
α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
.
Ci
,
ag (a
1
, . . . , a
n
) nazywamy ci
,
agiem
współrz
,
ednych wektora α w bazie (α
1
, . . . , α
n
), a element a
i
, dla każ-
dego i = 1, . . . , n, nazywa si
,
e i-t
,
a współrz
,
edn
,
a wektora α w tej bazie.

Baza i wymiar przestrzeni liniowej
93
Wniosek 11.1. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad ciałem
K i niech, dla pewnej liczby naturalnej n, (α
1
, . . . , α
n
) b
,
edzie baz
,
a
uporz
,
adkowan
,
a tej przestrzeni. Przyporz
,
adkujmy każdemu wektorowi
α ∈ V , ci
,
ag jego współrz
,
ednych w bazie (α
1
, . . . , α
n
). Otrzymane w ten
sposób odwzorowanie φ jest bijekcj
,
a zbioru V na zbiór K
n
. Przy tym
φ(α
i
) = ε
i
dla i = 1, . . . , n.
Definicja 11.5. Odwzorowanie φ określone w powyższym wniosku
nazywamy układem współrz
,
ednych wyznaczonym przez baz
,
e
(α
1
, . . . , α
n
).
11.3
Wymiar przestrzeni liniowej
Lemat 11.1. Niech wektory α
1
, . . . , α
n
tworz
,
a baz
,
e przestrzeni V
i niech α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
, przy czym a
j
6= 0. Wówczas wektory
α
1
, . . . , α
j−1
, α, α
j+1
, . . . , α
n
(11.1)
też tworz
,
a baz
,
e przestrzeni V .
Dowód. Zauważmy, że wektory (11.1) powstaj
,
a z wektorów α
1
, . . . ,
α
n
przez kolejne wykonanie nast
,
epuj
,
acych operacji elementarnych:
a
j
·w
j
, w
j
+a
1
·w
1
, . . . , w
j
+a
j−1
·w
j−1
, w
j
+a
j+1
·w
j+1
, . . . , w
j
+a
n
·w
n
. Za-
tem na mocy twierdzenia 11.7, wektory (11.1) tworz
,
a baz
,
e przestrzeni
V .
Twierdzenie 11.10 (Steinitza o wymianie). Jeśli wektory
α
1
, . . . , α
n
tworz
,
a baz
,
e przestrzeni liniowej V nad ciałem K, a wektory
β
1
, . . . , β
s
s
,
a liniowo niezależne, to
(i) s ≤ n oraz
(ii) spośród wektorów α
1
, . . . , α
n
można wybrać n − s wektorów,
które ł
,
acznie z wektorami β
1
, . . . , β
s
tworz
,
a baz
,
e przestrzeni V .
Dowód. Zastosujemy indukcj
,
e wzgl
,
edem s. Dla s = 0 teza jest
oczywista. Załóżmy, że teza zachodzi dla liczb mniejszych od pew-
nej liczby naturalnej s i rozpatrzmy s wektorów liniowo niezależnych

94
Wykłady z algebry liniowej I
β
1
, . . . , β
s
. Wektory β
1
, . . . , β
s−1
s
,
a liniowo niezależne, a wi
,
ec z założe-
nia indukcyjnego s − 1 ≤ n i istnieje n − s + 1 = n − (s − 1) wektorów
spośród wektorów α
1
, . . . , α
n
, które ł
,
acznie z β
1
, . . . , β
s−1
tworz
,
a baz
,
e
przestrzeni V . Dla uproszczenia znakowania przyjmiemy, że tymi wek-
torami s
,
a α
1
, . . . , α
n−s+1
.
Wykażemy najpierw, że s−1 < n. W przeciwnym razie byłoby n =
s − 1 (bo s − 1 ≤ n), a zatem już wektory β
1
, . . . , β
s−1
tworzyłyby baz
,
e
przestrzeni V , a st
,
ad wynikałoby, że β
s
∈ lin(β
1
, . . . , β
s−1
), co na mocy
twierdzenia 11.3 prowadzi do sprzeczności (gdyż wektory β
1
, . . . , β
s
s
,
a
liniowo niezależne). Wobec tego s − 1 < n, a st
,
ad s ≤ n. To dowodzi
(i).
Ponieważ wektory β
1
, . . . , β
s−1
, α
1
, . . . , α
n−s+1
tworz
,
a baz
,
e przestrzeni
V , wi
,
ec β
s
jest ich kombinacj
,
a liniow
,
a. Wobec liniowej niezależności
wektorów β
1
, . . . , β
s
i twierdzenia 11.3, w kombinacji liniowej przed-
stawiaj
,
acej β
s
, co najmniej jeden z wektorów α
1
, . . . , α
n−s+1
wyst
,
epuje
ze współczynnikiem różnym od zera. Bez zmniejszania ogólności roz-
ważań możemy przyj
,
ać, że a
n−s+1
6= 0. Wtedy z lematu 11.1 wektory
β
1
, . . . , β
s−1
, α
1
, . . . , α
n−s
, β
s
tworz
,
a baz
,
e przestrzeni V , czyli wektory
β
1
, . . . , β
s
, α
1
, . . . , α
n−s
tworz
,
a baz
,
e przestrzeni V , co kończy dowód
twierdzenia.
Wniosek 11.2. Jeśli n-elementowy zbiór jest baz
,
a przestrzeni li-
niowej V nad ciałem K, to każda baza tej przestrzeni składa si
,
e z do-
kładnie n wektorów.
Dowód. Niech wektory α
1
, . . . , α
n
tworz
,
a baz
,
e przestrzeni liniowej
V nad ciałem K. Niech X b
,
edzie inn
,
a baz
,
a tej przestrzeni. Gdyby
zbiór X miał wi
,
ecej niż n elementów, to byłyby one liniowo niezależne
i otrzymalibyśmy sprzeczność z twierdzeniem Steinitza o wymianie.
Zatem |X| ≤ n. Ale wektory α
1
, . . . , α
n
s
,
a liniowo niezależne i zbiór
skończony X jest baz
,
a przestrzeni V , wi
,
ec znowu z twierdzenia Ste-
initza o wymianie n ≤ |X|, czyli ostatecznie |X| = n.
Definicja 11.6. Liczb
,
e elementów dowolnej skończonej bazy prze-
strzeni liniowej V nad ciałem K nazywamy wymiarem przestrzeni V
i oznaczamy przez dim
K
V lub dim V , jeśli wiadomo nad jakim ciałem
rozpatrujemy przestrzeń V .

Baza i wymiar przestrzeni liniowej
95
W ten sposób wymiar jest określony dla wszystkich takich prze-
strzeni, które maj
,
a skończon
,
a baz
,
e. Jeśli dana przestrzeń liniowa V
nie ma skończonej bazy, to mówimy, że jej wymiar jest nieskończony
i piszemy dim V = ∞. Można udowodnić, że wszystkie bazy dowolnej
przestrzeni liniowej V maj
,
a t
,
e sam
,
a moc. Wobec tego można okre-
ślić wymiar dowolnej przestrzeni liniowej V jako moc dowolnej bazy
przestrzeni V .
Przykład 11.8. Ponieważ dla dowolnego ciała K przestrzeń K
n
posiada baz
,
e n-elementow
,
a (np. baz
,
e kanoniczn
,
a), wi
,
ec dim
K
K
n
= n.
Przykład 11.9. Ponieważ dla dowolnego ciała K zbiór {1} jest
baz
,
a przestrzeni liniowej K
K
, wi
,
ec dim
K
K = 1.
W szczególności
dim
C
C = 1 oraz dim
R
C = 2, gdyż zbiór {1, i} jest baz
,
a przestrzeni
C
R
.
Przykład 11.10. Ponieważ zbiór pusty jest baz
,
a przestrzeni ze-
rowej {Θ}, wi
,
ec dim{Θ} = 0.
Przykład 11.11.
Ponieważ zbiór {1, x, x
2
, . . .} jest baz
,
a prze-
strzeni R[x], wi
,
ec dim R[x] = ∞.
Przykład 11.12. Dla dowolnego ciała K w przestrzeni liniowej
K
∞
wektory
1
= [1, 0, 0, . . .],
2
= [0, 1, 0, . . .], . . . s
,
a liniowo niezależne.
Zatem z twierdzenia Steinitza o wymianie dim K
∞
= ∞.
Twierdzenie 11.11. Jeśli przestrzeń liniowa V ma wymiar n, to
każda jej podprzestrzeń W ma wymiar nie wi
,
ekszy niż n.
Dowód. Niech X b
,
edzie baz
,
a podprzestrzeni W . Wtedy zbiór X
jest liniowo niezależny, wi
,
ec na mocy twierdzenia Steinitza o wymianie
|X| ≤ n.
Twierdzenie 11.12. Dla dowolnej podprzestrzeni W przestrzeni
liniowej V wymiaru skończonego równoważne s
,
a warunki:
(i) dim W = dim V , (ii) W = V .
Dowód. (ii)⇒(i). Oczywiste. (i)⇒(ii). Oznaczmy n = dim V .
Wtedy istnieje baza {α
1
, . . . , α
n
} przestrzeni V . Ale dim W = n, wi
,
ec
istnieje baza {β
1
, . . . , β
n
} podprzestrzeni W . Zatem wektory β
1
, . . . , β
n

96
Wykłady z algebry liniowej I
s
,
a liniowo niezależne i na mocy twierdzenia Steinitza o wymianie można
je uzupełnić do bazy przestrzeni V , n − n = 0 wektorami wybranymi
spośród wektorów α
1
, . . . , α
n
. Zatem wektory β
1
, . . . , β
n
tworz
,
a baz
,
e
przestrzeni V , sk
,
ad V = lin(β
1
, . . . , β
n
) = W .
Z twierdzenia 11.8 wynika od razu nast
,
epuj
,
ace
Twierdzenie 11.13. Niech α
1
, . . . , α
n
b
,
ed
,
a wektorami przestrzeni
liniowej V . Wówczas dim lin(α
1
, . . . , α
n
) ≤ n. Ponadto
dim lin(α
1
, . . . , α
n
) = n wtedy i tylko wtedy, gdy wektory α
1
, . . . , α
n
s
,
a
liniowo niezależne.
Twierdzenie 11.14. Niech α
1
, . . . , α
n
b
,
ed
,
a wektorami przestrzeni
liniowej V wymiaru n. Wówczas równoważne s
,
a warunki:
(i) zbiór {α
1
, . . . , α
n
} jest baz
,
a przestrzeni V ,
(ii) zbiór {α
1
, . . . , α
n
} jest liniowo niezależny,
(iii) zbiór {α
1
, . . . , α
n
} generuje przestrzeń V .
Dowód. (i)⇒(ii). Oczywiste. (ii)⇒(iii). Wynika od razu z twier-
dzenia Steinitza o wymianie. (iii)⇒(i). Z założenia wynika, że V =
lin(α
1
, . . . , α
n
). Zatem dim lin(α
1
, . . . , α
n
) = n i na mocy twierdzenia
11.13 zbiór {α
1
, . . . , α
n
} jest liniowo niezależny. Zatem ostatecznie ten
zbiór jest baz
,
a przestrzeni V .
Twierdzenie 11.15. Niech V
1
i V
2
b
,
ed
,
a skończenie wymiarowymi
podprzestrzeniami przestrzeni liniowej V nad ciałem K. Wówczas pod-
przestrzenie V
1
∩ V
2
i V
1
+ V
2
s
,
a również skończenie wymiarowe i za-
chodzi wzór:
dim(V
1
+ V
2
) = dim V
1
+ dim V
2
− dim(V
1
∩ V
2
).
(11.2)
Dowód. Ponieważ V
1
∩V
2
jest podprzestrzeni
,
a przestrzeni skończe-
nie wymiarowej V
1
, wi
,
ec z twierdzenia 11.11 przestrzeń V
1
∩V
2
jest skoń-
czenie wymiarowa. Niech {α
1
, . . . , α
k
} b
,
edzie baz
,
a przestrzeni V
1
∩ V
2
.
Wtedy z twierdzenia Steinitza o wymianie ten zbiór można uzupełnić
do bazy {α
1
, . . . , α
n
, β
1
, . . . , β
s
} przestrzeni V
1
i można go też uzupeł-
nić do bazy {α
1
, . . . , α
k
, γ
1
, . . . , γ
r
} przestrzeni V
2
. Wtedy

Baza i wymiar przestrzeni liniowej
97
dim(V
1
∩V
2
) = k, dim V
1
= k +s i dim V
2
= k +r, wi
,
ec pozostaje wyka-
zać, że dim(V
1
+V
2
) = k+s+r. Ale V
1
+V
2
= lin(α
1
, . . . , α
k
, β
1
, . . . , β
s
)
+lin(α
1
, . . . , α
k
, γ
1
, . . . , γ
r
) = lin(α
1
, . . . , α
k
, β
1
, . . . , β
s
, γ
1
, . . . , γ
r
), wi
,
ec
wystarczy wykazać, że wektory α
1
, . . . , α
k
, β
1
, . . . , β
s
, γ
1
, . . . , γ
r
s
,
a li-
niowo niezależne. W tym celu weźmy dowolne skalary a
1
, . . . , a
k
, b
1
,
. . . , b
s
, c
1
, . . . , c
r
∈ K takie, że
a
1
◦ α
1
+ . . . + a
k
◦ α
k
+ b
1
◦ β
1
+ . . . + b
s
◦ β
s
+ c
1
◦ γ
1
+ . . . + c
r
◦ γ
r
= Θ.
Oznaczmy: α = a
1
◦ α
1
+ . . . + a
k
◦ α
k
, β = b
1
◦ β
1
+ . . . + b
s
◦ β
s
,
γ = c
1
◦ γ
1
+ . . . + c
r
◦ γ
r
. Wtedy γ = −(α + β) ∈ V
1
∩ V
2
. Za-
tem istniej
,
a d
1
, . . . , d
k
∈ K takie, że γ = d
1
◦ α
1
+ . . . + d
k
◦ α
k
,
sk
,
ad c
1
◦ γ
1
+ . . . + c
r
◦ γ
r
+ (−d
1
) ◦ α
1
+ . . . + (−d
k
) ◦ α
k
= Θ. Za-
tem z liniowej niezależności wektorów α
1
, . . . , α
k
, γ
1
, . . . , γ
r
mamy, że
c
1
= . . . = c
r
= −d
1
= . . . = −d
k
= 0, czyli γ = Θ oraz Θ = α + γ.
Zatem z liniowej niezależności wektorów α
1
, . . . , α
k
, β
1
, . . . , β
s
otrzy-
mamy, że a
1
= . . . = a
k
= b
1
= . . . = b
s
= 0 i ostatecznie wektory
α
1
, . . . , α
k
, β
1
, . . . , β
s
, γ
1
, . . . , γ
r
s
,
a liniowo niezależne.
Wniosek 11.3. Niech V
1
, V
2
b
,
ed
,
a podprzestrzeniami przestrzeni
liniowej V wymiaru n. Wtedy dim(V
1
∩ V
2
) ≥ dim V
1
+ dim V
2
− n.
Dowód. Ponieważ dim(V
1
+ V
2
) ≤ n, wi
,
ec z twierdzenia 11.15
uzyskujemy, że dim V
1
+ dim V
2
− dim(V
1
∩ V
2
) ≤ n, sk
,
ad mamy tez
,
e.

Rozdział 12
Izomorfizmy. Sumy proste.
Hiperpłaszczyzny
12.1
Izomorfizmy przestrzeni liniowych
Definicja 12.1. Niech V i W b
,
ed
,
a przestrzeniami liniowymi nad
ciałem K. Powiemy, że przestrzenie V i W s
,
a izomorficzne i piszemy
V ∼
= W , jeżeli istnieje bijekcja f : V −→ W spełniaj
,
aca warunki:
(1) ∀
α,β∈V
f (α + β) = f (α) + f (β) i (2) ∀
a∈K
∀
α∈V
f (a ◦ α) = a ◦ f (α).
Takie przekształcenia f nazywamy izomorfizmami liniowymi.
Twierdzenie 12.1. Niech V i W b
,
ed
,
a przestrzeniami liniowymi
wymiaru n nad ciałem K. Wtedy V ∼
= W . Jeśli wektory α
1
, . . . , α
n
tworz
,
a baz
,
e przestrzeni V , zaś wektory β
1
, . . . , β
n
tworz
,
a baz
,
e prze-
strzeni W , to istnieje dokładnie jeden taki izomorfizm f : V −→ W ,
że f (α
i
) = β
i
dla i = 1, . . . , n. W szczególności każda n-wymiarowa
przestrzeń liniowa nad ciałem K jest izomorficzna z przestrzeni
,
a K
n
.
Dowód. Z założenia oraz z twierdzenia 11.9 wynika, że f : V → W
dane wzorem
f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = a
1
◦ β
1
+ . . . + a
n
◦ β
n
dla a
1
, . . . , a
n
∈ K
(12.1)
jest dobrze określon
,
a bijekcj
,
a oraz f (α
i
) = β
i
dla i = 1, . . . , n.
Ponadto dla dowolnych a, a
1
, . . . , a
n
, b
1
, . . . , b
n
∈ K oraz dla
98

Izomorfizmy, sumy proste, hiperpłaszczyzny
99
α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
i β = b
1
◦ α
1
+ . . . + b
n
◦ α
n
mamy, że
α + β = (a
1
+ b
1
) ◦ α
1
+ . . . + (a
n
+ b
n
) ◦ α
n
, a ◦ α = (aa
1
) ◦ α
1
+
. . . + (aa
n
) ◦ α
n
, wi
,
ec f (α + β) = (a
1
+ b
1
) ◦ β
1
+ . . . + (a
n
+ b
n
) ◦ β
n
=
[a
1
◦ β
1
+ . . . + a
n
◦ β
n
] + [b
1
◦ β
1
+ . . . + b
n
◦ β
n
] = f (α) + f (β)
oraz f (a ◦ α) = (aa
1
) ◦ β
1
+ . . . + (aa
n
) ◦ β
n
= a ◦ (a
1
◦ β
1
+ . . . +
a
n
◦ β
n
) = a ◦ f (α). Zatem f jest izomorfizmem liniowym takim, że
f (α
i
) = β
i
dla i = 1, . . . , n. W szczególności mamy st
,
ad, że V ∼
= W
oraz V ∼
= K
n
. Niech teraz g : V −→ W b
,
edzie izomorfizmem liniowym
takim, że g(α
i
) = β
i
dla i = 1, . . . , n. Wtedy przez prost
,
a indukcj
,
e
wzgl
,
edem k można wykazać, że g(γ
1
+ . . . + γ
k
) = g(γ
1
) + . . . + g(γ
k
)
dla dowolnych γ
1
, . . . , γ
k
∈ V . Zatem dla dowolnych a
1
, . . . , a
n
∈ K
mamy, że g(a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = g(a
1
◦ α
1
) + . . . + g(a
n
◦ α
n
) =
a
1
◦ g(α
1
) + . . . + a
n
◦ g(α
n
) = a
1
◦ β
1
+ . . . + a
n
◦ β
n
, czyli g = f .
Wniosek 12.1. Jeśli α, β s
,
a niezerowymi wektorami przestrzeni li-
niowej V o skończonym wymiarze, to istnieje izomorfizm f przestrzeni
V na siebie taki, że f (α) = β.
Dowód. Ponieważ α 6= Θ i β 6= Θ, wi
,
ec zbiory {α} i {β} s
,
a li-
niowo niezależne. Z twierdzenia Steinitza o wymianie wynika zatem, że
można te zbiory uzupełnić do baz {α, α
1
, . . . , α
n−1
}, {β, β
1
, . . . , β
n−1
}
przestrzeni V . Wtedy z twierdzenia 12.1 wynika istnienie ż
,
adanego
izomorfizmu f .
Niech f : V −→ W b
,
edzie izomorfizmem liniowym. Wtedy z (12.1)
mamy, że f (Θ) = f (0 ◦ Θ) = 0 ◦ f (Θ) = Θ. Zatem
f (Θ) = Θ.
St
,
ad dla α ∈ V mamy, że f (α) + f (−α) = f (α + (−α)) = f (Θ) = Θ,
czyli
f (−α) = −f (α) dla każdego α ∈ V .
Zatem izomorfizm liniowy zachowuje działania dodawania wektorów,
mnożenia przez skalary, branie wektora przeciwnego i wektor zerowy.
St
,
ad izomorfizm liniowy zachowuje wszystkie własności algebraiczne

100
Wykłady z algebry liniowej I
(poj
,
ecie własności algebraicznej rozumiemy tutaj w intuicyjnym sen-
sie) przestrzeni liniowych i układów wektorów. Uwaga ta może po-
służyć do wprowadzenia ścisłej definicji własności algebraicznej prze-
strzeni liniowych jako własności zachowywanej przez wszystkie izomor-
fizmy liniowe. Można wykazać, że dla izomorfizmu liniowego f :
(I) jeśli podzbiór X ⊆ V jest liniowo niezależny (zależny lub jest
baz
,
a), to f (X) jest liniowo niezależny (odpowiednio zależny, jest baz
,
a),
(II) jeśli β, α
1
, . . . , α
n
∈ V i β jest kombinacj
,
a liniow
,
a wektorów
α
1
, . . . , α
n
, to f (β) jest kombinacj
,
a liniow
,
a wektorów f (α
1
), . . . , f (α
n
),
(III) jeśli dim V = n, to dim W = n.
W algebrze liniowej utożsamia si
,
e izomorficzne przestrzenie liniowe.
12.2
Suma prosta podprzestrzeni
Twierdzenie 12.2. Niech n ≥ 2 b
,
edzie liczb
,
a naturaln
,
a i niech
V
1
, . . . , V
n
b
,
ed
,
a podprzestrzeniami przestrzeni liniowej V . Nast
,
epuj
,
ace
warunki s
,
a równoważne:
(i) V
i
∩ (V
1
+ . . . + V
i−1
+ V
i+1
+ . . . + V
n
) = {Θ} dla i = 1, . . . , n;
(ii) jeśli α
1
+ . . . + α
n
= Θ, gdzie α
i
∈ V
i
dla i = 1, . . . , n, to
α
1
= . . . = α
n
= Θ.
Dowód. (i)⇒(ii). Weźmy dowolne α
i
∈ V
i
dla i = 1, . . . , n takie,
że α
1
+ . . . + α
n
= Θ. Wtedy dla i = 1, . . . , n: α
i
= (−α
1
) + . . . +
(−α
i−1
)+(−α
i+1
)+. . .+(−α
n
) ∈ V
i
∩(V
1
+. . .+V
i−1
+V
i+1
+. . .+V
n
) =
{Θ}, czyli α
i
= Θ dla i = 1, . . . , n.
(ii)⇒(i). Weźmy dowolne i = 1, . . . , n i niech
α ∈ V
i
∩ (V
1
+ . . . + V
i−1
+ V
i+1
+ . . . + V
n
). Wtedy istniej
,
a α
k
∈ V
k
dla
k = 1, . . . , i−1, i+1, . . . , n takie, że α = α
1
+. . .+α
i−1
+α
i+1
+. . .+α
n
,
sk
,
ad α
1
+ . . . + α
i−1
+ (−α) + α
i+1
+ . . . + α
n
= Θ. Zatem α
1
=
. . . = α
i−1
= −α = α
i+1
= . . . = α
n
= Θ, sk
,
ad α = Θ. Zatem
V
i
∩ (V
1
+ . . . + V
i−1
+ V
i+1
+ . . . + V
n
) = {Θ}.
Definicja 12.2. Mówimy, że przestrzeń liniowa V jest sum
,
a prost
,
a
swoich podprzestrzeni V
1
, . . . , V
n
, gdy V = V
1
+ . . . + V
n
oraz spełniony
jest którykolwiek warunek (a wi
,
ec oba warunki) powyższego twierdze-
nia. Piszemy wtedy V = V
1
⊕ . . . ⊕ V
n
. Jeśli V = V
1
⊕ V
2
, to mó-

Izomorfizmy, sumy proste, hiperpłaszczyzny
101
wimy, że podprzestrzeń V
2
jest dopełnieniem liniowym podprzestrzeni
V
1
(w przestrzeni V ).
Twierdzenie 12.3. Dla dowolnej podprzestrzeni V
1
przestrzeni
liniowej V istnieje podprzestrzeń W ⊆ V taka, że V = V
1
⊕ W .
Dowód. Z twierdzenia 11.5 podprzestrzeń V
1
posiada baz
,
e X.
Zatem z twierdzenia 11.4 istnieje podzbiór Y ⊆ V rozł
,
aczny z X i taki,
że zbiór X ∪ Y jest baz
,
a przestrzeni V . Ponadto V
1
= lin(X) oraz
V = lin(X ∪ Y ). Niech W = lin(Y ). Wtedy z twierdzenia 10.5 mamy,
że lin(X ∪ Y ) = lin(X) + lin(Y ), czyli V = V
1
+ W . Niech α ∈ V
1
∩ W .
Wtedy istniej
,
a α
1
, . . . , α
n
∈ X, β
1
, . . . , β
k
∈ Y , a
1
, . . . , a
n
, b
1
, . . . , b
k
∈
K takie, że α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
= b
1
◦ β
1
+ . . . + b
k
◦ β
k
, sk
,
ad
a
1
◦ α
1
+ . . . + a
n
◦ α
n
+ (−b
1
) ◦ β
1
+ . . . + (−b
k
) ◦ β
k
= Θ. Zatem z
liniowej niezależności zbioru X ∪ Y mamy, że a
1
= . . . = a
n
= −b
1
=
. . . = −b
k
= 0, czyli α = Θ i V
1
∩ W = {Θ}. Zatem V = V
1
⊕ W .
12.3
Hiperpłaszczyzny liniowe
Definicja 12.3.
Niech V b
,
edzie n-wymiarow
,
a przestrzeni
,
a li-
niow
,
a. Hiperpłaszczyzn
,
a liniow
,
a przestrzeni V nazywamy każd
,
a pod-
przestrzeń przestrzeni V o wymiarze n − 1.
Twierdzenie 12.4. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad cia-
łem K wymiaru n i niech V
1
b
,
edzie podprzestrzeni
,
a wymiaru k. Wów-
czas V
1
jest cz
,
eści
,
a wspóln
,
a n−k hiperpłaszczyzn liniowych przestrzeni
V .
Dowód. Niech {α
1
, . . . , α
k
} b
,
edzie baz
,
a podprzestrzeni V
1
. Z twier-
dzenia Steinitza o wymianie możemy j
,
a uzupełnić do bazy {α
1
, . . . , α
k
,
α
k+1
, . . . , α
n
} przestrzeni V . Niech W
i
= lin(α
1
, . . . , α
k
, . . . , α
k+i−1
,
α
k+i+1
, . . . , α
n
) dla i = 1, . . . , n − k. Wówczas W
1
, . . . , W
n−k
s
,
a hiper-
płaszczyznami zawieraj
,
acymi V
1
, sk
,
ad V
1
⊆ W
1
∩ . . . ∩ W
n−k
. Niech
α ∈ W
1
∩ . . . ∩ W
n−k
. Wtedy istniej
,
a a
1
, . . . , a
n
∈ K takie, że α =
a
1
◦ α
1
+ . . . + a
n
◦ α
n
. Dla liczb naturalnych i ≤ n − k mamy, że
α ∈ W
i
, wi
,
ec wektor α można przedstawić w postaci α = a
i1
◦ α
1
+
. . . + a
i k+i−1
◦ α
k+i−1
+ a
i k+i+1
◦ α
k+i+1
+ . . . + a
in
◦ α
n
. Z jednoznaczno-

102
Wykłady z algebry liniowej I
ści przedstawienia wektora α w postaci kombinacji liniowej wektorów
bazy (α
1
, . . . , α
n
) wynika, że a
k+i
= 0 dla wszystkich i = 1, . . . , n − k.
Wobec tego α = a
1
◦α
1
+. . .+a
k
◦α
k
∈ V
1
. Zatem W
1
∩. . .∩W
n−k
⊆ V
1
i ostatecznie V
1
= W
1
∩ . . . ∩ W
n−k
.
Twierdzenie 12.5. Niech l b
,
edzie liczb
,
a naturaln
,
a. Niech V
1
, . . . ,
V
l
b
,
ed
,
a hiperpłaszczyznami n-wymiarowej przestrzeni liniowej V . Wów-
czas dim(V
1
∩ . . . ∩ V
l
) ≥ n − l.
Dowód. Dla l = 1 teza jest oczywiście prawdziwa. Załóżmy, że
teza zachodzi dla pewnego naturalnego l = k i niech V
1
, . . . , V
k+1
b
,
ed
,
a
hiperpłaszczyznami przestrzeni V . Z założenia indukcyjnego wynika,
że dim(V
1
∩ . . . ∩ V
k
) ≥ n − k, a z wniosku 11.3 otrzymujemy
dim(V
1
∩ . . . ∩ V
k
∩ V
k+1
) ≥ dim(V
1
∩ . . . ∩ V
k
) + n − 1 − n. Zatem
dim(V
1
∩ . . . ∩ V
k
∩ V
k+1
) ≥ n − k + n − 1 − n = n − (k + 1). Z zasady
indukcji wynika zatem, że nasze twierdzenie jest prawdziwe dla każdej
liczby naturalnej l.
Z twierdzeń 12.4 i 12.5 wynika od razu nast
,
epuj
,
acy
Wniosek 12.2. Każda k-wymiarowa podprzestrzeń W n-wymiarowej
przestrzeni liniowej V daje si
,
e przedstawić jako przeci
,
ecie n − k, ale
nie mniejszej liczby hiperpłaszczyzn liniowych.
12.4
Podprzestrzenie przestrzeni
współrz
,
ednych
Twierdzenie 12.6. Podprzestrzeń W przestrzeni K
n
wyznaczona
przez równanie a
1
x
1
+. . .+a
n
x
n
= 0, gdzie a
1
, . . . , a
n
∈ K i co najmniej
jeden ze współczynników a
1
, . . . , a
n
jest różny od zera, jest hiperpłasz-
czyzn
,
a liniow
,
a.
Dowód.
Załóżmy, że współczynnik a
i
6= 0 dla pewnego i =
1, . . . , n. Podprzestrzeń W jest różna od K
n
, gdyż wektor ε
i
nie jest
rozwi
,
azaniem rozpatrywanego równania, a st
,
ad dim W ≤ n−1. Dla do-
wodu równości dim W = n−1 wystarczy wi
,
ec wskazać n−1 liniowo nie-
zależnych rozwi
,
azań równania a
1
x
1
+ . . . + a
n
x
n
= 0. Łatwo sprawdzić,

Izomorfizmy, sumy proste, hiperpłaszczyzny
103
że wektory ε
1
−
a
1
a
i
◦ ε
i
, . . . , ε
i−1
−
a
i−1
a
i
◦ ε
i
, ε
i+1
−
a
i+1
a
i
◦ ε
i
, . . . , ε
n
−
a
n
a
i
◦ ε
i
czyni
,
a zadość temu ż
,
adaniu.
Z twierdzeń 12.5 i 12.6 wynika od razu nast
,
epuj
,
acy
Wniosek 12.3. Podprzestrzeń przestrzeni K
n
wyznaczona przez
układ m równań jednorodnych liniowych ma wymiar nie mniejszy niż
n − m.
Twierdzenie 12.7. Każda hiperpłaszczyzna liniowa W przestrzeni
liniowej K
n
jest wyznaczona przez pewne równanie a
1
x
1
+ . . . + a
n
x
n
=
0, gdzie a
1
, . . . , a
n
∈ K.
Dowód. Niech wektory α
i
= [a
i1
, . . . , a
in
] dla i = 1, . . . , n − 1
tworz
,
a baz
,
e hiperpłaszczyzny W i niech V b
,
edzie podprzestrzeni
,
a opi-
san
,
a przez układ równań
a
11
x
1
+ . . . +
a
1n
x
n
= 0
a
21
x
1
+ . . . +
a
2n
x
n
= 0
..
.
..
.
. .. ...
..
.
..
.
a
n−1 1
x
1
+ . . . + a
n−1 n
x
n
= 0
.
(12.2)
Z wniosku 12.3 wynika, że dim V ≥ n − (n − 1) = 1, a wi
,
ec podprze-
strzeń V zawiera niezerowy wektor. Niech [b
1
, . . . , b
n
] b
,
edzie nieze-
rowym wektorem podprzestrzeni V . Przestrzeń V
1
wyznaczona przez
równanie b
1
x
1
+ . . . + b
n
x
n
= 0 jest na mocy twierdzenia 12.6 hiper-
płaszczyzn
,
a liniow
,
a. Ponadto z określenia wektora [b
1
, . . . , b
n
] wynika,
że wektory α
j
dla j = 1, . . . , n − 1 należ
,
a do hiperpłaszczyzny V
1
, a za-
tem W = lin(α
1
, . . . , α
n−1
) ⊆ V
1
. Ponieważ dim W = dim V
1
= n − 1,
wi
,
ec z twierdzenia 11.12, W = V
1
.
Z twierdzenia 12.7 i z wniosku 12.2 mamy natychmiast nast
,
epuj
,
acy
Wniosek 12.4. Każda k-wymiarowa podprzestrzeń przestrzeni li-
niowej K
n
jest wyznaczona przez układ złożony z n − k, ale nie mniej,
równań liniowych jednorodnych.

Rozdział 13
Rz
,
ad macierzy
13.1
Określenie rz
,
edu macierzy
Niech A b
,
edzie m×n - macierz
,
a nad ciałem K. Wówczas wiersze macie-
rzy A możemy w naturalny sposób traktować jako wektory przestrzeni
K
n
, zaś kolumny macierzy A możemy traktować jako wektory prze-
strzeni K
m
. Rz
,
edem wierszowym macierzy A nazywamy maksymaln
,
a
ilość jej liniowo niezależnych wierszy. Natomiast rz
,
edem kolumnowym
macierzy A nazywamy maksymaln
,
a ilość jej liniowo niezależnych ko-
lumn. Rz
,
ad wierszowy i rz
,
ad kolumnowy macierzy A oznaczamy od-
powiednio symbolami: r
w
(A) i r
k
(A).
Z tego określenia wynika od razu, że dla dowolnej macierzy A:
r
w
(A) = r
k
(A
T
) oraz r
k
(A) = r
w
(A
T
).
(13.1)
Ponadto z określenia rz
,
edu macierzy mamy natychmiast, że
r
w
(0
m×n
) = r
k
(0
m×n
) = 0.
(13.2)
Z twierdzenia 11.8 wynika od razu, że rz
,
ad wierszowy macierzy
A jest równy wymiarowi podprzestrzeni generowanej przez
jej wektory wierszowe, zaś rz
,
ad kolumnowy macierzy A jest
równy wymiarowi podprzestrzeni generowanej przez wektory
kolumnowe macierzy A.
104

Rz
,
ad macierzy
105
Ponadto z własności operacji elementarnych rz
,
ad wierszowy ma-
cierzy A nie zmienia si
,
e przy stosowaniu operacji elementar-
nych na wierszach tej macierzy oraz rz
,
ad kolumnowy macie-
rzy A nie zmienia si
,
e przy stosowaniu operacji elementarnych
na kolumnach tej macierzy.
Lemat 13.1. Jeżeli do pewnego wiersza macierzy dodamy inny jej
wiersz pomnożony przez dowolny skalar, to rz
,
ad kolumnowy tej macie-
rzy nie ulegnie zmianie.
Dowód. Niech A = [a
ij
] b
,
edzie m × n-macierz
,
a nad ciałem K.
Dla uproszczenia znakowania założymy, że do pierwszego wiersza ma-
cierzy A dodano drugi jej wiersz pomnożony przez skalar a ∈ K
i oznaczmy przez B = [b
ij
] macierz uzyskan
,
a w wyniku tej opera-
cji. Niech r = r
k
(A). Oznacza to, że pewne r-kolumn macierzy A s
,
a
liniowo niezależne. Dla uproszczenia znakowania załóżmy, że pierwsze
r-kolumny macierzy A s
,
a liniowo niezależne. Udowodnimy, że wówczas
pierwsze r-kolumny macierzy B też s
,
a liniowo niezależne. Niech A
j
oraz B
j
oznaczaj
,
a j-t
,
a kolumn
,
e macierzy A i B odpowiednio. Weźmy
dowolne x
1
, . . . , x
r
∈ K takie, że x
1
◦ B
1
+ . . . + x
r
◦ B
r
= Θ. Wtedy
x
1
◦
a
11
+ aa
21
a
21
..
.
a
m1
+ . . . + x
r
◦
a
1r
+ aa
2r
a
2r
..
.
a
mr
= 0
m×1
,
wi
,
ec
(a
11
+ aa
12
)x
1
+ . . . + (a
1r
+ aa
2r
)x
r
= 0
a
21
x
1
+ . . . +
a
2r
x
r
= 0
..
.
..
.
. .. ...
..
.
..
.
..
.
a
m1
x
1
+ . . . +
a
mr
x
r
= 0
,
sk
,
ad po odj
,
eciu od pierwszej równości równości drugiej pomnożonej
przez a uzyskamy, że x
1
◦ A
1
+ . . . + x
r
◦ A
r
= Θ. Zatem z liniowej nie-
zależności kolumn A
1
, . . . , A
r
wynika, że x
1
= . . . = x
r
= 0 i kolumny
B
1
, . . . , B
r
s
,
a liniowo niezależne. Zatem r
k
(B) ≥ r
k
(A). Ale macierz

106
Wykłady z algebry liniowej I
A powstaje z macierzy B przez dodanie do pierwszego wiersza dru-
giego wiersza pomnożonego przez skalar (−a), wi
,
ec z pierwszej cz
,
eści
dowodu r
k
(A) ≥ r
k
(B) i ostatecznie r
k
(A) = r
k
(B).
Z (13.1) i z lematu 13.1 wynika od razu, że prawdziwy jest też
nast
,
epuj
,
acy
Lemat 13.2. Jeżeli do pewnej kolumny macierzy dodamy inn
,
a
jej kolumn
,
e pomnożon
,
a przez dowolny skalar, to rz
,
ad wierszowy tej
macierzy nie ulegnie zmianie.
Lemat 13.3. Niech m, n ≥ 2 i niech A = [a
ij
] b
,
edzie m × n-
macierz
,
a nad ciałem K tak
,
a, że dla pewnych s, t jest a
st
6= 0 oraz
a
it
= 0 dla wszystkich i 6= s i a
sj
= 0 dla wszystkich j 6= t. Wówczas
oraz r
k
(A) = 1 + r
k
(A
st
) oraz r
w
(A) = 1 + r
w
(A
st
).
Dowód. Niech r = r
k
(A
st
). Istniej
,
a wówczas kolumny B
1
, . . . , B
r
macierzy A
st
, które s
,
a liniowo niezależne i takie, że każda kolumna
macierzy A
st
jest ich kombinacj
,
a liniow
,
a. Oznaczmy przez A
j
kolumn
,
e
macierzy A powstaj
,
ac
,
a przez dopisanie 0 w s-tym wierszu macierzy B
j
dla j = 1, . . . , r. Niech A
r+1
oznacza t-t
,
a kolumn
,
e macierzy A. Weźmy
dowolne x
1
, . . . , x
r+1
∈ K takie, że x
1
◦ A
1
+ . . . + x
r+1
◦ A
r+1
= Θ.
Wtedy x
r+1
a
st
= 0, sk
,
ad x
r+1
= 0 oraz x
1
◦ B
1
+ . . . + x
r
◦ B
r
= Θ.
Zatem z liniowej niezależności B
1
, . . . , B
r
jest x
1
= . . . = x
r
= 0. St
,
ad
kolumny A
1
, . . . , A
r+1
s
,
a liniowo niezależne. Niech X b
,
edzie dowoln
,
a
kolumn
,
a macierzy A o numerze różnym od t. Niech Y b
,
edzie kolumn
,
a
macierzy A
st
powstaj
,
ac
,
a z X przez wykreślenie s-tego wiersza (który
składa si
,
e z jednego zera!). Wtedy istniej
,
a a
1
, . . . , a
r
∈ K takie, że
Y = a
1
◦ B
1
+ . . . + a
r
◦ B
r
, sk
,
ad X = a
1
◦ A
1
+ . . . + a
r
◦ A
r
. Wynika
st
,
ad, że wszystkie kolumny macierzy A s
,
a kombinacjami liniowymi
kolumn A
1
, . . . , A
r
, A
r+1
. Oznacza to, że r
k
(A) = r + 1 = 1 + r
k
(A
st
).
Dowód drugiej cz
,
eści lematu wynika natychmiast z (13.1) i z pierw-
szej jego cz
,
eści.
Twierdzenie 13.1. Rz
,
ad kolumnowy dowolnej macierzy równy
jest jej rz
,
edowi wierszowemu.
Dowód. Indukcja wzgl
,
edem liczby m wierszy macierzy. Jeżeli
m = 1, to A = [a
1
a
2
. . .
a
n
] dla pewnych skalarów a
1
, . . . , a
n
.

Rz
,
ad macierzy
107
Jeżeli a
1
= . . . = a
n
= 0, to r
w
(A) = 0 = r
k
(A). Jeżeli zaś a
j
6= 0 dla
pewnego j = 1, . . . , n, to r
w
(A) = 1 = r
k
(A). Zatem teza zachodzi dla
m = 1.
Niech teraz m b
,
edzie liczb
,
a naturaln
,
a wi
,
eksz
,
a od 1 i tak
,
a, że teza
zachodzi dla wszystkich macierzy nad ciałem K, które maj
,
a mniej niż
m wierszy. Weźmy dowoln
,
a m × n-macierz A = [a
ij
] nad ciałem K.
Jeśli A = 0
m×n
, to r
w
(A) = 0 = r
k
(A). Niech zatem A 6= 0
m×n
. Wtedy
istniej
,
a k, l takie, że a
kl
6= 0. Jeśli n = 1, to r
w
(A) = r
k
(A
T
), wi
,
ec z za-
łożenia indukcyjnego r
k
(A
T
) = r
w
(A
T
) = r
k
(A), czyli r
w
(A) = r
k
(A).
Niech dalej n > 1. Niech B = [b
ij
] b
,
edzie macierz
,
a powstaj
,
ac
,
a z macie-
rzy A przez wykonanie operacji elementarnych: w
i
−
a
il
a
kl
·w
k
dla wszyst-
kich i 6= k. Wtedy r
w
(B) = r
w
(A) oraz z lematu 13.1, r
k
(B) = r
k
(A).
Niech dalej C b
,
edzie macierz
,
a powstaj
,
ac
,
a z macierzy B przez wyko-
nanie operacji elementarnych: k
j
−
b
kj
a
kl
· k
l
dla wszystkich j 6= l. Wtedy
r
k
(C) = r
k
(B) oraz z lematu 13.2, r
w
(C) = r
w
(B). Ale z lematu 13.3
mamy, że r
w
(C) = 1 + r
w
(C
kl
) oraz r
k
(C) = 1 + r
k
(C
kl
). Z założenia
indukcyjnego r
w
(C
kl
) = r
k
(C
kl
). Zatem r
w
(A) = 1 + r
k
(C
kl
) = r
k
(A).
13.2
Metody obliczania rz
,
edu macierzy
Wspóln
,
a wartość rz
,
edu kolumnowego i wierszowego macierzy A nazy-
wamy rz
,
edem macierzy A i oznaczamy przez r(A). Z twierdzenia 13.1
oraz z pocz
,
atkowej cz
,
eści tego rozdziału mamy od razu nast
,
epuj
,
ace
Twierdzenie 13.2. Operacje elementarne wykonywane na wier-
szach lub kolumnach macierzy nie zmieniaj
,
a jej rz
,
edu.
Z twierdzenia 13.1 oraz ze wzoru (13.1) wynika od razu nast
,
epuj
,
ace
Twierdzenie 13.3. Dla dowolnej macierzy A: r(A) = r(A
T
).
Twierdzenie 13.4. Niech A = [a
ij
] b
,
edzie tak
,
a m × n-macierz
,
a
nad ciałem K, że a
kl
6= 0 dla pewnych k, l oraz a
il
= 0 dla wszystkich

108
Wykłady z algebry liniowej I
i 6= k. Wtedy r(A) = 1 + r(A
kl
).
Dowód.
Oznaczmy przez B macierz powstaj
,
ac
,
a z macierzy A
przez wykonanie operacji elementarnych: k
j
−
a
kj
a
kl
· k
l
dla wszystkich
j 6= l. Wtedy B
kl
= A
kl
oraz na mocy twierdzenia 13.2, r(A) = r(B).
Ponadto z twierdzenia 13.1 i z lematu 13.3, r(B) = 1 + r(B
kl
). Zatem
r(A) = 1 + r(A
kl
).
Twierdzenie 13.5. Niech A = [a
ij
] b
,
edzie macierz
,
a kwadratow
,
a
stopnia n nad ciałem K. Wówczas równoważne s
,
a warunki:
(i) r(A) = n,
(ii) det(A) 6= 0.
Dowód. (i)⇒(ii). Ponieważ wszystkie kolumny A
1
, . . . , A
n
macie-
rzy A s
,
a liniowo niezależne i jest ich n, wi
,
ec tworz
,
a one baz
,
e prze-
strzeni K
n
. Wynika st
,
ad, że dla każdego i = 1, . . . , n istniej
,
a ska-
lary x
i1
, . . . , x
in
∈ K takie, że x
i1
◦ A
1
+ . . . + x
in
◦ A
n
= ε
i
. Niech
X = [x
ij
]
i,j=1,...,n
. Wtedy A · X = I
n
, sk
,
ad z twierdzenia Cauchy’ego
det(A) 6= 0.
(ii)⇒(i). Ponieważ det(A) 6= 0, wi
,
ec istnieje macierz X = [x
ij
] ∈
M
n
(K) taka, że A · X = I
n
. Wtedy dla każdego i = 1, . . . , n mamy,
że ε
i
= x
i1
◦ A
1
+ . . . + x
in
◦ A
n
, wi
,
ec kolumny macierzy A generuj
,
a
przestrzeń K
n
. St
,
ad na mocy twierdzenia 11.14 te kolumny s
,
a liniowo
niezależne, czyli r(A) = n.
Definicja 13.1. Niech A b
,
edzie m×n-macierz
,
a nad ciałem K oraz
niech k b
,
edzie liczb
,
a naturaln
,
a tak
,
a, że k ≤ min{m, n}. Minorem
stopnia k macierzy A nazywamy wyznacznik macierzy kwadratowej
stopnia k, która powstaje z macierzy A przez wykreślenie m−k wierszy
oraz n − k kolumn.
Twierdzenie 13.6. Rz
,
ad niezerowej macierzy jest równy maksy-
malnemu stopniowi jej niezerowego minora.
Dowód. Niech A b
,
edzie niezerow
,
a m × n-macierz
,
a nad ciałem K.
Oznaczmy przez k maksymalny stopień niezerowego minora macierzy
A oraz przez r rz
,
ad tej macierzy. Wtedy pewne r wierszy macierzy
A jest liniowo niezależnych. Wykreślaj
,
ac pozostałe wiersze uzyskamy
k × n-macierz B o rz
,
edzie r. Zatem z twierdzenia 13.1 pewne r kolumn

Rz
,
ad macierzy
109
macierzy B s
,
a liniowo niezależne. Wykreślaj
,
ac w macierzy B pozostałe
kolumny uzyskamy macierz kwadratow
,
a C stopnia r o rz
,
edzie r. Zatem
z twierdzenia 13.4, det(C) 6= 0. Ale det(C) jest minorem stopnia r
macierzy A, wi
,
ec r ≤ k.
Niech teraz D b
,
edzie macierz
,
a kwadratow
,
a stopnia k powstaj
,
ac
,
a z
macierzy A przez wykreślenie pewnych m − k wierszy i n − k kolumn
tak
,
a, że det(D) 6= 0. Wtedy z twierdzenia 13.4 mamy, że r(D) = k.
Niech X b
,
edzie macierz
,
a powstaj
,
ac
,
a z macierzy A przez wykreśle-
nie tych samych wierszy, co dla macierzy D. Wtedy r(X) ≤ k oraz
wszystkie kolumny macierzy D s
,
a liniowo niezależne, wi
,
ec r(X) ≥ k
i ostatecznie r(X) = k. St
,
ad z definicji rz
,
edu wierszowego macierzy
k ≤ r i ostatecznie r = k.
13.3
Twierdzenie Kroneckera-Capellie’go
Niech dany b
,
edzie teraz dowolny układ m-równań liniowych z n-
niewiadomymi x
1
, . . . , x
n
nad ciałem K:
a
11
x
1
+
a
12
x
2
+
. . . +
a
1n
x
n
= b
1
a
21
x
1
+
a
22
x
2
+
. . . +
a
2n
x
n
= b
2
..
.
..
.
. ..
..
.
a
m1
x
1
+ a
m2
x
2
+ . . . + a
mn
x
n
= b
m
,
(13.3)
Macierz
,
a współczynników układu (13.3) nazywamy macierz:
A =
a
11
a
12
. . .
a
1n
a
21
a
22
. . .
a
2n
..
.
..
.
. ..
..
.
a
m1
a
m2
. . . a
mn
,
(13.4)
zaś macierz
,
a uzupełnion
,
a układu (13.3) nazywamy macierz:
A
u
=
a
11
a
12
. . .
a
1n
b
1
a
21
a
22
. . .
a
2n
b
2
..
.
..
.
. ..
..
.
..
.
a
m1
a
m2
. . . a
mn
b
m
.
(13.5)

110
Wykłady z algebry liniowej I
Twierdzenie 13.7 (Kroneckera-Capellie’go). Układ (13.3) ma
rozwi
,
azanie wtedy i tylko wtedy, gdy r(A) = r(A
u
). Ponadto układ
(13.3) ma dokładnie jedno rozwi
,
azanie wtedy i tylko wtedy, gdy r(A) =
r(A
u
) = n.
Dowód.
Oznaczmy przez α
j
j-t
,
a kolumn
,
e macierzy A i niech
β = [b
1
, . . . , b
m
]. Układ (13.3) można wtedy zapisać jako równanie
wektorowe:
x
1
◦ α
1
+ . . . + x
n
◦ α
n
= β.
(13.6)
Jeżeli (a
1
, . . . , a
n
) jest rozwi
,
azaniem układu (13.3), to a
1
◦ α
1
+ . . . +
a
n
◦α
n
= β, sk
,
ad na mocy twierdzenia 10.4 i twierdzenia 10.6 mamy, że
lin(α
1
, . . . , α
n
, β) = lin(α
1
, . . . , α
n
), czyli r(A
u
) = r(A). Na odwrót,
załóżmy, że r(A
u
) = r(A). Wtedy
dim lin(α
1
, . . . , α
n
) = dim lin(α
1
, . . . , α
n
, β),
wi
,
ec z twierdzenia 11.12 mamy, że lin(α
1
, . . . , α
n
, β) = lin(α
1
, . . . , α
n
),
sk
,
ad β ∈ lin(α
1
, . . . , α
n
), czyli istniej
,
a a
1
, . . . , a
n
∈ K takie, że β =
a
1
◦ α
1
+ . . . + a
n
◦ α
n
i wówczas (a
1
, . . . , a
n
) jest rozwi
,
azaniem układu
Pozostaje udowodnić drug
,
a cz
,
eść twierdzenia. Załóżmy najpierw,
że r(A
u
) = r(A) = n. Wówczas kolumny α
1
, . . . , α
n
s
,
a liniowo nie-
zależne, wi
,
ec tworz
,
a baz
,
e podprzestrzeni lin(α
1
, . . . , α
n
). Ale wtedy
dim lin(α
1
, . . . , α
n
) = dim lin(α
1
, . . . , α
n
, β), sk
,
ad lin(α
1
, . . . , α
n
) =
lin(α
1
, . . . , α
n
, β), czyli β ∈ lin(α
1
, . . . , α
n
). Zatem z twierdzenia 11.9
istnieje dokładnie jeden ci
,
ag (a
1
, . . . , a
n
) ∈ K
n
taki, że β = a
1
◦ α
1
+
. . . + a
n
◦ α
n
, wi
,
ec układ (13.3) ma dokładnie jedno rozwi
,
azanie. Na
odwrót, załóżmy, że układ (13.3) posiada dokładnie jedno rozwi
,
azanie
(a
1
, . . . , a
n
). Wówczas z pierwszej cz
,
eści dowodu r(A
u
) = r(A). Wy-
starczy zatem wykazać, że wektory α
1
, . . . , α
n
s
,
a liniowo niezależne.
Ale jeżeli b
1
, . . . , b
n
∈ K s
,
a takie, że b
1
◦ α
1
+ . . . + b
n
◦ α
n
= Θ, to
(a
1
+ b
1
) ◦ α
1
+ . . . + (a
n
+ b
n
) ◦ α
n
= a
1
◦ α
1
+ . . . + a
n
◦ α
n
+ Θ = β, wi
,
ec
(a
1
+ b
1
, . . . , a
n
+ b
n
) jest rozwi
,
azaniem układu (13.3), sk
,
ad a
i
+ b
i
= a
i
,
czyli b
i
= 0 dla i = 1, . . . , n, a wi
,
ec wektory α
1
, . . . , α
n
s
,
a liniowo nie-
zależne.

Rz
,
ad macierzy
111
Z rezultatów uzyskanych dotychczas wynika, że można stosować
nast
,
epuj
,
acy schemat post
,
epowania dla znalezienia wszystkich rozwi
,
a-
zań układu (13.3). Najpierw obliczamy r(A) i r(A
u
). Jeżeli r(A) 6=
r(A
u
), to układ (13.3) nie ma rozwi
,
azania. Jeśli zaś r = r(A) = r(A
u
),
to układ posiada rozwi
,
azanie. Wyznaczamy wówczas r liniowo nieza-
leżnych wierszy w macierzy A
u
i wykreślamy wszystkie pozostałe jej
wiersze. W otrzymanej macierzy znajdujemy k liniowo niezależnych
kolumn. Nast
,
epnie w przekształconym układzie równań przenosimy
na praw
,
a stron
,
e wszystkie niewiadome o numerach pozostałych n − k
kolumn i stosujemy wzory Cramera dla obliczenia pozostałych nie-
wiadomych (natomiast niewiadome przenoszone na drugie strony s
,
a
dowolnymi elementami ciała K).

Rozdział 14
Przestrzenie ilorazowe
14.1
Konstrukcja przestrzeni ilorazowej
Niech W b
,
edzie podprzestrzeni
,
a przestrzeni liniowej V nad ciałem K.
W zbiorze V określamy relacj
,
e ∼ przyjmuj
,
ac, że dla dowolnych α, β ∈
V :
α ∼ β ⇔ α − β ∈ W
(14.1)
Ponieważ Θ ∈ W , wi
,
ec dla każdego α ∈ V , jest α − α ∈ W , sk
,
ad
α ∼ α i relacja ∼ jest zwrotna.
Weźmy dowolne α, β ∈ V takie, że α ∼ β. Wtedy α − β ∈ W , sk
,
ad
β − α = −(α − β) ∈ W , czyli β ∼ α i relacja ∼ jest symetryczna.
Weźmy dowolne α, β, γ ∈ V takie, że α ∼ β i β ∼ γ. Wtedy
α − β, β − γ ∈ W , sk
,
ad α − γ = (α − β) + (β − γ) ∈ W , czyli α ∼ γ
i relacja ∼ jest przechodnia.
W ten sposób pokazaliśmy, że ∼ jest relacj
,
a równoważności w zbio-
rze V . Dla α ∈ V przez α + W oznaczmy klas
,
e abstrakcji relacji ∼
o reprezentancie α. Pokażemy, że
α + W = {α + β : β ∈ W }
(14.2)
Rzeczywiście, jeżeli γ ∈ α + W , to γ ∼ α, sk
,
ad γ − α = β ∈ W oraz
γ = α + β. Na odwrót, jeżeli γ = α + β dla pewnego β ∈ W , to
γ − α = β ∈ W , sk
,
ad γ ∼ α i γ ∈ α + W .
112
Przestrzenie ilorazowe
113
Dla α ∈ V zbiór α + W b
,
edziemy dalej nazywali warstw
,
a o repre-
zentancie α wzgl
,
edem podprzestrzeni W . Z własności klas abstrakcji
relacji równoważności wynika, że dowolne dwie warstwy wzgl
,
edem pod-
przestrzeni W s
,
a albo równe albo rozł
,
aczne oraz przestrzeń V jest sum
,
a
rozł
,
aczn
,
a pewnych swoich warstw wzgl
,
edem W .
Zauważmy, że dla dowolnych α, β ∈ V :
α + W = β + W ⇔ α − β ∈ W.
(14.3)
Rzeczywiście, α + W = β + W ⇔ α ∼ β ⇔ α − β ∈ W .
Ponadto
Θ + W = W,
(14.4)
bo Θ + W = {Θ + β : β ∈ W } = {β : β ∈ W } = W .
Ze wzorów (14.3) i (14.4) wynika od razu, że dla każdego α ∈ V :
α + W = W ⇔ α ∈ W.
(14.5)
Zatem jedna warstwa może mieć wiele reprezentantów! Warstw
,
e W
b
,
edziemy nazywali warstw
,
a zerow
,
a. Zbiór wszystkich warstw prze-
strzeni V wzgl
,
edem podprzestrzeni W b
,
edziemy oznaczali przez V /W .
Zatem
V /W = {α + W : α ∈ V }.
(14.6)
Dla dowolnych α, β ∈ V określamy sum
,
e warstw α + W i β + W przy
pomocy wzoru:
(α + W ) + (β + W ) = (α + β) + W.
(14.7)
Sprawdzimy, że wzór (14.7) nie zależy od wyboru reprezentantów warstw.
W tym celu weźmy dowolne α
1
, β
1
∈ V takie, że α
1
∼ α i β
1
∼ β.
Wtedy α
1
−α, β
1
−β ∈ W , sk
,
ad (α
1
+β
1
)−(α+β) = (α
1
−α)+(β
1
−β) ∈
W , czyli (α
1
+ β
1
) + W = (α + β) + W na mocy wzoru (14.3).
Teraz określimy iloczyn warstwy α + W przez skalar a ∈ K:
a ◦ (α + W ) = a ◦ α + W.
(14.8)

114
Wykłady z algebry liniowej I
Sprawdzimy, że to określenie nie zależy od wyboru reprezentantów
warstw. W tym celu weźmy dowolne α
1
∈ V takie, że α
1
∼ α. Wtedy
α
1
− α ∈ W , sk
,
ad a ◦ (α
1
− α) ∈ W , czyli a ◦ α
1
− a ◦ α ∈ W , wi
,
ec
a ◦ α
1
+ W = a ◦ α + W na mocy (14.3).
Twierdzenie 14.1. Dla dowolnej podprzestrzeni W przestrzeni li-
niowej V nad ciałem K zbiór V /W z dodawaniem warstw określonym
wzorem (14.7) i mnożeniem warstw przez skalary określonym wzorem
(14.8) oraz z warstw
,
a zerow
,
a W tworzy przestrzeń liniow
,
a nad cia-
łem K (nazywamy j
,
a przestrzeni
,
a ilorazow
,
a przestrzeni V wzgl
,
edem
podprzestrzeni W ).
Dowód. Weźmy dowolne α, β, γ ∈ V . A1. Ponieważ α + β =
β + α, wi
,
ec (β + W ) + (α + W ) = (β + α) + W = (α + β) + W =
(α + W ) + (β + W ). A2. Ponieważ (α + β) + γ = α + (β + γ),
wi
,
ec [(α + W ) + (β + W )] + (γ + W ) = [(α + β) + W ] + (γ + W ) =
[(α + β) + γ] + W = [α + (β + γ)] + W = (α + W ) + [(β + γ) + W ] =
(α + W ) + [(β + W ) + (γ + W )]. A3. Ponieważ α + Θ = α, wi
,
ec
(α + W ) + W = (α + W ) + (Θ + W ) = (α + Θ) + W = α + W . A4.
Ponieważ α+(−α) = Θ, wi
,
ec (α+W )+((−α)+W ) = [α+(−α)]+W =
Θ + W = W . St
,
ad dla α ∈ V mamy wzór:
− (α + W ) = (−α) + W.
(14.9)
A5. Ponieważ dla a ∈ K jest a ◦ (α + β) = a ◦ α + a ◦ β, wi
,
ec
a ◦ [(α + W ) + (β + W )] = a ◦ [(α + β) + W ] = a ◦ (α + β) + W =
(a◦α+a◦β)+W = (a◦α+W )+(a◦β +W ) = a◦(α+W )+a◦(β +W ).
A6. Ponieważ dla a, b ∈ K jest (a + b) ◦ α = a ◦ α + b ◦ α, wi
,
ec
(a + b) ◦ (α + W ) = (a + b) ◦ α + W = (a ◦ α + b ◦ α) + W = (a ◦ α + W ) +
(b ◦ α + W ) = a ◦ (α + W ) + b ◦ (α + W ). A7. Ponieważ dla dowolnych
a, b ∈ K jest (ab) ◦ α = a ◦ (b ◦ α), wi
,
ec (ab) ◦ (α + W ) = (ab) ◦ α + W =
a ◦ (b ◦ α) + W = a ◦ (b ◦ α + W ) = a ◦ [b ◦ (α + W )]. A8. Ponieważ
1 ◦ α = α, wi
,
ec 1 ◦ (α + W ) = 1 ◦ α + W = α + W .

Przestrzenie ilorazowe
115
14.2
Baza i wymiar przestrzeni ilorazowej
Twierdzenie 14.2. Niech W i U b
,
ed
,
a podprzestrzeniami prze-
strzeni liniowej V nad ciałem K takimi, że V = W ⊕ U . Wówczas
przekształcenie f : U −→ V /W dane wzorem f (α) = α + W dla α ∈ U
jest izomorfizmem liniowym. W szczególności
V /W ∼
= U .
Dowód. Z określenia f mamy, że dla dowolnych α, β ∈ U , a ∈ K
jest f (α + β) = (α + β) + W = (α + W ) + (β + W ) = f (α) + f (β)
oraz f (a ◦ α) = a ◦ α + W = a ◦ (α + W ) = a ◦ f (α). Jeżeli zaś
f (α) = f (β), to α + W = β + W , sk
,
ad α − β ∈ W . Ale α, β ∈ U ,
wi
,
ec α − β ∈ W ∩ U = {Θ}, czyli α − β = Θ i α = β. Zatem f
jest różnowartościowe. Dowolna warstwa przestrzeni V /W ma postać
α + W dla pewnego α ∈ V . Ale V = W + U , wi
,
ec istniej
,
a β ∈ W i
γ ∈ U takie, że α = β+γ. St
,
ad α−γ ∈ W , wi
,
ec α+W = γ+W = f (γ).
Zatem f jest ”na”i ostatecznie f jest izomorfizmem liniowym.
Ponieważ izomorfizm liniowy przekształca baz
,
e na baz
,
e, wi
,
ec z twier-
dzenia 14.2 oraz z dowodu twierdzenia 12.3 mamy natychmiast nast
,
epu-
j
,
ace
Twierdzenie 14.3. Niech X b
,
edzie baz
,
a podprzestrzeni W prze-
strzeni liniowej V i niech Y ⊆ V b
,
edzie zbiorem liniowo niezależnym
rozł
,
acznym z X takim, że X ∪ Y jest baz
,
a przestrzeni V . Wtedy dla
dowolnych α, β ∈ Y mamy, że α + W = β + W wtedy i tylko wtedy,
gdy α = β oraz zbiór {α + W : α ∈ Y } jest baz
,
a przestrzeni ilorazowej
V /W .
Twierdzenie 14.4. Niech W b
,
edzie podprzestrzeni
,
a skończenie
wymiarowej przestrzeni liniowej V . Wówczas zachodzi wzór:
dim(V /W ) = dim V − dim W .
Dowód. Z twierdzenia 12.3 istnieje podprzestrzeń przestrzeni V
taka, że V = W ⊕ U . Zatem W ∩ U = {Θ}, wi
,
ec na mocy twierdzenia
11.15 mamy, że dim V = dim W + dim U . Ale na mocy twierdzenia
14.2 jest V /W ∼
= U , wi
,
ec dim(V /W ) = dim U = dim V − dim W .

116
Wykłady z algebry liniowej I
Przykład 14.1. Wyznaczymy baz
,
e i wymiar przestrzeni ilorazowej
R
4
/W dla W = lin([1, 1, 1, 1], [1, 2, 3, 4]). W tym celu najpierw za po-
moc
,
a operacji elementarnych wyznaczamy baz
,
e podprzestrzeni W . Po
wykonaniu operacji w
2
−w
1
uzyskamy, że W = lin([1, 1, 1, 1], [0, 1, 2, 3])
oraz wektory [1, 1, 1, 1], [0, 1, 2, 3] tworz
,
a baz
,
e podprzestrzeni W , gdyż
wektory [1, 1, 1, 1], [0, 1, 2, 3], [0, 0, 1, 0], [0, 0, 0, 1] tworz
,
a baz
,
e prze-
strzeni R
4
. Zatem z twierdzenia 14.3 wektory [0, 0, 1, 0]+W , [0, 0, 0, 1]+
W tworz
,
a baz
,
e przestrzeni ilorazowej R
4
, sk
,
ad dim(R
4
/W ) = 2.
Przykład 14.2. Niech W b
,
edzie podprzestrzeni
,
a przestrzeni Q
3
generowan
,
a przez wektory [1, 2, 3] i [0, 1, 0]. Sprawdzimy, czy zachodzi
równość warstw [1, 0, 1] + W oraz [2, 4, 5] + W . Na mocy (14.3) mamy,
że [2, 4, 5] + W = [1, 0, 1] + W ⇔ [2, 4, 5] − [1, 0, 1] ∈ W ⇔ [1, 4, 4] ∈ W .
Ale wektory [1, 2, 3] i [0, 1, 0] tworz
,
a baz
,
e podprzestrzeni W , wi
,
ec
[1, 4, 4] ∈ W ⇔ (wektory [1, 2, 3], [0, 1, 0], [1, 4, 4] s
,
a liniowo zależne).
Lecz po wykonaniu operacji w
3
− w
1
, w
3
− 2w
2
uzyskamy z tych wekto-
rów baz
,
e {[1, 2, 3], [0, 1, 0], [0, 0, 1]} przestrzeni Q
3
, wi
,
ec wektory [1, 2, 3],
[01, 0], [1, 4, 4] s
,
a liniowo niezależne i wobec tego [1, 0, 1]+W 6= [2, 4, 5]+
W .
Przykład 14.3. Niech K = Z
2
, V = K
4
oraz W b
,
edzie podprze-
strzeni
,
a przestrzeni V generowan
,
a przez wektory [1, 0, 1, 1], [1, 1, 0, 1],
[0, 1, 1, 0]. Wypiszemy wszystkie elementy przestrzeni ilorazowej V /W .
Po wykonaniu operacji w
2
− w
1
uzyskamy, że
W = lin([1, 0, 1, 1], [0, 1, 1, 0]) oraz wektory [1, 0, 1, 1], [0, 1, 1, 0] tworz
,
a
baz
,
e podprzestrzeni W , gdyż wektory [1, 0, 1, 1], [0, 1, 1, 0], [0, 0, 1, 0],
[0, 0, 0, 1] tworz
,
a baz
,
e przestrzeni V . Zatem z twierdzenia 14.3 wek-
tory [0, 0, 1, 0] + W i [0, 0, 0, 1] + W tworz
,
a baz
,
e przestrzeni ilorazowej
V /W . Ponieważ K = {0, 1}, wi
,
ec st
,
ad przestrzeń ilorazowa V /W
ma dokładnie 4 elementy: W , [0, 0, 1, 0] + W , [0, 0, 0, 1] + W oraz
([0, 0, 1, 0] + W ) + ([0, 0, 0, 1] + W ) = [0, 0, 1, 1] + W .
Ponadto W = {[0, 0, 0, 0], [1, 0, 1, 1], [0, 1, 1.0], [1, 1, 0, 1]}, wi
,
ec na
przykład [0, 0, 1, 0] + W = {[0, 0, 1, 0], [1, 0, 0, 1], [[0, 1, 0, 0], [1, 1, 1, 1]}.

Rozdział 15
Przekształcenia liniowe i ich
zastosowania
15.1
Przekształcenia liniowe i ich
własności
Definicja 15.1. Niech V i W b
,
ed
,
a przestrzeniami liniowymi nad
ciałem K. Przekształcenie f : V −→ W spełniaj
,
ace warunki:
(I) ∀
α,β∈V
f (α+β) = f (α)+f (β) oraz (II) ∀
α∈V
∀
a∈K
f (a◦α) = a◦f (α)
nazywamy przekształceniem liniowym przestrzeni V w przestrzeń W .
Stwierdzenie 15.1. Złożenie przekształceń liniowych jest prze-
kształceniem liniowym.
Dowód. Niech f : V −→ W i g : W −→ U b
,
ed
,
a przekształceniami
liniowymi. Wówczas dla dowolnych α, β ∈ V jest (g ◦ f )(α + β) =
g(f (α + β)) = g(f (α) + f (β)) = g(f (α)) + g(f (β)) = (g ◦ f )(α) +
(g ◦ f )(β) oraz dla dowolnych α ∈ V , a ∈ K jest: (g ◦ f )(a ◦ α) =
g(f (a ◦ α)) = g(a ◦ f (α)) = a ◦ g(f (α)) = a ◦ (g ◦ f )(α). Zatem g ◦ f
jest przekształceniem liniowym.
Stwierdzenie 15.2. Niech f : V −→ W b
,
edzie przekształceniem
liniowym przestrzeni liniowej V nad ciałem K w przestrzeń liniow
,
a W
nad ciałem K. Wówczas:
117

118
Wykłady z algebry liniowej I
(i) f (Θ) = Θ,
(ii) f (−α) = −f (α) dla każdego α ∈ V ,
(iii) f (α − β) = f (α) − f (β) dla dowolnych α, β ∈ V ,
(iv) f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = a
1
◦ f (α
1
) + . . . + a
n
◦ f (α
n
) dla
dowolnych a
1
, . . . , a
n
∈ K, α
1
, . . . , α
n
∈ V i dla dowolnego n ∈ N.
Dowód. (i). Na mocy (II) jest f (Θ) = f (0 ◦ Θ) = 0 ◦ f (Θ) = Θ.
(ii). Na mocy (I) i (i) mamy, że f (α)+f (−α) = f (α+(−α)) = f (Θ) =
Θ, wi
,
ec f (−α) = −f (α).
(iii). Na mocy (I) i (ii) jest f (α − β) = f (α + (−β)) = f (α) + f (−β) =
f (α) + (−f (β)) = f (α) − f (β).
(iv). Stosujemy indukcj
,
e wzgl
,
edem n. Dla n = 1 teza wynika z (II).
Załóżmy, że teza zachodzi dla pewnego naturalnego n i niech
a
1
, . . . , a
n+1
∈ K oraz α
1
, . . . , α
n+1
∈ V . Wtedy na mocy (I), (II)
i założenia indukcyjnego mamy, że f (a
1
◦ α
1
+ . . . + a
n+1
◦ α
n+1
) =
f ((a
1
◦ α
1
+ . . . + a
n
◦ α
n
) + a
n+1
◦ α
n+1
) = f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) +
f (a
n+1
◦ α
n+1
) = a
1
◦ f (α
1
) + . . . + a
n
◦ f (α
n
) + a
n+1
◦ f (α
n+1
). Zatem
teza zachodzi dla liczby n + 1.
Stwierdzenie 15.3. Niech f : V −→ W b
,
edzie przekształceniem
liniowym przestrzeni liniowej V nad ciałem K w przestrzeń liniow
,
a
W nad ciałem K. Wówczas zbiór Ker(f ) = {α ∈ V : f (α) = Θ}
zwany j
,
adrem f jest podprzestrzeni
,
a przestrzeni V . Ponadto f jest
różnowartościowe (tzn. f jest monomorfizmem liniowym) wtedy i tylko
wtedy, gdy Ker(f ) = {Θ}.
Dowód. Na mocy stwierdzenia 15.2(i) mamy, że Θ ∈ Ker(f ).
Niech a ∈ K, α, β ∈ Ker(f ). Wtedy na mocy (I) f (α + β) = f (α) +
f (β) = Θ + Θ = Θ, wi
,
ec α + β ∈ Ker(f ) oraz na mocy (II) f (a ◦ α) =
a ◦ f (α) = a ◦ Θ = Θ, sk
,
ad a ◦ α ∈ Ker(f ). Zatem Ker(f ) jest
podprzestrzeni
,
a przestrzeni V .
Załóżmy, że f jest różnowartościowe i niech α ∈ Ker(f ). Wtedy
f (α) = Θ. Ale na mocy stwierdzenia 15.2(i) jest Θ = f (Θ), wi
,
ec
f (α) = f (Θ), sk
,
ad α = Θ.
Zatem Ker(f ) = {Θ}.
Na odwrót,
załóżmy, że Ker(f ) = {Θ} i weźmy dowolne α, β ∈ V takie, że f (α) =
f (β). Wtedy na mocy stwierdzenia 15.2(iii) jest Θ = f (α) − f (β) =
f (α − β), czyli α − β ∈ Ker(f ). Zatem α − β = Θ, sk
,
ad α = β i f
jest monomorfizmem.

Przekształcenia liniowe i ich zastosowania
119
Uwaga 15.1. Każda podprzestrzeń W przestrzeni liniowej V nad
ciałem K jest j
,
adrem pewnego przekształcenia liniowego określonego
na V . Rzeczywiście, niech f : V −→ V /W b
,
edzie przekształceniem
danym wzorem f (α) = α + W dla α ∈ V . Wtedy dla α, β ∈ V , a ∈ K
mamy, że f (α + β) = (α + β) + W = (α + W ) + (β + W ) = f (α) + f (β)
oraz f (a ◦ α) = a ◦ α + W = a ◦ (α + W ) = a ◦ f (α). Zatem f jest
przekształceniem liniowym. Ponadto dowolna warstwa z przestrzeni
V /W jest postaci α + W = f (α) dla pewnego α ∈ V , wi
,
ec f jest ”na”.
Dla α ∈ V mamy, że α ∈ Ker(f ) ⇔ α + W = W ⇔ α ∈ W . Zatem
Ker(f ) = W . Oznacza to, że podprzestrzenie przestrzeni liniowej V
s
,
a to dokładnie j
,
adra pewnych przekształceń liniowych określonych na
V .
Przykład 15.1. Niech W b
,
edzie podprzestrzeni
,
a przestrzeni li-
niowej V nad ciałem K. Wtedy z twierdzenia 12.3 istnieje podprze-
strzeń U przestrzeni V taka, że W ⊕ U = V . St
,
ad każde α ∈ V
można zapisać w postaci α = β + γ dla pewnych β ∈ W oraz γ ∈ U .
Jeśli β
1
, β
2
∈ W i γ
1
, γ
2
∈ U s
,
a takie, że β
1
+ γ
1
= β
2
+ γ
2
, to
β
1
− β
2
= γ
2
− γ
1
∈ W ∩ U = {Θ}, sk
,
ad β
1
= β
2
i γ
1
= γ
2
. Oznacza
to, że przekształcenie f : V → U dane wzorem f (α) = γ dla α ∈ V
takiego, że α = β + γ i β ∈ W oraz γ ∈ U , jest dobrze określone. Niech
α
1
, α
2
∈ V , a ∈ K. Wtedy istniej
,
a β
1
, β
2
∈ W , γ
1
, γ
2
∈ U takie, że
α
1
= β
1
+ γ
1
i α
2
= β
2
+ γ
2
, sk
,
ad α
1
+ α
2
= (β
1
+ β
2
) + (γ
1
+ γ
2
) oraz
β
1
+β
2
∈ W i γ
1
+γ
2
∈ U . Zatem f (α
1
+α
2
) = γ
1
+γ
2
= f (α
1
)+f (α
2
).
Ponadto a ◦ α
1
= a ◦ β
1
+ a ◦ γ
1
oraz a ◦ β
1
∈ W i a ◦ γ
1
∈ U , wi
,
ec
f (a ◦ α
1
) = a ◦ γ
1
= a ◦ f (α
1
). St
,
ad f jest przekształceniem linio-
wym. Nazywamy je rzutem przestrzeni V na podprzestrzeń U wzdłuż
podprzestrzeni W . Ponieważ dla γ ∈ U jest γ = Θ + γ i Θ ∈ W , wi
,
ec
f (γ) = γ. Zatem f jest ”na”. Dla β ∈ W mamy, że β = β +Θ i Θ ∈ U ,
wi
,
ec f (β) = Θ, sk
,
ad W ⊆ Ker(f ). Jeśli zaś α ∈ Ker(f ), to istniej
,
a
β ∈ W i γ ∈ U takie, że α = β + γ i Θ = f (α) = γ, sk
,
ad α = β ∈ W .
Zatem ostatecznie W = Ker(f ).
Stwierdzenie 15.4.
Niech f : V −→ W b
,
edzie przekształceniem
liniowym przestrzeni liniowej V nad ciałem K w przestrzeń liniow
,
a W
nad ciałem K. Wówczas zbiór Im(f ) = f (V ) = {f (α) : α ∈ V } zwany

120
Wykłady z algebry liniowej I
obrazem f jest podprzestrzeni
,
a przestrzeni W .
Dowód. Ze stwierdzenia 15.2(i) mamy, że Θ = f (Θ) ∈ f (V ).
Niech α, β ∈ f (V ). Wtedy istniej
,
a α
1
, β
1
∈ V takie, że α = f (α
1
)
i β = f (β
1
). Zatem α + β = f (α
1
) + f (β
1
) = f (α
1
+ β
1
) ∈ f (V ) oraz
dla a ∈ K: a ◦ α = a ◦ f (α
1
) = f (a ◦ α
1
) ∈ f (V ). Zatem f (V ) jest
podprzestrzeni
,
a przestrzeni W .
Stwierdzenie 15.5. Niech f : V −→ W b
,
edzie przekształceniem
liniowym przestrzeni liniowej V nad ciałem K w przestrzeń liniow
,
a
W nad ciałem K. Wówczas dla dowolnych wektorów α
1
, . . . , α
n
∈
V : jeżeli wektory f (α
1
), . . . , f (α
n
) s
,
a liniowo niezależne, to wektory
α
1
, . . . , α
n
też s
,
a liniowo niezależne. Jeżeli dodatkowo f jest mono-
morfizmem, to wektory α
1
, . . . , α
n
∈ V s
,
a liniowo niezależne wtedy
i tylko wtedy, gdy wektory f (α
1
), . . . , f (α
n
) s
,
a liniowo niezależne.
Dowód. Niech α
1
, . . . , α
n
∈ V . Załóżmy, że wektory f (α
1
), . . . ,
f (α
n
) s
,
a liniowo niezależne. Weźmy dowolne a
1
, . . . , a
n
∈ K takie,
że a
1
◦ α
1
+ . . . + a
n
◦ α
n
= Θ. Wtedy na mocy stwierdzenia 15.2
mamy, że a
1
◦ f (α
1
) + . . . + a
n
◦ f (α
n
) = Θ, sk
,
ad z lnz wektorów
f (α
1
), . . . , f (α
n
) jest a
1
= . . . = a
n
= 0, czyli wektory α
1
, . . . , α
n
też
s
,
a liniowo niezależne.
Niech teraz dodatkowo f b
,
edzie monomorfizmem.
Załóżmy, że
wektory α
1
, . . . , α
n
s
,
a lnz i weźmy dowolne a
1
, . . . , a
n
∈ K takie, że
a
1
◦ f (α
1
) + . . . + a
n
◦ f (α
n
) = Θ. Wtedy ze stwierdzenia 15.2 mamy,
że f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = f (Θ), sk
,
ad a
1
◦ α
1
+ . . . + a
n
◦ α
n
= Θ.
Zatem z lnz wektorów α
1
, . . . , α
n
wynika, że a
1
= . . . = a
n
= 0, czyli
wektory f (α
1
), . . . , f (α
n
) s
,
a liniowo niezależne.
Definicja 15.2. Przekształcenie liniowe f : V −→ W nazywamy
epimorfizmem, jeżeli f (V ) = W (tzn. f jest ”na”). Przekształcenie
liniowe f : V −→ V przestrzeni V w siebie nazywamy endomorfizmem
przestrzeni V .
Uwaga 15.2. Z tych określeń wynika od razu, że izomorfizm li-
niowy jest to taki monomorfizm, który jest jednocześnie epimorfizmem.

Przekształcenia liniowe i ich zastosowania
121
Stwierdzenie 15.6. Niech f : V −→ W b
,
edzie izomorfizmem
przestrzeni liniowych V i W nad tym samym ciałem K. Jeżeli wek-
tory α
1
, . . . , α
n
tworz
,
a baz
,
e przestrzeni V , to wektory f (α
1
), . . . , f (α
n
)
tworz
,
a baz
,
e przestrzeni W .
Dowód. Ze stwierdzenia 15.5 wynika od razu, że wektory f (α
1
), . . . ,
f (α
n
) s
,
a liniowo niezależne. Weźmy dowolne β ∈ W . Wtedy istnieje
α ∈ V takie, że β = f (α). Zatem istniej
,
a a
1
, . . . , a
n
∈ K takie, że
α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
, sk
,
ad na mocy stwierdzenia 15.2 jest, że
β = a
1
◦f (α
1
) + . . . + a
n
◦f (α
n
). Zatem wektory f (α
1
), . . . , f (α
n
) gene-
ruj
,
a przestrzeń W i s
,
a liniowo niezależne, czyli tworz
,
a baz
,
e przestrzeni
W .
15.2
Twierdzenie o izomorfizmie
Twierdzenie 15.1 (o izomorfizmie). Niech f : V −→ W b
,
edzie
przekształceniem liniowym. Wówczas
V /Ker(f ) ∼
= Im(f ).
Dowód. Niech F : V /Ker(f ) −→ Im(f ) b
,
edzie przekształceniem
danym wzorem: F (α + Ker(f )) = f (α) dla α ∈ V . Jeśli α, β ∈ V s
,
a
takie, że α + Ker(f ) = β + Ker(f ), to α − β ∈ Ker(f ), czyli
Θ = f (α − β) = f (α) − f (β), sk
,
ad f (α) = f (β). Wynika st
,
ad, że
przekształcenie F jest dobrze określone (nie zależy od wyboru repre-
zentantów warstw). Dalej, dla α, β ∈ V i a ∈ K mamy, że
F ((α + Ker(f )) + (β + Ker(f ))) = F ((α + β) + Ker(f )) = f (α + β) =
f (α) + f (β) = F (α + Ker(f )) + F (β + Ker(f )) oraz
F (a ◦ (α + Ker(f ))) = F (a ◦ α + Ker(f )) = f (a ◦ α) = a ◦ f (α) =
a ◦ F (α + Ker(f )). Zatem F jest przekształceniem liniowym. Weźmy
dowolne β ∈ Im(f ). Wtedy istnieje α ∈ V takie, że β = f (α) =
F (α + Ker(f )). Zatem F jest epimorfizmem. W końcu dla α ∈ V
mamy, że α + Ker(f ) ∈ Ker(F ) ⇔ f (α) = Θ ⇔ α ∈ Ker(f ) ⇔
α + Ker(f ) = Ker(f ). St
,
ad na mocy stwierdzenia 15.3 F jest mono-
morfizmem i ostatecznie F jest izomorfizmem liniowym.

122
Wykłady z algebry liniowej I
Twierdzenie 15.2. Niech f : V −→ W b
,
edzie przekształceniem li-
niowym. Jeżeli przestrzeń V jest skończenie wymiarowa, to przestrzeń
Im(f ) też jest skończenie wymiarowa i zachodzi wzór:
dim V = dim Ker(f ) + dim Im(f ).
Dowód. Z twierdzenia o izomorfizmie V /Ker(f ) ∼
= Im(f ). Z twier-
dzenia 14.4 mamy, że dim(V /Ker(f )) = dim V − dim Ker(f ). Zatem
na mocy stwierdzenia 15.6 mamy, że dim Im(f ) = dim V −dim Ker(f ),
sk
,
ad dim Im(f ) + dim Ker(f ) = dim V .
Twierdzenie 15.3. Niech wektory α
1
, . . . , α
n
tworz
,
a baz
,
e prze-
strzeni liniowej V nad ciałem K i niech β
1
, . . . , β
n
b
,
ed
,
a dowolnymi
wektorami przestrzeni liniowej W nad ciałem K. Wówczas istnieje do-
kładnie jedno przekształcenie liniowe f : V −→ W takie, że f (α
i
) = β
i
dla każdego i = 1, . . . , n. Ponadto takie f jest dane wzorem:
f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = a
1
◦ β
1
+ . . . + a
n
◦ β
n
(15.1)
dla a
1
, . . . , a
n
∈ K. Przekształcenie f jest monomorfizmem wtedy
i tylko wtedy, gdy wektory β
1
, . . . , β
n
s
,
a liniowo niezależne. Ponadto
f jest epimorfizmem wtedy i tylko wtedy, gdy wektory β
1
, . . . , β
n
gene-
ruj
,
a przestrzeń W oraz f jest izomorfizmem wtedy i tylko wtedy, gdy
wektory β
1
, . . . , β
n
tworz
,
a baz
,
e przestrzeni W .
Dowód. Dla przekształcenia f danego wzorem (15.1) mamy, że
f (α
i
) = β
i
przy i = 1, . . . , n. Weźmy dowolne α, β ∈ V i dowolne
a ∈ K. Wtedy istniej
,
a a
1
, . . . , a
n
, b
1
, . . . , b
n
∈ K takie, że α = a
1
◦
α
1
+ . . . + a
n
◦ α
n
oraz β = b
1
◦ α
1
+ . . . + b
n
◦ α
n
. Zatem f (α + β) =
f ((a
1
+b
1
)◦α
1
+. . .+(a
n
+b
n
)◦α
n
) = (a
1
+b
1
)◦β
1
+. . .+(a
n
+b
n
)◦β
n
=
(a
1
◦ β
1
+ . . . + a
n
◦ β
n
) + (b
1
◦ β
1
+ . . . + b
n
◦ β
n
) = f (α) + f (β) oraz
f (a◦α) = f ((aa
1
)◦α
1
+. . .+(aa
n
)◦α
n
) = (aa
1
)◦β
1
+. . .+(aa
n
)◦β
n
=
a ◦ (a
1
◦ β
1
+ . . . + a
n
◦ β
n
) = a ◦ f (α). Zatem f jest szukanym prze-
kształceniem liniowym. Jeżeli g : V −→ W jest przekształceniem
liniowym takim, że g(α
i
) = β
i
dla i = 1, . . . , n, to ze stwierdzenia 15.2
mamy, że g(a
1
◦ α
1
+ . . . + a
n
◦ α
n
) = a
1
◦ g(α
1
) + . . . + a
n
◦ g(α
n
) =
a
1
◦ β
1
+ . . . + a
n
◦ β
n
= f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
) dla dowolnych
a
1
, . . . , a
n
∈ K. Ponieważ {α
1
, . . . , α
n
} jest baz
,
a przestrzeni V , wi
,
ec
st
,
ad g = f .

Przekształcenia liniowe i ich zastosowania
123
Jeżeli f jest różnowartościowe, to na mocy stwierdzenia 15.5 wek-
tory β
1
= f (α
1
), . . . , β
n
= f (α
n
) s
,
a liniowo niezależne. Na odwrót, za-
łóżmy, że wektory β
1
, . . . , β
n
s
,
a liniowo niezależne. Niech α ∈ Ker(f ).
Wtedy istniej
,
a a
1
, . . . , a
n
∈ K takie, że α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
, sk
,
ad
Θ = f (α) = a
1
◦ β
1
+ . . . + a
n
◦ β
n
, czyli a
1
= . . . = a
n
= 0 i α = Θ.
Zatem na mocy stwierdzenia 15.3 f jest monomorfizmem.
Jeżeli f jest epimorfizmem, to dla każdego β ∈ W istnieje α ∈ V
takie, że β = f (α). Ale α = a
1
◦ α
1
+ . . . + a
n
◦ α
n
dla pewnych
a
1
, . . . , a
n
∈ K, wi
,
ec ze wzoru (15.1) β = a
1
◦ β
1
+ . . . + a
n
◦ β
n
, czyli
wektory β
1
, . . . , β
n
generuj
,
a przestrzeń W . Na odwrót, załóżmy, że
wektory β
1
, . . . , β
n
generuj
,
a przestrzeń W . Weźmy dowolne β ∈ W .
Wtedy istniej
,
a a
1
, . . . , a
n
∈ K takie, że β = a
1
◦ β
1
+ . . . + a
n
◦ β
n
=
f (a
1
◦ α
1
+ . . . + a
n
◦ α
n
), czyli f jest epimorfizmem.
Ostatnia cz
,
eść twierdzenia wynika z jego pierwszej cz
,
eści.
15.3
Przykłady i zastosowania
przekształceń liniowych
Przykład 15.2. Niech V i W b
,
ed
,
a przestrzeniami liniowymi nad
tym samym ciałem K. Wówczas przekształcenie f : V −→ W dane
wzorem f (α) = Θ dla α ∈ V jest przekształceniem liniowym, bo dla
α, β ∈ V , a ∈ K: f (α + β) = Θ = Θ + Θ = f (α) + f (β) oraz
f (a ◦ α) = Θ = a ◦ Θ = a ◦ f (α). Przekształcenie to nazywamy
zerowym lub trywialnym.
Przykład 15.3. Niech V b
,
edzie przestrzeni
,
a liniow
,
a nad ciałem
K. Niech a ∈ K b
,
edzie dowolnym ustalonym elementem ciała K.
Wtedy przekształcenie φ
a
: V −→ V dane wzorem φ
a
(α) = a ◦ α dla
α ∈ V , jest liniowe, gdyż dla α, β ∈ V , b ∈ K mamy, że φ
a
(α + β) =
a ◦ (α + β) = a ◦ α + a ◦ β = φ
a
(α) + φ
a
(β) oraz φ
a
(b ◦ α) = a ◦ (b ◦ α) =
(ab)◦α = (ba)◦α = b◦(a◦α) = b◦φ
a
(α). To przekształcenie nazywamy
homoteti
,
a o współczynniku a.
Przykład 15.4. Niech W b
,
edzie podprzestrzeni
,
a przestrzeni li-
niowej V nad ciałem K. Wówczas przekształcenie f : W −→ V dane

124
Wykłady z algebry liniowej I
wzorem f (α) = α dla α ∈ W jest oczywiście liniowe. Jest ono po-
nadto monomorfizmem podprzestrzeni W w przestrzeń V . W szcze-
gólności przekształcenie identycznościowe id
V
: V −→ V dane wzorem
id
V
(α) = α dla α ∈ V , jest przekształceniem liniowym.
Przykład 15.5. Opiszemy wszystkie przekształcenia liniowe
f : K
n
→ K
m
dla ustalonego ciała K i dla dowolnych ustalonych liczb
naturalnych m, n. Ponieważ wektory ε
1
, ε
2
, . . . , ε
n
tworz
,
a baz
,
e prze-
strzeni K
n
oraz dla dowolnych x
1
, . . . , x
n
∈ K jest [x
1
, . . . , x
n
] =
x
1
◦ ε
1
+ . . . + x
n
◦ ε
n
, wi
,
ec na mocy twierdzenia 15.3 wszystkimi
przekształceniami liniowymi f : K
n
→ K
m
s
,
a jedynie przekształcenia
f postaci:
f ([x
1
, . . . , x
n
]) = x
1
◦ β
1
+ . . . + x
n
◦ β
n
,
dla dowolnych ustalonych β
1
, . . . , β
n
∈ K
m
. Ale dla j = 1, . . . , n ist-
niej
,
a a
ij
∈ K (i = 1, . . . , m) takie, że β
j
= [a
1j
, a
2j
, . . . , a
mj
], wi
,
ec
st
,
ad otrzymujemy tzw. wzór analityczny na dowolne przekształcenie
liniowe f : K
n
−→ K
m
:
f ([x
1
, . . . , x
n
]) = [a
11
x
1
+ . . . + a
1n
x
n
, . . . , a
m1
x
1
+ . . . + a
mn
x
n
]. (15.2)
Zauważmy ponadto, że jeżeli a
0
ij
∈ K dla i = 1, . . . , m, j = 1, . . . , n s
,
a
takie, że przekształcenie f dane wzorem (15.2) spełnia wzór
f ([x
1
, . . . , x
n
]) = [a
0
11
x
1
+ . . . + a
0
1n
x
n
, . . . , a
0
m1
x
1
+ . . . + a
0
mn
x
n
], to dla
β
0
j
= [a
0
1j
, a
0
2j
, . . . , a
0
mj
], j = 1, . . . , n, b
,
edziemy mieli, że β
0
j
= f (ε
j
) =
β
j
, czyli a
0
ij
= a
ij
dla wszystkich i, j. Wynika st
,
ad, że przekształcenie
liniowe f : K
n
−→ K
m
jest jednoznacznie wyznaczone przez m × n
macierz A = [a
ij
]. Ponadto z definicji mnożenia macierzy mamy, że
dla przekształcenia f danego wzorem (15.2) zachodzi wzór:
f ([x
1
, . . . , x
n
]) = A ·
x
1
x
2
..
.
x
n
.
(15.3)
Przy tych oznaczeniach mamy też, że f (K
n
) = lin(β
1
, . . . , β
n
) oraz
wektory β
1
, . . . , β
n
możemy traktować jako kolumny macierzy A, wi
,
ec

Przekształcenia liniowe i ich zastosowania
125
st
,
ad dla przekształcenia f mamy wzór:
dim Im(f ) = r(A).
(15.4)
Zatem z twierdzenia 15.2 mamy, że n = dim K
n
= dim Ker(f ) +
dim Im(f ), wi
,
ec na mocy wzoru (15.4):
dim Ker(f ) = n − r(A).
(15.5)
Zauważmy też, że [a
1
, . . . , a
n
] ∈ Ker(f ) wtedy i tylko wtedy, gdy
[a
1
, . . . , a
n
] jest rozwi
,
azaniem układu jednorodnego
a
11
x
1
+
a
12
x
2
+
. . . +
a
1n
x
n
= 0
a
21
x
1
+
a
22
x
2
+
. . . +
a
2n
x
n
= 0
..
.
..
.
. ..
..
.
a
m1
x
1
+ a
m2
x
2
+ . . . + a
mn
x
n
= 0
.
(15.6)
Wynika st
,
ad nast
,
epuj
,
ace
Twierdzenie 15.4. Zbiór rozwi
,
azań układu jednorodnego (15.6)
o macierzy współczynników A jest podprzestrzeni
,
a przestrzeni liniowej
K
n
wymiaru n − r(A).
Podamy teraz drugi sposób wyznaczania jednorodnego układu rów-
nań liniowych o zadanej podprzestrzeni rozwi
,
azań. Niech K b
,
edzie
ustalonym ciałem i niech V b
,
edzie dowoln
,
a podprzestrzeni
,
a przestrzeni
liniowej K
n
.
Wyznaczamy najpierw baz
,
e i wymiar podprzestrzeni
V . Niech wektory α
1
, . . . , α
s
tworz
,
a baz
,
e podprzestrzeni V . Wtedy
dim V = s. W praktyce wyznaczamy baz
,
e V w takiej postaci, aby
można było j
,
a uzupełnić w prosty sposób do bazy przestrzeni K
n
pewnymi wektorami bazy kanonicznej przestrzeni K
n
. Niech wektory
α
1
, . . . , α
s
, β
1
, . . . , β
n−s
tworz
,
a baz
,
e przestrzeni K
n
. Na mocy twier-
dzenia 15.3 istnieje dokładnie jeden epimorfizm f : K
n
−→ K
n−s
taki, że f (α
i
) = Θ dla wszystkich i = 1, . . . , s oraz f (β
j
) = ε
j
dla
j = 1, . . . , n − s. Z określenia f mamy, że V ⊆ Ker(f ). Ponadto
dim Im(f ) = dim K
n−s
= n − s, wi
,
ec z twierdzenia 15.2 mamy, że
n = dim K
n
= dim Ker(f ) + dim Im(f ), sk
,
ad dim Ker(f ) = s. Ale

126
Wykłady z algebry liniowej I
dim V = s oraz V ⊆ Ker(f ), wi
,
ec st
,
ad V = Ker(f ). Pozostaje za-
tem wyznaczyć wzór analityczny na przekształcenie f i w ten sposób
uzyskamy natychmiast ż
,
adany układ jednorodny.
Przykład 15.6. Znajdziemy układ jednorodny równań liniowych
nad ciałem R, którego przestrzeni
,
a rozwi
,
azań jest
V = lin([1, −1, 1], [1, 1, −1]). Najpierw znajdujemy baz
,
e przestrzeni
V :
1 −1
1
1
1 −1
w
2
−w
1
≡
1 −1
1
0
2 −2
1
2
·w
2
≡
1 −1
1
0
1 −1
. Zatem
baz
,
a przestrzeni V jest {[1, −1, 1], [0, 1, −1]}.
Nast
,
epnie uzupełniamy znalezion
,
a baz
,
e przestrzeni V do bazy całej
przestrzeni R
3
przy pomocy wektora [0, 0, 1]. Istnieje przekształcenie
liniowe f : R
3
−→ R takie, że f([1, −1, 1]) = 0, f([0, 1, −1]) = 0,
f ([0, 0, 1]) = 1. Wtedy f ([0, 1, 0]) = f ([0, 1, −1])+f ([0, 0, 1]) = 0+1 =
1 oraz f ([1, 0, 0]) = f ([1, −1, 1]) − f ([0, 1, −1]) = 0 − 0 = 0. Zatem dla
dowolnych x
1
, x
2
, x
3
∈ R mamy, że f([x
1
, x
2
, x
3
]) = x
1
· f ([1, 0, 0]) +
x
2
· f ([0, 1, 0]) + x
3
· f ([0, 0, 1]) = x
2
+ x
3
. Ale dim(Im f ) = 1, wi
,
ec
dim(Ker f ) = 3 − 1 = 2. Ponadto V ⊆ Ker f oraz dim(V ) = 2, wi
,
ec
V = Ker f . St
,
ad szukanym układem równań jest:
x
2
+ x
3
= 0.
Przykład 15.7. Znajdziemy układ jednorodny równań liniowych
nad ciałem R, którego przestrzeń rozwi
,
azań jest generowana przez wek-
tory: [1, −1, 1, −1, 1], [1, 1, 0, 0, 3], [3, 1, 1, −1, 7], [0, 2, −1, 1, 2].
Znajdujemy najpierw baz
,
e podprzestrzeni V generowanej przez
wektory: [1, −1, 1, −1, 1], [1, 1, 0, 0, 3], [3, 1, 1, −1, 7], [0, 2, −1, 1, 2].
1
1
0
0 3
1 −1
1 −1 1
3
1
1 −1 7
0
2 −1
1 2
w
2
−w
1
, w
3
−3w
1
≡
1
1
0
0
3
0 −2
1 −1 −2
0 −2
1 −1 −2
0
2 −1
1
2
w
2
+w
4
, w
3
+w
4
≡
1 1
0 0 3
0 0
0 0 0
0 0
0 0 0
0 2 −1 1 2
≡
1 1
0 0 3
0 2 −1 1 2
. Zatem baz
,
a
V jest {[1, 1, 0, 0, 3], [0, 2, −1, 1, 2]} oraz dim V = 2. Ponieważ nasze
wektory maj
,
a 5 współrz
,
ednych, wi
,
ec szukany układ równań b
,
edzie si
,
e

Przekształcenia liniowe i ich zastosowania
127
składał z 5 − 2 = 3 równań.
Ponadto baz
,
a przestrzeni R
5
jest {[1, 1, 0, 0, 3], [0, 2, −1, 1, 2],
[0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]}, wi
,
ec istnieje przekształcenie li-
niowe f : R
5
−→ R
3
takie, że
f ([1, 1, 0, 0, 3]) = [0, 0, 0],
(15.7)
f ([0, 2, −1, 1, 2]) = [0, 0, 0],
(15.8)
f ([0, 0, 1, 0, 0]) = [1, 0, 0],
(15.9)
f ([0, 0, 0, 1, 0]) = [0, 1, 0],
(15.10)
f ([0, 0, 0, 0, 1]) = [0, 0, 1].
(15.11)
Ponieważ wektory [1, 0, 0], [0, 1, 0], [0, 0, 1] tworz
,
a baz
,
e przestrzeni R
3
oraz należ
,
a do f (R
5
), wi
,
ec f (R
5
) = R
3
, czyli dim f (R
5
) = 3. Ale 5 =
dim R
5
= dim Ker(f ) + dim f (R
5
), wi
,
ec dim Ker(f ) = 5 − 3 = 2. Po-
nadto z (15.7) i (15.8) mamy, że V = lin([1, 1, 0, 0, 3], [0, 2, −1, 1, 2]) ⊆
Ker(f ) oraz dim V = 2, wi
,
ec V = Ker(f ). Pozostaje zatem wy-
znaczyć wzór analityczny na takie przekształcenie f .
Niech ε
1
=
[1, 0, 0, 0, 0], ε
2
= [0, 1, 0, 0, 0], ε
3
= [0, 0, 1, 0, 0], ε
4
= [0, 0, 0, 1, 0],
ε
5
= [0, 0, 0, 0, 1]. Wtedy dla dowolnych x
1
, x
2
, x
3
, x
4
, x
5
∈ R:
[x
1
, x
2
, x
3
, x
4
, x
5
] = x
1
◦ ε
1
+ x
2
◦ ε
2
+ x
3
◦ ε
3
+ x
4
◦ ε
4
+ x
5
◦ ε
5
.
Zatem z liniowości przekształcenia f mamy, że f ([x
1
, x
2
, x
3
, x
4
, x
5
]) =
x
1
◦ f (ε
1
) + x
2
◦ f (ε
2
) + x
3
◦ f (ε
3
) + x
4
◦ f (ε
4
) + x
5
◦ f (ε
5
).
Ze wzoru (15.8) mamy, że 2 ◦ f (ε
2
) − f (ε
3
) + f (ε
4
) + 2 ◦ f (ε
5
) =
[0, 0, 0], wi
,
ec 2 ◦ f (ε
2
) − [1, 0, 0] + [0, 1, 0] + 2 ◦ [0, 0, 1] = [0, 0, 0], sk
,
ad
f (ε
2
) = [
1
2
, −
1
2
, −1].
Ze wzoru (15.7) mamy, że f (ε
1
) + f (ε
2
) + 3 ◦ f (ε
5
) = [0, 0, 0], czyli
f (ε
1
) + [
1
2
, −
1
2
, −1] + 3 ◦ [0, 0, 1] = [0, 0, 0], sk
,
ad f (ε
1
) = [−
1
2
,
1
2
, −2].
St
,
ad
f ([x
1
, x
2
, x
3
, x
4
, x
5
]) = x
1
◦[−
1
2
,
1
2
, −2]+x
2
◦[
1
2
, −
1
2
, −1]+x
3
◦[1, 0, 0]+x
4
◦
[0, 1, 0] + x
5
◦[0, 0, 1] = [−
1
2
x
1
+
1
2
x
2
+ x
3
,
1
2
x
1
−
1
2
x
2
+ x
4
, −2x
1
−x
2
+ x
5
].
Zatem V = Ker(f ) jest zbiorem rozwi
,
azań układu równań:
−
1
2
x
1
+
1
2
x
2
+ x
3
= 0
1
2
x
1
−
1
2
x
2
+ x
4
= 0
−2x
1
−
x
2
+ x
5
= 0
.

Literatura
[1] A. Białynicki-Birula, Algebra liniowa z geometri
,
a, PWN, Warszawa
1976.
[2] A. Białynicki-Birula, Algebra, PWN, Warszawa 1971.
[3] L. Jeśmianowicz, J. Łoś, Zbiór zadań z algebry, PWN, Warszawa
1976.
[4] A. I. Kostrykin, Wstęp do algebry, PWN, Warszawa 1984.
[5] A. I. Kostrykin, Zbiór zadań z algebry, PWN, Warszawa 1995.
[6] A. Mostowski i M. Stark, Elementy algebry wyższej, PWN, War-
szawa 1972.
128
Document Outline
- Wstep
- Pojecie ciala
- Cialo liczb zespolonych I
- Cialo liczb zespolonych II
- Uklady równan liniowych
- Wyznaczniki I
- Wyznaczniki II
- Rozwiniecie Laplace'a i wzory Cramera
- Algebra macierzy
- Przestrzenie liniowe
- Podprzestrzenie przestrzeni liniowych
- Baza i wymiar przestrzeni liniowej
- Izomorfizmy. Sumy proste. Hiperplaszczyzny
- Rzd macierzy
- Przestrzenie ilorazowe
- Przeksztalcenia liniowe i ich zastosowania
- Literatura
Wyszukiwarka
Podobne podstrony:
3 wyklad algebra liniowa
Wyklad7ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Wyklad8ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Wyklad2ALG2001a, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych
Wyklad5ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Wykład 4 - 2 sem, 2 Semestr, Analiza matematyczna i algebra liniowa
Wyklad6ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Egzamin z algebry, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszyc
Algebra liniowa i geometria kolokwia AGH 2012 13
Algebra Liniowa 2 Definicje Twierdzenia Wzory Jurlewicz Skoczylas
Egzamin z Algebry Liniowej 2004
Geometia i Algebra Liniowa
Poprawa 1 go kolokwium z algebry liniowej
do wydruku sc, WTD, algebra liniowa
więcej podobnych podstron