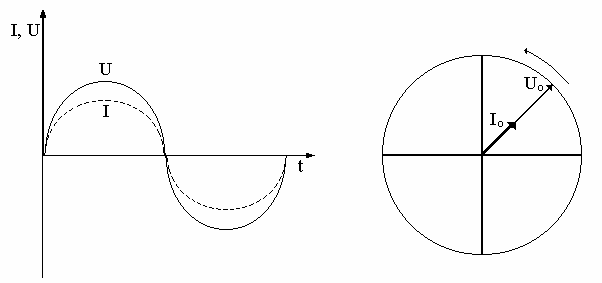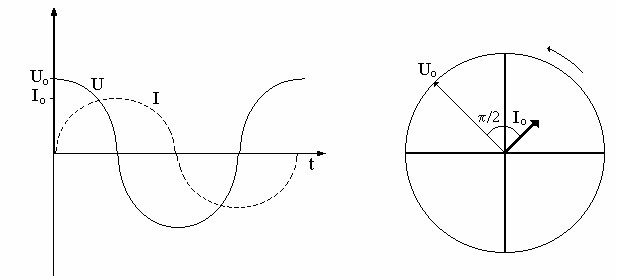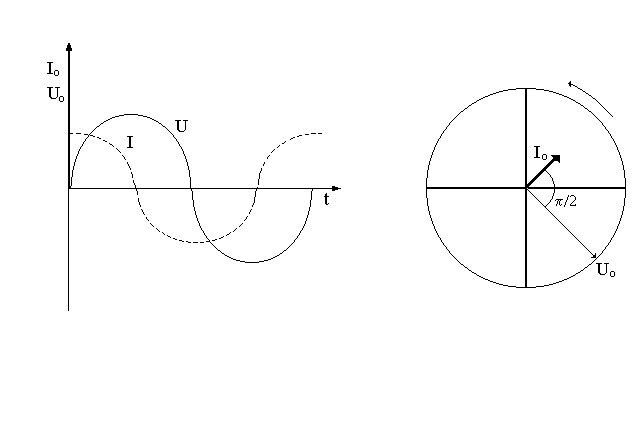Józef Zapłotny

Zakład Fizyki, Akademia Rolnicza Do u ytku wewn trznego

WICZENIE 36

ZAWADA OBWODÓW RLC

Kraków, luty 2007

SPIS TRE CI

I. CZ

TEORETYCZNA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

1. INDUKCJA ELEKTROMAGNETYCZNA .................................................................................................................. 2

2. REGUŁA LENZA ................................................................................................................................................. 3

3. SAMOINDUKCJA, INDUKCJA WZAJEMNA............................................................................................................. 3

4. PR DY ZMIENNE SINUSOIDALNIE ....................................................................................................................... 3

5. PRACA W OBWODZIE PR DU ZMIENNEGO, WARTO CI SKUTECZNE ..................................................................... 4

6. PRAWO OHMA W OBWODACH PR DU ZMIENNEGO............................................................................................. 4

6.1. Opór omowy (czynny) w obwodzie pr du zmiennego. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

6.2. Indukcyjno w obwodzie pr du zmiennego . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

6.3. Pojemno w obwodzie pr du zmiennego. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

7. SZEREGOWY OBWÓD RLC. ZAWADA................................................................................................................. 8

II. CEL WICZENIA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

III. WYKONANIE WICZENIA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

IV. OPRACOWANIE WYNIKÓW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

V. LITERATURA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

ZAKRES WYMAGANYCH WIADOMO CI:

Podstawowe wielko ci elektryczne: ładunek, potencjał, napi cie, nat enie pr du

elektrycznego, opór elektryczny. Prawa Ohma i Kirchhoffa. Indukcja elektromagnetyczna,

prawo Faradaya, reguła Lenza. Samoindukcja, indukcja wzajemna. Pole magnetyczne

przewodnika z pr dem - prawo Biota-Savarta. Pr dy elektryczne zmienne sinusoidalnie, praca

w obwodzie pr du zmiennego, warto ci skuteczne. Prawo Ohma w obwodach pr du

zmiennego - zawada. Pojemno elektryczna, indukcyjno obwodu, pojemno i

indukcyjno w obwodach pr du zmiennego (obwód szeregowy RLC), rezonans elektryczny.

2

I. CZ

TEORETYCZNA

1. Indukcja elektromagnetyczna

Je eli linie pola magnetycznego o indukcji magnetycznej B przechodz przez jak powierzchni , to strumie Φ tego pola magnetycznego mo na obliczy ze wzoru:

B

Φ

B dS

(1)

B =

S

gdzie S jest dowoln powierzchni ograniczon przez zamkni ty obwód. Jest to definicja strumienia magnetycznego. Jednostk strumienia magnetycznego Φ jest weber (Wb). Jeden

B

weber jest to strumie przenikaj cy przez powierzchni 1 m2 prostopadł do linii

jednorodnego pola magnetycznego o indukcji 1T (1WB = 1T ⋅ m2).

W przypadku gdy pole magnetyczne o indukcji magnetycznej B jest jednorodne i

równocze nie prostopadłe do powierzchni S, to strumie magnetyczny przechodz cy przez t powierzchni ma warto Φ = B S.

B

Zjawisko indukcji elektromagnetycznej odkrył fizyk angielski Faraday. Istot tego zjawiska

jest stwierdzenie faktu, e ka da zmiana strumienia indukcji magnetycznej przechodz cego

przez powierzchni ograniczon przewodnikiem tworz cym obwód zamkni ty powoduje

zawsze powstanie w tym zamkni tym obwodzie pr du elektrycznego, zwanego pr dem

indukcyjnym. Oboj tny jest sposób wytworzenia tej zmiany strumienia magnetycznego, mo e

to by :

a) wzgl dny ruch obwodu zamkni tego z przewodnika i magnesu,

b) zmiana poło enia obwodu, umieszczonego w stałym polu magnetycznym (np. jego obrót),

c) zmiana nat enia pola magnetycznego wzgl dem obwodu ustawionego prostopadle do pola

magnetycznego. Poniewa pr d w obwodzie zamkni tym płynie tylko wtedy, gdy istnieje w

nim ródło siły elektromotorycznej, czyli SEM, mo emy powiedzie , e zmienny strumie magnetyczny powoduje powstanie w zamkni tym obwodzie elektrycznym siły

elektromotorycznej, dzi ki której płynie w tym obwodzie pr d indukcyjny.

∆Φ

E

B

= −

(2)

∆ t

Dla zmian niesko czenie małych otrzymamy:

dΦ

E

B

= −

(3)

d t

3

Wzór (3) przedstawia matematycznie prawo Faradaya:

SEM indukowana w obwodzie zamkni tym jest równa szybko ci zmian strumienia

magnetycznego przenikaj cego ten obwód.

2. Reguła Lenza

Znak minus w dwóch ostatnich równaniach mówi nam o kierunku pr du indukcyjnego. W

praktyce kierunek powstaj cego pr du mo na okre li wykorzystuj c tzw. reguł Lenza: Pr d indukcyjny ma zawsze taki kierunek, e wytworzony przez strumie magnetyczny

przeciwdziała zmianom strumienia magnetycznego, który go wytworzył. Wynika to z zasady

zachowania energii.

3. Samoindukcja, indukcja wzajemna

Je eli w strumieniu magnetycznym, wytworzonym przez pr d płyn cy w jednej cewce

znajduje si druga cewka, to ka da zmiana pr du I w jednej z nich powoduje powstanie SEM

w drugiej - jest to indukcja wzajemna.

Z drugiej strony, je eli zmienia si nat enie pr du I płyn cego przez cewk , to powoduje

to tym samym zmian strumienia magnetycznego, który, zgodnie z reguł Lenza, b dzie

indukował w tej samej cewce SEM - jest to zjawisko samoindukcji lub indukcji własnej. Dla tego zjawiska prawo indukcji elektromagnetycznej przybierze nast puj c posta :

def

dφ

dI

E = −

= −L

(4)

dt

dt

gdzie L jest współczynnikiem samoindukcji cewki. Jego warto zale y od geometrii obwodu i wła ciwo ci magnetycznych o rodka, w którym obwód si znajduje. Jednostk współczynnika

samoindukcji 1 henr (H). 1 Henr jest to indukcyjno takiego obwodu, w którym zmiana nat enia pr du o 1 A w ci gu 1 s powoduje powstanie SEM samoindukcji równej 1 V.

4. Pr dy zmienne sinusoidalnie

Je eli w stałym i jednorodnym polu magnetycznym obraca si ze stał szybko ci k tow ω

wokół osi prostopadłej do tego pola ramka wykonana z przewodnika, to strumie magnetyczny

przechodz cy przez ramk zmienia si periodycznie zgodnie ze wzorem:

φ = φ cos ωt. W ramce tej indukuje si SEM indukcji E, zale na od szybko ci zmian ο

strumienia magnetycznego dΦ/dt. Warto E zmienia si w czasie wg wzoru:

Φ

E

d

= −

= −ωΦ sin

sin

(5)

0

ωt = E0

ωt

dt

gdzie: E jest amplitud SEM, ω = 2πf = 2π/T jest pr dko ci k tow ramki.

o

4

5. Praca w obwodzie pr du zmiennego, warto ci skuteczne

Pr d indukcyjny wzbudzony w ramce zmienia si równie sinusoidalnie z szybko ci

k tow ω:

I = Io sin ωt

(6)

Je eli do ródła napi cia zmiennego doł czymy opornik o oporze R, to w czasie dt, tak małym, e mo emy przyj , i nat enie pr du I jest stałe, pr d ten wykonuje prac :

2

2

2

dW = I R dt = Io R sin ωt dt

(7)

W czasie jednego okresu, czyli w czasie t = T, pr d płyn cy przez opornik wykona prac :

T

W = I

2

1 2

sin ω

(8)

0 R

t dt = I0 RT

2

0

W przypadku ka dego pr du zmiennego u ywa si jako wielko ci charakterystycznych

poj cia warto ci skutecznej napi cia i nat enia pr du. Je eli postawimy pytanie, jaki pr d

stały (o nat eniu I ) musiałby płyn przez opornik R w czasie T, eby wykonana przez ten sk

pr d praca była równa pracy wykonanej przez pr d zmienny to nale y porówna prac pr du

2

stałego wyra on wzorem W = I R T z prac wyra on wzorem (8):

sk

I 2 RT = I 2

(9)

0 R T

sk

2

Ζ powy szego wzoru otrzymamy wyra enie na warto skuteczn nat enia pr du:

I

I = 0 = 0,707

sk

I

(10)

0

2

i podobnie dla napi cia

U

U = 0 = 0,707

sk

U

(11)

0

2

Mierniki nat enia pr du (amperomierze) i napi cia (woltomierze) s wyskalowane w

warto ciach skutecznych.

6. Prawo Ohma w obwodach pr du zmiennego

Pierwsze prawo Ohma jest spełnione dla wszystkich warto ci napi cia i nat enia pr du

zmiennego, w tym równie warto ci maksymalnych, skutecznych i rednich. Równie prawa

Kirchhoffa s słuszne w obwodach pr du zmiennego.

5

6.1. Opór omowy (czynny) w obwodzie pr du zmiennego

Je eli w obwodzie pr du zmiennego znajduje si opornik o oporze R, to zale no mi dzy

napi ciem i nat eniem pr du przedstawia prawo Ohma wyra one wzorem U = I R, czyli nie ma przesuni cia fazy mi dzy napi ciem i nat eniem pr du (rys.1a i 1b).

a)

b)

Rys.1

6.2. Indukcyjno w obwodzie pr du zmiennego

Je eli natomiast w obwód pr du zmiennego wł czymy cewk o indukcyjno ci L, to przykładaj c do niej napi cie U = U sin ωt b dziemy mie zgodnie z II prawem Kirchhoffa

o

(U0+ E = 0):

ind

lub

U sin ω =

(12)

0

t L dI

dt

albo

dI = 1 U sinω

(13)

0

t dt

L

st d

U0

U0

U

I =

sin ωt dt = −

cosωt = 0 sin t

ω π

−

(14)

L

ωL

ωL

2

Amplituda napi cia na cewce wynosi U = I ω L. Je eli porównamy ten wzór z prawem

Lo

o

Ohma, to widzimy, e zamiast oporu R mamy tutaj wyra enie R = ω L, nazywane oporem L

indukcyjnym cewki. Ze wzoru (14) wida równie , e napi cie U wyprzedza pr d I o warto π/2, czyli o jedn czwart okresu (rys. 2a i 2b). Z tego wynika te fakt, e rednia moc tracona w cewce pozbawionej oporu omowego wynosi zero.

6

Cewk rzeczywist mo emy traktowa jako szeregowe poł czenie cewki idealnej o

współczynniku samoindukcji L i przewodnika o oporze omowym R, (rys. 3a). Zgodnie z II-im prawem Kirchhoffa napi cie na oporniku równe jest sumie sił elektromotorycznych w

obwodzie (U = U + E ), albo:

R

L

U = U −

=

+

=

sin ω

cosω

(15)

0

+

R

EL I R L dI R I

t LI0

t

dt

Poniewa U = U sin ωt, to po podstawieniu do powy szego równania otrzymamy:

o

Uo sin ωt = L Io ω sin (ωt + π/2) + R Io sin ωt

(16)

a)

b)

Rys.2

Wyrazy po prawej stronie równania (16) przedstawiaj sum dwóch drga harmonicznych o

tym samym okresie i ró nicy faz π/2. Aby znale drganie wypadkowe mo na przedstawi

drgania składowe graficznie (rys.3a). Suma geometryczna amplitud drga składowych daje

amplitud SEM U . Opór całkowity takiego obwodu znajdujemy buduj c trójk t prostok tny,

o

którego przyprostok tne b d równe R i Lω. Przeciwprostok tna takiego trójk ta (rys. 3b) jest równa oporowi pozornemu obwodu Z = R2 + L2 2

ω , inaczej jest nazywana zawad , a k t φ

równy jest przesuni ciu faz mi dzy nat eniem pr du i napi ciem.

ω

tg

L

Φ =

(17)

R

7

y

Lω

Z

U0

I0R

ϕ

I0Lω

ωt-ϕ

x

R

a)

b)

Rys 3

6.3. Pojemno w obwodzie pr du zmiennego

Kondensator nie stanowi przerwy w obwodzie pr du zmiennego. Zakładamy, jak dla cewki,

e napi cie zmienne przyło one do kondensatora wyra a si wzorem U = U sin ωt. Napi cie w

o

danej chwili na okładkach kondensatora o pojemno ci C wyra a si wzorem: U

q

=

(18)

C

Po zró niczkowaniu tego wzoru otrzymamy:

dU

dq

= 1

(19)

dt

C dt

Po podstawieniu za U (U = Uo sin ωt) a I zamiast dq/dt otrzymamy

ωU

1

cos

=

(20)

0

ωt

t

C

otrzymamy, e nat enie pr du płyn cego przez kondensator wynosi

I = ω C U cos ωt = ω C U sin (ωt + π/2)

(21)

o

o

Amplituda nat enia pr du płyn cego przez kondensator wynosi

I = U ωC

(22)

o

o

a wyra enie:

Z = 1

C

(23)

ω C

nazywa si oporno ci pojemno ciow Z kondensatora. Napi cie U na okładkach

C

kondensatora jest opó nione w fazie wzgl dem nat enia pr du I o π/2, czyli o jedn czwart okresu (rys. 4a i 4b). Z te przyczyny rednia moc tracona w idealnym kondensatorze wynosi

8

zero, tak jak w cewce. Opór pojemno ciowy i indukcyjny otrzymał równie nazw oporu

biernego.

a)

b)

Rys. 4

7. Szeregowy obwód RLC. Zawada

Je eli do obwodu pr du zmiennego wł czymy szeregowo poł czone rzeczywist cewk

posiadaj c opór omowy R i indukcyjno L oraz kondensator o pojemno ci C (rys. 5a), U0

UL

R

UR

ϕ

E

I

≈

L

0

C

UC

a)

b)

Rys.5

to wzajemne zale no ci mi dzy nat eniem pr du w poszczególnych elementach tego

obwodu, a napi ciami na nich przedstawia wykres na rys. 5b). Całkowity opór takiego

obwodu, czyli zawada, b dzie wyra ony wzorem:

Z = R2 +(R −

2

L

RC )

(24)

a po podstawieniu odpowiednich wyra e na R i R

L

C otrzymamy

2

Z = R2 +

L − 1

ω

(25)

ω C

9

Pomi dzy napi ciem i nat eniem pr du wyst puje przesuni cie fazowe φ wyra one

wzorem:

ω L − 1

ω

tg

C

φ =

(26)

R

Ze wzorów tych wynika, e w przypadku, gdy R = R , czyli gdy opór bierny cewki R

L

C

L

zrówna si z oporem biernym kondensatora R , opór całkowity, czyli zawada obwodu

C

szeregowego R, L i C pr du zmiennego równa si oporowi omowemu R obwodu, i nie ma

przesuni cia fazowego mi dzy napi ciem i nat eniem pr du. Przypadek ten nazywamy

napi ciowym rezonansem elektrycznym takiego obwodu. Wyst puje on wtedy, gdy mi dzy L,

C i ω zachodzi zale no :

ω =

1

2π f =

(27)

LC

Nat enie pr du osi ga wówczas warto maksymaln : I =U/R.

Moc pr du zmiennego w przypadku, mi dzy napi ciem i nat eniem pr du istnieje

przesuni cie fazowe φ, przedstawia wzór:

P = I U cos φ

(28)

sk

sk

Cos φ nazywamy współczynnikiem mocy pr du zmiennego.

Gdy Φ = π/2, P = 0. Z sytuacj zbli on do przypadku mamy do czynienia wtedy, gdy w

obwodzie elektrycznym jest du a indukcyjno , albo du a pojemno , a opór omowy tego

obwodu jest bardzo mały. Pr d taki nazywamy jałowym.

II. CEL WICZENIA

Celem wiczenia jest:

a) wyznaczenie współczynnika samoindukcji cewki z otwartym i zamkni tym strumieniem

magnetycznym,

b) wyznaczenie pojemno ci kilku kondensatorów z pomiarów ich oporu biernego,

c) sprawdzenie zjawiska rezonansu elektrycznego.

10

III. WYKONANIE WICZENIA

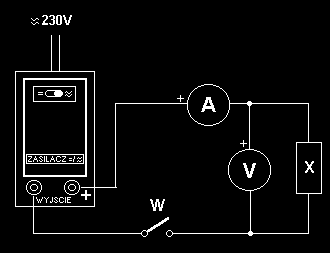
1. Zestawi schemat obwodu zgodnie z poni szym rysunkiem podł czaj c w miejsce X cewk bez zwory (W - wył cznik). Przeł cznik znajduj cy si na zasilaczu musi by w pozycji

„=” a mierniki przeł czone na pomiary stałopr dowe. Po zamkni ciu obwodu wył cznikiem W odczyta napi cie Us i nat enie pr du Is w obwodzie.

Rys. 6

2. Zamkn zwor strumie magnetyczny w rdzeniu cewki i odczyta wskazania mierników.

3. Wył czy obwód wył cznikiem W. Przeł cznik na zasilaczu ustawi w poło enie „≈” a mierniki przeł czy na pomiar pr du zmiennego. Zamkn obwód wył cznikiem W.

Zanotowa warto ci napi cia U i nat enia pr du I w obwodzie.

L

L

4. Zamkn zwor strumie magnetyczny w rdzeniu cewki i odczyta napi cie U i nat enie

L1

pr du I .

L1

5. Wł czy do obwodu zamiast cewki kondensator C1 a nast pnie C2. Powtórzy pomiary dla

kondensatorów poł czonych szeregowo i równolegle.

6. W obwód z rysunku wł czy szeregowo cewk i jeden z kondensatorów. Zanotowa

napi cie i nat enie pr du.

7. Dla obwodu z punktu 6 powtórzy pomiar napi cia i nat enia pr du przy zamkni tym

strumieniu magnetycznym cewki. Wyniki pomiarów zapisa w poni szej tabelce:

11

Tabela wyników

Element

Napi cie

Nat enie pr du

badany

Zakres

Wychylenie Warto Zakres

Wychylenie Warto

wolt. [V] wskazówki

[V]

amp. [A] wskazówki

[A]

Cewka bez

PR D zwory

STAŁY Cewka ze

zwor

Cewka bez

zwory

P

Cewka ze

R

zwor

I

D

kondensator

II

kondensator

Z

kondensatory

M

poł czone

I

szeregowo

E

N

kondensatory

N

poł czone

Y

równolegle

cewka bez

zwory i jeden

kondensator

cewka ze

zwor i jeden

kondensator

IV. OPRACOWANIE WYNIKÓW

1. Obliczy opór omowy cewki (czyli dla pr du stałego) ze wzoru:

U

R

S

=

IS

2. Obliczy zawad cewki ze wzoru:

U

Z

L

=

L

IL

Obliczy zawad cewki po zamkni ciu strumienia magnetycznego w rdzeniu cewki.

4. Korzystaj c ze wzoru

12

Z =

2 +

2

2

2

4π

L

R

f L

obliczy współczynnik indukcji L cewki bez zwory i ze zwor zamykaj c strumie magnetyczny.

5. Obliczy zawad kondensatorów i ich poł cze ze wzoru

U

Z

C

=

C

IC

6. Korzystaj c ze wzoru (23) obliczy pojemno ka dego kondensatora i ich poł cze .

7. Obliczy zawad dla szeregowego poł czenia kondensatora i cewki z otwartym i

zamkni tym strumieniem magnetycznym. Otrzymany wynik porówna z warto ci oporu

omowego cewki obliczon w punkcie 1.

8. Dyskusj bł dów przeprowadzi dla oporu omowego cewki i pojemno ci jednego

kondensatora metod pochodnej logarytmicznej, a dla jednego współczynnika indukcji

cewki metod ró niczki zupełnej.

V. LITERATURA

1. Bolton W., Zarys Fizyki, cz

2, W-wa 1988

2. Frisz S., Timoriewa A., Kurs Fizyki, t.2, PWN, W-wa 1955

3. Kapu ci ska Maria, Fizyka, W-wa 1975

4. Orear Jay, Fizyka, t.1, WN-T, W-wa 1990

5. Resnick R., Halliday D., Fizyka, t.2, PWN, W-wa 1994