Zaprojektować licznik synchroniczny na przerzutnikach D modulo n, gdzie n wynosi 4, 5 lub 6, w zależności
od bitów c1c2, jak podano poniżej
c1c2 modulo
00
4
01
5
10
6
Niech c4= c c , c
c c , c
c c
1
2
5=
1 2
6=
1
2
Tabele przejść dla układu zrealizowanego na przerzutnikach D będą wyglądały następująco: d2d1d0 mod 4: d2d1d0 mod 5: d2d1d0 mod 6: d2d1d0
0 0 0
0 0 1
0 0 1
0 0 1
0 0 1
0 1 0
0 1 0
0 1 0
0 1 0
0 1 1
0 1 1
0 1 1
0 1 1
0 0 0
1 0 0
1 0 0
1 0 0
0 – –
0 0 0
1 0 1
1 0 1
0 – –
0 – –
0 0 0
1 1 0
0 – –
0 – –
0 – –
1 1 1
0 – –
0 – –
0 – –
Z tabel przejść można odczytać że:
d2= d d d c + d d d c
2
1
0
4
2
1
0 6
d1= d ⊕ d ⋅ d d
1
0
2
1
d0= d + c d
0
2
2
Zaprojektować układ sterowania załączeniem trzech urządzeń, umożliwiający załączanie i wyłączanie po
jednym urządzeniu na minutę. Wejściem układu jest zadawana ilość urządzeń która docelowo ma pracować,
sygnał zegara (minutowego), natomiast wyjściem układu jest ilość urządzeń która w danej minucie ma być
włączona.
Dla przykładu, jeśli wszystkie urządzenia są wyłączone (ilość załączonych wynosi 0), a na wejściu układu pojawi się liczba 3 (trzy urządzenia należy włączyć), układ będzie co minutę włączał po jednym urządzeniu.
Następnie jeśli zadana ilość pracujących urządzeń zostanie zmniejszona do 1, układ zmniejszy w pierwszej minucie ilość pracujących urządzeń do 2, a w kolejnej do 1.
Z treści zadania wynika, że układ musi pamiętać ile urządzeń jest obecnie włączonych – 0, 1, 2 lub 3. Liczba 3
zmieści się na dwóch bitach (dwóch elementach pamięci – przerzutnikach).
Graf pracy układu można przedstawić następująco:
1,2,3
2,3
3
0
1
2
3
0
0,1
0,1,2
0
1
2
3
W kółkach znajduje się bieżący stan układu, tożsamy z wyjściem układu (ilość włączonych urządzeń), natomiast warunki przejść pomiędzy stanami to ilość urządzeń które docelowo mają zostać włączone.
Tabela przejść układu będzie wyglądała następująco (s1s0 to stan układu, a c1c0 to zadana ilość urządzeń): s
(t+1)
1s0 c1c0 s1s0
00 00
00
00 01
01
00 10
01
00 11
01
01 00
00
01 01
01
01 10
10
01 11
10
Układy sekwencyjne - przykłady
1/4
10 00
01
10 01
01
10 10
10
10 11
11
11 00
10
11 01
10
11 10
10
11 11
11
Powyższa tabela przejść koresponduje z grafem pracy układu.
Aby wyznaczyć s1 użyta zostanie metoda Quinne’a-McCluskey’a: 0110 011– –11–
1010
101–
1– 1–
1100
1–10
11– –
0111
110–
1011
11–0
1101
–111
1110
1–11
1111
11–1
111–
s1 = s0c1 + s1c1 + s1s0
Dla wyznaczenia s0 użyta zostanie metoda tabeli Karnough: c1c0
00 01 11 10
s1s0
00 0 1 1 1
01 0 1 0 0
11 0 0 1 0
10 1 1 1 0
s0= s ( c ⊕ s ) + c ( c ⊗ s ) 0
1
1
0
1
1
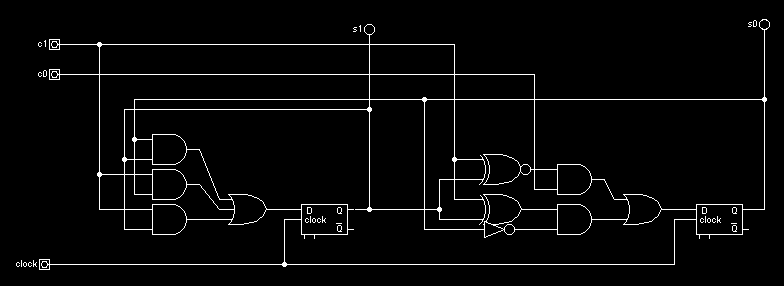
Schemat układu:
Układy sekwencyjne - przykłady
2/4
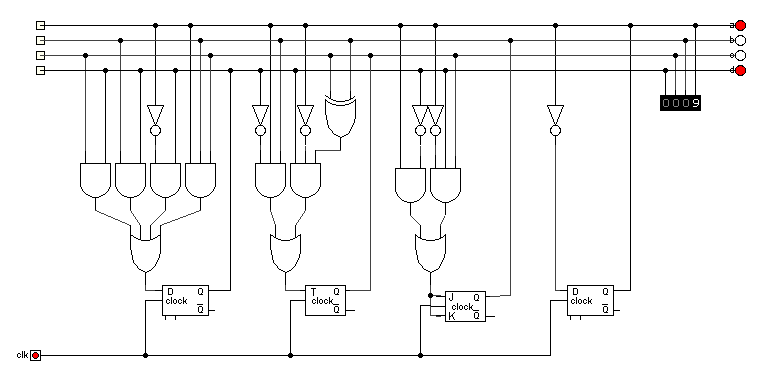
Zaprojektować licznik 4-bitowy z dwoma przeciwbieżnymi pętlami jak na poniższym grafie. Kolejne stopnie
(licząc od najbardziej znaczącego bitu) zrealizować na przerzutnikach: D, T, JK i D.
0
1
2
3
4
10
11
12
13
14
15
9
8
7
6
5
Tabela przejść licznika będzie następująca
nt dcbat nt+1 dcbat+1
0 0000
1 0001
1 0001
2 0010
2 0010
3 0011
3 0011
4 0100
4 0100
5 0101
5 0101
6 0110
6 0110
7 0111
7 0111
8 1000
8 1000
9 1001
9 1001
0 0000
10 1010 15 1111
11 1011 10 1010
12 1100 11 1011
13 1101 12 1100
14 1110 13 1101
15 1111 14 1110
Zgodnie z treścią zadania, najstarszy stopień licznika ma zostać zrealizowany na przerzutniku D. Funkcja logiczna podana na jego wejście sterujące będzie miała realizować dt+1 (stan Qt+1 przerzutnika zależy tylko od wejścia D, nie zależy od stanu poprzedniego Qt – w naszym przypadku dt). Tabela Karnough będzie wyglądać następująco:
ba
Dd
00 01 11 10
00 0 0 0 0
01 0 0 1 0
dc 11 1 1 1 1
10 1 0 1 1
Dd = cd + bd + d
a + abc
Kolejny stopień ma zostać zrealizowany na przerzutniku T. Zgodnie z zasadą działania tego przerzutnika, wyjście zmienia swój stan, gdy na wejściu T podana jest 1, a nie zmienia stanu gdy na wejściu T podane jest 0.
Zatem analizując stany kolumn ct i ct+1 tabeli przejść licznika, dochodzimy do następującej tabeli Karnough określającej funkcję logiczną którą należy podać na wejście T przerzutnika: ba
Tc
00 01 11 10
00 0 0 1 0
01 0 0 1 0
dc 11 1 0 0 0
10 0 0 0 1
Tc = dab + d a( c ⊕ b) Przedostatni stopień ma zostać zrealizowany na przerzutniku JK. Uwzględniając, że tabela przejść tego typu przerzutnika jest następująca:
JK Qt
Qt+1
0 – 0
0
1 – 0
1
– 1 1
0
– 0 1
1
Układy sekwencyjne - przykłady
3/4
postępując podobnie jak dla poprzednich stopni, dochodzimy do poniższej tabeli Karnough funkcji Jb i Kb: ba
Jb Kb 00 01 11 10
00 0– 1– –1 –0
01 0– 1– –1 –0
dc 11 1– 0– –0 –1
10 0– 0– –0 –0
Jb = Kb = ad + d
a c
Dla stopnia najmłodszego bitu, realizowanego na przerzutniku D, można zauważyć że a
= a , dlatego
t +1
t
Da = a
Uwaga: przerzutnik JK musi być zwykłym przerzutnikiem, nie przerzutnikiem typu JK-MS. Ponieważ w programie DigitalWorks zaimplementowany jest przerzutnik JK-MS, należy zrobić swoje makro przerzutnika JK.
Układy sekwencyjne - przykłady
4/4
Wyszukiwarka
Podobne podstrony:
Synchroniczne uklady sekwencyjne - przyklad, elektrotechnika, elektronika, szpytma
15 Język Instruction List Układy sekwencyjne Działania na liczbach materiały wykładowe
Podstawy Automatyki Lab 10 CW3 Układy sekwencyjne elektroniczne
E7Cyfrowe uklady sekwencyjne id Nieznany
Zadania 4, układy sekwencyjno-czasowe
2 Instrukcja do laboratorium układy sekwencyjne
03 Uklady sekwencyjne id 472117 (2)
IO8Cyfrowe uklady sekwencyjne
Zadania 2, układy sekwencyjne
Ćwiczenia, Instrukcja do ćwiczenia 4, Układy sekwencyjne - przerzutniki asynchroniczne i synchronicz
Macierze i układy równań przykłady
203 uklady sekwencyjne 2, Politechnika Wrocławska - Materiały, logika ukladow cyfrowych, sprawozdani
układy sekwencyjne, sem 4, Elektronika I i II, Elektronika II
10 Cyfrowe Uklady Sekwencyjne Nieznany
układy sekwencyjne, wip, Elektronika 2
203 uklady sekwencyjne - liczniki, Politechnika Wrocławska - Materiały, logika ukladow cyfrowych, sp
Sprawozdanie - Układy Sekwencyjne, nauka, PW, Sem 4, Elektronika II lab
więcej podobnych podstron