Ćwiczenia nr 3: Obiekty proste odnawialne z zerowym czasem odnowy 1
Elementy teorii niezawodności, ćwiczenia
Elementy teorii niezawodnoś ci
Ćwiczenia nr 3: Obiekty proste odnawialne z
zerowym czasem odnowy
Jedynymi
istotnymi
zdarzeniami
w
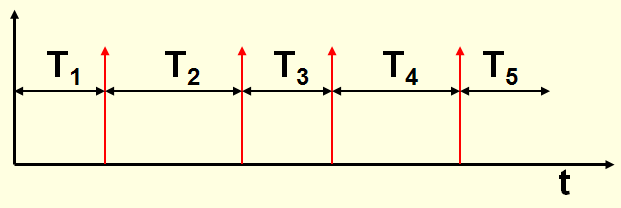
eksploatacji obiektu prostego odnawialnego z zerowa odnową są chwile uszkodzeń , które przy zerowej odnowie, są jednocześ nie chwilami odnów.
Przyjmujemy rozkład czasu T do uszkodzenia dla strumienia ogólnego:
– rozkład gamma z parametrami a, b t
t
a
1
1
1
−
−
−1 −
*
b
a
a
bx
a
a
bx
F t
( )
1
= ∫
b x
e
dx =
b ∫ x e dx , f ( s) 1
=
Γ( a)
Γ( a)
b + s
0
0
, … -rozkład Erlanga 2 rzędu z parametrem
n 1
-
(λt) i
i
1
−λ
λt
λ
λ
λ
λ
t
( )
2
− t
− t
− t
*
F (t) = 1− ∑
e
=1− ∑
e
=1 − e − λ te , f ( s) =
i=0
!
i
i=
!
i
λ + s
0
Strumienie odnów
Proste
Ogólne
Wszystkie zmienne losowe , , … mają identyczne
Wszystkie zmienne losowe oprócz mają identyczne rozkłady określone:
rozkłady jak w strumieniu prostym, ma inny rozkład
• dystrybuantą ,
określony:
• gęstością ,
• dystrybuantą ,
• transformatą Laplace’a ,
• gęstością ,
•
wartością oczekiwaną ,
• transformatą Laplace’a ,
• odchyleniem standardowym .
• wartością oczekiwaną ,
• odchyleniem standardowym .
Michał Kapałka
mkapalka@wat.edu.pl
Ćwiczenia nr 3: Obiekty proste odnawialne z zerowym czasem odnowy 2
Elementy teorii niezawodności, ćwiczenia
Miary niezawodnościowe
1. Czas do r-tej odnowy
- zmienna losowa dla której:
Dystrybuanta:
Transformata Laplace’a funkcji %&:
∞
Gęstość :
' ( ')*)+)
!
!
∞
Dla strumienia prostego
Dla strumienia ogólnego
! "#
! "#
! "#
! "#
Dla , - ∞ zmienna losowa dąŜy do rozkładu normalnego ."/ · 1, 2 · √/#
• Zadanie 1: Wyznaczyć prawdopodobieństwo tego, Ŝe 7-me uszkodzenie wystąpi po chwili , 6
a
a
1
1
b λ
1 b λ
*
*
P( S ≥ t ) = 1− K ( t ), K ( s) =
f ( s) f ( s)
=
=
7
1
7
1
7
1
(
)
2
12
6
*
s
s b + s λ + s
s b + s λ + s
• Zadanie 2: Wyznaczyć prawdopodobieństwo tego, Ŝe do chwili , będzie co najmniej 5 napraw
4
a
a
1
1
b λ
1 b λ
*
*
P( S < t ) = K ( t ), K ( s) =
f ( s) f ( s)
=
=
5
2
5
2
5
1
(
)
2
8
4
*
s
s b + s λ + s
s b + s λ + s
2. Proces stochastyczny 4 - liczba odnowień do chwili t
5., 6 / 5 7 ,
5., 6 / 5 7 , 1 9 8,
5., / 8, 9 8: ,
5., 7 / 5: 6 , 8: ,
5., / 5., 7 / 5., 6 / 1
Dla , - ∞ proces ., dąŜy do
, "2 ·
. <
√,#
1 ,
=
1
• Zadanie 3: Wyznaczyć prawdopodobieństwo tego, Ŝe do chwili , będzie dokładnie 8 uszkodzeń P( N ( t ) = )
8 = K ( t ) − K ( t ), 3
8
3
9
3
7
8
a
2
a
14
a
2
a
16
1
b λ
1 b λ
1
b λ
1 b λ
*
K ( s)
=
=
*
K ( s)
=
=
8
s b + s λ + s
s b + s λ + s
9
s b + s λ + s
s b + s λ + s
Michał Kapałka
mkapalka@wat.edu.pl
Ćwiczenia nr 3: Obiekty proste odnawialne z zerowym czasem odnowy 3
Elementy teorii niezawodności, ćwiczenia
3. Funkcja odnowy > - oczekiwana liczba odnowień do chwili t
> ?4
Równanie odnowy:
> > ·
Dla strumienia prostego
Dla strumienia ogólnego
1 BA
1 BA
@A
A 1 9 BA
@A A 1 9 BA
4. Gęstość odnowy C
E@,
D, E,
Dla strumienia prostego
Dla strumienia ogólnego
BA
BA
@A
1 9 BA
@A 1 9 BA
• Zadanie 4: Wyznaczyć oczekiwaną liczbę napraw do chwili ,F
a
b
*
1
f
s
b +
1 (
)
1
s
*
H ( t ) = ?, H ( s) =
=
4
*
2
s 1 − f ( s)
s
λ
1 −
λ + s
• Zadanie 5: Wyznaczyć oczekiwaną liczbę uszkodzeń w przedziale czasu ,G, ,H
@,H 9 @,G ?
Jak w poprzednim punkcie.
5. Miary graniczne dla - ∞ @, 1
,
lim
N-O , 1 ; EQR ESżUVD ,: @, 1
\
Tw. Blackwella
XYZ[> \ 9 > ]
-O
• Zadanie 6: Wyznaczyć oczekiwaną graniczną liczbę uszkodzeń w przedziale ,^, ,_
lim( H t
( )
R ,
/. `/QRb%R
8
− H( )
7 ) = a
t
_ 9 ,^, Θ ` λ
t 7 ∞
→
Θ
t − t
λ
8
7
lim( H ( t ) − H ( t ) =
=
t − t
8
7 )
(
)
t
∞
→
7
2
2 8
7
λ
• Zadanie 7: Wyznaczyć oczekiwaną graniczną liczbę napraw do chwili ,c lim H ( ) = t
t
t→∞
Θ
@,c 2 ,c
Michał Kapałka
mkapalka@wat.edu.pl
Ćwiczenia nr 3: Obiekty proste odnawialne z zerowym czasem odnowy 4
Elementy teorii niezawodności, ćwiczenia
• Zadanie 8: Wyznaczyć rozkład granicznej liczby uszkodzeń w chwili , e σ
N ( t) → N ( m,σ '), gdzie
= t
m
, σ ' =
t , pamiętamy, Ŝe dla rozkładu Erlanga σ √
3
λ
t→∞
Θ
2
Θ
2
t
σ t
λ
λ
λ t
λ t
10
10
zatem N(t
10
10
N
,
= N t ,
t
N
3
10
3
10
=
10) dąŜy do rozkładu
,
Θ
2
2
2
Θ2
2 2
λ
• Zadanie 9: Wyznaczyć graniczne prawdopodobieństwo tego, Ŝe do chwili , będzie co najmniej 50
uszkodzeń
P( S
< t ) = K ( t ) ≅ F
( t )
50
11
50
11
normalny
11
100
100
Ge fgh ."50 · 1, 2 · √50# , N ( m,σ ') = N (50Θ,σ 50 )
= N
,
N-O
λ
λ
• Zadanie 10: Wyznaczyć graniczne prawdopodobieństwo tego, Ŝe do chwili , będzie mniej niŜ 100 napraw
P( S
≥ t ) = 1− K ( t ) ≅ 1− F
( t )
100
12
100
12
normalny
12
200 10 2
ee fgh ."100 · 1, 2 · √100# N ( , m σ ') = N (100Θ,σ 100)
= N
,
N-O
λ
λ
6. Prawdopodobieństwo k , \braku uszkodzenia w przedziale , \
k , \ 9 \ ([ 9 \ 9 )]C)+)
l
Tw. Smitha
O
XYZ ( mn 9 oC)+)
-O
( 'p+p
l
q
Prawdopodobieństwo graniczne braku uszkodzenia w przedziale ,, , r
O
5r XYZ5,, , r
-O
([1 9 sU] +t
\
• Zadanie 11: Wyznaczyć prawdopodobieństwo tego, Ŝe w przedziale (t13,t14) nie będzie uszkodzeń t
P( t , t
1 F ( t )
1 F ( t
τ ) h(τ ) dτ
13
14 )
13
= − 1 14 + ∫[ −
14 −
]
0
a
b
b + s
h(t) wyznaczamy z formuły
*
h
( s) =
, zatem h(t)=λ, więc
2
λ
1−
λ + s
t
t
14
13
1
−λ ( t −
a
a−1 − bx
−λ(
τ
1
t 4 −
)
14
P( t , t
1
b
x
e
dx
e
λ
τ
( t
τ ) e
h(τ ) dτ
14
13 ) =
−
∫
+ ∫[
) +
14 −
]
Γ( a)
0
0
Michał Kapałka
mkapalka@wat.edu.pl
Ćwiczenia nr 3: Obiekty proste odnawialne z zerowym czasem odnowy 5
Elementy teorii niezawodności, ćwiczenia
• Zadanie 12: Wyznaczyć graniczne prawdopodobieństwo tego, Ŝe w przedziale czasu (t15,t16) nie będzie uszkodzeń
ze wzoru
O
k\ ([1 9 s,] +
\
∞
∞
∞
1
2
−
λ
λ
t
λ
−λ t
−λ t
−λ
mamy P(
t
t
t
e
λ te dt
e
dt
te
dt
16 − 15 ) =
∫
+
=
∫
+
∫
θ
2
2
1
t 6 − 1
t 5
1
t 6 − 1
t 5
1
t 6 − 1
t 5
Uwaga:
1
b
( &uvwxE& R&uvwx 9R(&u vwxE& 7. Pozostały czas zdatności y , jeśli od ostatniej odnowy minął czas t
5zN 7 r 5,, , r
y k , \ 9
\ ([ 9 \ 9 )]C)+)
l
Dla duŜych t:
O
y ([1 9 sU] +t
\
O
1 2
`z ( 5rEr 2 21
e
Michał Kapałka
mkapalka@wat.edu.pl