
Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
1
Ćwiczenia nr 2. Redundancja układowa, pasywna
1. Redundancja układowa
Redundancja nazywana jest inaczej rezerwowaniem lub nadmiarem. W systemach oznacza
to istnienie dodatkowych zdolności funkcjonalnych ponad te, które są wymagane dla
prawidłowego funkcjonowania systemu. Redundancję wprowadza się do systemu w celu
zwiększenia jego niezawodności. Jednak wiadomo, że nie każdy nadmiar zwiększa
niezawodność systemów.
Nadmiar układowy (strukturalny) – w tym przypadku system posiada dodatkowe elementy,
które w razie awarii elementów podstawowych mogą pełnić ich rolę w systemie.
2. Klasyfikacja rezerwowania układowego
Klasyfikację sposobów włączania elementów rezerwowych, czyli klasyfikację rezerwowania
układowego przedstawia poniższy schemat.
Rezerwowanie ogólne – polega na rezerwowaniu całego systemu identycznymi systemami
(na przykład zapasowymi).
Rezerwowanie rozdzielcze - ma miejsce wtedy, gdy oddzielnie każdy element jest
rezerwowany pewną liczbą elementów.
Rezerwowanie mieszane - występuje wtedy, gdy dla część i systemu stosujemy ogólną
rezerwę układową, a dla części rezerwowanie rozdzielcze.
Rezerwowane przesuwające - się może być stosowane wtedy, gdy element rezerwowy może
być włączany zamiast dowolnego elementu podstawowego.
Ze względu na sposób włączenia w układ elementów stanowiących rezerwę:
Rezerwowanie pasywne – elementy rezerwowe są na stałe włączone do systemu wraz z
elementami podstawowymi.
Rezerwowanie aktywne – elementy rezerwowe są włączane do systemu dopiero w
przypadku awarii elementów podstawowych (przełącznik: idealny, rzeczywisty).

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
2
Ze względu na warunki w jakich przebywają elementy stanowiące rezerwę:
Rezerwa gorąca – oznacza obciążenie całkowite elementu stanowiącego rezerwę
Rezerwa ciepła – oznacza obciążenie częściowe elementu stanowiącego rezerwę
Rezerwa zimna – oznacza obciążenie zerowe elementu stanowiącego rezerwę
3. Charakterystyka rozmiarów rezerwowania
Krotność rezerwowania
κ
charakteryzuje rozmiar rezerwowania. Jest to stosunek liczby n
r
elementów rezerwowych do liczby n
p
elementów rezerwowanych:
p
r
n
n
=
κ
4. Miara redundancji
Aby móc ocenić zysk wynikający z zastosowanej redundancji układowej trzeba mieć
możliwość porównania niezawodności systemu z redundancją z niezawodnością systemu
podstawowego (bez elementów rezerwowych).
Wprowadza się pojęcie miary redundancji strukturalnej (zysk z rezerwowania), która to
miara jest ściśle związana ze wskaźnikiem niezawodności, jaki jest w danym momencie
rozważany:
)
(
)
(
*
)
(
t
w
t
w
t
w
=
η
Gdzie,
•
w(t) - rozważany wskaźnik niezawodności,
przy czym
•
w(t) – jest rozważanym wskaźnikiem dla systemu z jego podstawowymi elementami
(bez nadmiarowych),
•
w*(t) – jest rozważanym wskaźnikiem dla systemu z uwzględnieniem elementów
nadmiarowych.
Jako wskaźnik niezawodności może służyć, np. funkcja niezawodności
).
(t
R
Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
3
Zadanie 1
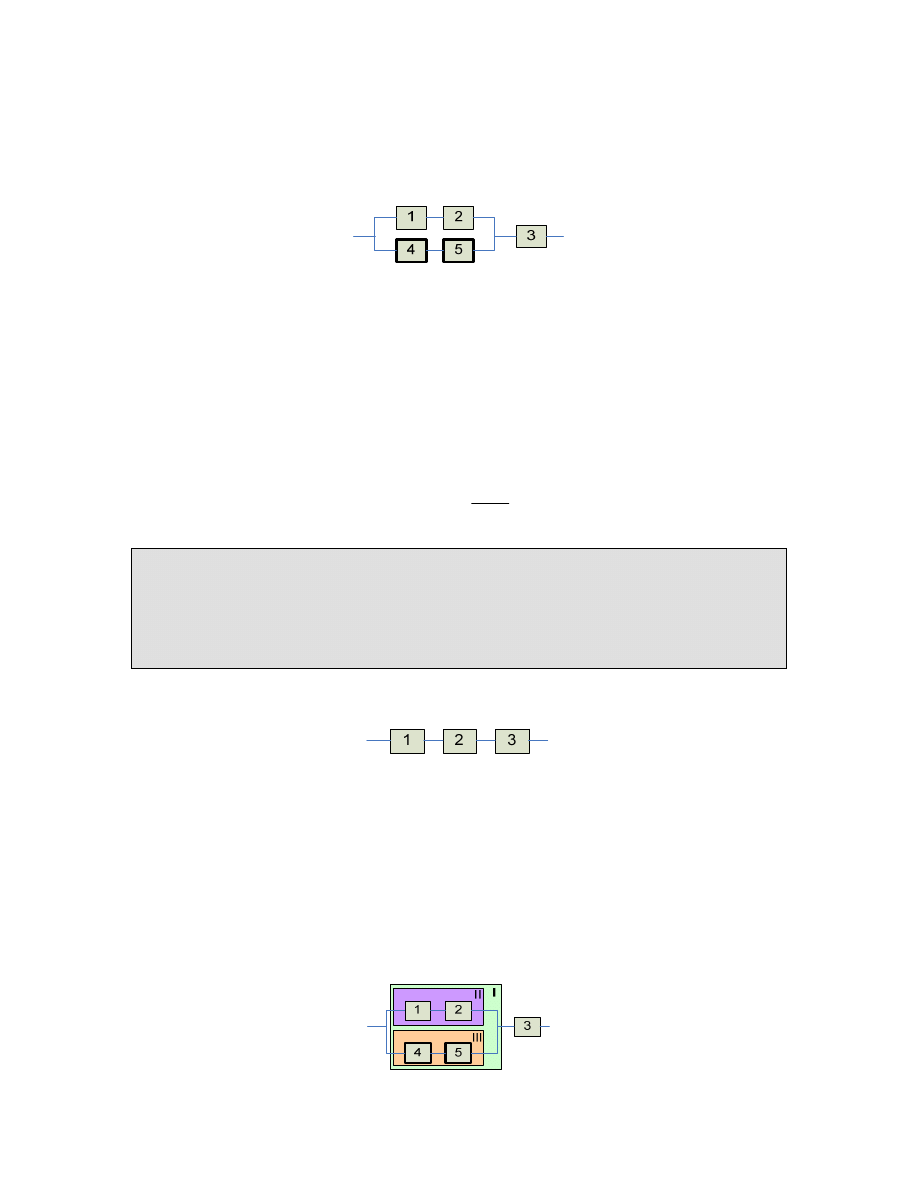
Rozpatrujemy strukturę niezawodnościową z redundancją układową, pasywną, ogólną
złożoną z elementów identycznych, nieodnawialnych o wykładniczym rozkładzie czasu do
uszkodzenia z parametrem a. Schemat blokowy struktury niezawodnościowej przedstawiony
jest na rysunku.
Elementy 4 i 5 stanowią redundancję pasywną dla elementów 1 i 2.
Zatem
at
i
e
t
F
t
F
−
−
=
=
1
)
(
)
(
at
i
e
t
R
t
R
−
=
=
)
(
)
(
Wyznaczyć zysk z redundancji dla wskaźników
)
(t
R
i
}
{T
E
.
Miara redundancji strukturalnej dla wskaźnika R(t) jest postaci
)
(
)
(
)
(
*
)
(
t
R
t
R
t
S
S
t
R
=
η
W świetle teorii niezawodności systemów istnienie redundancji układowej zmienia strukturę
niezawodnościową w odniesieniu do struktury niezawodnościowej systemu podstawowego
(bez redundancji). Jest oczywiste, że struktura niezawodnościowa systemu z redundancją jest
nieredukowalna i koherentna, ponieważ elementy rezerwowe nie mogą być pasywne. Wobec
tego wszystkie metody badania niezawodności systemów, omawiane do tej pory, nadają się
do badania niezawodności systemów zawierających elementy rezerwowe.
Schemat blokowy struktury niezawodnościowej systemu podstawowego
Funkcja niezawodności systemu podstawowego o szeregowej strukturze niezawodnościowej
wyraża się następująco
at
at
at
at
S
e
e
e
e
t
R
t
R
t
R
t
R
3
3
2
1
)
(
)
(
)
(
)
(
−
−
−
−
=
⋅
⋅
=
=
Sprawdzamy czy nie popełniliśmy błędu w obliczeniach
1
)
0
(
0
=
= e
R
S
Schemat blokowy struktury niezawodnościowej systemu z redundancją
W celu ułatwienia obliczeń wyznaczamy podsystemy.

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
4
at
at
at
at
at
I
S
e
e
e
e
e
t
R
t
R
t
R
5
3
4
2
3
*
2
)
2
(
)
(
)
(
)
(
−
−
−
−
−
−
=
−
=
=
at
at
at
at
III
II
I
e
e
e
e
t
F
t
F
t
F
4
2
2
2
2
1
)
1
)(
1
(
)
(
)
(
)
(
−
−
−
−
+
−
=
−
−
=
=
at
II
e
t
R
t
R
t
R
2
2
1
)
(
)
(
)
(
−
=
=
at
III
e
t
R
t
R
t
R
2
5
4
)
(
)
(
)
(
−
=
=
Sprawdzamy czy nie popełniliśmy błędu w obliczeniach
1
1
2
2
)
0
(
0
0
=
−
=
−
=
e
e
R
S
A więc zysk z redundancji dla wskaźnika
)
(t
R
wynosi
at
at
at
at
S
S
t
R
e
e
e
e
t
R
t
R
t
2
3
5
3
*
)
(
2
2
)
(
)
(
)
(
−
−
−
−
−
=
−
=
=
η
Wartość miary redundancji strukturalnej w chwili t=0 przyjmuje wartość 1 (
1
)
0
(
)
(
=
t
R
η
).
Możemy w prosty sposób sprawdzić, czy nie popełniliśmy błędu w obliczeniach.
Wiadomo, że
1
0
0
=
=
⋅
−
e
e
λ
, więc
1
1
2
2
)
0
(
0
)
(
=
−
=
−
=
e
t
R
η
Natomiast dla
∞
→
t
otrzymujemy
2
0
2
2
)
(
)
(
=
−
=
−
=
∞
−∞
e
t
R
η
Wniosek. Zatem mamy podwójny wzrost wartości wskaźnika niezawodności R(t) dla
dostatecznie dużych t.
Miara redundancji strukturalnej dla wskaźnika E{T} jest postaci
}
{
}
{
*
}
{
S
S
T
E
T
E
T
E
=
η
Wartość oczekiwana czasu zdatności dla systemu bez redundancji
a
dt
e
dt
t
R
T
E
at
s
s
3
1
)
(
}
{
0
3
0
=
=
=
∫
∫
∞
−
∞
Wartość oczekiwana czasu zdatności dla systemu z redundancją
a
a
a
a
dt
e
dt
e
dt
e
e
dt
t
R
T
E
at
at
at
at
S
s
15
7
15
3
10
5
1
3
2
2
)
2
(
)
(
}
{
0
5
0
3
0
5
3
0
*
*
=
−
=
+
=
−
=
−
=
=
∫
∫
∫
∫
∞
−
∞
−
∞
−
−
∞
A więc zysk z redundancji dla wskaźnika E{T} wynosi
5
7
1
3
15
7
3
1
15
7
}
{
}
{
*
}
{
=
=
=
=
a
a
a
a
T
E
T
E
S
S
T
E
η
Wniosek. Zatem mamy 1,4 wzrost wartości wskaźnika niezawodności E{T} dla dostatecznie
dużych t. Poprawa nie jest już tak wielka, jak w przypadku wskaźnika R(t).

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
5
Zadanie 2
Rozpatrujemy strukturę niezawodnościową z redundancją układową, pasywną złożoną z
elementów identycznych, odnawialnych. Schemat blokowy struktury niezawodnościowej
przedstawiony jest na rysunku.
Elementy 4 i 5 stanowią redundancję pasywną dla elementów 1 i 2.
Zatem
at
i
e
t
F
t
F
−
−
=
=
1
)
(
)
(
bt
i
e
t
G
t
G
−
−
=
=
2
)
(
)
(
Wyznaczyć zysk z redundancji dla wskaźników
)
(t
k
g
i
g
K .
Miara redundancji strukturalnej dla wskaźnika
)
(t
k
g
jest postaci
)
(
)
(
)
(
*
)
(
t
k
t
k
t
S
S
g
g
g
t
k
=
η
Schemat blokowy struktury niezawodnościowej systemu podstawowego
Funkcja
)
(t
k
S
g
systemu podstawowego o szeregowej strukturze niezawodnościowej wyraża
się następująco
)
(
)
(
)
(
)
(
3
2
1
t
k
t
k
t
k
t
k
g
g
g
g
S
=
wiadomo, że
t
b
a
g
e
b
a
a
b
a
b
t
k
i
)
(
)
(
+
−
+
+
+
=
oznaczmy
)
(
)
(
t
d
t
k
i
g
=
więc
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
3
3
2
1
t
d
t
d
t
d
t
d
t
k
t
k
t
k
t
k
g
g
g
g
S
=
⋅
⋅
=
=
Schemat blokowy struktury niezawodnościowej systemu z redundancją
W celu ułatwienia obliczeń wyznaczamy podsystemy.

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
6
)
(
)
(
2
))
(
)
(
2
)(
(
)
(
)
(
)
(
5
3
4
2
*
3
t
d
t
d
t
d
t
d
t
d
t
k
t
k
t
k
gI
g
g
S
−
=
−
=
=
)
(
)
(
2
1
))
(
1
))(
(
1
(
))
(
1
))(
(
1
(
)
(
1
4
2
2
2
t
d
t
d
t
d
t
d
t
k
t
k
t
k
III
II
I
g
g
g
+
−
=
−
−
=
−
−
=
−
)
(
)
(
)
(
)
(
2
2
1
t
d
t
k
t
k
t
k
g
g
g
II
=
=
)
(
)
(
)
(
)
(
)
(
)
(
2
5
4
t
d
t
d
t
d
t
k
t
k
t
k
g
g
g
III
=
⋅
=
=
A więc zysk z redundancji dla wskaźnika
)
(t
k
g
wynosi
2
)
(
2
3
5
3
*
)
(
2
)
(
2
)
(
)
(
)
(
2
)
(
)
(
)
(
+
+
+
−
=
−
=
−
=
=
+
−
t
b
a
g
g
t
k
e
b
a
a
b
a
b
t
d
t
d
t
d
t
d
t
k
t
k
t
S
S
g
η
Wartość miary redundancji strukturalnej w chwili t=0 przyjmuje wartość 1 (
1
)
0
(
)
(
=
t
k
g
η
).
Możemy w prosty sposób sprawdzić, czy nie popełniliśmy błędu w obliczeniach.
Wiadomo, że
1
0
0
=
=
⋅
−
e
e
λ
, więc
1
1
2
2
2
)
0
(
2
2
0
)
(
=
−
=
+
+
+
−
=
+
+
+
−
=
−
b
a
a
b
a
b
e
b
a
a
b
a
b
t
k
g
η
Natomiast dla
∞
→
t
otrzymujemy
2
2
)
(
2
2
)
(
+
−
=
+
+
+
−
=
∞
∞
−
b
a
b
e
b
a
a
b
a
b
t
k
g
η
Miara redundancji strukturalnej dla wskaźnika
g
K
jest postaci
S
S
g
g
g
K
K
K
*
=
η
Graniczny współczynnik gotowości dla systemu bez redundancji
3
2
1
g
g
g
g
K
K
K
K
S
=
wiadomo, że
b
a
b
K
i
g
+
=
oznaczmy
d
K
i
g
=
3
3
2
1
d
K
K
K
K
g
g
g
g
S
=
=
Graniczny współczynnik gotowości dla systemu z redundancją
5
3
4
2
*
2
)
2
(
3
d
d
d
d
d
K
K
K
gI
g
g
S
−
=
−
=
=
4
2
2
2
2
1
)
1
)(
1
(
)
1
)(
1
(
1
d
d
d
d
K
K
K
III
II
I
g
g
g
+
−
=
−
−
=
−
−
=
−
2
2
1
d
K
K
K
g
g
g
II
=
=
2
5
4
d
d
d
K
K
K
g
g
g
III
=
⋅
=
=
A więc zysk z redundancji dla wskaźnika
g
K
wynosi
2
2
3
5
3
2
2
2
+
−
=
−
=
−
=
b
a
b
d
d
d
d
g
K
η
Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
7
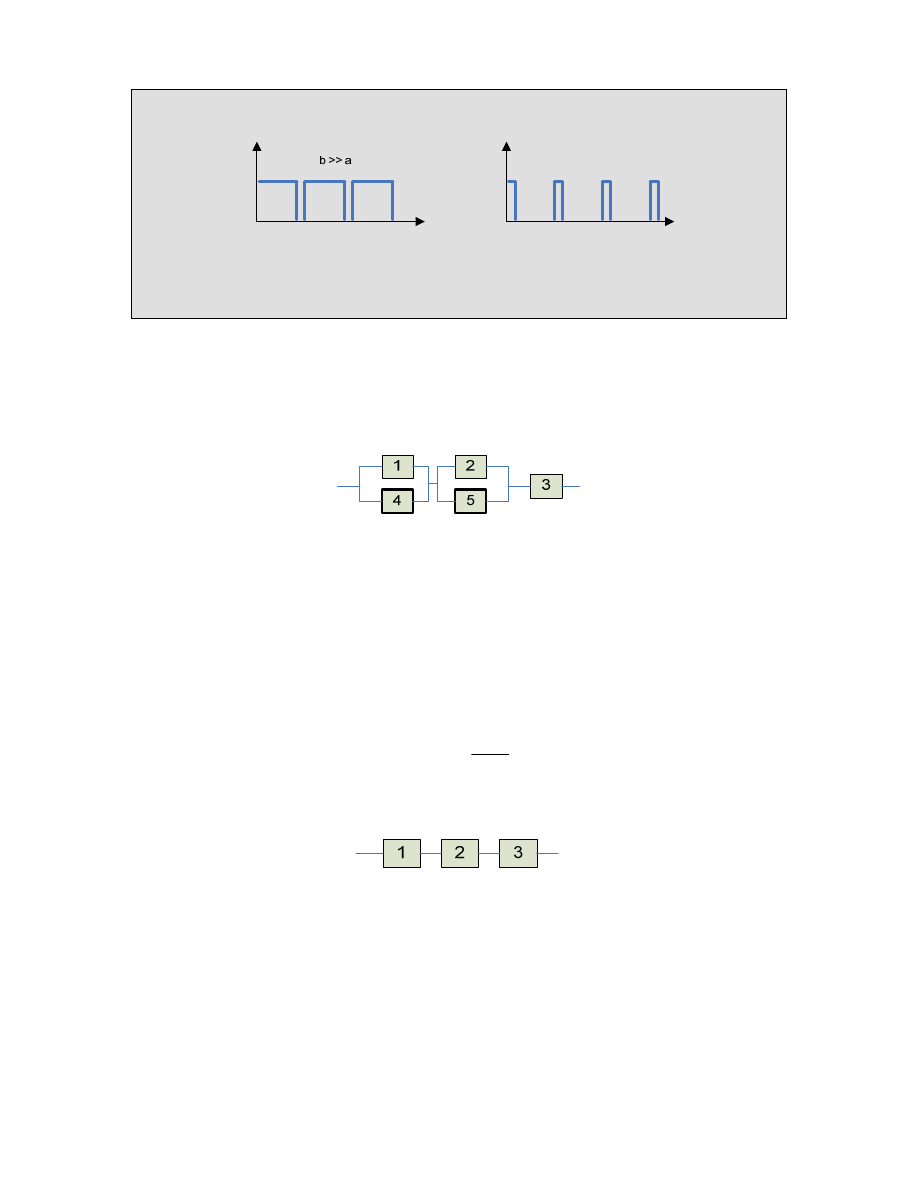
Zysk z redundancji uzależniony jest nie tylko od liczby elementów rezerwowych, ale również
od parametrów a i b rozkładów F(t) i G(t)
a >> b
1
1
2
)
(
)
(
=
−
≈
t
t
k
g
η
2
0
2
)
(
)
(
=
−
≈
t
t
k
g
η
Wniosek. Zysk z redundancji rośnie, im obiekty podstawowe są gorsze.
Zadanie 3
Rozpatrujemy strukturę niezawodnościową z redundancją układową, pasywną złożoną z
elementów identycznych, nieodnawialnych o wykładniczym rozkładzie czasu do uszkodzenia
z parametrem a. Schemat blokowy struktury niezawodnościowej przedstawiony jest na
rysunku.
Elementy 4 i 5 stanowią redundancję pasywną, rozdzielczą dla elementów 1 i 2.
Zatem
at
i
e
t
F
t
F
−
−
=
=
1
)
(
)
(
at
i
e
t
R
t
R
−
=
=
)
(
)
(
Wyznaczyć zysk z redundancji dla wskaźników
)
(t
R
i
}
{T
E
.
Miara redundancji strukturalnej dla wskaźnika R(t) jest postaci
)
(
)
(
)
(
*
)
(
t
R
t
R
t
S
S
t
R
=
η
Schemat blokowy struktury niezawodnościowej systemu podstawowego
Funkcja niezawodności systemu podstawowego o szeregowej strukturze niezawodnościowej
wyraża się następująco
at
at
at
at
S
e
e
e
e
t
R
t
R
t
R
t
R
3
3
2
1
)
(
)
(
)
(
)
(
−
−
−
−
=
⋅
⋅
=
=

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
8
Schemat blokowy struktury niezawodnościowej systemu z redundancją
W celu ułatwienia obliczeń wyznaczamy podsystemy.
=
−
−
=
−
−
=
=
−
−
−
−
−
−
−
−
−
)
2
)(
2
(
)
2
)(
2
(
)
(
)
(
)
(
)
(
2
3
2
2
2
3
*
at
at
at
at
at
at
at
at
at
II
I
S
e
e
e
e
e
e
e
e
e
t
R
t
R
t
R
t
R
at
at
at
at
at
at
at
e
e
e
e
e
e
e
5
4
3
5
4
4
3
4
4
2
2
4
−
−
−
−
−
−
−
+
−
=
+
−
−
=
at
at
at
at
I
e
e
e
e
t
F
t
F
t
F
2
4
1
2
1
)
1
)(
1
(
)
(
)
(
)
(
−
−
−
−
+
−
=
−
−
=
=
at
at
at
at
II
e
e
e
e
t
F
t
F
t
F
2
5
2
2
1
)
1
)(
1
(
)
(
)
(
)
(
−
−
−
−
+
−
=
−
−
=
=
Sprawdzamy czy nie popełniliśmy błędu w obliczeniach
1
1
4
4
4
4
)
0
(
0
0
0
=
+
−
=
+
−
=
e
e
e
R
S
A więc zysk z redundancji dla wskaźnika
)
(t
R
wynosi
at
at
at
at
at
at
S
S
t
R
e
e
e
e
e
e
t
R
t
R
t
5
3
5
4
3
*
)
(
4
4
4
4
)
(
)
(
)
(
−
−
−
−
−
−
+
−
=
+
−
=
=
η
Wartość miary redundancji strukturalnej w chwili t=0 przyjmuje wartość 1 (
1
)
0
(
)
(
=
t
R
η
).
Możemy w prosty sposób sprawdzić, czy nie popełniliśmy błędu w obliczeniach.
Wiadomo, że
1
0
0
=
=
⋅
−
e
e
λ
, wi
ę
c
1
1
4
4
4
4
)
0
(
0
0
)
(
=
+
−
=
+
−
=
e
e
t
R
η
Natomiast dla
∞
→
t
otrzymujemy
4
0
0
4
4
4
)
(
)
(
=
+
−
=
+
−
==
∞
−∞
−∞
e
e
t
R
η
Wniosek.
Zatem mamy poczwórny wzrost warto
ś
ci wska
ź
nika niezawodno
ś
ci R(t) dla
dostatecznie du
ż
ych t.
Miara redundancji strukturalnej dla wska
ź
nika E{T} jest postaci
}
{
}
{
*
}
{
S
S
T
E
T
E
T
E
=
η
Warto
ść
oczekiwana czasu zdatno
ś
ci dla systemu
bez redundancji
a
dt
e
dt
t
R
T
E
at
s
s
3
1
)
(
}
{
0
3
0
=
=
=
∫
∫
∞
−
∞

Ćwiczenia 2
Niezawodność systemów komputerowych, ćwiczenia
Arkadiusz Wrzosk
awrzosk@wat.edu.pl
9
Warto
ść
oczekiwana czasu zdatno
ś
ci dla systemu
z redundancją
=
+
−
=
+
−
=
=
∫
∫
∫
∫
∫
∞
−
∞
−
∞
−
∞
−
−
−
∞
0
5
0
4
0
3
0
5
4
3
0
*
*
4
4
)
4
4
(
)
(
}
{
dt
e
dt
e
dt
e
dt
e
e
e
dt
t
R
T
E
at
at
at
at
at
at
S
s
a
a
a
a
a
15
8
15
15
3
20
5
1
4
4
3
4
=
−
+
=
+
−
=
A wi
ę
c zysk z redundancji dla wska
ź
nika E{T} wynosi
5
8
1
3
15
8
3
1
15
8
}
{
}
{
*
}
{
=
=
=
=
a
a
a
a
T
E
T
E
S
S
T
E
η
Wniosek.
Zatem mamy 1,6 wzrost warto
ś
ci wska
ź
nika niezawodno
ś
ci R(t) dla dostatecznie
du
ż
ych t. Poprawa nie jest ju
ż
tak wielka, jak w przypadku wska
ź
nika R(t).
Porównuj
ą
c wyniki z zadaniem 1 mo
ż
na zauwa
ż
y
ć
,
ż
e rezerwowanie rozdzielcze jest lepsze
od rezerwowania ogólnego. Wynika to z faktu,
ż
e struktura niezawodno
ś
ciowa jest lepsza, im
wi
ę
cej zawiera
ś
cie
ż
ek zdatno
ś
ci.
Wyszukiwarka
Podobne podstrony:
etn cwiczenia nr 1 zadania
etn cwiczenia nr 1 id 164456
etn cwiczenia nr 6 id 164467
etn cwiczenia nr 3
etn, cwiczenia nr 3
etn, cwiczenia nr 10
etn, cwiczenia nr 7
etn, cwiczenia nr 2
etn, cwiczenia nr 8
etn cwiczenia nr 2,3 zadania
etn cwiczenia nr 4
etn cwiczenia nr 5 id 164464
etn cwiczenia nr 2
więcej podobnych podstron