WPŁYW PARAMETRÓW UKŁADU REGULACJI NA PRACĘ
NAPĘDU PRĄDU STAŁEGO
1. CEL I ZAKRES ĆWICZENIA
Celem ćwiczenia jest zapoznanie się z wpływem parametrów, ograniczeń
oraz realizacji przekształtnika i układu sterowania na właściwości statyczne
i dynamiczne układu napędowego złożonego z silnika obcowzbudnego prądu stałego
i przekształtnika energoelektronicznego.
Zakres
ćwiczenia
obejmuje
badania
symulacyjne
różnych
realizacji
energoelektronicznego układu napędowego z silnikiem obcowzbudnym prądu stałego,
wykonane w programie MATLAB-SIMULINK. Modele uwzględniają różny stopień
uproszczenia elementów układu napędowego, co wpływa na stopień adekwatności
przeprowadzanych symulacji oraz czas wykonywania obliczeń. Badania obejmują
wpływ ograniczeń, nastaw regulatorów, uwzględnienie cyfrowej realizacji układu
sterowania i modeli obwodów mocy na właściwości dynamiczne i statyczne napędu.
W ramach ćwiczenia wyznaczana jest reakcja na skokową zmianę wielkości zadanej
i zakłócenia, badana jest praca w stanie ustalonym oraz proces nawrotu silnika.
2. WPROWADZENIE TEORETYCZNE
O dobrych właściwościach dynamicznych i statycznych napędu decyduje
prawidłowy dobór silnika, przekształtnika zasilającego oraz układu sterowania.
Ważną rolę przy projektowaniu układu sterowania pełni odpowiedni dobór
zastosowanych w nim regulatorów. Podczas projektowania regulatorów pomocne są
programy symulacyjne pozwalające na dobre zamodelowanie układu napędowego
i jego układu regulacji. Należy zaznaczyć, że dobór złożoności modelu układu
napędowego musi stanowić kompromis między czasem wykonywania obliczeń
a dokładnością (zbieżnością z rzeczywistością) otrzymywanych wyników.
W ćwiczeniu wykorzystywane jest oprogramowanie MATLAB-SIMULINK,
pozwalające na modelowanie układów analogowych i cyfrowych. Umożliwia ono
stosowanie modeli wyprowadzanych z opisu matematycznego obiektów, jak również
wykorzystanie gotowych modeli „elektrycznych” ułatwiających przeprowadzenie
symulacji. Wybór metody modelowania prowadzi do różnych poziomów
odzwierciedlenia układu rzeczywistego oraz różnych czasów trwania obliczeń.
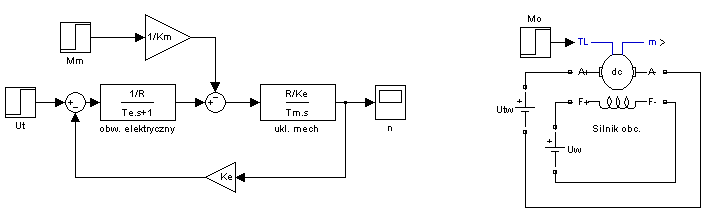
2.1. Model silnika obcowzbudnego prądu stałego
Ćwiczenie niniejsze dotyczy układów napędowych z silnikiem obcowzbudnym
prądu stałego, którego schemat przedstawiono na rys. 4.1.a. Podczas pracy takiego
układu z prędkością mniejszą bądź równą prędkości znamionowej strumień
wzbudzenia silnika pozostaje stały (ϕ = const.). Przy takim założeniu silnik opisują zależności (4.1-4.3):
d i ( t)
u ( t) = e( t) + R i ( t)
T
+ L
,
(4.1)
T
T T
T
dt
e( t) = kϕω( t) = k n( t)
M ( t) = k i
ϕ ( t) = k i( t) ,
(4.2)
e
m
dω( t)
π d n( t)
M ( t) = M ( t) + J
= M ( t) + J
,
(4.3)
m
m
dt
30 dt
gdzie:
u T , i T – odpowiednio napięcie zasilające silnik i prąd twornika,
e – siła elektromotoryczna indukowana w tworniku,
R T , L T – odpowiednio rezystancja i indukcyjność uzwojenia twornika,
ω , n – odpowiednio prędkość kątowa i prędkość obrotowa silnika,
M, M m – odpowiednio moment elektromagnetyczny i moment obciążenia silnika,
J – moment bezwładności silnika .
Stałe k e oraz k m wyznacza się z danych znamionowych silnika (zależność 4.4): U
− R I
30
N
T N
k =
k
= k
,
(4.4)
e
m
e
n N
π
Wprowadzając w równaniach silnika elektromagnetyczną stałą czasową
L
JR
(
T
T =
) oraz elektromechaniczną stałą czasową (
T
T =
) uzyskuje się
e
m
R
2
T
km
następującą postać operatorową równań opisujących silnik obcowzbudny:
Wpływ parametrów układu regulacji na pracę napędu prądu stałego
3
1
R
I ( s)
T
=
( U ( s) − E( s))
T
T
,
(4.5)
1 + sT e
E( s) = k n( s) M ( s) = k I ( s) M ( s) = k I ( s) ,
(4.6)
e
m T
m
m m
R T
k
n( s)
e
=
( I ( s) − I ( s))
T
M
,
(4.7)
sT m
Z równań (4.5-4.7) wynika, że obwód elektryczny w silniku można traktować jako
układ inercyjny I rzędu w której oprócz wymuszenia występuje wolnozmienne
zakłócenie (siła elektromotoryczna E). Część mechaniczną traktuje się natomiast jako układ całkujący, w którym moment (prąd twornika) jest wymuszeniem, natomiast
moment obciążenia (prąd I m) jest zakłóceniem, które może zmieniać się dowolnie.
Model funkcjonalny silnika zbudowany w programie MATLAB-SIMULINK
w oparciu o powyższe zależności przedstawia rys. 4.1.a.. Na rys. 4.1.b. przedstawiono
model
silnika
obcowzbudnego
dostępny
w
bibliotece
SimPowerSystem,
odpowiadający układowi elektrycznemu.
a) b)
Rys. 4.1 Modele symulacyjne silnika obcowzbudnego prądu stałego : a) model bazujący na opisie matematycznym, b) model „elektryczny”
2.2. Modele przekształtników energoelektronicznych
Przekształtnikami energoelektronicznymi, które są wykorzystywane w układach
napędowych z silnikiem prądu stałego, są prostowniki tyrystorowe oraz przekształtniki
tranzystorowe. W zależności od potrzeb modeluje się je w różny sposób.
Najprostszym rozwiązaniem jest zastosowanie inercji I rzędu o wzmocnieniu k PE
i stałej czasowej T PE. Wzmocnienie k PE zależy od przyjętego w układzie sygnału wejściowego. Dla przekształtnika tranzystorowego oraz prostownika ze sterowaniem
opartym na funkcji arcus cosinus jest ono zawsze stałe. Dla prostownika
tyrystorowego ze sterowaniem opartym na generacji przebiegu piłokształtnego
wzmocnienie to jest zmienne i przyjmuje się jego średnią wartość.
Przekształtniki energoelektroniczne charakteryzują się działaniem nieciągłym
o zmiennym opóźnieniu. W prostowniku tyrystorowym zmienne opóźnienie związane
jest z brakiem możliwości reakcji na zmianę wartości zadanej kąta opóźnienia
załączenia aż do chwili generacji sygnału wyzwalającego kolejny tyrystor.
Przyjmuje się, że średnie opóźnienie T PE jest równe połowie czasu pomiędzy chwilami wyzwalania kolejnych tyrystorów (dla prostownika trójfazowego mostkowego
T PE = 1,67 ms). W przekształtniku tranzystorowym zmienne opóźnienie związane jest
z realizacją zmiany wypełnienia w układzie licznikowym generującym sygnały
sterujące tranzystorami. Stała czasowa T PE jest równa w tym przypadku połowie okresu pracy tranzystorów ( T PE = T I/2).
Pełniejsze odwzorowanie działania przekształtników energoelektronicznych
polega na uwzględnieniu przełączenia zaworów w modelu funkcjonalnym.
Model prostownika można zbudować jako generator przebiegów będących
fragmentami przebiegów sinusoidalnych o określonej amplitudzie, zależnych
od zadanego kąta opóźnienia załączenia tyrystora (problemem staje się
tu uwzględnienie prądów nieciągłych). Prądy tyrystorów oraz prąd wejściowy należy
modelować jako iloczyny prądu wyjściowego oraz funkcji stanu zaworów (zależnych
od napięć wejściowych i kąta opóźnienia załączenia).
Model przekształtnika tranzystorowego (przy sterowaniu symetrycznym
i przy założeniu stałej wartości napięcia obwodu pośredniczącego) można
zamodelować w oparciu o następujące zależności:
u ( t) = U
(2 S
( t) − )
1 ,
(4.8)
T
DC
T1,T4
i
( t) = i ( t) S
( t)
i
( t) = i ( t) 1
( − S
( t)) ,
(4.9)
T1,T4
T
T1,T4
T2,T3
T
T1,T4
i
( t) = i ( t)(2 S
( t) − )
1 ,
(4.10)
DC
T
T1,T4
gdzie:
S T1,T4 – funkcja stanu tranzystorów T1 i T4 (0 - tranzystory wyłączone,
1 - tranzystory załączone), przy sterowaniu symetrycznym funkcja stanu
tranzystorów T2 i T3 jest dopełnieniem S T1,T4,
Wpływ parametrów układu regulacji na pracę napędu prądu stałego
5
U DC, i DC – odpowiednio napięcie i prąd obwodu pośredniczącego napięcia stałego, i T1,T4, i T2,T3 – prądy odpowiednich tranzystorów w przekształtniku.
Zastosowanie modeli funkcjonalnych przekształtników wymaga odpowiedniego
przygotowania plików symulacyjnych (większy nakład pracy), ale umożliwia
stosunkowo dokładne modelowanie pracy przekształtnika, przy zachowaniu krótkich
czasów symulacji.
Najbliższe rzeczywistości modele przekształtników (uwzględniające specyfikę
zaworów, ich dynamikę oraz układy odciążające) dostępne są w bibliotece
SimPowerSystem. Wykorzystanie ich jest proste i intuicyjne, należy jednak
nadmienić, że wprowadzenie takich modeli powoduje potrzebę zastosowania
zmiennokrokowych metod rozwiązywania równań różniczkowych sztywnych
oraz znacząco wydłuża czas symulacji.
2.3. Modelowanie układu sterowania napędu
Modelowanie elementów układu sterowania zależy od sposobu realizacji
tego układu. W przypadku modelowania układu analogowego należy korzystać
z elementów ciągłych, natomiast przy modelowaniu układu mikroprocesorowego
elementów dyskretnych. Ciągły model regulatora PI (opisanego zależnością 4.11)
przestawiono na rys. 4.2.a. Przy realizacji dyskretnej regulatora korzysta się
z dyskretnego układu całkującego. W rzeczywistych układach przekształcających
energię
występują
ograniczenia
związane
z
parametrami
znamionowymi
zastosowanych przy ich budowie elementów (np. ograniczony prąd lub napięcie
wyjściowe z przekształtnika DC/DC). Z tego względu sygnał wyjściowy z integratora
oraz całkowity sygnał wyjściowy (rys. 4.2.a.) są ograniczone.
a) b) Rys. 4.2 Model regulatora PI(a) oraz wyjścia z modulacją szerokości impulsów PWM(b)
Rys. 4.2.b przedstawia model wyjścia z modulacją szerokości impulsów (PWM –
pulse width modulation) występującego w mikrokontrolerach. Napięcie zadane
zapamiętywane jest w ekstrapolatorze zerowego rzędu (układ próbkujaco-pamiętający)
działającym z częstotliwością równą częstotliwości przełączeń. Zadana wartość
napięcia jest realizowana poprzez odpowiednie wypełnienie, które wyznaczane jest
przez podzielenie napięcia zadanego przez wartość napięcia obwodu pośredniczącego.
Układ licznikowy (Timer) generuje przebieg piłokształtny o zakresie zmian (-1;1)
i częstotliwości równej częstotliwości przełączeń tranzystorów. Na wyjściu układu
porównującego pojawia się sygnał sterujący zaworem energoelektronicznym.
Opisane powyżej wyjście z modulacją szerokości impulsów wykorzystywane jest
do sterowania zaworami pełnosterowalnymi np. w przekształtnikach DC/DC.
W przypadku modelowania układu sterowania napędu z prostownikiem tyrystorowym
należy zamodelować funkcję określająca kąt opóźnienia załączenia na podstawie
napięcia zadanego, układ synchronizacji oraz układ wyzwalania tyrystorów.
W układach sterowania występują jeszcze dodatkowo sprzężenia od wybranych
wielkości modelowane najczęściej jako stałe wzmocnienia lub inercje I rzędu.
W przypadku modelowania mikroprocesorowej realizacji układu sterowania,
należy na wejściach pomiarowych zastosować układy próbkujaco-pamiętające
(element Zero-order Hold), wykorzystać całkowanie dyskretne oraz na wyjściach (celem zamodelowania opóźnień związanych z procesem obliczeniowym) zastosować
elementy opóźniające (element Unit Delay). Dodatkowo możliwe jest modelowanie szumu pomiarowego w przetwornikach poprzez zastosowanie na wejściach
pomiarowych dodatkowych źródeł przebiegów losowych.
2.4. Dobór nastaw regulatorów w układzie sterowania
Typową strukturę układu regulacji silnika prądu stałego (tzw. szeregową
lub kaskadową) przedstawia rys. 4.3.a. W strukturze tej silnik obcowzbudny jest
zasilany z przekształtnika energoelektronicznego (tu: prostownika tyrystorowego).
Napięcie zadane dla przekształtnika energoelektronicznego ( U S) jest sygnałem wyjściowym z wewnętrznego regulatora prądu silnika Reg. I. Prąd zadany I Z
wyznaczany jest natomiast w zewnętrznym regulatorze prędkości Reg. n.
Filtr wejściowy F ogranicza szybkość zmian prędkości zadawanej z zadajnika.
W układach sterowania z silnikiem obcowzbudnym prądu stałego najczęściej
korzysta się z regulatorów PI o transmitancji:
1 + sT
K ( s) = k ⋅ (
R ) ,
(4.11)
PI
R
sT R
gdzie:







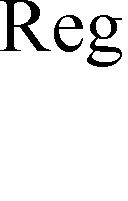



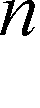











































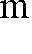

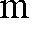
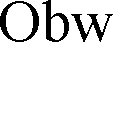

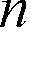












Wpływ parametrów układu regulacji na pracę napędu prądu stałego
7
k R – wzmocnienie proporcjonalne regulatora,
T R – czas zdwojenia regulatora.
a)
b)
1 k m
1
1+ sT
1
Rn
+ sT
k
1 R
R
k
RI
PE
T
T
e
k
k
Rn
RI
1+ sT
sT
sT
1
F
Rn
RI
+ sT
1+ sT
sT
PE
e
m
k e
Rys. 4.3 Struktura kaskadowa układu sterowania napędu prądu stałego (a) oraz odpowiadający jej schemat blokowy (b)
Dobór nastaw regulatorów można przeprowadzić miedzy innymi na podstawie
kryterium optimum modułowego oraz kryterium optimum symetrycznego
opracowanych przez Kesslera. Kryterium optimum modułowego stosuje się
w układach, gdzie szybkie tłumienie zakłóceń nie jest najważniejsze, natomiast ważna
jest szybka reakcja na wielkość zadaną. Kryterium optimum symetrycznego stosuje się
dla obiektów całkujących, gdzie najważniejsza jest szybka reakcja na zakłócenia.
Kryterium optimum modułowego (dobór nastaw regulatora prądu)
Przy doborze nastaw regulatora prądu zakłada się, że zmiany prędkości następują
dużo wolniej niż elektromagnetyczna stała czasowa silnika. Dzięki temu można
pominąć wpływ zakłócenia, jakim jest w pętli regulacji prądu siła elektromotoryczna
(rys. 4.3 b). Korzystając z zależności (4.5) i przyjmując, że przekształtnik opisany jest
inercją I rzędu, transmitancję układu otwartego pętli regulacji prądu opisuje zależność:
1
R
k
T
PE
K
( s) =
⋅
,
(4.12)
OI
1 + sT 1+ sT
e
PE
Transmitancja ta jest iloczynem inercji I rzędu z dużą i małą stałą czasową.
Dla takiego obiektu, zgodnie z kryterium optimum modułowego, nastawy regulatorów
dobiera się z zależności:
T
e
k
=
T = T
R
R
e ,
(4.13)
1
2 T k
PE PE R T
Zamknięta pętla regulacji przyjmuje wtedy postać:
1
K ( s) =
,
(4.14)
Z
2
2
1+ s 2 T
+ s 2 T
PE
PE
Zastosowanie kryterium optimum modułowego zapewnia współczynnik tłumienia
w transmitancji (4.14) wynoszący 0,707, co powoduje, że w odpowiedzi układu na
sygnał zadany występuje przeregulowanie 4,3%. Przy dalszej syntezie układu regulacji
pomija się człon związany z drugą potęgą zmiennej s.
Kryterium optimum symetrycznego (dobór nastaw regulatora prędkości)
Przy doborze nastaw regulatora prędkości otwarta pętla układu regulacji składa się
z układu całkującego i inercji I rzędu (uproszczonej transmitancji z zależności 4.14), odpowiadającej
pętli
zamkniętej
regulacji
prądu.
Korzystając
z
(4.7)
oraz uproszczonej zależności (4.14) otrzymuje się następującą transmitancjaę układu
otwartego pętli regulacji prędkości:
R T
k
1
e
K
( s) =
,
(4.15)
On
sT 1+ s 2 T
m
PE
Transmitancja ta jest iloczynem układu całkującego i inercji z małą stałą czasową.
Dla takiego obiektu, zgodnie z kryterium optimum symetrycznego, nastawy
regulatorów dobiera się z zależności:
T
m
k
=
T = 8 T
R
R
PE ,
(4.16)
R T
4 T PE k e
Wpływ parametrów układu regulacji na pracę napędu prądu stałego
9
Zamknięta pętla regulacji zapewnia przy takich nastawach szybkie tłumienie
zakłócenia, jednak przy skokowej zmianie wielkości zadanej w prędkości następuje
przeregulowanie na poziomie 43 %, co jest spowodowane występowaniem członu
forsującego w liczniku transmitancji układu zamkniętego. W celu zniwelowania tego
członu na wejściu regulatora można zastosować dodatkowy filtr w postaci inercji
I rzędu o stałej czasowej równej czasowi zdwojenia regulatora.
2.5. Uwagi końcowe
Opisane powyżej metody doboru parametrów regulatorów nie uwzględniają
występujących w układach napędowych ograniczeń. Ograniczenia dla regulatora prądu
wynikają z minimalnej i maksymalnej wartości kąta opóźnienia w prostowniku
tyrystorowym lub z wartości napięcia obwodu pośredniczącego w przypadku
przekształtnika tranzystorowego. Ograniczenia dla regulatora prędkości dobiera się do
założonej przeciążalności w zastosowanym przekształtniku. Efektem występowania
ograniczeń jest to ,że regulatory mają ograniczony wpływ na dynamikę układu przy
reakcji na skokową zmianę wielkości zadanej, ponieważ przez większość czasu
trwania reakcji na zmianę wielkości zadanej układ pracuje na ograniczeniu. Działanie
regulatorów można natomiast zaobserwować przy reakcji na skokową zmianę
wielkości zakłócającej, gdzie najczęściej wpływ ograniczeń jest niewielki.
Ograniczenia mają dodatkowo znaczenie w układach z przekształtnikami
charakteryzujących się dużą szybkością, gdzie mogą pojawić się oscylacje.
W przypadku mikroprocesorowych realizacji układów sterowania należy również
uwzględnić niedokładności przetworników analogowo-cyfrowych, których szumy
mogą pobudzać oscylacje w układzie regulacji, przy zbyt dużych wzmocnieniach.
Opóźnienia w mikroprocesorowym układzie sterowania powinny być również
uwzględnione w procesie projektowania układu regulacji.
Podsumowując
należy
zaznaczyć,
że
nastawy
regulatorów
otrzymane
na podstawie optimum symetrii i optimum modułu powinny być traktowane jako
bazowe i powinny one zostać dostrojone do konkretnej realizacji układu sterowania.
3. STANOWISKO LABORATORYJNE
Stanowisko jest wyposażone w komputer PC wraz z oprogramowaniem
MATLAB-SIMULINK i plikami obliczeniowymi pozwalającymi na przeprowadzenie
symulacji dla różnych modeli układu napędowego z silnikiem i przekształtnikiem
energoelektronicznym. W ramach ćwiczenia symulowany jest rozruch silnika, reakcja
na skokową zmianę momentu obciążenia oraz rewersja prędkości. Dla każdej
z kolejnych symulacji rejestrować ich czas trwania.
4. PRZEBIEG ĆWICZENIA
1. Wyznaczyć nastawy regulatorów prądu i prędkości dla silnika prądu stałego o
zadanych parametrach. Przeprowadzić symulacje dla napędu bez uwzględniania
ograniczeń i modelu prostownika tyrystorowego w postaci transmitancji I rzędu.
2. Przeprowadzić symulacje dla modelu prostownika tyrystorowego w postaci inercji
I rzędu oraz przy uwzględnieniu ograniczeń. W razie konieczności dla układu z
ograniczeniami dokonać korekty nastaw regulatorów.
3. Przeprowadzić analizę wpływu wartości wzmocnienia i czasu zdwojenia
w regulatorze prądu i prędkości na pracę napędu.
4. Przeprowadzić badania symulacyjne takie jak w punktach 1 - 3 dla przekształtnika
tranzystorowego zamodelowanego w postaci inercji I rzędu.
5. Przeprowadzić
symulacje
dla
modelu
funkcjonalnego
przekształtnika
tranzystorowego uwzględniającego przełączanie tranzystorów.
6. Przeprowadzić
symulacje
dla
modelu
funkcjonalnego
przekształtnika
tranzystorowego z uwzględnieniem dyskretnej realizacji układu sterowania. W
razie konieczności dokonać korekty nastaw regulatorów.
7. Przeprowadzić symulacje dla modeli „elektrycznych” prostownika tyrystorowego
i przekształtnika tranzystorowego dostępnych w bibliotece SimPowerSystem.
W ramach sprawozdanie umieścić uzyskane w poszczególnych symulacjach
oscylogramy wraz z opisem kolejnych zmian. W postaci tabelarycznej zebrać czasy
trwania poszczególnych symulacji. Całość podsumować wnioskami.
5. LITERATURA
1. Tunia H., Kaźmierkowski M. P.: Automatyka napędu przekształtnikowego,
PWN, Warszawa 1987.
2. SimPowerSystemTM User’s Guide, Matlab & Simulink, dokumentacja
techniczna firmy The MathWorks, 2005
3. Simulink® User’s Guide, Matlab & Simulink, dokumentacja techniczna
firmy The MathWorks, 2005
Wyszukiwarka
Podobne podstrony:
Przemiennik? DC Wpływ parametrów układu regulacji na pracę napędu prądu stałego
Przemiennik AC-DC, Wpływ parametrów układu regulacji na pracę napędu prądu stałego - pytania
Wpływ układu autonomicznego na prace serca
Modelowanie napędu prądu stałego
Układ automatycznej regulacji prędkości obrotowej silnika prądu stałego
Sprawozdanie pomiary i regulacja napięcia oraz natężenia prądu stałego
Wpływ układu współczulnego i przywspółczulnego na pracę serca
Wpływ układu pomiarowego na efekty aktywnej regulacji drgań konstrukcji ramowych
Wpływ wolnych rodników na pracę serca
Wpływ rozwoju społeczeństwa informacyjnego na regulacje prawne, Zarządzanie i inżynieria produkcji,
04 02 Polecenia na prace kwalifikacje uprawnienia
wpływ parametrów reologicznych na dostępność ketoprofenu
Wir├│wki1 , Zanieczyszczenia paliw i olejów smarowych i ich wpływ na pracę silników
Obróbka skrawaniem, wplyw parametrow skrawania na temperature skrawania, POLITECHNIKA ŚWIĘTOKRZYSKA
5 WPŁYW PARAMETRÓW TECHNOLOGICZNYCH NA WŁAŚCIWOŚCI WYPRASEK WTRYSKOWYCH, Studia, Przetwórstwo Tworzy
Ćw 6 Wpływ kompensacji równoległej na pracę linii elektroenergetycznych WN i NN
1 Wpływ mechaniki ruchu pojazdów na parametry projektowo - e, pdu
DERMATOLOGIA Szkodliwy wpływ nikotyny i promieni UV na organizm człowieka, PRACE PISEMNE na studia,
więcej podobnych podstron