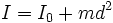Rzeszów, dn. 13.11.12r.

Sprawdzanie twierdzenia Steinera za pomocą wahadła fizycznego.

Ćwiczenie nr 18.

Laboratorium – Fizyka

Arkadiusz Bednarz

79326 (1imd)

L1 grupa: 1

str. 1

Spis treści:

1. Zarys teoretyczny

2. Cel

e i

l p

i rze

rz b

e ie

b g

ie ć

w

ć icz

ic e

z n

e ia

3. Obliczenia i ze

z s

e ta

s w

ta ien

ie ie

ie w

ynik

i ów

4. Wnioski

1. Zarys teoretyczny

Twierdzenie Steinera – twie

i r

e dze

dz n

e ie

i mechaniki oraz

a

z wytr

t zymał

a ośc

ł

i

ośc

i mat

a e

t r

e ia

i ł

a ó

ł w opisu

opi ją

j c

ą e

c

e sposób

znajdowania momentu bez

be wła

ł dności

ośc dan

da ej

e

j brył

y y

y wzg

z lę

l de

ę

m dan

da ej

e

j osi

osi przy

z

y dan

da ym momencie

i

e bez

be wła

wł dn

a

ości

i

względem osi równole

ol g

e łe

ł j

e

j i

i prze

z c

e h

c odzą

odz c

ą e

c j

e

j pr

p ze

z z

e środek masy bryły. Jego autorem jest Ja J k

a ob St

S e

t i

e n

i er

e .

Mówi, że moment

e

nt bezwł

be

adnośc

zwł

i

adnośc

i brył

bry y

ł

y szty

szt wnej

wne

j wzglę

wzgl de

ę

m

de dowolne

dowol

j

ne

j osi

osi je

j st

e

st równy

równy sumie

i

e moment

e u

nt bezwł

be

adnośc

zwł

i

adnośc

i

wzglę

wzgl de

ę

m

de osi

osi równole

równol gł

e e

gł j

e

j do danej

dane

j i

i przec

prze hodząc

c

e

hodząc j

e

j prze

z

prze środek

ode

k masy

y brył

bry y

ł

y oraz il

i oc

l

zy

oc nu

zy

nu masy

asy brył

bry y

ł

y i

i kwadrat

k

u

wadrat

odle

odl gł

e ośc

gł

i

ośc

i mię

i dzy

ę

dzy ty

t m

y i

i dwie

dwi m

e a osiam

osi

i, co można wyrazić wzorem

gdzie:

– momen

e t

t bez

be wła

ł d

a ności

ośc

i względe

ę

m

de osi

i prze

z c

e h

c odzą

odz c

ą e

c j

e

j pr

ze

z z

e środek masy,

– momen

e t

t bez

be wła

ł d

a ności

ośc

i względe

ę

m

de osi

i równole

ol g

e łe

ł j

e

j do pie

pi r

e w

r sze

z j

e

j osi,

osi

– odle

odl g

e łość

ł

ość mię

i dz

ę

y

y osia

osi mi,

i

– masa bryły.

Momen

e t

t bez

be wła

ł d

a ności

ośc

i osią

osi ga

a minimal

a n

l ą

ą war

a tość

t

,

ość gdy

y oś prze

z c

e h

c odzi

odz

i prze

z z

e

z środek

ode mas

a y.

2. Cel

Ce

l i

i pr

p zeb

e i

b e

i g

e ćwic

i z

c en

e i

n a

i

Ce

C l: W

y

W zna

zn czyć dw

d oma sp

s o

p s

o o

s b

o a

b mi moment

n be

b zwładn

d o

n ś

o c

ś i I0 br

b y

r ły (t

( a

t rc

r zy)

) względe

d m os

o i

s pr

p o

r s

o t

s op

o a

p dł

d e

ł j

e

do

d

o pł

p as

a zc

s zyzny tarc

r zy pr

p ze

r cho

h d

o zą

d cej

e

j pr

p ze

r z j

z ej

e

j śr

ś o

r d

o e

d k masy. Por

Po ó

r w

ó na

n ć ot

o rzy

r

mane

n wyni

n ki.

Przebieg:

a) Zmierz

r yć śr

ś e

r dn

d i

n cę

ę tar

a c

r zy D pr

p zy

r

po

p moc

o y su

s w

u miark

r i (U

( WA

W GA: w kol

o ej

e ny

n ch

h po

p m

o iara

r ch

h

na

n leży br

b a

r ć po

p d

o

d uw

u agę ró

r ż

ó n

ż e

n pu

p n

u k

n ty ob

o wodu tarczy).

b) Zmierzyć odległości ri po

p m

o iędzy

d

śr

ś o

r d

o k

d iem tarc

r zy, a dzi

d ewięc

ę iom

o a os

o i

s ami ob

o r

b o

r t

o u. W

W tym celu

u

na

n leży w ot

o wor

o ze

r śr

ś o

r d

o k

d ow

o ym i w ot

o wor

o ze

r od

o p

d o

p w

o ia

i da

d j

a ą

j cym da

d ne

n j

e os

o i

s ob

o r

b o

r t

o u

u um

u ieś

e c

ś ić

ć pr

p ę

r ciki

o

o j

edn

d a

n kow

o ej

e gru

r b

u o

b ś

o c

ś i i

zmierzy

r

ć su

s w

u miark

r ą od

o l

d egłoś

o ć

ś

ć po

p m

o iędzy

d

pr

p ę

r cikami. Wy

W ni

n ki po

p m

o iaru

r

u

na

n leży zwiększ

s yć (z

( mni

n ejs

j zy

s

ć)

) o

o gru

r b

u o

b ś

o ć

ś pr

p ę

r ci

c ka.

c) Dla każde

żd j

e z dzi

d ewięci

c u

u os

o i

s

i ob

o r

b o

r t

o u

u wyzna

zn czyć czas

s ti du

d że

u j l

ic

i zby

zb (n

( =

n 50

5 )

0

) ok

o re

r s

e ó

s w

ó

w waha

h ń.

ń

Dzieląc t

en

n c

zas

s pr

p ze

r z lic

i zbę

zb waha

h ń

ń zna

zn l

a eźć ok

o re

r sy

s dr

d g

r ań

ń Ti dl

d a

l po

p s

o zc

s zegól

ó ny

n ch

h os

o i

s .

d) Wyniki po

p m

o iaró

r w

ó um

u ieśc

ś ić

i

ć w tabe

b l

e kach.

h

str. 2

3. Obliczenia i zestawienie wyników a) Tabele pomiarowe

Pomiar

∅ ݌ݎęݐܽ 1

∅ ݌ݎęݐܽ 2

∅1 ሾ݉݉ሿ ± 0,05 [݉݉]

∅1 ሾ݉݉ሿ ± 0,05 [݉݉]

1

2,35

2,50

2

2,40

2,50

3

2,45

2,45

4

2,40

2,40

5

2,45

2,40

6

2,45

2,45

Średnia wartość

2,416667

2,45

Tabela 1: Zestawienie wyników pomiarów średnic prętów Nr osi

ݎ௜[݉݉]

ݐ௜[ݏ]

ܶ௜[ݏ]

±0,05 [݉݉]

±0,01 [ݏ]

±0,01 [ݏ]

1

9,77

70,01

1,40

2

19,57

51,28

1,03

3

29,42

44,12

0,88

4

39,27

40,44

0,81

5

48,67

38,56

0,77

6

58,62

37,96

0,76

7

68,37

37,61

0,75

8

78,32

37,43

0,75

9

88,02

37,12

0,74

Tabela 2: Zestawienie wyników pomiarów głównych Wartości średnie zostały wyznaczone przy pomocy średniej arytmetycznej.

ݎ௜[݉݉] - promień przesunięcia środka ciężkości ݐ௜[ݏ] - czas pomiaru 50 wahnięć

ܶ ሾݏሿ

௜

= ݐ௜/݊ – okres wahnięcia

n = 50 – liczba wahnięć

Wielkość ݎ௜[݉݉] została wyznaczona poprzez odjęcie od zmierzonego r, połówek średnic obu prętów użytych podczas pomiaru tej wielkości (zawartych w tabeli nr 1).

Pomiar

Średnica płyty

Grubość płyty

ܦ = 2ܴ [݉݉] ± 0,05[݉݉]

ℎ [݉݉] ± 0,05[݉݉]

1

196,05

10,00

2

195,75

10,15

3

195,85

10,10

4

195,95

10,20

5

195,95

10,15

6

196,00

10,05

7

195,80

10,05

8

196,05

10,00

9

195,85

10,10

10

195,90

10,05

Średnia wartość

195,915

10,085

Tabela 3: Zestawienie wyników pomiarów płyty str. 3

b) Obliczenie masy płyty i błędu pomiarowego ߩ

௞௚

= 7,8 ∗ 10ଷ [

] – gęstość materiału

௠య

ߩ = ݉/ܸ - wzór na gęstość, który po przekształceniu da nam wzór na masę.

݉ = ߩ ∗ ܸ [݇݃] - masa

ܸ

஽మ

= ߨ ∗

∗ ℎ [݉ଷ] - wzór na objętość

ସ

ܦଶ

݉

(195,915 ∗ 10ିଷ)ଶ

= ߩ ∗ ߨ ∗

∗ ℎ = 7,8 ∗ 10ଷ ∗ 3,14 ∗ 10,085 ∗ 10ିଷ ∗

= 2,3701 [݇݃]

4

4

Rachunek błędu wykonam metodą pochodnej logarytmicznej

∆ܦ – błąd pomiaru średnicy płyty (wartość zawarta w tabeli nr 3)

∆ℎ - błąd pomiaru grubości płyty (wartość zawarta w tabeli nr 3)

∆ܦ

∆ℎ

0,05

0,05

∆݉ = ݉ ∗ ൬2 ∗ ܦ + ൰ = 2,3701 ∗ ൬2 ∗

+

൰ = 0,0129 [݇݃]

ℎ

195,915

10,085

c) Moment bezładności płyty względem środka ciężkości i błąd pomiarowy ܦଶ

ܫ

1

(195,915 ∗ 10ିଷ)ଶ

଴ =

∗ ݉ ∗

= 0,5 ∗ 2,3701 ∗

= 11,372 ∗ 10ିଷ [݇݃ ∗ ݉ଶ]

2

4

4

Rachunek błędu wykonam metoda pochodnej logarytmicznej

∆ܦ

∆݉

0,05

0,0129

∆ܫ

൰

଴ = ܫ଴ ∗ ൬2 ∗ ܦ + ݉ ൰ = 11,372 ∗ 10ିଷ ∗ ൬2 ∗

+

195,915

2,3701

= 0,06799 ∗ 10ିଷ ሾ݇݃ ∗ ݉ଶሿ

d) Moment bezładności dla kolejnych przesuniętych osi i rachunek błędów

ܶ

ܫ

௜ ∗ ݉ ∗ ݃ ∗ ݎ௜

ଶ

௜ =

− ݉ ∗ ݎ

4 ∗ ߨଶ

௜

Dokonam teraz obliczeń przykładowych dla 1 osi (osie zapisane są w tabeli nr 2).

Pozostałe zostały obliczone tą samą metodą.

ܶ

ܫ

ଵ ∗ ݉ ∗ ݃ ∗ ݎଵ

1,4 ∗ 2,3701 ∗ 9,81 ∗ 9,77 ∗ 10ିଷ

ଶ

ଵ =

− ݉ ∗ ݎ =

− 2,3701 ∗ (9,77 ∗ 10ିଷ )ଶ

4 ∗ ߨଶ

ଵ

4 ∗ 3,14ଶ

0,31796

=

− 0,00022 = 0,00806 − 0,00022 = 0,00784[݇݃ ∗ ݉ଶ]

39,4384

Rachunek błędu wykonam metodą różniczki zupełnej ܫ

௜ = ݂(ܶ௜, ݉, ݎ௜)

str. 4

݉ ∗ ݃ ∗ ݎ

ܶ

ܶ

ଵ

ଵ ∗ ݃ ∗ ݎଵ

ଵ ∗ ݉ ∗ ݃

∆ܫ

ቚ

ଶฬ

ฬ

ଵ = ቚ

∗ ∆ܶ

− ݎ

∗ ∆݉ + ฬ

− ݉ ∗ 2 ∗ ݎ ∗ ∆ݎ

4 ∗ ߨଶ

ଵ + ฬ

4 ∗ ߨଶ

ଵ

4 ∗ ߨଶ

ଵ

ଵ

= ቤ2,3701 ∗ 9,81 ∗ ሺ9,77 ∗ 10ିଷ ሻቤ ∗ 0,01

4 ∗ ߨଶ

+ ቤ1,4 ∗ 9,81 ∗ ሺ9,77 ∗ 10ିଷ ሻ − ሺ9,77 ∗ 10ିଷ ሻଶቤ ∗ 0,0129

4 ∗ ߨଶ

+ ฬ1,4 ∗ 2,3701 ∗ 9,81 − 2,3701 ∗ 2 ∗ ሺ9,77 ∗ 10ିଷ ሻฬ ∗ 0,05 ∗ 10ିଷ

4 ∗ ߨଶ

= 8,0623 ∗ 10ିହ + 4,2851 ∗ 10ିହ + 4011,7 ∗ 10ିହ = 0,04024ሾ݇݃ ∗ ݉ଶሿ

A oto tabelaryczne zestawienie wszystkich wyników Nr osi

ܫ

௜

∆ܫ௜(ܶ௜)

∆ܫ௜(݉)

∆ܫ௜(ݎ௜)

∆ܫ௜

1

0,00784

0,00784

0,00784

0,00784

0,040241

2

0,01092

0,01092

0,01092

0,01092

0,028092

3

0,01325

0,01325

0,01325

0,01325

0,022751

4

0,01507

0,01507

0,01507

0,01507

0,019458

5

0,01651

0,01651

0,01651

0,01651

0,017277

6

0,01809

0,01809

0,01809

0,01809

0,015794

7

0,01924

0,01924

0,01924

0,01924

0,01448

8

0,02003

0,02003

0,02003

0,02003

0,013241

9

0,02016

0,02016

0,02016

0,02016

0,011949

Średnia

0,01568

0,02036

Tabela 4: Zestawienie pomiarów e) Zestawienie wyników

ܫ଴ = 0,01137

±

0,000068 ሾ݇݃ ∗ ݉ଶሿ

ܫଵ = 0,00784

±

0,040241 ሾ݇݃ ∗ ݉ଶሿ

ܫଶ = 0,01092

±

0,028092 ሾ݇݃ ∗ ݉ଶሿ

ܫଷ = 0,01325

±

0,022751 ሾ݇݃ ∗ ݉ଶሿ

ܫସ = 0,01507

±

0,019458 ሾ݇݃ ∗ ݉ଶሿ

ܫହ = 0,01651

±

0,017277 ሾ݇݃ ∗ ݉ଶሿ

ܫ଺ = 0,01809

±

0,015794 ሾ݇݃ ∗ ݉ଶሿ

ܫ଻ = 0,01924

±

0,01448

ሾ݇݃ ∗ ݉ଶሿ

ܫ଼ = 0,02003

±

0,013241 ሾ݇݃ ∗ ݉ଶሿ

ܫଽ = 0,02016

±

0,011949 ሾ݇݃ ∗ ݉ଶሿ

4. Wnioski

Możemy zaobserwować wzrost momentu bezładności wraz z odsunięciem osi, dla której mierzymy moment. Jednym z czynników wpływających na dokładność pomiarów i opartych na nich następnie obliczeniach była bezwładność oka ludzkiego, ponieważ bardzo trudno jest dokładnie określić moment amplitud drgań. Dodatkowo układ pomiarowy narażony był na drgania przenoszone na stół

przez podłoże. Wahadło należy odchylić o mały kat ߙ , aby równanie ruchu zachowało liniowość.

Błędy przy pomiarach czasu drgań spowodowane były głównie błędami przyrządu pomiarowego (stopera). Nie bez znaczenia pozostaje niedokładność odczytu suwmiarki przy pomiarze odległości d.

Istotny wpływ na wartości odchyleń miały zaokrąglenia wartości ߨ oraz stałej g.

str. 5