Blok 9: Moment bezwładności. Moment siły

Zasada zachowania momentu pędu

I.

Moment bezwładności

Omawiając ruch postępowy ciała, posługujemy się pojęciami przemieszczenia, szybkości, przyspieszenia tego ciała oraz wypadkowej siły na nie działającej. W opisie ruchu postępowego zwykle traktujemy ciała jako punkty materialne. Nawet, jeśli ciało ma duże rozmiary, wszystkie powyższe wielkości fizyczne wiążemy ze środkiem masy ciała, a samo ciało zastępujemy przez punkt materialny o masie równej masie badanego ciała.

W opisie ruchu obrotowego taka konstrukcja myślowa przestaje być uzasadniona, ponieważ w przypadku tego ruchu ma znaczenie nie tyle wartość masy ciała, ile rozkład masy w przestrzeni.

Dlatego musimy wziąć pod uwagę rozmiary i kształt badanego ciała, którego nie możemy już

traktować jak punktu materialnego, ale musimy je rozważać jako bryłę sztywną.

Miarą bezwładności ciała w ruchu postępowym jest masa ciała.

Miarą bezwładności ciała w ruchu obrotowym jest moment bezwładności.

Moment bezwładności I ciała względem osi O definiuje się, dzieląc bryłę sztywną na małe fragmenty o masach m : I = ∑

2

m r , gdzie r jest odległością fragmentu bryły o masie m od

i

i i

i

i

i

wybranej osi O, a sumowanie przebiega po wszystkich fragmentach. Można zdefiniować moment bezwładności bardziej dokładnie za pomocą całki: I = ∫ 2

r dm , gdzie całkowanie przebiega po

V

całej objętości V bryły sztywnej.

Moment bezwładności jest wielkością addytywną, tzn. moment bezwładności układu brył

sztywnych względem osi O jest sumą momentów bezwładności poszczególnych ciał tego układu względem osi O.

Moment bezwładności punktu materialnego względem osi przechodzącej przez ten punkt jest równy zero.

Oś wybierana do obliczania momentu bezwładności ciała jest najczęściej osią obrotu tego ciała.

Jeśli oś ta jest osią symetrii ciała, wyznaczenie momentu bezwładności bardzo często staje się proste. Momenty bezwładności, I podstawowych brył względem ich osi symetrii można znaleźć O

w tablicach matematycznych.

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

53

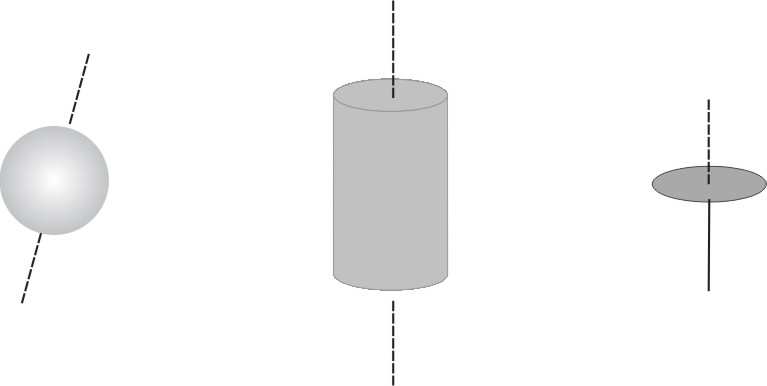
kula

pełny walec

pełny cienki krąż ek

2

2

I

= MR

1

2

I

= MR

1

2

I

= MR

O

5

O

2

O

2

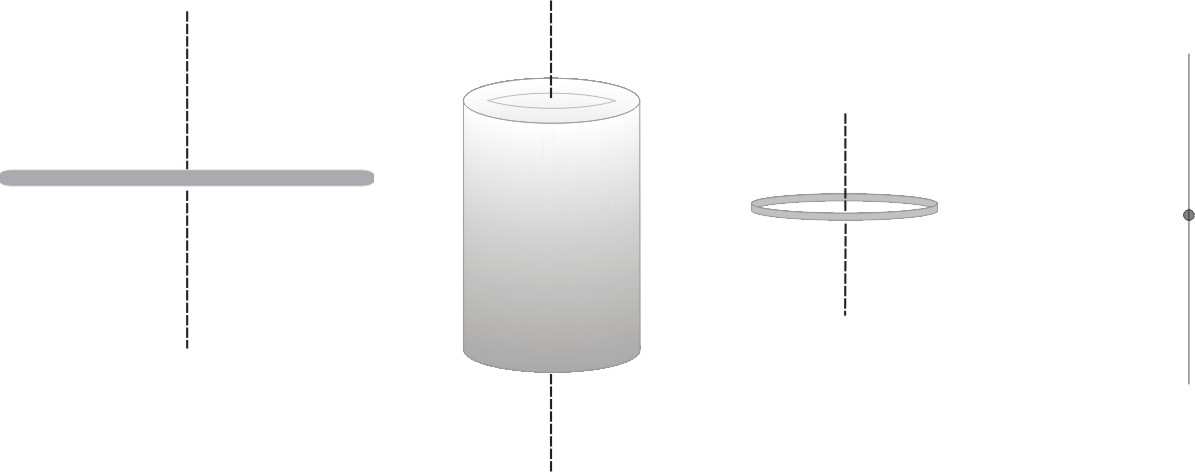
cienki prę t

cienkoś cienna rura

cienki pierś cień punkt materialny

1

2

I

= ML

2

I

= MR

2

I

= MR I = 0

O

12

O

O

O

Moment bezwładności bryły o masie M względem osi obrotu innej niż oś symetrii, można obliczyć z twierdzenia Steinera,

2

I

= I + Md

A

0

ale pod pewnymi warunkami: I to moment bezwładności bryły względem którejś z jej osi 0

symetrii, osie O i A są równoległe do siebie, a odległość między nimi wynosi d .

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

54

► Przykład 9.1: Cztery kulki, każda o masie m = 5 g , znajdują się w wierzchołkach kwadratu o boku a = 1 m . Oblicz moment bezwładności układu kulek względem osi zawierającej jeden z boków kwadratu oraz względem osi zawierającej przekątną kwadratu. Kulki traktujemy jak punkty materialne.

Moment bezwładności układu względem wybranej osi O jest równy sumie momentów bezwładności poszczególnych elementów tego układu względem tej osi.

Chcąc obliczyć moment bezwładności dowolnej bryły względem dowolnej osi A, korzystamy z twierdzenia Steinera:

2

I

= I + Md , gdzie M to masa bryły, I to moment bezwładności bryły A

0

0

względem którejś z jej osi symetrii (najczęściej znany z tablic), osie O i A są równoległe do siebie, a odległość między nimi wynosi d .

Moment bezwładności punktu materialnego względem osi przechodzącej przez ten punkt I = 0 .

0

Moment bezwładności układu kulek względem jednego z boków kwadratu: 2

2

2

2

I

= 4I + 2Ma = 0 + 2Ma = 2 ⋅ ,

0 005 kg ⋅ m

1

= ,

0 01 kg ⋅ m

A

0

Moment bezwładności układu kulek względem przekątnej D kwadratu (uwaga: D

d =

):

2

2

2

2

 2 a 

2

2

2

I

= 4I + 2Md = 0 + 2Md = 2M

 = Ma = 0,005 kg ⋅1m = 0 0

, 05 kg ⋅ m

A

0

2





► Przykład 9.2: Oblicz moment bezwładności cienkiego jednorodnego pręta o długości L i masie m, względem osi prostopadłej do niego i przechodzącej przez:

• punkt odległy od środka pręta o L/4

• punkt leżący na końcu pręta

Moment bezwładności cienkiego, jednorodnego pręta względem osi prostopadłej do niego i przechodzącej przez jego środek wynosi:

1

2

I =

ML , gdzie M to masa pręta, a L to jego

0

12

długość. Moment bezwładności względem innej równoległej osi obliczamy z tw. Steinera: 2

I

= I + Ma i w tym przypadku:

A

0

• a = L / 4 , stąd

1

2

L 2

7

2

I

= ML + M( ) = ML

A

12

4

48

• a = L / 2 , stąd

1

2

L 2

1

2

I

= ML + M( ) = ML

A

12

2

3

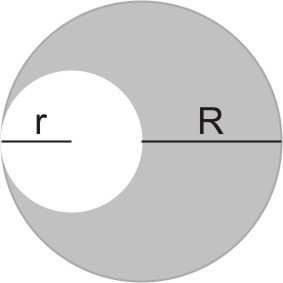
► Przykład 9.3: Z jednorodnej kuli o masie M i promieniu R wycięto kulę o promieniu

R

r =

, której środek znajdował się w odległości r od środka

2

dużej kuli. Ile wynosi moment bezwładności wydrążonej kuli względem osi przechodzącej przez punkt stanowiący środek masy pełnej dużej kuli i stycznej do wydrążenia?

Moment bezwładności pełnej kuli względem osi O to suma momentu

bezwładności względem osi O kuli wydrążonej i momentu bezwładności wydrążenia. Zatem: I

= I

− I

dziurawe

kuli

wydrazenia

2

2

I

= MR , a

2

2

2

2

7

2

7

I

= I + Ma = mr + mr = mr =

( ) =

MR , bo

wydrazenia

0

5

5

(M

5

8 ) R 2

7

2

kuli

5

2

160

m = M / 8 .

Zatem

2

2

7

2

64−7

2

57

2

I

= MR −

MR =

MR =

MR

dziurawe

5

160

160

160

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

55

II.

Moment siły

Moment siły M jest wielko

ścią wektorową zdefiniowaną względem osi obrotu, jako: M = r × F ,

gdzie r - ramię siły F .

Kierunek wektora M jest prostopadły do płaszczyzny wyznaczonej przez wektory r i F , a zwrot

M można określić z reguły dla iloczynu wektorowego.

Ramię siły F to wektor prostopadły do osi obrotu, którego początek leży na tej osi, a koniec

znajduje się w punkcie przyłożenia siły F . Moment siły jest zatem obliczany zawsze względem jakiejś osi.

Warto

ść momentu siły: M = r ⋅ F ⋅ sin

(

∠ r, )

F .

Moment siły jest przyczyną zmiany ruchu obrotowego bryły sztywnej o momencie bezwładności I , nadając jej przyspieszenie kątowe, ε :

M

ε =

I

Jest to tzw. II zasada dynamiki dla ruchu obrotowego bryły sztywnej.

Jeśli suma momentów wszystkich sił działających na ciało jest równa zeru, to ciało obraca się ze stałą szybkością kątową, ω

.

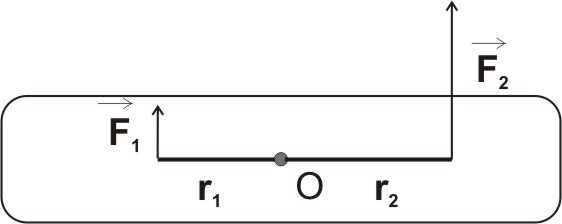
► Przykład 9.4: Stosunek wartości sił działających na F

1

bryłę sztywną wynosi 1 =

. Jaki warunek spełniają

F

3

2

długości ramion tych sił, jeżeli wiadomo, że bryła

obraca się ruchem jednostajnym wokół osi O

prostopadłej do płaszczyzny rysunku?

Jeżeli bryła obraca się ruchem obrotowym z jednostajną prędkością kątową, to z II zasady dynamiki dla ruchu obrotowego, wypadkowy moment sił działających na bryłę jest równy zeru:

M = 0 , czyli M +

M = 0 Moment siły F : M = r × F , gdzie r jest ramieniem siły, czyli 1

2

1

1

1

1

1

wektorem prostopadłym do osi obrotu, którego początek leży na tej osi , a koniec znajduje się w

punkcie przyło

żenia siły F . Podobnie obliczamy moment siły F : M = r × F . Ponieważ

1

2

2

2

2

wektory M i M są do siebie równoległe i mają przeciwne zwroty, to równanie wektorowe na 1

2

sumę momentów sił można przedstawić w postaci algebraicznej (wybieram oś OX prostopadłą do płaszczyzny rysunku i np. zwróconą za tę płaszczyznę.):

r

F

1

M −

M = 0 ⇒ r F sin (

∠ r , F ) = r F sin (

∠ r , F ) ⇒ r F = r F

2

1

⇒

=

= . Czyli

1

2

1 1

1

1

2

2

2

2

1 1

2

2

r

F

3

1

2

długość r ramienia siły F jest trzykrotnie mniejsza od długości r ramienia siły F .

2

2

1

1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

56

III.

Moment pędu. Zasada zachowania momentu pędu

Moment pędu L jest wielkością wektorową zdefiniowaną względem punktu, jako:

L = r × p , gdzie

r - ramię pędu p .

Kierunek wektora L jest prostopadły do płaszczyzny wyznaczonej przez wektory r i p , a zwrot

L można określić z reguły dla iloczynu wektorowego.

Warto

ść momentu pędu: L = r ⋅ p ⋅ sin ∠(r, p) .

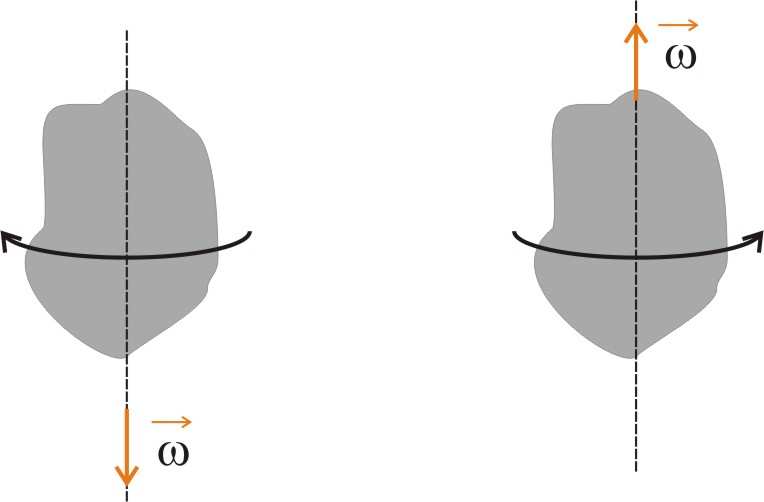
Cz

ęściej stosowana jest druga definicja momentu pędu: L = I ⋅ ω , gdzie ω

jest wektorem

prędkości kątowej bryły, o kierunku pokrywającym się osią obrotu i zwrocie określonym zgodnie z regułą śruby prawoskrętnej.

Moment pędu można powiązać z momentem siły poprzez tzw. uogólnioną postać II zasady dynamiki dla ruchu obrotowego bryły sztywnej:

∆

L = M ⋅ ∆t

Zasada zachowania momentu pędu.

Jeżeli wypadkowy moment sił działających na bryłę sztywną jest równy zeru, to moment pędu bryły

nie ulega zmianie: M =

0 ⇒ L

∆ = 0

IV.

Energia kinetyczna ruchu obrotowego. Zasada zachowania energii mechanicznej

Ciało poruszając się ruchem obrotowym posiada energię kinetyczną ruchu obrotowego: I 2

ω

E

=

K

2

Całkowita energia mechaniczna bryły sztywnej w ruchu obrotowym nie ulega zmianie wtedy i tylko wtedy, gdy wypadkowa sił niezachowawczych działających na ciało jest równa zeru i moment sił

zewnętrznych działających na ciało jest równy zeru.

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

57

► Przykład 9.5: Dwa krążki obracają się niezależnie w przeciwne strony z prędkościami kątowymi o wartościach: ω i ω na jednej osi przechodzącej przez ich środki i prostopadłej do ich powierzchni.

1

2

W pewnej chwili krążek górny spada na krążek dolny i krążki te „zlepiają się”. Oblicz prędkość kątową złączonych krążków, jeżeli masa górnego krążka wynosi m , a jego promień r , natomiast masa 1

1

dolnego krążka wynosi m , a jego promień r . Oblicz zmianę energii kinetycznej układu i wyjaśnij, 2

2

dlaczego jest ona różna od zera (tzn. dlaczego nie obowiązuje zasada zachowania energii).

Zderzenie idealnie niesprężyste. Obowiązuje zasada zachowania momentu pędu, ale nie obowiązuje zasada zachowania energii mechanicznej:

L = L , czyli I ⋅ ω − I ⋅ ω = (I + I ) ⋅ ω . Podstawiamy dane z zadania: p

k

1

1

2

2

1

2

k

2

2

m r ⋅ ω − m r ⋅ ω

1

2

1

2

1

2

1

2

m r ⋅ ω − m r ⋅ ω = ( m r + m r ) ⋅ ω , stąd

1 1

1

2 2

2

ω =

.

2

1 1

1

2

2 2

2

2

1 1

2

2 2

k

k

2

2

m r + m r

1 1

2 2

Zmiana energii kinetycznej:

(I + I )

2

⋅ ω

I

2

ω

I

2

ω

(I + I ) (I ⋅ ω − I ⋅ ω )2

I

2

ω

I

2

ω

E

1

2

k

1

1

2

2

1

2

1

1

2

2

1

1

2

2

∆

=

−

−

=

⋅

−

−

.

k

2

2

2

2

(I + I )2

2

2

1

2

Po skróceniu pierwszego iloczynu ułamków oraz sprowadzeniu wszystkich trzech składników do wspólnego mianownika, otrzymujemy:

− I⋅ ⋅ I ⋅ (ω + ω )2

∆E

1

2

1

2

=

. Zmiana energii układu jest ujemna tak, jak tego się

k

2(I + I )

1

2

spodziewaliśmy.

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu

operacyjnego KAPITAŁ LUDZKI

58