Dane:

Obliczenia i szkice

Wyniki

Temat: Zaprojektować przekładnie zębatą dwustopniową o zębach skośnych korygowanych dla następujących danych:

I. Założenia wstępne

N1 = 21[kW]

n1=1000[Obr/min] N1 = 34[kW]

Uc = 18,2

n1 = 3000[Obr/min]

Uc = 19

η =10 %

0

η = 100%

Materiał na koła zębate:

Stal nawęglana 15 HN

HB

= 650 MPa

nom

[

]

k = 56 MPa

o

[

]

Z = 570 MPa

o

[

]

Materiał na wały maszynowe:

Stal do azotowania 40 H

HB

= 587 MPa

nom

[

]

k = 47 MPa

o

[

]

Z = 450 MPa

o

[

]

Przyjmuje wartość obciążenia jednostkowego Qu = 3,85 [MPa]

Zastosowana korekcja typu P

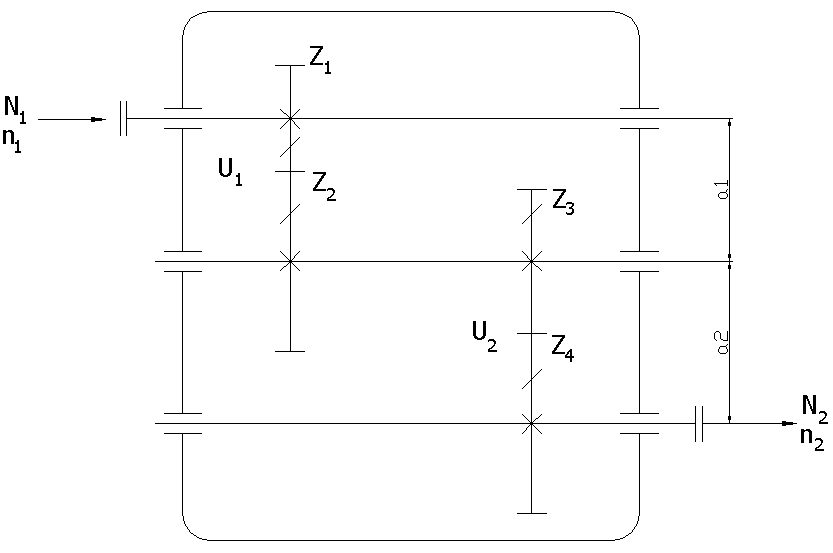
1. Schemat przekładni:

Dane:

Obliczenia i szkice

Wyniki

II. Wstępne określenie wymiarów przekładni zębatej

1.Dobór przełożenia na poszczególne stopnie:

U

1

> U

opt

c

U

> 4, 27

1 opt

Dobieram wartość przełożenia zgodnie z zalecanymi zakresami doboru

przeło

żenia pierwszego stopnia dla przekładni dwustopniowych.

Rys 252 str. 344 Ludwik Muller - Przekładnie zębate

u1 = 5

u = 5

1

u = u ⋅ u

c

1

2

u2 = 3,64

uc

u =

= 3,64

2

u 1

N1 = 21[kW]

2. Wstępne obliczenie średnicy zębnika:

u1 = 5

κ = 0,7

d = 0, 075[ m]

1

Qu = 3,85 [MPa]

N ⋅ ( u +1)

1

=

⋅

n

d

270 3

[ mm]

1=1000[Obr/min]

1

n ⋅ Q ⋅κ ⋅ u

1

u

1

k = 1, 25

p

d = 75, 0[ mm]

1

przyjmuje d = 0, 075[ m]

1

3. Obliczenie odległości osi kół:

u1 = 5

a = 0, 225[ m]

d = 0, 075[ m]

a = 0,5 ⋅ d ⋅ ( u +1)[ mm]

1

1

1

a = 225[ mm]

Dane:

Obliczenia i szkice

Wyniki

4. Obliczenie szerokości koła

d = 0, 075[ m]

1 κ =

= κ ⋅

=

0, 7

b

d [ mm]

b

0, 0525[ m]

1

b = 52,5[ mm]

przyjmuje b = 0, 0525[ mm]

κ = 0,7

5. Dobór liczby zębów w zębniku z oraz kole z : 1

2

β =15°

π

z =

= 16,74

1

κ ⋅ tgβ

ale że przyjmujemy następnie korekcje dodatnią możemy przyjąć liczbę

z1=16

zębów: z

1=16

u

1 = 5

= ⋅ =

z

z

u z

80

1=16

2

1

1

Przyjmuje liczbę zębów: z

z

2=80

2=81

6. Obliczenie modułu normalnego:

a = 0, 225[ m]

2 ⋅ a

m =

⋅cos β = 4, 49[ mm]

z

n

1=16

z + z

1

2

z

2=81

m = 4,5 mm

n

[ ]

Przyjmuje wartość modułu normalnego: m = 4, 5 mm n

[ ]

II. Obliczenia geometryczne kół śrubowych

1. Obliczenie przełożenia na pierwszym stopniu przekładni: z1=16

z2=81

u1 = 5

u1 = 5

2. Obliczenie modułu w przekroju czołowym:

m = 4,5 mm

n

[ ]

1

1

=

m = m ⋅

= 4,65 mm

n

[ ]

1, 015 =

cos β

m = 4, 65 [ mm]

cos β

=

sec β

Przyjmuje m = 4, 65 [ mm]

3. Wymagany luz:

j = 0,135[ mm]

j = 0,135[ mm]

4. Wysokość głowy narzędzia:

f

h = 5, 6 mm

a 0

[ ]

o = 1

c

h = f + c ⋅ m = 5, 6 mm a 0

( o o)

[ ]

o =

,

0 25

m = 4, 65[ mm]

Dane:

Obliczenia i szkice

Wyniki

5. Obliczenie średnicy podziałowej:

z1=16

z2=81

- zębnika: d = z ⋅ m ⋅ sec β = 74, 53[ mm]

d

1

1

n

1=75[mm]

przyjmuje d

1=86[mm]

m = 4,5 mm

n

[ ]

sec β = ,

1 015

- koła: d = z ⋅ m ⋅ sec β = 372, 7[ mm]

2

2

n

d2=373 [mm]

przyjmuje d2=433[mm]

6. Obliczenie kąt zarysu w przekroju czołowym na średnicy podziałowej:

o

α = 20

tgα = tgα ⋅sec β = 0, 3768

o

'

α = 20 39

on

on

sec β = ,

1 015

α = arctg(0,3696) = 20 o 39'

7. Obliczenie kąta pochylenia linii zęba na walcu zasadniczym:

o

α = 20

n 0

sin β = cos(α ) ⋅ sin(β ) = 0, 2456

15 o

β =

b

n 0

o

'

o

'

β =

β =

14 04

14 04

b

b

8. Obliczenie zastępczej liczby zębów:

z

1

z =

o

'

β = 14 07

1

n

2 β ⋅

β

b

- zębnika:

cos

cos

b

z = 18

15 o

β =

z = 18

1

n

1

n

z

1=16

z = 18

z

= u ⋅ z

1

n

- koła: n 2

1

n

u1 = 5

z

=

91

n 2

z

= 91

n 2

9. Wielkość pomocnicza:

o

α = 20

0, 5

c = 0, 484

n 0

c =

= 0,484

15 o

β =

2

2

tg α + cos β

n 0

10. Obliczenie średnicy koła zasadniczego dla:

z1=16

d = 2 ⋅ z ⋅ m ⋅ [

c mm]

b

n

- zębnika

1

1

=

d =

69,8[ mm]

d

70[ mm]

1

b

z

1

b

2=81

=

przyjmuje d

70[ mm]

1

b

m = 4,5 mm

n

[ ]

d

= 2⋅ z ⋅ m ⋅ [

c mm]

c = 0, 484

- koła b 2

2

n

d

=

348,8[ mm]

d

= 349[ mm]

b 2

b 2

przyjmuje d

= 349[ mm]

b 2

11. Obliczenie kąta przyporu na średnicy tocznej w przekroju czołowym:

aw=225 [mm]

- zakładam wartość odległości osi: aw=225 [mm]

m = 4,5 mm

n

[ ]

a

c = 0, 484

sec

w

α =

w

+

z

m ( z

z ) c

1=16

n

1

2

z

α =

2=81

sec

1, 06

w

o

'

α = 20 06

w

o

'

α = arccos(0,93) = 20 06

w

Dane:

Obliczenia i szkice

Wyniki

z1=16

12. Obliczam sume współczynników przesunięcia zarysu:

z2=81

o

α = 20

z + z

j

( x + x ) = 0,89

on

1

2

( x + x ) =

⋅( invα − invα) −

1

2

o

'

α =

1

2

w

20 06

2 ⋅ tg 20°

2 ⋅ m ⋅sin α

w

n

o

'

α = 20 39

( x + x ) = 0,89

1

2

j = 1

,

0 5[ m ]

m

m = 4,5 mm

n

[ ]

13. Współczynniki przesunięcia zarysu:

- dobrane zostały na podstawie wskazówek i wykresu:

x1 = +0,3

x2 = +0,6

14. Obliczenie rozsunięcia kół podziałowych:

aw=225 [mm]

d1=75[mm]

a

∆ = a − 0,5⋅( d + d =1

a

∆ =1

w

1

2 )

d2=373[mm]

15. Obliczenie średnicy koła tocznego:

-zębnika:

z

1

d

=

⋅2⋅ [

a mm]]

a

1

w

w=225 [mm]

z + z

1

2

dw1=74[mm]

d

= 74[ mm]

z

1

w

1=16

z

przyjmuje d

2=81

w1=74[mm]

z 2

d

= 2⋅ a ⋅

[ mm]

w 2

- koła

z + z

1

2

d

= 375,8[ mm]

dw2=376[mm]

w 2

przyjmuje dw2=376[mm]

16. Obliczenie średnic podstaw:

d1=75[mm]

d2=373[mm]

- zębnika

ha0 = 5,6 [mm]

d

= d − 2⋅ h + 2⋅ m ⋅ x [ mm]

f 1

1

0

n

1

m = 4,5 mm

d

= 67[ mm]

n

[ ]

d

=

66,5[ mm]

f 1

f 1

x

1 = 0,3

przyjmuje d

= 67[ mm]

x

f 1

2 = 0,6

- koła

d

= 368[ mm]

f 2

d

= d − 2⋅ h + 2⋅ m ⋅ x = 367,2[ mm]

f 2

2

0

n

2

przyjmuje d

= 368[ mm]

f 2

d1=75[mm]

17. Obliczenie średnic wierzchołków:

d2=373[mm]

- zębnika

d

= d + 2⋅ m + ∆ a − 2⋅ m ⋅ x [ mm]

1

a

1

n

n

2

a

∆ =1

=

d

=

79, 6[ mm]

d

80[ mm]

1

a

1

a

m = 4,5 mm

n

[ ]

przyjmuje d

= 80[ mm]

1

a

x

1 = +0,3

- koła

x

2 = +0,6

d

= d + 2⋅ m + ∆ a − 2⋅ m ⋅ x [ mm]]

a 2

2

n

n

1

d

= 380[ mm]

a 2

d

=

380[ mm]

a 2

przyjmuje d

= 380[ mm]

a 2

Dane:

Obliczenia i szkice

Wyniki

18. Obliczenie kąta przyporu na wierzchołkach:

d

= 80[ mm]

tgα = 0, 553

1

a

1

a

d

= 380[ mm]

2

d

a 2

1

a

tgα =

−1 = 0,553

1

a

d

2

b1=70[mm]

d 1

b

d

tgα

= 0,431

b2=349[mm]

a 2

2

da 2

tgα

=

−1 = 0,431

a 2

2

d

b 2

19. Obliczenie częściowego wskaźnika przyporu:

o

'

α = 20 39

tgα = 0, 553

z

ε = 0,449

1

a

1

ε =

⋅( tgα − tgα) = 0,449

1

1

1

⋅π

tgα

= 0,431

2

a

a 2

z1=16

ε =

z

0, 698

2=81

2

z 2

ε =

⋅( tgα − tgα) = 0,698

2

2

2

a

⋅π

20.Obliczenie wskaźnika przyporu:

ε = 0,449

1

ε =

ε = ε +ε =

ε =1,147

0, 698

1,147

1

2

2

III. Sprawdzenie zazębienia

1. Wyznaczenie kąta przyporu na średnicy wierzchołkowej: d

= 80[ mm]

1

a

d

= 380[ mm]

d 1

b

a 2

cosα =

= 0,88

1

a

o

'

α = 28 21

d

- zębnika

d

1

a

b1= 70[mm]

1

a

d

b2= 349[mm]

d

- koła

b 2

cosα

=

= 0,92

a 2

da 2

o

'

α = 23 18

a 2

2. Wyznaczenie wartości funkcji ewolwentowej

o

'

α = 28 21

1

a

α = α −α

- zębnika inv

tg

= 0,045

invα = 0, 045

a 1

a 1

1

a

a 1

o

'

α = 23 18

- koła invα

= 0,024

invα

= 0,024

a 2

a 2

a 2

3. Wyznaczenie grubości zęba na średnicy wierzchołkowej d

= 80[ mm]





1

a

π

2 ⋅ x 1

s = d ⋅ 

+

⋅ tgα + invα − invα  = 6,52[ mm]

d

= 380[ mm] - zębnika 1 a

1

a

0

0

1

a

 ⋅

a 2

2 z

z



1

1

s = 6,52[ mm]

1

a

x

1 = +0,3

 π

2 x



⋅

x

2

2 = +0,6

s

= d ⋅

+

⋅ tgα + invα − invα 5,96[ mm]

- koła a 2

a 2

0

0

a 2

invα = 0, 045

 2 ⋅ z

z



2

2

a 1

s

= 5,96[ mm]

invα

= 0,024

a 2

a 2

=

>

⋅ =

o

α =

S

6, 52

0, 4 m

1,86

20

1

a

o

=

>

⋅ =

z

S

5, 96

0, 4 m

1,86

1=16

a 2

z

2=81

Warunek spełniony

Dane:

Obliczenia i szkice

Wyniki

3. Obliczenie kąta przyporu na kole ograniczającym czynną część

ewolwenty (interferencja)

z1=16

- zębnika

z2=81

z

tgα

= 0,041

2

α = α − ⋅ α − α =

1

A

tg

tg

( tg

tg

)

0, 041

1

A

w

a 2

w

z

1

o

'

α = 28 21

1

a

o

'

α = 23 18

tgα

= 0,332

a 2

-koła

A 2

o

'

α = 20 06

z

w

1

tgα

= tgα −

⋅( tgα − tgα ) = 0,332

A 2

w

1

a

w

z

2

4. Obliczenie kąta zarysu w punkcie podcięcia ewolwenty o

α = 20

o

4( f + c − ρ − x )

f

α = α −

=

tgα

= 0,3

1

P

o = 1

- zębnika

0

0

0

1

tg

tg

0, 3

1

P

0

z sin 2α

c

1

0

o =

,

0 25

ρ

4( f + c − ρ − x )

- koła

0

0

0

2

tgα

= tgα −

= 0,36

o =

,

0 25

P 2

0

z sin 2α

tgα

= 0,36

P 2

2

0

5. Sprawdzenie warunku uniknięcia interferencji

- zębnika

tgα

= 0,041

tgα

≥ tgα

1

A

1

A

1

P

tgα

= 0,332

0, 041 ≤ 0, 3

A 2

tgα

= 0,3

- koła

1

P

tgα

≥ tgα

tgα

= 0,36

A 2

P 2

P 2

0, 332 ≤ 0, 36

Warunek nie jest spełniony w obu kołach

6. Sprawdzenie warunku podcinania zęba

- zębnika

tgα

= 0,3

tgα

P

> 0

1

P

1

tgα

= 0,36 - koła

P 2

tgα

P

> 0

2

Warunek spełniony w obu kołach (dodatnia korekcja)

7. Sprawdzenie wskaźnika przyporu:

ε =1,147

ε > ,12

Warunek spełniony

8. Sprawdzenie luzu wierzchołkowego:

a=225[mm]

d

= 80[ mm] - zębnika:

1

a

= −

⋅

+

=

d

= 380[ mm]

c

a

0, 5 ( d

d )

1, 5

c = 1,5

1

f 1

a 2

1

a 2

d

= 67[ mm] - koła

f 1

c = a − 0,5 ⋅ ( d

+ d ) = 1

c = 1

d

= 368[ mm]

2

f 2

1

a

2

f 2

Warunek spełniony

Dane:

Obliczenia i szkice

Wyniki

9. Sprawdzenie poślizgu:

u

1=5

- zębnika

o

'

α = 28 21

u +1

tgα

η = 0,39

1

a

I

η =

(1

w

−

) = 0,39

1

1

o

'

α = 23 18

u

tgα

I

a 1

a 2

o

'

α =

20 06

w

- koła

tgα

η = 0,90

2

η = ( u +1)(1

w

−

) = 0, 90

2

I

α

tg a 2

Warunek spełniony

IV. Obliczenia wytrzymałościowe

1. Przełożenie obliczonego stopnia przekładni:

z

1=16

z 2

u =

= 5,05

z

2=81

z 1

przyjmuje u=5

u=5

2. Obliczenie średnicy podziałowej:

- zębnika

z ⋅ m

1

n

d =

= 74,54[ mm]

z

1

β

d = 75[ mm]

1=16

cos

1

z2=81

przyjmuje d = 75[ mm]

1

m = 4, 5 mm

n

[ ]

z ⋅ m

β =

2

n

d =

= 377,36[ mm]

15°

- koła 2

cos β

d = 377,36[ mm]

2

przyjmuje d = 200[ mm]

2

3. Obliczenie średnicy tocznej:

z

1

d

= 2⋅ a ⋅

= 74,23[ mm]

- z

1

w

ębnika

z + z

1

2

z

1=16

=

z

d

75[ mm]

2=81

1

w

przyjmuje d

= 75[ mm]

1

w

a=225[mm]

z

2

d

= 2⋅ a ⋅

= 375,77[ mm]

- koła w 2

z + z

1

2

d

= 376[ mm]

w 2

przyjmuje d

= 376[ mm]

w 2

Dane:

Obliczenia i szkice

Wyniki

4. Obliczenie średnicy tocznej w przekroju normalnym: d

= 75[ mm]

- z

1

w

ębnika

d

1

w

d

=

= 79,71[ mm]

d

= 376[ mm]

1

w n

2 β

w 2

cos

b

=

o

'

β =

d

80[ mm]

14 04

1

w n

b

przyjmuje d

= 80[ mm]

1

w n

- koła

dw 2

d

=

= 399,6[ mm]

w 2 n

2

cos β

b

d

= 400[ mm]

w 2 n

przyjmuje d

= 400[ mm]

w 2 n

5. Obliczenie modułu tocznego w przekroju normalnym: d

= 75[ mm]

1

w

⋅

β

15 o

β =

d

cos

m

= 4,5

1

w

m

=

= 4,5

wn

wn

z

z

1=16

1

6. Obliczenie współczynnika skrócenia głowy:

a = 0, 5⋅( z + z ⋅ m = 211,58

o

1

2 )

x + x

z

1

2

1=16

B = 2 ⋅

= 0,0186

p

+

z

z

z

2=81

1

2

B = 0, 014009

r

m = 4, 65 [ mm]

a = a ⋅ (1+ B ) = 214,54

o

r

x1 = +0,3

x2 = +0,6

a − ao

y = 0,574 [ mm]

y = ( x + x ⋅

= 0,574 mm

1

2 )

[ ]

m

7. Obliczenie średnicy wierzchołków:

d = 75[ mm]

1

d = 373[ mm]

- zębnika

2

d

= d + 2⋅( x +1− y)⋅ m = 81,75[ mm]

x

1

a

1

1

n

1 = +0,3

d

= 82[ mm]

x

1

a

2 = +0,6

przyjmuje d

= 82[ mm]

1

a

y = 0,574 [ mm]

- koła

m = 4, 5 mm

n

[ ]

d

= d + 2⋅( x +1− y)⋅ m = 382,54[ mm]

d

= 383[ mm]

a 2

a 2

2

2

n

przyjmuje d

= 383[ mm]

a 2

8. Obliczeniowa wysokość zęba liczona od średnicy tocznej: d

= 82[ mm]

1

a

- z

d

= 383[ mm]

ębnika

a 2

'

h = 0, 5⋅ d − d

= 3,5

'

h = 3,5

1

( 1 a

1

w )

d

= 75[ mm]

1

1

w

- koła

'

h = 3,5

d

= 376[ mm]

2

w 2

'

h = 0, 5⋅ d − d

= 3,5

2

( a 2 w 2)

Dane:

Obliczenia i szkice

Wyniki

9. Wyznaczenie wielkości pomocniczej:

α = 20 o

- zębnik

n 0

100 h '

ε = 0,78

'

h = 3,5

1

ε = f (α ,

) = 0, 78

01

1

01

nw

d

'

h = 3,5

n 1

w

2

- koło

d

= 80[ mm]

ε =

1

w n

100 h '

0, 95

2

ε = f (α ,

) = 0,95

02

d

= 400[ mm]

02

nw

w 2 n

d

nw 2

10. Obliczenie częściowego współczynnika przyporu w przekroju normalnym:

ε = 0,78

01

ε =

- z

0, 95

ębnika

02

h '

ε = 0,61

'

h = 3,5

1

ε = ε ⋅

= 0,61

1 n

1

1 n

01

m

'

wn

h = 3,5

2

m

= 4,5

ε = 0,74

wn

- koła

2 n

h '

2

ε = ε ⋅

= 0,74

2 n

02

m

wn

11. Obliczenie wskaźnika przyporu w przekroju normalnym: ε = 0,61

ε = ε +ε =1,35

ε =1,35

1 n

n

1 n

2 n

n

ε = 0,74

2 n

12. Obliczenie czołowego wskaźnika przyporu:

ε =1,35

2

ε = ε ⋅cos β =1,27

ε =1,27

n

α

n

b

α

o

'

β =14 04

b

13. Obliczenie poskokowego wskaźnika przyporu:

15 o

β =

⋅

β

ε =

m = 4, 5 mm

b sin

ε =

=

1,83

β

n

[ ]

1,83

β

π ⋅ m

b = 0, 0525[ m]

n

14. Obliczenie prędkości obwodowej:

n1=1000[obr/min]

d ⋅ n

v = 3,93[ m / s]

1

w

1

v =

= 3,93[ m / s]

d

= 75[ mm]

- zębnika

1

w

19100

15. Określenie wypadkowej odchyłki kinetycznej na podziałce koła:

'

f = 45

'

f = 50

t 1

t 2

'

'

f =

f + f = 67, 27µ m

f = 67, 27µ m

t

t 1

t 2

t

16. Odczytanie odchyłki kierunku zęba:

Fβ = 25[ m

µ ]

Fβ = 25[ m

µ ]

Dane:

Obliczenia i szkice

Wyniki

17. Obliczenie współczynnika wielkości zęba:

b = 0, 0525[ m]

2

y = 0, 64 +

= 0,77

m

y = 0, 77

m = 4, 5 mm

b ⋅ m

m

n

[ ]

n

18. Obliczenie sumy chropowatości powierzchni zębów: R = 0, 64 µ m

h = R + R = 1, 28 µ m

h = 1, 28[µ m]

z 1

z 2

[ ]

z 1

[ ]

R

= 0,64 µ m

z 2

[ ]

19. Obliczenie współczynników wpływu oleju na wielkość i rozkład nacisków:

v = 3,93[ m / s]

- zębnika

0, 6

y = 0, 7 +

=1,29

h

2

 800 

y = 1, 29

h

1+ 



 v ν

⋅ 

20. Określenie współczynnika zależnego od kąta pochylenia linii zęba: y = f (β ) = 0,916

=

β

y

0, 916

β

21. Obliczenie zastępczej liczby zębów:

z1=16

- zębnika

z2=81

z

1

z =

=17,61

1 n

2

cos β ⋅ cos β

z1n=18

b

o

'

β =14 04

b

- koła

z

15 o

β =

z

2n=90

2

z

=

= 89,12

2 n

2

cos β ⋅ cos β b

22. Obliczenie współczynnika zależnego od położenie punktu o

α = 20

jednoparowej współpracy zębów:

nw

π

z

2

1n=18

y = 1−

(1− ε ) = 0, 626

ε

1

n

=

tgα z

y

0, 626

ε

nw

1

n

ε = 0,61

1 n

23. Określenie współczynnika zależnego od kąta przyporu na średnicy tocznej w przekroju normalnym:

o

α = 20

y = f (α ) = 3,11

y = 3,11

nw

c

nw

c

24. Obliczenie wypadkowej wartości współczynników y i c

ε

y :

y

y = 3,11

c

y =

=1,95

y = 1,95

c

1

y

1

y = 0, 626

ε

ε

25. Obliczenie współczynnika podziału sił na obie pary zębów: 1

ε =

q =

= 0,741

1, 35

ε

q = 0, 741

n

ε

ε

n

Dane:

Obliczenia i szkice

Wyniki

26. Określenie współczynnika kształtu zęba:

z1n=18

z2n=90

- zębnika

q = 2, 78

1

x1 = +0,3

q = f ( z , x ) = 2, 78

1

1

n

1

x2 = +0,6

- koła

q = f ( z , x ) = 2,58

q = 2, 58

2

n 2

2

2

27. Określenie współczynnika nierównomierności rozkładu obciążenia:

ε =1,83

ε

β

>1

β

ε =1,27

K = 0, 79

α

1

s

K =

s

εα

N1 = 21[kW]

28. Obliczenie nominalnego obciążenia kół:

n1=1000[Obr/min]

a=225[mm]

7

2

10 ⋅ N ⋅ ( u +1)

Q = 1,35[ MPa]

Q =

=1,35[ MPa]]

b = 0, 0525[ m]

2

2,1⋅ n ⋅ b ⋅ a

1

u=5

29. Obliczenie wielkości pomocniczej:

z1=16

v = 3,93[ m / s]

2

v ⋅ z

u

1

u

P =

⋅

= 0,077

P = 0, 077

1=5

2

800

1+ u

k

30. Obliczenie wielkości pomocniczej:

p =

,

1 25

Q = 1,35[ MPa]

4 ⋅ f

B = 2,13

f = 67, 27µ m

t

B =

= 2,13

t

Q ⋅ k ⋅ d

d

= 75[ mm]

p

1

w

1

w

31. Obliczenie współczynnika sił dynamicznych:

B = 2,13

P = 0, 077

3

2

P

K = 1, 068

d

ε =

K = 1+

⋅

⋅(1+ B) = 1,068

1,83

d

β

3

1+ 0,5 ⋅ε

β 1 +

P

k

32. Określenie wielkości pomocniczej:

p =

,

1 25

K = 1, 068

d

7, 5 ⋅ Fβ

d

= 75[ mm]

A =

=1,39

1

w

A = 1,39

Q ⋅ k ⋅ k ⋅ d

Q = 1,35[ MPa]

p

d

1

w

Fβ = 25[ m

µ ]

33. Określenie współczynnika nierównomierności rozkładu obciążenia:

A = 1,39

k = 1,38

r

k = f ( )

A = 1, 38

r

34. Określenie współczynnika wpływu odkształceń sprężystych na nierównomierności rozkładu:

k

= f ( ukladu) =1,1

r 0

k

= 1,1

r 0

35. Obliczenie wypadkowego współczynnika nierównomierności k = 1,38

rozkładu obciążenia na szerokości koła:

r

k

= 1,1

r 0

k

= k + k −1 =1, 48

k

=1,48

rw

r

r 0

rw

Dane:

Obliczenia i szkice

Wyniki

k = 1, 25

36. Obliczenie całkowitego obciążenia zęba w warunkach p

normalnych:

k = 1, 068

d

Q = 2,11[ MPa]

k

=1,48

c

rw

Q = Q ⋅ K ⋅ K ⋅ K ⋅ K = 2,11[ MPa]

c

p

d

rw

s

k = 0, 79

s

Q = 1,35[ MPa]

37. Obliczenie granicznej wytrzymałości zęba na naciski: HB = 587[ MPa]

- zębnika

HB

= 587 MPa

nom

[

]

2



HB 

k = 56 MPa

k = k ⋅ 

 = 56 MPa

k = 56 MPa

z 1

[

]

z 1

01

[

]

01

[

]

 HB



nom

k

= 47 MPa

02

[

]

- koła

HB = 650[ MPa]

2

 HB 

k

= 47 MPa

z 2

[

]

k

= k ⋅

 = 47 MPa

z 2

02

[

]

HB

= 650 MPa

nom

[

]

 HB



nom

38. Określenie granicznej liczby zębów na złamanie:

- zębnika

Z = 570 MPa

Z = 570 MPa

z 1

[

]

z 1

[

]

- koła

Z

= 450 MPa

Z

= 450 MPa

z 2

[

]

z 2

[

]

39. Określenie współczynnika karbu u podstawy zęba:

- zębnika

y = 1

y

k

= 1

k 1

1

- koła

y

y

k

= 1

k

= 1

2

2

40. Określenie współczynnika stanu powierzchni u podstawy zębów:

- zębnika

y

=1

y

=1

1

p

1

p

- koła

y

= 1

y

= 1

p 2

p 2

V. Współczynniki bezpieczeństwa

k = 56 MPa

1. Obliczenie współczynnika bezpieczeństwa na naciski: z 1

[

]

k

= 47 MPa

z 2

[

]

- zębnika

y = 1, 29

k ⋅ y ⋅ y

u

X

=12,24

h

z 1

m

h

X

=

⋅

=12, 24

1

p

1

p

y = 0, 77

Q ⋅ y ⋅ y

u +1

m

c

1

β

y = 1,95

1

X

= 6, 45

y = 0, 916

-koła

p 2

β

k ⋅ y ⋅ y

u

z 2

m

h

y = 3,11

X

=

⋅

= 6, 45

c

p 2

Q ⋅ y ⋅ y

u +1

β

u

c

c

1=5

Q = 2,11[ MPa]

c

Dane:

Obliczenia i szkice

Wyniki

2. Obliczenie współczynnika bezpieczeństwa na złamanie: Z = 570 MPa

z 1

[

] - zębnika

Z

= 450 MPa

z 2

[

]

Z ⋅ y

z 1

m

=

=

Q = 2,11[ MPa]

X

6, 31

z 1

c

Q ⋅ z ⋅ q ⋅ q ⋅ y ⋅ y X

= 6,31

z 1

c

1

ε

1

k 1

1

p

y = 0, 77

m

q = 0, 741

ε

- koła

X

= 5,37

q = 2, 78

Z ⋅ y

z 2

1

z 2

m

X

=

= 5,37

z 2

q = 2, 58

Q ⋅ z ⋅ q ⋅ q ⋅ y ⋅ y 2

c

1

ε

2

k 2

p 2

y

k

= 1

1

y

k

= 1

2

y

=1

1

p

y

=1

1

p

z1=16

3. Sprawdzenie warunku wytrzymałościowego:

,

1 2 < X

p

< 2

1

,

1 2 < X

p

< 2

X

=12,24

2

1

p

1, 2 < X < 4

X

= 6, 45

z 1

p 2

1, 2 < X

< 4

X

= 6,31

z 2

z 1

X z 1 =1,6

X

= 5,37

z 2

X

X

z 1

1

p

=1,6

X

1

p

X

X z 2

z 2 =1,3

=1,3

X

X p 2

p 2