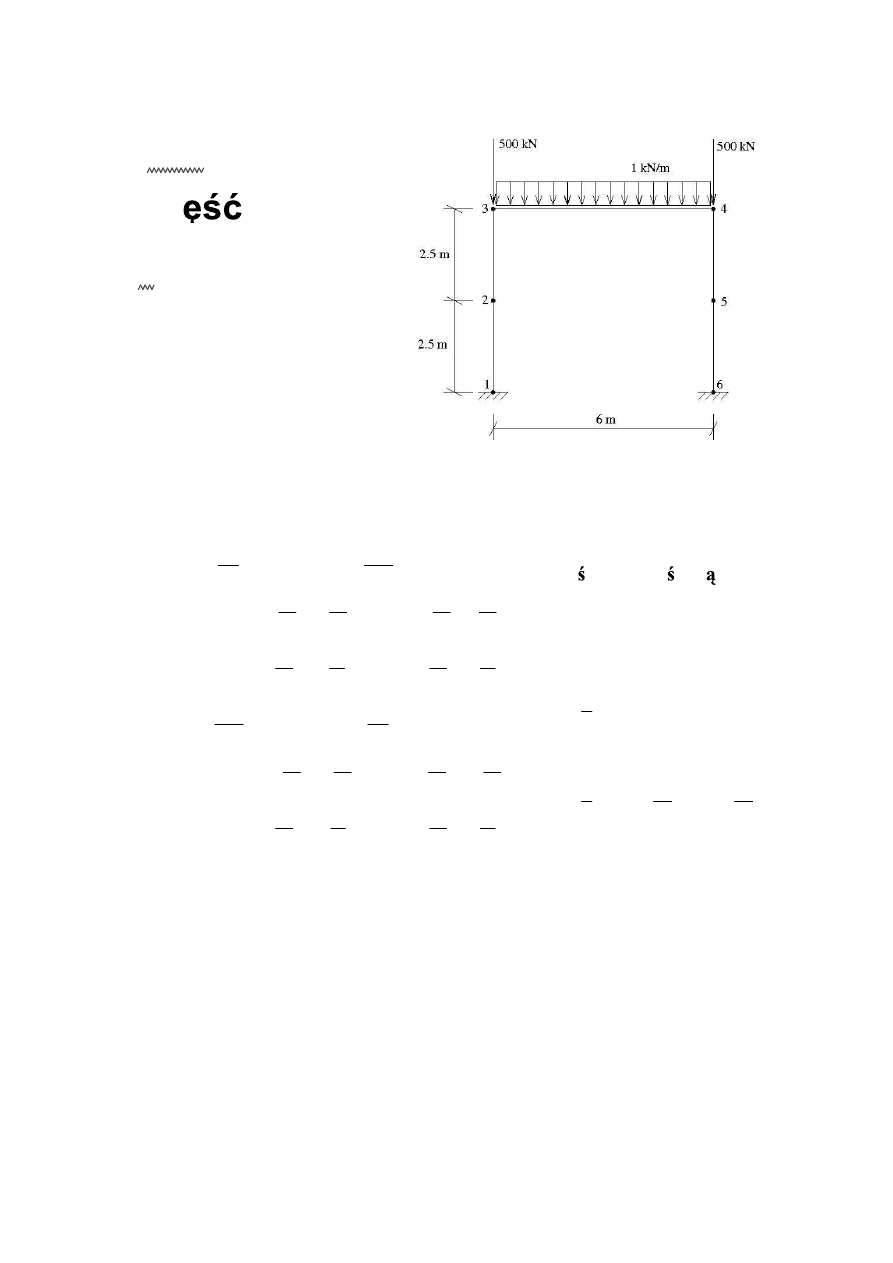
ORIGIN
1
:=
Cz
I: statyka
E
210 10
6
⋅
:=
A
53.4 10
4
−
⋅
:=
I
5740 10
8
−
⋅
:=
EA
E A
⋅
:=
EI
E I
⋅
:=
Te a
( )
cos a
( )
sin a
( )
−
0
0
0
0
sin a
( )
cos a
( )
0
0
0
0
0
0
1
0
0
0
0
0
0
cos a
( )
sin a
( )
−
0
0
0
0
sin a
( )
cos a
( )
0
0
0
0
0
0
1
:=
Długo ci i warto ci k tów
transformacji dla
poszczególnych
elementów
L1
2.5
:=
L3
6
:=
ke L
( )
EA
L
0
0
EA
−
L
0
0
0
12
EI
L
3
⋅
6
EI
L
2
⋅
0
12
−
EI
L
3
⋅
6
EI
L
2
⋅
0
6
EI
L
2
⋅
4
EI
L
0
6
−
EI
L
2
⋅
2
EI
L
⋅
EA
−
L
0
0
EA
L
0
0
0
12
−
EI
L
3
⋅
6
−
EI
L
2
⋅
0
12
EI
L
3
⋅
6
−
EI
L
2
⋅
0
6
EI
L
2
⋅
2
EI
L
⋅
0
6
−
EI
L
2
⋅
4
EI
L
⋅
:=
a1
π
2
:=
a3
0
:=
L2
2.5
:=
L4
2.5
:=
L5
2.5
:=
a2
π
2
:=
a4
π
−
2
:=
a5
π
−
2
:=
Macierze agregacji
B1
6 18
,
0
:=
B2
6 18
,
0
:=
B3
6 18
,
0
:=
B4
6 18
,
0
:=
B5
6 18
,
0
:=
B1
1 1
,
1
:=
B1
2 2
,
1
:=
B1
3 3
,
1
:=
B1
4 4
,
1
:=
B1
5 5
,
1
:=
B1
6 6
,
1
:=
B2
1 4
,
1
:=
B2
2 5
,
1
:=
B2
3 6
,
1
:=
B2
4 7
,
1
:=
B2
5 8
,
1
:=
B2
6 9
,
1
:=
B3
1 7
,
1
:=
B3
2 8
,
1
:=
B3
3 9
,
1
:=
B3
4 10
,
1
:=
B3
5 11
,
1
:=
B3
6 12
,
1
:=
B4
1 10
,
1
:=
B4
2 11
,
1
:=
B4
3 12
,
1
:=
B4
4 13
,
1
:=
B4
5 14
,
1
:=
B4
6 15
,
1
:=
B5
1 13
,
1
:=
B5
2 14
,
1
:=
B5
3 15
,
1
:=
B5
4 16
,
1
:=
B5
5 17
,
1
:=
B5
6 18
,
1
:=
1/7

Macierze sztywno ci
k1
ke L1
(
)
:=
k2
ke L2
(
)
:=
k3
ke L3
(
)
:=
k4
ke L4
(
)
:=
k5
ke L5
(
)
:=
T1
Te a1
(
)
:=
T2
Te a2
(
)
:=
T3
Te a3
(
)
:=
T4
Te a4
(
)
:=
T5
Te a5
(
)
:=
K1
T1
T
k1
⋅
T1
⋅
:=
K2
T2
T
k2
⋅
T2
⋅
:=
K3
T3
T
k3
⋅
T3
⋅
:=
K4
T4
T
k4
⋅
T4
⋅
:=
K5
T5
T
k5
⋅
T5
⋅
:=
Agregacja do globalnej macierzy sztywno ci
K
B1
T
K1
⋅
B1
⋅
B2
T
K2
⋅
B2
⋅
+
B3
T
K3
⋅
B3
⋅
+
B4
T
K4
⋅
B4
⋅
+
B5
T
K5
⋅
B5
⋅
+
:=
Macierz funkcji kształtu
Nk1 x L
,
(
)
1
x
L
−
:=
Nk2 x L
,
(
)
x
L
:=
Nb1 x L
,
(
)
1
3
x
L
2
⋅
−
2
x
L
3
⋅
+
:=
Nb2 x L
,
(
)
L
x
L
2
x
L
2
⋅
−
x
L
3
+
⋅
:=
Nb3 x L
,
(
)
3
x
L
2
⋅
2
x
L
3
⋅
−
:=
Nb4 x L
,
(
)
L
x
L
3
x
L
2
−
⋅
:=
N x L
,
(
)
Nk1 x L
,
(
)
0
0
Nb1 x L
,
(
)
0
Nb2 x L
,
(
)
Nk2 x L
,
(
)
0
0
Nb3 x L
,
(
)
0
Nb4 x L
,
(
)
:=
Wektor prawej strony
q3 x
( )
0
1
−
:=
L3c
6
:=
i
1 6
..
:=
P3
i
0
L3c
x
N x L3c
,
(
)
1 i
,
q3 x
( )
1
⋅
N x L3c
,
(
)
2 i
,
q3 x
( )
2
⋅
+
⌠
⌡
d
:=
Pw
18
0
:=
Pw
8
500
−
:=
Pw
11
500
−
:=
F
B3
T
P3
⋅
Pw
+
:=
2/7
Wektor warunków brzegowych
Wb
1
2
3
16
17
18
:=
Kb
K
:=
Fb
F
:=
Warunki brzegowe
i
1 18
..
:=
j
1 6
..
:=
Kb
i Wb
j
,
0
:=
Kb
Wb
j
( )
i
,
0
:=
Kb
Wb
j
Wb
j
,
1
:=
Fb
Wb
j
0
:=
Wektor rozwi zania - przemieszczenia w złowe
Q
Kb
1
−
Fb
⋅
:=
Q
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0
0
0
-4
-1.36626094·10
-3
-1.12136615·10
-5
5.44807292·10
-6
1.69708389·10
-3
-2.2427323·10
-4
-2.19959418·10
-6
-1.69708389·10
-3
-2.2427323·10
-4
2.19959418·10
-4
1.36626094·10
-3
-1.12136615·10
-5
-5.44807292·10
0
=
3/7

Wektor reakcji
R
K Q
⋅
F
−
:=
reakcje dla wezła 1
R
1
0.63436996
=
R
2
503
=
R
3
1.05564673
−
=
reakcje dla wezła 2
R
4
0
=
R
5
0
=
R
6
0
=
reakcje dla wezła 3
R
7
1.49880108
−
10
14
−
×
=
R
8
1.70530257
10
13
−
×
=
R
9
1.33226763
10
15
−
×
=
reakcje dla wezła 4
R
10
1.37667655
10
14
−
×
=
R
11
1.13686838
10
13
−
×
=
R
12
1.33226763
−
10
15
−
×
=
reakcje dla wezła 5
R
13
1.2625689
10
15
−
×
=
R
14
1.13686838
−
10
13
−
×
=
R
15
0
=
reakcje dla wezła 6
R
16
0.63436996
−
=
R
17
503
=
R
18
1.05564673
=
Równowaga globalna
Równowaga na osi X
R
1
R
7
+
R
16
+
1.46549439
−
10
14
−
×
=
Równowaga na osi Y
R
2
R
14
+
R
17
+
2
−
500
⋅
+
6
−
4.54747351
−
10
13
−
×
=
Równowaga momentu wzgledem punktu A(0,0)
R
3
R
18
+
500 6
⋅
−
6 3
⋅
−
R
17
6
⋅
+
9.09494702
−
10
13
−
×
=
4/7

Siły przyw złowe
element 1
element 2
element 3
Q1
B1 Q
⋅
:=
Q2
B2 Q
⋅
:=
Q3
B3 Q
⋅
:=
S1
K1 Q1
⋅
:=
S2
K2 Q2
⋅
:=
S3
K3 Q3
⋅
P3
−
:=
s1
T1 S1
⋅
:=
s2
T2 S2
⋅
:=
s3
T3 S3
⋅
:=
s1
503
0.63436996
−
1.05564673
−
503
−
0.63436996
0.53027816
−
=
s2
503
0.63436996
−
0.53027816
503
−
0.63436996
2.11620306
−
=
s3
0.63436996
3
2.11620306
0.63436996
−
3
2.11620306
−
=
element 4
element 5
Q4
B4 Q
⋅
:=
Q5
B5 Q
⋅
:=
S4
K4 Q4
⋅
:=
S5
K5 Q5
⋅
(
)
:=
s4
T4 S4
⋅
:=
s5
T5 S5
⋅
:=
s4
503
0.63436996
2.11620306
503
−
0.63436996
−
0.53027816
−
=
s5
503
0.63436996
0.53027816
503
−
0.63436996
−
1.05564673
=
5/7

Cz
II: stateczno
Macierz geometryczna
Etap II
Ksig N L
,
(
)
N
30 L
⋅
0
0
0
0
0
0
0
36
3 L
⋅
0
36
−
3 L
⋅
0
3 L
⋅
4 L
2
⋅
0
3
−
L
⋅
L
2
−
0
0
0
0
0
0
0
36
−
3
−
L
⋅
0
36
3
−
L
⋅
0
3 L
⋅
L
2
−
0
3
−
L
⋅
4L
2
⋅
:=
Macierze geometryczne dla elementów
ks1
Ksig s1
4
L1
,
(
)
:=
ks2
ks1
:=
ks4
ks1
:=
ks5
ks1
:=
ks3
Ksig s3
4
L3
,
(
)
:=
Ks1
T1
T
ks1
⋅
T1
⋅
:=
Ks2
T2
T
ks2
⋅
T2
⋅
:=
Ks3
T3
T
ks3
⋅
T3
⋅
:=
Ks4
T4
T
ks4
⋅
T4
⋅
:=
Ks5
T5
T
ks5
⋅
T5
⋅
:=
Agregacja do globalnej macierzy geometrycznej
Ks
B1
T
Ks1
⋅
B1
⋅
B2
T
Ks2
⋅
B2
⋅
+
B3
T
Ks3
⋅
B3
⋅
+
B4
T
Ks4
⋅
B4
⋅
+
B5
T
Ks5
⋅
B5
⋅
+
:=
Ksb
Ks
:=
Warunki brzegowe
i
1 18
..
:=
j
1 6
..
:=
Ksb
i Wb
j
,
0
:=
Ksb
Wb
j
( )
i
,
0
:=
genvals Kb
Ksb
−
,
(
)
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5
8.8949998410
3
3.5054230910
241.072764
204.33656328
91.97174554
77.66967808
6.75702037
29.11031256
24.02775446
308
1.7976931310
308
1.7976931310
308
1.7976931310
308
1.7976931310
308
1.7976931310
308
1.7976931310
308
1.7976931310
=
lambda1
min genvals Kb
Ksb
−
,
(
)
(
)
:=
lambda1
6.75702037
=
6/7

Obliczenie wektora formy utraty statecznooci dla
minimalnej warto ci własnej (w przykładzie jest to 7)
genvecs Kb
Ksb
−
,
(
)
7
〈 〉
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0
0
0
0.40211608
-3
1.1833140710
-0.27302088
1
-3
2.3666281410
-0.1329186
1
-3
-2.3666281410
-0.1329186
0.40211608
-3
-1.1833140710
-0.27302088
0
=
7/7
Wyszukiwarka
Podobne podstrony:
Rozwiązanie stateczności ramy MES, Mathcad
Mathcad Mechanika stateczno Ť¦ç 2
ROZWIĄZANIE RAMY METODĄ PRZEMIESZCZEŃ
Mathcad rozwiazanie rurociag Pilch
mes rama statecznosc
Przykład rozwiązania tarczy MES-wersja 3
Przykład rozwiązania tarczy MES-wersja 2
mes podstawy ramy wykł
Algorytm rozwiązania MES
mes zad 1 ramy wykł
Mathcad Mechanika stateczno Ť¦ç 2
mes zad 1 ramy wykł
Przykład rozwiązania tarczy MES wersja 1(1)
statecznosc mes
mes podstawy ramy wykł
więcej podobnych podstron