Wykład MES

ALGORYTM ROZWIĄZANIA - PRZYKŁADY

ALGORYTM ROZWIĄZANIA - PRZYKŁADY

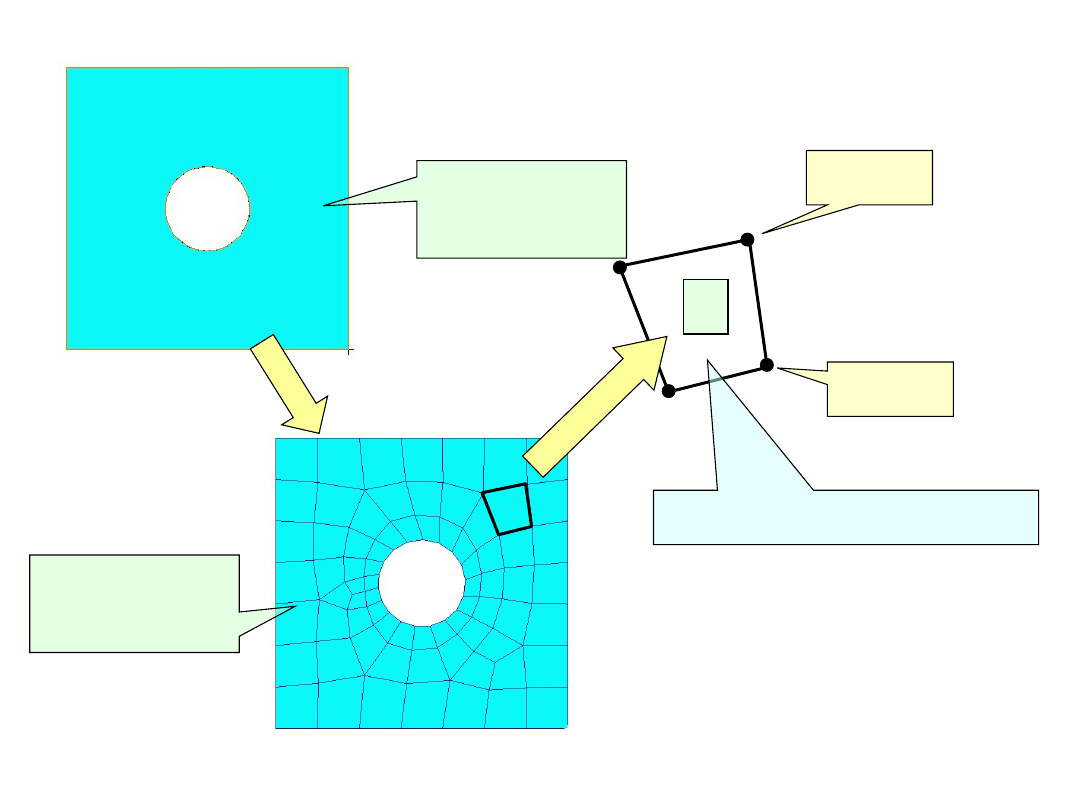
ELEMENT SKOŃCZONY

węzeł

węzeł

Element skończony

Geometri

a

Podział na

elementy

K

ELEMENT SKOŃCZONY

Element skończony

– podobszar

oryginalnej geometrii

konstrukcji

o prostym kształcie

Właściwości mechaniczne elementu,

zależność pomiędzy przemieszczeniami i

obciążeniami, opisuje

macierz sztywności

Kształt elementu określany jest poprzez

podanie położenia charakterystycznych

punktów -

węzłów

ALGORYTM PROGRAMU MES

• Przedstawienie modelu ciągłego jako zbioru

elementów i połączeń

• Obliczenie macierzy sztywności elementów -

K

e

• Połączenie macierzy sztywności wszystkich

elementów w globalną macierz struktury -

K

• Utworzenie wektora obciążeń -

F

• Rozwiązanie równania macierzowego

K*u = F

względem przemieszczeń

u

• Obliczenie sił w elementach
• Obliczenie naprężeń i odkształceń w

elementach

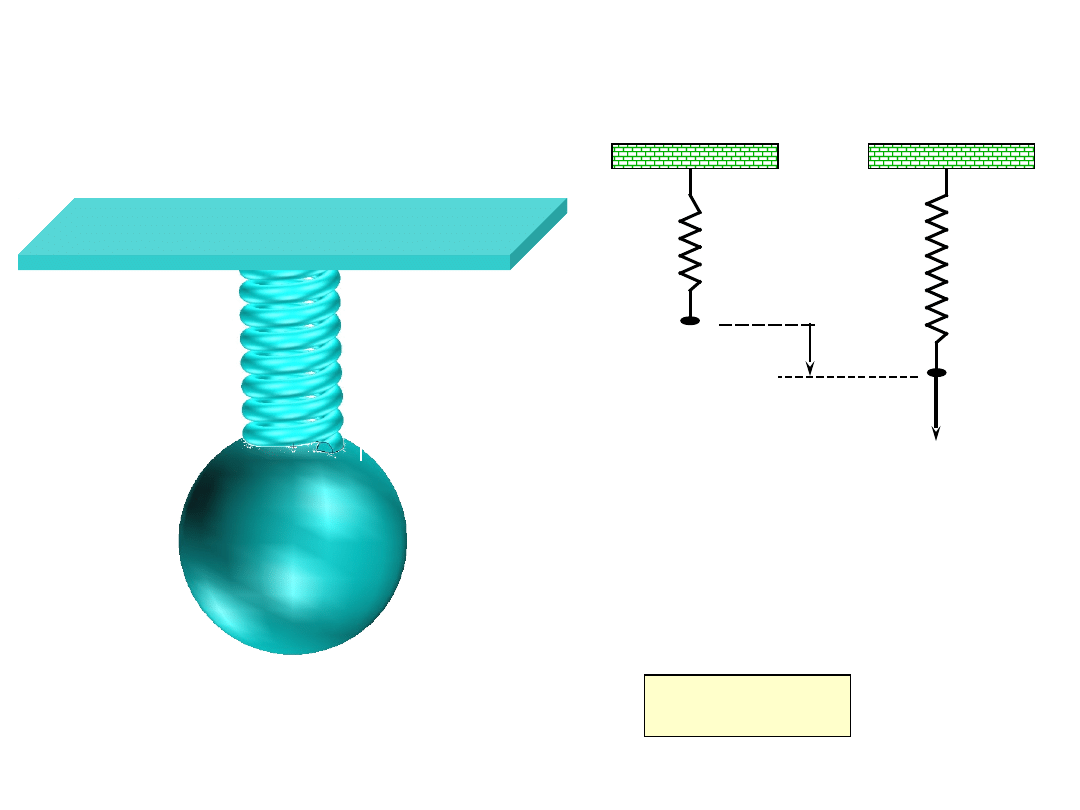
MODEL

MATEMATYCZNY

k * u = F

k – sztywność
sprężyny u –
wydłużenie sprężyny
F – siła w sprężynie

F

u

k

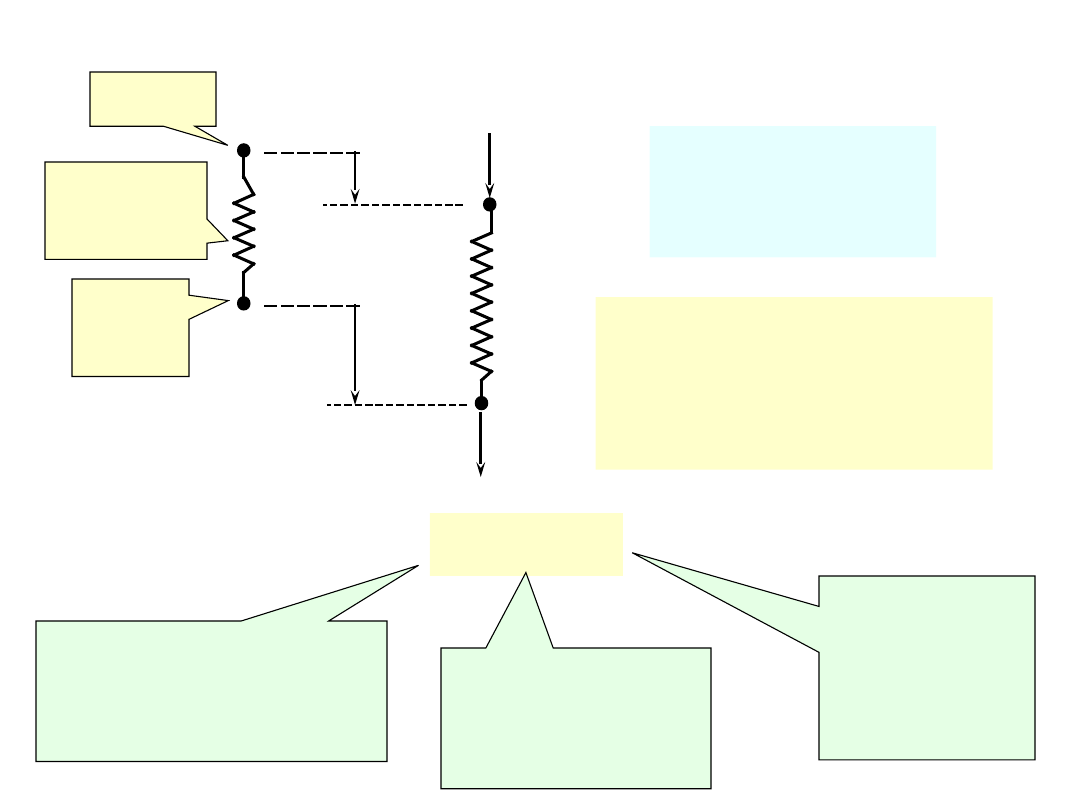
MODEL

MATEMATYCZNY



























1

2

1

2

1

2

F

u

u

k

F

u

u

k



















































2

1

2

1

F

F

u

u

k

k

k

k

F

U

K





macierz

sztywności

elementu

wektor

przemieszcze

ń węzłowych

wektor

obciążeń

węzłowyc

h

elemen

t

węzeł

węze

ł

k

u

2

u

1

F

2

F

1

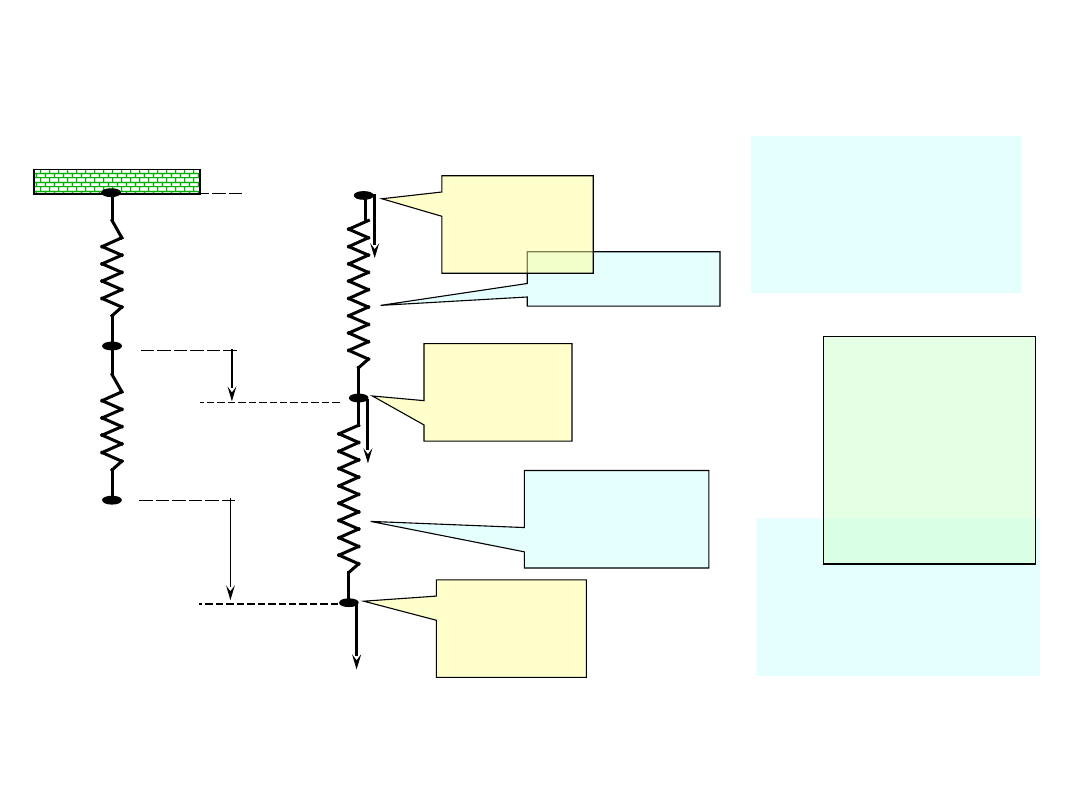
PRZYKŁAD I – układ sprężyn

F

2

u

2

k

1

u

1

u

3

F

1

F

3

k

2

element I

węzeł

1

węzeł

2

węzeł

3

element

II





















1

1

1

1

I

k

k

k

k

K





















2

2

2

2

II

k

k

k

k

K

macierze

sztywnośc

i

elementó

w

PRZYKŁAD I – stopnie swobody

Każdy z 3 węzłów ma 1 możliwość ruchu –

przesunięcie w kierunku pionowym

Układ ma 3 niezależne możliwości

ruchu

Niezależne możliwości ruchu układu

nazywamy

stopniami swobody

Wymiar macierzy układu równy jest

liczbie stopni swobody

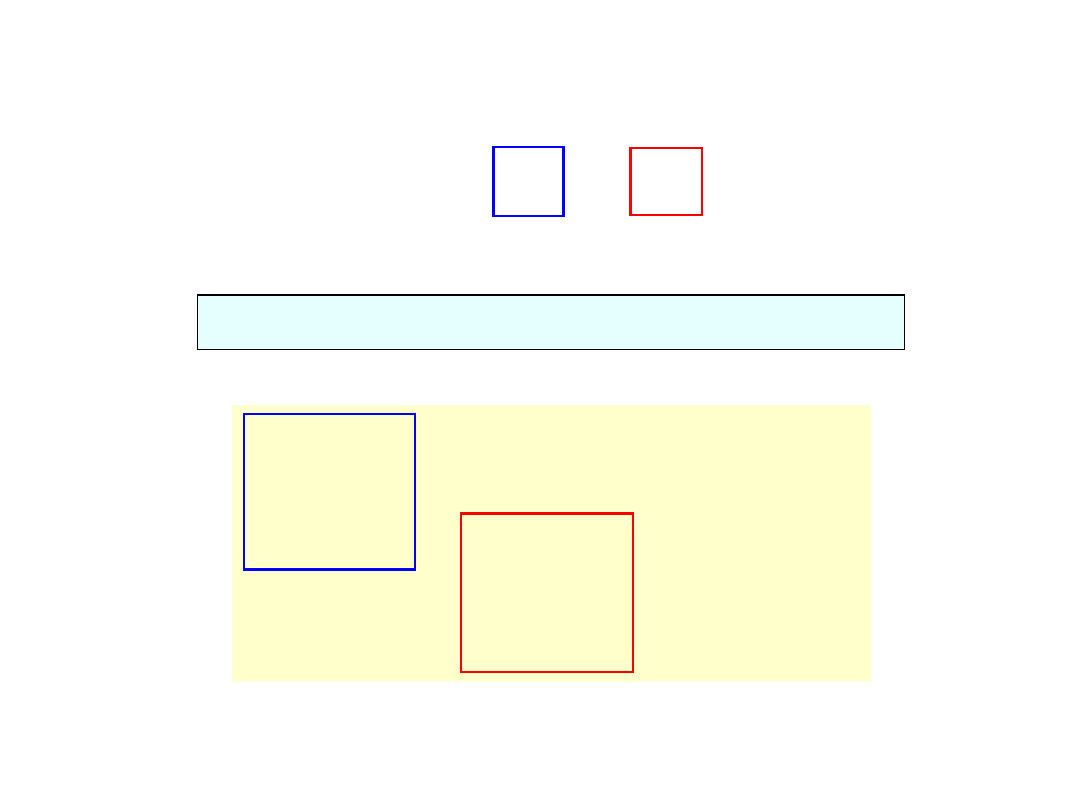
PRZYKŁAD I – macierz

sztywności



























































































3

2

1

3

2

1

2

2

2

2

1

1

1

1

F

F

F

u

u

u

k

k

-

0

k

-

k

k

k

-

0

k

-

k

II

I

K

K

K





Wymiar macierzy układu równy jest 3

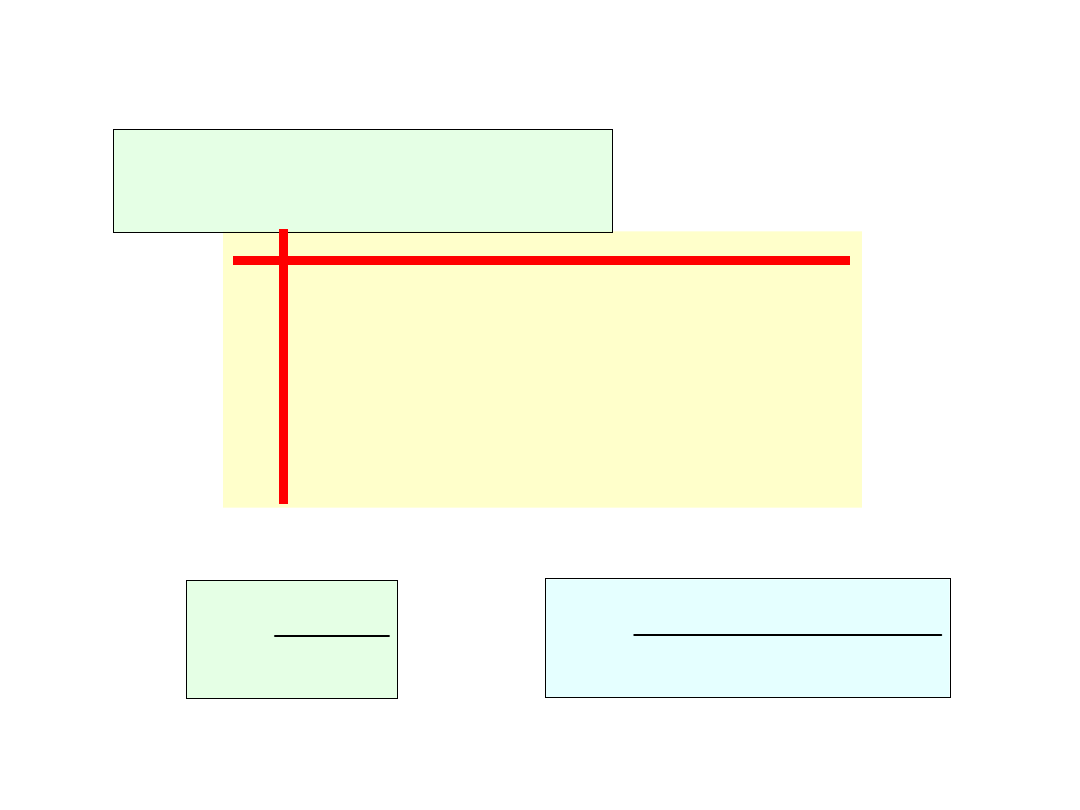
PRZYKŁAD I – rozwiązanie

układu



























































































3

2

1

3

2

2

2

2

2

1

1

1

1

F

F

F

u

u

0

k

k

-

0

k

-

k

k

k

-

0

k

-

k

Z warunków zadania : u

1

= 0

1

3

2

2

k

F

F

u









2

1

3

2

2

3

1

3

k

k

F

F

k

F

k

u











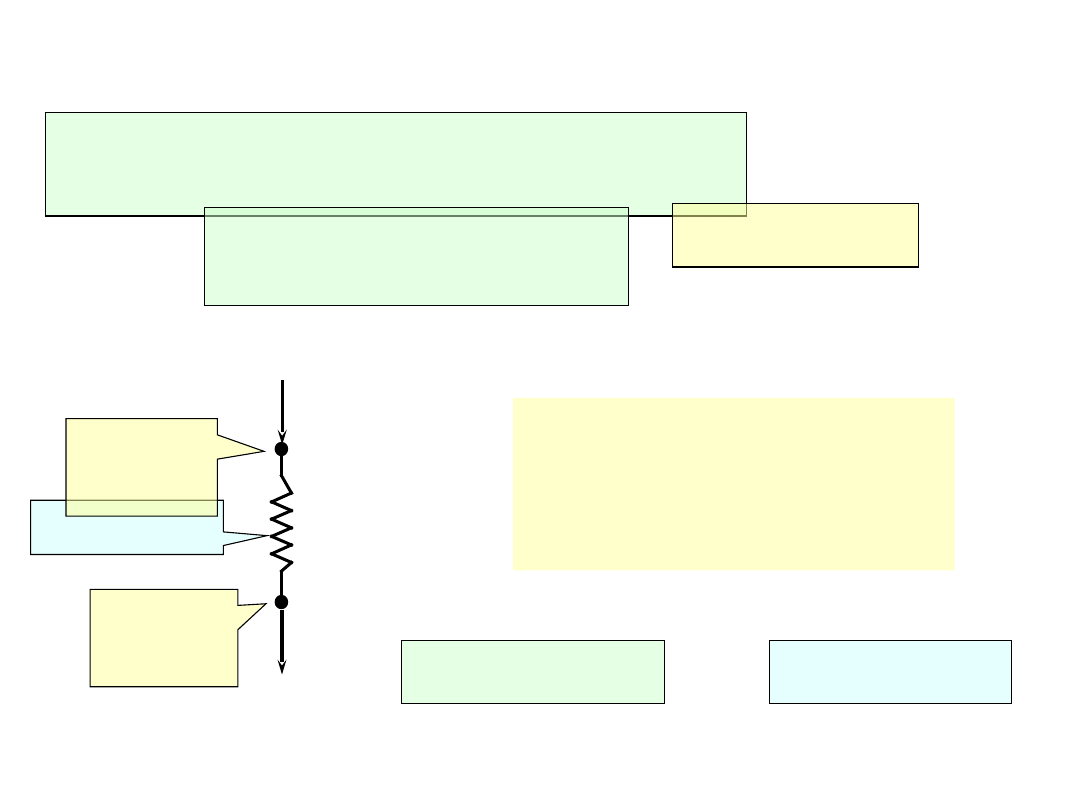
PRZYKŁAD I – obliczenie reakcji

Z warunków zadania siła F

1

jest

reakcją





3

2

1

F

F

F







obliczenie sił w węzłach elementów





3

2

1

-

I

F

F

P











3

2

2

-

I

F

F

P























































2

-

I

1

-

I

2

1

1

1

1

1

P

P

u

u

k

k

k

k

element I

węzeł

1

węzeł

2

P

I-1

P

I-2

k

1

Z pierwszego

równania:

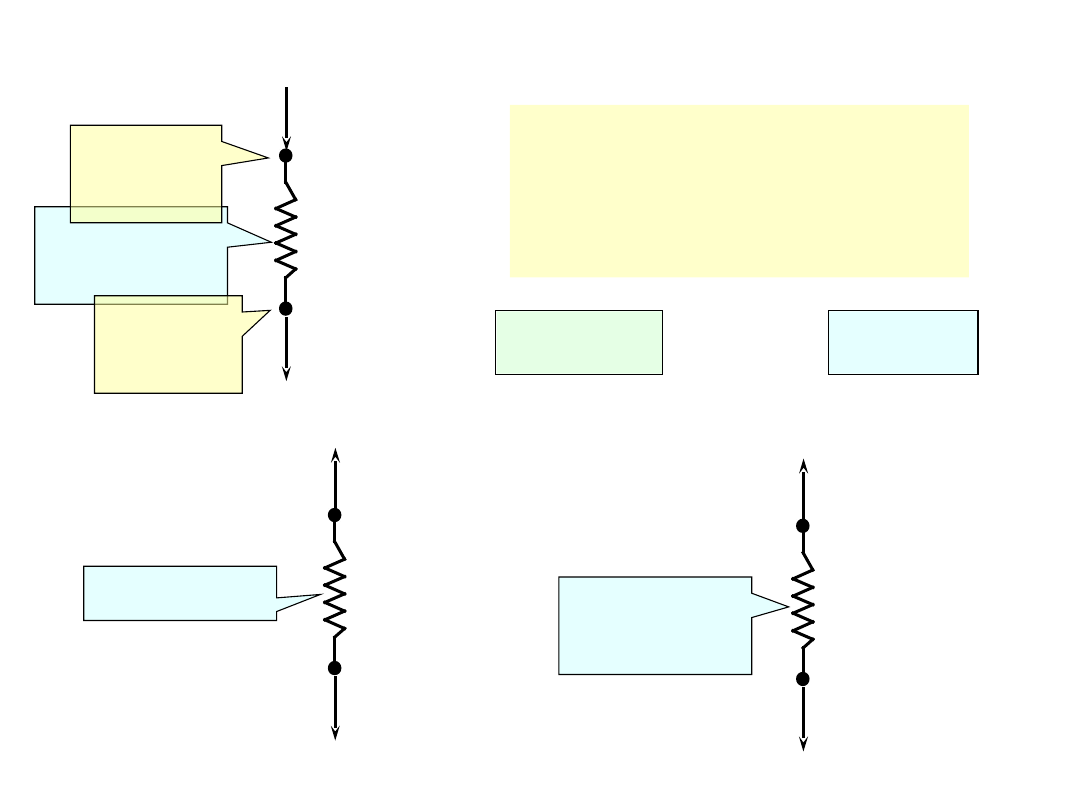
PRZYKŁAD I – obliczenie sił



















































2

-

II

1

-

II

3

2

2

2

2

2

P

P

u

u

k

k

k

k

element

II

węzeł

2

węzeł

3

3

1

-

II

F

P





3

2

-

II

F

P 

P

II-1

P

II-2

k

2

F

2

+F

3

element I

F

2

+F

3

k

1

element

II

F

3

k

2

F

3

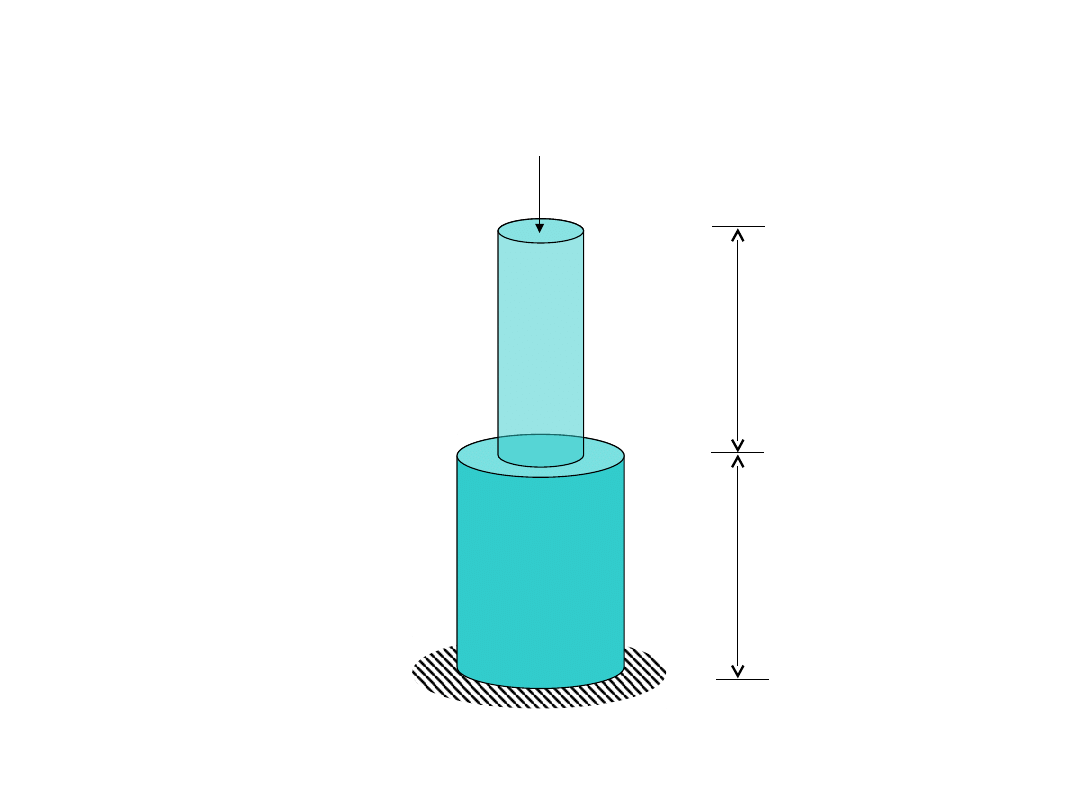
PRZYKŁAD II – słup

L = 50 mm

L = 50 mm

A = 20 mm

2

E = 210000 N/mm

2

A = 50 mm

2

E = 210000 N/mm

2

F = 1000 N

Model ciągły

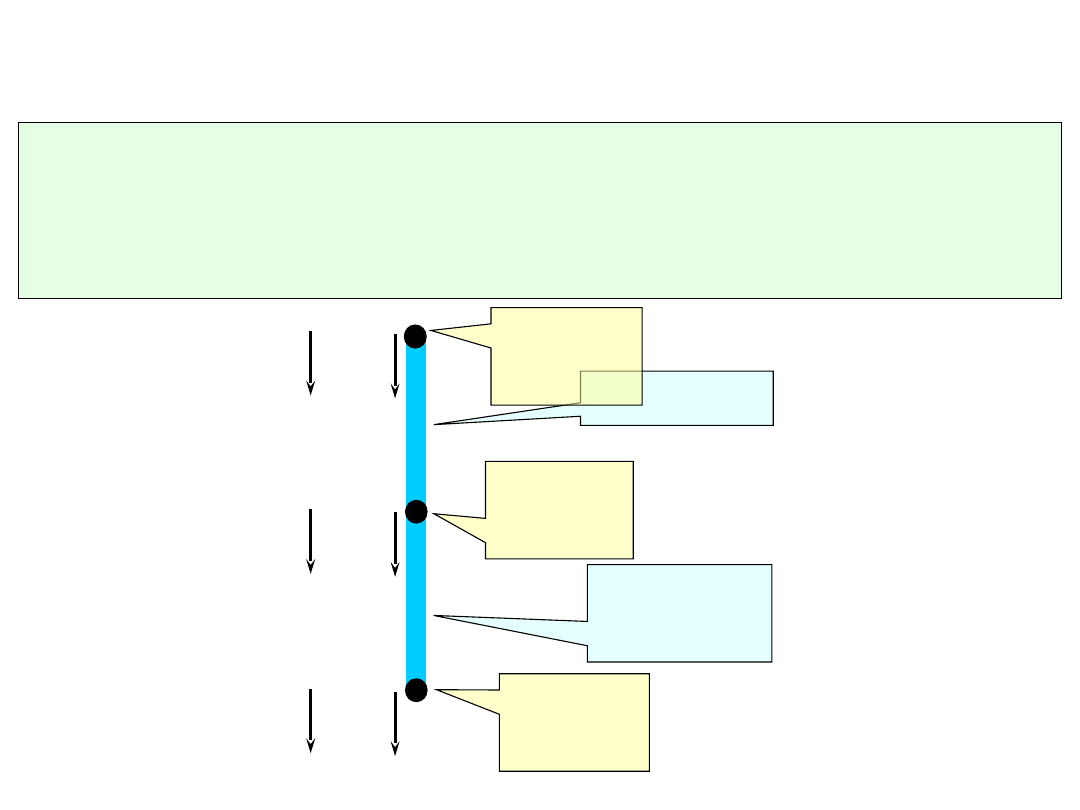
PRZYKŁAD II – słup model

dyskretny

element I

węzeł

1

węzeł

2

węzeł

3

element

II

u

2

u

1

u

3

Wybór elementu:

jednowymiarowy element prętowy z dwoma stopniami

swobody,

po jednym stopniu swobody w każdym węźle

F

2

F

1

F

3

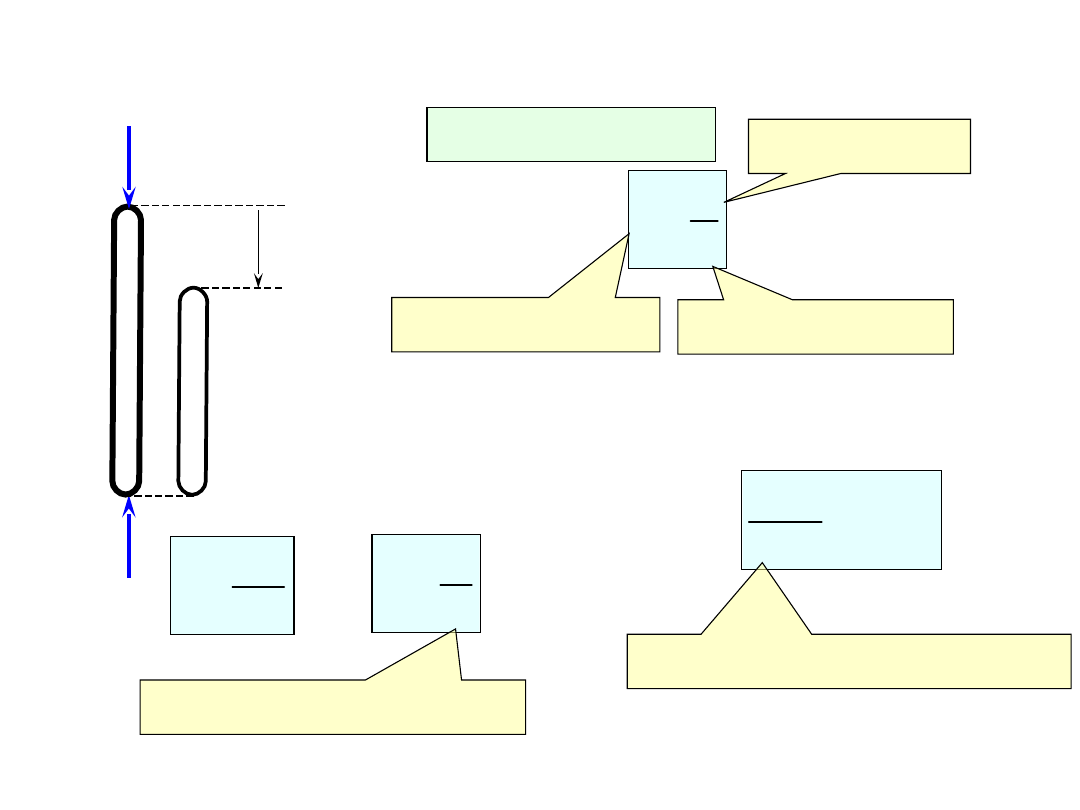
PRZYKŁAD II – sztywność na

ściskanie

F

F

L

L

Prawo Hooke’a

E

σ

ε 

odkształcenie

naprężenia

moduł Younga

L

ΔL

ε 

A

F

σ 

pole przekroju pręta

F

ΔL

L

A

E





Sztywność na ściskanie

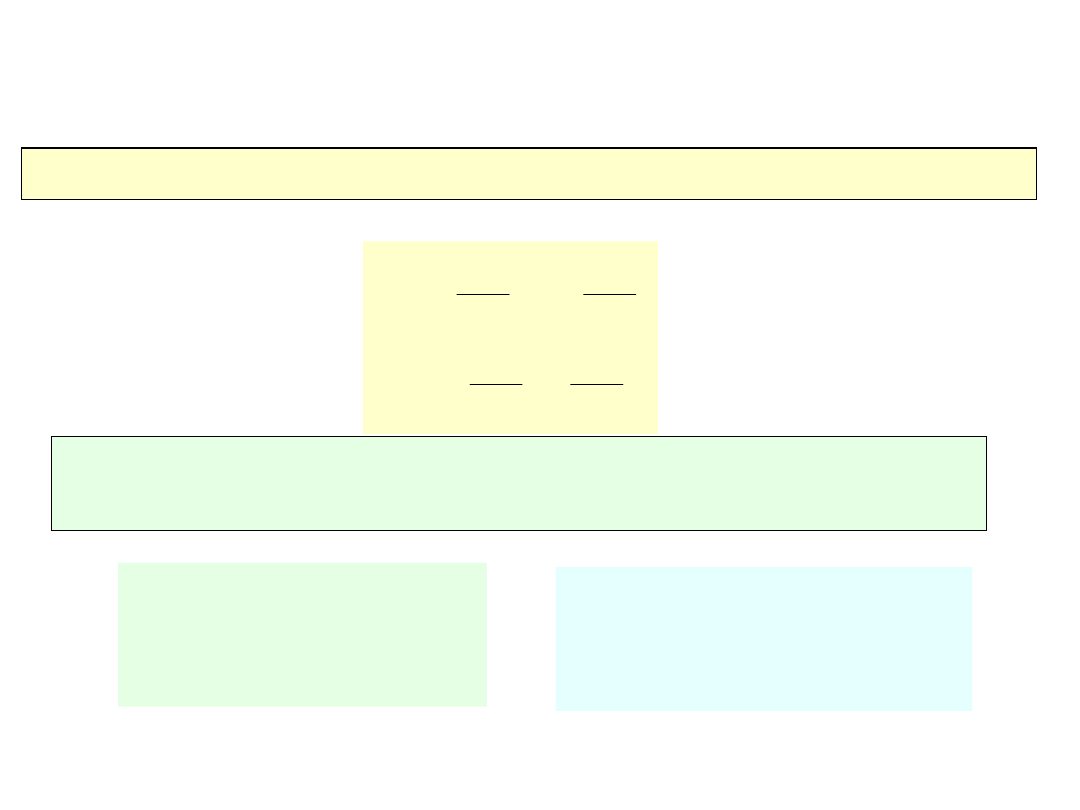
PRZYKŁAD II – macierz sztywności

elementu































L

EA

L

EA

L

EA

L

EA

K

1000

84

84

84

84

K

I























1000

210

210

210

210

K

II























Ogólna postać macierzy sztywności elementu ściskanego

Wartości liczbowe macierzy sztywności obydwu

elementów

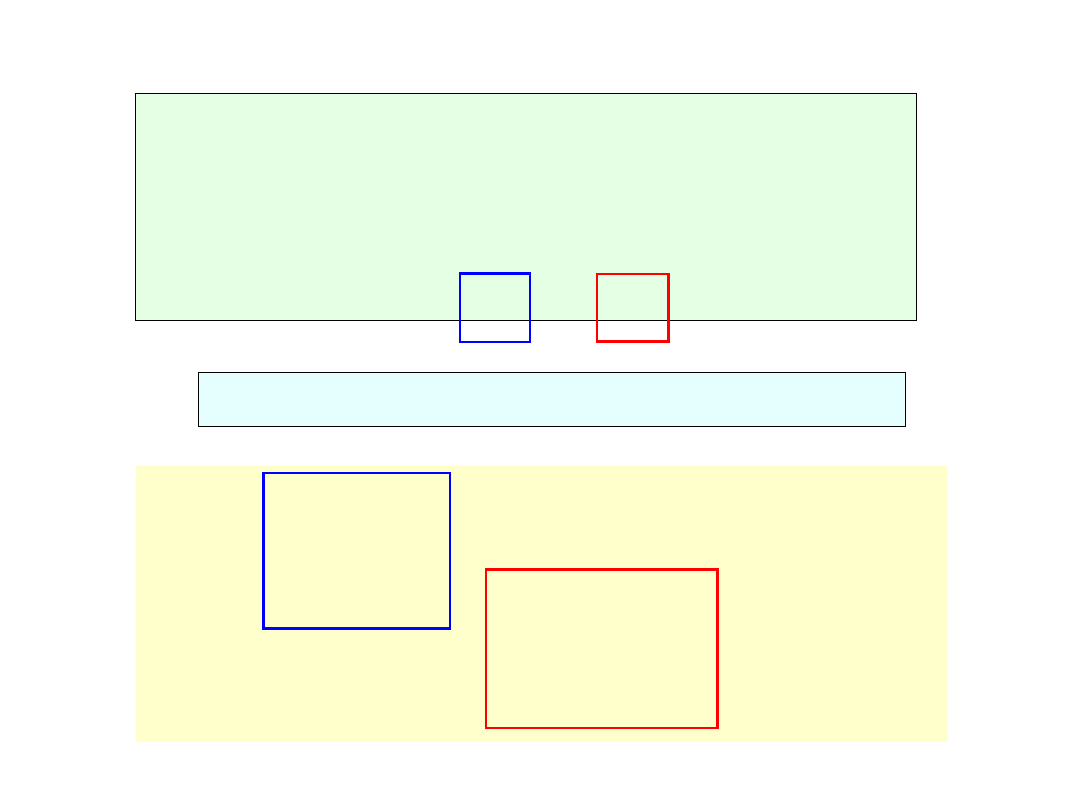
PRZYKŁAD II – macierz sztywności

układu

Globalna macierz sztywności

jest sumą macierzy sztywności

elementów

z uwzględnieniem numeracji stopni

swobody





























































































3

2

1

3

2

1

F

F

F

u

u

u

210

210

-

0

210

-

210

84

84

-

0

84

-

84

1000

II

I

K

K

K





Wymiar macierzy układu równy jest 3

PRZYKŁAD II – rozwiązanie układu

równań

Z warunków

zadania :

u

3

=

0 siła F

3

jest

reakcją

F

1

=

1000
F

2

= 0





























































































3

2

1

F

0

1000

0

u

u

210

210

-

0

210

-

210

84

84

-

0

84

-

84

1000

[mm]

0.0167

u

1



[mm]

0.0047

u

2



PRZYKŁAD II – obliczenie reakcji

Z trzeciego równania

układu :

F

3

=

-1000*210*u

2

F

3

= -1000

[N]

obliczenie sił w węzłach elementów





















































2

-

I

1

-

I

2

1

P

P

u

u

84

84

84

84

1000

element I

węzeł

1

węzeł

2

[N]

1000

P

1

-

I



[N]

1000

P

2

-

I





P

I-1

P

I-2

PRZYKŁAD II – obliczenie sił





















































2

-

II

1

-

II

2

P

P

0

u

210

210

210

210

1000

element

II

węzeł

2

węzeł

3

[N]

1000

P

1

-

II



[N]

1000

P

2

-

II





P

II-1

P

II-2

element I

1000

1000

element

II

1000

1000

PRZYKŁAD II – obliczenie

naprężeń

L

)

u

(u

L

ΔL

ε

1

2

I

I

I







0.00024

ε

I





L

)

u

(u

L

ΔL

ε

2

3

II

II

II







0.000095

ε

II





I

I

ε

E

σ





]

2

I

[N/mm

-50

σ 

II

II

ε

E

σ





]

2

II

[N/mm

-20

σ 

I

2

I

I

A

P

σ





II

2

II

II

A

P

σ





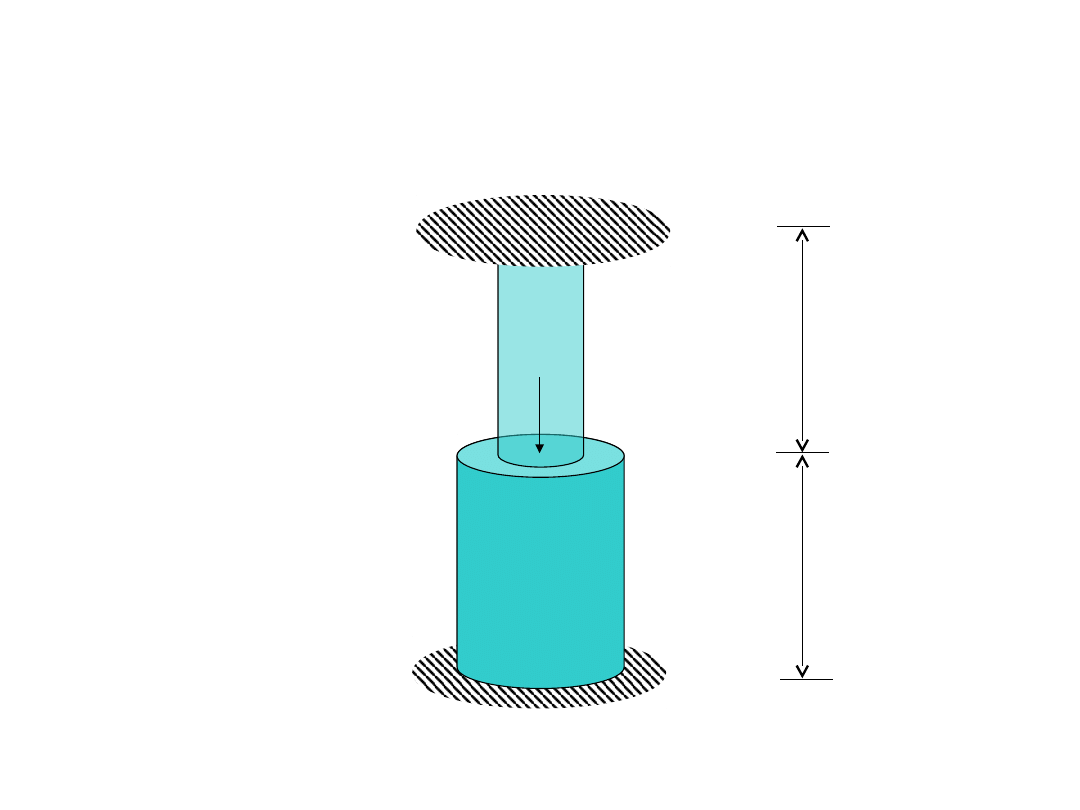
PRZYKŁAD III – słup

L = 50 mm

L = 50 mm

A = 20 mm

2

E = 210000 N/mm

2

A = 50 mm

2

E = 210000 N/mm

2

F = 1000 N

Model ciągły

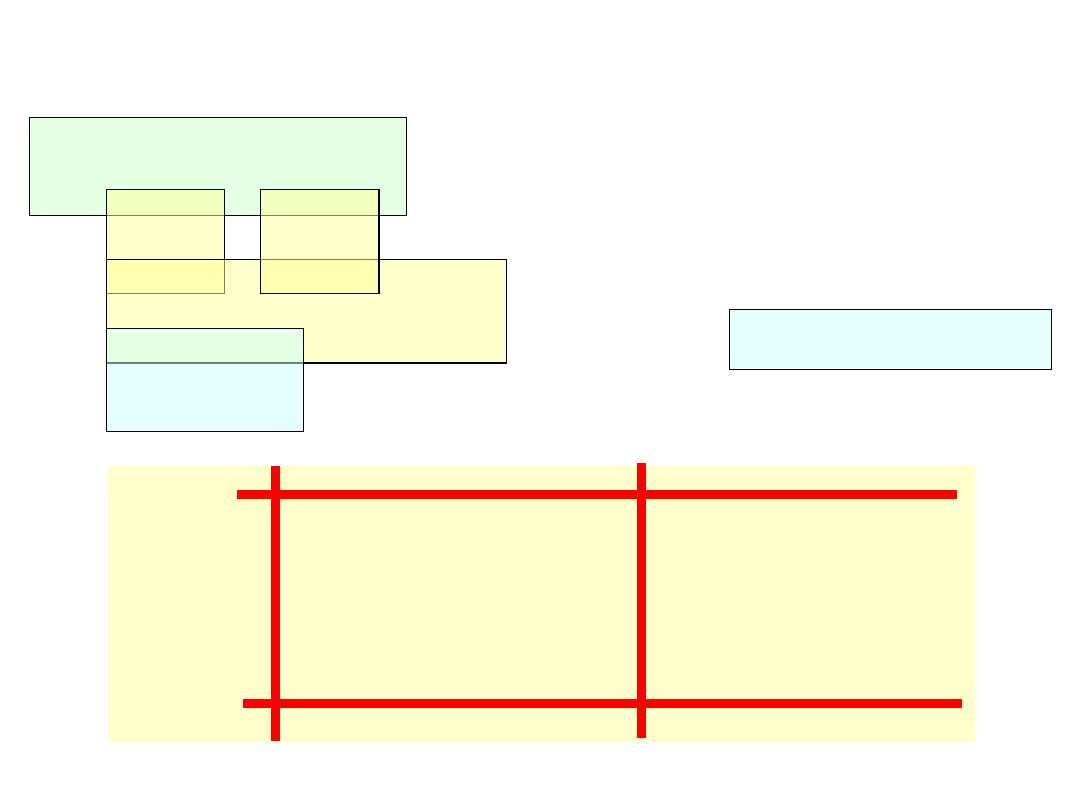
PRZYKŁAD III – rozwiązanie układu

równań

Z warunków

zadania :

u

1

=

0 siły F

1

i F

3

są

reakcjami

F

2

=

1000





























































































3

1

2

F

1000

F

0

u

0

210

210

-

0

210

-

210

84

84

-

0

84

-

84

1000

[mm]

0.0034

u

2



u

3

=

0

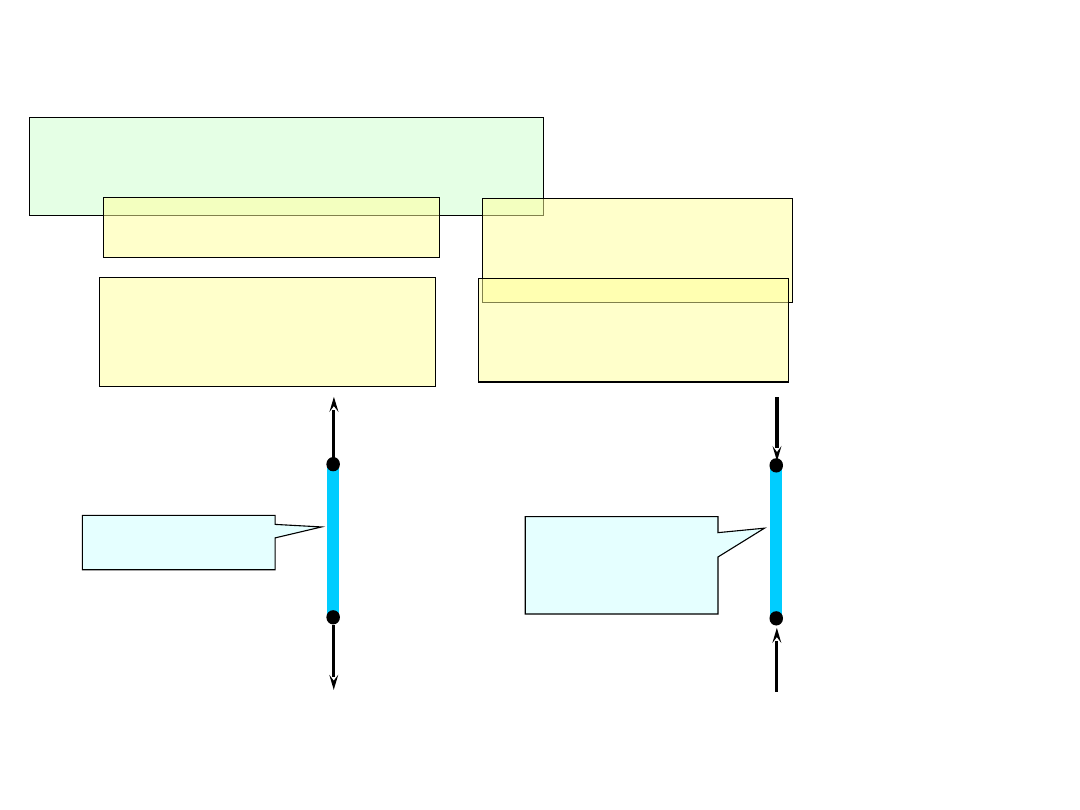
PRZYKŁAD III – obliczenie reakcji

Z trzeciego równania

układu :

F

1

= -1000*84*u

2

F

1

= -285.715

[N]

F

3

=

-1000*210*u

2

F

3

= -714.285

[N]

element I

285

285

element

II

715

715