Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
1/4
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
22:
Z
HODNÉ A
PODOBNÉ ZOBRAZENIA
1. príklad (236/Pr. 1)
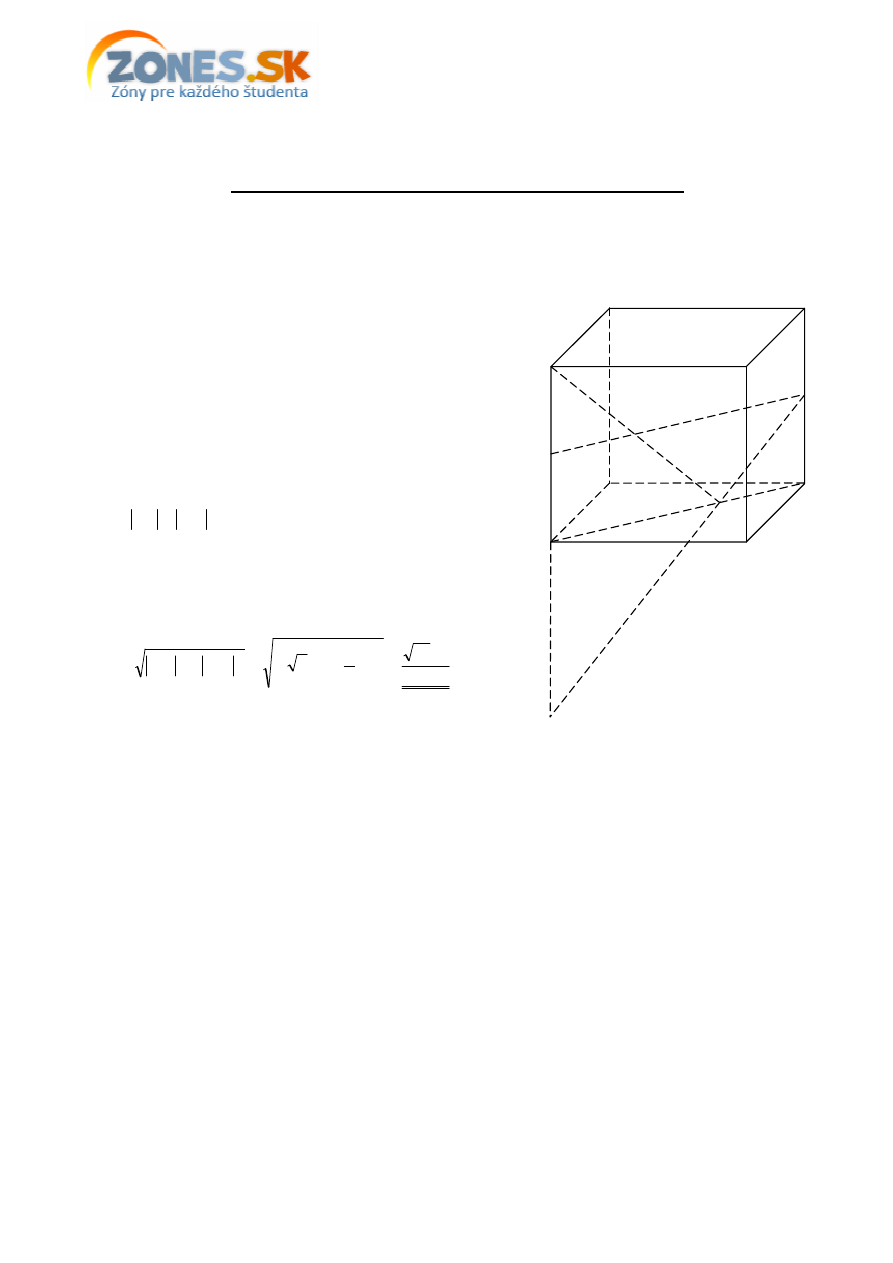
Zadanie: Bod
L
je stredom hrany
CG
kocky
ABCDEFGH
s d
ĺ
žkou hrany
a
. Ur
č
te d
ĺ
žku
x
najkratšej lomenej
č
iary
EXL
, ak bod
X
patrí rovine
ABC
. (Máme ur
č
i
ť
d
ĺ
žku
svetelného lú
č
a, ktorý vychádza z bodu
E
a po odraze
od zrkadla
ABC
dopadá do bodu
L
.)
Riešenie:
Zostrojíme bod
E
′
súmerne združený s bodom
E
pod
ľ
a
roviny
ABC
. Priamka
L
E
′
pretne rovinu
ABC
v bode
X
, pre ktorý platí, že d
ĺ
žka lomenej
č
iary
EXL
je
najmenšia. (Zo súmernosti pod
ľ
a roviny
ABC
vyplýva,
že
X
E
EX
′
=
, teda d
ĺ
žka lomenej
č
iary
EXL
je rovnaká
ako d
ĺ
žka
č
iary
XL
E
′
a tá je najkratšia, ke
ď
ležia body
L
X
E
,
,
′
na priamke.) Treba ešte ur
č
i
ť
d
ĺ
žku
x
č
iary
EXL
. Tá sa rovná d
ĺ
žke úse
č
ky
L
E
′
, ktorú vypo
č
ítame
z pravouhlého trojuholníka
ML
E
′
, kde
M
je stred hrany
EA
.
Teda
( )
2
17
2
3
2
2
2
2
2
a
a
a
E
M
LM
x
⋅
=
+
=
′
+
=
.
2. príklad (240/4)
Zadanie: Zostrojte pä
ť
uholník
ABCDE
, ak sú dané stredy všetkých jeho strán:
5
4
3
2
1
,
,
,
,
S
S
S
S
S
.
Riešenie:
Zo zadania môžeme zapísa
ť
nieko
ľ
ko stredových súmerností:
A
A
S
A
E
S
E
D
S
D
C
S
C
B
S
B
A
S
S
S
S
S
S
S
S
S
S
S
→
⇒
→
→
→
→
→
:
:
:
:
:
:
5
4
3
2
1
5
4
3
2
1
o
o
o
o
Vieme, že zložením párneho po
č
tu stredových súmerností vzniká identita alebo posunutie
a združovaním nepárneho po
č
tu stredových súmerností vzniká stredová súmernos
ť
. V našom
prípade sme zložili nepárny po
č
et stredových súmerností a vznikla nám teda stredová súmernos
ť
so stredom v bode
A
(pretože je samodružný). Pä
ť
uholník sa teraz dá zostroji
ť
nasledujúcim
postupom:
1. Zvolíme
si
ľ
ubovo
ľ
ný
bod
L
a zobrazíme
ho
v zloženej
stredovej
súmernosti
L
L
S
S
S
S
S
S
′
→
:
5
4
3
2
1
o
o
o
o
.
2. Zostrojíme stred úse
č
ky
L
L
′
a dostaneme tak bod
A
.
3. Zostrojíme ostatné body pä
ť
uholníka cez ostatné stredové súmernosti.
A
H
G
F
E
D
C
B
E’
L
X
M
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
2/4
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
22:
Z
HODNÉ A
PODOBNÉ ZOBRAZENIA
3. príklad (241/5)
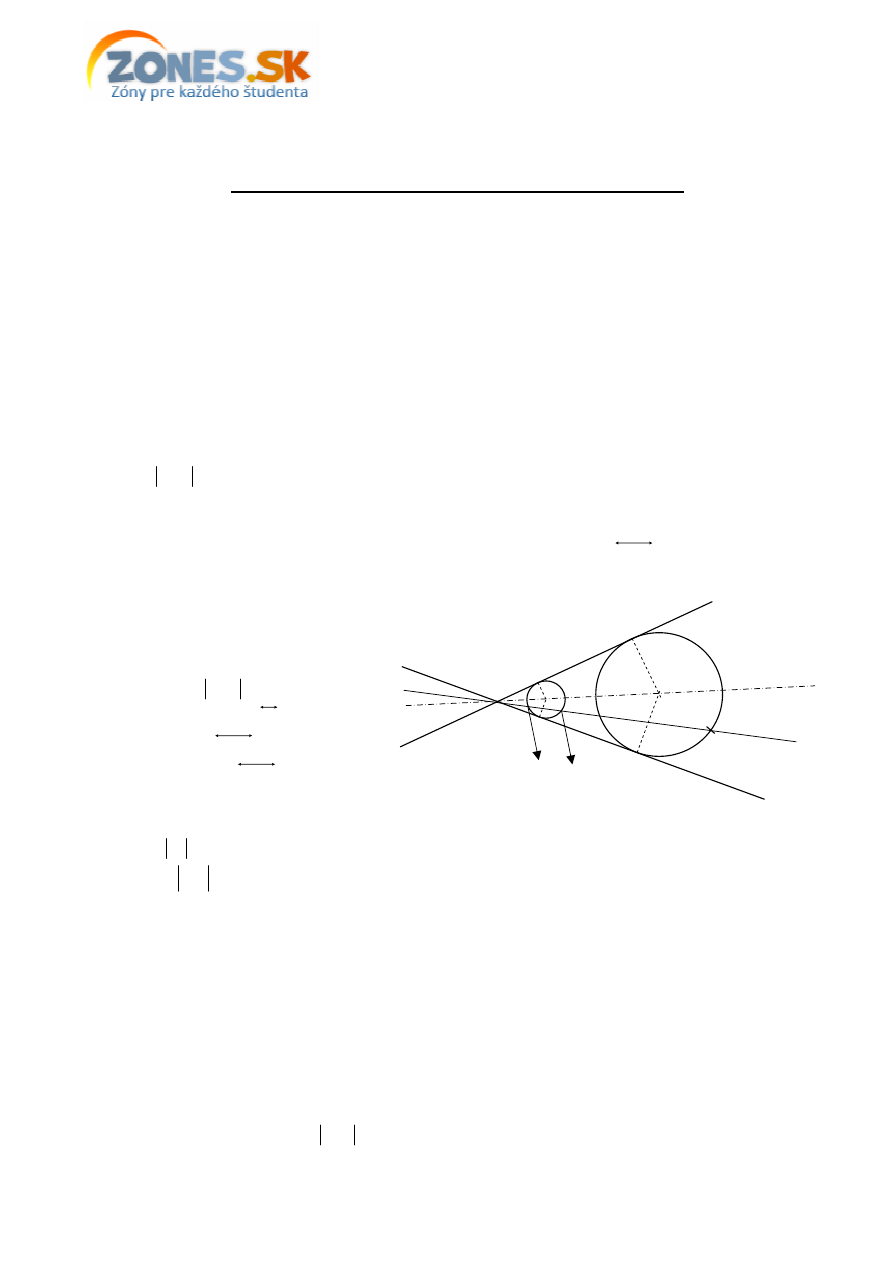
Zadanie: Dané sú dve rôznobežky
q
p,
a mimo nich bod
A
. Zostrojte všetky kružnice, ktoré
prechádzajú bodom
A
a dotýkajú sa
p
aj
q
.
Riešenie:
Aby sme zostrojili kružnice požadovaných vlastností, sta
č
í nám zostroji
ť
ich stredy, ich polomer už
potom
ľ
ahko zistíme ako vzdialenos
ť
nájdených stredov od bodu
A
(alebo od jednej z priamok).
Vieme, že spomínané stredy ležia na osi uhla priamok
q
p,
(resp. na osi susedného uhla k uhlu
priamok
q
p,
, pod
ľ
a toho, kde sa nachádza bod
A
). Vieme teda zostroji
ť
takú pomocnú kružnicu
P
k
, ktorá síce nebude prechádza
ť
bodom
A
, ale bude sa dotýka
ť
oboch priamok, teda
(
)
q
S
S
k
P
P
P
,
,
. Potom vieme, že v rovno
ľ
ahlosti so stredom v bode
q
p
V
∩
∈
sa zobrazí kružnica
P
k
do kružnice
k
(
)
k
k
H
P
V
→
:
. V opa
č
nej rovno
ľ
ahlosti sa zase zobrazí kružnica
k
do kružnice
P
k
,
a teda aj bod
A
do bodu
P
A
. Teda body
P
A
A
V
,
,
ležia na jednej priamke. Ke
ď
že vieme zostroji
ť
kružnicu
P
k
, vieme zostroji
ť
aj bod
P
A
a pomocou rovnobežky s
P
P
A
S
cez bod
A
aj stred
S
kružnice
k
.
Postup:
1.
A
q
p
,
,
2. os uhla priamok
q
p
,
3.
∈
P
P
S
S
;
osi
4.
(
)
q
S
S
k
k
P
P
P
P
,
,
;
5.
{
}
P
P
P
P
P
k
VA
A
A
A
A
∩
=
*
*
,
;
,
6.
P
P
A
S
l
l
A
l
||
;
∧
∈
7.
P
P
A
S
l
l
A
l
||
;
*
*
*
∧
∈
8.
∩
∈
l
S
S;
os
9.
∩
∈
*
*
*
;
l
S
S
os
10.
(
)
SA
S
k
,
11.
(
)
A
S
S
k
*
*
*
,
4. príklad (241/11)
Zadanie: Dokážte, že
ť
ažnice trojuholníka sa pretínajú v jednom bode.
Dôkaz (priamy, cez rovno
ľ
ahlos
ť
):
Nech
ABC
∆
je
ľ
ubovo
ľ
ný a
1
1
1
,
,
C
B
A
nech sú postupne stredy strán
AB
AC
BC
,
,
.
2
C
nech je stred
1
1
B
A
. Ozna
č
me
1
1
BB
AA
T
∩
∈
. Dôkaz prevedieme v štyroch krokoch:
(
)
(
)
2
1
1
2
1
1
,
,
:
2
:
2
:
C
C
C
C
C
H
k
B
A
H
k
A
B
H
C
C
C
⇒
→
⇒
=
→
=
→
ležia na jednej priamke
(
)
(
)
( )
uu
ABT
T
B
A
AB
B
A
AB
B
A
k
B
A
H
k
A
B
H
C
C
∆
≈
∆
⇒
=
⇒
=
→
=
→
1
1
1
1
1
1
1
1
2
||
2
:
2
:
A
S
S
P
k
P
k
V
p
q
A
P
*
P
A
1.
2.
3.
pozn.: kvôli preh
ľ
adnosti chýba v obrázku
druhé riešenie a tiež niektoré
č
asti postupu
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
3/4
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
22:
Z
HODNÉ A
PODOBNÉ ZOBRAZENIA
(
)
(
)
2
1
1
2
1
1
,
,
:
2
:
2
:
C
C
T
C
C
H
k
B
B
H
k
A
A
H
T
T
T
⇒
→
⇒
=
→
=
→
ležia na jednej priamke
4.
(
)
T
C
C
C
,
,
,
.
3
.
1
2
1
⇒
∧
ležia na jednej priamke
1
CC
T
∈
⇒
Bod
T
teda leží na všetkých troch
ť
ažniciach,
Č
BTD.
A
B
C
A
1
B
1
C
1
T
C
2
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
4/4
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
22:
Z
HODNÉ A
PODOBNÉ ZOBRAZENIA
5. príklad (241/14)
Zadanie: Je daný lichobežník
ABCD
, ktorého základne sú
AB
a
CD
, pri
č
om
CD
AB
>
. Vnútri úse
č
ky
AD
zostrojte bod
P
a vnútri úse
č
ky
BC
bod
Q
tak, aby platili zárove
ň
vz
ť
ahy
AB
PQ
||
a
AQ
PC
||
.
Riešenie:
Zostrojíme bod
BC
AD
V
∩
∈
.
( )
( )
VB
VC
VQ
VB
VQ
VQ
VC
VB
VQ
VA
VP
uu
ABV
PQV
VQ
VC
VA
VP
uu
AQV
PCV
⋅
=
⇒
=
⇒
=
⇒
∆
≈
∆
=
⇒
∆
≈
∆
Pomocou odvodeného vz
ť
ahu zostrojíme bod
Q
a bod
P
zostrojíme pomocou zadaného poznatku
AV
P
AB
PQ
∈
∧
||
.
pozn.: Pri zostrojení
VQ
využijeme Euklidovu vetu o odvesne. Euklidove vety vyzerajú takto:
1. o výške:
(
)
b
a
b
a
c
c
v
v
c
c
⋅
=
⇒
=
⋅
2
2. o odvesne:
c
c
a
a
⋅
=
2
a
c
c
b
b
⋅
=
2
A
B
C
D
P
Q
V
v
c
a
c
b
a
b
c